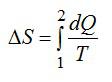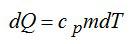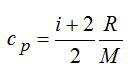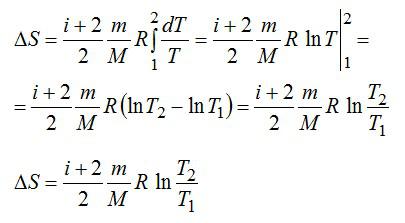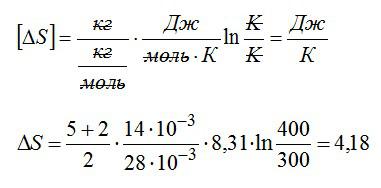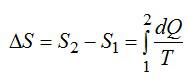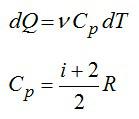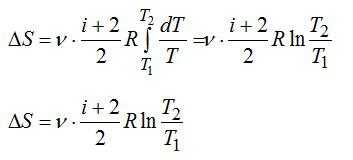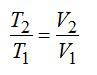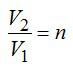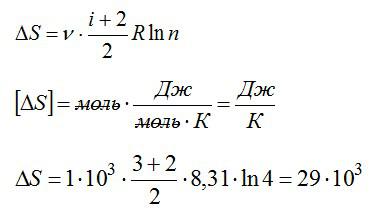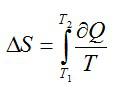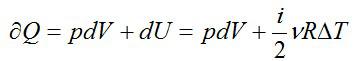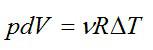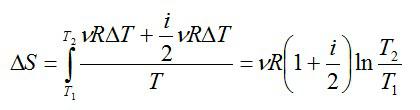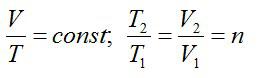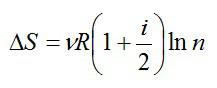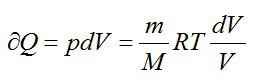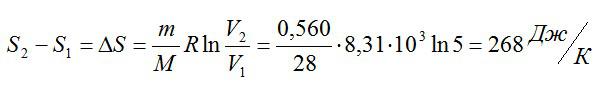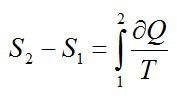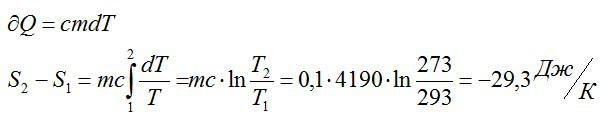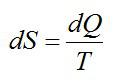Как найти изменение энтропии при нагревании газа

Расчет
изменения энтропии в процессах идеального
газа производится по формуле

dS
= d
(
C_V
ln T
+ R
ln V).
(70)

Изотермический
процесс.
Так как T
= const,
то в формуле (70) первое слагаемое при
дифференцировании обратится в нуль: dS
= R
d
(ln
V).
Интегрируя, получаем:

^.
(71)

Из
формулы (71) видно, что энтропия возрастает
при увеличении объёма газа. Из закона
Бойля-Мариотта p₁V₁
= p₂V₂
можно произвести замену V₂/V₁
= p₁/p₂.
Таким образом, получаются формулы

<sup>.

(72)</sup>

Изохорный
процесс.
Так как V
= const,
то в формуле (70) второе слагаемое при
дифференцировании обратится в нуль:
dS =  C_V
d
(ln
T).
Интегрируя, получаем: S
= 
C_V
ln
(T₂/T₁),
т.е. энтропия возрастает при увеличении
температуры. Отношение T₂/T₁
можно заменить отношением p₂/p₁.

Изменение
энтропии можно найти и другим способом,
используя молярную теплоёмкость:

^{ Q
= 
C}_V
^dT;

^.
(73)

Изобарный
процесс
(p
= const).
Для вычисления S
по формуле (70) необходимо выразить
температуру Т
или объём V
из уравнения Менделеева-Клапейрона,
например, подставим объём V = RT/p
в формулу (70):

,

Постоянные
величины при дифференцировании обратятся
в нуль.

,

.

Вычислить
S
можно, используя молярную теплоёмкость
(кроме того, при р
= const
возможна замена T₂/T₁
= V₂/V₁):

^{ Q
= 
C}_P
^dT;

^.
(74)

^{Адиабатический
процесс.
,
так как Q = 0}
(энтропия
не изменяется). При адиабатном расширении
газа энтропия возрастает за счет
увеличения объёма, но уменьшается за
счет понижения температуры, и эти два
процесса полностью компенсируют друг
друга.

Энтропия
обладаетаддитивностью:
энтропия системы равна сумме энтропий
тел, входящих в систему. Для нахождения
S
в газовых процессах выбираются любые
удобные для расчетов процессы.

Изменение
энтропии при нагревании тел:
Q
= cm
(t₂
– t₁),

^{Q
= cm
dT;}

^;

^,
(75)

где
с
– удельная теплоёмкость.

Изменение
энтропии при плавлении.

^{Q
= m,
Q
= 
dm,}

^{. (76)}

Интегрирование
ведется от 0 до m,
так как идет процесс появления новой
фазы вещества. Температура плавления
Т_ПЛ
и удельная теплота плавления 
– величины постоянные.

Аналогичной
формулой выражается изменение
энтропии при парообразовании.
Только в формулу (76) подставляются
температура кипения Т_ПАР
и удельная теплота парообразования r.

Если
вещество нагревалось, плавилось,
нагревалось, испарялось и т.д., то общее
изменение энтропии будет равно сумме
^{изменений
энтропии в отдельных процессах:}
.

14. Цикл Карно

Теплота
и работа
как две формы передачи энергии
неравноценны.
Если механическая работа всегда может
самопроизвольно перейти в тепловую
энергию, то обратный процесс возможен
лишь в тепловых машинах (двигателях).

Круговым
процессом,
или циклом,
называется такая совокупность
термодинамических процессов, в результате
которых система возвращается в исходное
состояние. Все преобразователи энергии
(двигатели) работают циклически, т.е.
процессы преобразования тепла в работу
периодически повторяются.

Тепловой
машиной
называется периодически действующее
устройство, совершающее работу за счет
получаемого извне количества теплоты.
Тепловая машина состоит из нагревателя,
рабочего тела (газ) и холодильника (рис.
30).

Пусть
рабочее тело (газ), получив от нагревателя
количество теплоты Q₁,
расширяясь от V₁
до V₂,
совершает работу (поднимает поршень).
Для того чтобы вернуться в начальное
состояние, надо газ сжать. Чтобы работа
за цикл была больше нуля, необходимо
сжатие осуществлять при более низком
давлении и температуре, т.е. передать
часть тепла Q₂
холодильнику. Обычно холодильником
служит атмосфера.

Поскольку
за цикл изменение внутренней энергии
равно нулю, то из первого начала
термодинамики следует, что работа равна
A
= Q₁
– Q₂.

Для
характеристики эффективности тепловой
машины вводят коэффициент
полезного действия (КПД)
как отношение совершенной за цикл работы
к полученному количеству теплоты:

^.
(77)

Циклом
с максимальным КПД,
в котором отсутствуют бесполезные
потери тепла, является
цикл
Карно,
состоящий из двух изотерм и двух адиабат.
Рассмотрим цикл Карно на диаграмме
(p, V),
изображенной на рис. 31. Для простоты
расчётов возьмём 1 моль газа (из
дальнейших расчетов будет видно, что
при произвольном числе молей величина

сокращается).

Процесс
1–2.
Газ получает от нагревателя (с температурой
Т₁)
количество теплоты Q₁
и расширяется. Наилучшим процессом
является изотермическое расширение,
так как U
= 0 и всё коли- ^{чество
теплоты идет на совершение работы:}

.

Процесс
2–3.
В точке 2 рабочее тело отключают от
нагревателя и заключают в адиабатическую
оболочку. Дальнейшее расширение идет
в адиабатическом режиме:

Q
= 0, A₂
= U
= C_V
(T₁

T₂).

Невыгодно
просто охладить газ (при постоянном
объёме). Газ, адиабатически расширяясь,
продолжает совершать работу.

Процесс
3–4.
Газ, соединив с холодильником, сжимают
изотермически, чтобы не повышать его
внутреннюю энергию:

^Т₂
^{= const,
U
= 0,}

^.

Процесс
4–1.
Газ сжимают адиабатно, чтобы он нагрелся
до температуры нагревателя: Q
= 0, A₄
= – U
= C_V
(T₂
– T₁).

^{КПД
равен}

^.

Можно
показать, что V₂/V₁
= V₃/V₄.
Для этого запишем уравнения адиабаты
для процессов 2–3 и 1–4 и поделим одно
уравнение на другое:

^{Следовательно,}

<sup>.

(78)</sup>

При
выводе формулы КПД не пришлось делать
никаких предположений о свойствах
рабочего тела и устройстве тепловой
машины. Следовательно, мы пришли к
теоремам
Карно:

1.
КПД цикла Карно не зависит от рода
рабочего тела и определяется только
температурами нагревателя и холодильника.

2.
КПД любой необратимой машины (реальной)
всегда меньше, чем КПД обратимой машины
(Карно), работающей в тех же условиях
(Т₁,
Т₂).

Существуют
различные формулировки
второго
начала термодинамики.

Формулировка
Кельвина:
невозможен вечный двигатель второго
рода, т.е. такой периодически действующий
двигатель, который бы полностью превращал
в работу количество теплоты, взятое от
теплового резервуара (т.е. работал бы
только за счет охлаждения одного
источника теплоты Q₁
= A).

Формулировка
Клаузиуса:
невозможен циклический процесс,
единственным результатом которого была
бы передача теплоты от менее нагретого
тела к более нагретому (т.е. теплота не
может самопроизвольно переходить от
тела, менее нагретого, к более нагретому).

Если
провести цикл, изображенный на рис. 31,
в обратном направлении, то получится
циклхолодильной
машины.
На приведение машины в действие
затрачивается работа А
(рис. 32). При этом машина отбирает за
цикл от тела с температурой Т₂
количество теплоты Q₂
и отдает телу с более высокой температурой
Т₁
количество теплоты Q₁
= Q₂
+ A.
Эффективность холодильной машины
характеризуется её холодильным
коэффициентом,
который определяется как отношение
отнятой от охлаждаемого тела теплоты
Q₂
к работе А,
которая затрачивается на приведение
машины в действие:

Холодильный

коэффициент

^.
(79)

Следовательно,
без совершения работы нельзя отбирать
теп­лоту от менее нагретого тела и
отдавать её более нагретому (см.
формулировку Клаузиуса).

Подсчитаем
КПД цикла Карно дляТ₁
= 100 С
и Т₂
= 0 С,
получим около 27%. Для увеличения КПД
обычно увеличивают температуру
нагревателя. Примеры КПД: паровоз – 9%,
карбюраторный двигатель – 25–30%, дизель
– 30–40%, паровая турбина (с температурой
пара 500 С)
– 30–40%.

Предельно
просто выглядит цикл Карно на диаграмме
(T, S).
Количества теплоты Q₁
и Q₂
на рис. 33 – это площади двух прямоугольников
(рис. 29):

^.

ТРИЗ-задание
22. Молекулярный
двигатель

Что
такое «молекулярный
двигатель»?
Существует ли он? Если существует, то
где применяется?

ТРИЗ-задание
23. Эволюция
топлива

Из
истории известно, что вначале в двигателях
использовалось твёрдое топливо (дрова,
уголь), затем – жидкое (бензин), а сегодня
уже используется газ и электричество.
Какой закон развития технических систем
подтверждает эта тенденция?

ТРИЗ-задание
24. Альтернативные
источники энергии

В
настоящее время большое внимание
уделяется экологически чистым
альтернативным источникам энергии
(вместо сжигания нефтепродуктов). Так,
например, для получения электричества
можно использовать энергию морских
волн. В одной из таких конструкций
электрогенератор с воздушной турбиной
закреплён вверху трубы, которая нижним
концом вертикально опущена в море.
Волны, как поршень, перемещают воздух
вверх и вниз по трубе, вращая лопатки
турбины на оси электрогенератора. Если
лопатки турбины имеют обычную конструкцию,
то такая установка имеет недостаток –
низкий КПД, так как ось генератора
вращается с остановками то в одну, то в
другую сторону. Как сделать так, чтобы
ось электрогенератора вращалась только
в одну сторону независимо от направления
движения воздуха в трубе? В ТРИЗ существуют
различные информационные фонды, в
частности, фонд геометрических эффектов.
Разработайте такую геометрическую
форму лопатки турбины, которая бы
обеспечивала вращение ротора турбины
только в одном направлении при изменении
направления «ветра» на противоположное.
Изготовьте макет такой турбины из бумаги
и проверьте своё техническое решение.
(Подсказка – турбина
Уэльса.)

Соседние файлы в папке папа Жужа

• #
• #
• #

Энтропия – это фундаментальная физическая величина. Введение этого понятия завершило этап становления понятийного аппарата термодинамики. Следующим этапом развития этой науки было выяснение физического смысла энтропии.

Установление принципа Больцмана (формулы Больцмана) и таким образом связи между термодинамикой и статистической физикой, позволило энтропии покинуть пределы физики и войти в другие области знаний.

Энтропия – это общезначимое понятие, применяемое во множестве наук, например, в:

• физике;
• химии;
• билогии;
• космологии;
• теории информации.

Введено это понятие было Р. Клаузиусом. Важные работы посвятил энтропии Л. Больцман, М. Планк.

Важно, что выражение (1) определяет не саму энтропию, а ее изменение, или разность энтропий. При помощи данной формулы можно вычислить, каково изменение энтропии, если термодинамическая система переходит из одного состояния в другое, но нельзя понять, какова энтропия каждого из этих состояний.

Напомним формулу Больцмана для энтропии, так как она нам поможет понять физический смысл, процессов, которые происходят с энтропией:

$S=klnW, left( 2 right)$

где ($W$) – термодинамическая вероятность (статистический вес состояния), то есть количество способов, реализации данного состояния термодинамической системы. $W$ ≥1; $k$- постоянная Больцмана.

Изменение энтропии, исходя из статистической формулы Больцмана, найдем как:

$S_{2}-S_{1}=klnfrac{W_{2}}{W_{1}}left( 2.1 right)$).

«Изменение энтропии» 👇

Вычисление изменения энтропии в изотермическом процессе

Вычислим изменение энтропии в одном моле идеального газа при изотермическом процессе ($T=const$). Оттолкнемся от первого начала термодинамики в дифференциальной форме:

$delta Q=dU+pdV, left( 3 right)$,

где $dU$ – изменение внутренней энергии идеального газа; $pdV$=$delta A$ – работа, совершаемая газом.

Найдем отношение всех слагаемых выражения (3) и температуры:

$frac{delta Q}{T}=C_{V}frac{dT}{T}+frac{p}{T}dVleft( 4 right)$.

где $C_V$ – теплоемкость газа при $V=const$.

Для идеального газа справедливо уравнение Менделеева – Клапейрона, учитывая, что у нас 1 моль газа:

$pV=RTto frac{p}{T}=frac{R}{V}left( 5 right)$.

Учтем:

$frac{dT}{T}=dleft( ln T right),, frac{dV}{V}=dleft( ln V right)left( 6 right)$.

в этом случае мы можем записать для уравнения (4):

$frac{delta Q}{T}=dleft( C_{V}lnT+RlnV right)left( 7 right)$.

По определению (1), и принимая во внимание (7), запишем:

$dS=dleft( C_{V}lnT+RlnV right)left( 8 right)$.

Формула (8) показывает нам, что в изотермическом процессе изменяется только второе слагаемое правой части:

• при увеличении объема энтропия увеличивается,
• с уменьшением объема энтропия уменьшается.

Данный результат очевиден, так как если увеличивается объем, то возрастает количество мест, которое смогут занять частицы при неизменяющемся их количестве. Следовательно, растет число разных возможностей расположения на этих местах (увеличивается количество пространственных микросостояний). Увеличение числа микросостояний означает увеличение энтропии (см формулу (2)).

Изменение энтропии в изохорическом процессе

Рассмотрим изохорный процесс в идеальном газе ($V=const$ или $dV=0$). Из формулы (7) для изохорного процесса следует:

$dS=dleft( C_{V}lnT+RlnV right)=d(C_{V}lnT)left( 9 right)$.

После интегрирования (9), получим:

$S_{2}-S_{1}=C_{V}ln left( frac{T_{2}}{T_{1}} right)left( 10 right)$.

Формула (10) показывает, что в изохорическом процессе при увеличении температуры происходит рост энтропии. Данный результат можно пояснить так:

1. при увеличении температуры растет средняя энергия частиц газа;
2. увеличивается количество возможных энергетических состояний.

Изменение энтропии в адиабатном процессе

Адиабатный процесс характеризуется тем, что он происходит без теплообмена (δQ=0). Исследуя адиабатный процесс в идеальном газе, за основу для вычисления энтропии примем выражение (8). Найдем интеграл правой и левой частей этого выражения, получим:

$S_{2}-S_{1}=C_{V}ln left( frac{T_{2}}{T_{1}} right)+Rln {left( frac{V_{2}}{V_{1}} right)left( 11 right).}$

Запишем уравнение адиабатного процесса в параметрах $T,V$:

$T_{1}V_{1}^{gamma -1}=T_{2}V_{2}^{gamma -1}left( 12 right)$.,

где $gamma =frac{C_{p}}{C_{V}}-$ показатель адиабаты. Возьмем натуральные логарифмы от обеих частей выражения (12), имеем:

$ln left( frac{T_{2}}{T_{1}} right)=left( gamma -1 right)ln left( frac{V_{1}}{V_{2}} right)=-left( gamma -1 right)ln left( frac{V_{2}}{V_{1}} right)left( 13 right)$.

Преобразуем выражение (11), приняв во внимание формулу (13):

$S_{2}-S_{1}=C_{V}left[ -left( gamma -1 right)ln left(frac{V_{2}}{V_{1}} right) right]+Rln left( frac{V_{2}}{V_{1}} right)=-C_{V}left( frac{C_{p}}{C_{V}}-1 right)ln left( frac{V_{2}}{V_{1}}right)$
$+Rln {left( frac{V_{2}}{V_{1}} right)=left[ -C_{V}left(frac{C_{p}}{C_{V}}-1 right)+R right]ln {left( frac{V_{2}}{V_{1}}right)=left[ C_{V}-C_{p}+R right]ln left( frac{V_{2}}{V_{1}} right)}}left( 14 right)$.

Вспомним соотношение Майера:

$R=C_{p}-C_{V}left( 15 right)$

и сделаем вывод о том, что изменение энтропии в адиабатном процессе нет:

$S_{2}-S_{1}=0.$

Адиабатный процесс является изоэнтропийным ($S=const$).

При адиабатном расширении газа увеличение энтропии может идти только за счет увеличения объема, но при этом происходит уменьшение температуры, и энтропия уменьшается из-за уменьшения температуры. Данные тенденции взаимно компенсируют друг друга.

Рассмотрим пример. Два сосуда разного объема содержат по $nu$ молей одинакового идеального газа. Температуры газов равны $ T_1$ и $ T_2$. Сосуды соединяют, газы перемешиваются. Система приходит в состояние равновесия. Определим изменение энтропии в этом процессе.

Будем считать, что изобарное расширение каждого из газов до конечного объема является обратимым. В этом процессе температура каждой из газовых компонент изменяется до конечной температуры $frac{T_{1}+T_{2}}{2}$. Найдем изменение энтропии каждого из газов по отдельности:

$Delta S_{1}=intlimits_a^b frac{dT}{T} =nu c_{p}ln left(frac{T_{1}+T_{2}}{2T_{1}} right)left( 16 right)$,

где $a=T_{1};b=frac{T_{1}+T_{2}}{2}$ $c_p$ – молярная теплоемкость газа при постоянном давлении.

Изменение энтропии второго газа запишем аналогично:

$Delta S_{2}=nu c_{p}ln left( frac{T_{1}+T_{2}}{2T_{2}} right)left( 17right)$.

Поскольку энтропия является аддитивной величиной, то полное изменение энтропии найдем как сумму:

$Delta S_{2}=Delta S_{1}+Delta S_{2}=nu c_{p}ln left( frac{T_{1}+T_{2}}{2T_{1}} right)+c_{p}ln left(frac{T_{1}+T_{2}}{2T_{2}} right)=nu c_{p}ln frac{left( T_{1}+T_{2} right)^{2}}{4T_{1}T_{2}}=2nu$ $c_{p}lnleft( frac{T_{1}+T_{2}}{2sqrt {T_{1}T_{2}} } right)$.

Мы уже решали задачи на первый закон термодинамики. Как известно, где первый – там и второй. В сегодняшней статье занимаемся физикой и разбираем примеры задач на второе начало термодинамики.

Хотите ежедневно получать интересную и полезную для студентов рассылку? Присоединяйтесь к нам в телеграме.

Второй закон термодинамики: задачи с решениями

Задача на второй закон термодинамики №1

Условие

Определить изменение энтропии 14 г азота при изобарном нагревании eгo oт 27°C дo 127°C.

Решение

Изменение энтропии вычисляем по формуле:

Для элементарного количества теплоты в изобарном процессе можно записать:

Удельная теплоемкость при постоянном давлении:

Для двухатомного газа число степеней свободы молекулы i=5 (три поступательных и две вращательных).

С учетом сказанного, формулу для энтропии можно переписать так:

Выполним проверку размерности и подставим значения, не забывая переводить Цельсии в Кельвины:

Ответ: 4,18 кДж/К.

Задача на второй закон термодинамики №2

Условие

1 кмоль гелия, изобарически расширяясь, увеличил объем в 4 раза. Найти изменение энтропии при этом расширении.

Решение

Изменение энтропии:

При постоянном давлении (в изобарном процессе) элементарное количество теплоты, полученное газом при температуре Т и молярная теплоемкость, запишутся так:

где ν – число молей газа, i – число степеней свободы молекулы газа (для молекулы инертного газе Не i=3). С учетом этого можно записать выражение для изменения энтропии:

При изобарном процессе справедлив закон Гей-Люссака:

По условию задачи:

Решая уравнения, получаем ответ:

Ответ: 29 Дж/К.

Задача на второй закон термодинамики №3

Условие

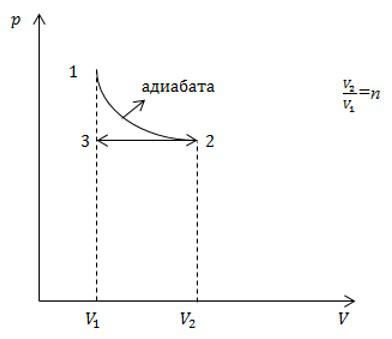
С идеальным газом определенного числа молей последовательно провели два процесса, указанных на рисунке. Какое приращение энтропии в результате получили? Считать, что число степеней свободы молекулы газа равно i.

Решение

Процесс 1-2 является адиабатным. Энтропия в адиабатном процессе не изменяется, следовательно, изменение энтропии происходит только в процессе 2-3, который является изобарным. Запишем в соответствии со вторым началом термодинамики:

Теперь запишем первое начало термодинамики для изобарного процесса:

Давление в процессе остается постоянным, поэтому:

Подставим это выражение в выражение для энтропии, и с учетом первого начала, запишем:

Для изобарного процесса выполняется закон Гей-Люссака:

С учетом этого, запишем окончательное решение:

Ответ: см. выше.

Задача на второй закон термодинамики №4

Условие

Найдите изменение энтропии двухатомного азота массой 0,560 кг при изотермическом расширении. Известно, что объем увеличился в 5 раз.

Решение

Запишем первое начало термодинамики для изотермического процесса:

Изменение энтропии вычислим следующим образом:

Ответ: 268 Дж/К.

Задача на второй закон термодинамики №5

Условие

Как изменилась энтропия воды массой 0,1 кг при ее охлаждении с Т1=293 К до Т2=273 К?

Решение

Изменение энтропии находим в соответствии со вторым началом термодинамики:

Считая, что изменение происходит при постоянном объеме, для элементарного этапа можно записать:

Ответ: -29,3 Дж/ К.

Вопросы на 2 закон термодинамики

Вопрос 1. Сформулируйте второй закон (второе начало) термодинамики.

Ответ. Второй закон термодинамики устанавливает: 

В изолированных системах самопроизвольно могут протекать только такие процессы, при которых энтропия системы возрастает, и процесс может идти самопроизвольно до такого состояния, при котором энтропия обладает максимальным для данных условий значением.

Второе начало термодинамики имеет несколько формулировок, первая из которых принадлежит Сади Карно. Вот пример второго закона термодинамики в его формулировке: теплота не может самоприозвольно переходить от холодного (менее нагретого) тела к горячему (более нагретому).

Хотите больше объяснений и примеров второго закона термодинамики? Читайте нашу отдельную статью на эту тему.

Вопрос 2. Что такое энтропия?

Ответ. Энтропия – физическая величина, одна из функций состояния термодинамической системы. Приращение энтропии вычисляется по формуле:

Энтропия показывает направление процессов и является мерой неупорядоченности в системе. Например, сахар в стакане лежит в виде кусочка, а потом его размешивают по всему стакану. В первом случае энтропия мала, а во втором – велика.

Вопрос 3. Что такое вечный двигатель второго рода?

Ответ. Вечный двигатель второго рода, или перпетум мобиле второго рода – это такая тепловая машина, которая превращает всю теплоту, полученную от нагревателя, в работу. По сути, это тепловая машина, которая работает без холодильника, а коэффициент ее полезного действия равен единице.

Эмпирически установлено, что создание такой машины невозможно.

Вопрос 4. Сформулируйте постулат второго начала термодинамики.

Ответ. Это постулат, вытекающий из невозможности построения вечного двигателя второго рода:

Невозможен круговой процесс, единственным результатом которого было бы произведение работы за счет охлаждения теплового резервуара.

Данная формулировка принадлежит Томсону.

Вопрос 5. Что такое тепловая смерть Вселенной?

Ответ. Это гипотеза, предложенная Клаузиусом в 1865 году. Главная ее идея состоит в том, что энтропия Вселенной, согласно 2 началу термодинамики, постоянно растет. Это значит, что со временем все макроскопические процессы прекратятся, и Вселенная придет в состояние термодинамического равновесия с температурой абсолютного нуля. Данная гипотеза считается ошибочной, так как Больцман объяснил, что Вселенную нельзя рассматривать как замкнутую систему.

Нужна помощь в решении задач на 2 закон термодинамики и написании студенческих работ? Обращайтесь в проверенный студенческий сервис с любыми заданиями в любое время.