Как найти модуль изменения импульса шарика при ударе?
Свободно падающий шарик
массой 200 г ударился о пол со скоростью 5,0 м/с и подпрыгнул на высоту 80 см.
Чему равен модуль изменения импульса шарика при ударе?
Решение.
Изменение импульса
шарика при ударе равно: Dp = p2 – p1 . Из рисунка видим, что модуль изменения импульса: Dp = p2 + p1 = mv1 + mv2 , где v2 – скорость шарика
после удара, которую найдем из закона сохранения механической энергии (нет
сопротивления воздуха): mgh = mv22/2 => v2 = ^(2gh). Тогда Dp = m(v1 + v2) = m(v1 + ^(2gh)) = 1,8 кг•м/с.
Ответ: Dp = 1,8 кг•м/с.
Источник: Пособие-репетитор для подготовки к централизованному тестированию. С.Н.Капельян, Л.А.Аксенович.
Условие задачи:
Найти модуль изменения импульса шарика массой 20 г за 3 с свободного падения. Сопротивление воздуха не учитывать.
Задача №2.1.31 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=20) г, (Delta t=3) с, (Delta p-?)
Решение задачи:
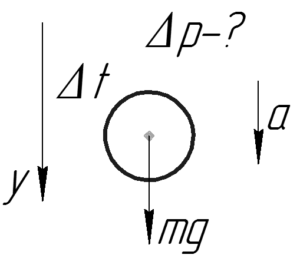Согласно второму закону Ньютона в общем виде:
[F = frac{{Delta p}}{{Delta t}}]
В этой формуле (F) – это равнодействующая сила, действующая на шарик. На него действует только одна сила – сила тяжести:
[F = mg]
Имея две вышеприведенные формулы, в итоге получим:
[mg = frac{{Delta p}}{{Delta t}} Rightarrow Delta p = mgDelta t]
Переведем массу шарика в систему СИ.
[20; г = frac{{20}}{{1000}}; кг = 0,02; кг]
Изменение импульса шарика равно:
[Delta p = 0,02 cdot 10 cdot 3 = 0,6; кг cdot м/с]
Ответ: 0,6 кг·м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.30 На участке дороги, где для автотранспорта установлена предельная скорость 30 км/ч
2.1.32 Определить натяжение каната, к которому подвешена клеть подъемной машины
2.1.33 Парашютист, достигнув в затяжном прыжке скорости 55 м/с, раскрыл парашют
Если
оба шара отклонить на равные углы и
одновременно освободить их, то они,
сталкиваясь друг с другом, в любой момент
времени будут иметь скорости равные по
величине, но разные по знаку.
Закон сохранения
импульса для удара 2-х шаров имеет вид:
,
(1)
где
и
– скорости непосредственно перед ударом
1-го и 2-го шаров соответственно,
и
–
скорости сразу после удара 1-го и 2-го
шаров.
Для изменения
импульсов:
∆
=
m1(
–
), (1a)
∆
=
m2(
–
).
(1б)
Из закона сохранения
импульса (1):
∆
=
– ∆
.
Изменение импульса
каждого (любого) шара за один удар равно:
∆
=
– m1
(
+
),
∆
=m2
(
+
),
∆
=
– ∆
,m1
(
+
)
= m2
(
+
).
(2)
Рассчитать
скорость шаров можно из следующих
рассуждений. При освобождении шара от
магнита он опускается с высоты h,
при этом его потенциальная энергия
переходит в кинетическую энергию по
закону сохранения полной механической
энергии (рис. 2):
,
где
– скорость непосредственно перед ударом
в нижней точке траектории,g
– ускорение свободного падения. Отсюда
.
Из рис. 2 видно,
что
.
Учитывая,
что для малых углов значение синуса
можно заменить значением аргумента, а
угол равен отношению дуги S
к длине подвеса, получим выражение для
скорости до удара:
,
(3)
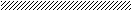
l
l
– h
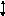
h
S0
Рис.
2. К вычислению скорости шара.
где
S0
– расстояние по дуге, пройденное шаром
до 1-го удара. Аналогичным образом
рассчитывается скорость шара после
первого удара:
.
(4)
С
учетом (3) и (4), формула (2) принимает
расчетный вид:
.
(5)
1.
Включить электромагниты и подвести к
ним шары. Записать значение S0.
Отключая электромагниты, определить
S1
– дугу отклонения после 1-го удара.
Повторить опыт несколько раз. Вычислить
скорости шаров в момент удара и величину
изменения импульса.
Результаты занести
в таблицу и оценить погрешность опыта.
Упражнение 2. Определение коэффициента восстановления.
Коэффициент
восстановления К
по определению равен отношению
относительной скорости после удара
шаров к относительной скорости до удара.
Коэффициент восстановления характеризует
степень упругости удара, т.к. для абсолютно
упругого удара К
= 1, а для
абсолютно неупругого К
= 0, во всех
остальных случаях (реальный удар): 0<K<1.
В случае m1
= m2
имеем:
. (6)
С учетом формул
(3) и (4) формула (6) принимает вид:
.
Проведя
n
столкновений, и, рассуждая так же,
получим:
,
,
….
,
,
, (7)
где
S0
– дуга начального отклонения; Sn
– дуга n-го
отклонения при n
ударе.
Зная
коэффициент восстановления, можно
подсчитать энергию деформации – ту
часть кинетической энергии относительного
движения, которая переходит во внутреннюю.
Так как в нашем случае массы одинаковы,
получаем:
,
где
W
– энергия остаточной деформации одного
шара после первого удара. Отсюда
.
Или
в процентах от кинетической энергии
данного шара к моменту удара имеем
,
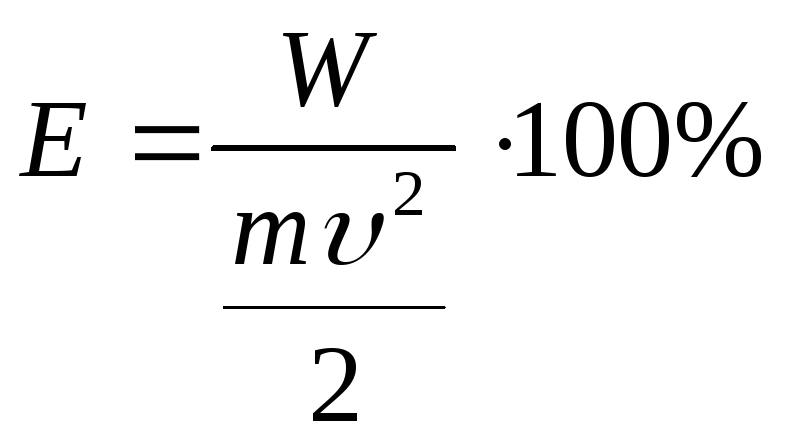(8)
Выполнение работы.
-
Включить
электромагниты (тумблер К1)
и подвести к ним шары. Записать S0. -
Выключить
электромагниты и, отсчитав 10-15 ударов,
зафиксировать Sn. -
К
по формуле (7). -
Повторить пункты
1-3 не менее 5 раз. -
Найти
Кср
и оценить погрешность. -
По формуле (8)
оценить долю потерянной энергии при
одном ударе.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В статье обсуждается, что такое изменение импульса, и формулы о том, как найти изменение импульса.
Изменение импульса есть разница в движении. Когда объект находится в движении, ударяется или сталкивается с другим объектом, приложенная сила ускоряет объект, изменяя его движение. Изменение импульса рассчитывается по формуле импульса или по закону сохранения импульса.
Говорят, что движущийся объект имеет импульс. Количество импульса, полученного объектом, пропорционально его массе и скорости вместе взятым. Следовательно, изменение одной величины может вызвать изменение импульса. Это означает, что если вы увеличиваете или уменьшаете массу объекта, его импульс изменяется. Точно так же импульс также изменяется, когда вы увеличиваете или уменьшаете его скорость.
Изменение скорости означает, что объект ускоряется, а мы узнали, что ускорение вызывается силой. Так чем больше ускорение, вызванное силой, тем больше изменение ее импульса!!!
Предположим, что объект покоится или не имеет импульса, тогда требуется достаточная сила для преодоления трения, чтобы объект двигался с некоторым импульсом. Если объект уже находится импульс и сила применяется в противоположном направлении, его импульс уменьшится. Но если сила приложена в том же направлении, то импульс увеличится.
Большая сила, приложенная за короткое время, вызывает значительное изменение импульса.. Если сила мала, но действует в течение длительного времени, также происходит значительное изменение количества движения. Это означает, что когда сила применяется к объекту, уже получившему импульс, в течение определенного периода времени, его импульс изменяется.
Подробнее о Моментум
Примеры изменения моментума
Примеры изменения импульса объясняют, как изменяется импульс при воздействии силы.
- Длинный прыжок
- Удар по мячу
- Вождение автомобиля
- футбол или регби
- Игровая площадка Slide
Длинный прыжок
Чтобы набрать обороты перед прыжком, спортсмен пробегает определенную дистанцию. Как только спортсмен набирает некоторый импульс после бега, они прикладывают силу к земле для прыжка, которая меняет его импульс, и спортсмен прыгает вперед. После прыжка спортсмену необходимо снова приложить большую силу к земле, чтобы остановить движение, что снова меняет его импульс.
(Кредит: Shutterstock)
Удар по мячу
Мяч набирает обороты, когда игрок бросает его во время таких видов спорта, как крикет или бейсбол. Когда отбивающий ударяет по мячу битой, сила, приложенная к мячу, меняет свой импульс, и затем мяч движется в направлении приложенной силы. Импульс мяча снова меняется, когда он останавливается или ловится полевым игроком.
(Кредит: Shutterstock)
Вождение автомобиля
Управление транспортным средством, таким как легковой или грузовой автомобиль, предполагает постоянное изменение импульса. Мы прикладываем усилие к его ускоряющей лопатке, чтобы ускорить транспортное средство. Чтобы внезапно остановить транспортное средство, мы прикладываем силу к его тормозной лопасти, которая изменяет импульс транспортного средства в соответствии с приложенной силой.
футбол или регби
В футболе или регби нападающий аккумулирует максимальный импульс, когда он ведет мяч или несет мяч вблизи побережья ворот, минуя других игроков. Затем защитники у побережья ворот пытаются остановить или изменить импульс нападающего, захватив его.
Слайды для детских площадок
Когда дети начинают скользить по игровой площадке с высоты, они получают импульс вниз. Но трение, присутствующее на поверхности скольжения игровой площадки, изменяет импульс скольжения детей, противодействуя их движению, предотвращая их падение в конце скольжения.
Подробнее о примерах Momentum
Изменение формулы импульса
Формула изменения количества движения рассчитывается с использованием второго закона Ньютона и кинематических уравнений движения.
Второй закон Ньютона показывает, что тело ускоряется под действием силы. Поскольку сила, приложенная в течение определенного интервала времени, изменяет движение объекта, она также вызывает изменение импульса. Произведение силы и временного интервала называется «импульсом», который измеряет изменение импульса.
Компания первое кинематическое уравнение движения является,
vf = Vi + в
vf– vi = в
Согласно Второй закон Ньютона, F = ма, а = F/а
vf-vi=(Ф/м)*t
м (vf– vi) = футов
мΔv=Ft
Принимая во внимание, что RHS в приведенном выше уравнении называется «Импульс’ (обозначается J), а LHS – формула Изменение импульса (ΔP)
Следовательно, мы также можем написать как,
J=Ft=mΔv=ΔP…………. (*)
Импульс = изменение импульса
Уравнение (*) также известно как ‘Импульс – уравнение изменения импульса.
Чем значительнее импульс, тем значительнее изменение импульса.
Сила силы, приложенная к объекту, зависит от того, как долго он действует. Понятие импульса количественно определяет действие силы.
Узнайте больше об уравнениях кинематики.
Предположим, что нападающий массой 40 кг ведет мяч со скоростью 10 м/с. Когда он приближается к защитнику за 0.10 секунды, он ведет мяч на высокой скорости, например 15 м/с, чтобы успешно обойти защитника.
(Кредит: Shutterstock)
Каков первоначальный импульс ударника?
Каков окончательный импульс нападающего, когда к нему приближается защитник?
Каково изменение импульса стикера?
Какую силу прикладывает защитник, чтобы остановить нападающего?
Рассчитайте Импульс, примененный защитником.
Данный:
m = 40 кг
vi = 10 м / с
vf = 15 м / с
t = 0.10 с
Найти:
- Pi =?
- Pf =?
- ΔP =?
- Ф =?
Формула:
- Р = мв
- ΔР = Рf -Пi
- Ft = ΔP
Решения:
Начальный импульс ударника рассчитывается как
Pi = мвi
Pi = 40 x 10
Pi = 400
Начальный импульс бойка 400кг.м/с
Конечный импульс ударника рассчитывается как
Pf = мвf
Pf = 40 x 15
Pf = 600
Конечный импульс бойка 600кг.м/с
Изменение импульса ударника рассчитывается как
ΔР = Рf -Пi
ΔP = 600 – 400
ΔP = 200
Изменение импульса бойка 200 кг.м/с.
Сила, приложенная защитником, чтобы остановить нападающего, рассчитывается по формуле изменения импульса-импульса.
Ft = ΔP
Подставляя все значения,
F (0.10) = 200
F = 200/0.10
F = 2000
Сила примененная защитником, составляет 2000 Н.
Импульс защитника рассчитывается как
Дж = фут
J = 2000 х 0.10
J = 200
Импульс защитника на нападающего 200Н.с.
Узнайте больше о Net Force.
Как рассчитать изменение импульса?
Изменение импульса рассчитывается по закону сохранения импульса.
Когда на объект действует внешняя сила, мы можем вычислить изменение его импульса по формуле импульса. Но когда нет внешней силы, суммарный импульс сталкивающихся объектов остается прежним. Вот как мы можем рассчитать изменение импульса из-за столкновения, используя закон сохранения импульса.
Предположим, что два объекта имеют импульс P1 и Р2 из-за их массы m1 И м2 и скорость u1 и ты2. В результате столкновения их импульс меняется на P1 “ и Р2 “ так как их скорость меняется на v1 и v2.
Согласно сохранение импульса,
m1u1 + м2u2 = м1v1 + м2v2
Поскольку мы хотим рассчитать изменение импульса, переставляя члены m1 в левой части и m2 в правой,
m1u1 – M1v1 = м2u2 – M2v2
P1f– П1i = P2f-P2i
ΔP1 = ΔP2
Изменение импульса объекта 1 = изменение импульса объекта 2
Подробнее о моментуме после столкновения
Когда два шара массами 5 кг и 3 кг движутся навстречу друг другу со скоростью 8 м/с и 15 м/с соответственно, а после столкновения первый шар удаляется со скоростью 5 м/с.
Вычислите изменение импульса первого шара.
Вычислите изменение скорости второго шара после удара.
Данный:
m1 = 5 кг
m2 = 3 кг
u1 = 8 м / с
u2 = 15 м / с
v1 = 5 м / с
Найти:
- ΔP1 =?
- v2 =?
Формула:
- ΔP1 = P1f– П1i
- m1u1 – M1v1 = м2u2 – M2v2
Решения:
Изменение импульса первого шара рассчитывается как
ΔP1 = P1f– П1i
ΔP1 = м1u1 – M1v1
Подставляя все значения,
ΔP1 = 5 х 8-5 х 5
ΔP1 = 40 – 25
ΔP1 = 25
Изменение импульса первого шара равно 25 кг.м/с.
Изменение скорости второго мяча после столкновения рассчитывается как
m1u1 – M1v1 = м2u2 – M2v2
Подставляя все значения,
25 = 3х15 – 3в2
25 = 45 — 3в2
v2 = -20/3
v2 = -6.66
Изменение скорости второго шара равно -6.6 м/с.
Подробнее о импульсе перед столкновением.
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Определение
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2 = m1v1отн2 = m1(v1 – v2)
p1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1 и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103 (кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:
∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар |
|
|
|
Конечная скорость после удара:
v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. |
Абсолютно упругий удар |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. |
Пуля пробила стенку |
|
|
|
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) |
Радиус-вектор тела повернул на 180 градусов |
|
|
|
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой:
|
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
Или:
F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Реактивная сила:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Определение
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
Важно!
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:
Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:
Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17695
На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?
а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22730
Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.
Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek = 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22520
Снаряд, имеющий в точке О траектории импульсp0, разорвался на два осколка. Один из осколков имеет импульс −p1
. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:
Сделаем чертеж:
Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:
Выразим массу груза:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20.1k
