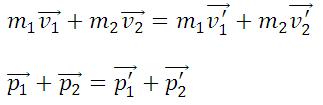Как найти изменение импульса шарика при ударе

Импульс. Закон сохранения импульса.
При решении динамических задач необходимо знать какие силы действуют на тело, закон, позволяющий рассчитать конкретную силу. Цель: получить решение задачи механики исходя из начальных условий, не зная конкретного вида взаимодействия.
Законы Ньютона в полученной ранее форме не позволяют решать задачи на движение тела с переменной массой и при скоростях, сравнимых со скоростью света. Цель: получить записи законов Ньютона в форме, справедливой для этих условий.
Импульс силы    Векторная физическая величина, являющаяся мерой действия силы за некоторый промежуток времени. – импульс силы за малый промежуток времени t. Вектор импульса силы сонаправлен с вектором силы.	[ I ]= Нс
Импульс тела. (Количество движения)      Векторная физическая величина, являющаяся мерой механического движения и равная произведению массы тела на его скорость. Вектор импульса тела сонаправлен с вектором скорости тела.	[ p ]=  кг м/с
Основное уравнение динамики.
Из второго закона Ньютона:
Тогда получим: – второй закон Ньютона в импульсной  форме
( Dt = t – t0 = t  при t = 0).
Импульс силы равен изменению импульса тела  Вектора импульса силы и изменения импульса тела сонаправлены.
Неупругий удар (шарик “прилипает” к стенке):
Абсолютно упругий удар (шарик отскакивает с прежней по величине скоростью):
Закон сохранения импульса.
До взаимодействия
После взаимодействия
Согласно 3 з-ну Ньютона: , следовательно:
Геометрическая (векторная) сумма импульсов взаимодействующих тел, составляющих замкнутую систему, остается неизменной.
Замкнутой называется система тел, взаимодействующих только друг с другом и не взаимодействующих с другими телами. Можно пользоваться и для незамкнутых систем, если сумма внешних сил, действующих на тела системы, равна нулю, или процесс происходит очень быстро, когда внешними воздействиями можно пренебречь (взрыв, атомные процессы).
В общем виде: т.к. система замкнутая, то , следовательно
Примеры применения закона сохранения импульса: Любые столкновения тел (биллиардных шаров, автомобилей, элементарных частиц и т.д.); Движение воздушного шарика при выходе из него воздуха; Разрывы тел, выстрелы и т.д.

Основные теоретические сведения

[custom_ads_shortcode1]

Импульс тела

К оглавлению…

Импульсом (количеством движения) тела называют физическую векторную величину, являющуюся количественной характеристикой поступательного движения тел. Импульс обозначается р. Импульс тела равен произведению массы тела на его скорость, т.е. он рассчитывается по формуле:

Направление вектора импульса совпадает с направлением вектора скорости тела (направлен по касательной к траектории). Единица измерения импульса – кг∙м/с.

Общий импульс системы тел равен векторной сумме импульсов всех тел системы:

Изменение импульса одного тела находится по формуле (обратите внимание, что разность конечного и начального импульсов векторная):

где: pн – импульс тела в начальный момент времени, pк – в конечный. Главное не путать два последних понятия.

Абсолютно упругий удар – абстрактная модель соударения, при которой не учитываются потери энергии на трение, деформацию, и т.п. Никакие другие взаимодействия, кроме непосредственного контакта, не учитываются. При абсолютно упругом ударе о закрепленную поверхность скорость объекта после удара по модулю равна скорости объекта до удара, то есть величина импульса не меняется. Может поменяться только его направление. При этом угол падения равен углу отражения.

Абсолютно неупругий удар – удар, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело. Например, пластилиновый шарик при падении на любую поверхность полностью прекращает свое движение, при столкновении двух вагонов срабатывает автосцепка и они так же продолжают двигаться дальше вместе.

[custom_ads_shortcode2]

Закон сохранения импульса

К оглавлению. . .

При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой.

В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называется законом сохранения импульса (ЗСИ). Следствием его являются законы Ньютона. Второй закон Ньютона в импульсной форме может быть записан следующим образом:

Как следует из данной формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:

Аналогично можно рассуждать для равенства нулю проекции силы на выбранную ось. Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:

Аналогичные записи можно составить и для остальных координатных осей. Так или иначе, нужно понимать, что при этом сами импульсы могут меняться, но именно их сумма остается постоянной. Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны.

[custom_ads_shortcode3]

Сохранение проекции импульса

К оглавлению…

Возможны ситуации, когда закон сохранения импульса выполняется только частично, то есть только при проектировании на одну ось. Если на тело действует сила, то его импульс не сохраняется. Но всегда можно выбрать ось так, чтобы проекция силы на эту ось равнялась нулю.

Тогда проекция импульса на эту ось будет сохраняться. Как правило, эта ось выбирается вдоль поверхности по которой движется тело.

[custom_ads_shortcode1]

Многомерный случай ЗСИ. Векторный метод

К оглавлению…

В случаях если тела движутся не вдоль одной прямой, то в общем случае, для того чтобы применить закон сохранения импульса, нужно расписать его по всем координатным осям, участвующим в задаче. Но решение подобной задачи можно сильно упростить, если использовать векторный метод. Он применяется если одно из тел покоится до или после удара. Тогда закон сохранения импульса записывается одним из следующих способов:

Из правил сложения векторов следует, что три вектора в этих формулах должны образовывать треугольник. Для треугольников применяется теорема косинусов.

[custom_ads_shortcode2]

Математика

В этом разделе представлены теория и задачи по математике, необходимые для успешной подготовки к ЦТ или ЕГЭ. Список основных тем из школьной математики:

Смотрите также:

• Все учебные материалы
• Справочники
• Задачники и учебники

[custom_ads_shortcode3]

Физика

В этом разделе представлены теория и задачи по физике, необходимые для успешной подготовки к ЦТ или ЕГЭ. Список основных тем из школьной физики:

Смотрите также:

• Все учебные материалы
• Справочники
• Задачники и учебники

[custom_ads_shortcode1]

Формулы, методы и другая справочная информация

В этом разделе сайта представлены различные списки формул по физике и математике, а также приведена другая необходимая справочная информация. Знание физических и математических формул и методов является одним из ключевых элементов успешной подготовки к ЦТ или ЕГЭ. В этом разделе смотрите:

[custom_ads_shortcode2]

Итоговые тесты по физике и математике

В этом разделе сайта представлены итоговые тесты по физике и математике, которые позволят абитуриентам успешно повторить изученный материал и систематизировать свои знания по физике и математике. Решение этих тестов поможет поступающим успешно сдать ЦТ или ЕГЭ.

Подробнее…

[custom_ads_shortcode3]

Другая полезная информация для абитуриентов

В этом разделе сайта представлены различные советы и рекомендации по подготовке и сдаче ЦТ и ЕГЭ. А также советы о том, как правильно организовать процесс изучения физики и математики дома для абитуриентов. В этом разделе смотрите:

[custom_ads_shortcode1]

Высшая математика

В этом разделе сайта приведена теория, задачи, тесты и формулы по высшей математике. Эта информация поможет поступившим в ВУЗы ученикам разобраться в этом сложном предмете и получить отличные оценки на экзаменах в ВУЗе. Представлена информация в следующих категориях:

• Основы высшей математики
• Теоретические сведения
• Теория вероятностей

[custom_ads_shortcode2]

Материалы для поступающих в Польшу

В этом разделе собраны материалы, которые помогут ученикам подготовится и поступить в польский университет. В основном материалы представляют из себя польские тесты по многим предметам, в том числе по физике и математике, но имеется также и другая полезная информация.

Подробнее…

[custom_ads_shortcode3]

Научно-популярные статьи

В этом разделе собраны различные интересные факты в виде научно-популярных статей, в которых сложные вещи излагаются простым языком без лишних формул. Эти статьи помогут убедиться в особенной занимательности науки, полюбить физику и математику, а также отвлечься и развеяться во время трудоемкой и скучной подготовки к экзаменам.

Подробнее…

Пуля 22-го калибра имеет массу всего 2 г. Если кому-нибудь бросить такую пулю, то он легко сможет поймать ее даже без перчаток. Если же попытаться поймать такую пулю, вылетевшую из дула со скоростью 300 м/с, то даже перчатки тут не помогут.

Если на тебя катится игрушечная тележка, ты сможешь остановить ее носком ноги. Если на тебя катится грузовик, следует уносить ноги с его пути.

Импульс это векторная величина, которая определяется по формуле

Импульс служит мерой того, насколько велика должна быть сила, действующая в течение определенного времени, чтобы остановить или разогнать его с места до данной скорости. Направление вектора импульса всегда совпадает с направлением вектора скорости.

Если тело покоится, импульс равен нулю. Ненулевым импульсом обладает любое, движущееся тело. Например, когда мяч покоится, его импульс равен нулю.

После удара он приобретает импульс. Импульс тела изменяется, так как изменяется скорость.

[custom_ads_shortcode1]

Импульс силы

Это векторная величина, которая определяется по формуле.

Изменение импульса тела равно импульсу равнодействующей всех сил, действующих на тело. Это иная формулировка второго закона Ньютона

Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела. Пример. Масса мяча равна 400 г, скорость, которую приобрел мяч после удара – 30 м/с.

Сила, с которой нога действовала на мяч – 1500 Н, а время удара 8 мс. Найти импульс силы и изменение импульса тела для мяча.

[custom_ads_shortcode2]

Изменение импульса тела

Как определить изменение импульса тела? Необходимо найти численное значение импульса в один момент времени, затем импульс через промежуток времени. От второй найденной величины отнять первую. Внимание! Вычитать надо вектора, а не числа. То есть из второго вектора импульса отнять первый вектор. Смотрите вычитание векторов. Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара. 1) Во время удара на мяч действуют две силы: сила реакции опоры, сила тяжести.

Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола. 2) Изменение импульса тела изображено на рисунке

3) Из второго закона Ньютона.

[custom_ads_shortcode3]

Главное запомнить

1) Формулы импульса тела, импульса силы; 2) Направление вектора импульса; 3) Находить изменение импульса тела

[custom_ads_shortcode1]

Вывод второго закона Ньютона в общем виде

[custom_ads_shortcode2]

График F(t). Переменная сила

Импульс силы численно равен площади фигуры под графиком F(t).

Если же сила непостоянная во времени, например линейно увеличивается F=kt, то импульс этой силы равен площади треугольника. Можно заменить эту силу такой постоянной силой, которая изменит импульс тела на ту же величину за тот же промежуток времени

Средняя равнодействующая сила.

Источники:

• www.eduspb.com
• educon.by
• educon.by
• fizmat.by

Если
оба шара отклонить на равные углы и
одновременно освободить их, то они,
сталкиваясь друг с другом, в любой момент
времени будут иметь скорости равные по
величине, но разные по знаку.

Закон сохранения
импульса для удара 2-х шаров имеет вид:

,
(1)

где
и– скорости непосредственно перед ударом
1-го и 2-го шаров соответственно,и–
скорости сразу после удара 1-го и 2-го
шаров.

Для изменения
импульсов:

∆=
m₁(–), (1a)

∆=
m₂(–).
(1б)

Из закона сохранения
импульса (1):

∆=
– ∆.

Изменение импульса
каждого (любого) шара за один удар равно:

∆=
– m₁
(+),
∆=m₂
(+),

∆=
– ∆,m₁
(
+
)
= m₂
(
+
).
(2)

Рассчитать
скорость шаров можно из следующих
рассуждений. При освобождении шара от
магнита он опускается с высоты h,
при этом его потенциальная энергия
переходит в кинетическую энергию по
закону сохранения полной механической
энергии (рис. 2):

,

где

– скорость непосредственно перед ударом
в нижней точке траектории,g
– ускорение свободного падения. Отсюда

.

Из рис. 2 видно,
что

.

Учитывая,
что для малых углов значение синуса
можно заменить значением аргумента, а
угол равен отношению дуги S
к длине подвеса, получим выражение для
скорости до удара:

,
(3)



l
l
– h

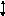
h

S₀

Рис.
2. К вычислению скорости шара.

где
S₀
– расстояние по дуге, пройденное шаром
до 1-го удара. Аналогичным образом
рассчитывается скорость шара после
первого удара:

.
(4)

С
учетом (3) и (4), формула (2) принимает
расчетный вид:

.
(5)

1.
Включить электромагниты и подвести к
ним шары. Записать значение S₀.
Отключая электромагниты, определить
S₁
– дугу отклонения после 1-го удара.
Повторить опыт несколько раз. Вычислить
скорости шаров в момент удара и величину
изменения импульса.

Результаты занести
в таблицу и оценить погрешность опыта.

Упражнение 2. Определение коэффициента восстановления.

Коэффициент
восстановления К
по определению равен отношению
относительной скорости после удара
шаров к относительной скорости до удара.
Коэффициент восстановления характеризует
степень упругости удара, т.к. для абсолютно
упругого удара К
= 1, а для
абсолютно неупругого К
= 0, во всех
остальных случаях (реальный удар): 0<K<1.
В случае m₁
= m₂
имеем:

. (6)

С учетом формул
(3) и (4) формула (6) принимает вид:

.

Проведя
n
столкновений, и, рассуждая так же,
получим:

,
,
….,,

, (7)

где
S₀
– дуга начального отклонения; S_n
– дуга n-го
отклонения при n
ударе.

Зная
коэффициент восстановления, можно
подсчитать энергию деформации – ту
часть кинетической энергии относительного
движения, которая переходит во внутреннюю.
Так как в нашем случае массы одинаковы,
получаем:

,

где
W
– энергия остаточной деформации одного
шара после первого удара. Отсюда

.

Или
в процентах от кинетической энергии
данного шара к моменту удара имеем

,
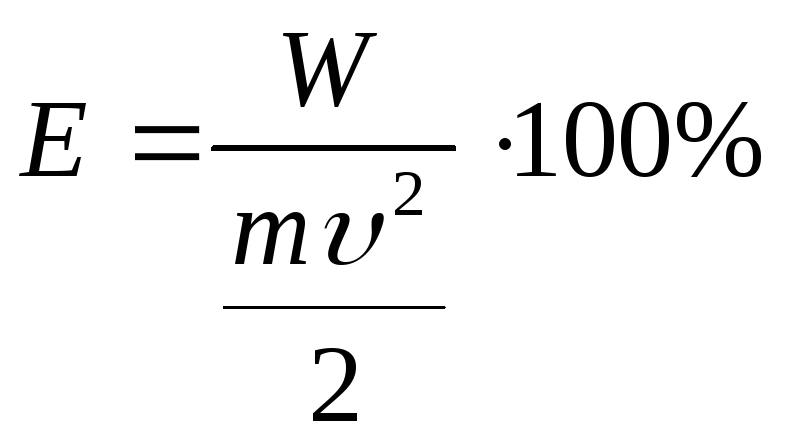(8)

Выполнение работы.

1. Включить
   электромагниты (тумблер К₁)
   и подвести к ним шары. Записать S₀.

2. Выключить
   электромагниты и, отсчитав 10-15 ударов,
   зафиксировать S_n.

3. К
   по формуле (7).

4. Повторить пункты
   1-3 не менее 5 раз.

5. Найти
   К_ср
   и оценить погрешность.

6. По формуле (8)
   оценить долю потерянной энергии при
   одном ударе.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Эта статья посвящена задачам на одну из самых важных тем школьного курса физики — закон сохранения импульса. Такие задачи можно часто встретить в экзаменационных билетах. В статье использованы задачи, предлагавшиеся на вступительных экзаменах по физике в Московском физико-техническом институте, на физических факультетах Московского государственного университета, Новосибирского государственного университета и в ряде других вузов.

Импульсом (или количеством движения) материальной точки называется произведение ее массы на скорость. Так как скорость — это вектор, а масса — величина скалярная, то импульс — тоже векторная величина. Направление вектора импульса совпадает с направлением вектора скорости.

Если у нас имеется несколько материальных точек или частиц, то можно говорить об импульсе системы материальных точек. Он равен векторной сумме импульсов отдельных точек. Так, например, если у нас имеется две материальные точки, одна из которых имеет массу m₁ и скорость 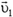, а вторая — массу m₂ и скорость 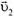, то импульс  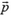системы этих материальных точек равен сумме  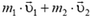(рис. 1). Важно не забывать, что импульсы частиц складываются векторно, то есть геометрически (по правилу треугольника или по правилу параллелограмма). В том случае, когда скорости частиц направлены вдоль одной прямой, импульсы можно складывать алгебраически. При этом импульсы частиц, движущихся в противоположные стороны, следует брать с противоположными знаками.

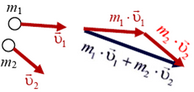
Рис. 1.

Для того чтобы найти импульс тела, различные точки которого имеют разные скорости, его разбивают мысленно на маленькие части (в пределе бесконечно маленькие) и затем складывают импульсы этих частей. Найдем таким способом импульс однородного диска, вращающегося вокруг своей оси. Ясно, что всегда можно найти два таких элемента диска с массами Δm, линейные скорости которых равны по абсолютной величине и противоположно направлены (рис. 2). Сумма импульсов этих элементов, очевидно, равна нулю. А так как диск можно всегда разбить на пары таких элементов, то отсюда следует, что импульс всего диска равен нулю.

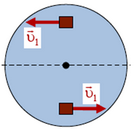
Рис. 2.

Иное дело, если диск катится по горизонтальной поверхности (рис. 3). Пусть скорость центра диска равна 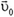. Скорость любого малого элемента Δm диска можно представить как сумму линейной скорости  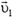ее вращения вокруг центра диска (в системе координат, связанной с центром диска) и скорости  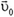ее поступательного движения: 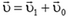. Импульс диска равен сумме импульсов отдельных его элементов, то есть

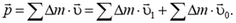
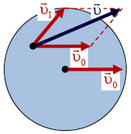
Рис. 3.

Но первый член в этой сумме, очевидно, равен импульсу диска в системе координат, связанной с его центром. В этой системе координат центр диска неподвижен и импульс диска равен нулю. Поэтому импульс диска, катящегося по горизонтальной плоскости, равен 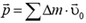. Вынося постоянный множитель  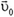за знак суммы, найдем

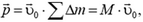
где М — масса диска.

Импульс тела зависит от системы координат. Пусть в системе координат В тело массы m движется со скоростью 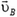. Его импульс 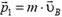. Система координат В движется со скоростью  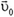относительно системы координат А. Чтобы найти импульс тела в системе координат A, надо к  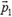прибавить  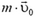— произведение массы тела на скорость системы координат В относительно системы координат А. Это правило — следствие того, что скорость любой точки в системе координат В складывается из скорости этой точки в системе координат А и скорости системы координат В относительно системы координат А (рис. 4): 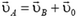. Отсюда

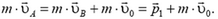
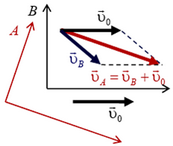
Рис. 4.

Пользуясь понятием «импульс», второй закон Ньютона можно записать так:

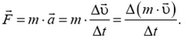
Если на тело действует сила 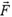 в течение времени Δt то импульс тела изменяется на величину 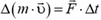. Произведение силы  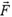на время ее действия Δt называют импульсом силы. И говорят, что изменение импульса тела равно импульсу действующей на него силы.

Воспользовавшись такой формой записи второго закона Ньютона, найдем, например, среднюю силу, действующую на плиту, с которой абсолютно упруго сталкивается шарик массы m, летящий со скоростью 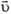 под углом α к плите (рис. 5). Время соударения шарика с плитой равно τ.

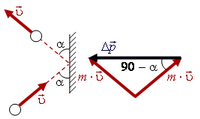
Рис. 5.

Так как столкновение абсолютно упруго, то шарик отскакивает от плиты под таким же углом α, под каким подлетает к ней, и с той же по величине скоростью 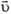. Нетрудно найти изменение импульса  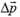шарика при ударе. Оно равно

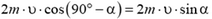
и направлено перпендикулярно плите. Эго означает, что при столкновении шарика с плитой на шарик действует средняя сила

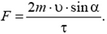
Согласно третьему закону Ньютона точно такая же сила, но направленная противоположно, действует на плиту.

Если одна и та же сила действует на два тела одно и то же время, то импульсы этих тел меняются одинаково, независимо от их начальных масс или скоростей. Пусть, например, две частицы с массами m и 2m движутся так, как показано на рисунке 6, а — первая, частица (m) движется со скоростью 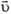 в направлении, перпендикулярном направлению движения второй частицы (2m), скорость которой равна 2.

          

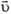                                    а                                                  б

Рис. 6.

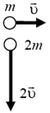
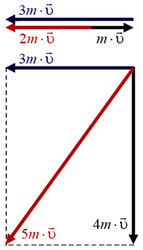
На частицы в некоторый момент времени начинают действовать одинаковые силы, причем эти силы действуют на частицы одинаковое время. После прекращения действия сил частица массы m движется со скоростью 2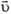 в направлении, противоположном направлению ее первоначального движения. С какой скоростью и в каком направлении движется вторая частица после прекращения действия силы?

Найдем импульс силы, действующей на каждую частицу. Нужно не забывать, что импульс и изменение импульса — величины векторные. Импульс первой частицы изменился по направлению и по величине и стал равным 2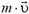. Изменение импульса первой частицы равно 3 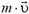(рис. 6, б). Так как и на вторую частицу действует такая же сила в течение того же самого времени, то и импульс второй частицы меняется на 3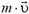. Сложив первоначальный импульс второй частицы с изменением импульса, найдем, что импульс частицы массы 2m стал равен 5 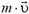и направлен под углом  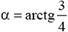к направлению первоначального движения этой частицы (см. рис. 6, б). Разделив импульс частицы на ее массу, найдем, что скорость частицы массы 2m после прекращения действия силы равна 2,5.

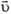Теперь решим более сложную задачу.

Космический корабль, имеющий лобовое сечение S = 50 м² и скорость υ = 10 км/сек, попадает в облако микро-метеоров, плотность которого n = 1 м^-3 (то есть в одном кубическом метре пространства находится один микрометеор). Масса каждого микрометеора m = 0,02 г. Насколько должна возрасти сила тяги двигателя, чтобы скорость корабля не изменилась? Удар микрометеоров об обшивку корабля считать абсолютно неупругим.

За время Δt корабль сталкивается с микрометеорами, которые в начальный момент находились от него на расстоянии, меньшем 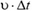(рис. 7).

Рис. 7.

Масса М всех этих микрометеоров равна 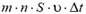. До столкновения с кораблем скорости и импульсы микрометеоров были равны нулю, а после неупругого столкновения с кораблем скорости микрометеоров стали равны υ. Это означает, что при столкновении микрометеора с обшивкой корабля микрометеор приобретает импульс m·υ. Микрометеоры, попавшие на обшивку корабля за время Δt, приобретают суммарный импульс

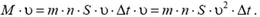
Это означает, что на микрометеоры действует сила

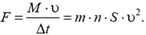
Согласно третьему закону Ньютона такая же по величине сила, но направленная в противоположную сторону, действует на обшивку корабля. Поэтому для того, чтобы при попадании корабля в облако метеоров его скорость не изменилась, сила тяги двигателя корабля должна увеличиться на 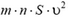 = 10⁵ H.

Если на тело не действуют силы или действующие силы взаимно уравновешиваются, то импульс тела не меняется. Точно так же, если на систему тел не действуют внешние силы (такая система тел называется замкнутой или изолированной), то суммарный импульс системы тел не меняется.

Решим такую задачу. Нейтрон с энергией E = 10^–15 Дж поглощается первоначально неподвижным, ядром кадмия (А = 112). Определить скорость вновь образовавшегося ядра (А = 113).

Система нейтрон — ядро изолированная, и ее импульс не меняется.

Если массу нейтрона обозначить m, а его скорость υ, то 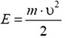. Отсюда мы найдем, что скорость нейтрона до его столкновения с ядром кадмия была равна 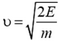. До столкновения импульс нейтрона был равен 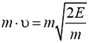, а импульс ядра был равен нулю. Поэтому до столкновения импульс системы был равен 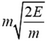. Если скорость ядра, образовавшегося в результате поглощения нейтрона ядром кадмия, обозначить u, а его массу М, то импульс этого ядра равен М·и. Запишем теперь закон сохранения импульса:

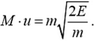
Отсюда найдем, что

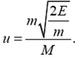
Напомним еще раз, что импульс — величина векторная. Поэтому, когда мы говорим о сохранении импульса изолированной системы, важно помнить, что сохраняется не только величина импульса, но и его направление. Сохраняются и составляющие импульса по любым направлениям, например по двум осям координат.

Решим, используя это, следующую задачу.

Ядро массы m, летящее со скоростью 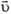, распадается на две части одинаковой массы, причем один из осколков деления летит со скоростью  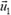под углом α к направлению полета ядра до его распада. Найти скорость и направление полета второго осколка ядра.

Введем такую систему координат: ось х направим по скорости ядра до распада (рис. 8). Если скорость второго осколка ядра обозначить 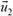, а угол, который образует вектор  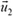с направлением скорости ядра до распада (с осью х), обозначить β, то на основании закона сохранения импульса мы можем записать:

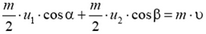
— для составляющих импульсов по оси x,

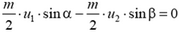
— для составляющих импульсов по оси у.

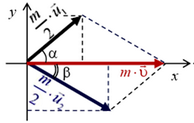
Рис. 8.

Из этих уравнений находим

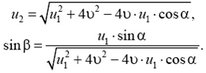
Если система не изолирована и на нее действует некоторая сила 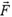, то полный импульс системы не сохраняется. Однако сохраняется составляющая импульса в направлении, перпендикулярном силе 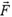. На этом основано решение большого числа задач.

Решим, например, такую задачу.

На железнодорожной платформе, движущейся со скоростью υ, укреплено орудие. Ствол орудия направлен в сторону движения платформы и приподнят над горизонтом. Орудие произвело выстрел, после чего скорость платформы уменьшилась в n раз. Найти скорость u снаряда (относительно земли), если он вылетает из ствола под углом α к горизонту. Масса снаряда m, масса платформы с орудием (без снаряда) М.

Система орудие — платформа — снаряд не является изолированной: на нее действует сила тяжести и сила реакции Земли. Однако в горизонтальном направлении на платформу с пушкой и снаряд внешние силы не действуют. Это означает, что горизонтальная составляющая импульса системы не должна при выстреле измениться. Поэтому

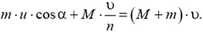
Отсюда

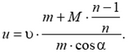
Если система частиц или тел изолирована и ее импульс не меняется, то не меняется и скорость центра масс системы (центра тяжести). В частности, если в некоторый момент система двигалась так, что скорость центра масс была равна нулю, то эта скорость остается равной нулю все время. Поэтому не меняется и положение центра масс.

Рассмотрим пример.

Человек массы m находится на корме лодки массы М, стоящей в пруду. Длина лодки L. На сколько сдвинется лодка относительно берега, если человек перейдет с кормы лодки на нос?

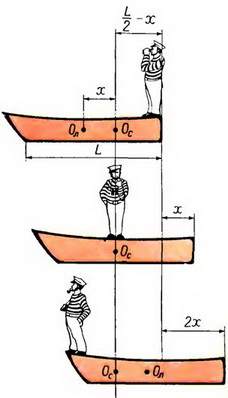
Рис. 9.

Так как в горизонтальном направлении на систему лодка — человек силы не действуют, положение ее центра масс должно сохраниться. Но положение центра масс системы определяется положением центров масс лодки и человека (рис. 9). Пусть первоначально расстояние между центром масс системы (О_с) и центром масс лодки (О_л) равно х.

Тогда 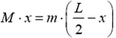, откуда 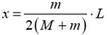. Когда человек перейдет с кормы лодки на ее середину, то, очевидно, положение его центра масс должно совпадать с положением центра масс системы. Следовательно, и положение центра масс лодки должно также совпадать с положением центра масс системы, то есть лодка должна переместиться на расстояние х. На такое же расстояние переместится лодка при переходе человека на нос. Следовательно, полное перемещение лодки

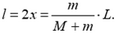
Упражнения

1. Найти среднюю силу, действующую на плиту при абсолютно неупругом столкновении с ней шарика массы m, летящего со скоростью υ в направлении, составляющем с плитой угол α. Время соударения равно τ.

2. С какой силой давит на плечо ручной пулемет при стрельбе, если масса пули m = 10 г, ее скорость при вылете υ = 800 м/сек и скорострельность пулемета n = 600 выстрелов в минуту?

3. Два шарика падают в облаке пыли. Во сколько раз отличаются скорости шариков, если диаметр одного из них вдвое больше диаметра другого?

4. Шарик, летящий горизонтально со скоростью υ, ударяется о тяжелую стальную плиту, движущуюся ему навстречу со скоростью u. С какой скоростью будет двигаться шарик после абсолютно упругого соударения? Силой тяжести пренебречь.

5. Пуля массы m, летящая горизонтально со скоростью υ, попадает в кубик, лежащий на гладком полу, и пробивает его насквозь. Масса кубика М. Скорость пули после вылета равна u. Какая часть первоначальной энергии пули перешла в тепло?

6. При взрыве снаряда массы М = 60 кг образовались три одинаковых осколка. Их общая кинетическая энергия равна E = 2,9 10⁷ Дж. Какую максимальную скорость может иметь один из осколков, если до разрыва снаряд летел со скоростью υ = 800 м/сек?

7. Шарик массы m, летящий со скоростью υ, сталкивается под углом α с кубиком массы М, стоящим на гладком полу (рис. 10). Найти скорость шарика после удара. Удар считать абсолютно упругим.

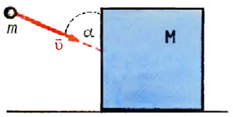
Рис. 10.

8. Шарик массы m, летящий со скоростью υ, составляющей угол α с горизонтом, попадает в покоящуюся платформу с песком массы М (рис. 11) и застревает в песке. Найти скорость платформы.

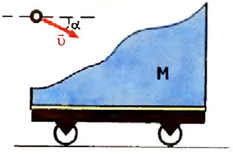
Рис. 11.

Ответы

1. Изменение импульса шарика равно 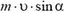. Поэтому

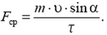
2. 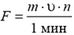= 80 Н.

3. Сила сопротивления, действующая на шарик, пропорциональна площади сечения шарика и квадрату его скорости

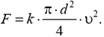
Эта сила растет с увеличением скорости и при некоторой скорости становится равной силе тяжести m·g. После этого скорость шарика не меняется. Так как 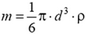 (ρ —плотность шарика), то .

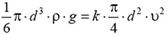Отсюда 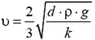. Таким образом, 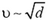. Это означает, что отношение скоростей шариков равно .

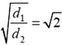То есть скорость шарика с вдвое большим диаметром в 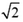 раз больше скорости второго шарика.

4. υ + 2u. Указание. Перейти в систему координат, связанную с плитой. Система шарик — плита не изолированная, так как скорость плиты не меняется.

5. Скорость кубика равна 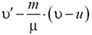. В тепло перешла энергия 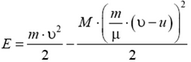. Разделив это выражение на 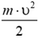, найдем, что в тепло перейдет  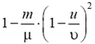часть энергии пули.

6. υ_max ≈ 1500 м/с. Указание. Скорость одного из осколков максимальна, если он будет лететь в направлении полета снаряда, а два других осколка — в противоположную сторону.

7. В вертикальном направлении составляющие скорости шарика 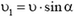 не меняются. В горизонтальном направлении система изолирована. Записав законы сохранения энергии импульса, нетрудно найти, что горизонтальная составляющая скорости шарика будет равна 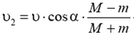. Скорость шарика после столкновения равна

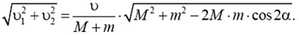
8.

Определение

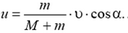
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:

p = mv

Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).

Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).

Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.

Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:

10 г = 0,01 кг

Импульс равен:

p = mv = 0,01∙300 = 3 (кг∙м/с)

Относительный импульс

Определение

Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:

p_1отн2 = m₁v_1отн2 = m₁(v₁ – v₂)

p_1отн2 — импульс первого тела относительно второго, m₁ — масса первого тела, v_1отн2 — скорость первого тела относительно второго, v₁ и v₂ — скорости первого и второго тела соответственно в одной и той же системе отсчета.

Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.

Сначала переведем единицы измерения в СИ:

15 т = 15000 кг

p_1отн2 = m₁(v₁ – v₂) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙10³ (кг∙м/с)

Изменение импульса тела

ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:

∆p = p – p₀ = p + (– p₀)

∆p — изменение импульса тела, p — конечный импульс тела, p₀ — начальный импульс тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар
	Конечная скорость после удара: v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0.
Абсолютно упругий удар
	Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p.
Пуля пробила стенку
	Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v)
Радиус-вектор тела повернул на 180 градусов
	Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
	Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой:

Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.

В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.

Вычисляем:

Второй закон Ньютона в импульсном виде

Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:

Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:

Подставим это выражение во второй закон Ньютона и получим:

Или:

F∆t — импульс силы, ∆p — изменение импульса тела

Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?

Из формулы импульса силы выразим модуль силы:

Реактивное движение

Определение

Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.

Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.

Второй закон Ньютона в импульсном виде:

Реактивная сила:

Второй закон Ньютона для ракеты:

Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.

Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:

V = a∆t

Выразим ускорение из второго закона Ньютона для ракеты:

Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:

Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел

Определение

Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:

Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.

Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:

Закон сохранения импульса

Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:

Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.

Закон сохранения импульса в проекции на горизонтальную ось

Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:

Важно!

При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Неупругое столкновение с неподвижным телом	m1v1 = (m1 + m2)v
Неупругое столкновение движущихся тел	± m1v1 ± m2v2 = ±(m1 + m2)v
В начальный момент система тел неподвижна	0 = m1v’1 – m2v’2
До взаимодействия тела двигались с одинаковой скоростью	(m1 + m2)v = ± m1v’1 ± m2v’2

Сохранение  проекции импульса

В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.

Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.

Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:

m₂v₂ = (m₁ + m₂)v

Отсюда скорость равна:

Алиса Никитина | Просмотров: 19.9k

Лабораторная работа № 2

Тема: Изучение закона сохранения импульса

Цель: экспериментально проверить справедливость закона сохранения импульса тел при прямом упругом соударении

Оборудование: 1. Два металлических шарика разной массы.

                        2. Рама для подвеса шариков.

                        3. Измерительная линейка.

Теория

   Величина, равная произведению массы материальной точки на ее скорость, называется импульсом.

p=mυ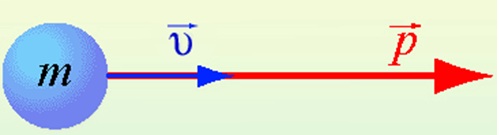  

p — импульс тела

m — масса тела

υ — скорость тела   

   Импульс тела направлен в ту же сторону, что и скорость тела.

   Единицей измерения импульса в СИ является 1 кг·м/с.

   Изменение импульса тела происходит при взаимодействии тел, например, при ударах.

   Для системы материальных точек полный импульс равен сумме импульсов. При этом следует иметь в виду, что импульс – это векторная величина, и поэтому в общем случае импульсы складываются как векторы, т.е. по правилу параллелограмма.

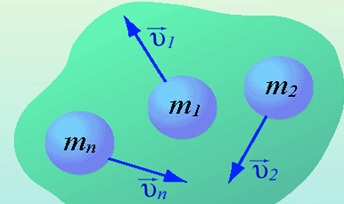
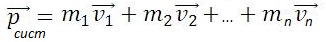
   Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой. Замкнутая система – это система тел, которые взаимодействуют только друг с другом.

   Закон сохранения импульса: в замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.

m₁, m₂ — массы взаимодействующих тел, кг

υ₁, υ₂ — скорости тел до столкновения, м/с

υ’₁, υ’₂ — скорости тел после столкновения, м/с

   Закон сохранения импульса можно сформулировать и так: если на тела системы действуют только силы взаимодействия между ними («внутренние силы»), то полный импульс системы тел не изменяется со временем, т.е. сохраняется. Этот закон применим к системе, состоящей из любого числа тел. Отметим еще раз, что импульс – величина векторная, поэтому сохранение полного импульса означает сохранение не только его величины, но и направления.

   Закон сохранения импульса выполняется при распаде тела на части и при абсолютно неупругом ударе, когда соударяющиеся тела соединяются в одно. Если распад или удар происходят в течение малого промежутка времени, то закон сохранения импульса приближенно выполняется для этих процессов даже при наличии внешних сил, действующих на тела системы со стороны тел, не входящих в нее, т.к. за малое время внешние силы не успевают значительно изменить импульс системы.

   Под ударом в механике понимается кратковременное взаимодейс­твие двух или более тел,  возникающее в результате их соприкосно­вения (соударение шаров, удар молота о наковальню и др.). Самым простым является прямой (центральный) удар, то есть такой удар, при котором скорости соударяющихся тел до удара направлены по линии, соединя­ющей центры тел. При соударении взаимодействие  длится такой короткий промежуток времени (иногда измеряемый тысячными долями секунды) и возни­кают столь большие внутренние силы взаимодействия, что внешними силами можно пренебречь и систему соударяющихся тел можно считать замкнутой и применять к ней закон сохранения импульса.

   В зависимости от упругих свойств тел соударения могут проте­кать весьма различно. Принято выделять два крайних случая: абсо­лютно упругий и абсолютно неупругий удары.

   Абсолютно упругим называется удар, при котором после взаимодействия тела полностью восстанавливают свою форму. Таких ударов в природе не существует, так как всегда часть энергии затрачивается на необратимую деформацию тел. Однако для некоторых  тел, например стальных закаленных шаров, потерями механической энергии при столкновении можно пренебречь и считать удар абсолютно упру­гим. В случае центрального абсолютно упругого удара двух тел с массами m₁, m₂  и скоростями υ₁, υ₂  до удара и υ′₁, υ′₂ после удара можно записать закон сохранения импульса тел:

   Абсолютно неупругим называется удар, при котором после соп­рикосновения тел они не восстанавливают полностью свою форму, со­единяются вместе и движутся как единое целое с одной скоростью. При этом ударе часть их механической энергии переходит в работу деформации тел (внутреннюю энергию). Столкновение двух шаров из пластилина, когда после столкновения шары слипаются и движутся вместе, является примером абсолютно неупругого удара. В случае центрального абсолютно неупругого удара двух тел с массами m₁, m₂  движущихся со скоростями υ₁, υ₂  до удара и υ′ после удара можно записать законы сохранения импульса тел:

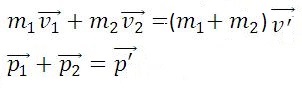
   Закон сохранения импульса служит основой для объяснения обширного круга явлений природы, применяется в различных науках:

1. Закон строго выполняется в явлениях отдачи при выстреле, явлении реактивного движения, взрывных явлениях и явлениях столкновения тел.
2. Закон сохранения импульса применяют: при расчетах скоростей тел при взрывах и соударениях; при расчетах реактивных аппаратов; в военной промышленности при проектировании оружия; в технике – при забивании свай, ковке металлов и т.д

Описание работы

Установка состоит из двух стальных шаров, на длинных подвесах и измерительной линейки под шарами. Центры масс соприкасающихся шарв лежат на одном уровне от точки подвеса. Отведя один из шаров (например, большей массы) в сторону и отпустив его, можно произвести прямой (центральный) удар шаров.

Если до столкновения один из шаров покоился υ₂=0, то выражение закона сохранения импульса упростится. При прямом ударе оба шара после столкновения движутся по одной прямой, поэтому от векторной формы записи закона сохранения импульса можно перейти к алгебраической и учитывая, что после столкновения оба шара движутся в одном направлении, получим:

m₁∙υ₁= m₁∙υ′₁ + m₂∙υ′₂ 

   

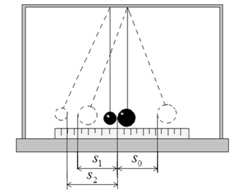
   рис. 2

   Для определения скорости первого шара υ₁ до удара  и скоростей шаров υ′₁ и υ′₂ после удара воспользуемся законом сохранения механической энергии. Потенциальная энергия шара в положении максимального отклонения равняется его кинетической энергии при ударе 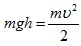, отсюда .

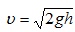   Высоту подъёма шара можно определить по его максимальному отклонению s от положения равновесия (рис.3,а).

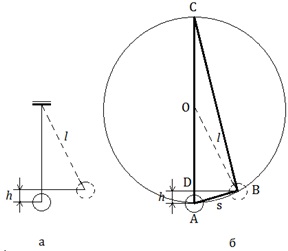
рис. 3

Треугольник АВС прямоугольный (опирается на диаметр). Катет АВ является средней пропорциональной величиной между гипотенузой АС=2l и своей проекцией на гипотенузу АD  (рис.3,б):  АВ²=АС·AD то есть 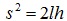, откуда 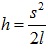. Следовательно, величины скоростей можно выразить так: 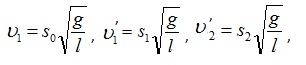где S₀,  S₁ – максимальные отклонения первого шара до и после удара; S₂ – максимальное отклонение второго шара после удара.

Запишем уравнение закона сохранения через выражения скоростей:

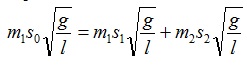  или  m₁∙S₀= m₁∙S₁ + m₂∙S₂.

Таким образом, проверка закона сохранения импульса в данной работе сводится к проверке справедливости последнего уравнения.

 При малых углах отклонения шара от положения равновесия S₀,  S₁ и S₂ можно заменить соответствующими величинами, отсчитанными по горизонтальной шкале.

Выполнение работы.

1. Перенесите рисунок 2 в отчет по работе.

2. Подготовьте в тетради таблицу для записи результатов измерений и вычислений:

№	m1, г	m2, г	S0, мм	S1, мм	S2, мм	m1∙S0, г∙мм с	m1∙S1, г∙мм с	m2∙S2, г∙мм с	m1∙S1 + m2∙S2, г∙мм с
1
2
3

3. Определите массы шаров m₁ и m₂. Запишите их результат в таблицу.

4. Отрегулируйте подвеску шаров так, чтобы их центры и точка касания находились на одной горизонтальной линии.

5. Отклоните шар большей массы на 3 см от положения расновесия (S₀) и затем отпустите его. Заметьте максимальное отклонение шара большей массы после удара (S₁). Повторите опыт 5 раз и найдите среднее значение отклонения S_1ср. Запишите его в таблицу (S₁).

6. Повторите опыт, но теперь заметьте после удара максимальное отклонение шара с меньшей массой (S₂). Повторите опыт 5 раз, и найдите среднее значение отклонения S_2ср. Запишите его в таблицу (S₂).

7. Повторите опыт, отклоняя шар большей массы на 4 см и 5 см. Результаты измерений запишите в таблицу.

8. Используя значения S₀, S₁ и S₂, вычислите импульс шара до удара m₁∙S₀ и сумму импульсов шаров после удара  m₁∙S₁ + m₂∙S₂ и внесите в таблицу их результаты.

9. Сравните импульс шара до удара с суммой импульсов шаров после удара. Запишите вывод по полученным результатам работы.

10. Ответьте на контрольные вопросы.

Контрольные вопросы

1. Что называется импульсом материальной точки? По какой формуле он находится? В каких единицах он измеряется?

2. Импульс – величина векторная или скалярная?

3. Запишите формулу и формулировку закона сохранения импульса.

4. При каких условиях выполняется закон сохранения импульса?

5. Какое соударение называется абсолютно упругим?

6. Для каких видов соударений выполняется закон сохранения импульса?

Вариант выполнения измерений.

1. Определяем массы шариков m₁ и m₂  при помощи динамометра (или весов) и записываем в таблицу:

m₁=62 г

m₂=27,5 г

2. Отклоняем большой шар от положения расновесия на 3 см и отпускаем его. 

S₀=3 см=30 мм

Замечаем его максимальное отклонение после удара. Повторяем опыт 5 раз, находим среднее значение отклонения и записываем в таблицу S_1ср.

S₁=13мм   S₁=15мм   S₁=18мм    S₁=14мм   S₁=16мм

S_1ср=(13мм+15мм+18мм+14мм+16мм)/5=15,2 мм

3. Повторяем этот же опыт, но теперь замечаем после удара отклонение шара меньшей массы. Повторяем опыт 5 раз, находим среднее значение и записываем в таблицу S_2ср.

S₂=31мм   S₂=34мм   S₂=36мм    S₂=35мм   S₂=32мм

S_2ср=(31мм+34мм+36мм+35мм+32мм)/5=34мм

4. Повторяем опыт, отклоняя шар большей массы на 4 см и 5 см. 

S₀=4 см=40 мм

S₁=18 мм   S₁=19 мм   S₁=23 мм    S₁=22 мм   S₁=18 мм

S_1ср=(18 мм+19 мм+23 мм+22 мм+18 мм)/5=20 мм

S₂=43 мм   S₂=44 мм   S₂=46 мм    S₂=47 мм   S₂=45 мм

S_2ср=(43 мм + 44 мм + 46 мм + 47 мм + 45 мм)/5=45 мм

S₀=5 см=50 мм

Результаты измерений записываем в таблицу.

№	m1, г	m2, г	S0, мм	S1, мм	S2, мм	m1∙S0, г∙мм с	m1∙S1, г∙мм с	m2∙S2, г∙мм с	m1∙S1 + m2∙S2, г∙мм с
1	62,0	27,5	30	15	34
2	62,0	27,5	40	20	45
3	62,0	27,5	50	25	56