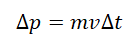Как найти изменение импульса за четверть периода

Спрятать решение

Источник: Рым­ке­вич А. П. Сбор­ник задач по фи­зи­ке для 9−11 клас­сов, М.: «Про­све­ще­ние», 1990 (322)

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Материальная точка массой 1 кг равномерно движется по окружности со скоростью 10 м/с. Найти изменение импульса за одну четверть периода; половину периода; период

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,857
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Импульс тела, закон сохранения импульса

теория по физике 🧲 законы сохранения

Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:

Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).

Направление импульса всегда совпадает с направлением скорости ( p ↑↓ v ), так как масса — всегда положительная величина (m > 0).

Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.

Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:

p = mv = 0,01∙300 = 3 (кг∙м/с)

Относительный импульс

Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:

p _1отн2— импульс первого тела относительно второго, m₁ — масса первого тела, v _1отн2 — скорость первого тела относительно второго, v ₁и v ₂ — скорости первого и второго тела соответственно в одной и той же системе отсчета.

Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.

Сначала переведем единицы измерения в СИ:

Изменение импульса тела

∆ p — изменение импульса тела, p — конечный импульс тела, p ₀ — начальный импульс тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар

Конечный импульс тела:

Модуль изменения импульса тела равен модулю его начального импульса:

Абсолютно упругий удар

Модули конечной и начальной скоростей равны:

Модули конечного и начального импульсов равны:

Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:

Пуля пробила стенку

Модуль изменения импульса тела равен разности модулей начального и конечного импульсов:

Радиус-вектор тела повернул на 180 градусов

Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:

Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали

Модули конечной и начальной скоростей равны:

Модули конечного и начального импульсов равны:

Угол падения равен углу отражения:

Модуль изменения импульса в этом случае определяется формулой:

Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.

В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.

Вычисляем:

Второй закон Ньютона в импульсном виде

Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:

Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:

Подставим это выражение во второй закон Ньютона и получим:

F ∆t — импульс силы, ∆ p — изменение импульса тела

Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?

Из формулы импульса силы выразим модуль силы:

Реактивное движение

Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.

Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.

Второй закон Ньютона в импульсном виде:

Второй закон Ньютона для ракеты:

Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.

Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:

Выразим ускорение из второго закона Ньютона для ракеты:

Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:

Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел

Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:

Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.

Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:

Закон сохранения импульса

Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.

Закон сохранения импульса в проекции на горизонтальную ось

Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:

• положителен, если его направление совпадает с направлением оси ОХ;
• отрицателен, если он направлен противоположно направлению оси ОХ.

При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Неупругое столкновение с неподвижным телом	m1v1 = (m1 + m2)v
Неупругое столкновение движущихся тел	± m1v1 ± m2v2 = ±(m1 + m2)v
В начальный момент система тел неподвижна	0 = m1v’1 – m2v’2
До взаимодействия тела двигались с одинаковой скоростью	(m1 + m2)v = ± m1v’1 ± m2v’2

Сохранение проекции импульса

В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.

Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.

Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:

Отсюда скорость равна:

Импульс частицы до столкновения равен − p ₁, а после столкновения равен − p ₂, причём p₁ = p, p₂ = 2p, − p ₁⊥ − p ₂. Изменение импульса частицы при столкновении Δ − p равняется по модулю:

Алгоритм решения

Решение

Запишем исходные данные:

Так как угол α = 90 о , вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:

Δ p = √ p 2 1 + p 2 2

Подставим известные данные:

Δ p = √ p 2 + ( 2 p ) 2 = √ 5 p 2 = p √ 5

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно

б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено

в) в интервалах 0–1 и 1–2 двигалось равномерно

г) в интервалах 0–1 и 1–2 двигалось равноускорено

Четверть числовой окружности

Если посмотреть на числовую окружность , то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).

(() (frac<3π><2>) (;2π)) – четвертая четверть

Почему так важно определять какой четверти принадлежит угол?

Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций .

Например, для любого угла из второй четверти – синус положителен, а косинус , тангенс и котангенс отрицательны. А для любого угла из первой четверти – все четыре функции будут положительны.

Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.

Пример (ЕГЭ):

Нам известен косинус, а найти нужно синус того же угла. Какая тригонометрическая формула связывает синус и косинус того же угла?
Основное тригонометрическое тождество. Запишем его.

Подставим известное, и проведем вычисления.

Про непостоянство четвертей:

Важно понимать, что, например, первой четверти принадлежат не только углы от (0) до (frac<π><2>) , но и углы от (2π) до (frac<5π><2>) , и от (4π) до (frac<9π><2>) , и от (6π) до (frac<13π><2>) и так далее. Ведь как только мы заканчиваем полный оборот – кончается четвертая четверть и опять начинается первая.

Кроме того, нужно помнить, что углы могут откладываться в отрицательную сторону (по часовой стрелке), и тогда мы попадем в первую четверть только в конце круга. Ведь сначала мы пройдем четвертую четверть, потом в третью и т.д.