Материальная точка массой 1 кг равномерно движется по окружности со скоростью 10 м/с. Найти изменение импульса за одну четверть периода; половину периода; период.
Спрятать решение
Решение.
Изобразим вектора скорости через четверть периода, половину периода и период (см. рис. слева).
Изменение импульса в векторном виде:
Изменение импульса через четверть периода равно (см. рис. справа)
Изменение импульса через половину периода равно
Изменение импульса через период равно
Ответ: 14 кг · м/с; 20 кг · м/с; 0.
Источник: Рымкевич А. П. Сборник задач по физике для 9−11 классов, М.: «Просвещение», 1990 (322)
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,651 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,896 -
разное
16,900
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Download Article
Learn the change in momentum formulas, plus when and how to use them
Download Article
- Change in Momentum Formulas
- How to Calculate Change in Momentum
- Example Problems
- Tips
|
|
|
Studying for a physics test? Or just trying to wrap your brain around change in momentum? You’re definitely not alone. Momentum is a pretty weird concept in science. Think of it as a measurement of “mass in motion.”[1]
The more massive something is, or the faster it moves, the more momentum it has. Change the speed or apply a force, and the momentum changes too. But if you want to calculate that change, you’ll need to know which formula to use. To make this easier, we’ve prepared a guide to finding the change in momentum. Keep reading for a crystal-clear breakdown, plus some example problems to help you ace that next test.
Things You Should Know
- The change in momentum can be calculated using two possible formulas: Δp = m(Δv) and Δp = F(Δt).[2]
- The formula Δp = m(Δv) tells us that the change in momentum (Δp) is equal to mass (m) multiplied by change in velocity (Δv).[3]
- The formula Δp = F(Δt) tells us that the change in momentum (Δp) is equal to the force applied to an object (F) multiplied by the total time the force was applied (Δt).[4]
- Use Δp = m(Δv) when you’re given mass (in kg) and velocities (in m/s). Use Δp = F(Δt) when you’re given a force (in Newtons, or “N”) and time (in seconds).
-

1
Formula #1: Δp = m(Δv) The change in momentum (Δp) is equal to mass (m) multiplied by change in velocity (Δv). Use this formula when you know the mass of an object, as well as the velocity it gained or lost.[5]
- The change in momentum (Δp) is expressed in kg m/s (kilogram meters per second).
- The mass is expressed in kg.
- The change in velocity is expressed in m/s (meters per second).
- Δv can also be expressed as vf – vi where vf = the object’s final velocity and vi = the object’s initial (or starting) velocity. Therefore, you might see the equation Δp = m(Δv) represented as Δp = m(vf – vi).
-

2
Formula #2: Δp = F(Δt) The change in momentum (Δp) is equal to the force applied to an object (F) multiplied by the total time the force was applied (Δt). Use this formula when you know the force applied to an object, as well as how long the force was applied.[6]
- The change in momentum (Δp) is expressed in kg m/s (kilogram meters per second).
- The force (F) is expressed in Newtons. In most cases, Newtons are abbreviated as “N”.
- The amount of time the force was applied (Δt) is expressed in seconds.
- Δt is also called the “time interval.”
Advertisement
-

1
Using Δp = m(Δv) Let’s say a 10 kg object accelerates from 10 m/s to 30 m/s. We know the mass (m) = 10 kg. To find the change in velocity (Δv), we subtract the final speed from the starting speed. Since 30 m/s – 10 m/s = 20 m/s, we know that Δv = 20 m/s. This means that Δp = 10 kg * 20 m/s. Therefore, Δp = 200 kg m/s.
- We knew to use the formula Δp =m(Δv) because we were provided with mass (in kg) and velocities (in m/s).
- Remember that the change in momentum (Δp) is always expressed in kg m/s.
-

2
Using Δp = F(Δt) Let’s say that a force of 12 Newtons is applied to an object for 45 seconds. We know that F = 12 N, and Δt = 45 s. This means that Δp = 12 N * 45 s. Therefore, Δp = 540 kg m/s.
- We knew to use the formula Δp = F(Δt) because we were provided with the Force (in N) and time (in seconds).
- The change in momentum (Δp) is always expressed in kg m/s, regardless of which formula you use.
Advertisement
-

1
Example 1: A stationary 55 kg sled is pushed down a hill until it reaches 11 m/s. What is the change in the sled’s momentum? Which formula should you use to calculate it?
- Since we were provided with mass and velocity, we should use the formula Δp = m(Δv).
- We know that m = 55kg.
- Because the sled was stationary when it began moving, we know that it accelerated from 0 m/s to 11 m/s. This means that Δv = 11 m/s – 0 m/s. Therefore, Δv = 11 m/s.
- We can now plug in the values for m and Δv into the formula: Δp = 55 kg * 11 m/s, which equals 605 kg m/s.
- Therefore, the sled’s change in momentum is 605 kg m/s.
-

2
Example 2: A rocket engine ignites and burns for 45 s, applying a force of 3 million N to a spacecraft. What’s the change in the rocket’s momentum? Which formula should you use?
- Since we’re provided with a force and a time, we should use the formula Δp = F(Δt).
- We know the force was 3,000,000 N.
- Because the rocket engine only applies a force while it’s burning, we know that the force was applied to the spacecraft for a total of 45 of seconds.
- We can now plug in the values for F and Δt into the formula: Δp = 3,000,000 N * 45 s, which equals 135,000,000 kg m/s.
- Therefore, the change in the rocket’s momentum is 135,000,000 kg m/s (or 1.35*10^8 kg m/s).
-

3
Example 3: A 14,000 kg aircraft accelerates from 200 m/s to 550 m/s. What’s the aircraft’s change in momentum?
- Because we have mass and velocity, we should use Δp =m(Δv).
- We know the mass is 14,000 kg.
- Because the plane accelerated from 200 m/s to 550 m/s, we know that Δv = 550 m/s – 200 m/s. Therefore, Δv = 350 m/s. In other words, the aircraft’s change in velocity is 350 m/s.
- Plugging in these values gives us Δp = 14,000 kg * 350 m/s, which equals 4,900,000 kg m/s.
- Therefore, the aircraft’s change in momentum is 4,900,000 kg m/s.
-

4
Example 4: A scientist observes a boat sitting in a lake. After 25 seconds, the boat’s engine begins applying a force of 400 N, accelerating the boat. When the engine stops, the scientist notes that they had observed the boat for a total of 60 seconds. What is the boat’s change in momentum?
- Because we’re provided with a force and a time, we should use the formula Δp = F(Δt).
- We know F = 400 N.
- We know that the scientist observed the boat for a total of 60 s. However, the boat’s engine did not begin applying a force until 25 s had passed. Therefore, to find the time that the force was actually applied (Δt), we need to find the difference between 60 s and 25 s. Δt = 60 s – 25 s. Therefore, Δt = 35 s. In other words, the force was applied to the boat for a total of 35 seconds.
- Plugging in the values for F and Δt into our formula, Δp = F(Δt), we know that Δp = 400 N * 35 s, which equals 14,000 kg m/s.
- Therefore, the boat’s change in momentum is 14,000 kg m/s.
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
When learning about momentum, you might encounter the concept of “Impulse,” defined as Force applied over time, represented by the value J. J = Δp. Because J and Δp have the same value, J can also be calculated using J = m(Δv) or Δp = F(Δt). Impulse and change in momentum have the same value and are both expressed in kg m/s (kilogram meters per second). You’ll encounter impulse again in future physics courses, where its distinction from change in momentum will be explained in greater detail.[7]
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Thanks to all authors for creating a page that has been read 6,066 times.
Did this article help you?
Get all the best how-tos!
Sign up for wikiHow’s weekly email newsletter
Subscribe
You’re all set!
Excelsior
Просветленный
(43602)
7 лет назад
Прежде всего: импульс — это ВЕКТОР. Изменение импульса — это разность конечного и начального импульсов, то есть тоже вектор.
За полный период изменение импульса будет равно нулю, так как начальный и конечный векторы одинаковы. За половину периода изменение импульса будет ПО МОДУЛЮ равно 2 mv и направлено туда же, куда и конечный импульс (потому что конечный и начальный импульсы направлены в противоположные стороны). Изменение импульса за четверть периода посчитать чуть-чуть сложнее, потому что конечный и начальный импульсы направлены под прямым углом друг к другу. Нарисуйте картинку и найдите разность векторов. Она будет гипотенузой в прямоугольном треугольнике, в котором конечный и начальный импульсы являются катетами. Справитесь?
Roman Petrov
Мудрец
(18248)
7 лет назад
Импульс меняет только направление. Момент импульса постоянен, если диссипации нет.
Для любой прямой x, проходящей через центр окружности и пересекающейся с ней, проекция импульса p на прямую x меняется по закону px(t)=mv*cos(2pi*t/T). От -mv до +mv.
Карен Гуюмджян
Просветленный
(40977)
7 лет назад
СОН!
Думаю.., вот-вот и поймаю..,
Думаю.., вот-вот и найду;
Как будто во сне обнимаю
Как будто поняв – упаду.
Но страх меня гонит куда-то,
Взвивая все мысли в крови…
Ищет, но где же лопата,
В руках или всё же в любви?
И внутренний голос собою…
Повторяя говорит – не суди;
Мы едины с твоею судьбою,
На правильном скажу ты пути!
И вдруг вдохновенье лопатой,
Трансформирует пар в облака;
Говорит мне: Карен ты не падай,
Гумно – это тоже рука.
Думаю.., вот-вот и поймаю,
Думаю.., вот-вот и найду;
Я истину во сне обнимаю,
Я истинной ко всем вам приду!
Erleker
Профи
(846)
7 лет назад
За 1/4 периода точка пройдет 1/4 окружности, то есть повернется на 90 градусов.
Изначально (если считать что точка была наверху) вектор импульса был направлен горизонтально, а затем стал вертикальным. Если в координатах (оси вертикальные и горизонтальные):
P1=m *v1 (векторно) =m*(v,0)=(mv,0)
P2=(0,mv)
Разность векторов:
ΔP=P2-P1=(0,mv)-(mv,0)=(-mv,mv)
Модуль вектора разности (видимо его и надо найти) соответственно:
lΔPl=√((ΔP)^2),где
(ΔP)^2=(-mv)^2+(mv)^2=2m^2 * v^2
Получается:
lΔPl=√2mv (а не 2mv)
Подставляем:
√2mv=√20 кг * м/с=4.47м/c (приблизительно)
Ответ: 4.47м/с
Можно и по-другому оформить: перенести два вектора в одну точку (по рисунку) и достроить до параллелограмма (в данном случае получится квадрат) и их вектор разности по правилу будет диагональю и по тереме Пифагора его модуль получится тоже lΔPl=√2mv.
Надеюсь, что объяснил толково:)
Если на тело массой m за определенный промежуток времени Δt действует сила F→, тогда следует изменение скорости тела ∆v→=v2→-v1→. Получаем, что за время Δt тело продолжает движение с ускорением:
a→=∆v→∆t=v2→-v1→∆t.
Основываясь на основном законе динамики, то есть втором законе Ньютона, имеем:
F→=ma→=mv2→-v1→∆t или F→∆t=mv2→-mv1→=m∆v→=∆mv→.
Изменение импульса
Импульс тела, или количество движения – это физическая величина, равная произведению массы тела на скорость его движения.
Импульс тела считается векторной величиной, которая измеряется в килограмм-метр в секунду (кг м/с).
Импульс силы – это физическая величина, равняющаяся произведению силы на время ее действия.
Импульс относят к векторным величинам. Существует еще одна формулировка определения.
Изменение импульса тела равняется импульсу силы.
При обозначении импульса p→ второй закон Ньютона записывается как:
F→∆t=∆p→.
Данный вид позволяет формулировать второй закон Ньютона. Сила F→ является равнодействующей всех сил, действующих на тело. Равенство записывается как проекции на координатные оси вида:
FxΔt=Δpx; FyΔt=Δpy; FzΔt=Δpz.
Рисунок 1.16.1. Модель импульса тела.
Изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось.
Одномерное движение – это движение тела по одной из координатный осей.
На примере рассмотрим свободное падение тела с начальной скоростью v0 под действием силы тяжести за промежуток времени t. При направлении оси OY вертикально вниз импульс силы тяжести Fт=mg, действующий за время t, равняется mgt. Такой импульс равняется изменению импульса тела:
Fтt=mgt=Δp=m(v–v0), откуда v=v0 + gt.
Запись совпадает с кинематической формулой определения скорости равноускоренного движения. По модулю сила не изменяется из всего интервала t. Когда она изменяема по величине, тогда формула импульса требует подстановки среднего значения силы Fср из временного промежутка t. Рисунок 1.16.2 показывает, каким образом определяется импульс силы, которая зависит от времени.
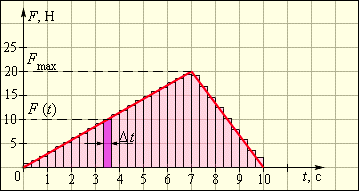
Рисунок 1.16.2. Вычисление импульса силы по графику зависимости F(t)
Необходимо выбрать на временной оси интервал Δt, видно, что сила F(t) практически неизменна. Импульс силы F(t)Δt за промежуток времени Δt будет равняться площади заштрихованной фигуры. При разделении временной оси на интервалы на Δti на промежутке от от 0 до t, сложить импульсы всех действующих сил из этих промежутков Δti, тогда суммарный импульс силы будет равняться площади образования при помощи ступенчатой и временной осей.
Применив предел (Δti→0), можно найти площадь, которая будет ограничиваться графиком F(t) и осью t. Использование определения импульса силы по графику применимо с любыми законами, где имеются изменяющиеся силы и время. Данное решение ведет к интегрированию функции F(t) из интервала [0; t].
Рисунок 1.16.2 показывает импульс силы, находящийся на интервале от t1=0 с до t2=10.
Из формулы получим, что Fср(t2-t1)=12Fmax(t2-t1)=100 Н·с=100 кг·м/с.
То есть, из примера видно Fср=12Fmax=10 Н.
Определение средней силы
Имеются случаи, когда определение средней силы Fср возможно при известных времени и данных о сообщенном импульсе. При сильной ударе по мячу с массой 0,415 кг можно сообщить скорость, равную v=30 м/с. Приблизительным временем удара является значение 8·10–3 с.
Тогда формула импульса приобретает вид:
p=mv=12,5 кг·м/с.
Чтобы определить среднюю силу Fср во время удара, необходимо Fср=p∆t=1,56·103 Н.
Получили очень большое значение, которое равняется телу массой 160 кг.
Когда движение происходит по криволинейной траектории, то начальное значение p1→ и конечное
p2→ могут быть различны по модулю и по направлению. Для определения импульса ∆p→ применяют диаграмму импульсов, где имеются векторы p1→ и p2→, а ∆p→=p2→-p1→ построен по правилу параллелограмма.
Для примера приводится рисунок 1.16.2, где нарисована схема импульсов мяча, отскакивающего от стены. При подаче мяч с массой m со скоростью v1→ налетает на поверхность под углом α к нормали и отскакивает со скоростью v2→ с углом β. При ударе в стену мяч подвергался действию силы F→, направленной также, как и вектор ∆p→.
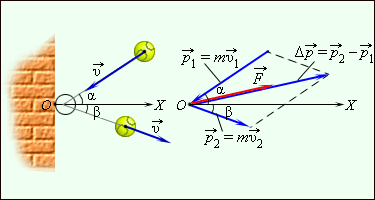
Рисунок 1.16.3. Отскакивание мяча от шероховатой стенки и диаграмма импульсов.
Если происходит нормальное падение мяча с массой m на упругую поверхность со скоростью v1→=v→, тогда при отскоке она изменится на v2→=-v→. Значит, за определенный промежуток времени импульс изменится и будет равен ∆p→=-2mv→. Используя проекции на ОХ, результат запишется как Δpx=–2mvx. Из рисунка 1.16.3 видно, что ось ОХ направлена от стенки, тогда следует vx<0 и Δpx>0. Из формулы получим, что модуль Δp связан с модулем скорости, который принимает вид Δp=2mv.
