Как найти изменение массы газа

1. Внутренняя энергия газа

Из курса физики основной школы вы знаете, что сумму кинетической энергии хаотического движения частиц и потенциальной энергии их взаимодействия называют внутренней энергией.

Внутренняя энергия U данной массы одноатомного идеального газа равна произведению средней кинетической энергии 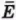одной молекулы на число молекул N:

U = 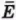N.

? 1. Объясните, почему внутренняя энергия U данной массы одноатомного идеального газа выражается формулой

Итак, внутренняя энергия идеального газа определяется только его абсолютной температурой и числом молекул в нем.

? 2. Объем одного моля газа при температуре 20 ºС и нормальном атмосферном давлении составляет 24 л.
а) Чему равна внутренняя энергия этого газа, если он одноатомный и его можно считать идеальным?
б) На какую высоту можно было бы забросить мяч массой 365 г, если бы можно было сообщить ему такую кинетическую энергию и пренебречь сопротивлением воздуха?

Выполнив это задание, вы сможете представить, как велика внутренняя энергия тела. Объясняется это тем, что скорость хаотического движения молекул в десятки и сотни раз превышает скорости движения окружающих нас тел. А кинетическая энергия пропорциональна квадрату скорости. Поэтому при увеличении скорости в 10 раз кинетическая энергия увеличивается в 100 раз, а при увеличении скорости в 100 раз кинетическая энергия увеличивается в 10 000 раз.

Внутреннюю энергию идеального одноатомного газа можно выразить также через его давление p и объем V.

? 3. Объясните, почему внутренняя энергия U данной массы одноатомного идеального газа выражается формулой

U = (3/2)pV.     (2)

Подсказка. Воспользуйтесь формулой (1) и уравнением состояния идеального газа.

? 4. Из формулы (1) следует, что внутренняя энергия одного моля газа зависит только от его абсолютной температуры и количества вещества (числа молекул). А из формулы (2) следует, что она зависит от давления и объема, но зато не зависит от количества вещества. Объясните, почему тут нет противоречия.

? 5. Ширина класса 5 м, длина 10 м, а высота – 4 м. Температура воздуха 20 ºС, давление равно нормальному атмосферному давлению.
а) Чему была бы равна внутренняя энергия газа, заполняющего класс, если бы он был одноатомным? (Воздух состоит в основном из двухатомных молекул. Как показывает расчет, выходящий за рамки нашего курса, внутренняя энергия двухатомного газа при тех же макроскопических параметрах в 5/3 раза больше, чем внутренняя энергия одноатомного газа.)
б) На какую высоту можно было бы поднять автомобиль массой 1 т, затратив такую энергию?
в) Есть ли в условии лишние данные?

Результаты выполнения этого задания раскроют, какая огромная энергия «окружает» каждого из нас! А ведь мы ее практически не замечаем, считая воздух «пустотой».

Большую внутреннюю энергию имеют, конечно, и другие тела. Например, внутренняя энергия литра кипятка больше внутренней энергии того же литра воды при комнатной температуре на величину, равную работе, которую надо совершить для того, чтобы поднять легковой автомобиль на двенадцать этажей!

При изучении тепловых явлений мы учитываем только кинетическую энергию хаотического движения молекул и потенциальную энергию их взаимодействия. А ведь есть еще и во много раз большая энергия взаимодействия частиц в атомных ядрах. Вы знаете о ней из курса физики основной школы. К ядерной физике мы вернемся в 11-м классе.

Соотношение между различными видами энергии, которыми обладает данное тело, схематически представлено на рисунке 42.1. Мы видим, что непосредственно наблюдаемая механическая энергия составляет лишь очень малую долю всей энергии тела. Соблюсти масштаб на этом рисунке невозможно, потому что тепловая внутренняя энергия в тысячи раз больше механической, а ядерная – в миллионы раз больше тепловой.

Два способа изменения внутренней энергии

Из курса физики основной школы вы знаете, что внутреннюю энергию тела можно изменить двумя способами:

• совершая работу над телом – например, сжимая газ (рис. 42.2, а);
• посредством теплопередачи, то есть без совершения работы, – например, при контакте с более горячим телом (рис. 42.2, б). (Теплопередачу называют иногда также теплообменом.)

Напомним, что меру изменения внутренней энергии при теплопередаче называют количеством теплоты и обозначают Q. Количество теплоты измеряют в джоулях.

Как мы знаем, внутренняя энергия данной массы идеального газа определяется только его температурой и числом молекул. Поэтому при постоянном числе молекул изменить внутреннюю энергию идеального газа можно только изменив его температуру.

Например, при сжатии газа в теплоизолированном сосуде газ нагревается вследствие того, что над ним производят работу. Нагревание газа может быть при атом весьма заметным.

Поставим опыт

Поместим кусочек сухой ваты в толстостенный прозрачный цилиндр и быстро (резким толчком) вдвинем в цилиндр поршень (рис. 42.3).

Воздух в цилиндре нагреется так сильно, что вата воспламенится.

Нагревание газа при сжатии используют в дизельных двигателях: при сжатии горючая смесь в цилиндре нагревается настолько, что воспламеняется без искры.

Газовый процесс, который происходит в теплоизолированном сосуде, то есть без теплопередачи, называют адиабатным. Адиабатным можно считать также процесс, когда тепло- передачей можно пренебречь: например, если процесс происходит за время, в течение которого не успевает произойти теплообмен с окружающей средой.

При адиабатном расширении газ охлаждается. По этой причине, например, образуются облака. Поднимающийся влажный воздух попадает в более разреженные слои атмосферы, расширяется и вследствие этого охлаждается. Как мы увидим далее, при охлаждении ниже определенной температуры (точки росы) содержащийся в воздухе водяной пар конденсируется: образуются капельки тумана, из которого и состоят облака.

Увеличить или уменьшить температуру газа можно, конечно, и посредством теплопередачи. Например, сосуд с газом можно поместить над огнем, в кипящую воду или в морозильную камеру.

? 6. Изменяется ли, н если да, то как внутренняя энергия данной массы идеального газа:
а) при изотермическом расширении? сжатии?
б) при изобарном расширении? сжатии?
в) при изохорном охлаждении? нагревании?
г) при адиабатном сжатии? расширении?

2. Первый закон термодинамики

Итак, внутренняя энергия газа U может изменяться как вследствие того, что ему сообщают количество теплоты Q, так и потому, что внешние силы совершают работу A над газом.

Согласно закону сохранения энергии

изменение внутренней энергии газа ∆U равно сумме количества теплоты Q, переданного газу, и работы A, совершенной над газом:

∆U = Q + A.     (3)

Закон сохранения энергии применительно к тепловым явлениям называют первым законом термодинамики. (Термодинамикой называют раздел физики, изучающий общие законы тепловых явлений.)

Как Q, так и A могут быть положительными, отрицательными или равными нулю. Если газ сжимают, то A > 0, а если он расширяется, то A < 0. Если объем газа не изменяется, то A = 0. Если газу передают некоторое количество теплоты, то Q > 0, а если газ отдает некоторое количество теплоты, то Q < 0.

В практических расчетах и при решении многих задач часто используют другую формулировку первого закона термодинамики. Дело в том, что при рассмотрении тепловых двигателей главный интерес представляет работа, совершенная самим газом (то есть силой давления, действующей со стороны газа на поршень; при расширении газа работа газа положительна).

Обозначим работу газа A_г. Она связана с работой A, совершенной внешними силами над газом, соотношением

A_г = –A.

При сжатии газа A > 0, A_г < 0; а при расширении газа A < 0, A_г > 0.

Используя понятие работы газа, первый закон термодинамики формулируют так:

количество теплоты, переданное газу, равно сумме изменения внутренней энергии газа и работы, совершенной газом:

Q = ∆U + A_г.     (4)

Чтобы использовать соотношения (3) и (4) на практике, надо уметь находить выражения для изменения внутренней энергии газа и работы газа (или работы внешних сил).

Как найти изменение внутренней энергии газа?

Для одноатомного идеального газа внутренняя энергия выражается формулой (1), поэтому для изменения ∆U внутренней энергии получаем:

∆U = (3/2)νR∆T.     (5)

Здесь ∆T = T₂ – T₁, ∆U = U₂ – U₁, а индексами 1 и 2 обозначены соответственно начальное и конечное состояния газа.

? 7. Начальная температура пяти молей гелия 100 ºС. Газ нагрели на 50 ºС.
а) Насколько увеличилась внутренняя энергия газа?
б) Есть ли в условии лишние данные?

Изменение внутренней энергии одноатомного идеального газа можно найти и с помощью формулы (2):

∆U = (3/2)∆(pV).     (6)

Здесь ∆(pV) – изменение произведения давления на объем. Например, при переходе газа из состояния 1 в состояние 2

∆(pV) = p₂V₂ – p₁V₁.     (7)

? 8. Чему равно изменение внутренней энергии одного моля одноатомного идеального газа:
а) при изобарном расширении, если давление газа равно p₀, а объем газа увеличился от V₀ до 3V₀?
б) при изохорном охлаждении, если объем газа равен V₀, а давление газа уменьшилось от p₀ до 0,5p₀?
в) в процессе, в котором начальные давление и объем газа равны p₀ и V₀, а конечные равны 2p₀ и 3V₀?
Есть ли в условии лишние данные?

Важным достоинством формулы (6) является то, что в нее не входят ни количество вещества в газе, ни его масса. Поэтому, например, если давление и объем газа остались неизменными, то не изменилась и внутренняя энергия газа, хотя при этом могла измениться его масса. Рассмотрим пример, в котором речь идет о воздухе, который состоит в основном из двух- атомных молекул. Их средняя кинетическая энергия при заданной температуре больше, чем у одноатомных молекул (двухатомные молекулы обладают еще кинетической энергией вращательного движения). Однако для выполнения следующего задания то, что воздух состоит из двухатомных молекул, несущественно.

? 9. До включения отопления температура воздуха в комнате объемом 60 м³ была равна 15 ºС. После включения отопления воздух нагрелся до 20 ºС. Давление воздуха постоянно и равно 10⁵ Па.
а) На сколько процентов увеличилась средняя кинетическая энергия молекул в воздухе?
б) Как изменилась внутренняя энергия воздуха в комнате?
в) На сколько процентов изменилась концентрация молекул воздуха?
г) Насколько изменилась масса воздуха в комнате?

Как найти совершенную газом работу?

Рассмотрим сначала изобарное расширение газа в цилиндре под поршнем (рис. 42.4). Газ давит на поршень с силой F = pS, где p – давление газа, S – площадь поршня.

Если поршень переместился на ∆x, то совершенная газом работа A_г = F * ∆x = pS * ∆x. Так как S * ∆x = ∆V, получаем, что при изобарном расшинерии работа газа выражается формулой

A_г = p * ∆V.     (8)

? 10. Используя рисунок 42.5, объясните, почему работа газа численно равна площади фигуры под графиком зависимости p(V).

Это свойство графика зависимости p(V) сохраняется и тогда, когда давление газа изменяется.

Пусть, например, график зависимости p(V) имеет вид, изображенный на рисунке 42.6. Процесс расширения газа мысленно разобьем на большое число этапов, в каждом из которых объем газа изменяется настолько мало, что его давление можно считать практически постоянным. Поскольку для каждого этапа работа газа численно равна площади под соответствующим участком графика, то и вся работа, совершенная газом при расширении, равна площади под всем графиком p(V).

? 11. Один моль идеального газа можно перевести из состояния 1 в состояние 2 многими способами. Рассмотрим процессы, которым соответствуют графики а и б (рис. 42.7).
а) В каком случае совершенная газом работа больше? Во сколько раз больше?
б) В каком случае изменение внутренней энергии газа больше? Во сколько раз больше?
в) В каком случае переданное газу количество теплоты больше? Во сколько раз больше?

На примере этого задания вы могли заметить, что изменение ∆U внутренней энергии данной массы идеального газа определяется только начальным и конечным состоянием газа.

Обусловлено это тем, что каждому состоянию данной массы газа (с определенными значениями p, V и T) соответствует одно определенное значение внутренней энергии, которое можно найти либо по формуле (1), либо по формуле (2).

А вот работа, совершенная газом при переходе из начального состояния в конечное, зависит от характера процесса, которым газ был переведен из начального состояния в конечное.

Действительно, работа газа численно равна площади под графиком зависимости p(V). А эта площадь зависит от того, какой вид имела функция p(V).

Если газ не расширяется, а сжимается (рис. 42.8), то внешние силы производят работу над газом. В таком случае говорят также, что газ производит отрицательную работу. Она численно равна взятой со знаком минус площади S под графиком зависимости p(V).

На том, что работа газа зависит от вида зависимости p(V), а не только от начального и конечного состояния, основан принцип действия тепловых двигателей (в следующем параграфе мы рассмотрим их подробнее).

В тепловых двигателях газ расширяется при высокой температуре. При атом давление газа велико, поэтому он совершает большую работу. А сжимают газ при более низкой температуре, когда давление газа меньше. Поэтому для того, чтобы вернуть газ в начальное состояние, внешние силы должны совершить меньшую работу.

Рассмотрим пример.

? 12. Газ совершает циклический процесс: переходит из состояния 1 в состояние 2 (рис. 42.9), а потом возвращается в состояние 1. При этом объем газа не должен быть меньше начального и больше конечного.

а) Какую максимально возможную работу может совершить газ при переходе 1–2, если давление газа не должно превышать 3p₀?
б) Какую минимально возможную работу должны совершить внешние силы при переходе 2–1, если давление газа не должно быть меньше p₀?
в) Насколько в этом случае работа газа при циклическом процессе больше работы внешних сил?

Применение первого закона термодинамики к изопроцессам и адиабатному процессу

? 13. Используя первый закон термодинамики, а также выражения для внутренней энергии и работы газа, объясните, почему:
а) при изохорном процессе A_г = 0, Q = ∆U, то есть сообщенное газу количество теплоты (напомним, что оно может быть как положительным, так и отрицательным) равно изменению внутренней энергии газа;
б) при изотермическом процессе ∆U = 0, Q = A_г, то есть сообщенное газу количество теплоты равно работе газа;
в) при изобарном процессе A_г ≠ 0, ∆U ≠ 0;
г) при адиабатном процессе Q = 0, A_г = –∆U, то есть при расширении газ совершает работу за счет уменьшения внутренней энергии, а при сжатии газа его внутренняя энергия увеличивается за счет работы внешних сил.
Подсказка. Если давление не изменяется, то ∆(pV) = p∆V.

Дополнительные вопросы и задания

14. На рисунках 42.10, а, б, в изображены графики трех процессов с данной массой одноатомного идеального газа. Чему равно изменение внутренней энергии газа для каждого из этих процессов при переходе 1–2?

15. При изобарном расширении данной массы одноатомного идеального газа его температура возросла от 0 ºС до 100 ºС. При этом газу было передано количество теплоты, равное 5 кДж.
а) Насколько изменилась внутренняя энергия газа?
б) Чему равно количество вещества в сосуде с газом?

Содержание:

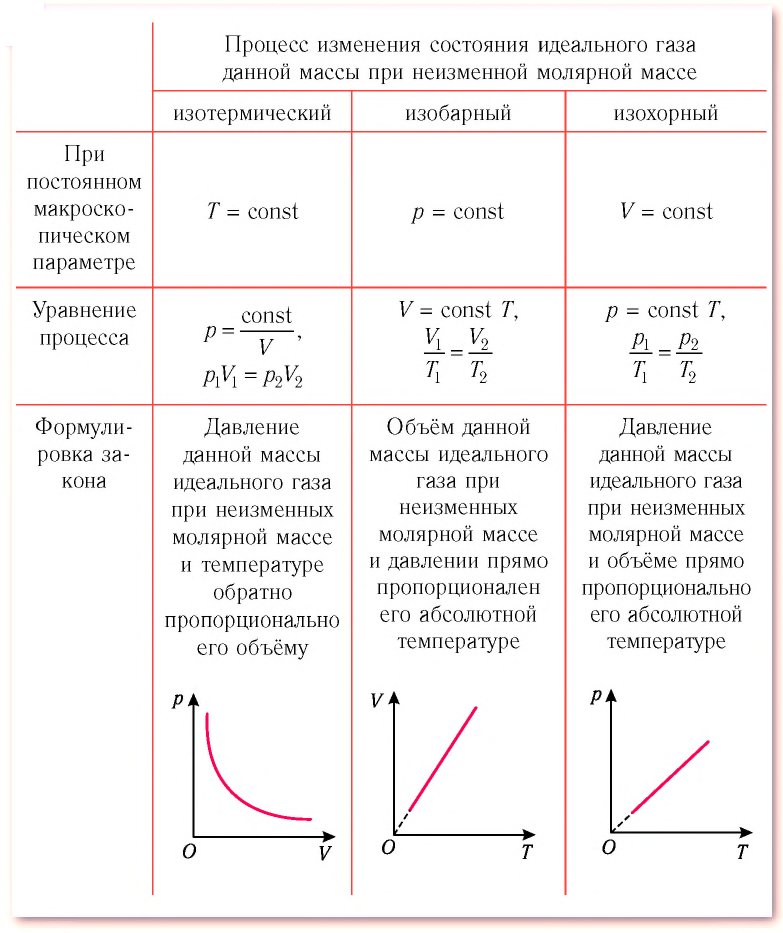
Изотермический, изобарный и изохорный процессы:

Свойство газов существенно изменять предоставленный им объём широко используют в тепловых двигателях. Анализируя процессы, происходящие с газом в этих устройствах, важно знать, каким законам подчиняются газы и каковы условия применимости этих законов.

Процессы в газах часто происходят так, что изменяются только два параметра из пяти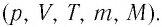

Изотермический процесс

Процесс изменения состояния физической системы при постоянной температуре 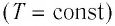называют изотермическим.

Если при переходе из начального состояния в конечное масса и молярная масса идеального газа не изменяются, то из уравнения Клапейрона—Менделеева следует:

 

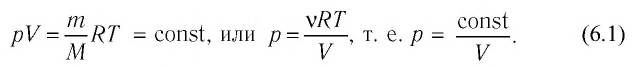
Давление данной массы газа при постоянных молярной массе и температуре обратно пропорционально его объёму.

Это утверждение называют законом Бойля—Мариотта.

Справедливость закона Бойля—Мариотта можно продемонстрировать экспериментально, используя установку, представленную на рисунке 18 в § 5.

Если медленно изменять объём газа, находящегося в сосуде, то вследствие теплообмена с окружающей средой можно поддерживать температуру газа в сосуде практически постоянной. При этом уменьшение объёма газа при вращении винта 3 повлечёт за собой увеличение его давления и некоторое незначительное увеличение температуры. И наоборот, увеличение объёма приведёт к уменьшению давления и некоторому незначительному уменьшению температуры газа*.

* Незначительное изменение температуры газа принципиально необходимо для теплообмена с термостатом — передача тепла возможна только при разных температурах тел.

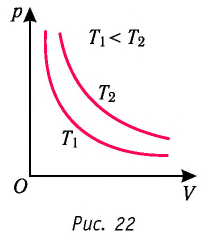
График изотермического процесса, совершаемого идеальным газом, в координатах 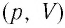представляет собой гиперболу (рис. 22). В физике такую кривую называют изотермой. Разным значениям температуры газа соответствуют разные изотермы. Согласно соотношениям (6.1) для одинаковых объёмов газов с одинаковыми количествами вещества и разными температурами чем больше давление, тем выше температура (рис. 22).

Многочисленные опыты показали, что исследованные газы подчиняются закону Бойля —Мариотта тем точнее, чем меньше их плотность. При значительном увеличении давления газа этот закон перестаёт выполняться.

Интересно знать:

Лёгкие расположены в грудной клетке, объём которой при дыхании периодически изменяется благодаря работе межрёберных мышц и диафрагмы. Когда грудная клетка расширяется, давление воздуха в лёгких становится меньше атмосферного, и воздух через воздухоносные пути устремляется в лёгкие — происходит вдох. При выдохе объём грудной клетки уменьшается, что вызывает уменьшение объёма лёгких. Давление воздуха в них становится выше атмосферного, и воздух из лёгких устремляется в окружающую среду.

Изобарный процесс

Процесс изменения состояния газа при постоянном давлении (р = const) называют изобарным.

В 1802 г. французский учёный Жозеф Гей-Люссак (1778-1850) рассмотрел этот процесс для воздуха, водорода, кислорода и азота.

Если при переходе из начального состояния в конечное масса и молярная масса газа не изменяются, то объём газа, как следует из уравнения Клапейрона—Менделеева:

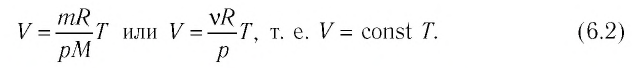
Объём данной массы газа при постоянных молярной массе и давлении прямо пропорционален абсолютной температуре.

Это утверждение называют законом Гей-Люссака.

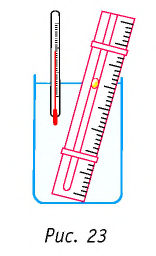
Справедливость закона Гей-Люссака можно продемонстрировать экспериментально, используя установку, представленную на рисунке 23. Жидкость в сосуде находится в тепловом равновесии с тонкой трубкой, заполненной воздухом, запертым капелькой масла. При увеличении температуры жидкости объём воздуха, находящегося в трубке под капелькой масла, возрастает и капелька движется вверх. При уменьшении температуры объём воздуха уменьшается — и капелька движется вниз.

Поскольку 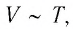то в координатах 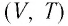график изобарного процесса, совершаемого идеальным газом, представляет собой прямую линию, продолжение которой проходит через начало координат (рис. 24). Эту линию называют изобарой.

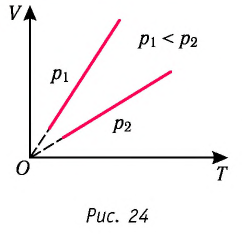
Изобара реальных газов не может быть продлена до нулевого значения температуры (на графике пунктирная линия), потому что при низких температурах все газы существенно отличаются от модели «идеальный газ» и при дальнейшем уменьшении температуры превращаются в жидкости.

В одних и тех же координатах 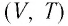можно построить несколько изобар, которые соответствуют разным давлениям данной массы идеального газа при неизменной молярной массе. Анализ соотношений (6.2) позволяет сделать вывод, что большему давлению соответствует меньший наклон изобары к оси температур (см. рис. 24).

Изохорный процесс

Процесс изменения состояния газа при постоянном объёме (V = const) называют изохорным.

Впервые этот процесс рассмотрел в 1787 г. французский учёный Жак Шарль (1746-1823)*.

* Несмотря на то что Шарль не опубликовал результаты своих исследований, история физики отдаёт приоритет открытия ему.

Если при переходе из начального состояния в конечное масса и молярная масса идеального газа не изменяются, то давление газа, как следует из уравнения Клапейрона—Менделеева:

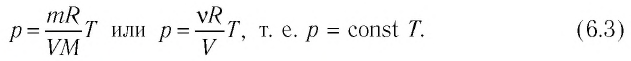
Давление данной массы газа при постоянных молярной массе и объёме прямо пропорционально абсолютной температуре.

Это утверждение называют законом Шарля.

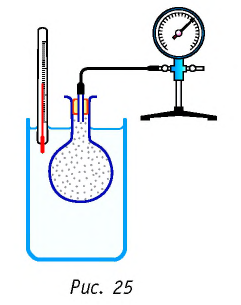
Справедливость закона Шарля можно продемонстрировать экспериментально, используя установку, представленную на рисунке 25. Колба, наполненная воздухом и соединённая с манометром, находится в тепловом равновесии с жидкостью в сосуде. При увеличении температуры жидкости давление воздуха в колбе возрастает, а при уменьшении температуры — давление воздуха уменьшается.

В координатах 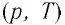график изохорного процесса, совершаемого идеальным газом, представляет собой прямую линию, продолжение которой проходит через начало координат (рис. 26). Эту линию называют изохорой.

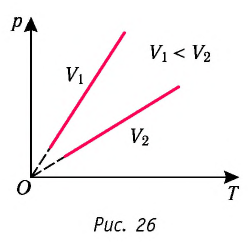
Как и в случае изобарного процесса, изохора реальных газов не может быть продлена до нулевого значения температуры.

В одних и тех же координатах 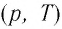можно построить несколько изохор, соответствующих разным объёмам данной массы газа при неизменной моляр- О ной массе. Анализ соотношений (6.3) показывает, что большему объёму соответствует меньший наклон изохоры к оси температур (см. рис. 26).

Пример №1

На рисунке 28 представлен график трёх процессов изменения состояния некоторой массы идеального газа. Как изменялись параметры газа на участках 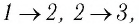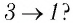Изобразите эти процессы в координатах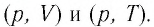

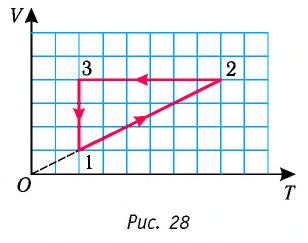
Решение. На участке 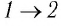объём газа прямо пропорционален абсолютной температуре, следовательно, процесс перехода газа из состояния 1 в состояние 2 является изобарным. Из графика следует, что в состоянии 2 температура и объём газа больше в 4 раза, чем в состоянии 1. Следовательно, в процессе изобарного расширения некоторой массы газа из состояния 1 в состояние 2 температура и объём газа увеличились. Это можно записать таким образом:

переход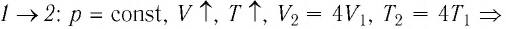  
происходит изобарное нагревание газа.

В процессе перехода газа из состояния 2 в состояние 3 остаётся постоянным объём (процесс изохорный), а температура газа уменьшается в 4 раза. Из соотношения (6.3) следует, что при изохорном охлаждении давление газа уменьшается пропорционально его абсолютной температуре. Поэтому можно записать:
переход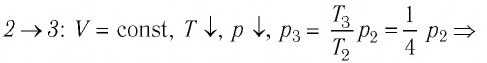
происходит изохорное охлаждение газа.

Процесс перехода газа из состояния 3 в состояние 1 — изотермический. При этом объём газа уменьшается в 4 раза, что влечёт за собой, согласно закону Бойля—Мариотта, увеличение давления газа в 4 раза:

• переход 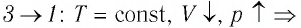 происходит изотермическое сжатие газа.

Опираясь на сделанные выводы, представим все три процесса в координатах 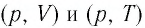(рис. 29, а, б).

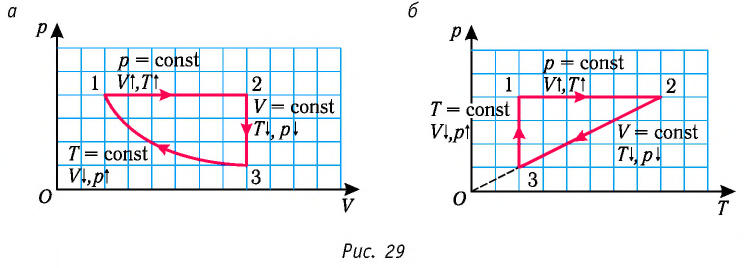
Пример №2

При изотермическом расширении идеального газа определённой массы его объём увеличился от 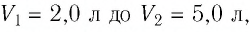а давление уменьшилось на 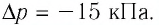Определите первоначальное давление газа.

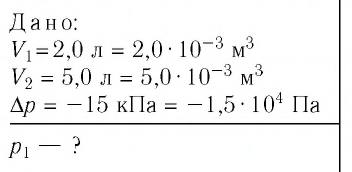
Решение. Так как температура и масса газа не изменяются, то его начальное и конечное состояния связаны законом Бойля—Мариотта, т. е. 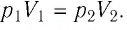 С учётом того, что 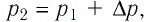получим:

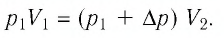
Откуда

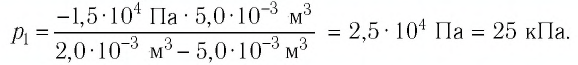
Ответ: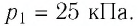 

Обобщение и систематизация определений:

Молекулы всех газов при одной и той же
температуре обладают одинаковой средней
кинетической энергией. Причем давление
газа при данной температуре зависит
только от числа молекул в единице объема
газа. В основе объяснений физических
свойств газов и законов газового
состояния лежит кинетическая теория.
Большинство законов газового состояния
было выведено для идеального газа.
Идеальным называют газ, в котором
молекулы рассматриваются как материальные
точки, обладающие массой, но не имеющие
при этом объёма, между которыми отсутствуют
силы взаимодействия.

При
больших объёмах и малых давлениях, когда
расстояние между молекулами во много
раз больше собственных размеров молекул,
а также при высоких температурах, когда
интенсивность хаотического движения
молекул велика и поэтому молекулы слабо
взаимодействуют между собой, складываются
условия, при которых реальный газ можно
с некоторым приближением считать
идеальным.

Закон Бойля — Мариотта.
Английский ученый
Бойль и независимо от него несколько
позднее французский физик Мариотт на
основании экспериментов пришли к выводу
о том, что объем данной
массы газа и его давление находятся в
обратно пропорциональной зависимости.

Эта зависимость между давлением и
объемом газа при постоянной температуре
выражается формулой:

, (1)

где V₁
и Р₁
– объем и абсолютное давление газа до
их изменения; V₂
и Р₂ –
то же, после изменения.

Из данной формулы можно получить
следующие математические выражения:

, (2)

или

при

. (3)

Из последней формулы следует,
что произведение
давления данной массы газа на его объем
постоянно, если температура газа не
меняется.

Закон
имеет практическое применение в газовом
хозяйстве. Он позволяет определять
объем газа при изменении его давленная
и давление газа при изменении его объема
при условии, что температура газа
остаётся постоянной.

Чем больше при постоянной
температуре увеличивается объем газа,
тем меньше становится его плотность.
Зависимость между
объёмом газа и его плотностью при
постоянной температуре выражается
формулой

, (4)

где V₁
и V₂
– объемы, занимаемые газом; ρ₁
и ρ₂
– плотности газа, соответствующие этим
объемам.

Если в формуле (1) заменим отношение
объемов газа отношением их плотностей,
то на основании формулы (4) можно получить.

или

(5)

Из формулы (5) можно сделать
вывод, что при одной
и той же температуре плотности газов
прямо пропорциональны давлениям, под
которым находятся эти газы, т.е. плотность
газа (при постоянной температуре) будет
тем больше, чем больше будет его давление.

Пример.
Объем газа при давлении 760 мм.рт.ст. и
при температуре 0°С составляет 300 м³.
Какой объем займет этот газ при абсолютном
давлении, равном 1520 мм.рт.ст. и при той
же температуре?

760 мм.рт.ст. = 101 320 Па = 101,3 кПа;

1520 мм.рт.ст. = 202 630 Па = 202,6 кПа.

Подставляем заданные
значения V₁,
Р₁,
и Р₂
в формулу (2):

Р₁ =
101,3 кПа; V₁
= 300 м³;
Р₂ =
202,6 кПа;

101,3 х 300 = 202,6 V₂,
откуда V₂
= (101,3
х 300)/202,6 = 150 м³.

Закон Гей-Люссака.
Французский химик Гей-Люссак впервые
установил зависимость объема газа от
температуры при постоянном давлении.
Сущность этой зависимости заключается
в том, что при постоянном
давлении относительное изменение объема
данной массы газа прямо пропорционально
изменению температуры.
Математически эта зависимость между
объемом и температурой газа при постоянном
давлении записывается следующим образом:

, (6)

где V
– объем газа, м³;
Т – абсолютная
температура, К.

Из формулы (6) следует, что
если определенный
объем газа нагревать при постоянном
давлении, то его объем изменится во
столько раз, во сколько раз изменится
его абсолютная температура.

Многочисленные опыты
показывают, что при нагревании газов
на 1 градус при постоянном давлении их
объем увеличивается на постоянную
величину, равную 1/273,2 первоначального
их объема. Эта величина называется
термическим
коэффициентом объемного расширения
и обозначается α
= 1/273,2 град^-1.

С учетом этого закон
Гей-Люссака можно сформулировать так:
объем данной массы
газа при постоянном давлении увеличивается
линейно при повышении температуры

; (7)

; (8)

, (9)

где V_t
и V₀
– объемы газа при
конечной и начальной температурах, м³;
t
и Т – начальная и конечная температуры,
^оС,
К; α – термический коэффициент объёмного
расширения.

Из формулы (9) следует, что
объем газа при постоянном
давлении прямо пропорционален его
абсолютной температуре.

Закон Шарля.
Согласно закону Шарля,
давление данной массы
газа при постоянном объеме прямо
пропорционально абсолютной температуре.
Из этого закона следует, что отношение
давлений массы газа при постоянном
объеме равно отношению его абсолютных
температур. Закон
выражается следующей формулой:

или

, (10)

где Р₁
и Р₂
– абсолютные давления; Т₁
и
Т₂
– абсолютные температуры
газа, К.

Из формулы (10) можно сделать вывод, что
при постоянном объеме давление газа
при нагревании увеличивается во столько
раз, во сколько раз увеличивается его
абсолютная температура.

Пример 1.
При температуре газа 27°С его давление
равно 4 МПа (40 кгс/см²).
Каково будет избыточное давление этого
газа при температуре 47°С?

Начальная абсолютная
температура газа равна:

,

конечная абсолютная
температура газа равна:

.

Атмосферное давление примем
равным 0,1 МПа (1 кгс/см²),
тогда абсолютное давление газа до
нагревания будет:

.

Искомое абсолютное давление
газа Р₂
по формуле (10) равное:

.

Следовательно, избыточное давление
газа после нагревания его до 47°С равно:

.

Пример 2.
Сжатый газ в баллоне при температуре
7°С имел избыточное давление 0,9МПа. После
нагревания давление в баллоне повысилось
до 1,1 МПа. До какой температуры был нагрет
газ?

Начальная абсолютная
температура газа:

.

Начальное абсолютное
давление газа:

.

Конечное абсолютное давление
газа:

.

Из формулы (10) после
преобразования ее относительно
неизвестной Т₂
получаем:

.

Следовательно, газ в баллоне был нагрет
до температуры 63°С.

Закон
Авогадро. Итальянский
ученый Амадео Авогадро выразил
предположение, что различные
газы, занимающие одинаковые объёмы при
равных условиях (одинаковые давление
и температура), содержат одинаковое
число молекул.

Это число для одной
грамм-молекулы (1 моль) любого газа
составляет около N
= 6,064 ^х
10²³
и называется числом Авогадро. В дальнейшем
было экспериментально установлено, что
1 грамм-молекула любого газа при нормальных
условиях занимает объем 22,4л.

В Международной системе
единиц производной является величина,
в 1000 раз большая моля, она называется
киломоль и
обозначается кмоль.
1 кмоль любого газа
при нормальных условиях (0°С и 101,3 кПа)
занимает объем 22,4 м³.
Зная эту величину, можно определить
плотность любого газа по формуле

, (11)

где М —
масса 1 кмоля газа, кг.

Пример 1.
Определить плотность метана при
нормальных условиях (О^оС
и 101,3 кПа):

.

Пример 2. В баллоне находится 100 кг
жидкого этана. Определить объем паров
этана, полученных при его полном испарении
в нормальных условиях.

Решение. Сначала определяют число
киломолей этана:

п = 100 : 30,07 = 3,33 (здесь 30,07 –
молекулярная масса этана).

Зная, что 1 киломоль этана при испарении,
т.е. в газообразном состоянии, занимает
объем 22,4 м³, находят объем паров
этана от испарения всего его количества:

V = 22,4 ^х
3,33 = 74,63 м³.

Уравнение Клапейрона —
Менделеева.
При одновременном изменении объема,
давления и температуры газа справедливы
законы и Бойля — Мариотта и Гей-Люссака.

Французский ученый Клапейрон пришел к
выводу о существовании для газов
некоторой универсальной функции. Русский
ученый Д.И. Менделеев вывел в более общем
виде уравнение состояния идеальных
газов, объединив уравнения законов
Бойля — Мариотта и Гей-Люссака в одно
общее математическое уравнение идеального
газа, которое называется уравнением
Клайперона—Менделеева:

. (12)

Величина

обозначается буквой “R”
называется газовой постоянной. Подставляя
обозначение газовой постоянной в формулу
(12), получаем выражение:

или

. (13)

Это
уравнение закона газового состояния
связывает все три основных параметра
данного количества газа: объем, абсолютное
давление и абсолютную температуру, и
оно относится к 1 молю газа.

Из уравнения следует, что
для определенного
количества газа произведение его объема
на абсолютное давление равно произведению
газовой постоянной на абсолютную
температуру газа. Числовое
значение газовой постоянной зависит
от величин параметров, входящих в
уравнение (13).

В Международной системе универсальная
газовая постоянная для 1 кмоля равна:

,

где 101325 – нормальное давление, Па.

Уравнением Клапейрона —
Менделеева часто пользуются при пересчете
характеристик газа. Формулы (14) и (15),
предназначенные для пересчета параметров,
характеризующих состояние газа в
нормальных и стандартных условиях,
получены путем соответствующих,
преобразований выражения

.

, (14)

, (15)

где V_Н V_ст
– объём газа при нормальных и стандартных
условиях, м³; V_t
– объём газа при реальных условиях, м³;
P_t –
давление газа при реальных условиях,
Па; Р – давление газа при нормальных и
стандартных условиях (101325 Па).

Закон Дальтона.
Смеси газов (паров),
близких по своим свойствам к идеальным,
характеризуются аддитивностью парциальных
давлений. Аддитивность
(от лат. additivus
– прибавляемый), свойство объекта, по
которому величина всего объекта равна
сумме величин частей объекта при любом
разбиении. Так, масса тела равна сумме
масс его частей.

Парциальным давлением
компонента ρ_i
газовой смеси называется то давление,
которое этот компонент оказывал бы,
если бы из смеси удалить все другие
компоненты при сохранении первоначальных
объема и температуры системы. Закон
аддитивности записывается следующим
образом:

(16)

где π — общее давление смеси
газов (паров). Из уравнения

следует, что

(17)

Подставив это выражение в уравнение
(17), получим

(18)

Следовательно

(19)

или

(20)

т.е. парциальное
давление компонента равно давлению
системы, умноженному на мольную долю
этого компонента в газовой фазе.

Пример. Известен молярный состав
смеси газов, %: метан – 90, этан – 5, пропан
– 2, азот – 2, бутаны – 1. Смесь находится
под давлением 12 МПа. Требуется определить
парциальное давление компонентов смеси.

Решение. Пользуясь уравнением, вычисляют
парциальное давление компонентов:

p_C1
= 0,9*12 = 10,8 МПа;

p_C2
= 0,05*12 = 0,6 МПа;

p_C3
= 0,02*12 = 0,24 МПа;

p_C4
= 0,02*12 = 0,24 МПа;

p_C5
= 0,01*12 = 0,12 МПа.

Законы реальных газов.
При повышении давления
объем реального газа становится меньше,
чем идеального. Это
обстоятельство учитывают введением
соответствующих поправок в законы
идеальных газов.

Так,
уравнение состояния реального газа
можно записать в виде:

(21)

где z
— коэффициент сжимаемости, являющийся
функцией приведенного давления Р_пр
= P/P_кр
и приведенной
температуры T_пр
= T/Т_кр;
Р_кр
и Т_кр
— критические давление и температура
(табличные значения).

Давление насыщенных
паров. Пары жидкости
могут быть насыщенными и ненасыщенными.
Насыщенным называется
пар, находящийся в равновесии с жидкостью.
Чем выше температура, тем выше давление,
при котором находится данная равновесная
система. Для насыщенных паров существует
однозначная зависимость между давлением
паров и температурой Р
= f(T).

Ненасыщенными (перегретыми)
парами называют пары, которые при данных
температуре и давлении образуют
однофазную систему.
Жидкая фаза отсутствует.

Известно, что жидкость
начинает кипеть при такой температуре,
при которой давление её насыщенных
паров Р
становится равным внешнему давлению
π. Давление насыщенных паров определяют
по табличным данным или эмпирическим
уравнениям (ур-е Антуана, Киреева).

Для определения ДНП
нефтепродуктов, представляющих собой
сложные смеси углеводородов различных
классов, предложены графики и формулы
(Кокса, Ашворта, Вильсона, BWR
и др.)

Закон Рауля. Этот закон
устанавливает зависимость между
парциальным давлением компонента,
входящего в состав раствора, его молярной
концентрацией в жидкой смеси Х
и упругостью пара того же чистого
компонента при заданной температуре
Q.

Парциальное давление компонента в
жидкой смеси равно его молярной
концентрации, умноженной на упругость
его паров в чистом виде при данной
температуре:

(22)

где р – парциальное давление
компонента в растворе.

По закону Рауля, сумма парциальных
давлений всех компонентов равна общему
давлению над смесью или общей упругости
паров смеси:

где
Х_nQ_n
– молярная концентрация и упругость
паров компонента соответственно.

Пример. Жидкая смесь состоит из
этана –60%, пропа­на –25 % и изобутана
–15 % (молярные доли). Требуется оп­ределить
общее давление системы при температуре
10⁰С.

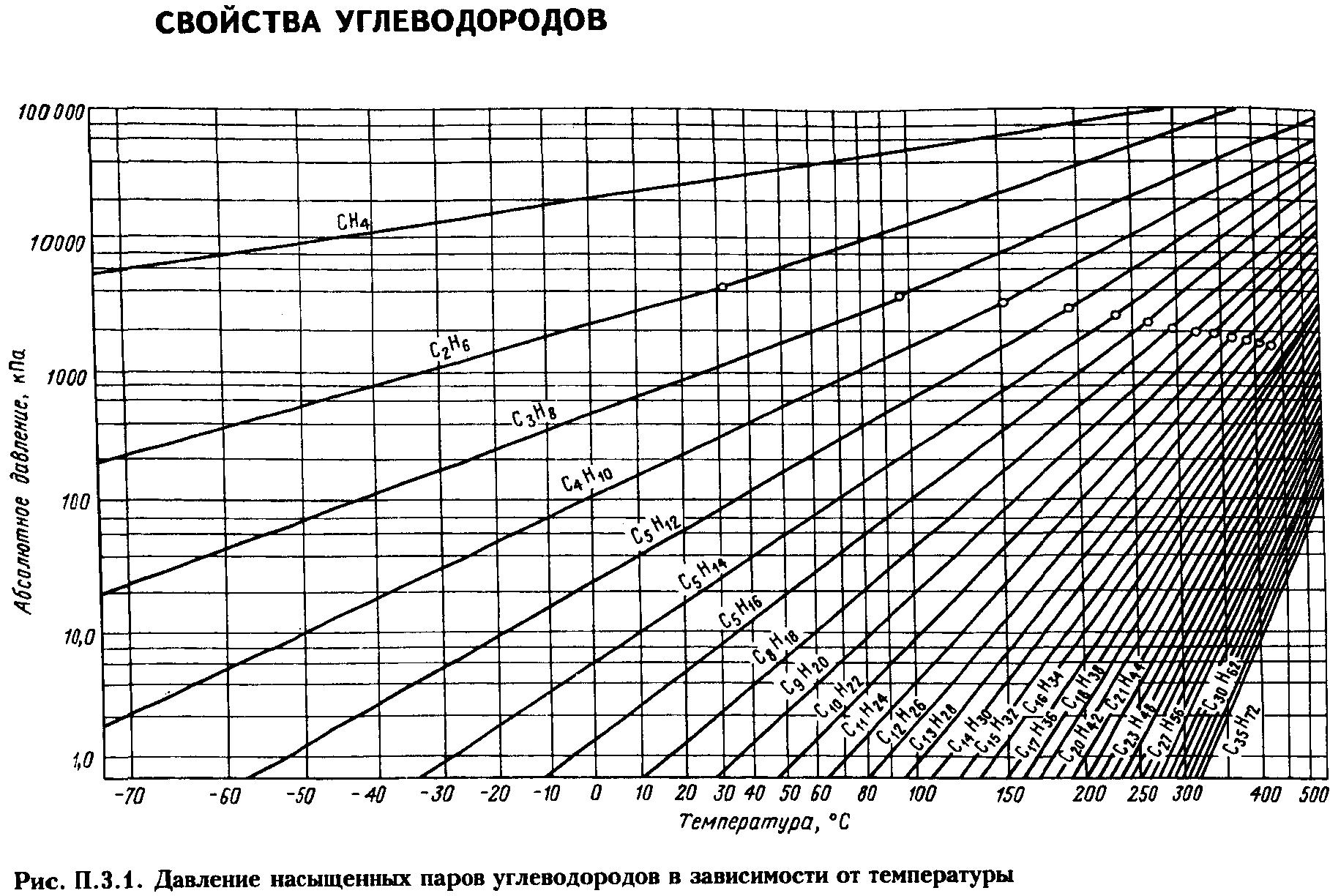
Решение. Сначала из рис. 2.1 (график Кокса)
находим давление насыщенных паров
компонентов в чистом виде при 10°С:

Q_C2
= 0,326 МПа; Q_C3
= 0,63 МПа; Q_C4
= 0,16 МПа

Затем по уравнению определим общее
давление системы:

Данные этого примера показывают, что
если бы указанная смесь транспортировалась
в жидком виде при 10°С, то трубопровод
работал под давлением 2,14 МПа.

Важным выводом, вытекающим из закона
Рауля, является то, что высококипящие
компоненты имеют низкую упругость,
содержатся в паровой фазе в малых
количествах; следователь­но, их
основная доля находится в жидкой фазе.
Что касается низкокипящих компонентов,
обладающих высокой упругостью, то они
легко переходят в газовую фазу. На этом
положении основана работа многих
установок по частичной стабилизации
газового конденсата при выветривании
– ступенчатом снижении давления смеси
с одновременным ее расширением.

23

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Уравнение состояния идеального газа

теория по физике 🧲 молекулярная физика, МКТ, газовые законы

Уравнение состояния идеального газа было открыто экспериментально. Оно носит название уравнения Клапейрона — Менделеева. Это уравнение устанавливает математическую зависимость между параметрами идеального газа, находящегося в одном состоянии. Математически его можно записать следующими способами:

Уравнение состояния идеального газа

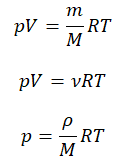
Внимание! При решении задач важно все единицы измерения переводить в СИ.

Пример №1. Кислород находится в сосуде вместимостью 0,4 м 3 под давлением 8,3∙10 5 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль.

Из основного уравнения состояния идеального газа выразим массу:

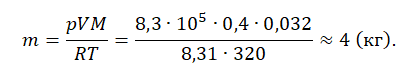
Уравнение состояния идеального газа следует использовать, если газ переходит из одного состояния в другое и при этом изменяется его масса (количество вещества, число молекул) или молярная масса. В этом случае необходимо составить уравнение Клапейрона — Менделеева отдельно для каждого состояния. Решая систему уравнений, легко найти недостающий параметр.

Подсказки к задачам

Важна только та масса, что осталась в сосуде. Поэтому:

Давление возросло на 15%	p2 = 1,15p1
Объем увеличился на 2%	V2 = 1,02V1
Масса увеличилась в 3 раза	m2 = 3m1
Газ нагрелся до 25 о С	T2 = 25 + 273 = 298 (К)
Температура уменьшилась на 15 К (15 о С)	T2 = T1 – 15
Температура уменьшилась в 2 раза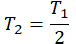
Масса уменьшилась на 20%	m2 = 0,8m1
Выпущено 0,7 начальной массы
Какую массу следует удалить из баллона?	Нужно найти разность начальной и конечной массы:
Газ потерял половину молекул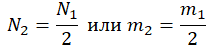
Молекулы двухатомного газа (например, водорода), диссоциируют на атомы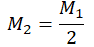
Озон (трехатомный кислород) при нагревании превращается в кислород (двухатомный газ)	M (O3) = 3Ar (O)∙10 –3 кг/моль M (O2) = 2Ar (O)∙10 –3 кг/моль
Открытый сосуд	Объем V и атмосферное давление pатм остаются постоянными
Закрытый сосуд	Масса m, молярная масса M, количество вещества ν, объем V, число N и концентрация n частиц, плотность ρ— постоянные величины
Нормальные условия	Температура T0 = 273 К Давление p0 = 10 5 Па
Единицы измерения давления	1 атм = 10 5 Па

Пример №2. В баллоне содержится газ под давлением 2,8 МПа при температуре 280 К. Удалив половину молекул, баллон перенесли в помещение с другой температурой. Определите конечную температуру газа, если давление уменьшилось до 1,5 МПа.

2,8 МПа = 2,8∙10 6 Па

1,5 МПа = 1,5∙10 6 Па

Так как половина молекул была выпущена, m₂ = 0,5m₁. Объем остается постоянным, как и молярная масса. Учитывая это, запишем уравнение состояния идеального газа для начального и конечного случая:

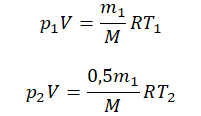
Преобразим уравнения и получим:

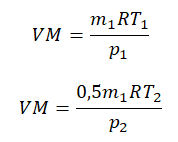
Приравняем правые части и выразим искомую величину:

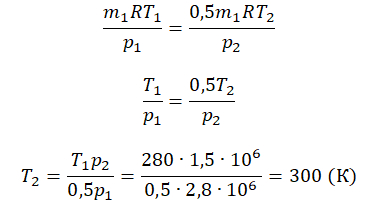
На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

ν R = p 1 V 1 T 1 . . = p 2 V 2 T 2 . .

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

pазбирался: Алиса Никитина | обсудить разбор | оценить

На высоте 200 км давление воздуха составляет примерно 10 –9 от нормального атмосферного давления, а температура воздуха Т – примерно 1200 К. Оцените плотность воздуха на этой высоте.

Уравнение состояния идеального газа

Содержание:

Уравнение состояния идеального газа получило название «уравнение Менделеева-Клапейрона». Давление смеси химически невзаимодействующих газов равно сумме их парциальных давлений: закон Дальтона.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Уравнение состояния идеального газа

Уравнение состояния идеального газа – это p = nkT называется уравнением Менделеева Клапейрона и оно даёт взаимосвязь трёх важнейших макроскопических параметров, описывающих состояние идеального газа давления, объёма и температуры. Поэтому уравнение Менделеева Клапейрона называется ещё уравнением состояния идеального газа.

Термодинамические параметры газа

В предыдущих главах было показано, что при описании свойств газа можно пользоваться величинами, характеризующими молекулярный мир (микромир), например энергией молекулы, скоростью ее движения, массой и т. п. Числовые значения таких величин мы можем определять только с помощью расчета. Все такие величины принято называть микроскопическими (от греческого «микрос» — малый).

Однако для описания свойств газов можно пользоваться и такими величинами, числовые значения которых находят простым измерением с помощью приборов, например давлением, температурой и объемом газа. Значения таких величин определяются совместным действием огромного числа молекул, поэтому они называются макроскопическими (от греческого «макрос» — большой).

Соотношение (4.1): устанавливает связь между микроскопическими и макроскопическими величинами для газов. Поэтому формулу (4.1) называют основным уравнением молекулярно-кинетической теории газов. Макроскопические величины, однозначно характеризующие состояние газа, называют термодинамическими параметрами газа. Важнейшими термодинамическими параметрами газа являются его объем V, давление р и температура Т.

Если взять определенную массу газа т, то при постоянных р, V и Т газ будет находиться в равновесном состоянии. Когда происходят изменения этих параметров, то в газе протекает тот или иной процесс. Если этот процесс состоит из ряда непрерывно следующих друг за другом равновесных состояний газа, то он называется равновесным процессом. Равновесный процесс должен протекать достаточно медленно, так как при быстром изменении параметров давление и температура не могут иметь соответственно одинаковые значения во всем объеме газа. В этой главе рассматриваются только равновесные процессы в газах, при которых масса газа остается постоянной.

Когда процесс в газе заканчивается, то газ переходит в новое состояние, а его параметры приобретают новые постоянные числовые значения, вообще говоря, отличные от их значений в начале процесса. Если же при постоянной массе газа значения всех его параметров в начале и в конце процесса окажутся одинаковыми, то процесс называется круговым или замкнутым.

Соотношение между значениями тех или иных параметров в начале и конце процесса называется газовым законом. Газовый закон, выражающий связь между всеми тремя параметрами газа, называется объединенным газовым законом.

Отметим еще, что такого процесса в газе, при котором изменялся бы только один параметр газа, не существует, так как значения этих параметров взаимосвязаны. Примером сказанного является закон Шарля, выражающий связь между р и Т.

Объединенный газовый закон. Приведение объема газа к нормальным условиям

Связь между давлением, объемом и температурой определенной массы газа устанавливается с помощью соотношения (4.9):

Поскольку обозначает число молекул в единице объема газа, то , где N — общее число молекул, V — объем газа. Тогда получим

Так как при постоянной массе газа N остается неизменным, — постоянное число, т. е.

Поскольку значения р, V и Т в (5.2) относятся к одному и тому же состоянию газа, можно следующим образом сформулировать объединенный газовый закон: при постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.

Следовательно, если числовые значения параметров в начале процесса, происходящего с какой-либо определенной массой газа, обозначить через р₁ , V₁ и Т₁, а их значения в конце процесса соответственно через р₂ , V₂ и Т₂, то

Формулы (5.2) и (5.3) представляют собой математическое выражение объединенного газового закона.

На практике иногда нужно установить, какой объем V₀ займет имеющаяся масса газа при нормальных условиях, т. е. при Т₀=273 К и при р₀=1,013 . 10 5 Па. Если значения параметров для этой массы газа в каком-либо произвольном состоянии, отличном от нормального, обозначить через р, V и Т, то на основании (5.3) получаем , или

Формула (5.4) позволяет приводить объем заданной массы газа к нормальным условиям.

Молярная газовая постоянная. Определение числового значения постоянной Больцмана

Формула (5.1) справедлива для любой массы газа, в которой содержится N молекул. Если применить эту формулу к одному молю какого-либо газа, то N нужно заменить постоянной Авогадро N_A, а V — объемом одного моля V_моль

Так как в одном моле любого газа содержится одно и то же число молекул N_A, то произведение имеет одинаковое значение для всех газов, т. е. не зависит от природы газа. Произведение обозначается R и называется молярной газовой постоянной. Таким образом,

Числовое значение R можно найти, если применить (5.5) к состоянию одного моля газа при нормальных условиях, так как при этом м 3 /моль (§ 3.6). Действительно,

Это числовое значение R в СИ необходимо запомнить, так как им часто пользуются при расчетах и при решении задач.

Теперь легко найти числовое значение постоянной Больнмана . Из (5.6) получаем . Подставляя сюда числовые значения R и , вычисляем :

Уравнение Клапейрона — Менделеева. Плотность газа

Выясним, как будет выглядеть соотношение (5.1), если в него ввести молярную газовую постоянную R. Так как N — полное число молекул в массе газа т, а — число молекул в одном моле, то

где — число молей в массе газа /т. Поэтому

Поскольку , а равно массе газа т, деленной на массу одного моля газа , то получаем

Соотношение (5.7) называется уравнением Клапейрона — Менделеева или уравнением состояния для произвольной массы идеального газа. Для одного моля идеального газа уравнение Клапейрона — Менделеева принимает вид

С помощью формулы (5.7) легко выяснить, какими величинами определяется плотность газа. Так как , то из (5.7) имеем

Зависимость средней квадратичной скорости молекул газа от температуры

Выясним теперь, как можно с помощью вычислений находить среднюю квадратичную скорость движения молекул газа . Поскольку средняя кинетическая энергия поступательного движения молекул газа равна (3/2) , то можно написать , откуда

Отметим, что под т в формуле (5.10) подразумевается масса одной молекулы в кг. Так как , получим . Поскольку а есть масса одного моля газа (§ 3.6), имеем

Наконец, из (5.9) следует, что , поэтому

Среднюю квадратичную скорость можно находить по любой из формул (5.10)—(5.12). Из функции Максвелла можно получить формулы для средней арифметической скорости и наивероятнейшей скорости. Средняя арифметическая скорость

Наконец, наивероятнейшую скорость вычисляют так:

(Используя график функции Максвелла (рис. 3.3), поясните, почему меньше , а меньше

Изохорический процесс

Процессы, при которых масса газа и один из его параметров остаются постоянными, называются изопроцессами (от греческого «изос» — равный, одинаковый). Поскольку имеется три параметра газа, существует три различных изопроцесса. Первый из них (изохорический) рассмотрен выше (§ 4.3). Процесс в газе, который происходит при постоянной массе и неизменном объеме, называется изохорическим (от греческого «хора» — пространство). Графики для этого процесса называются изохорами (рис. 4.3).

Отметим, что к любому изопроцессу применим объединенный газовый закон и формулы (5.3), (5.7) и (5.8) с учетом того, что один из параметров остается постоянным. При изохорическом процессе постоянным остается объем V, поэтому формула (5.3) после сокращения на V принимает вид

Итак, изохорический процесс подчиняется закону Шарля: при постоянной-массе газа и неизменном объеме давление газа прямо пропорционально его абсолютной температуре. Это видно и из уравнения Клапейрона — Менделеева (5.7):

Так как V, т, и R остаются постоянными, то из (5.7) следует, что р пропорционально Т. Отметим, что закон Шарля можно формулировать и так, как это было сделано в § 4.3.

Изобарический- процесс

Процесс в газе, который происходит при постоянной массе и неизменном давлении, называется изобарическим (от греческого «барос» — тяжесть). Этот процесс был изучен французским физиком Л. Гей-Люссаком в 1802 г.

Поскольку при изобарическом процессе р постоянно, то после сокращения на р формула (5.3) принимает вид

Формула (5.16) является математическим выражением закона Гей-Люссака: при постоянной массе газа и неизменном давлении объем газа прямо пропорционален его абсолютной температуре. (Это видно и из уравнения Клапейрона — Менделеева (5.7): так как р, т, и R постоянны, то объем V пропорционален Т.)

На рис. 5.1 схематически изображен опыт Гей-Люссака. Колба с газом помещается в сосуд с водой и льдом.

В пробку вставлена трубка, изогнутая таким образом, что свободный конец ее горизонтален. Газ в колбе отделен от окружающего воздуха небольшим столбиком ртути в трубке. Температуру газа определяют по термометру, а объем — по положению столбика ртути. Для этого на трубке нанесены деления, соответствующие определенному внутреннему объему трубки (при градуировке трубки можно учесть и расширение сосуда при нагревании, но оно сравнительно мало’).

Сначала по положению столбика ртути 1 определяют — объем газа при 0°С. Затем газ нагревают (столбик ртути перемещается в положение 2), в процессе нагревания записывают значения объема и температуры и строят график, который называется изобарой.

Оказывается, что изобара представляет собой прямую линию (рис. 5.2, а), которая пересекается с осью абсцисс в точке А.

Из подобия треугольников на рис. 5.2, а следует

Обозначив через , получим

Здесь — коэффициент объемного расширения газа (гл. 13).

Если повторять этот опыт для разных газов или для разных масс газа, то все графики будут пересекаться в точке А, соответствующей t=—273°С (рис. 5.2, б), т. е. коэффициент одинаков для всех газов. Это означает, что расширение газа при изобарическом процессе не зависит от его природы.

Отметим, что для газов коэффициенты и в формулах (4.2а) и (5.17) численно одинаковы, поэтому обычно пользуются одним .

Изотермический процесс

Процесс в газе, который происходит при постоянной температуре, называется изотермическим.

Изотермический процесс в газе был изучен английским ученым Р. Бойлем и французским ученым Э. Мариоттом. Установленная ими опытным путем связь получается непосредственно из формулы (5.3) после сокращения на Т:

Формула (5.18) является математическим выражением закона Бойля — Мариотта: при постоянной массе газа и неизменной температуре давление газа обратно пропорционально его объему. Иначе говоря, в этих условиях произведение объема газа на соответствующее давление есть величина постоянная:

Соотношение (5.19) можно получить и из (5.7) или (5.8), так как при постоянном Г справа в формулах (5.7) и (5.8) стоит постоянная величина. График зависимости р от V при изотермическом процессе в газе представляет собой гиперболу и называется изотермой. На рис. 5.3 изображены три изотермы для одной и той же массы газа, но при разных температурах Т.

Отметим еще, что из формулы (5.9) непосредственно вытекает, что при изотермическом процессе плотность газа изменяется прямо пропорционально давлению:

(Подумайте, как проверить закон Бойля — Мариотта на опыте.)

Внутренняя энергия идеального газа

Как отмечалось, силы взаимодействия молекул в идеальном газе отсутствуют. Это означает, что молекулярно-потенциальной энергии у идеального газа нет. Кроме того, атомы идеального газа представляют собой материальные точки, т. е. не имеют внутренней структуры, а значит, не имеют и энергии, связанной с движением и взаимодействием частиц внутри атома. Таким образом, внутренняя энергия идеального газа представляет собой только сумму знамений кинетической энергии хаотического движения всех его молекул:

Поскольку у материальной точки вращательного движения быть не может, то у одноатомных газов (молекула состоит из одного атома) молекулы обладают только поступательным движением. Так как среднее значение энергии поступательного движения молекул определяется соотношением(4.8): , то внутренняя энергия одного моля одноатомного идеального газа выразится формулой , где — постоянная Авогадро. Если учесть, что , то получим:

Для произвольной массы одноатомного идеального газа имеем

Если молекула газа состоит из двух жестко связанных атомов (двухатомный газ), то молекулы при хаотическом движении приобретают еще и вращательное движение, которое происходит вокруг двух взаимно перпендикулярных осей. Поэтому при одинаковой температуре внутренняя энергия двухатомного газа больше, чем одноатомного, и выражается формулой

Наконец, внутренняя энергия многоатомного газа (молекула содержит три или больше атомов) в два раза больше, чем у одно-атомного при той же температуре:

поскольку вращение молекулы вокруг трех взаимно перпендикулярных осей вносит в энергию теплового движения такой же вклад, как поступательное движение молекулы по трем взаимно перпендикулярным направлениям.

Отметим, что формулы (5.23) и (5.24) теряют силу для реальных газов при высоких температурах, так как при этом в молекулах возникают еще колебания атомов, что ведет к увеличению внутренней энергии газа. (Почему это не относится к формуле (5.22)?)

Работа газа при изменении его объема

Физический смысл молярной газовой постоянной. Опыт показывает, что сжатый газ в процессе своего расширения может выполнять работу. Приборы и агрегаты, действия которых основаны на этом свойстве газа, называют пневматическими. На этом принципе действуют пневматические молотки, механизмы для закрывания и открывания дверей на транспорте и т. д.

Представим себе цилиндр с подвижным поршнем, заполненный газом (рис. 5.4).

Пока давление газа внутри цилиндра и окружающего наружного воздуха одинаковы, поршень неподвижен. Пусть при этом температура газа и окружающей среды равна а давление равно р.

Будем теперь медленно нагревать газ в цилиндре до температуры . Газ при этом начинает изобарически расширяться (внешнее давление р остается постоянным), и поршень переместится из положения 1 в положение 2 на расстояние . При этом газ совершит работу против внешней силы. Сила F, совершающая эту работу, будет равна рS, где S — площадь сечения цилиндра. Из механики известно, что работа выражается формулой , или . Так как есть приращение объема газа в процессе его изобарического нагревания от до , имеем

Нетрудно сообразить, что при изохорическом процессе работа газа равна нулю, так как никакого изменения объема, занятого газом, в этом случае не происходит. Вообще следует помнить, что газ выполняет работу только в процессе изменения своего объема, т. е. при . Отметим, что при расширении газа работа газа положительна; при сжатии газа положительную работу выполняют внешние силы, а работа газа в этом случае отрицательна.

Выясним, как можно определить работу газа по графику зависимости р от V в том или ином газовом процессе. При изобарическом процессе график зависимости р от V представляет собой прямую линию, параллельную оси абсцисс, так как р постоянно. Из рис. 5.5 видно, что работа газа в этом случае численно равна заштрихованной площади.

Выясним, как найти работу газа при изотермическом процессе. На рис. 5.6 изображена изотерма идеального газа. При таком процессе газ выполняет работу, так как в этом случае отлично от нуля. Формулу (5.25) здесь применять нельзя, так как она верна при постоянном давлении р, а в изотермической процессе р изменяется. Однако можно взять такое малое приращение объема , при котором изменением давления можно пренебречь. Тогда приближенно можно считать, что при увеличении объема газа на давление остается постоянным. Работу при этом можно вычислять по формуле . На рис. 5.6 она выражается заштрихованной площадью.

Разбивая интервал на множество интервалов , настолько малых, что работу на каждом из них можно вычислять по формуле , полную работу газа найдем как сумму элементарных работ . Это означает, что работа газа будет равна сумме площадей, подобных заштрихованной площади на рис. 5.6. Следовательно, работа газа при изотермическом процессе выражается площадью, ограниченной двумя ординатами и , отрезком оси абсцисс и графиком зависимости р от V.

Можно строго доказать, что работа газа при любом процессе выражается площадью, ограниченной двумя ординатами, отрезком оси абсцисс и графиком того процесса в координатах V и р.

Выясним теперь физический смысл молярной газовой постоянной R. Применяя формулу (5.25) к одному молю идеального газа, получим

Но из уравнения Клапейрона — Менделеева (5.8) для одного моля можно записать для двух состояний газа:

Подставляя это выражение в (5.26), будем иметь , или

Из (5.27) следует, что молярная газовая постоянная численно равна работе, совершаемой одним молем идеального газа при его изобарическом нагревании на один кельвин.

Из соотношения видно, что постоянная Больцмана показывает, сколько работы в среднем приходится на одну молекулу идеального газа при изобарическом нагревании на один кельвин.

Услуги по физике:

Лекции по физике:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Уравнение Клапейрона-Менделеева

Что такое уравнение Клапейрона-Менделеева

Идеальный газ — это газ, в котором пренебрегают взаимодействием молекул газа между собой.

Идеальными считают разреженные газы. Особенно близкими к идеальным считают гелий и водород.

Идеальный газ — это упрощенная математическая модель, которая широко применяется для описания свойств и поведения реальных газов при атмосферном давлении и комнатной температуре.

Давление, объем и температура — это основные параметры состояния системы, и они связаны друг с другом. Соотношение, при котором определяется данная связь, называется уравнением состояния данного газа.

Существует эквивалентная макроскопическая формулировка идеального газа — это такой газ, который одновременно будет подчиняться закону Бойля-Мариотта и Гей-Люссака, то есть:

p V = c o n s t * T

В представленном выше уравнении состоянии газа под const подразумевается количество молей.

Свойства классического и квазиклассического идеального газа описываются уравнением состояния идеального газа, которое называется уравнением Менделеева-Клапейрона, ниже представлена формула Менделеева-Клапейрона.

p V = m M R T = n R T , где m — масса газа, M — молярная масса газа, R = 8 , 314 Д ж / ( м о л ь * К ) — универсальная газовая постоянная, T — температура (К), n — количество молей газа.

Таким образом давление и объем прямо пропорциональны количеству молей и температуре.

Также уравнение Клапейрона-Менделеева можно записать в ином виде:

p V = N k T , где N — это количество молекул газа массой m , k = 1 , 38 * 10 – 23 Д ж / К — постоянная Больцмана, которая определяет «долю» газовой постоянной, приходящуюся на одну молекулу и определяется по формуле:

N = m N A M , где

N A = 6 . 02 * 10 23 м о л ь – 1 ; — это постоянная Авогадро.

Какое значение имеет универсальная газовая постоянная

Универсальная газовая постоянная (R) — это величина, которая является константой, численно равная работе расширения одного моля идеального газа в изобарном процессе при увеличении температуры на 1 K.

Значение данной константы находится как произведение постоянной Больцмана ( k = 1 , 38 * 10 – 23 Д ж / К ) на число Авогадро ( N A = 6 . 02 * 10 23 м о л ь – 1 ) . Таким образом универсальная газовая постоянная принимает следующее значение: R = 8 , 314 Д ж / ( м о л ь * К ) .

Постоянную Больцмана используют в формулах, описывающих изучаемое явление или поведение рассматриваемого объекта с микроскопической точки зрения, тогда как универсальная газовая постоянная более удобна при расчетах, касающихся макроскопических систем, когда число частиц задано в молях.

Связь с другими законами состояния идеального газа

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса и один трех макропараметров (давление, температура или объем) — остаются неизменными.

Количественные зависимости между двумя параметрами газа при фиксированном третьем параметре называют газовыми законами, которые связывают эти параметры.

Изопроцессы — это термодинамические процессы, во время протекания которых количество вещества и один из макропараметров состояния: давление, объем, температура или энтропия — остается неизменным.

В зависимости от того, какой параметр остается неизменным различают разные процессы, которые выражаются законами, являющимися следствием уравнения состояния газа:

• изотермический процесс (T=const);
• изохорный процесс (V=const);
• изобарный процесс (p=const).

Изотермический процесс (T=const)

Процесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим.

Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой — термостатом. Им может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.

Согласно уравнению Клапейрона-Менделеева, в любом состоянии с неизменной температурой произведение давления газа на объем одно и то же, то есть постоянно:

Этот закон был открыт экспериментально английским ученым Бойлем и несколько позднее французским ученым Мариоттом. Именно поэтому он называется закон Бойля-Мариотта.

Закон Бойля-Мариотта справедлив для любых газов, а также для смеси газов (например, для воздуха).

Зависимость давления газа от объема при постоянной температуре изображается графической кривой — изотермой. Изотерма для различных температур представлена в координатах pV на рис.1. и представляет собой гиперболу.

Рис.1. Изотерма в pV — координатах.

Изохорный процесс (V=const)

Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным.

Из уравнения состояния следует, что отношение давлений газа данной массы при постоянно объеме равно отношению его абсолютных температур:

p 1 p 2 = T 1 T 2

Газовый закон был установлен экспериментально в 1787 г. французским физиком Ж. Шарлем и носит название закона Шарля: давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре.

Так, если в качестве одного из состояний газа выбрать состояние газа при нормальных условиях, тогда

p = p 0 T T 0 = p 0 γ T

Коэффициент γ называют температурным коэффициентом давления газа. Он одинаков для всех газов.

Зависимость давления газа от температуры при постоянном объеме изображается графически прямой, которая называется изохорой (Рис.2).

Рис.2 Изображение изохоры в pT-координатах.

Изобарный процесс (p=const)

Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным.

Из уравнения Клапейрона-Менделеева вытекает, что отношение объемов газа данной массы при постоянном давлении равно отношению его абсолютных температур.

V 1 V 2 = T 1 T 2

Если в качестве второго состояния газа выбрать состояние при нормальных условиях (нормальном атмосферном давлении, температуре таяния льда) следует:

V = V 0 T T 0 = V 0 α T

Этот газовый закон был установлен экспериментально в 1802 г французским ученым Гей-Люссаком.

Закон Гей-Люссака: объем данной массы газа при постоянном давлении прямо пропорционален абсолютной температуре.

Коэффициент α называют температурным коэффициентом объемного расширения газов.

Зависимость объема газа от температуры при постоянном давлении изображается графической прямой, которая называется изобарой (Рис.3).

Рис. 3. Изобара в VT-координатах.

Использование универсального уравнения для решения задачи

В реальности проводятся различные физико-химические процессы. Рассмотрим каким образом уравнение состояния идеального газа и законы, связанные с ним находят применение для решения физических и химических задач.

Определить давление кислорода в баллоне объемом 1 м 3 при температуре t = 27 C o . Масса кислорода 1 кг.

Так как в уравнении даны объем и температура — два из трех макроскопических параметров, а третий (давление) нужно определить, то мы можем использовать уравнение Клапейрона-Менделеева:

p V = n R T = m M R T

Не забываем перевести температуру в Кельвины:

T = t + 273 = 27 + 273 = 300 K

Молярная масса кислорода известна из таблицы Менделеева:

M ( O 2 ) = 2 * 16 = 32 г / м о л ь = 32 * 10 – 3 к г / м о л ь

Выразим из уравнения состояния давления и поставим все имеющиеся данные:

p = n R T V = m R T M V = 1 * 8 . 31 * 300 32 * 10 – 3 * 1 = 77 . 906 П а = 78 к П а

Ответ: p = 78 кПа.

Каким может быть наименьший объем баллона, содержащего кислород массой 6,4 кг, если его стенки при t = 20 C o выдерживают p = 1568 Н / с м 2 ?

Используем уравнение Менделеева-Клапейрона, из которого выражаем объем кислорода, который нужно найти:

p = n R T V = m R T M V

Молярная масса кислорода предполагается равной:

M ( O 2 ) = 2 * 16 = 32 г / м 3

Не забываем перевести температуру в Кельвины:

T = t + 273 = 20 + 273 = 293 K

Переводим давление: p = 15680000 Па

Выражаем из уравнения Клапейрона-Менделеева объем и подставляем значения, данные в условиях задачи:

V = n R T p = m R T M p = 6 . 4 * 8 . 31 * 293 15680000 * 32 * 10 – 3 = 3 . 1 * 10 – 2 м 3 = 31 л .

Используя уравнение состояния идеального газа, доказать, что плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .

Согласно уравнению Менделеева-Клапейрона:

p = n R T V = m R T M V

Плотность — это величина, характеризующая массу некоторого объема и находится по формуле:

ρ = m V и л и V = m ρ

Тогда p m ρ = n R T = m R T M

Откуда выражаем плотность газа:

Для водорода эта формула запишется следующим образом:

ρ H 2 = p M H 2 R T

По условию задачи водород и любой другой газ находятся при одинаковых условиях, откуда следует, что:

ρ H 2 M H 2 = p R T

Поставим последнее выражение в выражение для плотности любого газа:

ρ = M * ρ H 2 M H 2

Молярная масса водорода, исходя из таблицы Менделеева равна 2 г/моль и тогда. Молекулярная масса численно равная молярной и представляет собой массу молекулы в атомных единицах, поэтому в дальнейшем мы совершили переход к молекулярной массе.

ρ = M r * ρ H 2 2

Вывод: плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .

Рассмотрим несколько задач на законы, связанные с уравнение Клапейрона-Менделеева, то есть на изотермические, изохорные, изобарные процессы.

При уменьшении давления газа в 2,5 раза его объем увеличился на 12 л. Какой объем занимал газ в начальном состоянии, если температура на протяжении всего процесса оставалась постоянной?

По условию задачи температура в ходе всего процесса оставалась постоянной, откуда следует, что у нас изотермический процесс, и мы можем воспользоваться для решения законом Бойля-Мариотта.

p 1 V 1 = p 2 V 2 , г д е p 1 – давление газа в начальном состоянии (до расширения), V 1 — объем газа в начальном состоянии, p 2 = p 1 2 . 5 — давление газа в конечном состоянии (после расширения), V 2 = V 1 + ∆ V — объем газа в конечном состоянии.

Откуда можем найти начальный объем:

p 1 V 1 = p 1 2 . 5 ( V 1 + ∆ V ) = p 1 2 . 5 V 1 + p 1 2 . 5 ∆ V

V 1 ( p 1 – p 1 2 . 5 ) = p 1 2 . 5 ∆ V

p 1 2 . 5 V 1 ( 2 . 5 – 1 ) = p 1 2 . 5 ∆ V

V 1 = ∆ V 1 , 5 = 8 л

Ответ: первоначальный объем газа был равен 8 л.

Газ находится в баллоне при температуре 400 К. До какой температуры нужно нагреть газ, чтобы его давление увеличилось в 1,5 раза?

Так как нагревание газа по условиям данной задачи происходит при постоянном объеме, значит перед нами изохорный процесс.

При изохорном процессе:

p 1 T 1 = p 2 T 2

T 2 = p 2 T 1 p 1

p 2 p 1 = 1 . 5 T 2 = 1 . 5 * T 1 = 1 . 5 * 400 = 600 K

При 27°C объем газа равен 600 мл. Какой объем займет газ при 57°C, если давление будет оставаться постоянным?

Так как давление по условию остается постоянным, то можем использовать закон Гей-Люссака.

V 1 V 2 = T 1 T 2

V_2 – искомый объем

Для правильного расчета необходимо перевести температуры из Цельсий в Кельвины:

T 1 = 273 + 27 = 300 K

T 2 = 273 + 57 = 330 K

T 2 V 1 T 1 = V 2

V 2 = ( 600 * 330 ) / 300 = 660 м л

Газ в трубе плавильной печи охлаждается от температуры t 1 = 1150 ° С д о t 2 = 200 ° С . Во сколько раз увеличивается плотность газа при этом? Давление газа не меняется.

Так как по условию задания давления газа не изменяется, значит перед нами изобарный процесс. Для решения воспользуемся законом Гей-Люссака:

V 1 V 2 = T 1 T 2

Перейдем к абсолютной температуре:

T 1 = 1150 + 273 = 1423 K

T 2 = 200 + 273 = 473 K

Масса газа: m = ρ 1 V 1 = ρ 2 V 2

Использование этих формул приводит к следующему:

[spoiler title=”источники:”]

http://natalibrilenova.ru/uravnenie-sostoyaniya-idealnogo-gaza/

http://wika.tutoronline.ru/fizika/class/10/uravnenie-klapejronamendeleeva

[/spoiler]