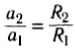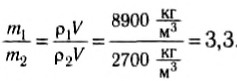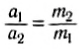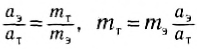Как найти изменение массы в физике

Содержание:

1. Масса
2. Второй закон Ньютона
3. Масса — мера инертности тела
4. Система единиц измерения механических величин
5. Примеры решения задач на второй закон Ньютона

Масса – это физическая величина, одна из основных характеристик материи, определяющая её инертные и гравитационные свойства, масса рассматривается как мера инертности тела по отношению к действующей на него силе и как источник поля тяготения равны (принцип эквивалентности), в международной системе единиц (си) обозначается в килограммах.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Масса

Всякое тело притягивается Землёй. Сила, с которой Земля притягивает тело, называется весом тела. С понятием веса тела тесно связано другое, более общее
понятие — масса тела.

Массой тела называется количество вещества, содержащегося в этом теле.

Масса литра воды в 1000 раз больше массы 1 см3 воды, масса бревна во много раз больше массы полена из такого же дерева. Словом, массы однородных тел тем больше, чем больше объёмы этих тел. При равенстве их объёмов равны и массы. Так, например, массы двух одинакового объёма кусков железа равны между собой. Если положить эти куски на чашки весов, то они окажутся в равновесии. Это даёт нам возможность измерять массы тел взвешиванием.

Рис. 98. Измерение массы тела.

Массы двух тел равны, если эти тела одинаково притягиваются Землёй в одном и том же месте,
т. е. если они уравновешивают друг друга на чашках рычажных весов. При этом совершенно безразлично, из каких веществ состоят эти тела. Если массу одного из этих тел принять за единицу массы, то и масса другого тела, которое уравновешивается первым, будет также равна единице массы.

За единицу массы принята масса платинового цилиндра, хранящегося в Сере (близ Парижа). Эта масса называется килограммом. В отличие от единицы силы, обозначаемой кГ, единица массы сокращённо обозначается кг.

В физике за единицу массы принимают 0,001 кг. Эта единица называется граммом (сокращённое обозначение—г).

В практике эталоны масс изготовляют в виде гирь различной величины.

Чтобы измерить массу тела, надо положить на одну чашку весов это тело, а на другую—гири. При равновесии весов масса тела равна массе гир,,. На рисунке 98 показано, что масса тела равна 0,5 кг.

Второй закон Ньютона

Во втором законе Ньютона устанавливается связь между силой, действующей на тело, массой тела и ускорением, с которым движется это тело.

Рис. 99. Прибор для установления зависимости ускорения от силы, действующей на тело.

Рассмотрим сначала, как зависит ускорение одного и того же тела от величины силы, действующей на тело. Проделаем следующий опыт (рис. 99). К тележке, которая может (с малым трением) двигаться по столу, прикреплён динамометр. К другому концу динамометра прикреплена нитка с грузом М, переброшенная через блок. По показаниям динамометра мы сможем определить силу, действующую на тележку. Пользуясь капельницей, отметим пути, пройденные тележкой при ускоренном движении за различные промежутки времени под действием постоянной силы. Измерения показывают, что пути эти пропорциональны квадратам времён. Таким образом, движение под действием постоянной силы есть равноускоренное движение.

Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле  определяем ускорение а.

Будем подвешивать к концам нити различные грузы, каждый раз измеряя динамометром силу и вычисляя соответствующее этой силе ускорение тележки.

Результаты таких измерений и вычислений отражены в таблице.

Из таблицы видно, что с увеличением силы в 1,5 раза ускорение увеличивается тоже в 1,5 раза; если сила увеличивается в 2 раза, в 2 раза увеличивается и ускорение, и т. д., т. е. ускорение тележки прямо пропорционально силе, действующей на тележку.

Математически это можно записать в виде формулы:

Чтобы установить, как зависит ускорение от массы тела, будем действовать на тележку какой-нибудь постоянной силой.

Нагружая тележку гирями, изменим массу движущихся тел.

Ускорение, получаемое тележкой, будем вычислять так же, как и в первом случае.

Результаты опытов снова занесём в таблицу.

Данные таблицы показывают, что при неизменной силе увеличение массы тела в два раза приводит к уменьшению ускорения в два раза, и наоборот, при уменьшении массы в два раза ускорение увеличивается в два раза, т. е. ускорение тележки с грузами обратно пропорционально их общей массе. Математически этот вывод можно
выразить формулой:

Итак, результаты опытов показывают, что ускорение, с которым движется тело, пропорционально действующей на тело силе и обратно пропорционально массе этого тела.

Кроме того, ускорение тела совпадает с этой силой по направлению.

Этот вывод, как показал Ньютон, имеет всеобщий характер; он носит название второго закона Ньютона.

Во втором законе Ньютона говорится о действии одной силы. Но практически на тело всегда действуют несколько сил. Нам уже известно, что в расчётных целях мы действие нескольких сил можем заменить действием одной силы — равнодействующей. Поэтому в случае, когда на тело действуют несколько сил, под силой, вызывающей ускорение тела, подразумевается их равнодействующая.

Второй закон Ньютона математически можно выразить в виде следующей формулы:

откуда

Величина силы равна произведению массы тела на ускорение.

Таким образом, второй закон Ньютона позволяет вычислить величину силы, если известна масса тела и ускорение, с которым оно движется.

В частности, на основании второго закона Ньютона вес тела Р можно выразить через массу этого тела т и ускорение свободного падения g:

Р = mg.

Из сопоставления формулы F=ma и P=mg видно, что

т. е. ускорение движения тела под действием некоторой силы во столько же раз больше или меньше ускорения свободного падения, во сколько раз действующая сила больше или меньше веса тела.

При решении задач с помощью указанного выше отношения однородные величины должны быть выражены в одних и тех же единицах.

Пример. Санки с седоком весят 70 кГ и скатываются с горы с ускорением  Определить силу, движущую санки.

Р=70 кГ;

g=
а =
F = ?

Из формулы определим F: 

Масса — мера инертности тела

Первый закон Ньютона утверждает, что всякое тело обладает свойством инерции, иначе говоря, всякое тело инертно. Какова мера инертности тела? Обратимся к следующему примеру.

Пусть по горизонтальному пути с одинаковой скоростью движутся два вагона, один пустой, другой гружёный. Пусть на каждый из них одновременно начали действовать одинаковые силы, тормозящие их движение. Какой из этих вагонов будет дольше сохранять своё движение? Опыт показывает, что гружёный вагон будет двигаться дольше, следовательно, можно сказать, что он обладает и большей инертностью. Но масса гружёного вагона больше массы пустого; отсюда следует, что чем больше масса тела, тем более оно инертно.

Рис. 100. Масса наковальни значительно больше массы молота.

Этот вывод непосредственно вытекает из второго закона Ньютона. Действительно, по второму закону Ньютона т. е. ускорение обратно пропорционально массе, а так как масса гружёного вагона больше массы пустого, то и ускорение его движения будет меньше (ускорение направлено против движения). Следовательно, гружёный вагон дольше будет сохранять своё движение.

Итак, масса тела является мерой его инертности. 

Из второго закона Ньютона  следует,что любая сколь угодно малая сила может вызвать ускоренное движение тела.

Не противоречит ли этому то, что мы иногда, толкая тяжёлый предмет, не можем сдвинуть его с места? Нисколько не противоречит. Дело в том, что между предметом и полом существует трение, и нам, чтобы привести его в движение,надо преодолеть это трение, а для этого сила, с которой мы толкаем предмет, должна быть больше силы трения, что не всегда бывает.

Изменение скорости тела зависит от массы тела и от времени действия силы на тело. Это видно хорошо на следующем опыте.

Положим на одну чашку весов тяжёлую плиту и уравновесим её гирями или каким-нибудь другим грузом. Если резко ударить небольшим молоточком по плите, то равновесие весов не нарушится.

Если же положить на чашки весов тела с малой массой, то уже при самом незначительном ударе равновесие весов нарушится.

Чем больше масса тела, тем меньшее изменение скорости вызывает действующая на него сила. Это учитывается в технике.

Рис. 101. Машина на массивном фундаменте.

Так, например, для уменьшения сотрясений от ударов делают массивными и прочно соединяют с землёй мостовые „быки“ и упоры; массивными делают наковальни: относительные размеры молота и наковальни видны на рисунке 100. По этой же причине станки и машины делают массивными и устанавливают их на массивные фундаменты. На рисунке 101 изображена машина, установленная на массивном основании.

Нам известен способ определения массы тела с помощью взвешивания тела на рычажных весах. Второй закон Ньютона даёт нам другой способ определения массы — как меры инертности тела по величине силы и ускорению:

Опытом проверено, что оба эти способа определения массы тела (по весу и по инертности) дают совершенно одинаковые результаты.

Система единиц измерения механических величин

Чтобы применять формулы для числовых расчётов, необходимо установить, в каких единицах измеряются физические величины.

Физические законы связывают физические величины определёнными зависимостями. Поэтому если произвольно выбрать единицы для измерения некоторых величин, то единицы для измерения других величин получатся на основе соответствующих законов. Например, в формуле s = vt дана зависимость между тремя величинами. Если мы произвольно выберем единицы каких-нибудь двух величин, то единица третьей величины определится из этого уравнения. Условившись, например, измерять путь в метрах, а время в секундах, мы должны будем измерять скорость в

Зависимости, существующие между физическими величинами, дают возможность составить такую совокупность единиц, в которой для измерения механических величин достаточно выбрать произвольно три единицы: единицу длины, единицу массы, или силы, и единицу времени; такая совокупность единиц называется системой единиц.

Выбранные произвольно единицы системы называются основными единицами, а все другие — производными единицами.

В физике принята система единиц, в которой основными единицами являются: единица длины—1 см (сотая часть международного метра), единица массы— 1 г (тысячная часть международного килограмма) и единица времени—1 сек ( средних солнечных суток, измеряемая весьма точными часами, которые систематически проверяются астрономическими наблюдениями) (Солнечные сутки—промежуток времени между двумя следующими друг за другом полуднями. Так как продолжительность солнечных суток в разные времена года несколько различна, то в практику введены средние солнечные сутки, продолжительность которых равна средней длительности суток за год).

Эта система называется системой единиц CGS (по первым буквам слов—сантиметр, грамм, секунда).

Единица скорости в этой системе единица ускорения 

Полагая в формуле F=ma второго закона Ньютона m = 1 г, получим единицу силы в системе CGS:

За единицу силы в системе CGS принимается такая сила, под действием которой масса в 1 г движется с ускорением, равным Эта единица называется диной (сокращённо дн).

В системе единиц, применяемой в настоящее время в СССР при электрических и магнитных измерениях, за основные единицы принимаются:

единица длины  — 1  м,

единица массы  — 1  кг,

единица времени  — 1 сек,

единица тока  — 1  ампер.

Сокращённо мы эту систему единиц будем называть MKSA (по первым буквам слов—метр, килограмм, секунда, ампер).

Единицей силы в системе MKSA будет такая сила, под действием которой масса в 1 кг движется с ускорением  Эта единица называется ньютон (сокращённо н). Таким образом,

Вычислим, сколько в одном ньютоне содержится дин. или  
В практике довольно широко распространена так называемая техническая система единиц. В этой системе основными единицами являются:

единица длины —1 м,

единица силы —1 кГ,

единица времени—1 сек.

Единица массы в этой системе единиц является производной и может быть определена из равенства т. е. единицей массы в технической системе единиц является масса, которая под действием силы в 1 кГ движется с ускорением

Сокращённое обозначение этой единицы—т. е. м. Таким образом,

Между различными единицами массы и силы существуют следующие соотношения:

1 кГ есть сила, с которой Земля притягивает массу в 1 кг и сообщает ей ускорение Отсюда:  или округлённо:

Так как то 1 кГ = 9,8 н.

Примеры решения задач на второй закон Ньютона

1.    Постоянная сила, равная 2 кГ, действует на тело, вес которого 19,6 кГ. С какой скоростью будет двигаться тело в горизонтальном направлении по прошествии 5 сек., если начальная скорость движения равна нулю?

Расчёты ведём в системе CGS.

Дано: F = 2 кГ=2*980000 дн = 1960000 дн;

m=19600 г; t = 5 сек. Найти 

Под действием постоянной силы тело будет двигаться равноускоренно. Скорость этого тела определим по формуле:

Время t дано по условиям задачи.

Ускорение найдем на основании второго закона:

Ответ: 
2.    Тело весом 98 кГ движется со скоростью, равной
Какую силу надо приложить, чтобы остановить это тело в течение 5 мин.? Расчёты провести в технической системе единиц.

Дано: Р = 98 кГ;  t = 300 сек. Найти F.

Искомую силу найдём на основании второго закона:

F = mа.

Под действием этой силы тело будет двигаться равнозамедленно, отрицательное ускорение его а определим по формуле;

Так как то

 и

По второму закону Ньютона Р = mg, откуда
 

Ответ. 

3. На тело, движущееся с начальной скоростью в  подействовали силой в 10 Г в направлении движения, после чего тело прошло за 5 сек. путь в 200 м. Определить вес тела. Расчёты провести в системе CGS.

Вес тела в системе CGS, выражаемый в динах, найдётся на основании второго закона Ньютона: 

Надо найти массу в граммах. Для этого воспользуемся тем F же вторым законом, ускорение а по условиям задачи вычислим по формуле:

откуда

Масса тела 

Ответ.

При решении физических задач мы производим математические действия не только с числовыми значениями величин, но и над их наименованиями. Если предварительно все величины, указанные в задаче, выразить в единицах одной системы единиц и правильно применить соотношения, существующие между физическими величинами, то ответ всегда получится в единицах этой системы. Это позволяет нам не загромождать вычисления наименованиями единиц; достаточно указать наименование величины только в окончательном результате.

Пример. Тело массой 0,01 кг, двигаясь равноускоренно без начальной скорости, за 1 мин. прошло в горизонтальном направлении путь, равный 18 м. Определить силу, действующую на тело.

Дано: m = 0,01 кг; t = 1 мин.; s = 18 м. Найти F.

Выражаем все данные в задаче величины в единицах одной системы, например в системе CGS.

m = 10 г; t = 60 сек.; s = 1800 см.

По второму закону Ньютона F = ma.    (1)

Масса дана, ускорение а находим по формуле пути равноускоренного движения: откуда

Подставим значение а из равенства (2) в равенство (1), получим:

Подставляя численные значения величин в равенство (3), определим величину силы F:

Услуги по физике:

1. Заказать физику
2. Заказать контрольную работу по физике
3. Помощь по физике

Лекции по физике:

1. Физические величины и их измерение
2. Основные законы механики
3. Прямолинейное равномерное движение
4. Прямолинейное равнопеременное движение
5. Сила
6. Взаимодействия тел
7. Механическая энергия
8. Импульс
9. Вращение твердого тела
10. Криволинейное движение тел
11. Колебания
12. Колебания и волны
13. Механические колебания и волны
14. Бегущая волна
15. Стоячие волны
16. Акустика
17. Звук
18. Звук и ультразвук
19. Движение жидкости и газа
20. Молекулярно-кинетическая теория
21. Молекулярно-кинетическая теория строения вещества
22. Молекулярно – кинетическая теория газообразного состояния вещества
23. Теплота и работа
24. Температура и теплота
25. Термодинамические процессы
26. Идеальный газ
27. Уравнение состояния идеального газа
28. Изменение внутренней энергии
29. Переход вещества из жидкого состояния в газообразное и обратно
30. Кипение, свойства паров, критическое состояние вещества
31. Водяной пар в атмосфере
32. Плавление и кристаллизация
33. Тепловое расширение тел
34. Энтропия
35. Процессы перехода из одного агрегатного состояния в другое
36. Тепловое расширение твердых и жидких тел
37. Свойства газов
38. Свойства жидкостей
39. Свойства твёрдых тел
40. Изменение агрегатного состояния вещества
41. Тепловые двигатели
42. Электрическое поле
43. Постоянный ток
44. Переменный ток
45. Магнитное поле
46. Электромагнитное поле
47. Электромагнитное излучение
48. Электрический заряд (Закон Кулона)
49. Электрический ток в металлах
50. Электрический ток в электролитах
51. Электрический ток в газах и в вакууме
52. Электрический ток в полупроводниках
53. Электромагнитная индукция
54. Работа, мощность и тепловое действие электрического тока
55. Термоэлектрические явления
56. Распространение электромагнитных волн
57. Интерференционные явления
58. Рассеяние
59. Дифракция рентгеновских лучей на кристалле
60. Двойное лучепреломление
61. Магнитное поле и электромагнитная индукция
62. Электромагнитные колебания и волны
63. Природа света
64. Распространение света
65. Отражение и преломление света
66. Оптические приборы и зрение
67. Волновые свойства света
68. Действия света
69. Линзы и получение изображений с помощью линз
70. Оптические приборы и глаз
71. Фотометрия
72. Излучение и спектры
73. Квантовые свойства излучения
74. Специальная теория относительности в физике
75. Теория относительности
76. Квантовая теория и природа поля
77. Строение и свойства вещества
78. Физика атомного ядра
79. Строение атома

Масса является одним из важных свойств материи. Это понятие применяют при решении задач различного характера, начиная от проблем в механике и заканчивая химическими расчетами. Рассмотрим в статье, с помощью каких формул массу в физике можно рассчитать.

Что это такое?

Прежде чем приводить формулы массы в физике, дадим ей определение. Этим термином называется физическая величина, которая пропорциональна количеству материи, заключенной в данном теле. Следует не путать ее с количеством вещества, которое выражается в молях. Масса в СИ вычисляется в килограммах. Другими ее единицами являются тонны и граммы.

Вам будет интересно:Слово “кворум”. Значение и происхождение термина. Нюансы определения

Масса бывает двух важных видов:

• инерционная;
• гравитационная.

Первый вид рассматриваемой физической величины характеризует инерционные свойства тела, то есть способность некоторой силы изменять скорость тела, а также кинетическую энергию, которой оно обладает.

Гравитационная масса связана с интенсивностью притяжения между любыми телами. Она играет важную роль в космосе, поскольку благодаря притяжению между звездами и планетами существует наша галактика и наша Солнечная система. Однако гравитационная масса проявляет себя и в повседневной жизни в виде наличия у всех тел некоторого веса.

Формулы для инерции

В физике формула нахождения массы инерционной имеет следующий вид:

m = F / a

Здесь F – сила, которая на тело действует и вызывает появление у него ускорения a. Формула показывает, что чем больше будет действующая сила и чем меньше она сообщит ускорение телу, тем больше инерционная масса m.

Помимо записанного выражения, следует привести еще одну формулу нахождения массы в физике, которая связана с явлением инерции. Эта формула имеет вид:

m = p / v

Здесь p – количество движения (импульс), v – скорость тела. Чем большим количеством движения обладает тело и чем меньше его скорость, тем большую инерционную массу оно имеет.

Формула для гравитации

Математическое описание явления гравитации стало возможным благодаря многочисленным наблюдениям за движением космических тел. Результаты всех этих наблюдений в XVII веке обобщил Исаак Ньютон в рамках закона всемирного тяготения. Согласно этому закону, два тела, которые имеют массы m1 и m2, друг к другу притягиваются с такой силой F:

F = G * m1 * m2 / r2

Где r – расстояние между телами, G – некоторая постоянная.

Если в данное выражение подставить значение массы нашей планеты и ее радиус, тогда мы получим следующую формулу массы в физике:

m = F / g

Здесь F – сила тяжести, g – ускорение, с которым тела падают на землю вблизи ее поверхности.

Как известно, наличие силы тяжести обуславливает то, что все тела имеют вес. Многие путают вес и массу, полагая, что это одна и та же величина. Обе величины действительно связаны через коэффициент g, однако вес – величина изменчивая (она зависит от ускорения, с которым движется система). Кроме того, вес измеряется в ньютонах, а масса в килограммах.

Весы, которыми человек пользуется в быту (механические, электронные), показывают массу тела, однако измеряют его вес. Перевод между этими величинами является лишь вопросом калибровки прибора.

Плотность и объем

Как было отмечено, масса – это неотъемлемое свойство материи, поэтому ее можно вычислить с помощью других физических характеристик тел. Этими характеристиками являются объем и плотность.

Объем представляет собой некоторую часть пространства, которая ограничена поверхностью тела. Измеряется он в кубических единицах длины, например, в м3.

Плотность – это свойство вещества, которое отражает количество материи, помещенной в единице объема.

Формула массы вещества через объем и плотность записывается так:

m = ρ * V

Чем больше объем тела и чем выше его плотность, тем большей массой оно обладает. В связи с этим фактом полезно вспомнить знаменитую загадку про то, что имеет большую массу: 1 тонна пуха или 1 тонна железа. В отсутствии выталкивающей архимедовой силы массы обоих веществ равны. Пух имеет гораздо меньшую плотность, чем железо, однако разница в плотности компенсируется аналогичной разницей в объеме.

Относительная

Понятие об относительной массе применяется в атомной физике и в химии. Поскольку массы атомов и молекул имеют очень маленькие значения (≈10-27 кг), то оперировать ими на практике при решении задач оказывается крайне неудобно. Поэтому сообществом ученых было решено использовать так называемую относительную массу, то есть рассматриваемая величина выражается в единицах массы по отношению к массе известного эталона. Этим эталоном стала 1/12 массы атома углерода, которая равна 1,66057*10-27 кг. Соответствующая относительная величина получила название атомной единицы (а. е. м.).

Формулу относительной массы M можно записать так:

M = ma / (1 / 12 * mC)

Где ma – масса атома в килограммах, mC – масса атома углерода в килограммах. Например, если в это выражение подставить значение массы атома кислорода, то его а. е. м. будет равна:

M = 26,5606 * 10-27 / (1,66057 * 10-27) = 15,9949.

Поскольку а. е. м. является относительной величиной, то она не имеет размерности.

Удобство применения этого термина на практике заключается не только в небольших и целых значениях этой единицы измерения. Дело в том, что значение а. е. м. совпадает по величине с молярной массой, выраженной в граммах. Последняя представляет собой массу одного моль вещества.

Энергия

Выше были приведены разные формулы, как найти массу в физике. Завершая статью, хотелось бы отметить связь массы и энергии. Это связь носит фундаментальный характер, который отражает пространственно-временные свойства нашей Вселенной. Соответствующая формула массы в физике, полученная Альбертом Эйнштейном, имеет вид:

E = m * c2

Квадрат скорости света c является коэффициентом перевода между массой и энергией. Это выражение говорит о том, что обе величины, по сути, являются одной и той же характеристикой материи.

Записанное выражение было подтверждено экспериментально при изучении ядерных реакций и реакций элементарных частиц.

Содержание:

Масса тела:

Согласно первому закону Ньютона в инерциальных системах отсчета скорость тела не изменяется при условии, что воздействие других тел скомпенсировано. А если это условие не выполняется?

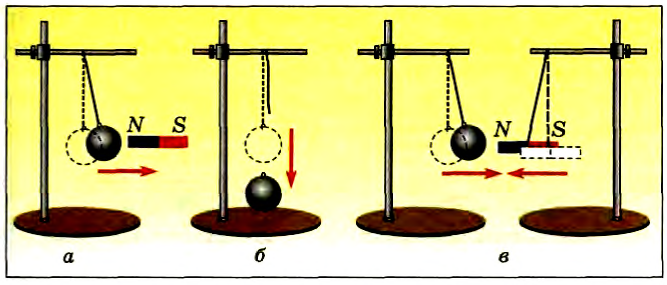
Проведем опыт с железным шариком, подвешенным на нити, прикрепленной к неподвижному штативу. Шарик покоится, так как воздействие нити компенсирует притяжение Земли. Если поднести сбоку к шарику магнит, то под его действием шарик начнет двигаться (рис. 29, а).

Если убрать магнит, а нить, на которой подвешен шарик, перерезать, то воздействие Земли не будет уравновешено, и, как вы уже хорошо знаете, шарик начнет двигаться ускоренно вниз (рис. 29. б).

Эти опыты и многочисленные наблюдения за различными телами в окружающем мире позволяют сделать вывод, что ускоренное движение тела — результат нескомпенсированного воздействия на него других тел.

А возможно ли какое-либо воздействие на конкретное тело без того, чтобы это тело также оказывало свое действие (противодействие)?

Если в нашем опыте с шариком мы подвесим рядом магнит на нити, то сможем наблюдать одновременное движение шарика и магнита друг к другу (рис. 29, в).

Ударяя по мячу (рис. 30), человек ощущает воздействие мяча во время удара. Если подержать за ручку тяжелый портфель некоторое время, то на ладони останутся вмятины из-за действия на нее этого груза.

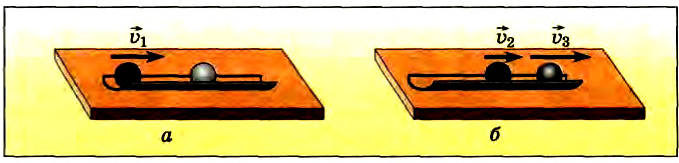
Чтобы исследовать, как происходит взаимодействие тел и от чего зависят их ускорения при этом, проведем несколько экспериментов. Возьмем два одинаковых по размеру шара — один из алюминия, а второй из железа — и рассмотрим их столкновение при движении по неподвижному горизонтальному металлическому желобу.

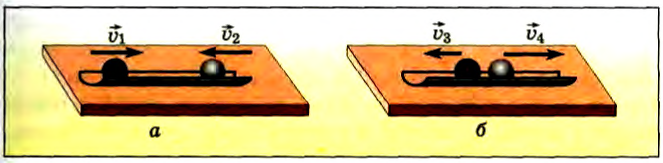
Пусть железный шар катится по желобу к покоящемуся алюминиевому шару (рис. 31, а). Мы увидим, что во время взаимодействия (столкновения) оба шара изменят свою скорость, т. е. будут иметь ускорения (рис. 31, б). Если оба шара движутся навстречу друг другу, то при столкновении их скорости также изменяются (рис. 32, а, б).

Рис. 31

Рис. 32

Значит, при взаимодействии оба шара изменяют свою скорость, но измерить и сравнить полученные ими при ударе ускорения в таком опыте сложно. Поэтому проведем опыт, в котором ускорения взаимодействующих тел можно достаточно просто определить.

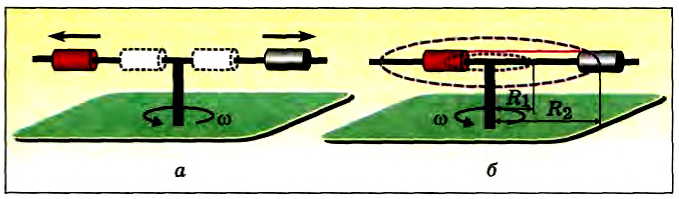
Для опыта используем два одинаковых по размеру цилиндра из алюминия и меди с просверленными вдоль их осей отверстиями. Вставим в отверстия цилиндров гладкий стержень, вдоль которого цилиндры могут легко скользить. Закрепим стержень с цилиндрами в установке, которая может вращать стержень с постоянной угловой скоростью в горизонтальной плоскости.

Если стержень вращать, то можно наблюдать скольжение цилиндров к концам стержня (рис. 33, а). Остановим вращение, свяжем цилиндры нитью и вновь приведем во вращение стержень.
Так как теперь цилиндры взаимодействуют друг с другом с помощью нити, то они будут вращаться вместе со стержнем, находясь на определенных расстояниях от оси вращения (рис. 33, б). Рассчитаем и сравним центростремительные ускорения цилиндров.

Рис. 33

Таким образом, модули ускорений относятся как радиусы окружностей, по которым вращаются центры цилиндров, и в нашем опыте это отношение равно 3,3.

Если провести этот опыт при другой угловой скорости вращения или связав цилиндры нитью другой длины, то радиусы окружностей изменятся, но их отношение, а значит, и отношение модулей ускорений останется тем же. Как объяснить постоянство отношений модулей ускорений для двух взаимодействующих цилиндров?

Ускорение характеризует быстроту изменения скорости тела. В 7-м классе вы познакомились с физической величиной — массой тела, от которой также зависела величина изменения скорости тела. Вы знаете, что, чем больше масса тела, тем труднее изменить его скорость.

Сравним массы медного и алюминиевого цилиндров. Так как их размеры одинаковы, то одинаковы и объемы, и отношение масс равно отношению плотностей меди и алюминия, т. е.:

Таким образом, сравнение отношений модулей ускорений и масс цилиндров показывает, что ускорения цилиндров обратно пропорциональны их массам:

Многочисленные эксперименты, проведенные учеными по исследованию самых разнообразных взаимодействий тел, показывают, что всегда выполняется полученная нами закономерность.

Отношение модулей ускорений двух взаимодействующих тел равно обратному отношению их масс.

Что же такое масса тела? Ответ на этот вопрос в полном объеме требует знания более сложных разделов физики.

Поэтому рассмотрим упрощенное представление о массе тела. В 8-м классе вы узнали, что все тела состоят из атомов и молекул, которые имеют массу. Тогда масса тела — это суммарная масса всех его частиц. На основании опытных данных упрощенное понятие «масса» можно охарактеризовать следующим образом:

1. масса тела — физическая скалярная величина, равная сумме масс всех частиц (или материальных точек), из которых оно состоит (свойство аддитивности);
2. для данной системы тел выполняется закон сохранения массы — при любых процессах в системе ее масса остается неизменной;
3. масса тела не зависит ни от взаимодействий, в которых тело участвует, ни от скорости движения тела;
4. масса тела при его взаимодействии с другими телами определяет модуль полученного телом ускорения.

Вы уже знаете, что единицей массы в СИ является 1 кг. Это масса специально изготовленного эталона (образца). Как, используя эталон массы, измерить массу определенного тела?

Если привести во взаимодействие эталон и тело неизвестной массы, а затем измерить их ускорения, то можно определить неизвестную массу тела:

Конечно, для обычных тел такой способ менее удобен, чем обычное взвешивание. Зато определение масс космических тел, например планет по ускорению их спутников или мельчайших частиц вещества (атомов, молекул и т. п.) по ускорению при их взаимодействии, производится практически всегда.

Главные выводы:

1. Тело движется ускоренно в инерциальной системе отсчета, если воздействие других тел на него нескомпенсировано.
2. При взаимодействии двух тел воздействие испытывают оба тела, а отношение модулей ускорений двух взаимодействующих тел равно обратному отношению их масс.
3. Масса тела — физическая скалярная аддитивная величина, не зависящая от взаимодействий, в которых участвует тело, и от его скорости.

Что такое масса тела

Наблюдение 1. Мяч падает на поверхность Земли, а потом отскакивает от неё -это пример взаимодействия двух тел. Мы уже знаем, что результатом взаимодействия тел является изменение их скорости и направления движения. Мяч после столкновения отскакивает почти с той же скоростью, что и падал, но в обратном направлении. В состоянии Земли практически не заметно никаких изменений, хотя на самом деле они есть, но бесконечно малые. В приведённом примере наглядно видно, что результаты взаимодействия тел для каждого из них будут разными и зависят от свойств этих тел. Ежедневный опыт и специальные исследования свидетельствуют, что в результате взаимодействия разные тела получают определённое изменение скорости за неодинаковые интервалы времени: одни за большие, другие — за меньшие. Движение того тела, которое в результате взаимодействия медленнее изменяет собственную скорость, более напоминает движение по инерции, поэтому говорят, что оно более инертно.

Инертность – это свойство тела, заключающееся в том, что для изменения его скорости при взаимодействии с любыми другими телами нужно определённое время.

Свойством инертности обладают все тела. Количественной мерой инертности тела является масса тела.

Масса тела – это физическая величина, характеризующая инертность тела. Чем больше масса тела, тем более оно инертно.

Существуют разные методы определения массы тела. Все они базируются на использовании свойств, присущих всем без исключения телам, например на свойстве инертности тел. На практике наиболее удобным оказался метод измерения массы, связанный с хорошо известным явлением взаимодействия всех тел с Землей.

• Заказать решение задач по физике

Наблюдение 2. Вы, наверное, неоднократно наблюдали, как падают капли дождя, снежинки, как оседают мелкие пылинки, как любое тело, поднятое над Землей и отпущенное, стремительно летит к Земле. Эти явления объясняются тем, что все физические тела притягиваются Землей, т. е. взаимодействуют с ней. Опыты показывают, что значение этого взаимодействия тем больше, чем больше масса тела.

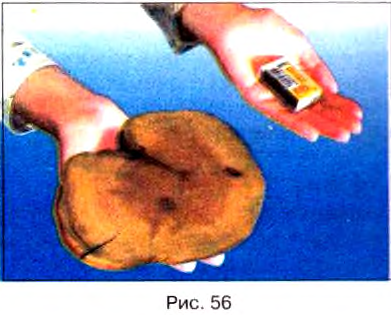
Опыт. Возьмём в одну руку спичечный коробок, а в другую — кусок дерева (рис. 56).

Оба тела вследствие притяжения их Землёй давят на удерживающие их руки. Большую нагрузку ощущаем в руке, держащей кусок дерева, т. е. он тяжелее спичечного коробка и соответственно его масса больше, чем у коробки.

Если массы тел близки по значению, если тела очень малы или слишком велики, то сравнить их массу на руках уже невозможно. Как можно измерить массу тела с достаточной точностью?

Для определения массы тела используют специальные приборы — весы. В магазинах, аптеках, на почте с помощью весов разных конструкций взвешивают продукты, лекарства, посылки и пр. Определение массы тела с помощью весов называют взвешиванием.

Массу тела обозначают малой латинской буквой 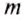. За единицу массы в СИ принят один килограмм (1 кг). Международный образец (эталон) (рис. 57, а) килограмма сохраняется во Франции (г. Севр близ Парижа). Он изготовлен из платиноиридиевого сплава и имеет форму цилиндра диаметром и высотой 39 мм (рис. 57, б). По этому образцу с большой точностью изготовлены копии для всех стран мира.

На практике применяют также кратные и дольные единицы массы: тонну (т), грамм (г), миллиграмм (мг):

Основной частью учебных весов (рис. 58) является стержень (коромысло весов), который может свободно поворачиваться вокруг оси, размещённой посреди стержня (в следующей главе вы узнаете, что такой механизм называют рычагом). К его концам подвешены чашки весов. Определение массы тела с помощью весов основано на том, что коромысло находится в равновесии при условии, что массы тел, лежащих на разных чашках, одинаковы. При этом коромысло весов располагается горизонтально, а стрелка прибора указывает на нулевую отметку. Таким образом, взвешивая тело на весах, сравнивают его массу с массой эталона.

Пример:

На одну чашку весов положим тело, массу которого нужно измерить, а на другую — гири с известными массами (рис. 59).

Гири подбираем такие, чтобы установилось равновесие. Определяем общую массу гирь, уравновесивших тело. Масса тела равна сумме масс гирь, т. е. 370 г. Результат записывают так:

= 370 г = 0,370 кг.

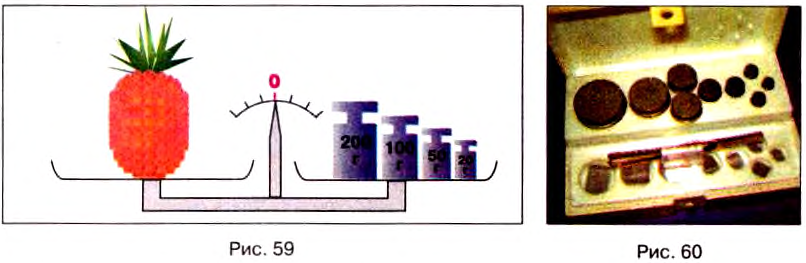
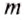
Для взвешивания используют специальный набор гирь разной массы. На рисунке 60 изображён набор гирь к учебным весам. В нём есть 9 гирь массой 100, 50, 20, 20, 10, 5, 2, 2 и 1 г. С их помощью можно подобрать любую массу от 1 до 210 г. Гири, масса которых меньше 1 г, изготавливают из алюминия в виде пластинок массой 500, 200, 200, 100, 50, 20, 20, 10 мг.

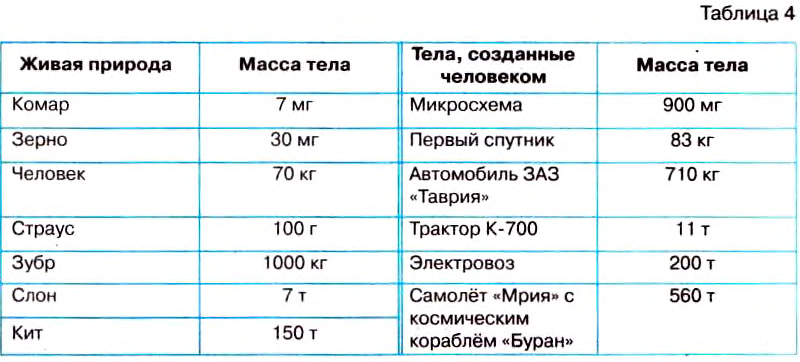
С помощью специальных весов можно измерять как большие, так и малые массы. В таблице 4 приведены массы тел живой природы, а также массы тел, созданных человеком.

Кстати:

Кроме системных существуют и другие единицы массы. Например, массу драгоценных камней измеряют в каратах: 1 карат = 0,2 г. В Киевской Руси единицей массы была 1 гривна, которая составляла приблизительно 410 г. Позднее эта единицу стали называть фунтом: 1 фунт = 0,025 пуда = 32 лота = 96 золотников = 9216 долей = 0,4 кг. Распространённой была и такая единица массы, как пуд (около 16 кг). Для взвешивания лекарств используются граны: 1 гран = 0,6 г. По традиции ещё применяют унцию, значение которой в зависимости от области применения лежит в пределах 28-31 г.

Пример №1

На столе лежит книжка. Вследствие взаимодействия с какими телами книжка находится в состоянии покоя?

Ответ: книжка взаимодействует с Землёй, а также со столом.

Пример №2

Почему с разбега можно прыгнуть на большее расстояние, чем без разбега?

Ответ: за счёт инерции.

Пример №3

На рисунке 61, а, б, в изображён процесс измерения массы воды с помощью весов. Какова масса сосуда с водой? Какова масса пустого сосуда? Какова масса воды в сосуде?

Ответ:

а)весы были уравновешены;

б)масса сосуда с водой составляла 70 г 200 мг = 70,2 г = 0,0702 кг;

в)масса пустого сосуда – 15 г 600 мг = 15,6 г = 0,0156 кг; масса воды в сосуде – 54 г 600 мг = 54,6 г = 0,0546 кг.

Определение массы

Для количественного выражения инертности тел пользуются физической величиной, которую называют массой.

Масса – это физическая величина, которая характеризует инертные свойства тела.

Очевидно, что масса стального шарика в предыдущем опыте была большей, чем алюминиевого, поэтому они и приобрели различную скорость.

Единицы массы

Как и всякая физическая величина, масса имеет единицу измерения. Основной единицей массы является килограмм (кг).

Килограмм равен массе международного прототипа килограмма.

Килограмм принадлежит к основным единицам Международной системы единиц (СИ). За единицу массы килограмм взята масса специально изготовленного образца (эталона) (рис. 43). Он сделан из сплава платины и иридия и имеет форму цилиндра. Сохраняется эталон массы в Международном бюро мер и весов в г. Севре, который находится вблизи Парижа.

Если тело имеет массу 1 кг, то под действием силы 1 Н его скорость каждую секунду изменяется на 1м/с.

Как и для других единиц измерения, для килограмма используют производные единицы:

• 1 г = 0,001 кг — 10^-3 кг;
• 1 мг = 0,000001 кг = 10^-6 кг;
• 1 т = 1000 кг = 10³ кг;
• 1 ц = 100 кг = 10² кг.

Для прямого измерения массы используют различные весы. Среди них самые распространенные и самые простые – рычажные (рис. 44). На этих весах сравнивают взаимодействие с Землей тела и эталонных грузов, положенных на чашки весов. На практике используют также и другие весы, которые приспособлены к различным условиям работы и имеют различную конструкцию.

Как увеличивается масса при скорости

Изменение массы тела при его движении рассматривается лишь в так называемом релятивистском случае, описываемом уравнениями релятивистской механики или специальной теорией относительности.

Вспомните из курса общей физики, что собой представляют преобразования Галилея. Данные преобразования являются некоторым способом для определения того, является ли данный случай релятивистским или нет. Релятивистский случай означает движение с достаточно большими скоростями. Величина таких скоростей приводит к тому, что преобразования Галилея становятся невыполнимы. Как известно, данные правила преобразования координат являются всего лишь переходом из одной системы координат, которая покоится, в другую (движущуюся).

Запомните, что скоростью, соответствующей случаю релятивистской механики, является скорость, близкая к скорости света. В этой ситуации вступают в силу преобразования координат Лоренца.

Выпишите из учебника по физике выражение для релятивистского импульса. Классическая формула импульса, как известно, представляет собой произведение массы тела на его скорость. В случае же больших скоростей к классическому выражению импульса добавляется типичная релятивистская добавка в виде корня квадратного из разницы единицы и квадрата отношения скорости тела и скорости света. Данный множитель должен стоять в знаменателе дроби, числителем которой является классическое представление импульса.

Обратите внимание на вид соотношения релятивистского импульса. Его можно разделить на две части: первая часть произведения – это отношение классической массы тела к релятивистской добавке, вторая часть – это скорость тела. Если провести аналогию с формулой для классического импульса, то первую часть релятивистского импульса можно принять за общую массу, свойственную случаю движения с большими скоростями.

Заметьте, что масса тела становится зависимой от величины его скорости в случае принятия за общий вид массы релятивистского выражения. Классическую массу, стоящую в числителе дроби, принято называть массой покоя. Из ее названия становится понятно, что тело обладает ей, когда его скорость равна нулю.

Если же скорость тела становится близка к скорости света, то знаменатель дроби выражения для массы стремится к нулю, а сама она стремится к бесконечности. Таким образом, при увеличении скорости тела его масса также растет. Причем по виду выражения для массы тела становится понятно, что изменения становятся заметны только тогда, когда скорость тела достаточно велика и отношение скорости движения к скорости света сравнимо с единицей.