Из трех состояний вещества газы претерпевают наибольшие изменения объема при изменении температуры и давления, но жидкости также претерпевают изменения. Жидкости не реагируют на изменения давления, но могут реагировать на изменения температуры, в зависимости от их состава. Чтобы рассчитать изменение объема жидкости по отношению к температуре, необходимо знать ее коэффициент объемного расширения. С другой стороны, все газы расширяются и сжимаются более или менее в соответствии с законом идеального газа, и изменение объема не зависит от его состава.
TL; DR (слишком долго; не читал)
Рассчитайте изменение объема жидкости при изменении температуры, посмотрев на коэффициент ее расширения (β) и используя уравнение ∆V = V 0 x β * ∆T. И температура, и давление газа зависят от температуры, поэтому для расчета изменения объема используйте закон идеального газа: PV = nRT.
Изменение объема жидкости
Когда вы добавляете тепло в жидкость, вы увеличиваете кинетическую и вибрационную энергию частиц, из которых она состоит. В результате они увеличивают диапазон своего движения в пределах сил, удерживающих их вместе как жидкость. Эти силы зависят от силы связей, удерживающих молекулы вместе и связывающих молекулы друг с другом, и различаются для каждой жидкости. Коэффициент объемного расширения – обычно обозначаемый строчной греческой буквой бета (β_) –_ является мерой количества, которое конкретная жидкость расширяет на степень изменения температуры. Вы можете посмотреть это количество для любой конкретной жидкости в таблице.
Как только вы узнаете коэффициент расширения (β _) _ для рассматриваемой жидкости, рассчитайте изменение объема по формуле:
ΔV = V 0 • β * (T 1 – T 0)
где ∆V – изменение температуры, V 0 и T 0 – начальный объем и температура, а T 1 – новая температура.
Изменения громкости для газов
Частицы в газе имеют большую свободу движения, чем в жидкости. Согласно закону идеального газа давление (P) и объем (V) газа взаимно зависят от температуры (T) и количества молей присутствующего газа (n). Уравнение идеального газа имеет вид PV = nRT, где R – постоянная, известная как постоянная идеального газа. В единицах СИ (метрических) значение этой константы составляет 8, 314 Дж ÷ моль – градус К.
Давление постоянно: переставляя это уравнение, чтобы изолировать объем, вы получаете: V = nRT ÷ P, и если вы сохраняете давление и число молей постоянными, у вас есть прямая зависимость между объемом и температурой: ∆V = nR∆T ÷ P где ∆V – изменение объема, а ∆T – изменение температуры. Если вы начинаете с начальной температуры T 0 и давления V 0 и хотите узнать объем при новой температуре T 1, уравнение становится:
V 1 = + V 0
Температура постоянна: если вы сохраняете температуру постоянной и позволяете давлению меняться, это уравнение дает вам прямую связь между объемом и давлением:
V 1 = + V 0
Обратите внимание, что объем больше, если T 1 больше, чем T 0, но меньше, если P 1 больше, чем P 0.
Давление и температура изменяются: когда температура и давление изменяются, уравнение становится:
V 1 = n • R • (T 1 – T 0) ÷ (P 1 – P 0) + V 0
Введите значения для начальной и конечной температуры и давления и значение для начального объема, чтобы найти новый объем.
При изучении
теплового объемного расширения удобно,
как и при линейном расширении, рассматривать
относительное изменение объема
Измерения показывают,
что в пределах не очень большого интервала
температур можно считать, что относительное
изменение объема пропорционально
изменению температуры:
(9.3.1)
Коэффициент
пропорциональности а называют
температурным
коэффициентом объемного расширения.
Он показывает, на какую долю своего
первоначального значения изменяется
объем тела при изменении температуры
на 1 К. Коэффициент объемного расширения,
как и коэффициент линейного расширения,
зависит от природы вещества и температуры.
Зависимость а от температуры незначительна
и ею можно пренебречь, если интервал
изменения температуры невелик. Для
большинства твердых тел коэффициент а
имеет порядок 10‑5—10-4
К-1,
т. е. очень мал по сравнению с коэффициентом
объемного расширения газов.
Из формулы
(9.3.1) легко найти выражение для объема
тела при любой температуре:
(9.3.2)
В
этой формуле значение начального объема
V0
обычно
берут при начальной температуре t0
=
0 °С. Однако и здесь, как в случае линейного
расширения, можно пользоваться формулой
(9.3.3)
где
V0
— объем тела при температуре 1x;
V2
—
объем тела при температуре t2;
Δt
= t2—
t1
Объем полого
(пустого) твердого тела (сосуда) при
нагревании увеличивается так, как если
бы это тело было сплошным. Объем полости
в твердом теле (сосуде) при его нагревании
увеличивается так, как увеличивался бы
объем тела, изготовленного из того же
вещества и имеющего форму и размер
полости.
Связь между коэффициентами линейного и объемного расширения
Коэффициент
линейного расширения α1
и
коэффициент объемного расширения а
связаны между собой. Эту связь можно
найти, рассматривая тепловое расширение
тела простой формы, например кубика с
ребром l0.
При
нагревании кубика на Δt
каждая
его сторона увеличится на Δl
и станет равной
(9.3.4)
Объем тела при
этом будет равен:
Но
V0
=и
V
= l3.
Следовательно,
(9.3.5)
Подставляя
I
из
уравнения (9.3.4) в уравнение (9.3.5), получим:
Так
как величина α1
очень
мала, то при малых изменениях температуры
членами
и
можно пренебречь по сравнению с членом
3α1.
Поэтому
(9.3.6)
Итак,
температурный
коэффициент объемного расширения равен
утроенному коэффициенту линейного
расширения.
Зависимость плотности вещества от температуры
При
изменении температуры тел изменяется
и их плотность. Пусть при температуре
t1
плотность
вещества равна ρ1,
а объем тела равен V1.
При
температуре t2
значения
этих величин стали соответственно
равными ρ2
и V2.
Так
как при изменении температуры масса
тела т
не
изменяется, то
Разделив почленно
второе равенство на первое, получим
отсюда
Пользуясь формулой (9.3.3), можно записать
(9.3.7)
Так
как αΔt
значительно меньше единицы, то для
приближенных расчетов можно упростить
эту формулу следующим образом:
Пренебрегая выражением (αΔt)2по сравнению с единицей, получим
(9.3.8)
При нагревании
плотность вещества уменьшается.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Изменение объема при нагревании, первый закон Гей-Люссака
Если
| Vt | объем газа при произвольной температуре t, | метр3 |
|---|---|---|
| V0 | объем газа при температуре 0°С, | метр3 |
| t | температура, | 0°С |
| β | коэффициент объемного расширения газа, | 1/K |
то
[ V_t = V_0 ( 1 + βt ) ]
Из формулы (1) следует, что при температуре t1
[ V_1 = V_0 ( 1 + βt_1 ) ]
[ V_1 = V_0 bigg( 1 + frac{t_1}{273.15} bigg) ]
[ V_1 = V_0 bigg( 1 + frac{t_1}{T_0} bigg) ]
[ V_1 = V_0 bigg( frac{T_0 + t_1}{T_0} bigg) ]
а при другой температуре t2 соответственно
[ V_2 = V_0 ( 1 + βt_2 ) ]
[ V_2 = V_0 bigg( 1 + frac{t_2}{273.15} bigg) ]
[ V_2 = V_0 bigg( 1 + frac{t_2}{T_0} bigg) ]
[ V_2 = V_0 bigg( frac{T_0 + t_2}{T_0} bigg) ]
Разделив первое равенство на второе, получим
[ frac{V_1}{V_2} = frac{T_0 + t_1}{T_0 + t_2} ]
или
[ frac{V_1}{V_2} = frac{T_1}{T_2} ]
или
[ frac{V}{T} = const ]
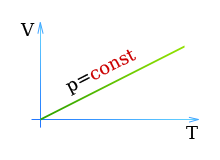
Первый закон Гей-Люссака
Первый закон Гей-Люссака гласит: При постоянном давлении объем газа V пропорционален абсолютной температуре газа T
[ V sim T qquad (enspace p = const enspace) ]
Изменение объема при нагревании, первый закон Гей-Люссака |
стр. 523 |
|---|
Термическим расширением называется изменение размеров и объёма тела под воздействием температуры.
При изменении температуры изменяются размеры твёрдых тел. Расширение под воздействием температуры характеризуется коэффициентом линейного термического расширения.
Изменение линейных размеров тела описывается формулой:
l=l0(1+α⋅Δt)
, где:
— первоначальная длина тела;
— коэффициент линейного термического расширения;
— разница температур.
Коэффициент линейного термического расширения показывает, на какую часть первоначальной длины или ширины изменится размер тела, если его температура повысится на (1) градус.
|
Рис. (1). Удлинения различных материалов |
|
Если рассматривать стержень твёрдого вещества длиной (1) метр, то при повышении температуры на один градус длина стержня изменится на такое число метров, которое равно коэффициенту линейного расширения |
Пример:
(10) км железнодорожного пути при увеличении температуры воздуха на (9) градусов (например, от (-5) до (+4)) удлиняются на
10000⋅0,000012⋅9=1,08
метра. По этой причине между участками рельсов оставляют промежутки.
|
Рис. (2). Поведение рельсов |
На этом рисунке видно, что происходит в жаркую погоду, если между участками рельсов оставлены неверные промежутки |
Термическое расширение надо учитывать и в трубопроводах, там используются компенсаторы — изогнутые трубы, которые при изменении температуры воздуха при необходимости могут сгибаться. На рисунке видно, что произойдёт, если не будет компенсатора.
Рис. (3). Трубопровод
Инженерам, проектирующим мосты, оборудование, здания, которые подвержены изменениям температуры, необходимо знать, какие материалы можно соединять, чтобы не образовались трещины.
Электрикам, которые протягивают линии электропередачи, необходимо знать, каким изменениям температуры будут подвержены провода. Если летом провода натянуты, то зимой они оборвутся.
При термическом расширении металлов используют автоматические выключатели тепловых приборов. Этот выключатель состоит из двух плотно соединённых пластин различных металлов (с различными термическими коэффициентами). Биметаллические пластины под воздействием температуры сгибаются или выпрямляются, замыкая или размыкая электрическую цепь.
|
Рис. (4). Биметаллические пластины, поведение при изменении температуры |
………………………………………………………………………….. Биметаллические пластины состоят из двух металлов с различными коэффициентами линейного расширения. При изменении температуры длина каждой пластины изменяется по-разному, в зависимости от этого пластины выгибаются либо вверх, либо вниз |
С изменением линейных размеров изменяется также и объём тела. Изменение объёма тела описывается формулой, похожей на формулу линейного расширения, только вместо коэффициента линейного термического расширения используется коэффициент объёмного термического расширения.
Изменение объёма тела под воздействием температуры описывается формулой:
V=V0(1+β⋅Δt)
, где:
— первоначальный объём тела;
— коэффициент объёмного термического расширения;
— разница температур.
Коэффициент объёмного термического расширения показывает, на какую часть первоначального объёма изменится объём тела после повышения температуры на (1) градус.
|
Вещество |
Коэффициент объёмного расширения β, K−1 |
|
Бензин |
(0,001100) |
|
Ртуть… |
(0,000181) |
|
Эфир |
(0,001650) |
|
Глицерин |
(0,000505) |
|
Нефть |
(0,000850) |
|
Керосин |
(0,000900) |
|
Спирт |
(0,001100) |
|
Вода |
(0,000208) |
Пример:
если объём спирта при температуре
−30°C
равен
500л
, то при температуре
25°C
его объём увеличится на
500⋅0,00011⋅(25−(−30))=3,025л.
Из формулы изменения объёма следует, что при повышении температуры объём жидкости увеличивается, но вода в очередной раз отличилась своими уникальными свойствами, так как при нагревании воды до определённой температуры она не расширяется, а сжимается.
|
Рис. (5). Изменение объёма в зависимости от температуры |
|
При нагревании воды с температуры таяния льда вначале у неё уменьшается объём, и только после 4°C её объём начинает увеличиваться |
Источники:
Рис. 4. Биметаллические пластины, поведение при изменении температуры. © ЯКласс.
Рис. 5. Изменение объёма в зависимости от температуры. © ЯКласс.