Однородным электрическим полем называют такое электрическое поле, вектор напряжённости которого не зависит от точки пространства ((vec{r(t)} =const)), где (vec{r(t)}) — радиус-вектор исследуемой точки.
Потенциальные и непотенциальные силы в электродинамике
Все силы можно разделить на потенциальные и непотенциальные.
Работа потенциальной силы зависит только от начального и конечного положения тела и от формы траектории не зависит. Сила Кулона является потенциальной.
Потенциальность кулоновских сил позволяет говорить о потенциальной энергии заряда в поле электрических сил. По определению потенциальной энергии полагается, что изменение потенциальной энергии при его переносе из точки (А) в точку (Б) в любом электрическом поле — это работа кулоновских сил при перемещении заряда между этими точками, взятая со знаком минус:
(A=-(E_Б-E_А)). ((1))
Энергия системы заряженных тел
Вокруг заряженного тела появляется электрическое поле, которое оказывает действие на другие заряды. Таким образом, система, состоящая из какого-либо набора заряженных тел, обладает потенциальной энергией, которую обычно называют кулоновской или электрической.
Изменение потенциальной энергии заряда в однородном электрическом поле
Рассмотрим изменение потенциальной энергии положительного заряда (q), если переместить его в однородном электрическом поле из точки (А) в точку (Б) по красной траектории (рис. (1)).
Рис. (1). Перемещение заряда в однородном поле
Она изменяется так же, как если бы заряд перемещался по прямой (чёрной) траектории, поскольку работа потенциальной силы зависит только от начальной и конечной точки траектории.
Сила, действующая на него, постоянна:
(vec{F}=q vec{E}). ((2))
Если ввести радиус-векторы начала и конца этой траектории (vec{r}_А) и (vec{r}_Б) соответственно, то перемещение этого заряда:
(vec{r}=(vec{r}_Б – vec{r}_А)). ((3))
Работу кулоновской силы можно записать как скалярное произведение силы на перемещение:
(A=vec{F}cdot {r}=q vec{E} (vec{r}_Б – vec{r}_А) ). ((4))
Выбрав за ноль потенциальной энергии начальную точку ((vec{r}_А)), перепишем формулу ((1)) в виде:
(A=-E_Б). ((5))
Из формулы ((4)) получим, что потенциальная энергия заряда, который расположен в точке с радиус-вектором (vec{r}_Б=vec{r}) в однородном электрическом поле, равна скалярному произведению радиус-вектора на вектор напряжённости электрического поля:
(E= -A=-q vec{E} cdot vec{r} ), ((6))
что в координатном виде может быть записано как:
(E=-q (E_x x+E_у y+E_z z).) ((7))
Энергия взаимодействия точечных зарядов
Для того чтобы найти энергию взаимодействия точечных зарядов, рассмотрим систему из двух положительных зарядов (q_1) и (q_2). Положим, что заряд (q_1) неподвижен.
Рассмотрим, какую работу совершит электрическое поле, которое создано зарядом (q_1), при перемещении заряда (q_2) из точки (А) в точку (Б) по красной траектории (рис. (2)).
Рис. (2). Перемещение заряда в поле точечного заряда
Как и в случае однородного электрического поля, вместо красной траектории будем рассматривать чёрную траекторию, где из точки (А) в точку (С) заряд перемещается вдоль линии, соединяющей эти два заряда, а из точки (С) в точку (Б) — по дуге окружности, центром которой является первый заряд.
В таком случае работа электрического поля на дуге (СБ) будет нулевой:
(A=vec{F} cdot vec{r}=|F|cdot |r|cos(pi/2)=0,) ((8))
поскольку сила Кулона всегда перпендикулярна перемещению. На участке (АС) сила Кулона сонаправлена с перемещением, а по модулю:
( F(r)=frac{k q_1q_2}{r^2}), ((9))
поэтому работу электрического поля можно рассчитать как:
(A=F(r_A)r+F(r_A+Delta r)Delta r+F(r_A+2Delta r) Delta r+F(r_A+3Delta r) Delta r+ldots +)
(+F(r_C-2Delta r) Delta r+ F(r_C-Delta r) r=sum limits_{r=r_A}^{r_C}F(r)Delta r=sum limits_{r=r_A}^{r_C} frac{k q_1 q_2}{r^2} cdot Delta r.) ((10))
В пределе, когда (Delta r) мало, эта сумма равна:
(A=-frac{k q_1 q_2}{r}). ((11))
Сравнивая формулы ((1)) и ((11)), получаем, что потенциальная энергия взаимодействия точечных зарядов:
(E=frac{k q_1q_2}{r}.) ((12))
Энергия системы (n) точечных зарядов
Если рассматривать систему, состоящую из (n) точечных зарядов, то её потенциальная энергия:
( E=frac{1}{2} sum limits_{i neq j} frac{k q_i q_j}{r_{i,j}}=frac{1}{2} left(frac{k q_1 q_2}{r_{12}}+frac{k q_2 q_1}{r_{21}}+frac{k q_2 q_3}{r_{23}}+frac{k q_3 q_2}{r_{32}}+ldots right),) ((13))
где (r_{i,j}) — это расстояние между (i)-м и (j)-м точечными зарядами, а множитель (frac{1}{2}) появляется из-за того, что в сумме дважды учитывается потенциальная энергия взаимодействия (i)-го и (j)-го точечных зарядов.
Свойство линий напряжённости электрического поля
Поскольку сила Кулона потенциальна, то, если перемещать заряд по любому замкнутому контуру, работа силы Кулона равна нулю.
Отсюда вытекает, что линия напряжённости электростатического поля не замкнута.
Докажем это от противного: предположим, что линия электрического поля замкнута (рис. (3)).
Рис. (3). Замкнутая линия электрического поля
Но тогда при перемещении положительного заряда по замкнутой линии электрического поля работа электрического поля будет равна:
(A=sum vec{F} cdot vec{r}). ((14))
Каждый член этой суммы положителен, поскольку сила всегда сонаправлена с перемещением (рис. (3)).
Мы пришли к противоречию. Следовательно, линии электрического поля не замкнуты.
Источники:
Рис. 1. Перемещение заряда в однородном поле. © ЯКласс.
Рис. 2. Перемещение заряда в поле точечного заряда. © ЯКласс.
Рис. 3. Замкнутая линия электрического поля. © ЯКласс.
Содержание:
Работа по перемещению заряда в электростатическом поле:
В повседневной жизни мы довольно часто, особенно в сухую погоду, встречаемся с ситуацией, когда, коснувшись какого-либо тела, чувствуем неприятный удар. Как показывает опыт, таких сюрпризов можно ожидать от тел, имеющих высокий потенциал.
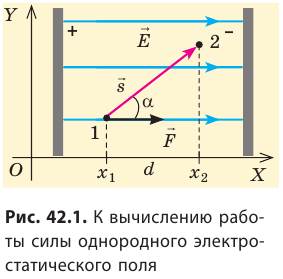
Работа по перемещению заряда в однородном электростатическом поле
Если электростатическое поле действует с некоторой силой на электрически заряженные тела, то оно способно совершить работу по перемещению этих тел.
Пусть в однородном электростатическом поле напряженностью
Вычислим работу А, которую совершает сила 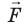
Поле однородное, поэтому сила 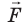
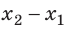
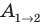
Обратите внимание! Если бы в данном случае заряд перемещался не из точки 1 в точку 2, а наоборот, то знак работы изменился бы на противоположный, то есть работа совершалась бы против сил поля.
Обратите внимание! Формула 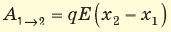
Потенциальным является любое электростатическое поле: работа электростатических (кулоновских) сил (как и работа гравитационных сил) не зависит от формы траектории, по которой перемещается заряд, а определяется начальным и конечным положениями заряда. Если траектория движения заряда замкнута, работа сил поля равна нулю.
Потенциальная энергия заряженного тела в поле, созданном точечным зарядом
Заряженное тело, помещенное в электростатическое поле, как и тело, находящееся в гравитационном поле Земли, обладает потенциальной энергией. Потенциальную энергию заряда, находящегося в электрическом поле, обычно обозначают символом 
Потенциальную энергию взаимодействия двух точечных зарядов Q и q, расположенных на расстоянии r друг от друга, определяют по формуле:
Обратите внимание: 1) потенциальная энергия взаимодействия зарядов положительна (


Что называют потенциалом электростатического поля
Потенциал 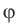

Единица потенциала в Си — вольт:
Из определения потенциала следует, что потенциал ϕ поля, созданного точечным зарядом Q, в точках, которые расположены на расстоянии r от данного заряда, можно рассчитать по формуле:
Из формулы ( *) видно: 1) если поле создано положительным точечным зарядом (Q > 0), то потенциал этого поля в любой точке является положительным ( ϕ > 0); 2) если поле создано отрицательным точечным зарядом (Q < 0), то потенциал этого поля в любой точке является отрицательным (ϕ < 0). Формула ( *) справедлива и для потенциала поля равномерно заряженной сферы (или шара) на расстояниях, которые больше ее радиуса или равны ему.
Если поле создано несколькими произвольно расположенными зарядами, потенциал ϕ поля в любой точке данного поля равен алгебраической сумме потенциалов 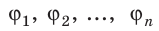
Как определяют разность потенциалов
Когда в электростатическом поле заряд движется из точки 1 в точку 2, это поле совершает работу, которая равна изменению потенциальной энергии заряда, взятому с противоположным знаком: 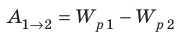
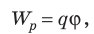
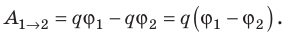
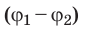
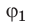
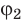
Разность потенциалов — скалярная физическая величина, равная отношению работы сил электростатического поля по перемещению заряда из начальной точки в конечную к значению этого заряда:
Единица разности потенциалов в Си — вольт: 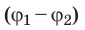
Разность потенциалов между двумя точками поля равна 1 В, если для перемещения между ними заряда 1 Кл электростатическое поле совершает работу 1 Дж. Обратите внимание: в подобных случаях разность потенциалов 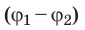
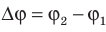
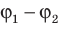
Как связаны напряженность однородного электростатического поля и разность потенциалов
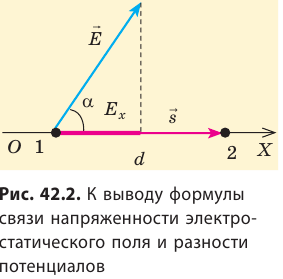
Рассмотрим однородное электростатическое поле на участке между точками 1 и 2, расположенными на расстоянии d друг от друга; пусть из точки 1 в точку 2 под действием поля перемещается заряд q (рис. 42.2).
Совершаемую полем работу можно найти двумя способами: 1) через разность потенциалов между точками 1 и 2: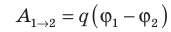
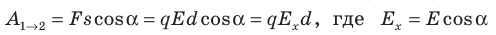
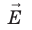
Приравняв оба выражения для работы, получим: 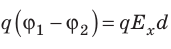
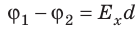
Если заряд перемещается в направлении напряженности электрического поля (
Из последней формулы следует единица напряженности в Си — вольт на метр:
Какие поверхности называют эквипотенциальными
Для визуализации электростатического поля кроме силовых линий используют также эквипотенциальные поверхности.
Эквипотенциальная поверхность — это поверхность, во всех точках которой потенциал электростатического поля имеет одинаковое значение.
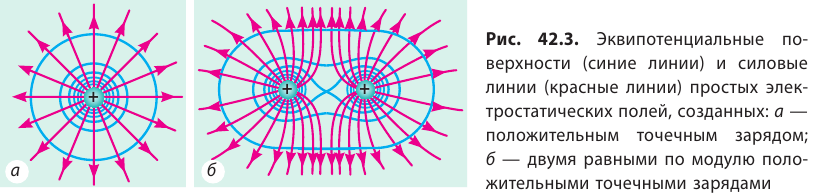
Для наглядности следует рассматривать не одну эквипотенциальную поверхность, а их совокупность. Однако графически изобразить совокупность поверхностей сложно, поэтому обычно изображают только линии пересечения эквипотенциальных поверхностей некоторой плоскостью (рис. 42.3).
Эквипотенциальные поверхности тесно связаны с силовыми линиями электростатического поля. Если электрический заряд перемещается по эквипотенциальной поверхности, то работа поля равна нулю, поскольку A=q ( 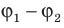
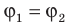
Работу электростатического поля также можно представить через силу 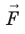
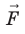
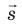
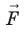
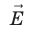
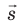
Таким образом, силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям (см. рис. 42.3).
Обратите внимание! Симметрия эквипотенциальных поверхностей повторяет симметрию источников поля. Так, поле точечного заряда сферически симметрично, поэтому эквипотенциальными поверхностями поля точечного заряда являются концентрические сферы; при однородном поле эквипотенциальные поверхности — это система параллельных плоскостей.
- Заказать решение задач по физике
Пример решения задачи
Электрон, начав движение из состояния покоя, прошел ускоряющую разность потенциалов –300 В. Какую скорость приобрел электрон? Масса электрона 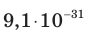
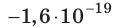
Заряд электрона — отрицательный, его начальная скорость 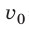
Решение:
Поиск математической модели, решение Согласно теореме о кинетической энергии:
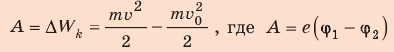
Таким образом, 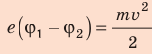
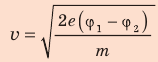
Проверим единицу, найдем значение искомой величины:
Ответ:
Выводы:
- Закон Ома для однородного участка электрической цепи
- Закон Ома для полной цепи
- Закон Ома для цепи переменного тока с последовательным соединением сопротивлений
- Сила и закон Ампера
- Волновое движение в физике
- Продольные и поперечные волны в физике
- Звуковые волны в физике
- Электрическое поле в физике
На прошлых уроках мы с вами говорили о том, что на помещённый
в электростатическое поле пробный заряд действует кулоновская сила, под
действием которой пробный заряд способен перемещаться вдоль линии напряжённости
поля. Из механики мы знаем, что при перемещении тела действующая на него сила
совершает работу. Логично предположить, что и электрическое поле также будет
совершать работу по перемещению в нём заряда.
В общем случае работа сил электрического поля зависит как от
начального и конечного положений перемещаемого заряда, так и от вида
траектории, по которой он движется.
Однако электростатическое поле имеет важную особенность. Работа
сил этого поля при перемещении заряда между двумя точками зависит только от
положения этих точек и не зависит от вида траектории.
Давайте вспомним, что физические поля, работа сил которых
не зависит от формы траектории, называют потенциальными (или консервативными).
Покажем, что электростатическое поле потенциально.
Итак, пусть положительный пробный заряд находится в
однородном электростатическом поле, созданном вертикальными параллельными
пластинами, находящимися на расстоянии d друг от друга и имеющими заряды противоположных знаков.
Предположим, что под действием электрической силы,
действующей со стороны поля, заряд перемещается из точки В в точку С
вдоль линии напряжённости рассматриваемого поля. При этом сила, с которой поле
действует на пробный заряд, совершает работу.
Давайте вспомним, что в общем случае работа постоянной силы
равна произведению модуля этой силы на модуль перемещения и на косинус угла
между ними:
Модуль электрической силы мы найдём, как произведение
величины пробного заряда и модуля напряжённости электростатического поля:
Так как направления силы и перемещения заряда совпадают, то
косинус угла между нами равен единице:
А модуль перемещения заряда равен расстоянию между точками В
и С.
Тогда работа силы однородного электростатического поля по
перемещению заряда прямо пропорциональна величине этого заряда, напряжённости
поля и расстоянию, пройденному зарядом в поле под действием электрической силы:
Теперь предположим, что заряд перемещается не вдоль силовой
линии поля, а под некоторым углом к ней.
Обозначив угол между направлением вектора силы и вектора
перемещения α, запишем формулу для работы поля в общем виде:
Для определения перемещения точки воспользуемся ΔMKN. Это прямоугольный треугольник, в котором гипотенуза
— это искомое перемещение, а один из острых углов — это угол между вектором
силы и вектором перемещения. Тогда очевидно, что произведение модуля вектора
перемещения на косинус угла альфа равно длине прилежащего к углу катета М):
Следовательно, работа поля вновь равна произведению величины
заряда, напряжённости поля и расстоянию, пройденному зарядом в поле под
действием силы:
И, наконец, пусть перемещение нашего заряда из одной точки
поля в другую происходит по криволинейной траектории.
Чтобы найти работу поля, разобьём траекторию движения заряда
на такие малые участки, что бы каждый из них можно было считать прямолинейным.Тогда
работа на поля на всей траектории будет равна алгебраической сумме работ,
совершаемых полем на каждом из маленьких участочков.
А теперь заметим, что в скобках стоит сумма длин
прямолинейных участков, на которые мы разбили траекторию заряда. А это есть ни
что иное, как расстояние между пластинами d.
Таким образом мы получаем уже знакомую нам формулу:
Таким образом действительно, работа силы однородного
электростатического поля по перемещению заряда из одной точки поля в другую не
зависит от формы траектории, по которой двигался пробный заряд, а зависит
только от начального и конечного положений заряда.
Тогда становится очевидным, что в случае движения заряда по
замкнутой траектории работа поля будет равна нулю, так как начальное и конечное
положения заряда совпадают. Следовательно, однородное электростатическое
поле потенциально. Это означает, что электростатическое и гравитационное
поля имеют похожие свойства, определяемые их потенциальным характером.
Применительно к электростатическому полю эти свойства
выражаются в следующем:
Во-первых, точечный электрический заряд, находящийся в любой
точке электростатического поля, обладает потенциальной энергией взаимодействия
с этим полем, значение которой определяют относительно произвольно выбираемой
нулевой точки. В нулевой точке потенциальную энергию заряда в поле принимают
равной нулю. Тогда потенциальная энергия взаимодействия точечного заряда с
электростатическим полем равна работе, которую совершили бы силы поля при
перемещении данного заряда из указанной точки поля в нулевую точку:
А во-вторых, работа сил электростатического поля по
перемещению электрического заряда из начальной точки в конечную равна изменению
потенциальной энергии, взятому с обратным знаком:
Знак «минус» в формуле означает, что если сила
электростатического поля совершает положительную работу (подобно силе
гравитационного поля Земли при падении мяча), то потенциальная энергия
заряженного тела в поле уменьшается. Тогда, согласно закону сохранения энергии,
кинетическая энергия заряженной частицы будет увеличиваться. На этом основано
ускорение заряженных частиц электростатическим полем.
Если работа сил электростатического поля отрицательна
(подобно работе силы гравитационного поля при движении мяча, брошенного вверх),
то потенциальная энергия заряда в поле увеличивается, а кинетическая энергия
наоборот уменьшается.
Обратим внимание ещё и на то, что потенциальная энергия —
это энергия взаимодействия, и её необходимо относить не к заряженной частице
или телу, а к системе в целом. В частности, для заряженной частицы, находящейся
в электростатическом поле, это потенциальная энергия взаимодействия
заряженной частицы с другими заряженными частицами или телами, являющимися
источниками этого поля.
Потенциальная энергия в поле сил тяжести
Изменение потенциальной
энергии измеряется работой сил тяжести
при
h2
= 0 и h1h
. (10)
Видно,
что работа, совершаемая силой тяготения
при изменении высоты тела над поверхностью
Земли, зависит только от начального и
конечного положения тела относительно
Земли и не зависит от формы пути, по
которому происходило перемещение из
начальной точки 1 в конечную точку 2.
Сила,
работа которой
при перемещении точки из одного
произвольного положения в другое не
зависит от формы траектории,
называется
консервативной.
Примерами
консервативных сил могут служить помимо
силы тяготения силы упругости,
электростатического взаимодействия
между заряженными телами.
При
перемещении материальной точки вдоль
замкнутой траектории работа консервативной
силы тождественно равна нулю.
Силы,
работа которых зависит от траектории
перемещения точки, называются
неконсервативными. К
неконсервативным силам относятся силы
трения, магнитные силы.
Правило знаков
Потенциальная
энергия определяется с точностью до
произвольной постоянной С.
Это не отражается на физических законах,
так как в них входит или разность
потенциальных энергий в двух положениях
тела, или производная Еп
по координатам. Поэтому потенциальную
энергию тела в некотором положении
(например, на поверхности Земли) выбирают
нулевой, а энергию тела в других положениях
отсчитывают относительно нулевого
уровня. Тогда
Eп
> 0 при h
> 0; Eп
< 0 при h
< 0 .
Потенциальная энергия в поле упругих сил
Потенциальная
энергия при упругой деформации – это
энергия взаимодействия отдельных частей
тела между собой силами упругости
;
, (11)
Изменение
потенциальной энергии упругого
деформирования определяется работой,
которую совершает внешняя сила при
удлинении пружины от величины х1
до величины х2
(х1
< х2)
.
(12)
Из
формулы (12) видно, что произведенная
работа не зависит от того, каким образом
произошло изменение длины пружины.
Упругая сила, так же как и сила тяготения,
консервативна.
Принимая
за нулевую потенциальную энергию
недеформированной пружины (Еп
= 0 при х =
0), получаем выражение потенциальной
энергии деформированной пружины в виде
.
(13)
С
увеличением деформации x
в два раза энергия упругого деформирования
увеличивается в 4 раза.
Силы и потенциальная энергия
Зная
потенциальную энергию как функцию
координат взаимодействующих материальных
точек, можно вычислить действующие на
эти точки силы.
Пусть
точка переместилась на бесконечно малую
величину
.
Если Fx
сила, действующая на нее, то работа этой
силы при таком перемещении будет равна
убыли потенциальной энергии:
(14)
Векторная форма
записи (14):
,
(15)
где
.
(16)
Вектор,
определяемый выражением (4.27), называется
градиентом скаляра Еп.
Для него наряду с обозначением grad Еп
применяется также обозначение Еп,
значок
(набла) означает символический вектор,
называемый оператором Гамильтона
или набла-оператором:
.
(17)

Энергия – важнейшее понятие в механике. Что такое энергия. Существует множество определений, и вот одно из них. Что такое энергия?
Энергия – это способность тела совершать работу.
Кинетическая энергия
Рассмотрим тело, которое двигалось под действием каких-то сил изменило свою скорость с
v
до
v
. В этом случае силы, действующие на тело, совершили определенную работу
A
. Работа всех сил, действующих на тело, равна работе равнодействующей силы. FрF1F2AF1scosα1F2scosα2Fрcosα.
Установим связь между изменением скорости тела и работой, совершенной действующими на тело силами. Для простоты будем считать, что на тело действует одна сила
F
, направленная вдоль прямой линии. Под действием этой силы тело движется равноускоренно и прямолинейно. В этом случае векторы
Fvas
совпадают по направлению и их можно рассматривать как алгебраические величины. Работа силы F равна AFs. Перемещение тела выражается формулой sv22v122a. Отсюда:
AFsFvvamavva
Amv22mv222mv222mv222.
None Кинетическая энергия – энергия движения тела. При нулевой скорости она равна нулю.
Определение. Кинетическая энергия
[custom_ads_shortcode1]
Терема о кинетической энергии
Вновь обратимся к рассмотренному примеру и сформулируем теорему о кинетической энергии тела. Работа приложенной к телу силы равна изменению кинетической энергии тела. Данное утверждение справедливо и тогда, когда тело движется под действием изменяющейся по модулю и направлению силы. AEK2EK1.

Таким образом, кинетическая энергия тела массы
m
, движущегося со скоростью
v
, равна работе, которую сила должна совершить, чтобы разогнать тело до этой скорости.
AmvEK
.
Чтобы остановить тело, нужно совершить работу Amv22EK
[custom_ads_shortcode2]
Потенциальная энергия
Кинетическая энергия – это энергия движения. Наряду с кинетической энергией есть еще потенциальная энергия, то есть энергия взаимодействия тел, которая зависит от их положения.
Например, тело поднято над поверхностью земли. Чем выше оно поднято, тем больше будет потенциальная энергия. Когда тело падает вниз под действием силы тяжести, эта сила совершает работу. Причем работа силы тяжести определяется только вертикальным перемещением тела и не зависит от траектории.
Вообще о потенциальной энергии можно говорить только в контексте тех сил, работа которых не зависит от формы траектории тела. Такие силы называются консервативными (или диссипативными).

Примеры диссипативных сил: сила тяжести, сила упругости. Когда тело движется вертикально вверх, сила тяжести совершает отрицательную работу. Рассмотрим пример, когда шар переместился из точки с высотой h1 в точку с высотой h2. При этом сила тяжести совершила работу, равную Amgh2h1mgh2mgh1.
Эта работа равна изменению величины
mgh
, взятому с противоположным знаком. Величина ЕПmgh – потенциальна энергия в поле силы тяжести. На нулевом уровне (на земле) потенциальная энергия тела равна нулю.
Определение. Потенциальная энергия
Потенциальная энергия – часть полной механической энергии системы, находящейся в поле диссипативных(консервативных) сил. Потенциальная энергия зависит от положения точек, составляющих систему. Можно говорить о потенциальной энергии в поле силы тяжести, потенциальной энергии сжатой пружины и т.
д. Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.
AEПEП
.
Ясно, что потенциальная энергия зависит от выбора нулевого уровня (начала координат оси OY). Подчеркнем, что физический смысл имеет изменение потенциальной энергии при перемещении тел друг относительно друга. При любом выборе нулевого уровня изменение потенциальной энергии будет одинаковым.
При расчете движения тел в поле гравитации Земли, но на значительных расстояниях от нее, во внимание нужно принимать закон всемирного тяготения (зависимость силы тяготения от расстояния до цента Земли). Приведем формулу, выражающую зависимость потенциальной энергии тела.
EПGmMr
.
Здесь
G
– гравитационная постоянная,
M
– масса Земли.
[custom_ads_shortcode3]
Потенциальная энергия пружины
Представим, что в первом случае мы взяли пружину и удлинили ее на величину
x
. Во втором случае мы сначала удлинили пружину на
x
, а затем уменьшили на
x
. В обоих случаях пружина оказалась растянута на
x
, но это было сделано разными способами. При этом работа силы упругости при изменении длины пружины на x в обоих случаях была одинакова и равнаAупрAkx22.
Величина
Eупрkx
называется потенциальной энергией сжатой пружины. Она равна работе силы упругости при переходе из данного состояния тела в состояние с нулевой деформацией.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter.
Тела, находящиеся в потенциальном поле, обладают способностью в определённых условиях совершать работу. Например, тело, поднятое над Землёй, когда его отпускают, приходит в движение под действием гравитационной силы, совершая работу. Следовательно, тела в данном поле обладают энергией, которую называют потенциальной. Эта энергия зависит от расположения тел, создающих поле, и от положения тела в этом поле, т.е. она зависит от взаимного расположения взаимодействующих тел. Однако от взаимного расположения тел или частей одного и того же тела зависят силы взаимодействия между ними. Итак, энергия, обусловленная взаимодействием тел или частей одного и того же тела, называется потенциальной. Величина потенциальной энергии тела может быть определена лишь с точностью до произвольной постоянной, значение которой зависит от выбора так называемого нулевого уровня, т.е. положения тела, в котором потенциальную энергию условно принимают за ноль. Потенциальная энергия равна той работе, которую совершают силы поля, действующие на тело, при переносе его из данной точки на нулевой уровень. Однако выбор нулевого уровня не отражается на физических законах. Потенциальная энергия тела, находящегося в гравитационном поле, вычисляется по формуле: иWp = mgh, (10) если за нулевой уровень энергии выбрать в бесконечности или на поверхности Земли. Здесь — гравитационная постоянная, М — масса Земли, m — масса тела, h — расстояние от тела до нулевого уровня, g — ускорение свободного падения. Потенциальная энергия деформированной пружины находится по формуле: (11) где k и х — коэффициент жёсткости и величина деформации пружины.
[custom_ads_shortcode1]
Теорема о потенциальной энергии
Работа Ap, совершаемая силами потенциального поля при переносе тела из положенияв положение, может быть выражена через потенциальные энергииWp1иWp2в этих положениях. Она равна Ap= Wp1 Wp2(Wp2 Wp1) Wp, (12) т.е. работа сил потенциального поля равна уменьшению потенциальной энергии перемещаемого тела или изменению потенциальной энергии тела, взятому с обратным знаком. Соотношение (12) называют теоремой о кинетической энергии.
[custom_ads_shortcode2]
Закон сохранения механической энергии
Предположим, что тело движется в гравитационном поле Земли. На него действуют сила тяжести и сила сопротивления воздуха. Тогда работа Aпри переходе тела из одного положения в другое складывается из работыAнксилы сопротивления воздуха (неконсервативная сила) и работыAксилы тяжести (консервативная сила), т.е.A = Aнк + Aк. Согласно теореме о кинетической энергии, запишем:A = Wк2 –Wк1, гдеWк1иWк2—кинетическая энергия тела в начальном и конечном положениях. Левые части последних равенств равны.Поэтому приравняем и их правые части, т.е. Aнк + Aк = Wк2 – Wк1. Согласно теореме о потенциальной энергии, Aк = Wp – Wp,гдеWpиWp—потенциальная энергия тела в данном поле в начальном и конечном положениях. Учитывая это, из предыдущего равенства получаемAнк = (Wк2 + Wp)–(Wк1 +Wp). ВеличинуW, равную сумме кинетической и потенциальной энергии тела, т.е.W = Wк+ Wp, называютполной механической энергиейилимеханической энергией. ТогдаWк1 +Wp=WиWк2+Wp=W, гдеWиW—полная механическая энергия тела в начальном и конечном положении. Итак, (13) т.е. изменение полной механической энергии тела в силовом поле равно работе неконсервативных сил, действующих на него. Тело, находящееся в силовом поле, можно рассматривать как механическую систему, состоящую из тел, создающих поле, и самого тела. Поэтому возможна и другая формулировка выражения (13): изменение полной механической энергии системы равно работе неконсервативных сил, действующих на неё. Если на механическую систему и внутри неё действуют только консервативные силы, то Aнк= 0 иW2=W1, т.е.
(14) Следовательно, в механической системе, в которой действуют только консервативные силы, полная механическая энергия величина постоянная. В этом и состоит закон сохранения механической энергии.
Тела, находящиеся в потенциальном поле, обладают способностью в определённых условиях совершать работу. Например, тело, поднятое над Землёй, когда его отпускают, приходит в движение под действием гравитационной силы, совершая работу. Следовательно, тела в данном поле обладают энергией, которую называют потенциальной. Эта энергия зависит от расположения тел, создающих поле, и от положения тела в этом поле, т.е. она зависит от взаимного расположения взаимодействующих тел. Однако от взаимного расположения тел или частей одного и того же тела зависят силы взаимодействия между ними. Итак, энергия, обусловленная взаимодействием тел или частей одного и того же тела, называется потенциальной. Величина потенциальной энергии тела может быть определена лишь с точностью до произвольной постоянной, значение которой зависит от выбора так называемого нулевого уровня, т.е. положения тела, в котором потенциальную энергию условно принимают за ноль. Потенциальная энергия равна той работе, которую совершают силы поля, действующие на тело, при переносе его из данной точки на нулевой уровень. Однако выбор нулевого уровня не отражается на физических законах. Потенциальная энергия тела, находящегося в гравитационном поле, вычисляется по формуле: иWp = mgh, (10) если за нулевой уровень энергии выбрать в бесконечности или на поверхности Земли. Здесь — гравитационная постоянная, М — масса Земли, m — масса тела, h — расстояние от тела до нулевого уровня, g — ускорение свободного падения. Потенциальная энергия деформированной пружины находится по формуле: (11) где k и х — коэффициент жёсткости и величина деформации пружины.
[custom_ads_shortcode3]
Теорема о потенциальной энергии
Работа Ap, совершаемая силами потенциального поля при переносе тела из положенияв положение, может быть выражена через потенциальные энергииWp1иWp2в этих положениях. Она равна Ap= Wp1 Wp2(Wp2 Wp1) Wp, (12) т.е. работа сил потенциального поля равна уменьшению потенциальной энергии перемещаемого тела или изменению потенциальной энергии тела, взятому с обратным знаком. Соотношение (12) называют теоремой о кинетической энергии.
[custom_ads_shortcode1]
Закон сохранения механической энергии
Предположим, что тело движется в гравитационном поле Земли. На него действуют сила тяжести и сила сопротивления воздуха. Тогда работа Aпри переходе тела из одного положения в другое складывается из работыAнксилы сопротивления воздуха (неконсервативная сила) и работыAксилы тяжести (консервативная сила), т.е.A = Aнк + Aк. Согласно теореме о кинетической энергии, запишем:A = Wк2 –Wк1, гдеWк1иWк2—кинетическая энергия тела в начальном и конечном положениях. Левые части последних равенств равны.Поэтому приравняем и их правые части, т.е. Aнк + Aк = Wк2 – Wк1. Согласно теореме о потенциальной энергии, Aк = Wp – Wp,гдеWpиWp—потенциальная энергия тела в данном поле в начальном и конечном положениях. Учитывая это, из предыдущего равенства получаемAнк = (Wк2 + Wp)–(Wк1 +Wp). ВеличинуW, равную сумме кинетической и потенциальной энергии тела, т.е.W = Wк+ Wp, называютполной механической энергиейилимеханической энергией. ТогдаWк1 +Wp=WиWк2+Wp=W, гдеWиW—полная механическая энергия тела в начальном и конечном положении. Итак, (13) т.е. изменение полной механической энергии тела в силовом поле равно работе неконсервативных сил, действующих на него. Тело, находящееся в силовом поле, можно рассматривать как механическую систему, состоящую из тел, создающих поле, и самого тела. Поэтому возможна и другая формулировка выражения (13): изменение полной механической энергии системы равно работе неконсервативных сил, действующих на неё. Если на механическую систему и внутри неё действуют только консервативные силы, то Aнк= 0 иW2=W1, т.е.
(14) Следовательно, в механической системе, в которой действуют только консервативные силы, полная механическая энергия величина постоянная. В этом и состоит закон сохранения механической энергии.
«Физика – 10 класс»Вспомните, какая связь существует между работой силы тяжести и потенциальной энергией. Почему работа силы упругости определяется её средним значением?
Согласно теореме об изменении кинетической энергии работа силы, действующей на тело, равна изменению его кинетической энергии:
Если же силы взаимодействия между телами являются консервативными, то, используя явные выражения для сил, мы показали (см. § 43), что работу таких сил можно также представить в виде разности двух значений некоторой величины, зависящей от взаимного расположения тел (или частей одного тела):
Здесь высоты h и h определяют взаимное расположение тела и поверхности Земли, а удлинения х и х — взаимное расположение частей тела, например витков деформированной пружины. Из формул (5.18) и (5.19) следует, что
Величину, равную произведению массы m тела на ускорение свободного падения g и на высоту h тела над поверхностью Земли, называют потенциальной энергией тела в поле силы тяжести и обозначают Еп:
Еп = mgh. (5.20)
Величину, равную половине произведения коэффициента упругости k тела на квадрат удлинения или сжатия х, называют потенциальной энергией упруго деформированного тела:
Введя понятие потенциальной энергии, мы получаем возможность выразить работу любых консервативных сил через изменение потенциальной энергии.
Под изменением величины понимают разность между её конечным и начальным значениями, поэтому Еп = Еп2 – Еп1. Следовательно, оба уравнения (5.19) можно записать так:
А = Еп1 — Еп2 = -(Еп2 — Еп1) = -ΔЕп, (5.22)
откуда ΔЕп = -А. Изменение потенциальной энергии тела равно работе консервативной силы, взятой с обратным знаком.
Например, при падении камня на Землю его потенциальная энергия убывает (ΔЕп < 0), но сила тяжести совершает положительную работу (А > 0).
Следовательно, А и ΔЕп имеют противоположные знаки в соответствии с формулой (5.22).
Нулевой уровень потенциальной энергии.
Согласно уравнению (5.22) работа консервативных сил определяет не саму потенциальную энергию, а её изменение. Поскольку работа определяет лишь изменение потенциальной энергии, то только изменение энергии в механике имеет физический смысл. Поэтому можно произвольно выбрать состояние системы, в котором её потенциальная энергия считается равной нулю. Этому состоянию соответствует нулевой уровень отсчёта потенциальной энергии.
Ни одно явление в природе или технике не определяется значением самой потенциальной энергии.
Важна лишь разность значений потенциальной энергии в конечном и начальном состояниях системы тел. Выбор нулевого уровня производится по-разному и диктуется условиями данной задачи. Обычно в качестве состояния с нулевой потенциальной энергией выбирают состояние системы с минимальным значением энергии. Тогда потенциальная энергия всегда положительна или равна нулю. Итак потенциальная энергия системы «тело — Земля» — величина, зависящая от положения тела относительно Земли, равная работе консервативной силы при перемещении тела из точки, где оно находится, в точку, соответствующую нулевому уровню потенциальной энергии системы. У пружины потенциальная энергия минимальна в отсутствие деформации, а у системы «камень — Земля» — когда камень лежит на поверхности Земли. Поэтому в первом случае а во втором случае Еп = mgh. Но к данным выражениям можно добавить любую постоянную величину С. При этом изменение потенциальной энергии, определяемое работой консервативной силы, останется прежним.
Изолированная система тел стремится к состоянию, в котором её потенциапьная энергия минимальна. Если не удерживать тело, то оно падает на землю (h = 0); если отпустить растянутую или сжатую пружину, то она вернётся в недеформированное состояние (х = 0).
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский.
Следующая страница «Закон сохранения энергии в механике»
Назад в раздел «Физика – 10 класс, учебник Мякишев, Буховцев, Сотский»
Законы сохранения в механике – Физика, учебник для 10 класса – Класс!ная физика Импульс материальной точки — Закон сохранения импульса — Реактивное движение. Успехи в освоении космоса — Примеры решения задач по теме «Закон сохранения импульса» — Механическая работа и мощность силы — Энергия. Кинетическая энергия — Примеры решения задач по теме «Кинетическая энергия и её изменение» — Работа силы тяжести. Консервативные силы — Работа силы упругости. Консервативные силы — Потенциальная энергия — Закон сохранения энергии в механике — Работа силы тяготения. Потенциальная энергия в поле тяготения — Примеры решения задач по теме «Закон сохранения механической энергии» — Основное уравнение динамики вращательного движения — Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси — Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»
Источники:
- zaochnik.com
- studfiles.net
- studfiles.net
- class-fizika.ru



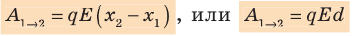
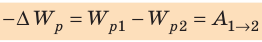
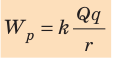
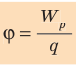
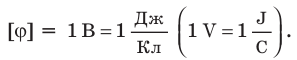
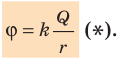
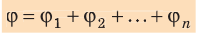
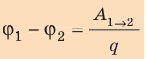
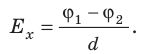
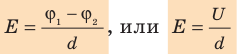
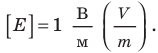
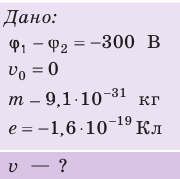
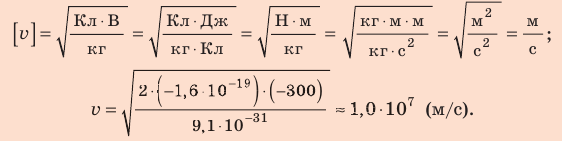
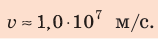



![[E=const]](https://fizikinfo.ru/wp-content/uploads/2019/07/Izmenenie-potentsialnoj-energii1.png)






![[Delta E=A]](https://fizikinfo.ru/wp-content/uploads/2019/07/Izmenenie-potentsialnoj-energii10.png)



