Как найти изменение потенциальной энергии заряда - Сайт, где вы сможете решить свои вопросы

Однородным электрическим полем называют такое электрическое поле, вектор напряжённости которого не зависит от точки пространства ((vec{r(t)} =const)), где (vec{r(t)}) — радиус-вектор исследуемой точки.

Потенциальные и непотенциальные силы в электродинамике

Все силы можно разделить на потенциальные и непотенциальные.

Работа потенциальной силы зависит только от начального и конечного положения тела и от формы траектории не зависит. Сила Кулона является потенциальной.

Потенциальность кулоновских сил позволяет говорить о потенциальной энергии заряда в поле электрических сил. По определению потенциальной энергии полагается, что изменение потенциальной энергии при его переносе из точки (А) в точку (Б) в любом электрическом поле — это работа кулоновских сил при перемещении заряда между этими точками, взятая со знаком минус:
(A=-(E_Б-E_А)). ((1))

Энергия системы заряженных тел

Вокруг заряженного тела появляется электрическое поле, которое оказывает действие на другие заряды. Таким образом, система, состоящая из какого-либо набора заряженных тел, обладает потенциальной энергией, которую обычно называют кулоновской или электрической.

Изменение потенциальной энергии заряда в однородном электрическом поле

Рассмотрим изменение потенциальной энергии положительного заряда (q), если переместить его в однородном электрическом поле из точки (А) в точку (Б) по красной траектории (рис. (1)).

Рис. (1). Перемещение заряда в однородном поле

Она изменяется так же, как если бы заряд перемещался по прямой (чёрной) траектории, поскольку работа потенциальной силы зависит только от начальной и конечной точки траектории.

Сила, действующая на него, постоянна:
(vec{F}=q vec{E}). ((2))
Если ввести радиус-векторы начала и конца этой траектории (vec{r}_А) и (vec{r}_Б) соответственно, то перемещение этого заряда:
(vec{r}=(vec{r}_Б – vec{r}_А)). ((3))
Работу кулоновской силы можно записать как скалярное произведение силы на перемещение:
(A=vec{F}cdot {r}=q vec{E} (vec{r}_Б – vec{r}_А) ). ((4))
Выбрав за ноль потенциальной энергии начальную точку ((vec{r}_А)), перепишем формулу ((1)) в виде:

(A=-E_Б). ((5))

Из формулы ((4)) получим, что потенциальная энергия заряда, который расположен в точке с радиус-вектором (vec{r}_Б=vec{r}) в однородном электрическом поле, равна скалярному произведению радиус-вектора на вектор напряжённости электрического поля:
(E= -A=-q vec{E} cdot vec{r} ), ((6))
что в координатном виде может быть записано как:
(E=-q (E_x x+E_у y+E_z z).) ((7))

Энергия взаимодействия точечных зарядов

Для того чтобы найти энергию взаимодействия точечных зарядов, рассмотрим систему из двух положительных зарядов (q_1) и (q_2). Положим, что заряд (q_1) неподвижен.

Рассмотрим, какую работу совершит электрическое поле, которое создано зарядом (q_1), при перемещении заряда (q_2) из точки (А) в точку (Б) по красной траектории (рис. (2)).

Рис. (2). Перемещение заряда в поле точечного заряда

Как и в случае однородного электрического поля, вместо красной траектории будем рассматривать чёрную траекторию, где из точки (А) в точку (С) заряд перемещается вдоль линии, соединяющей эти два заряда, а из точки (С) в точку (Б) — по дуге окружности, центром которой является первый заряд.

В таком случае работа электрического поля на дуге (СБ) будет нулевой:

(A=vec{F} cdot vec{r}=|F|cdot |r|cos(pi/2)=0,) ((8))

поскольку сила Кулона всегда перпендикулярна перемещению. На участке (АС) сила Кулона сонаправлена с перемещением, а по модулю:
( F(r)=frac{k q_1q_2}{r^2}), ((9))
поэтому работу электрического поля можно рассчитать как:

(A=F(r_A)r+F(r_A+Delta r)Delta r+F(r_A+2Delta r) Delta r+F(r_A+3Delta r) Delta r+ldots +)

(+F(r_C-2Delta r) Delta r+ F(r_C-Delta r) r=sum limits_{r=r_A}^{r_C}F(r)Delta r=sum limits_{r=r_A}^{r_C} frac{k q_1 q_2}{r^2} cdot Delta r.) ((10))
В пределе, когда (Delta r) мало, эта сумма равна:
(A=-frac{k q_1 q_2}{r}). ((11))
Сравнивая формулы ((1)) и ((11)), получаем, что потенциальная энергия взаимодействия точечных зарядов:
(E=frac{k q_1q_2}{r}.) ((12))

Энергия системы (n) точечных зарядов

Если рассматривать систему, состоящую из (n) точечных зарядов, то её потенциальная энергия:
( E=frac{1}{2} sum limits_{i neq j} frac{k q_i q_j}{r_{i,j}}=frac{1}{2} left(frac{k q_1 q_2}{r_{12}}+frac{k q_2 q_1}{r_{21}}+frac{k q_2 q_3}{r_{23}}+frac{k q_3 q_2}{r_{32}}+ldots right),) ((13))
где (r_{i,j}) — это расстояние между (i)-м и (j)-м точечными зарядами, а множитель (frac{1}{2}) появляется из-за того, что в сумме дважды учитывается потенциальная энергия взаимодействия (i)-го и (j)-го точечных зарядов.

Свойство линий напряжённости электрического поля

Поскольку сила Кулона потенциальна, то, если перемещать заряд по любому замкнутому контуру, работа силы Кулона равна нулю.
Отсюда вытекает, что линия напряжённости электростатического поля не замкнута.
Докажем это от противного: предположим, что линия электрического поля замкнута (рис. (3)).

Рис. (3). Замкнутая линия электрического поля

Но тогда при перемещении положительного заряда по замкнутой линии электрического поля работа электрического поля будет равна:
(A=sum vec{F} cdot vec{r}). ((14))
Каждый член этой суммы положителен, поскольку сила всегда сонаправлена с перемещением (рис. (3)).

Мы пришли к противоречию. Следовательно, линии электрического поля не замкнуты.

Источники:

Рис. 1. Перемещение заряда в однородном поле. © ЯКласс.

Рис. 2. Перемещение заряда в поле точечного заряда. © ЯКласс.

Рис. 3. Замкнутая линия электрического поля. © ЯКласс.

Источник

Потенциальная энергия заряженного тела в однородном электростатическом поле

Подробности: Обновлено 13.08.2018 18:35; Просмотров: 729

«Физика – 10 класс»

Вспомните из курса механики определение потенциальной энергии в поле силы тяжести.
Какие силы действуют на точечный заряд в электростатическом поле?
Какое поле называется однородным?

Заряженные тела притягивают или отталкивают друг друга. При перемещении заряженных тел, например листочков электроскопа, действующие на них силы совершают работу. Из механики известно, что система, способная совершить работу благодаря взаимодействию тел друг с другом, обладает потенциальной энергией. Значит, система заряженных тел обладает потенциальной энергией, называемой электростатической или электрической.

Понятие потенциальной энергии самое сложное в электростатике. Вспомните, как нелегко было представить себе, что такое потенциальная энергия в механике. Силу мы ощущаем непосредственно, а потенциальную энергию нет. На пятом этаже дома потенциальная энергия нашего тела больше, чем на первом. Но мы это никак не воспринимаем. Различие становится понятным, если вспомнить, что при подъёме вверх пришлось совершить работу, а также если представить себе, что произойдёт при падении с пятого этажа.

Энергия взаимодействия электронов с ядром в атоме и энергия взаимодействия атомов друг с другом в молекулах (химическая энергия) — это в основном электрическая энергия.

С точки зрения теории близкодействия на заряд непосредственно действует электрическое поле, созданное другим зарядом. При перемещении заряда действующая на него со стороны поля сила совершает работу. (В дальнейшем для краткости будем говорить просто о работе поля.) Поэтому можно утверждать, что заряженное тело в электрическом поле обладает энергией. Найдём потенциальную энергию заряда в однородном электрическом поле.

Работа при перемещении заряда в однородном электростатическом поле.

Однородное поле создают, например, большие параллельные металлические пластины, имеющие заряды противоположного знака. Это поле действует
на заряд q с постоянной силой = q, подобно тому как Земля действует с постоянной силой = m на камень вблизи её поверхности.

Пусть пластины расположены вертикально (рис. 14.31), левая пластина В заряжена отрицательно, а правая — положительно. Вычислим работу, совершаемую полем при перемещении положительного заряда q из точки 1, находящейся на расстоянии d1 от левой пластины, в точку 2, расположенную на расстоянии d2 от неё. Точки 1 и 2 лежат на одной силовой линии.
Электрическое поле при перемещении заряда совершит положительную работу:

А = qE(d1 – d2) = qEΔd. (14.12)

Работа по перемещению заряда в электрическом поле не зависит от формы траектории, подобно тому как не зависит от формы траектории работа силы тяжести.

Докажем это непосредственным расчётом.

Пусть перемещение заряда происходит по кривой (рис. 14.32). Разобьём эту кривую на малые перемещения. Сила, действующая на заряд, остаётся постоянной (поле однородно), а угол а между направлением силы и направлением перемещения будет изменяться. Работа на малом перемещении Δ равна ΔА = qElΔlcosa. Очевидно, что |Δ|cosa = Δd — проекция малого перемещения на горизонтальное направление. Суммируя работы на малых перемещениях, получаем А = qEd.

С помощью аналогичных рассуждений можно вывести формулу для работы кулоновской силы при перемещении заряда q₀ из точки 1 в точку 2 в неоднородном поле неподвижного точечного заряда q. При этом должно быть учтено, что сила зависит от расстояния до точечного заряда q. Для работы кулоновской силы в поле точечного заряда q справедливо выражение

Мы видим, что работа зависит только от положения начальной (r₁) и конечной (r₂) точек траектории и не зависит от формы траектории.

Электростатическая сила, действующая на заряды, является так же, как и силы тяжести, тяготения и упругости, консервативной силой.

Потенциальная энергия.

Поскольку работа электростатической силы не зависит от формы траектории точки её приложения, сила является консервативной, и её работа согласно формуле (5.22) равна изменению потенциальной энергии, взятому с противоположным знаком:

А = -(W_п2 – W_п1) = -ΔW_п. (14.13)

Сравнивая полученное выражение (14.12) с общим определением потенциальной энергии (14.13), видим, что ΔW_п = W_п2 – W_п1 = -qEd. Считаем, что в точке 2 потенциальная энергия равна нулю. Тогда потенциальная энергия заряда в однородном электростатическом поле равна:

W_п = qEd, (14.14)

где d — расстояние от точки 2 до любой точки, находящейся с точкой 2 на одной силовой линии.

Теперь получим формулу для потенциальной энергии заряда, находящегося в поле точечного заряда. Изменение потенциальной энергии заряда q0 при перемещении из точки 1 в точку 2 в неоднородном поле неподвижного точечного заряда q равно работе консервативной силы, взятой с обратным знаком:

Если считать, что в бесконечно удалённой точке потенциальная энергия равна нулю (при r2 → ∞ W_п2 — 0), то потенциальная энергия заряда q₀ в некоторой точке, находящейся на расстоянии r от точечного заряда q, создающего поле: Потенциальная энергия прямо пропорциональна заряду q₀, внесённому в поле.

Отметим, что формула (14.14) подобна формуле W_п = mgh для потенциальной энергии тела. Но заряд q в отличие от массы может быть как положительным, так и отрицательным.

Если поле совершает положительную работу, то потенциальная энергия заряженного тела при его свободном перемещении в поле в точку 2 уменьшается: ΔW_п < 0. Одновременно согласно закону сохранения энергии растёт его кинетическая энергия. И наоборот, если работа отрицательна (например, при свободном движении положительно заряженной частицы в направлении, противоположном направлению вектора напряжённости поля Е; это движение подобно движению камня, брошенного вверх), то ΔW_п > 0. Потенциальная энергия растёт, а кинетическая энергия уменьшается; частица тормозится.

На замкнутой траектории, когда заряд возвращается в начальную точку, работа поля равна нулю:

A= -ΔW_п = -(W_п1 – W_п1) = 0.

Это — свойство полей консервативных сил.

Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Электростатика – Физика, учебник для 10 класса – Класс!ная физика

Что такое электродинамика —
Электрический заряд и элементарные частицы. Закон сохранения заряд —
Закон Кулона. Единица электрического заряда —
Примеры решения задач по теме «Закон Кулона» —
Близкодействие и действие на расстоянии —
Электрическое поле —
Напряжённость электрического поля. Силовые линии —
Поле точечного заряда и заряженного шара. Принцип суперпозиции полей —
Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» —
Проводники в электростатическом поле —
Диэлектрики в электростатическом поле —
Потенциальная энергия заряженного тела в однородном электростатическом поле —
Потенциал электростатического поля и разность потенциалов —
Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности —
Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» —
Электроёмкость. Единицы электроёмкости. Конденсатор —
Энергия заряженного конденсатора. Применение конденсаторов —
Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»

Источник

Содержание:

Работа по перемещению заряда в электростатическом поле:

В повседневной жизни мы довольно часто, особенно в сухую погоду, встречаемся с ситуацией, когда, коснувшись какого-либо тела, чувствуем неприятный удар. Как показывает опыт, таких сюрпризов можно ожидать от тел, имеющих высокий потенциал.

Работа по перемещению заряда в однородном электростатическом поле

Если электростатическое поле действует с некоторой силой на электрически заряженные тела, то оно способно совершить работу по перемещению этих тел.

Пусть в однородном электростатическом поле напряженностью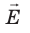

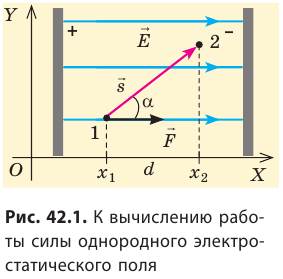
Вычислим работу А, которую совершает сила 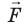, действующая на заряд со стороны электростатического поля. По определению работы: A=Fscosα.

Поле однородное, поэтому сила 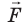постоянна, ее модуль равен: F=qE, а scosα=d=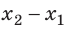является проекцией вектора перемещения на направление силовых линий поля. Следовательно, работа сил однородного электростатического поля по перемещению электрического заряда q из точки 1 в точку 2 ( 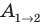) равна:

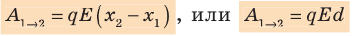
Обратите внимание! Если бы в данном случае заряд перемещался не из точки 1 в точку 2, а наоборот, то знак работы изменился бы на противоположный, то есть работа совершалась бы против сил поля.

Обратите внимание! Формула 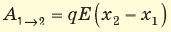будет справедлива в случаях движения заряда по любой траектории. То есть однородное электростатическое поле является потенциальным.

Потенциальным является любое электростатическое поле: работа электростатических (кулоновских) сил (как и работа гравитационных сил) не зависит от формы траектории, по которой перемещается заряд, а определяется начальным и конечным положениями заряда. Если траектория движения заряда замкнута, работа сил поля равна нулю.

Потенциальная энергия заряженного тела в поле, созданном точечным зарядом

Заряженное тело, помещенное в электростатическое поле, как и тело, находящееся в гравитационном поле Земли, обладает потенциальной энергией. Потенциальную энергию заряда, находящегося в электрическом поле, обычно обозначают символом . Согласно теореме о потенциальной энергии изменение потенциальной энергии заряда, взятое с противоположным знаком, равно работе, которую совершает электростатическое поле по перемещению заряда из точки 1 в точку 2 поля:

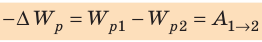
Потенциальную энергию взаимодействия двух точечных зарядов Q и q, расположенных на расстоянии r друг от друга, определяют по формуле:

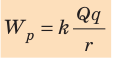
Обратите внимание: 1) потенциальная энергия взаимодействия зарядов положительна ( > 0), если заряды одноименные, и отрицательна ( < 0), если заряды разноименные; 2) если заряды бесконечно отдалить друг от друга (r → ∞), то = 0 (заряды не будут взаимодействовать). Таким образом, потенциальная энергия взаимодействия двух точечных зарядов равна работе, которую должно совершить электростатическое поле для увеличения расстояния между этими зарядами от r до бесконечности.

Что называют потенциалом электростатического поля

Потенциал 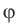электростатического поля в данной точке — это скалярная физическая величина, которая характеризует энергетические свойства поля и равна отношению потенциальной энергии электрического заряда, помещенного в данную точку поля, к значению q этого заряда:

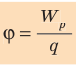
Единица потенциала в Си — вольт: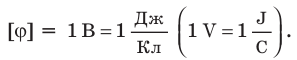

Из определения потенциала следует, что потенциал ϕ поля, созданного точечным зарядом Q, в точках, которые расположены на расстоянии r от данного заряда, можно рассчитать по формуле: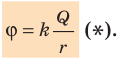

Из формулы ( *) видно: 1) если поле создано положительным точечным зарядом (Q > 0), то потенциал этого поля в любой точке является положительным ( ϕ > 0); 2) если поле создано отрицательным точечным зарядом (Q < 0), то потенциал этого поля в любой точке является отрицательным (ϕ < 0). Формула ( *) справедлива и для потенциала поля равномерно заряженной сферы (или шара) на расстояниях, которые больше ее радиуса или равны ему.

Если поле создано несколькими произвольно расположенными зарядами, потенциал ϕ поля в любой точке данного поля равен алгебраической сумме потенциалов 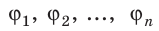полей, созданных каждым зарядом:

Как определяют разность потенциалов

Когда в электростатическом поле заряд движется из точки 1 в точку 2, это поле совершает работу, которая равна изменению потенциальной энергии заряда, взятому с противоположным знаком: 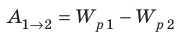. Поскольку 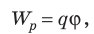то 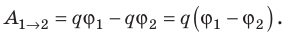Выражение 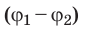называют разностью потенциалов, где 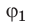— значение потенциала в начальной точке траектории движения заряда, 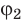— значение потенциала в ее конечной точке.

Разность потенциалов — скалярная физическая величина, равная отношению работы сил электростатического поля по перемещению заряда из начальной точки в конечную к значению этого заряда:

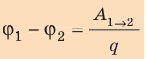
Единица разности потенциалов в Си — вольт: 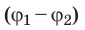= 1 В (V).

Разность потенциалов между двумя точками поля равна 1 В, если для перемещения между ними заряда 1 Кл электростатическое поле совершает работу 1 Дж. Обратите внимание: в подобных случаях разность потенциалов 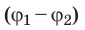− также называют напряжением (U). Важно не путать изменение потенциала 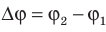и разность потенциалов (напряжение) .

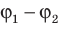Как связаны напряженность однородного электростатического поля и разность потенциалов

Рассмотрим однородное электростатическое поле на участке между точками 1 и 2, расположенными на расстоянии d друг от друга; пусть из точки 1 в точку 2 под действием поля перемещается заряд q (рис. 42.2).

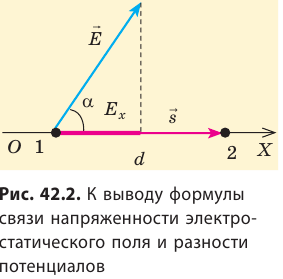
Совершаемую полем работу можно найти двумя способами: 1) через разность потенциалов между точками 1 и 2: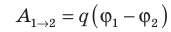; 2) через напряженность поля: 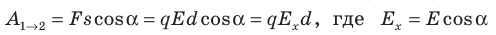— проекция вектора 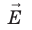на ось Ох, проведенную через точки 1 и 2.

Приравняв оба выражения для работы, получим: 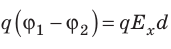, откуда: 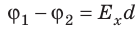, или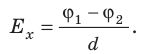

Если заряд перемещается в направлении напряженности электрического поля () , последняя формула примет вид:

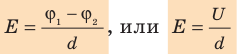
Из последней формулы следует единица напряженности в Си — вольт на метр:

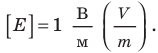
Какие поверхности называют эквипотенциальными

Для визуализации электростатического поля кроме силовых линий используют также эквипотенциальные поверхности.

Эквипотенциальная поверхность — это поверхность, во всех точках которой потенциал электростатического поля имеет одинаковое значение.

Для наглядности следует рассматривать не одну эквипотенциальную поверхность, а их совокупность. Однако графически изобразить совокупность поверхностей сложно, поэтому обычно изображают только линии пересечения эквипотенциальных поверхностей некоторой плоскостью (рис. 42.3).

Эквипотенциальные поверхности тесно связаны с силовыми линиями электростатического поля. Если электрический заряд перемещается по эквипотенциальной поверхности, то работа поля равна нулю, поскольку A=q ( 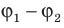), а на эквипотенциальной поверхности .

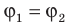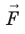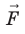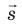Работу электростатического поля также можно представить через силу , действующую на заряд со стороны поля: A F= scosα , где α — угол между векторами и . Поскольку A = 0, а F ≠ 0 и s ≠ 0, то cosα = 0, то есть α = 90°. Это означает, что при движении заряда вдоль эквипотенциальной поверхности вектор силы 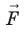, а следовательно, и вектор напряженности 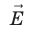поля в любой точке перпендикулярны вектору перемещения .

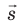Таким образом, силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям (см. рис. 42.3).

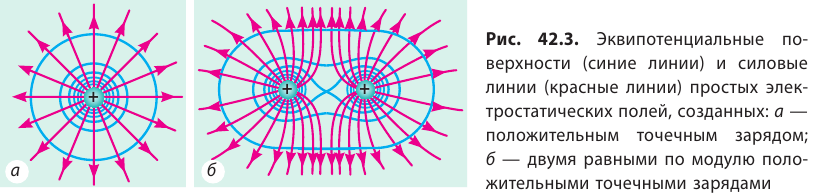
Обратите внимание! Симметрия эквипотенциальных поверхностей повторяет симметрию источников поля. Так, поле точечного заряда сферически симметрично, поэтому эквипотенциальными поверхностями поля точечного заряда являются концентрические сферы; при однородном поле эквипотенциальные поверхности — это система параллельных плоскостей.

Заказать решение задач по физике

Пример решения задачи

Электрон, начав движение из состояния покоя, прошел ускоряющую разность потенциалов –300 В. Какую скорость приобрел электрон? Масса электрона 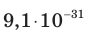кг, заряд 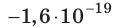Кл.

Заряд электрона — отрицательный, его начальная скорость 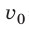= 0, поэтому под действием сил поля электрон будет двигаться в направлении, противоположном направлению силовых линий поля, то есть в направлении увеличения потенциала. Поле будет совершать положительную работу, в результате кинетическая энергия электрона и его скорость будут возрастать.

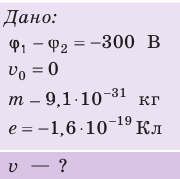
Решение:

Поиск математической модели, решение Согласно теореме о кинетической энергии:

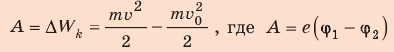— работа сил поля.

Таким образом, 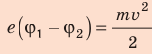, отсюда .

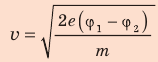Проверим единицу, найдем значение искомой величины:

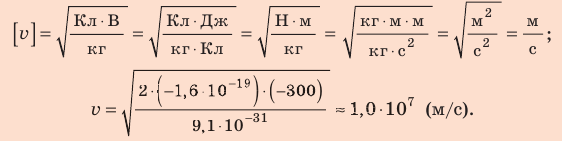
Ответ: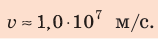

Выводы:

Закон Ома для однородного участка электрической цепи
Закон Ома для полной цепи
Закон Ома для цепи переменного тока с последовательным соединением сопротивлений
Сила и закон Ампера
Волновое движение в физике
Продольные и поперечные волны в физике
Звуковые волны в физике
Электрическое поле в физике

Источник

Потенциальная
энергия заряда в электрическом
поле. Работу,
совершаемую силами электрического поля
при перемещении положительного точечного
заряда q из
положения 1 в положение 2, представим
как изменение потенциальной энергии
этого заряда:

где W_п1 и W_п2 –
потенциальные энергии заряда q в
положениях 1 и 2. При малом перемещении
заряда q в
поле, создаваемом положительным точечным
зарядом Q,
изменение потенциальной энергии равно

При
конечном перемещении заряда q из
положения 1 в положение 2, находящиеся
на расстояниях r₁ и r₂ от
заряда Q,

Если
поле создано системой точечных
зарядов Q₁, Q₂,¼, Q_n,
то изменение потенциальной энергии
заряда q в
этом поле:

Приведённые
формулы позволяют найти
только изменение потенциальной
энергии точечного заряда q,
а не саму потенциальную энергию. Для
определения потенциальной энергии
необходимо условиться, в какой точке
поля считать ее равной нулю. Для
потенциальной энергии точечного
заряда q,
находящегося в электрическом поле,
созданном другим точечным зарядом Q,
получим

где C –
произвольная постоянная. Пусть
потенциальная энергия равна нулю на
бесконечно большом расстоянии от
заряда Q (при r ® ¥),
тогда постоянная C =
0 и предыдущее выражение принимает вид

При
этом потенциальная энергия определяется
как работа
перемещения заряда силами поля из данной
точки в бесконечно удаленную. В
случае электрического поля, создаваемого
системой точечных зарядов, потенциальная
энергия заряда q:

Потенциальная
энергия системы точечных зарядов. В
случае электростатического поля
потенциальная энергия служит мерой
взаимодействия зарядов. Пусть в
пространстве существует система точечных
зарядов Q_i (i =
1, 2, … ,n).
Энергия взаимодействия
всех n зарядов
определится соотношением

где r_ij – расстояние
между соответствующими зарядами, а
суммирование производится таким образом,
чтобы взаимодействие между каждой парой
зарядов учитывалось один раз.

Потенциал
электростатического поля. Поле
консервативной силы может быть описано
не только векторной функцией, но
эквивалентное описание этого поля можно
получить, определив в каждой его точке
подходящую скалярную величину. Для
электростатического поля такой величиной
является потенциал
электростатического поля,
определяемый как отношение потенциальной
энергии пробного заряда q к
величине этого заряда, j = W_п / q,
откуда следует, что потенциал численно
равен потенциальной энергии, которой
обладает в данной точке поля единичный
положительный заряд. Единицей измерения
потенциала служит Вольт (1 В).

Потенциал
поля точечного заряда Q в
однородной изотропной среде с
диэлектрической проницаемостью e :

3.
НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО
ПОЛЯ. Количественной
характеристикой силового действия
электрического поля на заряженные тела
служит векторная величина E,
называемая напряжённостью
электрического поля.

E = F / q_пр.

Она
определяется отношением силы F,
действующей со стороны поля на точечный
пробный заряд q_пр,
помещенный в рассматриваемую точку
поля, к величине этого заряда.

Понятие
«пробный заряд» предполагает, что этот
заряд не участвует в создании электрического
поля и так мал, что не искажает его, т.
е. не вызывает перераспределения в
пространстве зарядов, создающих
рассматриваемое поле. В системе СИ
единицей напряженности служит 1 В / м,
что эквивалентно 1 Н / Кл.

Электрическое
поле. Для
объяснения природы электрических
взаимодействий заряженных тел необходимо
допустить наличие в окружающем заряды
пространстве физического агента,
осуществляющего это взаимодействие. В
соответствии с теорией
близкодействия,
утверждающей, что силовые взаимодействия
между телами осуществляются через
посредство особой материальной среды,
окружающей взаимодействующие тела и
передающей любые изменения таких
взаимодействий в пространстве с конечной
скоростью, таким агентом является электрическое
поле.

Электрическое
поле создается как неподвижными, так и
движущимися зарядами. О наличии
электрического поля можно судить, прежде
всего, по его способности оказывать
силовое действие на электрические
заряды, движущиеся и неподвижные, а
также по способности индуцировать
электрические заряды на поверхности
проводящих нейтральных тел.

Поле,
создаваемое неподвижными электрическими
зарядами, называют стационарным
электрическим,
или электростатическим полем.
Оно представляет собой частный
случай электромагнитного
поля,
посредством которого осуществляются
силовые взаимодействия между электрически
заряженными телами, движущимся в общем
случае произвольным образом относительно
системы отсчета.

Напряженность
поля точечного заряда. Используя
закон Кулона (1.1) найдем выражение для
напряжённости электрического поля,
создаваемого точечным зарядом q в
однородной изотропной среде на
расстоянии r от
заряда:

(1.2)

В
этой формуле r –
радиус-вектор, соединяющий заряды q и q_пр.
Из (1.2) следует, что напряжённость E поля
точечного заряда q во
всех точках поля направлена радиально
от заряда при q >
0 и к заряду при q <
0.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

From Wikipedia, the free encyclopedia

Electric potential energy
Common symbols	U_E
SI unit	joule (J)
Derivations from other quantities	U_E = C · V² / 2

Electric potential energy is a potential energy (measured in joules) that results from conservative Coulomb forces and is associated with the configuration of a particular set of point charges within a defined system. An object may be said to have electric potential energy by virtue of either its own electric charge or its relative position to other electrically charged objects.

The term “electric potential energy” is used to describe the potential energy in systems with time-variant electric fields, while the term “electrostatic potential energy” is used to describe the potential energy in systems with time-invariant electric fields.

Definition[edit]

The electric potential energy of a system of point charges is defined as the work required to assemble this system of charges by bringing them close together, as in the system from an infinite distance. Alternatively, the electric potential energy of any given charge or system of charges is termed as the total work done by an external agent in bringing the charge or the system of charges from infinity to the present configuration without undergoing any acceleration.

The electrostatic potential energy, U_E, of one point charge q at position r in the presence of an electric field E is defined as the negative of the work W done by the electrostatic force to bring it from the reference position r_ref^{[note 1]} to that position r.^[1]^[2]^: §25-1

${displaystyle U_{mathrm {E} }(mathbf {r} )=-W_{r_{rm {ref}}rightarrow r}=-int _{{mathbf {r} }_{rm {ref}}}^{mathbf {r} }qmathbf {E} (mathbf {r'} )cdot mathrm {d} mathbf {r'} }$ ,

where E is the electrostatic field and dr’ is the displacement vector in a curve from the reference position r_ref to the final position r.

The electrostatic potential energy can also be defined from the electric potential as follows:

The electrostatic potential energy, U_E, of one point charge q at position r in the presence of an electric potential Phi is defined as the product of the charge and the electric potential.

$U_{{mathrm {E}}}({mathbf r})=qPhi ({mathbf r})$ ,

where Phi is the electric potential generated by the charges, which is a function of position r.

Units[edit]

The SI unit of electric potential energy is joule (named after the English physicist James Prescott Joule). In the CGS system the erg is the unit of energy, being equal to 10⁻⁷ Joules. Also electronvolts may be used, 1 eV = 1.602×10⁻¹⁹ Joules.

Electrostatic potential energy of one point charge[edit]

One point charge q in the presence of another point charge Q[edit]

A point charge q in the electric field of another charge Q.

The electrostatic potential energy, U_E, of one point charge q at position r in the presence of a point charge Q, taking an infinite separation between the charges as the reference position, is:

${displaystyle U_{E}(r)=k_{text{e}}{frac {qQ}{r}},}$

where ${displaystyle k_{text{e}}={frac {1}{4pi varepsilon _{0}}}}$ is the Coulomb constant, r is the distance between the point charges q and Q, and q and Q are the charges (not the absolute values of the charges—i.e., an electron would have a negative value of charge when placed in the formula). The following outline of proof states the derivation from the definition of electric potential energy and Coulomb’s law to this formula.

Outline of proof

The electrostatic force F acting on a charge q can be written in terms of the electric field E as

By definition, the change in electrostatic potential energy, U_E, of a point charge q that has moved from the reference position r_ref to position r in the presence of an electric field E is the negative of the work done by the electrostatic force to bring it from the reference position r_ref to that position r.

${displaystyle U_{E}(r)-U_{E}(r_{rm {ref}})=-W_{r_{rm {ref}}rightarrow r}=-int _{{r}_{rm {ref}}}^{r}qmathbf {E} cdot mathrm {d} mathbf {s} .}$

where:

r = position in 3d space of the charge q, using cartesian coordinates r = (x, y, z), taking the position of the Q charge at r = (0,0,0), the scalar r = |r| is the norm of the position vector,
ds = differential displacement vector along a path C going from r_ref to r,
${displaystyle W_{r_{rm {ref}}rightarrow r}}$ is the work done by the electrostatic force to bring the charge from the reference position r_ref to r,

Usually U_E is set to zero when r_ref is infinity:

${displaystyle U_{E}(r_{rm {ref}}=infty )=0}$

${displaystyle U_{E}(r)=-int _{infty }^{r}qmathbf {E} cdot mathrm {d} mathbf {s} }$

When the curl ∇ × E is zero, the line integral above does not depend on the specific path C chosen but only on its endpoints. This happens in time-invariant electric fields. When talking about electrostatic potential energy, time-invariant electric fields are always assumed so, in this case, the electric field is conservative and Coulomb’s law can be used.

Using Coulomb’s law, it is known that the electrostatic force F and the electric field E created by a discrete point charge Q are radially directed from Q. By the definition of the position vector r and the displacement vector s, it follows that r and s are also radially directed from Q. So, E and ds must be parallel:

Using Coulomb’s law, the electric field is given by

${displaystyle |mathbf {E} |=E={frac {1}{4pi varepsilon _{0}}}{frac {Q}{s^{2}}}}$

and the integral can be easily evaluated:

${displaystyle U_{E}(r)=-int _{infty }^{r}qmathbf {E} cdot mathrm {d} mathbf {s} =-int _{infty }^{r}{frac {1}{4pi varepsilon _{0}}}{frac {qQ}{s^{2}}}{rm {d}}s={frac {1}{4pi varepsilon _{0}}}{frac {qQ}{r}}=k_{e}{frac {qQ}{r}}}$

One point charge q in the presence of n point charges Q_i[edit]

Electrostatic potential energy of q due to Q₁ and Q₂ charge system: $U_{E}=q{frac {1}{4pi varepsilon _{0}}}left({frac {Q_{1}}{r_{1}}}+{frac {Q_{2}}{r_{2}}}right)$

The electrostatic potential energy, U_E, of one point charge q in the presence of n point charges Q_i, taking an infinite separation between the charges as the reference position, is:

${displaystyle U_{E}(r)=k_{text{e}}qsum _{i=1}^{n}{frac {Q_{i}}{r_{i}}},}$

where ${displaystyle k_{text{e}}={frac {1}{4pi varepsilon _{0}}}}$ is the Coulomb constant, r_i is the distance between the point charges q and Q_i, and q and Q_i are the assigned values of the charges.

Electrostatic potential energy stored in a system of point charges[edit]

The electrostatic potential energy U_E stored in a system of N charges q₁, q₂, …, q_N at positions r₁, r₂, …, r_N respectively, is:

${displaystyle U_{mathrm {E} }={frac {1}{2}}sum _{i=1}^{N}q_{i}Phi (mathbf {r} _{i})={frac {1}{2}}k_{e}sum _{i=1}^{N}q_{i}sum _{stackrel {j=1}{jneq i}}^{N}{frac {q_{j}}{r_{ij}}},}$

(1)

where, for each i value, Φ(r_i) is the electrostatic potential due to all point charges except the one at r_i,^{[note 2]} and is equal to:

${displaystyle Phi (mathbf {r} _{i})=k_{e}sum _{stackrel {j=1}{jneq i}}^{N}{frac {q_{j}}{mathbf {r} _{ij}}},}$

where r_ij is the distance between q_i and q_j.

Outline of proof

The electrostatic potential energy U_E stored in a system of two charges is equal to the electrostatic potential energy of a charge in the electrostatic potential generated by the other. That is to say, if charge q₁ generates an electrostatic potential Φ₁, which is a function of position r, then

${displaystyle U_{mathrm {E} }=q_{2}Phi _{1}(mathbf {r} _{2}).}$

Doing the same calculation with respect to the other charge, we obtain

${displaystyle U_{mathrm {E} }=q_{1}Phi _{2}(mathbf {r} _{1}).}$

The electrostatic potential energy is mutually shared by $q_{1}$ and $q_{2}$ , so the total stored energy is

${displaystyle U_{E}={frac {1}{2}}left[q_{2}Phi _{1}(mathbf {r} _{2})+q_{1}Phi _{2}(mathbf {r} _{1})right]}$

This can be generalized to say that the electrostatic potential energy U_E stored in a system of N charges q₁, q₂, …, q_N at positions r₁, r₂, …, r_N respectively, is:

${displaystyle U_{mathrm {E} }={frac {1}{2}}sum _{i=1}^{N}q_{i}Phi (mathbf {r} _{i}).}$

Energy stored in a system of one point charge[edit]

The electrostatic potential energy of a system containing only one point charge is zero, as there are no other sources of electrostatic force against which an external agent must do work in moving the point charge from infinity to its final location.

A common question arises concerning the interaction of a point charge with its own electrostatic potential. Since this interaction doesn’t act to move the point charge itself, it doesn’t contribute to the stored energy of the system.

Energy stored in a system of two point charges[edit]

Consider bringing a point charge, q, into its final position near a point charge, Q₁. The electric potential Φ(r) due to Q₁ is

${displaystyle Phi (r)=k_{e}{frac {Q_{1}}{r}}}$

Hence we obtain, the electrostatic potential energy of q in the potential of Q₁ as

${displaystyle U_{E}={frac {1}{4pi varepsilon _{0}}}{frac {qQ_{1}}{r_{1}}}}$

where r₁ is the separation between the two point charges.

Energy stored in a system of three point charges[edit]

The electrostatic potential energy of a system of three charges should not be confused with the electrostatic potential energy of Q₁ due to two charges Q₂ and Q₃, because the latter doesn’t include the electrostatic potential energy of the system of the two charges Q₂ and Q₃.

The electrostatic potential energy stored in the system of three charges is:

${displaystyle U_{mathrm {E} }={frac {1}{4pi varepsilon _{0}}}left[{frac {Q_{1}Q_{2}}{r_{12}}}+{frac {Q_{1}Q_{3}}{r_{13}}}+{frac {Q_{2}Q_{3}}{r_{23}}}right]}$

Outline of proof

Using the formula given in (1), the electrostatic potential energy of the system of the three charges will then be:

${displaystyle U_{mathrm {E} }={frac {1}{2}}left[Q_{1}Phi (mathbf {r} _{1})+Q_{2}Phi (mathbf {r} _{2})+Q_{3}Phi (mathbf {r} _{3})right]}$

Where $Phi ({mathbf {r}}_{1})$ is the electric potential in r₁ created by charges Q₂ and Q₃, $Phi ({mathbf {r}}_{2})$ is the electric potential in r₂ created by charges Q₁ and Q₃, and $Phi ({mathbf {r}}_{3})$ is the electric potential in r₃ created by charges Q₁ and Q₂. The potentials are:

${displaystyle Phi (mathbf {r} _{1})=Phi _{2}(mathbf {r} _{1})+Phi _{3}(mathbf {r} _{1})={frac {1}{4pi varepsilon _{0}}}{frac {Q_{2}}{r_{12}}}+{frac {1}{4pi varepsilon _{0}}}{frac {Q_{3}}{r_{13}}}}$

${displaystyle Phi (mathbf {r} _{2})=Phi _{1}(mathbf {r} _{2})+Phi _{3}(mathbf {r} _{2})={frac {1}{4pi varepsilon _{0}}}{frac {Q_{1}}{r_{21}}}+{frac {1}{4pi varepsilon _{0}}}{frac {Q_{3}}{r_{23}}}}$

${displaystyle Phi (mathbf {r} _{3})=Phi _{1}(mathbf {r} _{3})+Phi _{2}(mathbf {r} _{3})={frac {1}{4pi varepsilon _{0}}}{frac {Q_{1}}{r_{31}}}+{frac {1}{4pi varepsilon _{0}}}{frac {Q_{2}}{r_{32}}}}$

Where r_ij is the distance between charge Q_i and Q_j.

If we add everything:

${displaystyle U_{mathrm {E} }={frac {1}{2}}{frac {1}{4pi varepsilon _{0}}}left[{frac {Q_{1}Q_{2}}{r_{12}}}+{frac {Q_{1}Q_{3}}{r_{13}}}+{frac {Q_{2}Q_{1}}{r_{21}}}+{frac {Q_{2}Q_{3}}{r_{23}}}+{frac {Q_{3}Q_{1}}{r_{31}}}+{frac {Q_{3}Q_{2}}{r_{32}}}right]}$

Finally, we get that the electrostatic potential energy stored in the system of three charges:

${displaystyle U_{mathrm {E} }={frac {1}{4pi varepsilon _{0}}}left[{frac {Q_{1}Q_{2}}{r_{12}}}+{frac {Q_{1}Q_{3}}{r_{13}}}+{frac {Q_{2}Q_{3}}{r_{23}}}right]}$

Energy stored in an electrostatic field distribution in vacuum[edit]

The energy density, or energy per unit volume, ${textstyle {frac {dU}{dV}}}$ , of the electrostatic field of a continuous charge distribution is:

${displaystyle u_{e}={frac {dU}{dV}}={frac {1}{2}}varepsilon _{0}left|{mathbf {E} }right|^{2}.}$

Outline of proof

One may take the equation for the electrostatic potential energy of a continuous charge distribution and put it in terms of the electrostatic field.

Since Gauss’s law for electrostatic field in differential form states

${displaystyle mathbf {nabla } cdot mathbf {E} ={frac {rho }{varepsilon _{0}}}}$

where

then,

${displaystyle {begin{aligned}U&={frac {1}{2}}int limits _{text{all space}}rho (r)Phi (r),dV\&={frac {1}{2}}int limits _{text{all space}}varepsilon _{0}(mathbf {nabla } cdot {mathbf {E} })Phi ,dVend{aligned}}}$

so, now using the following divergence vector identity

we have

${displaystyle U={frac {varepsilon _{0}}{2}}int limits _{text{all space}}mathbf {nabla } cdot (mathbf {E} Phi )dV-{frac {varepsilon _{0}}{2}}int limits _{text{all space}}(mathbf {nabla } Phi )cdot mathbf {E} dV}$

using the divergence theorem and taking the area to be at infinity where

${displaystyle {begin{aligned}U&=overbrace {{frac {varepsilon _{0}}{2}}int limits _{{}_{text{ of space}}^{text{boundary}}}Phi mathbf {E} cdot dmathbf {A} } ^{0}-{frac {varepsilon _{0}}{2}}int limits _{text{all space}}(-mathbf {E} )cdot mathbf {E} ,dV\&=int limits _{text{all space}}{frac {1}{2}}varepsilon _{0}left|{mathbf {E} }right|^{2},dV.end{aligned}}}$

So, the energy density, or energy per unit volume ${textstyle {frac {dU}{dV}}}$ of the electrostatic field is:

${displaystyle u_{e}={frac {1}{2}}varepsilon _{0}left|{mathbf {E} }right|^{2}.}$

Energy stored in electronic elements[edit]

The electric potential energy stored in a capacitor is U_E=1/2 CV²

Some elements in a circuit can convert energy from one form to another. For example, a resistor converts electrical energy to heat. This is known as the Joule effect. A capacitor stores it in its electric field. The total electrostatic potential energy stored in a capacitor is given by

${displaystyle U_{E}={frac {1}{2}}QV={frac {1}{2}}CV^{2}={frac {Q^{2}}{2C}}}$

where C is the capacitance, V is the electric potential difference, and Q the charge stored in the capacitor.

Outline of proof

One may assemble charges to a capacitor in infinitesimal increments, , such that the amount of work done to assemble each increment to its final location may be expressed as

${displaystyle W_{q}=V,dq={frac {q}{C}}dq.}$

The total work done to fully charge the capacitor in this way is then

${displaystyle W=int dW=int _{0}^{Q}V,dq={frac {1}{C}}int _{0}^{Q}q,dq={frac {Q^{2}}{2C}}.}$

where is the total charge on the capacitor. This work is stored as electrostatic potential energy, hence,

${displaystyle W=U_{E}={frac {Q^{2}}{2C}}.}$

Notably, this expression is only valid if , which holds for many-charge systems such as large capacitors having metallic electrodes. For few-charge systems the discrete nature of charge is important. The total energy stored in a few-charge capacitor is

${displaystyle U_{E}={frac {Q^{2}}{C}}}$

which is obtained by a method of charge assembly utilizing the smallest physical charge increment where is the elementary unit of charge and Q = Ne where is the total number of charges in the capacitor.

The total electrostatic potential energy may also be expressed in terms of the electric field in the form

${displaystyle U_{E}={frac {1}{2}}int _{V}mathrm {E} cdot mathrm {D} ,dV}$

where is the electric displacement field within a dielectric material and integration is over the entire volume of the dielectric.

(A virtual experiment based on the energy transfert between capacitor plates reveals that an additional term must be taken into account when the electrostatic energy is expressed in terms of the electric field and displacement vectors ^[3].

While this extra energy cancels when dealing with insulators, in general it cannot be ignored, as for instance with semiconductors.)

The total electrostatic potential energy stored within a charged dielectric may also be expressed in terms of a continuous volume charge, rho ,

${displaystyle U_{E}={frac {1}{2}}int _{V}rho Phi ,dV}$

where integration is over the entire volume of the dielectric.

These latter two expressions are valid only for cases when the smallest increment of charge is zero () such as dielectrics in the presence of metallic electrodes or dielectrics containing many charges.

Notes[edit]

^ The reference zero is usually taken to be a state in which the individual point charges are very well separated (“are at infinite separation”) and are at rest.
^ The factor of one half accounts for the ‘double counting’ of charge pairs. For example, consider the case of just two charges.

References[edit]

^ Electromagnetism (2nd edition), I.S. Grant, W.R. Phillips, Manchester Physics Series, 2008 ISBN 0-471-92712-0
^ Halliday, David; Resnick, Robert; Walker, Jearl (1997). “Electric Potential”. Fundamentals of Physics (5th ed.). John Wiley & Sons. ISBN 0-471-10559-7.
^ Sallese (2016-06-01). “A new constituent of electrostatic energy in semiconductors”. The European Physical Journal B. 89 (6): 136. doi:10.1140/epjb/e2016-60865-4. ISSN 1434-6036. S2CID 120731496.

External links[edit]

Media related to Electric potential energy at Wikimedia Commons

Источник

Потенциальная энергия заряженного тела в однородном электростатическом поле

Работа по перемещению заряда в однородном электростатическом поле

Потенциальная энергия заряженного тела в поле, созданном точечным зарядом

Что называют потенциалом электростатического поля

Как определяют разность потенциалов

Как связаны напряженность однородного электростатического поля и разность потенциалов

Какие поверхности называют эквипотенциальными

Пример решения задачи

Definition[edit]

Units[edit]

Electrostatic potential energy of one point charge[edit]

One point charge q in the presence of another point charge Q[edit]

One point charge q in the presence of n point charges Qi[edit]

Electrostatic potential energy stored in a system of point charges[edit]

Energy stored in a system of one point charge[edit]

Energy stored in a system of two point charges[edit]

Energy stored in a system of three point charges[edit]

Energy stored in an electrostatic field distribution in vacuum[edit]

Energy stored in electronic elements[edit]

Notes[edit]

References[edit]

External links[edit]

Вам также может понравиться

Как решить задачу найди площадь многоугольника

Как найти инвесторов на землю

Как составить сбалансированное питание для собаки

Добавить комментарий Отменить ответ

One point charge q in the presence of n point charges Q_i[edit]