блабла ???
Мастер
(2156)
7 лет назад
р (давление жидкости на дно сосуда) =g(ускорение свободного падения) *h(уровень жидкости, высота) *ро (плотность жидкости)
Отсюда выражаем h
h=p/(ро*g)
Анна Краснова
Знаток
(361)
7 лет назад
Так как “Давление = высота столба жидкости * ускорение свободного падения * плотность жидкости”, “высота столба жидкости = Давление : ускорение свободного падения : плотность жидкости”
ZillaKami
Ученик
(47)
5 лет назад
р (давление жидкости на дно сосуда) =g(ускорение свободного падения) *h(уровень жидкости, высота) *ро (плотность жидкости)
Отсюда выражаем h
h=p/(ро*g)
12. Математическая модель изменения уровня жидкости в резервуаре, из которого жидкость откачивается насосом. Переходные процессы в
Производительность Fp постоянна.
Для нахождения зависимости уровня жидкости в аппарате L от входных величин Fпр и Fp (в м3/с) составим уравнение материального баланса аппарата:
где V — объем жидкости в аппарате, м3; t — время, с. Отсюда скорость изменения объема жидкости в аппарате:
Скорость изменения уровня жидкости L, если площадь горизонтального сечения аппарата А (в м2) неизменна по высоте
Рекомендуемые материалы
Таким образом, скорость изменения уровня в резервуаре пропорциональна разности потоков жидкости на входе и выходе. Уровень жидкости принимает постоянные значения во времени (скорость dL/dt=0) только при отсутствии рассогласования потоков Fпр и Fp.
Проинтегрируем уравнение (II,6) в пределах от 0 до t
Следовательно, выходная величина объекта пропорциональна интегралу от изменения его входных величин.
При ступенчатом изменении нагрузки объекта на величину ΔF уровень жидкости L изменяется по зависимости (рис II-5):
Рис. II-5. Переходная характеристика нейтрального объекта первого порядка.
Как следует из уравнения (II,8), скорость изменения выходной величины при ступенчатом возмущении ΔF постоянна и равна
При расчетах систем автоматизации уравнение динамики объекта представляют в относительных величинах. Предполагая, что Fnр является возмущением, a Fp — регулирующим воздействием (см. рис. II-1), имеем
где L0 и F0 — значения соответствующих величин при равновесном состоянии объекта.
Записав уравнение (II,6) в приращениях и введя относительные величины, получим уравнение динамики:
Из уравнения (II,11) видно, что отношение AL0/F0 имеет размерность времени. Его называют временем разгона объекта и обозначают через Tε. Под этим термином донимают время, в течение которого выходная величина объекта у, изменяясь с постоянной скоростью, достигает значения входной величины z. Время разгона Tε прямо пропорционально емкости объекта и характеризует его инерционные свойства.
Заменяя коэффициент в левой части уравнения (II,11) через Tε, получим уравнение динамики нейтрального объекта первого порядка в общем виде
Интегрируя уравнение (II,12), найдем
В нашем случае х=0. Величину, обратную Tε, часто называют скоростью разгона объекта ε, под которой понимают скорость изменения выходной величины у при предварительном ступенчатом изменении входной величины z, равном единице. Действительно, при единичном ступенчатом возмущений z—x=1(t) изменение выходной величины у подчиняется зависимости:
Передаточная функция нейтрального объекта первого порядка:
В динамическом отношении такой объект представляет собой интегрирующее звено.
Нейтральным объектам первого порядка присущи только емкостные (инерционные) свойства, что выражается, например при регулировании уровня L, степенью влияния величины Fnp—Fp на скорость dL/dt. Это влияние зависит от площади поперечного сечения аппарата. При большем значении А скорость изменения уровня меньше и наоборот (см. рис. II-5).
В лекции “61. Мостиковая гипотеза мышечного сокращения” также много полезной информации.
Для рассмотренного выше аппарата емкость равна
Из сравнения уравнений (II,6) и (II,16) следует, что емкость резервуара численно равна площади его горизонтального сечения. Единицей измерения емкости в данном случае является м2.
Емкость объектов зависит от протекающих в них процессов. Так емкость тепловых объектов, в которых осуществляется теплообмен при регулировании в них температуры, находят по изменению теплового потока Δq, Вт, вызывающего приращение температуры T на 1 °С в течение 1 ч:
Емкость аппарата зависит от теплоемкости ст, находящегося в нем продукта. Единицей измерения емкости теплового объекта является Дж/°С.
Урок посвящён решению задач по гидростатике об изменении уровня жидкости в сосуде. Рассматриваются два метода решения задач данного типа: через давление на дно и с использованием условия равновесия и закона Архимеда (через объёмы). Урок сопровождается компьютерной презентацией, в которой при решении задач используются статические модели в виде рисунков с фрагментарной анимацией.
Цели урока:
- Образовательные:
- учащиеся узнают способы решения задач по гидростатике об изменении уровня жидкости в сосуде и формулируют алгоритмы решения данного типа задач;
- учащиеся совершенствуют навыки решения задач об изменении уровня жидкости на дно сосуда;
- Развивающие:
- формирование умения применять изученные алгоритмы к решению конкретных задач;
- формирование умения анализировать условие задачи и выбирать наиболее рациональный способ решения задачи;
- формирование познавательного интереса к физике посредством решения задач повышенной сложности и через использование информационных технологий;
- Воспитательные:
- воспитание самостоятельности, любознательности;
- формирование коммуникативных навыков;
Необходимое оборудование:
- персональный компьютер;
- проектор;
- интерактивная доска или экран;
- компьютерная презентация «Уровень жидкости в сосудах»,
- документ-камера.
Хронометраж урока:
- Организационный момент – 1 мин.
- Постановка целей и задач урока (создание проблемной ситуации) – 2 мин.
- Изучение нового материала (решение проблемной задачи) – 15 мин.
- Закрепление изложенного материала при решении задач – 23 мин.
- Работа в группах – 15 мин.
- Презентация и защита – 8 мин.
- Подведение итогов – 3 мин.
- Организация домашнего задания – 1 мин.
Ход урока
| Содержание | Обоснование | |
| учитель | ученик | |
| I. Организационный момент. (1 мин.) | ||
| Приветствует учащихся, отмечает отсутствующих. | Слушают учителя, проверяют свою готовность к уроку. | Создание рабочей обстановки в классе, мобилизация учащихся для включения в учебный процесс, создание атмосферы взаимопонимания и сотрудничества. Воспитание дисциплины и организованности. |
| II. Постановка цели урока. Создание проблемной ситуации. (2 мин.) | ||
| Совместная с учащимися формулировка целей урока, формулирование учебных заданий. Постановка цели урока осуществляется в ходе анализа сложившейся проблемной ситуации, для создания которой учащимся предлагается проблемная задача (см. слайд №2 презентации) и задаётся вопрос о способах решения данной задачи. |
Совместно с учителем формулируют цели урока, осознают цели и задачи урока, записывают тему занятия в тетрадь. | Погружение учеников в проблематику занятия, обозначение образовательного объекта урока, создание необходимой образовательной среды. |
| III. Изучение нового материала. Решение проблемной задачи. (15 мин.) | ||
| При изучении способов решения проблемной задачи происходит актуализация знаний учащихся (закон Архимеда, условие плавания тел, гидростатическое давление, давление и т.п.) В зависимости от уровня класса решение задачи может быть выполнено непосредственно одним из учеников класса или коллективно в ходе эвристической беседы с помощью наводящих вопросов учителя. Учитель подводит учеников к формулировке алгоритмов решения задач. |
Решают проблемную задачу двумя способами (через давление на дно и через объёмы). Дают ответы на вопросы, дополняют ответы других учеников, корректируют свои знания. Совместно с учителем формулируют и записывают алгоритмы решения задач. | Актуализация знаний, осуществляемая в ходе решения задачи, необходима для перевода знаний, имеющихся у учащихся из потенциальных в активные. Это, в свою очередь, способствует развитию долговременной памяти. Полученные знания о способах решения задач систематизируются при формулировке алгоритмов решения задач. |
| IV. Закрепление изложенного материала при решении задач. (23 мин.) | ||
| Дальнейшее закрепление материала происходит при работе в группах с последующей презентацией своих решений. Для командной олимпиады учащимся предлагаются ключевые задачи по теме (см. слайд 13), первые две из которых являются обязательными. Для координации работы в группе учитель в каждой группе назначает координатора. Каждой группе перед началом работы раздаётся лист рефлексии. Учитель ставит задачу, объявляет режим работы, критерии оценки, даёт инструкцию о правилах работы в группе, напоминает требования к оформлению задачи, напоминает, что при решении необходимо выбирать наиболее рациональный способ решения. Наиболее рациональное решение задачи принесет группе дополнительный балл. По мере решения задач группой учитель получает оформленные решения, которые в случае отсутствия документ-камеры сканирует. Разбор начинается с защиты обязательных задач. Учитель задает наводящие вопросы, помогает выстраивать логическую связь, делает уточнения, обращает внимание на главное. |
Ученики работают в группе, координатор группы распределяет обязанности, определяет степень участия каждого члена группы в решении задач.
Учащиеся, обсудив задачу, записывают решение яркими чернилами на отдельном листе, сдают учителю и определяются с выбором ученика, который будет защищать ту или иную задачу. |
Групповая работа требует от учащегося коммуникативных навыков: он должен приспособиться к темпу работы других членов группы, должен правильно понимать их, ясно формулировать свои мысли, учитывать мнение группы.При презентации и защите решения задачи формируются и развиваются такие навыки как умения задавать и отвечать на вопросы, отстаивать свою точку зрения, а также навыки публичного выступления. |
| V. Подведение итогов. (3 мин.) | ||
| Подведение итогов урока осуществляется в ходе эвристической беседы, целью которой является побуждение учащихся к осознанию личной значимости своих действий и достижений на уроке, определение успешности урока. Задачей учителя является создание ситуации успеха, сопоставление целей урока с его результатами. Учитель совместно с учениками формулирует основные выводы занятия. Учитель организует индивидуальную и коллективную рефлексию деятельности, обозначает и оценивает достигнутые результаты, подводит итоги работы в группах, выставляет оценки. Отмечает наиболее активных учащихся. Благодарит за работу на уроке. |
Формулируют основные выводы урока. Координатор группы оказывает помощь в выставлении оценок членам группы. Учащиеся самостоятельно определяют параметры личных образовательных результатов и их место и роль в общем результате урока. |
Происходит индивидуальная рефлексия каждого по осознанию происходящего на уроке и его роли в выполнении задач урока и задач группы. |
| VI. Организация домашнего задания. (1 мин.) | ||
| Учитель сообщает домашнее задание. Домашнее задание дифференцированно по уровню сложности, в зависимости от способностей, а также желания самого ученика. Для организации домашнего задания могут быть использованы оставшиеся не решенными ключевые задачи и задания для самостоятельного решения. Так, например, опираясь на таксономии Блума и Карпинчика, оно может выглядеть следующим образом: А) задачи для самостоятельного решения №2, №3 (см. список задач в документе Microsoft Word на слайде 13); В) ключевые задачи №4, №5; С) задачи для самостоятельного решения №6, №7. |
Записывают домашнее задание в соответствие со своим уровнем притязаний, уточняют неясности. | Ученики осмысляют информацию о домашнем задании и задают уточняющие вопросы. Используемый дифференцированный подход к выполнению домашнего задания побуждает учеников к рефлексии. |
Литература:
- Гельгафт И.М., Генденштейн Л.Э., Кирик Л.А. 1001 задача по физике с решениями. Учебное пособие. – Харьков-Москва, 1995. – 592 с.
- Городские олимпиады по физике г. Нижнего Новгорода. 2004-2008 гг. Сборник задач. – Н.Новгород: Институт прикладной физики РАН, 2009. – 52 с.
- Подлесный Д.В. Анализ давления на дно сосуда в задачах гидростатики. // Потенциал, №10, 2005. – С. 42-45
- Полянский С.Е. Поурочные разработки по физике. – М.: ВАКО, 2004. –240 с.
- Черноуцан А. Гидростатика в стакане. // Квант, №3, 2008. – С. 47-50.
- Чивилёв В.И. Олимпиада «Физтех-2005». // Потенциал, №5, 2005. – С. 59-61.
1
Урок «Изменение уровня жидкости в сосуде» Авторы-составители: Н.В. Ларионова, к.п.н., учитель физики высшей категории; В.С.Ларионов, учитель физики высшей категории.
2
ЗАДАЧА В цилиндрическом сосуде с водой плавает кусок льда. Изменится ли уровень воды в сосуде, если лёд растает? ?
3
ЦЕЛЬ УРОКА Изучить 2 способа решения задач об изменении уровня жидкости в сосуде. Сформулировать алгоритмы решения. ЦЕЛЬ УРОКА
4
2 СПОСОБА РЕШЕНИЯ ЗАДАЧИ через объёмычерез давление на дно
5
АНАЛИЗ V 0 – первоначальный объём жидкости в сосуде, V 1 – «добавочный» объём, V 2 – «добавочный» объём после некоторых манипуляций с содержимым сосуда, S – площадь дна сосуда, h 0, h 1, h 2 – уровни жидкости в сосуде. V 0 +V 1 =Sh 1 V 0 +V 2 =Sh 2
6
1.Запишем условие плавания для кусочка льда: Fа = Fт. Fа = Fт. 2.Воспользуемся законом Архимеда: ρ ж gV в.ж = m л g, где m л – масса льда, V в.ж (V 1 ) – объём вытесненной жидкости. 3. Откуда V в.ж = m л /ρ ж. 4. После таяния льда объём воды в сосуде увеличился на ΔV (V 2 ) ΔV= m л /ρ ж. (Очевидно, что масса талой воды равна массе льда.) 5. Откуда следует, что V в.ж. = ΔV, т.е. h 1 = h 2. РЕШЕНИЕ
7
ОТВЕТ: Уровень воды в сосуде не изменится.
8
1. Записать условие плавания тела: F т = F а. (1) 2. Воспользоваться законом Архимеда: F а = ρ ж gV в.ж. (2) 3. Используя уравнения (1) и (2) и расписав F т выразить объём вытеснённой жидкости V в.ж. (V 1 ) 4. Рассчитать на сколько измениться уровень воды в сосуде по сравнению с изначальным (до погружения тела в воду) после таяния льда (или других действий): Δ V ( V 2 ). 5. Сравнить V в.ж. (V 1 ) с Δ V ( V 2 ) и сформулировать ответ. АЛГОРИТМ решения задачи через объёмы
9
2 СПОСОБА РЕШЕНИЯ ЗАДАЧИ через объёмычерез давление на дно 1. F т = F а 2. F а = ρ ж gV в.ж 3. V 1 4. V 2 5. V 1 ? V 2
10
h1h1 h2h2 1.С одной стороны, силу давления на дно в 1-ом и во 2-ом случаях можно выразить следующим образом F д1 = (m л +М)g, F д2 = (m в +М)g, где m л – масса льда, M – первоначальная масса воды в стакане без льда, m в – масса воды, образовавшейся после таяния льда. Т.к. m л = m в, то F д1 = F д2. 2. С другой стороны: F д1 = p 1 S = gh 1 S, F д2 = p 2 S = gh 2 S. 3. Т.к. F д1 = F д2, то h 1 = h 2. РЕШЕНИЕ
11
ОТВЕТ: Уровень воды в сосуде не изменится.
12
1. Содержимое сосуда не изменилось, поэтому не изменилась и сила давления на дно сосуда: F д1 = F д2. (1) 2. Выразить F д1 и F д2, воспользовавшись определительной формулой давления p = F д /S и формулой гидростатического давления p= ρ gh : F д1 = …, F д2 =… (2) 3. Из уравнений (1) и (2) выразить высоты h 1 и h 2 и сравнить. АЛГОРИТМ решения задачи через давление на дно сосуда
13
2 СПОСОБА РЕШЕНИЯ ЗАДАЧИ через объёмычерез давление на дно 1. F т = F а 2. F а = ρ ж gV в.ж 3. V в.ж. 4. Δ V. 5. V в.ж. ? Δ V 1. F д1 = F д2. 2. p = F д /S F д1 = … p= ρ gh F д2 =… 3. (1) и (2) h 1 ? h 2
14
через объёмычерез давление на дно 1. F т = F а 2. F а = ρ ж gV в.ж 3. V 1 4. V 2 5. V 1 ? V 2 1. F д1 = F д2. 2. p = F д /S F д1 = … p= ρ gh F д2 =… 3. (1) и (2) h 1 ? h 2 Алгоритмы Изучить 2 способа решения задач об изменении уровня жидкости в сосуде. Сформулировать алгоритмы решения. ЗАДАЧИ УРОКА
15
1. В цилиндрическом сосуде с водой плавает кусок льда, в котором находится пузырёк воздуха. Изменится ли уровень воды в сосуде, если лёд растает? 2. В цилиндрическом сосуде с водой плавает кусок льда с вмёрзшим в него стальным шариком. Изменится ли уровень воды в сосуде, если лёд растает? 3. В цилиндрическом сосуде на поверхности воды плавает стальная кастрюля. Изменится ли уровень воды в сосуде, если кастрюлю утопить? 4. В небольшом бассейне плавает лодка. Как изменится уровень воды в бассейне, если лежащий на дне лодки камень бросили в воду? 5. В небольшом бассейне плавает полузатопленная лодка, причём уровень воды в лодке совпадает с уровнем воды в бассейне. Из лодки зачерпнули ведро воды и вылили в бассейн. Как изменился уровень воды в бассейне? КЛЮЧЕВЫЕ ЗАДАЧИ
16
Библиография 1. Гельгафт И.М., Генденштейн Л.Э., Кирик Л.А задача по физике с решениями. Учебное пособие. – Харьков-Москва, – 592 с. 2. Городские олимпиады по физике г. Нижнего Новгорода гг. Сборник задач. – Н.Новгород: Институт прикладной физики РАН, –52с. 3. Подлесный Д.В. Анализ давления на дно сосуда в задачах гидростатики. // Потенциал, 10, – С Полянский С.Е. Поурочные разработки по физике. – М.: ВАКО, –240с. 5. Черноуцан А. Гидростатика в стакане. // Квант, 3, – С Чивилёв В.И. Олимпиада «Физтех-2005». // Потенциал, 5, – С.59-61
Условие задачи:
В цилиндрический сосуд с водой, с площадью дна 150 см2, опускают тело массой 1 кг, с плотностью 800 кг/м3 (вода – 1000 кг/м3) и площадью горизонтального сечения 50 см2. Вода при этом из сосуда не выливается. Найти изменение уровня воды в сосуде.
Задача №3.3.8 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(S=150) см2, (m=1) кг, (rho=800) кг/м3, (rho_{в}) кг/м3, (S_1=50) см2, (h-?)
Решение задачи:
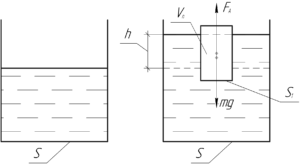Поскольку плотность материала (rho), из которого изготовлено тело, меньше, чем плотность воды, значит тело плавает, погрузившись частично в воду. К такому выводу можно прийти, если предположить, что тело плавает, и записать условие плавания тел:
[{F_А} = mg;;;;(1)]
Распишем силу Архимеда (F_А) в левой части и массу (m) в правой, тогда получим такое равенство:
[{rho _в}g{V_п} = rho Vg]
[{rho _в}{V_п} = rho V]
Так как из условия понятно, что (rho_{в} > rho), значит (V_{п} < V), то есть мы доказали наше суждение выше.
Известно, что тело вытесняет объем воды, равный объему погруженной части тела. Значит справедливо равенство:
[Sh = {V_п}]
[h = frac{{{V_п}}}{S}]
Объем погруженной части тела можно узнать из равенства (1), предварительно расписав в левой части силу Архимеда:
[{rho _в}g{V_п} = mg]
[{V_п} = frac{m}{{{rho _в}}}]
В итоге искомое изменение уровня воды (h) найдем по формуле:
[h = frac{m}{{{rho _в}S}}]
Переведем площадь дна сосуда (S) в систему СИ и произведем вычисления:
[150;см^2 = 150 cdot {10^{ – 4}};м^2]
[h = frac{1}{{1000 cdot 150 cdot {{10}^{ – 4}}}} = 0,067;м = 67;мм]
Ответ: 67 мм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.3.7 В стакане, наполненном до краев водой, плавает кусок льда. Как изменится давление
3.3.9 Вес куска железа в воде 1,67 Н. Найти его объем
3.3.10 Груз какой массы может поднять аэростат объемом 100000 м3 на высоту 40 км?
