§3. Изменение физической величины
Изучая физику, часто приходится использовать понятие изменения физической величины. При этом следует иметь в виду, что изменение какой-либо физической величины можно характеризовать либо её приращением, либо убылью. Приращением называется разность конечного и начального значений этой величины, в то время как убыль, напротив, представляет собой разность начального и конечного её значений.
Иными словами, убыль и приращение отличаются знаком. Мы чаще будем пользоваться понятием приращения и обозначать его в соответствии со сложившейся традицией с помощью греческой буквы «дельта»: `Delta`.
Таким образом, если этот символ стоит перед обозначением какой-либо векторной или скалярной величины, то такое выражение означает приращение соответствующей величины.
Так, выражение `Deltavec A` означает приращение вектора A→vec A , а выражение `Delta x` – приращение скалярной величины xx. Вместе с тем во избежание недоразумений следует проявлять известную осторожность при использовании символа `Delta`. Например, убедитесь самостоятельно, что, вообще говоря, `|DeltavecA|!=Delta|vecA|`, хотя в некоторых частных случаях возможно равенство.

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение дополнительного образования детей
«Заочная физико-техническая школа Московского физико-технического института (государственного университета)»
ФИЗИКА
Кинематика
Задание №2 для 9-х классов
(2012 – 2013 учебный год)
г. Долгопрудный, 2012

2012-2013 уч. год, № 2, 9 кл. Физика. Кинематика
Составитель: А.Ю. Чугунов, магистр естественных наук.
Физика: задание №2 для 9-х классов (2012 – 2013 учебный год), 2012, 28 с.
Дата отправления заданий по физике и математике – 29 октября 2012г.
Учащийся должен стараться выполнять все задачи и контрольные вопросы в заданиях. Некоторая часть теоретического материала, а также часть задач и контрольных вопросов, являются сложными и потребуют от учащегося больше усилий при изучении и решении. В целях повышения эффективности работы с материалом они обозначены символом «*» (звёздочка). Мы рекомендуем приступать к этим задачам и контрольным вопросам в последнюю очередь, разобравшись вначале с более простыми.
Составитель
Чугунов Алексей Юрьевич
Подписано 02.07.12. Формат 60×90 1/16.
Бумага типографская. Печать офсетная. Усл. печ. л. 1,75. Уч.-изд. л. 1,55. Тираж 1500. Заказ №6-з.
Заочная физико-техническая школа Московского физико-технического института (государственного университета)
ООО «Печатный салон ШАНС»
Институтский пер., 9, г. Долгопрудный, Московская обл., 141700.
ЗФТШ, тел./факс (495) 408-51-45 – заочное отделение
тел./факс (498) 744-6 3-51 – очно-заочное отделение
тел. (498) 755-55-80 – очное отделение
e-mail: zftsh@mail.mipt.ru
Наш сайт: www.school.mipt.ru
© ЗФТШ , 2012
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
2

2012-2013 уч. год, № 2, 9 кл. Физика. Кинематика
Введение
Предлагаемое Задание посвящено изложению кинематических способов описания механического движения. Кинематика представляет собой раздел механики, в котором изучается движение тел без исследования причин, вызывающих это движение и определяющих тот или иной его характер. Такой подход позволяет выявить особенности различных вариантов механического движения и рассмотреть их физические закономерности.
§1. Система отсчёта
Впредыдущем Задании по физике механическое движение было оп-
ределено как всякое изменение положения тел или их частей в пространстве относительно друг друга с течением времени. Следова-
тельно, чтобы узнать, движется ли конкретное тело и как оно движется, необходимо указать, относительно каких тел (объектов) рассматривает-
ся это движение. Тела, относительно которых рассматривается изучаемое движение, называются телами отсчёта, а само движение при этом является относительным.
Вто же время выбор одного лишь тела отсчёта не даёт возможности полностью описать изучаемое движение, поэтому с телом отсчёта связывают так называемую систему координат, а отсчёт времени ведут с помощью часов, наличие которых предполагается изначально. Выбор той или иной системы координат для решения конкретной задачи осуществляется по соображениям удобства. Наиболее привычной и распространённой для нас является декартова прямоугольная система координат, с которой мы и будем работать в дальнейшем. Тело отсчёта и связанная с ним система координат в совокупности с часами для отсчёта времени образуют систему отсчёта.
§2. Физические модели
Реальные движения тел порой так сложны, что при их изучении необходимо постараться пренебречь несущественными для рассмотрения деталями. С этой целью в физике прибегают к моделированию, т. е. к составлению упрощённой схемы (модели) явления, позволяющей понять его основную суть, не отвлекаясь на второстепенные обстоятельства. Среди общепринятых физических моделей важную роль в механике играют модель материальной точки и модель абсолютно твёрдого тела.
Материальная точка – это тело, геометрическими размерами которого в условиях задачи можно пренебречь и считать, что вся масса тела сосредоточена в геометрической точке.
Абсолютно твёрдое тело (просто твёрдое тело) – это система, состоящая из совокупности материальных точек, расстояния между которыми в условиях задачи можно считать неизменными.
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
3

2012-2013 уч. год, № 2, 9 кл. Физика. Кинематика
Модель материальной точки применима прежде всего в случаях, когда размеры тела много меньше других характерных размеров в условиях конкретной задачи. Например, можно пренебречь размерами искусственного спутника по сравнению с расстоянием до Земли и рассматривать спутник как материальную точку. Это – верно! Но вместе с тем не стоит ограничиваться лишь подобными случаями.
Дело в том, что сложное движение реального тела можно «разложить» на два простых вида движения: поступательное и вращательное (см. Задание №1). Если при сложном движении заменить тело материальной точкой, то мы исключим из рассмотрения вращение тела, т. к. говорить о вращении точки вокруг самой себя бессмысленно (точка не имеет геометрических размеров). Следовательно, заменив тело материальной точкой при сложном движении, мы допустим ошибку. Однако часто в случаях, когда тело движется поступательно, не вращаясь, его можно считать материальной точкой независимо от размеров, формы и пройденного им пути.
Модель абсолютно твёрдого тела можно применять, когда в условиях рассматриваемой задачи деформации реального тела пренебрежимо малы. Так, например, в задании, посвящённом вопросам статики (Задание №4), мы будем изучать условия равновесия твёрдого тела и при решении задач часто применять указанную модель. Вместе с тем, данная модель неуместна, если суть задачи состоит, например, в изучении деформаций тела в результате тех или иных воздействий в процессе его движения или в состоянии покоя.
Таким образом, мы будем изучать механическое движение не самих реальных тел, а упомянутых выше моделей. Из них основной и наиболее употребимой для нас станет модель материальной точки. В то же время там, где это необходимо, мы будем ради наглядности изображать на рисунках тела не в виде точек, а в виде объектов, геометрические размеры которых не равны нулю.
§3. Изменение физической величины
Изучая физику, часто приходится использовать понятие изменения физической величины. При этом следует иметь в виду, что изменение какой-либо физической величины можно характеризовать либо её приращением, либо убылью. Приращением называется разность конечного и начального значений этой величины, в то время как убыль, напротив, представляет собой разность начального и конечного её значений. Иными словами, убыль и приращение отличаются знаком. Мы чаще будем пользоваться понятием приращения и обозначать его в соответствии со сложившейся традицией с помощью греческой буквы «дельта»: . Таким образом, если этот символ стоит перед обозначением ка- кой-либо векторной или скалярной величины, то такое выражение означает приращение соответствующей величины.
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
4
2012-2013 уч. год, № 2, 9 кл. Физика. Кинематика
Так, выражение A означает приращение вектора A, а выражение
x − приращение скалярной величины x. Вместе с тем во избежание недоразумений следует проявлять известную осторожность при ис-
|
пользовании символа |
. Например, убедитесь самостоятельно, что, |
|
|
вообще говоря, |
r |
r |
|
A ≠ |
A , хотя в некоторых частных случаях возмож- |
но равенство.
§4. Способы описания движения
В кинематике существуют три способа аналитического описания движения материальной точки в пространстве. Рассмотрим их, ограничившись случаем движения материальной точки на плоскости, что позволит нам при выборе системы отсчёта задавать лишь две координатные оси.
|
y |
A |
y |
1 |
|
r |
r1 |
r |
|
|
2 |
|||
|
O |
x |
O |
r2 |
|
x |
|||
|
Рис. 1 |
Рис. 2 |
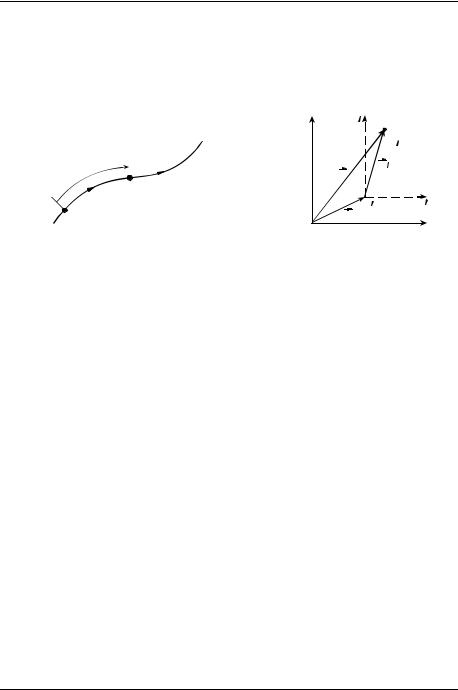
1. Векторный способ. В этом способе положение материальной точки A задаётся с помощью так называемого радиус-вектора r , кото-
рый представляет собой вектор, проведённый из точки O, соответ-
ствующей началу отсчёта выбранной системы координат, в интере-
сующую нас точку A (рис. 1). В процессе движения материальной точки её радиус-вектор может изменяться как по модулю, так и по направ-
лению, являясь функцией времени rr = rr(t ).
Геометрическое место концов радиус-вектора rr(t ) называют
траекторией точки A. В известном смысле траектория движения представляет собой след (явный или воображаемый), который «оставляет за собой» точка A после прохождения той или иной области про-
странства. Понятно, что геометрическая форма траектории зависит от выбора системы отсчёта, относительно которой ведётся наблю-
дение за движением точки.
Пусть в процессе движения по некоторой траектории в выбранной системе отсчёта за промежуток времени t тело (точка A ) перемести-
лось из начального положения 1 с радиус-вектором r1 в конечное положение 2 с радиус-вектором r2 (рис. 2). Приращение r радиусвектора тела в таком случае равно: r = rr2 −rr1.
Вектор rr, соединяющий начальное и конечное положения тела,
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
5

2012-2013 уч. год, № 2, 9 кл. Физика. Кинематика
называют перемещением тела.
|
Отношение |
r r |
t называют средней скоростью (средним векто- |
||
|
ром скорости) |
vср |
тела за время t : |
rr. |
|
|
vrср = |
(1) |
|||
|
Вектор vrср |
t |
r , так как от- |
||
|
коллинеарен и сонаправлен с вектором |
личается от последнего лишь скалярным неотрицательным множителем 1/ t.
Предложенное определение средней скорости справедливо для лю-
|
бых значений |
t, |
кроме t =0. Однако ничто не мешает брать проме- |
|
жуток времени |
t |
сколь угодно малым, но отличным от нуля. |
Для точного описания движения вводят понятие мгновенной скорости, то есть скорости в конкретный момент времени t или в конкретной точке траектории. С этой целью промежуток времени t устремляюr т к нулю. Вместе с ним будет стремиться к нулю и перемещение r. При этом отношение r / t стремится к определённому значению, не зависящему от t.
Величина, к которой стремится отношение r / t при стремлении t к нулю, называется мгновенной скоростью v :
|
vr= rt при |
t →0. |
|
Теперь заметим, что чем меньше |
t, тем ближе направление r к |
направлению касательной к траектории в данной точке. Следовательно,
вектор мгновенной скорости направлен по касательной к траектории
вданной точке в сторону движения тела.
Вдальнейшем там, где это не повлечёт недоразумений, мы будем опr ускать прилагательное «мгновенная» и говорить просто о скорости
vтела (материальной точки).
Движение тела принято характеризовать также ускорением, по которому судят об изменении скорости в процессе движения. Его опреде-
|
ляют через отношение приращения вектора скорости |
v тела к про- |
|
|
межутку времени t, в течение которого это приращение произошло. |
||
|
Ускорениемr ar |
тела называется величина, к которой стремится от- |
|
|
ношение v / |
t при стремлении к нулюзнаменателя |
t : |
|
r |
v |
|||
|
a |
= |
t |
при t →0. |
(2) |
|
При уменьшении t ориентация вектора |
v будет приближаться к |
определённому направлению, которое принимается за направление вектора ускорения a. Заметим, что ускорение направлено в сторону малого приращения скорости, а не в сторону самой скорости!
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
6

2012-2013 уч. год, № 2, 9 кл. Физика. Кинематика
Таким образомr , зная зависимость r (t), можно найти скорость v и
ускорение a тела в каждый момент времrени. В этой связи возникает и обратная задача о нахождении скорости v(t) и радиус-вектора r (t) по
известной зависимости от времени ускорения a. Для однозначного решениrя этой задачи необходимо знать начальные условия, т. е. ско-
рость v0 и радиус-вектор r0 тела в начальный момент времени t = 0. Напомним, что в системе СИ единицами длины, скорости и ускоре-
ния являются соответственно метр (м), метр в секунду (м/с) и метр на секунду в квадрате (м/с2 ).
|
y |
||
|
y |
A |
|
|
r |
||
|
O |
x |
x |
|
Рис. 3 |
Рис. 4 |
2. Координатный способ. В этом способе положение материальной точки A на плоскости в произвольный момент времени t определяется двумя координатамиr x и y, которые представляют собой проекции
радиус-вектора r тела на оси Ox и Oy соответственно (рис. 3). При
движении тела его координаты изменяются со временем, т. е. являются функциями t: x = x(t) и y = y(t). Если эти функции известны, то они
определяют положение тела на плоскости в любой момент времени.
В свою очередь, вектор скорости v можно спроецировать на оси координат и определить таким образом скорости vx и vy изменения ко-
ординат тела (рис. 4). В самом деле, vx и vy будут равны значениям, к
которым стремятся соответственно отношения x / t и y / t при
стремлении к нулю промежутка времени t.
Аналогично с помощью проецирования вектора a определяются ускорения ax и ay тела по направлениям координатных осей.
Таким образом, зная зависимости x(t) и y(t), можно найти не толь-
ко положение тела, но и проекции его скоростиr и ускорения, а следовательно, модуль и направление векторов v и a в любой момент време-
ни. Например, модуль вектора скорости будет равен v = vx2 + vy2 , a его
направление может быть задано углом между этим вектором и любой осью координат. Так угол α между вектором v и осью Ox определя-
ется отношением tgα = vy / vx . Аналогичными формулами определяются модуль и направление вектора a.
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
7

2012-2013 уч. год, № 2, 9 кл. Физика. Кинематика
Обратная задача – нахождение скорости и зависимостей x(t) и y(t)
по заданному ускорению – будет иметь однозначное решение, если кроме ускорения заданы ещё и начальные условия: проекции скорости и координаты точки в начальный момент времени t =0.
3. Естественный (или траекторный) способ. Этот способ применя-
ют тогда, когда траектория материальной точки известна заранее. На заданной траектории LM (рис. 5) выбирают начало отсчёта – непод-
вижную точку O, а положение движущейся материальной точки A определяют при помощи так называемой дуговой координаты l, ко-
торая представляет собой расстояние вдоль траектории от выбран-
ного начала отсчёта O до точки A. При этом положительное направление отсчёта координаты l выбирают произвольно, по соображениям удобства, например так, как показано стрелкой на рисунке 5.
Движение тела определено, если известны его траектория, начало отсчёта O, положительное направление отсчёта дуговой координа-
ты l и зависимость l(t).
Следующие два важных механических понятия – это пройденный путь и средняя путевая скорость.
По определению, путь S − это длина участка траектории, пройденного телом за промежуток времени t.
Ясно, что пройденный путь – величина скалярная и неотрицатель-
|
ная, а потому его нельзя сравнивать с перемещением |
r , |
представ- |
|||||||||||||
|
ляющем собой вектор. Сравнивать можно только путь |
S |
и модуль |
|||||||||||||
|
перемещения |
rr |
. Очевидно, что |
S ≥ |
rr |
. |
||||||||||
|
Средней путевой скоростью |
vср |
тела называют отношение пути |
|||||||||||||
|
S к промежутку времени |
t, |
в |
течение, которого |
этот путь |
|||||||||||
|
был пройден: |
S . |
||||||||||||||
|
v |
= |
(3) |
|||||||||||||
|
ср |
t |
r |
|||||||||||||
|
Определённая ранее средняя скорость vср (см. формулу (1)) и сред- |
|||||||||||||||
|
няя путевая скорость отличаются друг от друга так же, как |
r отлича- |
ется от S, но при этом важно понимать, что обе средние скорости
имеют смысл только тогда, когда указан промежуток времени усред-
нения t. Само слово «средняя» означает усреднение по времени. Пример 1. Городской троллейбус утром вышел на маршрут, а через
8 часов, проехав в общей сложности 72 км, возвратился в парк и занял своё обычное место на стоянке. Какова средняя скорость vср и средняя
путевая скорость vср троллейбуса?
Решение. Поскольку начальное и конечное положения троллейбуса
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
8
2012-2013 уч. год, № 2, 9 кл. Физика. Кинематика
|
совпадают, то его перемещение |
r равно нулю r =0, следовательно, |
|||||
|
vrср = rr/ t =0 и |
vrср |
= 0. Но средняя путевая скорость троллейбуса не |
||||
|
равна нулю: |
S |
72км |
||||
|
vср = |
= |
=9 км/ч. |
||||
|
t |
||||||
|
8ч |
|
M |
y |
y |
A |
||
|
K |
K |
||||
|
l |
r |
r |
|||
|
A |
x |
||||
|
O |
O |
r0 |
O |
||
|
L |
x |
||||
|
Рис. 5 |
Рис. 6 |
§5. Преобразование скорости и ускорения при переходе в другую систему отсчёта
В рамках классической механики скорость и ускорение тела преобразуются по определённым правилам при переходе от одной системы отсчёта к другой.
Пусть имеются две произвольные системы отсчёта K и K′ (рис. 6). Известны скорость v′ и ускорение a′ тела (точки A ) в K′− системе.
Рассмотрим случай, когда K′− система движется поступательно по отношениюr к K − системе, и определим значения скорости v и ускорения a тела в K − системе.
|
Если за малый промежуток времени |
t |
тело (точка A ) перемести- |
|||||||||
|
лось относительно K |
′ |
−системы на величину |
′ |
K |
′ |
− система пе- |
|||||
|
r , а |
|||||||||||
|
реместилась относительно K − системы на |
r0 , то из правила вектор- |
||||||||||
|
ного сложения следует, что перемещение |
r |
тела |
относительно |
||||||||
|
K − системы |
будет равно |
r = |
r |
+ |
r′ |
Разделив обе части этого |
|||||
|
r0 |
r . |
||||||||||
|
равенства на |
t и обозначив через v0 |
скорость K′− системы относи- |
|||||||||
|
тельно K − системы, получим: |
r |
r′ |
|||||||||
|
v = v0 |
+ v . |
(4) |
|||||||||
|
Рассуждая аналогично, найдём формулу преобразования ускорения: |
|||||||||||
|
r |
r′ |
(5) |
|||||||||
|
a = a0 |
+ a . |
||||||||||
|
Из формулы (5) вытекает важное следствие: при a0 |
= 0 |
ускорения ar |
|||||||||
|
и ar′ равны. Иными словами, если система отсчёта K′ |
движется посту- |
пательно без ускорения относительно системы отсчёта K, то ускоре-
ния тела в обеих системах отсчёта будут одинаковы.
Переход из одной системы отсчёта в другую довольно часто приме-
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
9
2012-2013 уч. год, № 2, 9 кл. Физика. Кинематика
няется на практике и, порой, существенно облегчает решение некоторых физических задач, поэтому к данному приёму желательно привыкнуть и научиться умело его использовать.
Часто встречаются задачи, в которых два тела движутся независимо друг от друга в некоторой системе отсчёта и требуется определить ка- кие-либо величины (перемещение, скорость), характеризующие движение одного тела относительно другого. В таких случаях, как правило, удобно перейти в систему отсчёта, связанную с тем телом, относительно которого рассматривается движение другого тела, и применить полученные выше формулы преобразований. Относительные перемеще-
ние и скорость двух тел определяются векторной разностью их перемещений и скоростей, заданных по отношению к одной и той же (ча-
ще всего – неподвижной) системе отсчёта. Рассмотрим следующий пример.
v2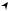
v1
Рис. 7 Рис. 8
Пример 2. Два корабля движутся с постоянными скоростями v1 и vr2 под углом α друг к другу (рис. 7). Найти скорость первого корабля
|
относительно второго. |
|||||||||||||||
|
Решение. Перейдём в |
систему отсчёта, связанную со вторым ко- |
||||||||||||||
|
раблём, |
движущимся со скоростью v2 . В этой системе отсчёта относи- |
||||||||||||||
|
тельная |
скорость |
v′ |
первого корабля |
согласно |
(4) |
будет равна |
|||||||||
|
vr′= vr1 −vr2 . Вектор |
v′ определим геометрически, |
используя правило |
|||||||||||||
|
построения векторной разности (рис. |
8). Из треугольника BDE с по- |
||||||||||||||
|
мощью теоремы косинусов найдём модуль искомого вектора: |
|||||||||||||||
|
v′= |
v12 + v2 |
2 −2v1v2 cosα. |
|||||||||||||
|
Направление вектора v′ зададим, например, углом β |
(рис. 8), кото- |
||||||||||||||
|
рый определим из |
BDE по теореме синусов: |
v1 |
= |
v′ |
. Отсюда |
||||||||||
|
sin β |
|||||||||||||||
|
sinα |
|||||||||||||||
|
sin β |
= |
v1 |
sinα = |
v1 sinα |
. |
||||||||||
|
v′ |
|||||||||||||||
|
v12 |
+ v2 |
2 −2v1v2 cosα |
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
10
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Изменение – физическая величина
Cтраница 1
Изменение физической величины во времени называется процессом. Процесс может характеризоваться постоянными параметрами. У синусоидального напряжения или тока, например, такими параметрами являются амплитуда, частота, начальная фаза. Их измерение к динамическим не относится.
[2]
Изменение физической величины во времени, как уже говорилось в разд.
[4]
Изменение физической величины во времени называется процессом. Процесс может характеризоваться постоянными параметрами. У синусоидального напряжения или тока, например, такими параметрами являются амплитуда, частота, начальная фаза. Их измерение к динамическим не относится.
[6]
Изменение физической величины во времени, как уже говорилось в разд.
[8]
Изменение физической величины, используемое для передачи данных.
[9]
Изменение физической величины вдоль любого направления случайного поля аналогично случайному процессу с той лишь разницей, что роль времени играет пространственная координата. Оно задается соответствующими многомерными функциями распределения вероятности физической величины.
[10]
Расчет изменения физических величин в косой ударной волне по формулам ( 46 7) – ( 46 12) сопряжен с большими вычислительными трудностями. Поэтому был предложен ряд диаграмм и графических методов, облегчающих эти расчеты.
[11]
Для определения характера изменения физической величины с течением времени нужно построить, используя оператор Гамильтона и оператор данной величины, оператор производной, а для него найти среднее в соответствующем состоянии.
[12]
Сигнал, в котором изменение физической величины, используемой для передачи, происходит непрерывным образом: в случае передачи информации – в соответствии со значением физической величины той же или другой природы; в случае передачи команды – в соответствии с уровнем требуемого воздействия.
[13]
Несмотря на случайный характер изменения физической величины, между ее значениями при различных значениях аргумента ( например, при различных значениях времени или в различных точках пространства) существует определенная связь. Для оценки этой взаимосвязи применяется корреляционная, или автокорреляционная, функция.
[14]
Задача заключается в описании изменения физических величин, характеризующих свойства полимеров, при этом преобразовании масштаба.
[15]
Страницы:
1
2
3
4
Применение производной в физике и технике
- Скорость и ускорение
- Физические величины как производные от других величин
- Примеры
п.1. Скорость и ускорение
Рассматривая физический смысл производной (см. §42 данного справочника), мы выяснили, что:
Производная функции (y=f(x)) в точке (x_0) равна скорости изменения функции в этой точке.
Например:
Рассмотрим прямолинейное равноускоренное движение.
Уравнение этого движения имеет вид: $$ x(t)=x_0+v_0t+frac{at^2}{2} $$ где (x(t)) – ккордината тела в произвольный момент времени (t, x_0) – начальная координата, (v_0) – начальная скорость, (a=const) – ускорение, действующее на тело.
Чтобы найти скорость тела из этого уравнения, нужно найти производную от координаты по времени: $$ v(t)=x'(t)=left(x_0+v_0t+frac{at^2}{2}right)’=0+v_0cdot 1+frac a2cdot 2t=v_0+at $$ Чтобы найти ускорение, нужно найти производную от скорости: $$ a(t)=v'(t)=x”(t)=(v_0+at)’=0+acdot 1=a=const $$
п.2. Физические величины как производные от других величин
Если рассматривать уравнение процесса (s=f(t)), его производной будет величина $$ f'(t)=lim_{triangle trightarrow 0}frac{triangle s}{triangle t} $$ Такие величины часто встречаются в различных разделах физики и техники.
Исходная величина (процесс)
Производная по времени
Координата (x(t))
Скорость (v(t)=x'(t))
Ускорение (a(t)=v'(t)=x”(t))
Угол поворота (varphi(t))
Угловая скорость (omega(t)=omega'(t))
Угловое ускорение (beta(t)=omega'(t)=varphi”(t))
Масса горючего ракеты (m(t))
Скорость расходования горючего (u(t)=m'(t))
Температура тела (T(t))
Скорость нагрева (v_T(t)=T'(t))
Заряд (q(t))
Сила тока (I(t)=q'(t))
Работа (A(t))
Мощность (N(t)=A'(t))
Магнитный поток (Ф(t))
ЭДС индукции (varepsilon(t)=-Ф'(t))
Число атомов радиоактивного вещества (N(t))
Скорость радиоактивного распада (I(t)=-N'(t))
Конечно же, в физике далеко не обязательно берут производную только по времени.
Например, для теплоты Q(T) теплоемкость равна C(T)=Q'(T), где T – температура.
А для процесса теплопереноса температура u(x,t) в точке с координатой x в момент времени t определяется уравнением теплопроводности: $$ frac{partial u(x,t)}{partial t}-a^2frac{partial^2 u(x,t)}{partial x^2}=f(x,t) $$ и производные берутся по времени (left(frac{partial u}{partial t}right)) и по координате (left(frac{partial u}{partial x}right)), причем по координате берется производная второго порядка (left(frac{partial^2 u}{partial x^2}right)).
Поэтому в физике для производных чаще используются обозначения Лейбница, в которых хорошо видна как функция, так и аргумент.
Например, для производных функции от одной переменной: (frac{partial varphi}{partial t}, frac{partial p}{partial V}, frac{partial Q}{partial T},…)
Для производных функций от многих переменных: (frac{partial u}{partial t}, frac{partial u}{partial x}, frac{partial u}{partial y}, frac{partial u}{partial z},…)
п.3. Примеры
Пример 1. Тело массой 6 кг движется прямолинейно по закону (x(t)=t^2+t+1) (м). Найдите: 1) кинетическую энергию тела через 3 с после начала движения; 2) силу, действующую на тело в это время.
1) Кинетическая энергия равна (E=frac{mv^2}{2})
Скорость тела: (v(t)=x'(t)=(t^2+t+1)’=2t+1)
Через 3 с: (v(3)=2cdot 3+1=7) (м/с)
Подставляем: (E=frac{6cdot 7^2}{2}=147) (Дж)
2) Сила по второму закону Ньютона: (F=ma)
Ускорение тела: (a(t)=v'(t)=(2t+1)’=2) (м/с^2)
Ускорение постоянно.
На тело действует постоянная сила: (F=6cdot 2=12) (Н)
Ответ: 147 Дж; 12 Н
Пример 2. Маховик вращается по закону (varphi (t)=4t-0,5t^2) (рад)
Найдите момент времени, в который маховик остановится.
Угловая скорость: (omega(t)=varphi ‘(t)=(4t-0,5t^2 )’=4-0,5cdot 2t=4-t)
В момент остановки угловая скорость равна 0. Решаем уравнение: $$ 4-t=0Rightarrow t=4 (c) $$ Ответ: 4 c
Пример 3. Ракету запустили вертикально вверх с начальной скоростью 40 м/с. В какой момент времени и на какой высоте ракета достигнет наивысшей точки (g≈10м/с2)?
Выберем начало отсчета на земле ((y_0=0)), направим ось y вверх.
Начальная скорость направлена вверх, её проекция на ось положительна.
Ускорение свободного падения направлено вниз, его проекция отрицательна.
Уравнение движения: $$ y(t)=y_0+v_{0y}t+frac{g_y t^2}{2}=0+40t-frac{10t^2}{2}=40t-5t^2 $$ В верхней точке траектории ракета останавливается, её скорость равна 0.
Найдем скорость: $$ v(t)=y'(t)=40-5cdot 2t=40-10t $$ Найдем момент остановки в верхней точке: $$ 40-10t_0=0Rightarrow t_0=frac{40}{10}=4 (c) $$ Найдем высоту подъема в верхней точке: $$ H_{max}=y(t_0)=40cdot 4-5cdot 4^2=80 (м) $$ Ответ: 4 с, 80 м
Пример 4. Через поперечное сечение проводника проходит заряд (q(t)=ln(t+1)) (Кл). В какой момент времени сила тока в проводнике равна 0,1 А?
Сила тока: $$ I(t)=q'(t)=(ln(t+1))’=frac{1}{t+1} $$ По условию: $$ frac{1}{t_0+1}=0,1Rightarrow t_0+1=frac{1}{0,1}=10Rightarrow t_0=9 (c) $$ Ответ: 9 c
Пример 5. Колесо вращается так, что угол его поворота пропорционален квадрату времени. Первый оборот оно сделало за 8 с. Найдите угловую скорость через 48 с после начала вращения.
По условию угол поворота (varphi (t)=At^2)
Один оборот (2pi) радиан был сделан за 8 с. Получаем уравнение: (Acdot 8^2=2pi)
Находим коэффициент (A=frac{2pi}{8^2}=frac{pi}{32})
Уравнение движения (varphi(t)=frac{pi}{32}t^2) (рад)
Угловая скорость (omega(t)=varphi ‘(t)=left(frac{pi}{32}t^2right)’=frac{pi}{32}cdot 2t=frac{pi}{16}t) (рад/с)
Через 48 секунд (omega(48)=frac{pi}{16}cdot 48=3pi) рад/с – полтора оборота в секунду.
Ответ: (3pi) рад/с
Пример 6. Для нагревания 1 кг жидкости от 0°С до t°C необходимо (Q(t)=1,7t+at^2+bt^3) Дж теплоты.
Известно, что теплоемкость жидкости при температуре 100°С равна 1,71 Дж/К, а для нагревания 1 кг этой жидкости 0°С до 50°C требуется 85,025 Дж теплоты. Найдите коэффициенты a и b.
Теплоемкость: (C(t)=Q'(t)=1,7cdot 1+acdot 2t+bcdot 3t^2=1,7+2at+3bt^2)
По условию: begin{gather*} C(100)=1,7+2acdot 100+3bcdot 100^2-1,71\ 200a+30000b=0,01 end{gather*} Кроме того: begin{gather*} Q(50)=1,7cdot 50+acdot 50^2+bcdot 50^3=85,025\ 2500a+125000b=0,025 end{gather*} Получаем линейную систему: begin{gather*} begin{cases} 200a+30000b=0,01 |:2\ 2500a+125000b=0,025 |:25 end{cases} Rightarrow begin{cases} 100a+15000b=0,005\ 100a+5000b=0,001 end{cases} \ 15000b-5000b=0,005-0,001\ 10000b=0,004\ b=4cdot 10^{-3}cdot 10^{-4}=4cdot 10^{-7} left(frac{Дж}{K^3}right)\ a=frac{0,001-5000b}{100}=frac{10^{-3}-5cdot 10^3cdot 4cdot 10^{-7}}{100}=frac{10^{-3}-2cdot 10^{-3}}{100}=-frac{10^{-3}}{100}\ a=-10^{-5} left(frac{Дж}{K^2}right) end{gather*} Ответ: (a=-10^{-5}frac{Дж}{K^2}; b=4cdot 10^{-7}frac{Дж}{K^3})
Пример 7*. Лестница длиной 5 м стояла вертикально. Потом её нижний конец стали перемещать по полу с постоянной скоростью (v=2) м/с. С какой по абсолютной величине скоростью в зависимости от времени опускается верхний конец лестницы? Постройте график полученной функции.
 |
Лестница со стенами образует прямоугольный треугольник, для которого справедлива теорема Пифагора: $$ x^2(t)+y^2(t)=5^2 $$ Нижний конец движется с постоянной скоростью, его уравнение движения по полу: $$ x(t)=vt=2t $$ Отсюда получаем уравнение движения верхнего конца по стенке: begin{gather*} y^2(t)=25-x^2(t)=25-(2t)^2=25-4t^2\ y(t)=sqrt{25-4t^2} end{gather*} |
Время (tgeq 0) имеет ограничение сверху (25-4t^2geq 0Rightarrow t^2leq frac{25}{4}Rightarrow 0leq tleq 2,5 (с))
Скорость скольжения верхнего конца по стенке: begin{gather*} u_y(t)=y'(t)=left(sqrt{25-4t^2}right)’=frac{1}{2sqrt{25-4t^2}}cdot (25-4t^2)’=frac{-8t}{2sqrt{25-4t^2}}\ u_y(t)=-frac{4t}{sqrt{25-4t^2}} end{gather*} Знак «-» указывает на направление скорости вниз и связан с уменьшением координаты (y(t)) со временем. Абсолютная величина найденной скорости: begin{gather*} u(t)=|u_y(t)|=frac{4t}{sqrt{25-4t^2}} end{gather*} 1) ОДЗ: (0leq tleq 2,5)
2) Четность – нет, т.к. функция определена только на положительных t.
Периодичность – нет.
3) Асимптоты:
1. Вертикальная
Рассмотрим односторонние пределы begin{gather*} lim_{trightarrow +0}left(frac{4t}{sqrt{25-4t^2}}right)=frac05=0\ lim_{trightarrow 2,5-0}left(frac{4t}{sqrt{25-4t^2}}right)=frac{10}{0}=+infty end{gather*} При подходе к правой границе (t=2,5) слева функция стремится к (+infty).
В точке (t=2,5) – вертикальная асимптота.
2. Горизонтальных асимптот нет, т.к. ОДЗ ограничено интервалом.
3. Наклонных асимптот нет.
4) Первая производная begin{gather*} u'(t)=4cdotfrac{1cdotsqrt{25-4t^2}-tcdotfrac{-8t}{2sqrt{25-4t^2}}}{25-4t^2}=4cdotfrac{25-4t^2+8t^2}{2(25-4t^2)^{frac32}}=frac{2(4t^2+25)}{(25-4t^2)^{frac32}} end{gather*} (u'(t)gt 0) на всей ОДЗ, функция возрастает.
5) Вторая производная begin{gather*} u”(t)=frac{2(4t^2+25)}{(25-4t^2)^{frac32}}=2cdotfrac{8tcdot(25-4t^2)^{frac32}-(4t^2+25)cdot frac32sqrt{25-4t^2}cdot (-8t)}{(25-4t^3)}=\ =2cdotfrac{8tcdot(25-4t^2)+8tcdotfrac32cdot (4t^2+25)}{(25-4t^2)^{frac52}}=8tcdotfrac{50-8t^2+12t^2+75}{(25-4t^2)^{frac52}}=frac{8t(4t^2+25)}{(25-4t^2)^{frac52}} end{gather*} (u”(t)gt 0) на всей ОДЗ, функция выпуклая вниз.
6) Пересечение с осями
В начале координат: (t=0, u=0)
7) График
Ответ: (u(t)=frac{4t}{sqrt{25-4t^2}})
Пример 8. Под действием нагрузки деталь с поперечным сечением в виде прямоугольника площадью 17 см2 начинает деформироваться. Одна из сторон прямоугольника растет с постоянной скоростью 1 см/ч, а вторая – уменьшается со скоростью 0,5 см/ч. Найдите скорость изменения площади поперечного сечения через 45 мин после начала деформации, если известно, что в этот момент его площадь равна 20 см2.
Длина первой стороны в зависимости от времени: (a(t)=a_0+1cdot t) (см),
время – в часах.
Длина второй стороны: (b(t)=b_0-0,5cdot t).
Площадь в начальный момент: (S_0=a_0 b_0=17 (см^2))
Площадь в произвольный момент t: begin{gather*} S(t)=a(t)cdot b(t)=(a_0+t)(b_0-0,5t)=a_0 b_0+(-0,5a_0+b_0)t-0,5t^2=\ =17+(-0,5a_0+b_0)t-0,5t^2 end{gather*} По условию при (t=45 мин=frac34 ч): begin{gather*} Sleft(frac34right)=17+(-0,5a_0+b_0)cdotfrac34-0,5cdotleft(frac34right)^2=20\ (-0,5a_0+b_0)cdotfrac34=20-17+frac{9}{32}=3+frac{9}{32}\ (-0,5a_0+b_0)=frac43left(3+frac{9}{32}right)=4+frac38=4frac38 end{gather*} Получаем: begin{gather*} S(t)=17+4frac38t-0,5t^2 end{gather*} Скорость изменения площади: begin{gather*} S'(t)=0+4frac38cdot 1-0,5cdot 2t=4frac38-t end{gather*} Через 45 мин: begin{gather*} S’left(frac34right)=4frac38-frac34=3+frac{11}{8}-frac34=3+frac{11-6}{8}=3frac58=3,625 (см^2/ч) end{gather*} Ответ: 3,625 см2/ч
оксана николаевна кузнецова
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Зависимые и независимые величины
Одним из основных инструментов для описания окружающего нас мира являются величины.
Определение 1
Величина – это такое свойство предмета или объекта, которое можно измерить.
Например, рост человека, высота столба, ширина забора, скорость полета.
Величины могут быть связанными между собой, зависимыми или независимыми одна от другой.
Например, длина стороны квадрата связана с площадью квадрата. При изменении длины стороны квадрата изменится и его площадь.
Рассмотрим еще один пример. Ученик идет в школу с некоторой скоростью (первая величина). В портфеле у него находится некоторое количество учебников (вторая величина).
При изменении скорости движения (первой величины) учеником количество учебников (второй величины) при этом не изменится. Следовательно, величины являются независимыми.
Иногда непосредственно повлиять на нужную величину невозможно. Тогда для изменения такой величины необходимо повлиять на промежуточную величину, от которой она зависит.
В таких случаях необходимо понимать связь между величинами, то, как при изменении одной величины изменится другая величина.
Описание изменения величины
Пример 1
Описание изменения температуры.
В полдень наблюдалось изменение температуры на $+6$ градусов, а к вечеру температура изменилась на $–4$ градуса.
Замечание 1
Уменьшение величины выражается с помощью отрицательных чисел, а увеличение – с помощью положительных чисел.
«Изменение величин» 👇
Пример 2
Описание изменения количества денег на счете телефона.
На счету мобильного телефона было $50$ рублей. На второй день количество денежных средств изменилось на $–14$ рублей. Число $–14$ – отрицательное, что указывает на уменьшение количества денег, которые были потрачены, например, на смс-сообщения, выход в Интернет и звонки. Остаток на счете составил $36$ рублей. За третий день количество денег изменилось на $–8$ рублей, а значит, уменьшилось, т.к. $–8$ – отрицательное число. На счету осталось $28$ руб. На четвертый день счет был пополнен на $20$ руб., т.е. количество денег увеличилось, т.к. число $20$ – положительное. Остаток на счете составил $48$ рублей.
Пример 3
Пример.
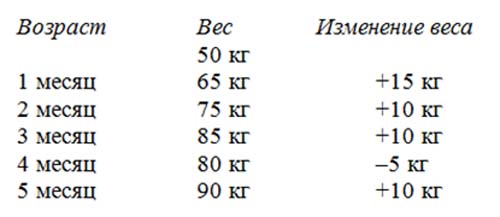
Описание изменения веса тигренка.
При рождении тигренок весил $50$ кг. За первый месяц его вес изменился на $+15$ кг, т.е. увеличился. За $2$-й и $3$-й месяц вес изменялся на $10$ кг. За $4$-й месяц вес тигренка изменился на $–5$ кг, т.е. уменьшился. Возможно, тигренок болел. В следующем месяце тигренок снова поправился на $10$ кг.
Изменение координаты точки на прямой
Замечание 2
При перемещении точки по координатной прямой ее координата будет изменяться. Причем при перемещении вправо изменение координаты (увеличение) описывается положительным числом, а при перемещении влево (уменьшении) – отрицательным числом.
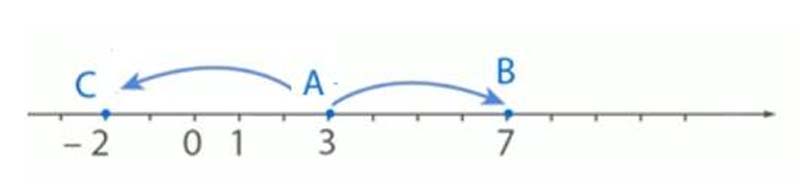
Например, при перемещении точки $A$ в точку $B$ изменение координаты составляет $+4$ единицы. При перемещении точки $A$ в точку $C$ координата изменится на $–5$ единиц.
Пример 4
Найти изменение координаты точки при ее перемещении по координатной прямой:
- от $A$ до $B$;
- от $B$ до $A$;
- от $A$ до $C$;
- от $B$ до $C$;
- от $C$ до $K$.
Решение.
- Перемещение от $A$ до $B$. Точка сдвинулась вправо на $3$ единицы, следовательно, перемещение равно $+3$ (или просто $3$).
- Перемещение от $B$ до $A$. Точка сдвинулась влево на 3 единицы, следовательно, перемещение равно $–3$ единицы.
- Перемещение от $A$ до $C$. Точка сдвинулась влево, т.е. перемещение будет отрицательным числом и составит $–7$ единиц.
- Перемещение точки $B$ в точку $C$ равно $–10$ единиц.
- Перемещение точки $C$ в точку $K$ составляет $12$ единиц, т.к. она сместилась вправо на $12$ единичных отрезков.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме