Ранее мы достаточно плотно познакомились с процессами и методами работы с ними. Среди часто используемых способов работы с процессами выделяются два: уравнение Менделеева-Клапейрона (для описания состояния идеального газа) и первое начало термодинамики. Из нескольких друг за другом идущих разных процессов можно составить общий циклический процесс.
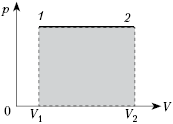
Круговой процесс (цикл) – составной термодинамический процесс, в результате совершения которого рабочее тело (газ) возвращается в исходное состояние. Таким образом, начальное и конечное состояние газа (давление газа , объём газа
и температура газа
) одинаковы. Попробуем изобразить такой процесс в координатах
(рис. 1).

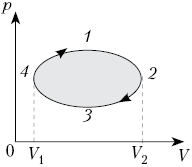
Рис. 1. Примеры циклических процессов
Например, наш циклический процесс 1.1 состоит из двух изохор, двух изотерм, а процесс 1.2 — из двух изобар и двух изохор. Таким образом, исходя из текстовых условий любой задачи и знания общего вида изопроцессов (именно из них чаще всего составляется цикл), можно нарисовать рисунок.
Для энергетического описания процесса (или цикла) через первое начало термодинамики необходимо обдумать два вопроса:
- как изменяется внутренняя энергия газа (
)
- чему равна работа газа (
)
- где
Для циклов есть небольшие фишки, которые удобно использовать для убыстрения задачи.
Так, изменение внутренней энергии газа зависит только от изменения температуры, а т.к. в цикле начальное и конечное состояние газа одинаково, то изменение внутренней энергии идеального газа за цикл равно 0 ().

Рис. 2. Графическая интерпретация работы газа
Поиск работы для газа также можно несколько упростить. Попробуем в координатах нарисовать график изобарического процесса и найти работу газа (рис. 2). Пусть газ находится в состоянии (давление
и объём
), далее газ изобарически перевели в состояние 2 (давление
и объём
). Тогда по определению работы газа:
(1)
Геометрически (рис. 2), произведение давления на разность объёмов численно равна площади прямоугольника, ограниченного сверху прямой (процессом), а снизу осью. В целом, эту логику можно расширить на любые процессы, тогда работа газа численно равна площади под кривой в координатах .
Также в рамках школьной физики присутствует условное деление циклов на прямые и обратные:
Прямой цикл – круговой, в котором рабочее тело совершает положительную работу за счёт сообщённой ему теплоты.
Обратный цикл — круговой, в котором рабочее тело совершает отрицательную работу.
Анализируя (1) вопрос о положительной и отрицательной работе, сводится к вопросу о соотношении между начальным и конечным объёмами, если:
— газ расширяется, работа положительна,
— газ сжимается, работа отрицательна.
Для графиков можно использовать следующую логику: в случае, если площадь под графиком расширения газа больше соответствующей площади для сжатия, значит цикл — прямой (рис. 3), если наоборот — обратный (рис. 4).

Рис. 3. Прямой циклический процесс

Рис. 4. Обратный циклический процесс
Таким образом, разница в прямом и обратном цикле может быть в очерёдности процессов. Так, прямой процесс, в нашем примере, — это 1-2-3-4-1, а обратный — 1-4-3-2-1.
Вывод: в задачах на циклические процессы нужно быть очень внимательным при прочтении, т.к. часть слов будет иметь глубокий физический смысл. Лучше всего процессы в таких задачах прорисовывать на графиках в координатах . Если график уже есть, то это к лучшему. Определяемся с конкретными изопроцессами, заданными в задаче, и используем это знание или через уравнение Менделеева-Клапейрона, или через первое начало термодинамики.
2.1 Найдем температуры в характерных точках цикла
Найдем
температуру Т1 :
Т1 = t1+273К
(1)
Т1=180C+273К=291
[К]
Найдем
температуру Т2 :
Т2=Т1εК-1
(2)
Т2=291×91,33-1 =599,46 [К]
Найдем
температуру Т3 :
Т3=Т2×λ (3)
Т3=599,46×3,8=2277,94 [K]
Найдем
температуру Т4 :
Т4=Т3×ρ (4)
Т4=2234,4×1=2277,94 [К]
Найдем
температуру Т6 :
Т6=Т1×ευ
(5)
Т6=291×1=291 [К]
Найдем
температуру Т5 :
λр=ρк×λ (6)
λр =11,33×3,8=3,8
Т5=Т6×λр
(7)

Т5=291×3,8=1105,8
[К]
2.2 Найдем давление в характерных точках цикла
Найдем
давление P1:
P1=Pa
= 96 [кПа]
Найдем
давление Р2:
Р2=Р1
k
(8)
Р2=96×103×91.33= 1783,68 [кПа]
Найдем
давление Р3:
Р3 = Р2 × λ
(9)
Р3=1783,68 ×103 ×3,8=6777,98 [кПа]
Найдем
давление Р4:
Р4=Р3
Р4=6777,98 [кПа]
Найдем
давление Р5:
Р5=
(10)
Р5 =
=
364,79 [кПа]
3 Изменение внутренней энергии каждого термодинамического процесса цикла
3.1 Определяем изменения внутренней
энергии по процессам цикла
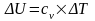
(11)
Изменение
внутренней энергии на участке (1-2):

=0,7164×
(599,46-291) = 220,98 [кДж/кг]
Изменение
внутренней энергии на участке (2-3):

=0,7164
×(2277,94-599,46) = 1202,46 [кДж/кг]
Изменение
внутренней энергии на участке (3-5):

=0,7164
×(1105,8-2277,94) =-839,72 [кДж/кг]
Изменение
внутренней энергии на участке (5-1):

=0,7164
×(291-1105,8) = -583,72 [кДж/кг]
Изменение
внутренней энергии в целом за цикл:

=220,98+1202,46-839,72-583,72=0
[кДж/кг]
4 Изменение энтальпии каждого термодинамического процесса цикла
4.1 Определяем изменения энтальпии по процессам цикла

(12)
Изменение
энтальпии на участке (1-2):

=1,0036
×(599,46-291)=309,57 [кДж/кг]
Изменение
энтальпии на участке (2-3):


=1,0036
×(2277,94- 599,46)=1684,52 [кДж/кг]
Изменение
энтальпии на участке (3-5):

=1,0036
×(1105,8-2277,94 )=-1176,35 [кДж/кг]
Изменение
энтальпии на участке (5-1):

=1,0036
×(291-1105,8)=-817,73 [кДж/кг]
Определяем
изменение энтальпии в целом за цикл:

=309,57+1684,52-1176,35-817,73=0
5 Изменение энтропии каждого термодинамического процесса цикла
5.1 Определяем изменения энтропии по
процессам цикла

(13)
Изменение
энтропии на участке (1-2):

=1,0036×
ln
=0,72
[(кДж×кг)/К]
Изменение
энтропии на участке (2-3):

=0,7164×ln
=0,95
[(кДж×кг)/К]
Изменение
энтропии на участке (3-5):
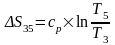
=1,0036×ln
=-0,72
[(кДж×кг)/К]

Изменение
энтропии на участке (5-1):

=0,7164×ln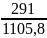
=-0,95
[(кДж×кг)/К]
Определяем
изменение энтропии в целом за цикл:

=0,72+0,95-0,72-0,95=0
6 КОЛИЧЕСТВО ПОДВЕДЕННОЙ И ОТВЕДЕННОЙ
ТЕПЛОТЫ
Так как мы знаем значения сυ
и ср найдем количество удельной
теплоты подведенной в цикле q1
и количество отведенной теплоты к
холодному источнику q2
:
q1=cυ
×(T3-T2)+cр×(T4-T3) (14)
q1=0,7164×(2277,94-599,46)+1,0036×(2277,94-2277,94)=1202,46
[кДж]
q2=cυ
×(T5-T1)+cр×(T6-T1) (15)
q2=0,7164×(1105,8-291)+1,0036×(291-291)=583,72
[кДж]
7 ТЕРМИЧЕСКИЙ КПД ЦИКЛА
Термический
КПД равен:
ηt
=1- q2
/q1 (16)
ηt
=1-(583,72/1202,46)=0,52
Работа
цикла равна:
WЦ=q1-q2
(15)
WЦ =1202,46-583,72=618,74
[кДж]

Сравниваем
циклы:

=1-
=0,88
Wy=q1ηt
(17)
Wy
=1202,46×0,52=625,27 [кДж]
Так как

,
то при использовании цикла Карно КПД
был бы выше, чем при использовании цикла
с подводом теплоты при V=const.
8 СРЕДНЕЕ ДАВЛЕНИЕ ЦИКЛА ДЛЯ ПОРШНЕВЫХ
ДВС
Одним из важнейших показателей работы
двигателей внутреннего сгорания является
среднее цикловое давление, найдем Рt
:

(18)
Рt=
=1123,62 [кПа]
9 ПОСТРОЕНИЕ В КООРДИНАТАХ p,v
и T,s
9.1 Рассчитаем объем камеры сгорания и
полный объем цилиндра
Rвоздуха=287 [Дж/(кг×К)]
V1=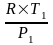
(19)
V2=
=0,86
[м3 /кг]
V1=
=

=
0,04 [м3 /кг]

Определим
характерные точки:
где
Р0=101325[Па];
Т0=273[К] .

=1,0036×ln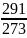
– 287×ln
= 15,55 [(кДж×кг)/К]
S2=0,95+15,55=16,5
[(кДж×кг)/К]


Рисунок
2 Диаграмма цикла с подводом теплоты
при V=const в
P,V координатах


Рисунок
3 Диаграмма цикла с подводом теплоты
при V=const в
P,V координатах

БИБЛИОГРАФИЧЕСКИЙ
СПИСОК
-
Амирханов,
Р.А. Проектирование систем теплоснабжения
сельского хозяйства [Текст] : учеб.
пособие / Р.А. Амирханов, Б.Х. Драганов.
– Краснодар : 2001. – 200 с.
-
Баскаков А.П. Теплотехника [Текст]:
учебник / А.П. Баскаков, Б.В. Берг, О.К.
Витт. – М. : Энергоатомидат, 1991. – 224 с.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ТЕРМОДИНАМИКА
Внутренней энергией тела в молекулярно-кинетической теории называется суммарная кинетическая энергия хаотического движения всех молекул тела плюс суммарная потенциальная энергия взаимодействия этих молекул друг с другом (но не с другими телами).
Внутренняя энергия одноатомного идеального газа
В одноатомном идеальном газе молекулы не взаимодействуют друг с другом, по этому его внутренняя энергия такого газа будет определяться как кинетическая энергия беспорядочного движения молекул.
Тогда внутренняя энергия будет определяться как произведение средней кинетической энергии и количества молекул из которых состоит наш газ:
![]()
Вспоминаем что средняя кинетическая энергия поступательного движения молекул определяется как:
![]()
А количество молекул в газе можно найти следующим образом:
![]()
Делаем небольшие алгебраические преобразования.
![]()
Так как произведение числа Авогадро ![]() и постоянную Больцмана
и постоянную Больцмана ![]() называют универсальной газовой постоянной
называют универсальной газовой постоянной ![]() , получаем:
, получаем:
![]()
Из полученного уравнения видно что внутренняя энергия одноатомного идеального газа напрямую зависит от его температуры. В таком случае изменение внутренней энергии можно определить как:
![]()
Работа газа при изобарном процессе
![]()
Работа газа при произвольном процессе равна площади под гафиком процесса в координатах (P,V). При линейной зависимости давления от объема равна:
![]()
Первый закон термодинамики количество теплоты сообщаемое газу идет на изменение внутренней энергии этого газа (![]() ), а так же на совершение работы этим газом (
), а так же на совершение работы этим газом (![]() ).
).
![]()
Применение первого закона термодинамики к изопроцессам.
Изобарный ![]()
![]()
Изохорный ![]()
![]()
Изотермический ![]()
![]()
Адиабатный ![]()
![]()
Адиабатный процесс — процесс протекающий без внешнего теплообмена с окружающей средой.
Еще одна интерпретация первого закона термодинамики звучит следующим образом: «Изменение внутренней энергии (![]() ) тела происходит в результате теплообмена (теплопередачи) либо совершения работы (
) тела происходит в результате теплообмена (теплопередачи) либо совершения работы (![]() ) над этим телом».
) над этим телом».
![]()
Количество теплоты (![]() ) — энергия которую приобретает или теряет тело в результате теплообмена.
) — энергия которую приобретает или теряет тело в результате теплообмена.
Теплопередача — это процесс передачи тепла от более нагретого тела жидкости или газа к менее нагретому. Можно выделить три вида теплопередачи: 1. Теплопроводность — передача тепла между различными частями одного тела, либо между телами при их непосредственном контакте; 2. Конвекция — вид теплообмена, при котором тепло передается струями и потоками жидкости или газа; 3. Излучение — передача тепла с помощью инфракрасного спектра электромагнитных волн.
Количество теплоты при нагревании или охлаждении
![]()
Удельная теплоемкость (![]() ) — количество теплоты необходимое чтоб нагреть 1 килограмм данного вещества на 1 градус.
) — количество теплоты необходимое чтоб нагреть 1 килограмм данного вещества на 1 градус.
Количество теплоты при плавлении (кристаллизации) При плавлении тело получает тепло, по этому количество теплоты берется со знаком плюс, а при кристаллизации, жидкость напротив отдает свою энергию, по этому количество теплоты имеет отрицательное значение.
![]()
![]()
Удельная теплота плавления и кристаллизации (![]() ) — количество теплоты необходимое для того, чтоб расславить 1 килограмм данного вещества.
) — количество теплоты необходимое для того, чтоб расславить 1 килограмм данного вещества.
Количество теплоты при парообразовании (конденсации) При кипении жидкость получает тепло, по этому количество теплоты берется со знаком плюс, а при конденсации, пар напротив теряет энергию, по этому количество теплоты имеет отрицательное значение.
![]()
![]()
Удельная теплота парообразования и конденсации (![]() ) — количество теплоты необходимое для того, чтоб превратить в пар 1 килограмм жидкости.
) — количество теплоты необходимое для того, чтоб превратить в пар 1 килограмм жидкости.
Количество теплоты выделяемое при сгорании топлива
![]()
Удельная теплота сгорания (![]() ) — количество теплоты выделяемое при сгорании одного килограмма топлива.
) — количество теплоты выделяемое при сгорании одного килограмма топлива.
Уравнение теплового баланса В изолированной системе в результате теплообмена устанавливается тепловое равновесие, а католичества теплоты получаемые или отдаваемые телами этой системы в сумме будут равны нулю.
![]()
Тепловая машина
Тепловая машина — устройство, преобразующее тепловую энергию в механическую работу (тепловой двигатель) или механическую работу в тепло (холодильник).
В циклическом процессе изменение внутренней энергии за цикл равно нулю, а работа выполняемая машиной за цикл ![]() будет равна разности теплоты полученной от нагревателя
будет равна разности теплоты полученной от нагревателя ![]() и теплоты отданной холодильнику
и теплоты отданной холодильнику ![]() .
.
![]()
КПД циклического процесса
![]()
КПД идеальной тепловой машины работающей по циклу Карно
![]()
![]() — соответственно температуры нагревателя и холодильника.
— соответственно температуры нагревателя и холодильника.
§7. Круговые процессы (циклы)
называется термодинамический процесс с телом, в результате совершения которого тело, пройдя через ряд состояний, возвращается в исходное состояние.
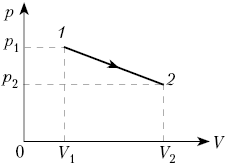
Если все процессы в цикле равновесные, то цикл считается равновесными. Его можноизобразить графически, и получится замкнутая кривая. На рис. 7 показан график зависимости давления `p` от объёма `V` (диаграмма $$ p-V$$) для некоторого цикла `1–2–3–4–1`, совершаемого газом. На участке `4–1–2` газ расширяется и совершает положительную работу `A_1`, численно равную площади фигуры $$ {V}_{1}412{V}_{2}$$. На участке `2–3–4` газ сжимается и совершает отрицательную работу $$ {A}_{2}$$, модуль которой равен площади фигуры $$ {V}_{2}234{V}_{1}$$. Полная работа газа за цикл $$ A={A}_{1}+{A}_{2}$$, т. е. положительна и равна площади фигуры `1–2–3–4–1`, изображающей цикл на диаграмме $$ p-V$$.
называется круговой процесс, в котором тело совершает положительную работу за цикл. Прямой равновесный цикл на диаграмме $$ p-V$$ изображается замкнутой кривой, которая обходится по часовой стрелке. Пример прямого цикла дан на рис. 7.
называется круговой процесс, в котором тело совершает отрицательную работу за цикл. На диаграмме $$ p-V$$ замкнутая кривая равновесного обратного цикла обходится против часовой стрелки.
В любом равновесном цикле работа за цикл равна по модулю площади фигуры, ограниченной кривой на диаграмме $$ p-V$$.
В круговом процессе тело возвращается в исходное состояние, т. е. в состояние с первоначальной внутренней энергией. Это значит, что изменение внутренней энергии за цикл равно нулю: $$ ∆U=0$$. Так как по первому закону термодинамики для всего цикла $$ Q=∆U+A$$, то $$ Q=A$$. Итак, алгебраическая сумма всех количеств теплоты, полученной телом за цикл, равна работе тела за цикл.
На некоторых участках прямого цикла тело получает от окружающих тел количество теплоты $$ {Q}^{+}$$ $$ ({Q}^{+}>0)$$, а на некоторых отдаёт $$ {Q}^{-}$$ т. е. получает отрицательное количество теплоты `«-Q^(-)»` `(Q^(-)>0)`.
За цикл тело совершает положительную работу `A`.
Коэффициентом полезного действия прямого цикла называется величина $$ eta ={displaystyle frac{A}{{Q}^{+}}}$$.
Поскольку $$ A={Q}^{+}+(-{Q}^{-})$$, то
$$ eta ={displaystyle frac{{Q}^{+}-{Q}^{-}}{{Q}^{+}}}=1-{displaystyle frac{{Q}^{-}}{{Q}^{+}}}$$. (20)
Для обратного цикла коэффициент полезного действия не вводится.
Спецвыпуск
Г. А.
Белуха
Работа газа в термодинамике
··· Орловский выпуск ···
Г.А.БЕЛУХА,
школа № 4, г. Ливны, Орловская обл.
Работа газа в термодинамике
Методические рекомендации по
изучению темы, 10-й класс
При изучении работы газа в
термодинамике учащиеся неизбежно сталкиваются с
трудностями, обусловленными слабыми навыками
вычисления работы переменной силы. Поэтому к
восприятию этой темы необходимо готовиться,
начиная уже с изучения работы в механике и решая
с этой целью задачи на работу переменной силы
путём суммирования элементарных работ на всём
пути с помощью интегрирования.
Например, при вычислениях работы силы
Архимеда, силы упругости, силы всемирного
тяготения и т.п. надо учиться суммировать
элементарные величины с помощью простейших
дифференциальных соотношений типа dA = Fds.
Опыт показывает, что старшеклассники легко
справляются с этой задачей, – дугу траектории, на
которой сила увеличивается или уменьшается,
нужно разбить на такие промежутки ds, на
которых силу F можно считать постоянной
величиной, а затем, зная зависимость F = F(s),
подставить её под знак интеграла. Например, 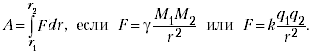
Работа этих сил вычисляется с помощью
простейшего табличного интеграла 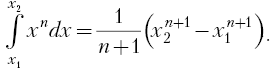
Такая методика облегчает адаптацию
будущих студентов к восприятию курса физики в
вузе и устраняет методические сложности,
связанные с умением находить работу переменной
силы в термодинамике и др.
После того как учащиеся усвоили, что
такое внутренняя энергия и как найти её
изменение, целесообразно дать обобщающую схему:
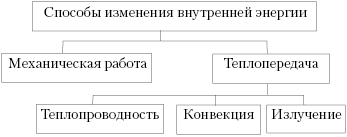
Усвоив, что работа – это один из
способов изменения внутренней энергии,
десятиклассники легко рассчитывают работу газа
в изобарном процессе. На данном этапе необходимо
подчеркнуть, что сила давления газа на всём пути
не меняется, и по третьему закону Ньютона |F2| = |F1|,
знак работы находим из формулы A = Fs cos![]() . Если
. Если ![]() = 0°, то A > 0,
= 0°, то A > 0,
если ![]() = 180°,
= 180°,
то A < 0. На графике зависимости р(V)
работа численно равна площади под графиком.
Пусть газ расширяется или сжимается
изотермически. Например, газ сжимается под
поршнем, давление изменяется, и в любой момент
времени 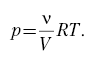
При бесконечно малом перемещении
поршня на dl мы получим бесконечно малое
изменение объёма dV, а давление р можно
считать постоянным. По аналогии с нахождением
механической работы переменной силы, составим
простейшее дифференциальное соотношение dA = pdV,
тогда 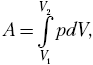 и, зная
и, зная
зависимость р (V), запишем 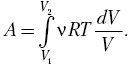 Это табличный интеграл
Это табличный интеграл
типа 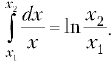 Работа
Работа
газа в этом случае отрицательна, т.к. ![]() = 180°:
= 180°:
![]()
т.к. V2 < V1.
Полученную формулу можно переписать,
используя соотношение 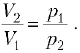
Для закрепления решим задачи.
1. Газ переходит из состояния 1
(объём V1, давление р1) в
состояние 2 (объём V2, давление р2)
в процессе, при котором его давление зависит от
объёма линейно. Найдите работу газа.
Решение. Построим примерный
график зависимости p от V. Работа равна
площади под графиком, т.е. площади трапеции:
![]()
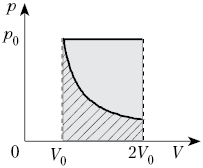
2. Один моль воздуха, находящийся при
нормальных условиях, расширяется от объёма V0
до 2V0 двумя способами – изотермически
и изобарно. Сравните работу, совершённую
воздухом в этих процессах.
Решение
При изобарном процессе Ap = р0![]() V, но р0 =
V, но р0 = ![]() RT0/V0,
RT0/V0,
![]() V = V0,
V = V0,
следовательно, Ap = ![]() RT0.
RT0.
При изотермическом процессе:
![]()
Сравним: ![]()
Изучив первый закон термодинамики и
его применение к изопроцессам и закрепив
решением задач тему о работе в термодинамике,
учащиеся подготовились к восприятию наиболее
сложной части термодинамики «Работа циклов и КПД
тепловых машин». Этот материал я излагаю в
следующей последовательности: работа циклов –
цикл Карно – КПД тепловых машин – круговые
процессы.
 Круговым
Круговым
процессом (или циклом) называется
термодинамический процесс, в результате
которого тело, пройдя ряд состояний,
возвращается в исходное состояние. Если все
процессы в цикле равновесные, то цикл считается
равновесным. Его можно изобразить графически в
виде замкнутой кривой.
На рисунке показан график зависимости
давления p от объёма V (диаграмма p, V)
для некоторого цикла 1–2–3–4–1. На участках 1–2
и 4–1 газ расширяется и совершает
положительную работу А1, численно
равную площади фигуры V1412V2.
На участке 2–3–4 газ сжимается и совершает
работу А2, модуль которой равен
площади фигуры V2234V1. Полная
работа газ за цикл А = А1 + А2,
т.е. положительна и равна площади фигуры 12341.
Если равновесный цикл изображается
замкнутой кривой на р, V-диаграмме,
которая обходится по часовой стрелке, то работа
тела положительна, а цикл накзывается прямым.
Если замкнутая кривая на р, V-диаграмме
обходится против часовой стрелки, то газ
совершает отрицательную работу за цикл, а цикл
называется обратным. В любом случае модуль
работы газа за цикл равен площади фигуры,
ограниченной графиком цикла на р, V-диаграмме.
В круговом процессе рабочее тело
возвращается в исходное состояние, т.е. в
состояние с первоначальной внутренней энергией.
Это значит, что изменение внутренней энергии за
цикл равно нулю: ![]() U = 0.
U = 0.
Так как, по первому закону термодинамики, для
всего цикла Q = ![]() U + A, то Q = A.
U + A, то Q = A.
Итак, алгебраическая сумма всех количеств
теплоты, полученных за цикл, равна работе тела за
цикл: Aц = Qн + Qх = Qн
– |Qх|. 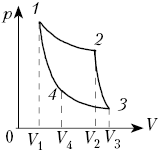
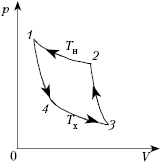
Рассмотрим один из круговых процессов
– цикл Карно. Он состоит из двух изотермических и
двух адиабатических процессов. Пусть рабочим
телом является идеальный газ. Тогда на участке 1–2
изотермического расширения, согласно первому
закону термодинамики, всё получаемое газом тепло
идёт на совершение положительной работы: Q12 = A12.
То есть нет никаких потерь тепла в окружающее
пространство и никакого изменения внутренней
энергии: ![]() U = 0,
U = 0,
т.к. T12 = const (потому что газ –
идеальный).
На участке 2–3 адиабатного
расширения газ совершает положительную работу
за счёт изменения внутренней энергии, т.к. Qад = 0
= ![]() U23 + Aг23
U23 + Aг23 ![]() Aг23 = –
Aг23 = –![]() U23.
U23.
Здесь также нет потерь тепла, по определению
адиабатного процесса.
На участке 3–4 над газом
совершается положительная работа внешней силой,
но он не нагревается (изотермический процесс).
Благодаря достаточно медленно протекающему
процессу и хорошему контакту с холодильником газ
успевает отдавать получаемую за счёт работы
энергию в виде тепла холодильнику. Сам же газ
совершает при этом отрицательную работу: Q34 = Aг34
< 0.
На участке 4–1 газ адиабатно (без
теплообмена) сжимается до исходного состояния.
При этом он совершает отрицательную работу, а
внешние силы – положительную: 0 = ![]() U41 + Aг41
U41 + Aг41
![]() Aг41 = –
Aг41 = –![]() U41.
U41.
Таким образом, за цикл газ получает
тепло только на участке 1–2, изотермически
расширяясь:
![]()
Холодильнику тепло отдаётся только
при изотермическом сжатии газа на участке 3–4:
![]()
Согласно первому закону термодинамики
Aц = Qн – |Qx|;
поэтому
![]()
КПД машины, работающей по циклу Карно,
найдём по формуле 
Согласно закону Бойля–Мариотта для
процессов 1–2 и 3–4, а также уравнению
Пуассона для процессов 2–3 и 4–1, легко
доказать, что ![]()
(Хорошо бы увидеть, как автор это
делает: ведь уравнение Пуассона для диабаты
идеального газа надо ещё получить. – Ред.)
После сокращений получим формулу КПД
тепловой машины, работающей по циклу Карно: ![]()
 Работу тепловых машин, работающих по
Работу тепловых машин, работающих по
обратному циклу, методически правильно, как
показывает опыт, изучать на примере работы
обратного цикла Карно, т.к. он обратим и его можно
провести в обратном направлении: расширять газ
при понижении температуры от Tн до Tx
(процесс 1–4) и при низкой температуре Tx
(процесс 4–3), а затем сжимать (процессы 3–2
и 2–1). Теперь двигатель совершает работу,
чтобы привести в действие холодильную машину.
Рабочее тело отнимает количество теплоты Qx
у продуктов внутри при низкой температуре Tх,
а отдаёт количество теплоты Qн
окружающим телам, за пределами холодильника, при
более высокой температуре Tн. Таким
образом, машина, работающая по обратному циклу
Карно, уже не тепловая, а идеальная холодильная.
Роль нагревателя (отдающего тепло) выполняет
тело с более низкой температурой. Но, сохранив
названия элементов, как в тепловой машине,
работающей по прямому циклу, мы можем
представить блок-схему холодильника в следующем
виде:
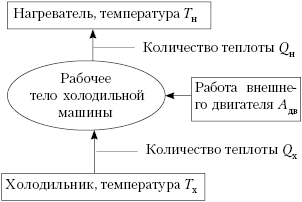
Обратим внимание, что тепло от
холодного тела переходит в холодильной машине к
телу с более высокой температурой не
самопроизвольно, а за счёт работы внешней силы.
Важнейшей характеристикой
холодильника является холодильный коэффициент ![]() , определяющий
, определяющий
эффективность работы холодильника и равный
отношению количества теплоты, отнятого от
холодильной камеры Qх к затраченной
энергии внешнего источника ![]()
За один обратный цикл рабочее тело
получает от холодильника количество теплоты Qх
и отдаёт в окружающее пространство количество
теплоты Qн, что больше Qх на
работу Aдв, совершаемую
электродвигателем над газом за цикл: |Qн| = |Qх| + Адв.
Энергия, затраченная двигателем
(электроэнергия в случае компрессорных
электрических холодильников), идёт на полезную
работу над газом, а также на потери при
нагревании обмоток двигателя электрическим
током QR и на трение в схеме Атр.
Если пренебречь потерями на трение и
джоулево тепло в обмотках двигателя, то
холодильный коэффициент
![]()
Учитывая, что в прямом цикле
![]()
после несложных преобразований
получим:
![]()
Последнее соотношение между
холодильным коэффициентом и КПД тепловой машины,
которая может работать и по обратному циклу,
показывает, что холодильный коэффициент может
быть больше единицы. В этом случае тепла
отнимается от холодильной камеры и возвращается
в комнату больше, чем для этого используется
энергии двигателем.
В случае идеальной тепловой машины,
работающей по обратному циклу Карно (идеального
холодильника), холодильный коэффициент имеет
максимальное значение:
![]()
В реальных холодильниках ![]() т.к. не вся получаемая
т.к. не вся получаемая
двигателем энергия идёт на работу над рабочим
телом, о чём написано выше.
Решим задачу:
• Оцените стоимость изготовления 1 кг
льда в домашнем холодильнике, если температура
испарения фреона –tх °С,
температура радиатора tн °С.
Стоимость одного киловатт-часа электроэнергии
равна Ц. Температура в комнате t.
Дано:
m, c, t, tн, tх,
![]() , Ц.
, Ц.
____________
Д – ?
Решение
Стоимость Д изготовления льда равна
произведению работы электродвигателя на тариф Ц:
Д = ЦА.
Для превращения воды в лёд с
температурой 0 °С необходимо отвести от неё
количество теплоты Q = m(ct + ![]() ). Считаем
). Считаем
приближённо, что над фреоном совершается
обратный цикл Карно с изотермами при
температурах Tн и Tх.
Используем формулы для холодильного
коэффициента: по определению, ![]() = Q/A и для
= Q/A и для
идеального холодильника ![]() ид = Tх/(Tн – Tх).
ид = Tх/(Tн – Tх).
Из условия следует, что ![]()
![]()
![]() ид.
ид.
Решаем совместно три последних
уравнения:
![]()
Разбирая с учащимися эту задачу,
необходимо обратить внимание на то, что основная
работа холодильного устройства идёт не на
охлаждение продуктов, а на поддержание
температуры внутри холодильного шкафа путём
периодической откачки тепла, проникающего
сквозь стенки холодильника.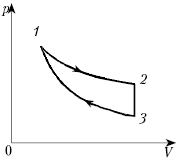
Для закрепления темы можно решить
задачу:
• КПД тепловой машины, работающей по
циклу, состоящему из изотермического процесса 1–2,
изохорического 2–3 и адиабатического 3–1,
равен ![]() , а
, а
разность максимальной и минимальной температур
газа в цикле равна ![]() T. Найдите работу, совершённую
T. Найдите работу, совершённую ![]() моль одноатомного
моль одноатомного
идеального газа в изотермическом процессе.
Решение
При решении задач, в которых
фигурирует КПД цикла, полезно предварительно
проанализировать все участки цикла, используя
первый закон термодинамики, и выявить участки,
где тело получает и отдаёт тепло. Проведём
мысленно ряд изотерм на р, V-диаграмме.
Тогда станет ясно, что максимальная температура
в цикле на изотерме, а минимальная – в т. 3.
Обозначим их через T1 и T3
соответственно.
На участке 1–2 изменение
внутренней энергии идеального газа U2 – U1 = 0.
По первому закону термодинамики, Q12 = (U2 – U1) + А12.
Так как на участке 1–2 газ расширялся, то
работа газа А12 > 0. Значит, и
подведённое к газу количество теплоты на этом
участке Q12 > 0, причём Q12 = А12.
На участке 2–3 работа газа равна
нулю. Поэтому Q23 = U3 – U2.
Воспользовавшись выражениями U2=
![]() cVT1
cVT1
и тем, что T1 – T3 = ![]() T, получим Q23 = –
T, получим Q23 = –![]() cV
cV ![]() T < 0.
T < 0.
Это означает, что на участке 2–3 газ получает
отрицательное количество теплоты, т.е. отдаёт
тепло.
На участке 3–1 теплообмена нет,
т.е. Q31 = 0 и, по первому закону
термодинамики, 0 = (U1 – U3) + A31.
Тогда работа газа
A31 = U3 – U1 = ![]() cV(T3 –T1) = –
cV(T3 –T1) = –![]() cV
cV ![]() T.
T.
Итак, за цикл газ совершил работу A12 + А31 = А12 – ![]() cV
cV ![]() T и получил
T и получил
тепло только на участке 1–2. КПД цикла
![]()
Так как ![]() то работа газа на изотерме равна
то работа газа на изотерме равна
![]()
Геннадий Антонович Белуха –
заслуженный учитель РФ, педагогический стаж 20
лет, ежегодно его ученики занимают призовые
места на различных этапах всероссийской
олимпиады по физике. Хобби – компьютерная
техника.
