Как найти измеренное значение напряжения

4.1 Основные значения измеряемых напряжений и токов

На практике
часто измеряют напряжения, несколько
реже – токи. Это объясняется тем, что для
измерения тока измеряемую цепь необходимо
разрывать, что не всегда возможно или
желательно. Измеряемые электрические
сигналы (токи или напряжения) представляют
собой, как правило, сложные функции
времени. Поэтому для анализа и сравнения
различных сигналов стремятся использовать
такие их значения, которые характеризовали
бы сигналы любой формы. Наиболее
распространенными являются следующие
значения (параметры) напряжений и токов:
амплитудное, среднее, средневыпрямленное
и среднеквадратическое. Рассмотрим
суть этих значений применительно к
напряжению.

Амплитудное
(пиковое) значение представляет собой
наибольшее или наименьшее мгновенное
значение переменной составляющей
сигнала за время измерения

(4.1)

где
– операция нахождения максимального
значения сигнала U(t)
на интервале измерения Т.

В общем случае
положительные и отрицательные пиковые
значения переменного напряжения могут
быть различными.

Среднее
значение
(постоянная составляющая) напряжения
определяется выражением

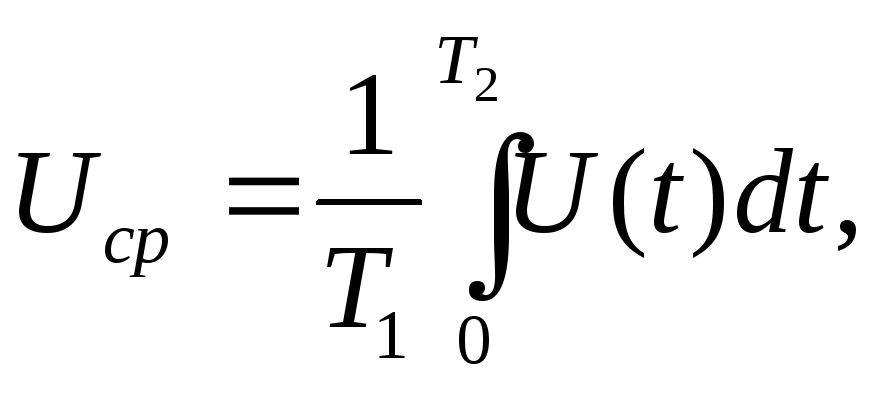(4.2)

где Т₁
– время наблюдения или период электрического
колебания; Т₂
– время действия измеряемого напряжения.

Интервалы Т₁
и Т₂
не всегда равны друг другу. При измерении
среднего значения импульсных напряжений
время действия измеряемого напряжения
меньше периода электрического колебания
(Т₂
< Т₁).

По физическому
смыслу U_сp
– это постоянная составляющая сигнала
U(t) за время Т₁,
а графически — это высота прямоугольника
с основанием Т₁,
площадь которого равна площади,
определяемой функцией U{t)
и осью времени за один .

Средневыпрямленное
значение
напряжения

(4.3)

Графически U_св
– это высота прямоугольника с основанием
Т₁,
площадь которого равна площади,
определяемой функцией U(t) над и под осью
времени. При таком определении считается,
что операция нахождения средневыпрямленного
значения осуществляется с помощью двух
полупериодного детектора средневыпрямленных
значений. Заметим, что для однополярных
сигналов U_сp
и U_св
равны между собой.

Среднеквадратическое
значение напряжения – это корень
квадратный из среднего значения
квадрата напряжения:

(4.4)

Среднеквадратическое
значение периодического сигнала сложной
формы может определяться также как
сумма квадратов постоянной составляющей
и среднеквадратических значений
отдельных гармоник, т.е.

(4.5)

Постоянную
составляющую U₀
и гармоники U₁,U₂,…U_n
находят путем разложения сложной
функции времени U{t)
в ряд Фурье.

Пиковое,
среднеквадратическое и средневыпрямленное
значения напряжений сигналов любой
формы связаны между собой коэффициентами
амплитуды К_а,
формы K_ф
и усреднения K_у:

(4.6)

Конкретные значения
Ка и Кф зависят от формы сигналов и
вычисляются с использованием формул
(4.2), (4.3) и (4.4). Например, основные
соотношения между значениями для
синусоидального сигнала U(t)
= U_msinωt
будут равны:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

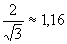
Метод и средства для измерения напряжения и тока.

При измерении напряжения и тока используют прямые и косвенные способы. Прямые измерения основаны на сравнении измеряемой величина с мерой этой величины или на непосредственной оценке измеряемой величины по отчетному устройству измерительного прибора. Косвенные измерения основаны на прямых измерениях другой величины, функционально связанной с измеряемой величиной. Например, косвенное измерение тока выполняют при помощи вольтметра, измеряющего напряжение на известном сопротивлении R0, и расчете тока по формуле

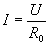
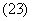
Погрешность косвенного метода измерения зависит от погрешности прямого измерения и погрешности расчета по функциональной зависимости (23). Сопротивление, используемое при косвенном измерении тока, называют шунтом. Дополнительная погрешность при косвенных измерениях обусловлена перераспределением тока между шунтом и вольтметром при изменении температуры окружающей среды. Для снижения температурной погрешности применяют специальные схемы компенсации,

В зависимости от рода тока приборы делят на четыре группы;

1) вольтметры постоянного напряжения (группа В2),
2) вольтметры переменного напряжения (группа ВЗ),
3) вольтметры импульсного напряжения (группа В4),
4) вольтметры селективные (группа В6).

Универсальные приборы, предназначенные для измерения постоянного и импульсного напряжения и тока, выделены в группу В7.

Программа работы

1. Определение основной погрешности, вариация показаний и поправку вольтметра.
2. Определение чувствительности и цены деления вольтметра.
3. Определение входного сопротивления вольтметра.
4. Определение частотного диапазона вольтметра.
5. Исследование влияния формы напряжения на показание вольтметра.
6. Определение погрешности при прямых и косвенных измерениях тока.

Порядок выполнения работы.

1. Определение основной погрешности, вариация показаний и поправки вольтметра выполняют по схеме, изображенной на рис. 1. В качестве поверяемого прибора используют вольтметр типа МПЛ-46, а образцовый служит цифровой вольтметр типа В2-23. Перед проведением измерений прибор В2-23 включить в сеть и выждать 10…15 мин. Затем произвести установку нуля и калибровку вольтметра И2-23 в соответствии с инструкцией по пользованию прибором. Кроме того, необходимо выполнить установку нуля вольтметра МПЛ-46, пользуясь корректором.

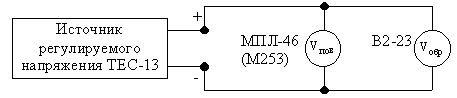
Для выполнения п.1 программы поверяемый вольтметр МПЛ-46 устанавливают на диапазон 15 В и измеряют напряжение на всех оцифрованных делениях шкалы, изменяя входное напряжение регулируемого источника ТЕС-13. Измерение напряжения на каждом оцифрованном делении шкалы МПЛ-46 производят дважды: один раз при возрастании напряжения (показание образцового вольтметра U’_обр), а второй раз при убывание напряжения (показание образцового вольтметра U’’_обр). При этом на образцовом вольтметре В2-23 необходимо выбрать поддиапазон, обеспечивающий не менее трех значащих цифр. Результаты измерений занести в ф.1.

Действительные значения на оцифрованных делениях шкалы поверяемого вольтметра определяют как среднее значение двух измерений U_ср=(U’_обр+U’’_обр)/2.
Расчет погрешности измерений выполняют по формулам:
Абсолютная погрешность U=U_пов-U_ср,
Относительная погрешность 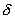=(U/ U_пов)*100%,
Приведенная погрешность _п=(U/ U_ном) *100%,
где U_ном=15 В – номинальное значение напряжения поверяемого.
Вариацию показаний вольтметра определяют по формулам:
Абсолютное значение вариации U=U’_обр-U’’_обр,
Приведенное значение вариации _в=(U_обр/ U_ном)*100%,
Поправку вольтметра вычисляют по формуле П=-U.
Из полученных значений _п и _в необходимо выбрать наибольшее и сравнить их с классом точности К_u поверяемого вольтметра. Если _{п макс} и _{в макс} окажутся больше К_u, то поверяемый вольтметр нельзя использовать с указанным классом точности.

Источник

Параметры переменного напряжения

Как вы помните из предыдущей статьи, переменное напряжение — это напряжение, которое меняется со временем. Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами.

Среднее значение напряжения

Среднее значение переменного напряжения Uср — это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.

Например,чему равняется среднее значение напряжения за эти два полупериода? В данном случае ноль вольт. Почему так? Площади S1 и S2 равны. Но все дело в том, что площадь S2 берется со знаком «минус». А так как площади равны, то в сумме они дают ноль: S1+(-S2)=S1-S2=0. Для бесконечного по времени синусоидального сигнала среднее значение напряжения также равняется нулю.

То же самое касается и других сигналов, например, двухполярного меандра. Меандр — это прямоугольный сигнал, у которого длительности паузы и импульса равны. В этом случае его среднее напряжение также будет равняться нулю.

Средневыпрямленное значение напряжения

Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая «пробивает пол» берут не с отрицательным знаком, а с положительным.

средневыпрямленное значение напряжения будет уже равняться не нулю, а S1+S2=2S1=2S2. Здесь мы суммируем площади, независимо от того, с каким они знаком.

На практике средневыпрямленное значение напряжения получить легко, использовав диодный мост. После выпрямления синусоидального сигнала, график будет выглядеть вот так:

Для того, чтобы примерно узнать, чему равняется средневыпрямленное напряжение, достаточно узнать максимальную амплитуду синусоидального сигнала Umax и сосчитать ее по формуле:

Среднеквадратичное значение напряжения

Чаще всего используют среднеквадратичное значение напряжения или его еще по-другому называют действующим. В литературе обозначается просто буквой U. Чтобы его вычислить, тут уже простым графиком не отделаешься. Среднеквадратичное значение — это значение постоянного напряжения, который, проходя через нагрузку (скажем, лампу накаливания), выделяет за тот же промежуток времени такое же количество мощности, какое выделит в этой нагрузке переменное напряжение. В английском языке среднеквадратичное напряжение обозначается так: RMS (rms) — root mean square.

Связь между амплитудным и среднеквадратическим значением устанавливается через коэффициент амплитуды K_a:

Вот некоторые значения коэффициента амплитуды K_a для некоторых сигналов переменного напряжения:

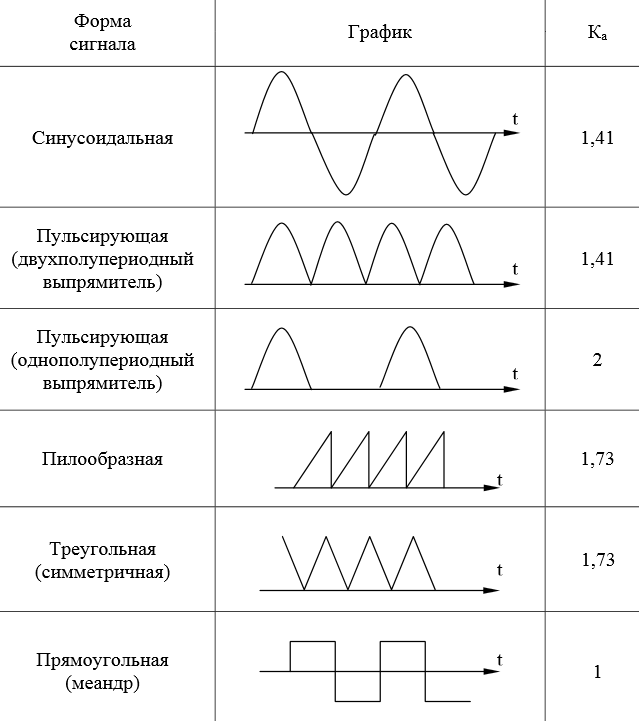
Более точные значения 1,41 и 1,73 — это √2 и √3 соответственно.

Как измерить среднеквадратичное значение напряжения

Для правильного замера среднеквадратического значения напряжения у нас должен быть мультиметр с логотипом T-RMS. RMS — как вы уже знаете — это среднеквадратическое значение. А что за буква «T» впереди? Думаю, вы помните, как раньше была мода на одно словечко: «тру». «Она вся такая тру…», «Ты тру или не тру?» и тд. Тру (true) — с англ. правильный, верный.

Так вот, T-RMS расшифровывается как True RMS — «правильное среднеквадратическое значение». Мои токоизмерительные клещи могут замерять этот параметр без труда, так как на них есть логотип «T-RMS».

мультиметр с True RMS

Проведем небольшой опыт. Давайте соберем вот такую схемку:

Выставим на моем китайском генераторе частоты треугольный сигнал с частотой, ну скажем, 100 Герц

генератор частоты

А вот осциллограмма этого сигнала. Внизу, в красной рамке, можно посмотреть его параметры

треугольный сигнал

И теперь вопрос: чему будет равно среднеквадратическое напряжение этого сигнала?

Так как один квадратик у нас равняется 1 Вольт (мы это видим внизу осциллограммы в красной рамке), то получается, что амплитуда Umax этого треугольного сигнала равняется 4 Вольта. Для того, чтобы рассчитать среднеквадратическое напряжение, мы воспользуемся формулой:

Итак, смотрим нашу табличку и находим интересующий нас сигнал:

Для нас не важно, пробивает ли сигнал «пол» или нет, главное, чтобы сохранялась форма сигнала. Видим, что наш коэффициент амплитуды K_a= 1,73.

Подставляем его в формулу и вычисляем среднеквадратическое значение нашего треугольного сигнала

Проверяем нашим прибором, так ли оно на самом деле?

Супер! И в правду Тrue RMS.

Замеряем это же самое напряжение с помощью моего китайского мультиметра

Он меня обманул :-(. Он умеет измерять только среднеквадратическое значение синусоидального сигнала, а у нас сигнал треугольный.

Самый интересный сигнал в плане расчетов — это двуполярный меандр, ну тот есть тот, который «пробивает пол».

Его амплитудное Umax, средневыпрямленное Uср.выпр. и среднеквадратичное напряжение U равняется одному и тому же значению. В данном случае это 1 Вольт.

Вот вам небольшая картинка, чтобы не путаться

среднее, среднеквадратичное и пиковое значения напряжения

Сред. — средневыпрямленное значение сигнала. Это и есть площадь под кривой
СКЗ — среднеквадратичное напряжение. Как мы видим, для синусоидальных сигналов, оно будет больше, чем средневыпрямленное.
Пик. — амплитудное значение сигнала
Пик-пик. — размах или двойная амплитаду. Или иначе, амплитуда от пика до пика.

Так что же все-таки показывает мультиметр при измерении переменного напряжения? Показывает он НЕ амплитудное, НЕ среднее и НЕ среднее выпрямленное напряжение, а среднее квадратическое, то есть действующее напряжение! Об этом всегда помним.

Источник

Среднее значение напряжения

среднее значение напряжения за период

меандр

Средневыпрямленное значение напряжения

выпрямленное переменное напряжение после диодного моста

Среднеквадратичное значение напряжения

Вот некоторые значения коэффициента амплитуды K_aдля некоторых сигналов переменного напряжения:

Более точные значения 1,41 и 1,73 — это √2 и √3 соответственно.

Как измерить среднеквадратичное значение напряжения

мультиметр с True RMS

Проведем небольшой опыт. Давайте соберем вот такую схемку:

Выставим на моем китайском генераторе частоты треугольный сигнал с частотой, ну скажем, 100 Герц

генератор частоты

А вот осциллограмма этого сигнала. Внизу, в красной рамке, можно посмотреть его параметры

треугольный сигнал

И теперь вопрос: чему будет равно среднеквадратическое напряжение этого сигнала?

Итак, смотрим нашу табличку и находим интересующий нас сигнал:

Подставляем его в формулу и вычисляем среднеквадратическое значение нашего треугольного сигнала

Проверяем нашим прибором, так ли оно на самом деле?

Супер! И в правду Тrue RMS.

Замеряем это же самое напряжение с помощью моего китайского мультиметра

Самый интересный сигнал в плане расчетов — это двуполярный меандр, ну тот есть тот, который «пробивает пол».

Вот вам небольшая картинка, чтобы не путаться

среднее, среднеквадратичное и пиковое значения напряжения

Сред. — средневыпрямленное значение сигнала. Это и есть площадь под кривой
СКЗ — среднеквадратичное напряжение. Как мы видим, для синусоидальных сигналов, оно будет больше, чем средневыпрямленное.
Пик. — амплитудное значение сигнала
Пик-пик. — размах или двойная амплитаду. Или иначе, амплитуда от пика до пика.

Источник

Что такое действующее значение напряжения

Содержание

1 Как измеряется
- 1.1 Практический пример
2 Импульсный электрический заряд
- 2.1 Расчёт кривой
- 2.2 Вычисления
3 Сила переменного тока
4 Вывод
5 Видео по теме

Всем нам известно о 220 вольт в бытовой розетке. Но если подключить к ней вольтметр, напряжение каждый раз будет разным. При этом зачастую напряжение может быть даже больше данной величины. Постараемся в данном материале разобраться — почему это происходит, что такое действующее значение переменного тока, и как его можно рассчитать с помощью различных вариантов.

Как измеряется

Электродинамические параметры в сети постоянно изменяются. Это связано с тем, что они представлены синусоидальным однополярным импульсом разной амплитуды. При измерении напряжения в цепи переменного тока, каждый раз будет получен разный результат. А при вычислении усреднённого параметра, он всегда будет составлять 0.

Получается, что математически вычислить данный параметр невозможно. Есть возможность получить только усреднённый параметр, который зависит от полупериода синусоидальной волны. Однако использовать его на практике или для каких-то вычислений нельзя.

Для решения этой проблемы и стали применять такое понятие, как действующее значение для расчёта силы тока и напряжения. Параметр определяется по характеристикам постоянного тока в цепи, генерирующей тепловую энергию такого же объёма, как и при подаче в цепь переменного тока.

Практический пример

Определение выше будет непонятным для человека, который не имеет особых познаний в области электротехники и электродинамики. Чтобы понять его смысл, предлагается рассмотреть следующий пример:

Доступны две идентичные электроцепи (длина, элементы цепи и сечение проводников у них совпадают).
В каждую включён одинаковый резистор — электронный компонент, который изменяет свое сопротивление в зависимости от подаваемого тока.
Обе цепи подключаются к источникам электроэнергии, имеющим одинаковое напряжение.

Но между цепями есть одна разница. На первую электроцепь подаётся постоянный, а на вторую — переменный ток. По одной из них пойдёт стабильный электроток, а по другой потечет импульсный электрозаряд, который постоянно изменяется и имеет синусоидальной график.

Чтобы найти количества тепла в цепи с сопротивлением, используется такая формула:

После произведения ряда замеров и вычислений можно увидеть, что выделяемое тепло в этих двух электроцепях имеет одинаковую величину. Например, в цепи с постоянным током при подаче напряжения 30 вольт выделяется тепло 200 Джоуль (или Дж). Если вторая цепь имеет идентичные характеристики, то выделение тепла в ней также составит 200 Дж. Получается, что напряжение 30В в этих электроцепях — это и есть эффективное напряжение.

Импульсный электрический заряд

Вышеприведенный пример позволяет только определить действующее и среднее значение напряжения переменного тока. Но на практике такой метод также не применяется, из–за того, что получить доступ к источнику переменного напряжения не всегда представляется возможным. Поэтому параметры цепи рассчитываются с помощью формул, которые основаны на синусоидальных кривых.

Стоит отметить, что действующее напряжение не всегда формируется путём плавного изменения определённого импульсного электрозаряда. Кривая зачастую имеет форму, отличную от привычной нам синусоиды:

Прямоугольную (меандр);
треугольную;
трапециевидную
и другие.

То есть график электротока может иметь отличную, но при этом стабильную форму. Наглядным примером такого варианта является кривая осциллографа, регистрирующая ритмы сердцебиения человека.

Но независимо от действующего в сети импульсного заряда, во время расчётов используется именно синусоида. Это объясняется тем, что погрешности в расчетах будут крайне малыми. Поэтому ими можно пренебречь, ведь они не скажутся на конечном результате:

Частота импульса в жилых домах составляет 50 Гц. За 1 сек электрический импульс проходит через фазу 100 раз. Это означает, что работающая от сети лампочка за секунду 100 раз загорается и тухнет, а электрический заряд при этом изменяется довольно плавно. Но человек этого не замечает из-за невосприимчивости человеческого зрения к сверхбыстрым колебаниям.
Одинаковая площадь фигур. Независимо от формы кривой периода, описывающей переменный электроток идентичных параметров, площадь их фигур всегда будет одинаковой. Следовательно, при любых расчетах получится одно и то же эффективное значение переменного синусоидального тока. Поэтому эффективные значения не зависят от формы кривой. На них оказывает влияние именно величина амплитуды.

Форма кривой импульса важна только для сверхточных расчётов в лабораторных условиях. Также она учитывается для работы суперкомпьютеров. В остальных случаях синусоида позволит вычислить действующее значение переменного синусоидального тока.

Расчёт кривой

Синусоида — это периодическая функция, которую можно всегда описать с помощью уравнения. Если взять её за основу, то на входе имеются следующие исходные данные:

Т — амплитуда;
φ — начальная фаза;
ωt — угловая скорость.

По этим входным характеристикам находим другие переменные параметры:

Uт — амплитудное напряжение;
Uм — действующие в момент измерения значения напряжения;
ωt + φ — фактическая фаза в точке измерения.

Т.к. начальная фаза равняется нулю, на выходе формула кривой будет иметь следующий вид:

Uм = Uт·sin(ωt + φ) = Uт·sin(ωt)

Теперь необходимо обратиться к закону выделения тепла, который еще называется законом Джоуля-Ленца. Согласно него квадрат напряжения — это произведение выделяемого тепла на сопротивление проводника.

Формулы для расчета тепловой энергии в электроцепях:
с постоянным током	с переменным током
Q = U²/R	Q = U_м²/R

U_м — величина постоянного напряжения;
U_м — величина действующего напряжения;
R — сопротивление проводника.

Мы видим, что при расчетах количества тепла в цепи переменного тока, пользуется именно действующим значением переменного тока.

Из данных формул вытекают два важных нюанса, на которые стоит обратить внимание:

В расчетах используется среднеквадратичное значение напряжения (СКЗ). Это связано с тем, что величина напряжения постоянно изменяется и можно получить только какую-то усредненную величину.
Амплитуда постоянного тока довольно условная величина. Ее используют в расчетах, чтобы только описать период синусоиды переменного электрозаряда.

Вычисления

Волны синусоид будут одинаковыми. Однако в пределах периода в каждой точке измерения напряжения будут отличаться. Поэтому, чтобы уравнять между собой среднеквадратичное напряжение постоянного и переменного электротока по тепловыделению, требуется рассчитать объём выделенного тепла в течение времени, равного 1 периоду:

В уравнение теперь можно подставить выражение расчёта мгновенного напряжения

Uм = Uт·sin(ωt + ф) = Uт·sin(ωt)

После математического преобразования можно рассчитать действующее значение электрического напряжения:

U = Uт / √2 = 0,707·Uм

Теперь найдем амплитудное напряжение по формуле:

Uт = U·√2

Амплитудное напряжение так же имеет и другое название – максимально возможное эффективное мгновенное значение напряжения.

Сила переменного тока

С помощью амперметра находим амплитудную силу тока в цепи. Используя её вместе с периодом, который равен 1/50 секунд, можно применить описанную выше формулу, чтобы рассчитать среднеквадратичное значение напряжения. В результате этого будет получена действующие значения силы тока.

Действующее значение тока можно рассчитать, когда других исходных параметров нет, но нам известно эффективное значение величины напряжения в цепи. Следовательно, можно воспользоваться всем нам известным законом Ома вычисления значения силы тока:

U = I·R и I = U/R

где:

U — будет действующим напряжением переменного синусоидального тока;
R — сопротивление проводника, которое всегда можно узнать в любом справочнике, зная состав материала проводника.

Ранее электропроводку делали из алюминия и меди, которые отличались довольно высоким сопротивлением. Эффективное значение реальной силы тока этих металлов было меньше 6.5А. По этой причине в старых домах зачастую срабатывает автоматический выключатель, если одновременно подключить в сеть несколько приборов. Сегодня открыты сложные сплавы с низким сопротивлением. Они позволяют достичь с действующее значение силы переменного тока около 16А даже в обычных современных многоквартирных домах.

С уменьшением сопротивления проводника, прямопропорционально возрастает мощность и тепловыделение. При том надо помнить о том, что у каждого сплава есть свой определенный температурный предел. Поэтому в жилых сетях сила тока часто не превышает 20 ампер, а при резком ее скачке, например, при неполадках на подстанции, электронная часть устройств просто сгорает. Для предотвращения таких случаев и подключаются автоматы, которые при регистрации высоких действующих значений размыкают цепь на данном участке. Более мощные источники электроэнергии встречаются только в промышленных трехфазных сетях с напряжением 380В.

Вывод

Мы рассмотрели в данной статье — что называют действующим значением силы тока и напряжения, а так же как определяют эти значения переменного тока в электроцепи. Это эффективные значения переменного тока, под действием которого выделяется точно такое же количества тепла, как и в цепи постоянного тока, имеющей аналогичные характеристики.

Видео по теме

Источник

Особенности измерения переменных напряжений и токов

В радиолюбительской практике приходится сталкиваться с необходимостью измерения переменных напряжений и токов не только синусоидальной формы, но и сигналов другой формы: прямоугольных импульсов, выходных напряжений одно- и двухполупериодных выпрямителей, выходных напряжений тиристорных регуляторов и пр. Форма сигнала существенно влияет на показания измерительного прибора. Дело в том, что шкалы большинства вольтметров переменного напряжения (как цифровых, так и стрелочных) градуируются в действующих значениях переменного напряжения. При этом в большинстве таких приборов в основу измерения переменного напряжения (или тока) положен способ измерения средневыпрямленного значения напряжения или тока.

Основные параметры переменного напряжения

Дадим некоторые определения. Переменное напряжение характеризуется следующими основными параметрами: амплитудным (пиковым) значением Ua, средним значением Ucp, средневыпрямленным значением Ucpв, действующим (среднеквадратическим, эффективным) значением Uд.

*Амплитудное значение**—это наибольшее или наименьшее за период значение величины.*

Среднее значение за период — это среднеинтегральное за период значение величины, которое математически может быть определено следующим образом:

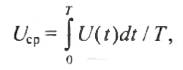
где U(t) — мгновенное значение напряжения.

Для двухполярных напряжений, форма которых симметрична относительно горизонтальной оси (например, для синусоидального) Ucp = 0. Часто говорят также, что среднее значение напряжения — это его постоянная составляющая. Очевидно, что для синусоидального симметричного напряжения постоянная составляющая равна нулю. Именно поэтому вольтметр постоянного напряжения, включенный для измерения такого напряжения, покажет нулевое значение. Это связано с тем, что любой вольтметр постоянного тока представляет собой выпрямитель с инерционным элементом. В стрелочных приборах функцию инерционного элемента выполняет магнитоэлектрический прибор. В цифровых вольтметрах такую функцию выполняет либо фильтр нижних частот, образованный резистором и конденсатором, либо усреднение производится самим аналого-цифровым преобразователем измерительного прибора.

Средневыпрямленное значение за период — это среднеинтегральное за период значение модуля величины, которое математически может быть определено по формуле:

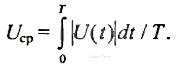
Эту величину несложно измерить, применив двухполупериодный выпрямитель. Эта величина характеризует перенос заряда электрическим током и геометрически равна высоте прямоугольника, у которого основание равно длине одного полупериода, а площадь прямоугольника равна площади под одной полуволной синусоиды.

Действующим (среднеквадратическим, эффективным) значением переменной величины называют такое постоянное значение этой величины, которое производит такое же тепловое действие, как и переменная величина. Поскольку тепловое действие электрического тока пропорционально квадрату тока (или напряжения), действующее значение можно определить как корень квадратный из среднего за период квадрата мгновенного значения величины, т. е.

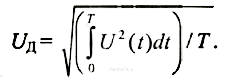
Все вышеуказанные значения напряжений связаны между собой коэффициентами амплитуды Ка и формы Кф. При этом Ка = Uа/ Uд, Кф= Uд /Ucpв. Иногда для удобства расчетов вводят коэффициент усреднения Ку = Ка Кф = Uа/ Ucpв. Эти коэффициенты позволяют определять любой параметр переменного напряжения, если известны форма напряжения и один из его параметров.

Формы и параметры, наиболее часто встречающиеся в практике радиолюбителя электрических сигналов различной формы, показаны на рис. 1 и в табл.1.

Напомним, что скважностью Q импульсов называют отношение периода следования импульсов к длительности одного импульса.

Особый интерес представляет измерение выходного напряжения регулятора с фазоимпульсным управлением (рис. 1, з). Его форма характеризуется углом α включения коммутирующего элемента (обычно это триодный или симметричный тиристор). Значение угла α может находиться в пределах от 0 до 180°. Коэффициенты формы и амплитуды являются функциями этого угла:

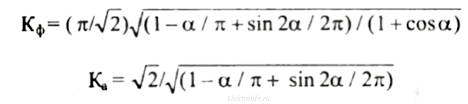
при 0 < α < 90° и

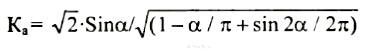
при 90° < α < 180°.

В данных формулах значение угла α измеряется в радианах (один радиан равен примерно 57,3°). Для удобства расчетов в приведенной ниже таблице 2 даны значения Кф, Ка и Ку для различных значений угла α, измеренного в градусах.

значения Кф, Ка и Ку для различных значений угла α, измеренного в градусах

Таблица 2

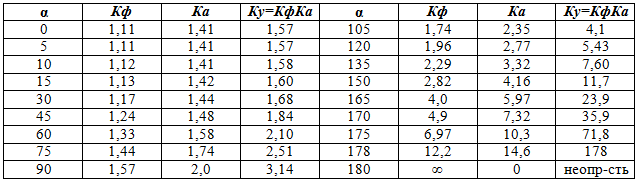
Из таблицы хорошо видно, что с увеличением угла значения Кф и Ка все более и более отклоняются от значений, приведенных в табл. 1 для синусоидального напряжения (1,11 и 1,41 соответственно).

Методика измерения переменных напряжений

В радиолюбительской практике возникает необходимость измерить действующее или среднее (средневыпрямленное), реже — амплитудное (пиковое) значения напряжений.

Приборы для измерения переменных напряжений отличаются принципом действия. Так, в приборах электромагнитной системы отклонение стрелки пропорционально действующему значению переменного напряжения или тока. При этом форма напряжения значения не имеет. Следовательно, для измерения действующих значений переменного напряжения произвольной формы желательно применять приборы электромагнитной системы. На шкалы таких приборов наносится соответствующий знак (рис. 2, а).

Особенности измерения переменных напряжений и токов

Рисунок 2. Условные обозначения на шкалах приборов: а — электромагнитной системы; б — магнитоэлектрической системы

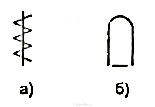
Приборы магнитоэлектрической системы реагируют на средневыпрямленное значение измеряемой величины и имеют на шкалах знак, показанный на рис. 2, б. Такие приборы весьма широко распространены и на их основе изготавливается подавляющее большинство авометров (тестеров). Практически все цифровые авометры широкого применения также реагируют на средневыпрямленное значение измеряемой величины. Отсюда следует, что для измерения средневыпрямленных значений переменных величин желательно применять именно такие приборы, поскольку форма сигнала на показания прибора не влияет.

Шкалы всех вольтметров, независимо от принципа действия прибора, градуируются в действующих значениях синусоидального напряжения. Это объясняется тем, что эти вольтметры чаще всего применяются для измерения синусоидальных напряжений как наиболее часто встречающихся в практике. Поэтому, если измеряется синусоидальное напряжение, прибор показывает значение Uд. Если же форма напряжения отличается от синусоидальной, потребуется пересчет показаний с учетом коэффициентов формы и амплитуды. Исключение составляют пиковые вольтметры, шкалы которых градуируются в амплитудных значениях Ua. При отсутствии такого вольтметра его несложно сделать самостоятельно, добавив к вольтметру постоянного тока диодный выпрямитель и конденсатор (рис. 3).

Рисунок 3. Пиковый вольтметр

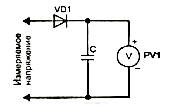
С учетом вышеизложенного, последовательность измерений переменной величины может быть следующей.

С помощью осциллографа определяется форма измеряемого сигнала и по таблице 1 и рисунку 1 определяются коэффициенты формы и амплитуды. Для выходного напряжения фазоимпульсного (рис. 1, з) регулятора необходимо определить угол включения α, который приблизительно можно оценить осциллографом.
Выясняют принцип действия измерительного прибора, и в каких значениях проградуирована его шкала.
Считывают показания со шкалы прибора и корректируют их с учетом Ка и Кф.

Примеры

Пример 1. Измеряется синусоидальное напряжение вольтметром переменного тока магнитоэлектрической системы. Шкала отградуирована в действующих значениях. Показание вольтметра равно 100 В. Из табл. 1 определяем К_а = 1,41 и К_ф = 1,11. По формулам K_a = U_a/ U_д, К_ф = U_д / U_cp_в вычисляем: амплитудное значение напряжения U_a = К_а • U_д = 1,41 • 100 = 141 (В) и средневыпрямленное значение U_cp_в = U_д / К_ф = 100:1,11 =90 (В).

Пример 2. Цифровым вольтметром постоянного тока, у которого измерительный узел реагирует на средневыпрямленное значение напряжения, измеряется напряжение на выходе двухполупериодного
выпрямителя (рис. 1, б). Прибор показывает 50 В. Из табл. 1 определяем коэффициенты формы и амплитуды для измеряемого двухполупериодного напряжения: К_а = 1,41 и К_ф= 1,11. Находим действующее значение измеряемого напряжения U_д = К_фU_cp_в = 1,11• 50 = 55,5 (В), а затем амплитудное значение U_a *= К_а*** U_д = 1,41•55,5 = 78,3 (В). Чтобы убедиться в правильности расчетов, понадобятся квадратичный вольтметр и осциллограф (или пиковый вольтметр). Подключенный к входу двухполупериодного выпрямителя квадратичный вольтметр должен показать 55,5 В. Определенная по изображению на экране осциллографа амплитуда напряжения должна составить примерно 78,3 В. При отсутствии осциллографа можно измерить амплитудное значение напряжения пиковым вольтметром, воспользовавшись приведенной на рис. 3 схемой. Показание вольтметра в этом случае также должно составить 78,3 В.

Если переменное напряжение той же величины (55,5 В действующего значения) будет подано на однополупериодный выпрямитель, то подключенный к нагрузке вольтметр постоянного тока покажет вдвое меньшее, по сравнению с предыдущим случаем, значение — 25 В.

Пример 3. Используется тот же вольтметр, что и в примере 2. Измеряемое напряжение имеет форму, показанную на рис. 1, з. Угол α = 90° (определен с помощью осциллографа). Показание вольтметра равно 40 В, то есть (U_cp_в = 40 В. Из табл. 2 определяем коэффициенты формы и амплитуды для измеряемого напряжения для указанного угла α: К_а = 2,0 и К_ф= 1,57. Находим действующее значение измеряемого напряжения U_д = К_фU_cp_в = 1,57•40 = 62,8 (В), а затем амплитудное значение U_a *= К_а*** U_д = 2•62,8 = 125,6 (В).

Пример 4. Измеряемое напряжение имеет форму, аналогичную показанной на рис. 1.з, но вторая полуволна имеет отрицательную полярность (то есть речь идет о переменном напряжении). Фазовый угол α = 90° (определен с помощью осциллографа). Для измерения переменного напряжения используется квадратичный вольтметр, шкала которого проградуирована в действующих значениях напряжения. Вольтметр доказывает 62,8 В. Следовательно, действующее значение напряжения и составляет эти самые 62,8 В. Из табл. 2 определяем коэффициенты формы и амплитуды измеряемого напряжения для указанного угла α: К_а = 2,0, К_ф = 1,57. Находим средневыпрямленное значение измеряемого напряжения U_cp_в = U_д / К_ф = 62,8:1,57 = 40 (В), а затем амплитудное значение U_a = К_а U_д = 2,0•62,8 = 125,6 (В).

Как видим, в двух последних примерах напряжение было измерено вольтметрами разного принципа действия, но результаты оказались одинаковыми. Это подтверждает правильность измерений и расчетов, а также свидетельствует о том, что средневыпрямленное и действующее значения переменного напряжения не зависят от знака этого напряжения.

Итоги

Исходя из рассмотренных выше примеров, можно сформулировать последовательность действий по измерению переменных напряжений:

1) Зная принцип действия прибора и способ градуировки шкалы прибора, вычисляется значение той величины, на которую непосредственно реагирует измерительный узел прибора (для квадратичного вольтметра — действующее значение напряжения, для вольтметра на базе прибора магнитоэлектрической системы — средневыпрямленное значение и т. п.).

2) Зная форму сигнала, по таблице определяются коэффициенты формы и напряжения.

3) Вычисляются искомые значения напряжения.

Все, что было сказано выше относительно измерения напряжений, в полной мере может быть применено и к измерению переменных токов. Однако далеко не все ампервольтомметры (тестеры) широкого применения имеют предел измерения переменного тока, а если таковой предел имеется, то максимальное значение тока не превышает обычно 10 А. Казалось бы, можно использовать режим измерения постоянного тока (имеется в каждом ампервольтомметре) и, добавив мостовой выпрямитель, измерять переменный ток. Однако при этом на диодах выпрямителя будет выделяться значительная мощность, а падение напряжения на измерительной цепи значительно возрастет (до 2…3 В), что может привести к снижению точности измерений за счет влияния измерительной цепи на работу устройства.

Источник

4.1 Основные значения измеряемых напряжений и токов