Андрей Андреев, Полина Ачева, Алексей Панов
«Квантик» №12, 2020
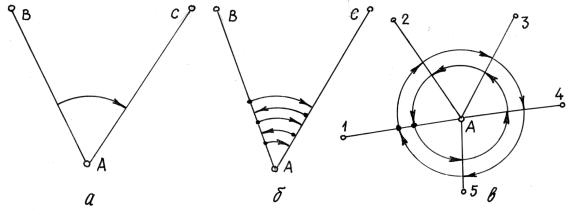
В школьной геометрии угол — это фигура, состоящая из двух лучей, выходящих из одной точки (рис. 1). Эта точка называется вершиной угла, а лучи — его сторонами. Угол разбивает плоскость на две части: на рисунке 2 они окрашены в зелёный и жёлтый цвет. Эти части называются плоскими углами.
Измерить угол можно обычным транспортиром, который размечен в градусах от 0° до 180° (рис. 3, слева).
Плоские углы удобно измерять круговым транспортиром, размеченным от 0° до 360° (рис. 3, справа). Конечно, для научных и технических измерений углов нужны более точные приборы: например, такие, как на рисунке 4. Слева там изображён один из астрономических инструментов Тихо Браге, с которым он проводил свои высокоточные наблюдения. Результаты этих наблюдений позволили Кеплеру вывести законы движения планет. Справа — современный электронный теодолит, используемый в геодезии.
А можно ли измерять углы, не применяя вообще никаких инструментов?
«Ручное измерение» углов. Об этом методе мы прочли в книге «Музыка сфер. Математика и астрономия», написанной Розой Марией Рос. Цитируем:
…Существует очень простой, хотя и не слишком точный, способ измерения углов вручную. Если мы вытянем руку перед собой, то растопыренная ладонь будет указывать интервал в 20°, кулак — 10°, большой палец — 2°, мизинец — 1°. Этот способ могут использовать и взрослые, и дети, так как размеры ладони человека увеличиваются пропорционально длине его руки.
Поясним сказанное. Пусть мы наблюдаем за двумя звёздами, расположенными на небе недалеко друг от друга. Направление взгляда на каждую из них задаёт луч. Угол между этими двумя лучами (с вершиной в глазу наблюдателя) мы и хотим измерить. Его величина называется угловым расстоянием между звёздами. Вытянем правую руку с растопыренной ладонью, как на рисунке 5 справа. Если кончик большого пальца закрывает одну звезду, а кончик мизинца — другую, угловое расстояние между звёздами можно оценить в 20°. Прикладывая ладони друг к другу, можно измерять углы до 40° (рис. 5, справа внизу).
Напомним: в направлении Мерак → Дубхе расположена Полярная звезда, указывающая путь на север.
Решив задачи, вы сможете проверить себя, так как известно, что расстояние Дубхе — Полярная звезда примерно в 5 раз больше расстояния Мерак — Дубхе.
Конечно, ручное измерение углов не позволяет добиться хорошей точности. Сейчас мы опишем бесприборный метод измерения углов, позволяющий проводить измерения со сколь угодно высокой точностью. Начнём с нескольких экспериментов.
Эксперименты с треугольниками: «60°» ≠ 60°. Мы купили несколько одинаковых треугольников, как на рисунке 7. Углы этого треугольника по стандарту должны быть равны 30°, 60° и 90°, но мы хотим проверить, так ли это на самом деле. Начнём со среднего по величине из этих углов, обозначив его α. Итак, верно ли, что α = 60°?
Эксперимент № 1: поворачиваем треугольники. Выложим на плоскость один за другим шесть треугольников, как на рисунке 8: каждый получен из соседнего поворотом на угол α.
Видно, что первый и последний треугольники не сомкнулись, и это означает, что в сумме шесть одинаковых углов α дают меньше 360°, то есть 6α < 360° и, значит, α < 60°. Выходит, мы купили дефектные треугольники.
На рисунке 8 также видно, что в промежуток между первым и последним треугольником ещё один такой же треугольник никак не поместится. Это говорит о том, что в сумме семь одинаковых углов α больше 360°, то есть 7α > 360°, откуда α > 360°/7. Объединим полученные два неравенства и запишем их в виде
( frac{360°}{7} < α < frac{360°}{6}.)
Эксперимент № 2: переворачиваем треугольники. На рисунке 9 представлен другой способ выкладывания треугольников. Каждый треугольник получается из соседнего переворотом вокруг их общей стороны на 180°. Этот способ даёт такую же оценку измеряемого угла, но он будет удобнее для нас в дальнейшем.
Практический совет: чтобы треугольники не смещались при малейшем прикосновении, не укладывайте их на скользкую поверхность. На видео мы воспользовались оборотной стороной коврика для ванной: она сделана из материала, не скользящего даже по влажному гладкому полу ванной комнаты, и идеально подходит для наших экспериментов.
Уменьшаем число треугольников, увеличиваем точность измерения. Первое усовершенствование: будем использовать единственный экземпляр треугольника. Опять обозначим один из его углов через α. Нарисуем на плоскости луч и совместим вершину угла с вершиной луча, а одну из сторон угла направим вдоль луча, как на рисунке 7. Перевернём треугольник вокруг другой стороны угла (не лежащей на луче). Потом перевернём треугольник вокруг другой стороны угла, опять перевернём и т. д., пока максимально не приблизимся к нарисованному лучу. Так мы определим максимальное k, для которого kα < 360° и при этом (k + 1)α > 360°, то есть
( frac{360°}{k+1} < α < frac{360°}{k}.)
На видео показан новый процесс измерения для уже знакомого треугольника с углом, близким к 60°, где k получилось равным 6.
Следующая цель — максимально увеличить точность оценки угла. Понятно, что, делая наши перевороты треугольника, совсем не обязательно останавливаться перед начальным лучом. Можно сделать ещё один или даже несколько полных оборотов вокруг начальной точки луча! Пусть n — общее число сделанных оборотов, k — экспериментально полученное нами число, такое, что kα < n · 360° и одновременно (k + 1)α > n · 360°. Тогда выполняется двойное неравенство:
( frac{n·360°}{k+1} < α < frac{n·360°}{k}.)
С увеличением n дроби, стоящие слева и справа, сближаются, и угол α определяется всё точнее — и безо всяких приборов!
Как выглядит это измерение для n = 3 и нашего треугольника, вы можете посмотреть на видео, там k оказалось равным 18. Мы провели измерения для n = 1, 2, …, 8 и для каждого n нашли соответствующее k. Результаты см. в таблице.
Судя по последней строке, 57,6° < α < 58,8°. Но можно поступить чуть хитрее и заменить значение 57,6° стоящим над ним в седьмой строке 58,6°, получив гораздо более точную оценку 58,6° < α < 58,8°.
Об измерении плоских углов. Всё сказанное об измерении угла треугольника применимо и к измерению плоского угла, который можно представлять себе вырезанным из очень тонкого и жёсткого листа пластика (рис. 10). В связи с этим задача.
В пункте б можно обойтись и без циркуля, если есть деревянный угольник с данным углом, о котором мы хотим выяснить, равен ли он 31°.
И напоследок — небольшой список увлекательных книг, в которых обсуждается измерение углов в астрономии и геометрии, с небольшими аннотациями.
- Роза Мария Рос. Музыка сфер. Астрономия и математика (М.: Де Агостини, 2014). В этой замечательной книге рассказывается о планетах и звёздах, об измерении углов, космических расстояний и времени.
- Александр Шень. Космография (М.: МЦНМО, 2019). В книге разбираются основные вопросы космографии: как движутся звёзды по небу, отчего бывают зима и лето, почему Луна видна в форме серпа, когда и как происходят затмения. Прочитав её, вы поймёте, что астрономия не может обойтись без измерения углов.
- Яков Перельман. Занимательная геометрия на вольном воздухе и дома, 7-е изд. (М.-Л.: ГИТТЛ, 1950). Обязательно обратите внимание на эту книгу. В третьей главе разобрано много задач на измерение углов подручными средствами и подробно рассказано о простейших устройствах для измерения углов, в том числе о посохе Якова и о грабельном угломере.
Особо рекомендуем раздел «Определение величины данного угла без всяких измерений» (с. 138–140), где описан метод измерения углов, «предложенный в 1946 г. З. Рупейка из Каунаса». По-видимому, этот раздел был добавлен редактором седьмого издания книги Б. А. Кордемским. Сам Яков Перельман скончался в 1942 году в блокадном Ленинграде. - Александр Шень. Геометрия в задачах (М.: МЦНМО, 2017). Второй раздел этой книги как раз называется «Измерение углов». Там много интересных задач, над которыми стоит подумать. Среди них мы выделим задачу № 38.
Художник Мария Усеинова
Добрый день, уважаемые гости!
Сегодня, я хотел бы описать полезный совет, как очень быстро построить или измерить любой угол с помощью обычного строительного угольника, когда других инструментов попросту нет под рукой.
Нам сейчас совершенно не потребуются ни угломеры, ни транспортиры и построение угла будет произведено угольником всего лишь в три шага.
1. Построение
Шаг №1
Как мы знаем, угол — это место на плоскости между двумя пересекающимися линиями (или сторонами какого-либо предмета), которые выходят из одной точки, называемой вершиной угла.
Итак, при построении угла, ставим угольник делением “0” (ноль) см. в вершину будущего угла и от этой точки проводим прямую в нужном вам направлении, от которой необходимо построить угол (эта прямая может являться одной из граней или сторон детали, заготовки или фигуры).
После чего, на этой прямой откладываем 10 см и ставим точку (штрих).
Отметив 10 см, из этой точки проводим к прямой перпендикуляр:
Шаг №2
Для примера, мне нужно построить угол 26°! В вашем же случае он может быть любым: 13°, 25°, 49°, 74° и пр.
Берем смартфон, заходим в приложение “калькулятор”, переводим его в инженерный режим и вводим нужный вам угол. Я ввел “26″.
Далее, нажимаем кнопку “tan” или “tg”, которая обозначает “вычислить тангенс угла”.
Машина мне вывела число 0,487. Из школы мы знаем, что тангенс угла — это отношение противолежащего нашему углу катета к прилежащему. И, зная один катет 10 см и отношение катетов 0,487, мы за одну секунду вычисляем второй катет, который равен 4,87 см.
Скорее, вы теперь поняли, для чего я взял первый катет именно 10 единиц.
Для простоты вычислений! На 10 проще всего умножать, переставив запятую на один разряд вправо.
Шаг №3
Я округляю 4,87 до десятых и на перпендикуляре отмечаю 4,9 см.
Чертим гипотенузу и получаем искомый угол!
Я решил перепроверить построенный угол и приложил угольник Свенсона:
Всё верно! Получил 26°.
2. Измерение
Сейчас мы построили угол, а при измерении угла — производим все то же самое, только в обратном порядке. Измеряя угол, мы будем знать оба катета, а соответственно и их отношение. Вводим в калькуляторе значение отношения противолежащего катета к прилежащему и нажимаем кнопку “arctg”, “atg” или “tan -1”, которая обозначает обратную тангенсу функцию — арктангенс.
На дисплее калькулятора мы увидим значение нашего угла!
…написано много, а на деле все занимает не более одной минуты…
Спасибо за внимание!
Геометрия
7 класс
Урок №5
Измерение углов
Перечень рассматриваемых вопросов:
- Измерительные инструменты.
- Градусная мера угла; биссектриса.
- Транспортир.
- Классификация углов.
Тезаурус:
Градус – угол, равный одной сто восьмидесятой части развернутого угла.
Градусная мера угла – положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Минута – 1/60 часть градуса.
Секунда – 1/60 часть минуты.
Луч – часть прямой, состоящий из всех точек, лежащих по одну сторону от заданной точки, которая является началом луча.
Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Стороны угла – лучи, из которых состоит угол.
Вершина угла – общее начало сторон угла.
Биссектриса – это луч, исходящий из вершины угла и делящий его на два равных угла.
Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Ранее вы уже познакомились с геометрической фигурой – уголи его составными элементами.
Сегодня мы продолжим изучать углы, познакомимся с их классификацией и будем измерять углы с помощью транспортира.
Измерение углов аналогично измерению отрезков – оно основано на сравнении, только отрезки сравнивались с отрезком, принятым за единицу измерения, а углы с углом, тоже принятым за единицу измерения.
Обычно за единицу измерения углов принимают градус.
Градус – угол, равный 1/180 части развёрнутого угла.
Положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу, называется градусной мерой угла.
Для измерения углов используют транспортир. Вспомним, как проводить измерение углов с помощью транспортира.
Транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах на той же шкале.
Например:
∠О = 50°
Но обычно говорят кратко – угол О равен 50 градусам.
Если масштабныйугол не укладываетсяцелое число раз в измеряемом угле, тоединицу измерения делят ещё на части.
Определённые части градуса носят специальные названия.
Части градуса.
Минута – 1/60 часть градуса.
Обозначается «´».
Секунда – 1/60 часть минуты.
Обозначается «´´».
Например:
∠А = 40 ° 15´ 16 ´´
Далее, аналогично понятию равные отрезки, ведём понятие равные углы.
Дваугла считаются равными, если градус и его части укладываются в этих углах одинаковое число раз, т.е. равные углы имеют равные градусные меры.
Если один угол меньше другого, то градус в нём (или его часть) укладываются в этом углу меньшее число раз, чем в другом, т.е. меньший угол имеет меньшую градусную меру.
Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
∠АОС =∠АОL + ∠LОС,
∠АОL = 64°,
∠LОС = 64°,
∠АОС = 64° + 64° = 128°.
Далее рассмотрим классификацию углов.
Мы уже знаем, что есть развёрнутый угол, его градусная мера сто восемьдесят градусов.
Но есть и другие углы.
Например, прямой угол, его градусная мера девяносто градусов;
острый угол, его градусная мера меньше девяноста градусов;
тупой угол, его градусная мера больше девяноста градусов, но меньше ста восьмидесяти.
Выполним практическое задание – построим биссектрису угла с помощью транспортира.
Мы знаем, что биссектриса – это луч, исходящий из вершины угла и делящий его на два равных угла.
∠АОС = 128°,
128° : 2 = 64°,
OL – биссектриса ∠АОС.
Поэтому для начала определим градусную меру ∠АОС, она составляет 128°, тогда биссектриса этого угла, исходя из определения, составит 64 °.
Итак, сегодня получили представление о том, как измерять и изображать угол с помощью транспортира. Перейдем к практическим заданиям.
Способы измерения на местности.
Измерение углов на местности проводят с помощью различных приборов. Один из таких – астролябия, она состоит из диска (лимб), разбитого на градусы и вращающейся вокруг центра диска линейки (алидады). На концах алидады есть окошечки, которые нужны, чтобы устанавливать её в определённом направлении.
Опишем, как происходит измерение углов с помощью этого прибора. При измерении углов астролябию устанавливают в его вершине, например, точке О, при этом лимб должен находится горизонтально плоскости угла, а отвес, в центе диска, совпадать с вершиной угла.
Затем устанавливаем алидаду вдоль одной из сторон угла, например, АО, отмечаем деление, напротив которого находится указатель алидады.
Далее поворачиваем алидаду по часовой стрелке, пока она не совпадёт со второй стороной угла, у нас это сторона ОВ, отмечаем деление, напротив которого оказался указатель алидады. Теперь можно найти градусную меру измеряемого угла, как разность второго и первого измерения.
Тренировочные задания.
1. Луч ВК делит развернутый ∠ОВС на два угла, разность которых равна 56°. Найдите образовавшиеся углы.
Решение: нарисуем рисунок, исходя из условия задачи.
Обозначим ∠СВК за х, тогда ∠ОВК= х + 56°, исходя из условия задачи (разность углов равна 56°). Развёрнутый угол равен 180°. Составим уравнение и решим его.
х + х +56 =180,
2х= 180 – 56,
2х= 124,
х = 124:2,
х = 62° (∠СВК).
Тогда ∠ОВК= х + 56°= 62° +56° = 118°.
Ответ: ∠СВК = 62°; ∠ОВК = 118°.
2. Чему равен ∠ЕОА, если ∠ВОА = 130° 54´, а ∠ВОЕ = 105° 76´?
Решение: Найдём ∠ЕОА = ∠ВОА – ∠ВОЕ, т.к. ОЕ – луч, проведённый из вершины ∠ВОА и делящий этот угол на 2 части. Подставим в выражение градусные меры углов и найдём градусную меру ∠ЕОА. Так как в градусе 60 минут, то 105° 76´ = 106° 16´.
∠ЕОА = 130° 54´ – 106° 16´ = 24° 38´.
Ответ: ∠ЕОА = 24° 38´.
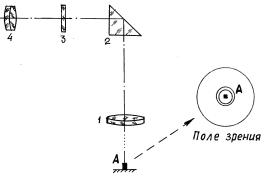
Рис. 5.11. Устройство оптического центрира
Установка зрительной трубы и отсчетной системы для наблюдений заключается в установке четкого (по глазу) изображения сетки нитей вращением окулярного колена зрительной трубы и четкого изображения шкал ГК и ВК вращением окулярного колена зрительной трубки отсчетной системы.
Многие теодолиты снабжены оптическими центрирами (рис. 5.11). Установка теодолита в рабочее положение (центрирование и горизонтирование) с помощью оптического центрира выполняется приближениями.
Найти в поле зрения оптического центрира точку, над которой производится центрирование, и закрепить в грунте или на твердой поверхности ножки штатива, следя за тем, чтобы изображение точки находилось как можно ближе к центру поля зрения центрира.
Выполнить установку пузырька цилиндрического уровня с помощью ножек
штатива, а затем – с помощью подъемных винтов подставки, как это выполняется при использовании отвеса.
При нарушении условия центрирования необходимо ослабить становой винт и переместить теодолит на головке штатива до совмещения центра поля зрения оптического центрира с вершиной измеряемого угла. Повторить действия по центрированию и горизонтированию по ножкам штатива и подъемным винтам подставки до достижения желаемого результата.
Горизонтирование может считаться удовлетворительным, если при любом положении колонки теодолита пузырек цилиндрического уровня при горизонтальном круге будет отклоняться от своего среднего положения не более чем на 2 деления ампулы.
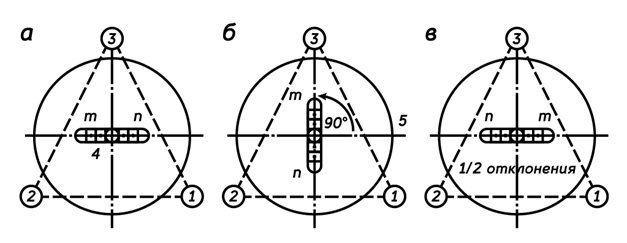
Горизонтальные углы измеряют способом приемов, способом повторений и способом круговых приемов (рис. 5.12) при двух положениях колонки: круг лево (КЛ) – вертикальный круг расположен слева от наблюдателя; круг право (КП) – вертикальный круг расположен справа от наблюдателя.
Здесь мы рассмотрим только приведенные способы измерения углов. При высокоточных измерениях существуют и другие способы.
Измерение горизонтального угла при одном из положений колонки (КП или КЛ) называется полуприемом. Два полуприема составляют полный прием. Наблюдения можно начинать с любого полуприема.
115
45.1.Способ приемов
1.Установить теодолит в рабочее положение.
2.Пользуясь прицельным приспособлением, размещенным на зрительной трубе, навести его светлый крест на наблюдаемую точку В. Зажать (легко) зажимные винты сначала колонки, затем – зрительной трубы. Вращением кремальеры фокусирующей системы, наблюдая в трубу, добиться четкого изображения объекта.
Рис. 5.12. Измерение горизонтальных углов.
а– способ приемов; б – способ повторений; в – способ круговых приемов
3.Наводящими винтами колонки и зрительной трубы переместить изображение наблюдаемой точки на вертикальную нить сетки нитей недалеко от центрального перекрестия (либо вывести изображение точки точно в центр сетки нитей).
4.Взять отсчет по шкале горизонтального круга (см. табл. 5.2, отсчет
117º 36,5′).
5.Открепить колонку и зрительную трубу и выполнить наведение на точку С (по аналогии с наведением на т. В: пп. 2-4). Отсчет – 236º 01,0′.
6.Перед сменой круга ослабить зажимной винт подставки и повернуть колонку в любую сторону (на 1о – 2о). Затем этот винт снова закрепить.
Ослабить зажимные винты колонки и зрительной трубы, перевести трубу через зенит и повернуть колонку на 180о. Такое положение колонки соответствует измерениям во втором полуприеме.
В теодолите Т15, например, не имеется наводящего устройства в подставке. Однако такую же функцию выполняет у него курковый зажим. Перед сменой круга необходимо нажать на курок зажима и слегка повернуть колонку. Затем снова отпустить зажим нажатием на вторую защелку.
7.Выполнить последовательно все действия по пп. 2-5 с записью отсчетов в журнал.
Вычисления в журнале заключаются в определении разностей отсчетов на правое (С) и левое (В) направления:
236º01,0′ – 117º36,5′ = 118º24,5′ (КЛ); 58º43,5′ – 300º18,5′ = (58º43,5′ + 360º) – 300º18,5′ = 118º25,0′ (КП).
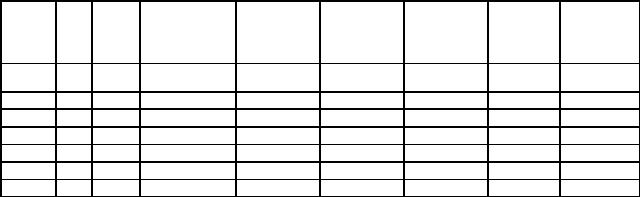
Таблица 5.2
116
|
№ |
№№ |
КП |
Отсчеты по |
Разность |
Среднее |
Отсчеты |
Место |
Значение |
|
стан- |
КЛ |
ГК |
отсчетов |
значение |
по ВК |
нуля |
угла |
|
|
то- |
||||||||
|
ции |
чек |
угла |
МО |
наклона |
||||
|
В |
117º36,5′ |
+1º36,5′ |
-0,75′ |
+1º37,25′ |
||||
|
С |
КЛ |
236º01,0′ |
118º24,5′ |
– 3º20,0′ |
-1,0′ |
– 3º19,0′ |
||
|
А |
118º24,75′ |
|||||||
|
В |
300º18,5′ |
– 1º38,0′ |
||||||
|
КП |
118º25,0′ |
|||||||
|
С |
58º43,5′ |
+3º18,0′ |
||||||
При получении отрицательного результата к меньшему значению следует прибавить 360º.
Можно вычислить и угол β’, дополняющий угол β до 360о. Для этого из отсчета на левое (В) направление необходимо вычесть отсчет на правое (С) направление:
(117º36,5′ + 360º) – 236º01,0′ = 241º 35,5′; 300º18,5′ – 58º43,5′ = 241º35,0′.
Если разность в значениях горизонтального угла, полученного в полуприемах, не будет превышать двойной точности теодолита, то вычисляют среднее значение угла из полуприемов.
Если разность будет больше допустимой, то измерение угла необходимо выполнить заново.
45.2. Способ повторений
Принцип измерения углов способом повторений (рис. 5.12 б) заключается в многократном (n раз) откладывании угла на шкале горизонтального круга, т.е. производится n раз суммирование горизонтального угла. Затем полученную сумму делят на число n, что дает значение искомого угла. Действия по измерению угла выполняются по следующей схеме (теодолит установлен в рабочее положение).
1.Выполнить визирование на т. В и записать полученный на нее отсчет в журнал (табл. 5.3, отсчет 33º16,0′).
2.Открепить колонку и зрительную трубу и выполнить наведение на
т.С. Взять контрольный отсчет на т. С.
3.Ослабить зажимной винт подставки и выполнить наведение на т. В, пользуясь наводящим устройством подставки. В результате этого отсчет на т. С переведется на т. В, поскольку алидада горизонтального круга и сам горизонтальный круг остаются неподвижными друг относительно друга.
Алидада – отсчетное приспособление горизонтального и вертикального кругов. Ось вращения алидады должна совпадать с осью вращения соответственного круга. В системе вертикального круга алидада всегда остается неподвижной, а вращается относительно нее вертикальный круг, жестко связанный со зрительной трубой. В системе горизонтального круга подвижными являются и горизонтальный круг и его алидада.
117
В теодолите Т15, например, после выполнения п. 2 необходимо взвести курок куркового зажима и затем выполнить наведение на т. В, пользуясь теми же наводящими устройствами.
4. Открепить колонку и зрительную трубу и выполнить действия по пп. 1, 2 и 3 n раз (в примере табл. 5.3 – n = 3) и записать последний отсчет на т. С
(200º56,5′).
5. Поменять круг и выполнить все действия по пп. 1 – 4.
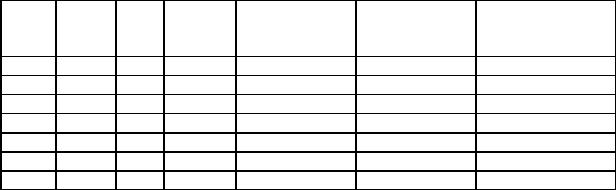
|
Таблица 5.3 |
|||||
|
№ |
№№ |
КП |
Число |
Значение угла |
Среднее значение |
|
стан- |
точек |
КЛ |
повто- |
Отсчеты по ГК в полуприеме |
угла |
|
ции |
В |
рений |
33º16,0′ |
||
|
КЛ |
3 |
55º53’30” |
|||
|
А |
С |
200º56,5′ |
55º53’45” |
||
|
В |
214º49,5′ |
||||
|
КП |
3 |
55º54’00” |
|||
|
С |
22º31,5′ |
Обработка журнала заключается в следующем:
– вычислить разности отсчетов в полуприемах и разделить их на число повторений n:
(200º56,5′ – 33º16,0′) : 3 = 55º53’30”; (22º31,5′ + 360º – 214º49,5′) : 3 = 55º54’00”.
При переходе через 0º (360º) N раз к последнему отсчету в точке С следует прибавить N360º. В примере N = 1;
– вычислить среднее значение угла:
(55º53’30 – 55º5400 ) : 2 = 55º53’45”.
45.3. Способ круговых приемов
Этот способ (рис. 5.12 в) используется при измерении углов между несколькими направлениями. Часто такие измерения приходится выполнять при сгущении геодезических и маркшейдерских сетей методом триангуляции. Методика измерений следующая (теодолит установлен в рабочее положение).
1.Устанавливают примерно нулевые индексы лимба и алидады горизонтального круга. Алидаду закрепляют. При свободном лимбе трубу наводят на первую точку, например, при КЛ, и берут на нее отсчет (0о01’15,6″) – табл. 5.4.
2.Алидаду освобождают (лимб при этом остается неподвижным), зрительную трубу наводят по часовой стрелке поочередно на точки 2, 3, 4, 5
иберут на них отсчеты (66о36’24,3″ и т д.).
3.Заканчивают наблюдение в первом полуприеме наведением на первую точку с регистрацией контрольного отсчета на нее (0о01’15,0″).
118
Работа с теодолитом – тема настоящей инструкции. Ниже поэтапно приведена методика измерения теодолитом, аккуратное выполнение пунктов которой обеспечит получение точных результатов. Настоящая инструкция предполагает, что пользователь обладает начальными знаниями о том, как работать с теодолитом, знаком с основными узлами и принципом работы прибора.
Установка теодолита в рабочее положение
Измерение горизонтальных углов теодолитом предполагает установку прибора в вершине определяемого угла. Для этого сначала ставят штатив так, чтобы центр площадки для установки штатива был примерно над точкой, а плоскость площадки – горизонтальна. Только после этого теодолит закрепляют на штативе, центрируют и горизонтируют прибор.
Центрирование теодолита – это проецирование оси вращения алидады и лимба по отвесной линии на вершину определяемого угла с точностью для механического отвеса ± 5 мм, ± 1-2 мм для оптического отвеса. Сначала проводится центрирование штатива с помощью механического отвеса с точностью 10-15 мм. При этом необходимо установить штатив горизонтально, чтобы регулировка подъемных винтов позволила произвести горизонтирование прибора. При установке прибора на штатив, производим окончательное центрирование теодолита, передвигаем оптический теодолит, ослабив становой винт.
Горизонтирование теодолита – это последовательное горизонтирование плоскости лимба горизонтального угломерного круга (ГУК) и приведение вертикальной оси вращения в отвесное положение. Процесс горизонтирования контролируется по цилиндрическому уровню алидады ГУК и производится посредством подъёмных винтов теодолита. Поворачивая алидаду, направляют ось уровня по двум подъёмным винтам и перемещают пузырёк уровня в центр. Затем следует повернуть алидаду на 90° и, используя третий подъёмный винт, вновь перевести пузырёк в центр. Действия необходимо повторять до тех пор, пока пузырек не станет сходить с середины при всех позициях алидады горизонтального круга. Допустимое его отклонение не больше двух делений шкалы цилиндрического уровня.
Горизонтирование теодолита
Для получения достоверного результата работа с теодолитом требует соблюдения двух геометрических условий:
- ось вращения прибора находится в вертикальном положении;
- ось цилиндрического уровня – в горизонтальном положении.
Измерение горизонтального угла теодолитом
Визирование
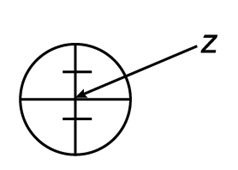
Визирование – совмещение центра сетки нитей с точкой.
Сетка нитей – это стеклянная пластина с нанесёнными на нём линиями (характер их нанесения может быть разным). Пересечение средних линий называют центром сетки нитей Z.
Наведение центра нитей на точку
Для визирования теодолита на точку необходимо:
- Закрепить лимб.
- Открепить алидаду для того, чтобы по грубому визиру, расположенному наверху зрительной трубы, установить прибор примерно на искомую точку.
- Закрепить алидаду.
- Для наблюдения установить зрительную трубу так, чтобы сетка нитей имела резкое изображение. Эта операция называется установкой по глазу и производится вращением окулярного колена.
- Установить зрительную трубу так, чтобы точка визирования была видна наилучшим образом. Эта операция называется установкой по предмету и производится вращением кремальеры.
- Навести центр сетки нитей точно на точку визирования посредством наводящих винтов алидады и зрительной трубы. Если вертикальный круг оказывается с правой стороны от трубы, если смотреть со стороны окуляра, говорят “круг право” (КП). Если вертикальный круг оказался слева – “круг лево” (КЛ).
Измерение горизонтального угла β
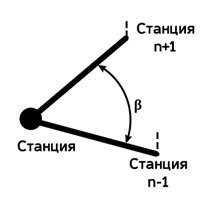
Измерение горизонтального угла теодолитом предполагает установку прибора в вершине измеряемого горизонтального угла (т.н. станция), а рейки на станциях n+1 и n–1.
Перекрестие сетки нитей совмещают с самой нижней видимой точкой рейки так, чтобы вертикальная нить совпадала с осью рейки.
Затем выполняют следующую последовательность действий (первый полуприём):
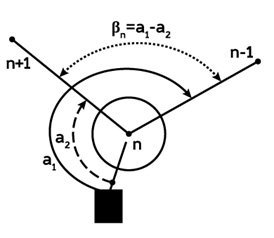
- наводят центр сетки нитей на вершину заднего (правого) угла (n – 1) и снимают отсчёт по лимбу горизонтального круга – отсчёт а1;
- наводят на вершину переднего (левого) угла (n + 1) снимают отсчет а2;
- определяют значение угла при круге лево βкл=а1-а2.
Измерение горизонтального угла на станции n:
β – горизонтальный угол
До начала второго полуприёма (КП) разблокируют зрительную трубу и переводят через положение зенита. Затем разблокируют алидаду и поворачивают прибор на 180° , проводят измерения при КП. При втором полуприёме (КП) визирование и измерения производят аналогично, различия в значениях угла в двух полуприёмах (С) не должно превышать двойной точности прибора (t): С < 2t.
Измерение горизонтального угла β на станции n (КЛ):
n – станция
n–1 –- вершина заднего угла
n+1 – вершина переднего угла
а1 – отсчёт на вершину заднего угла
а2 – отсчёт на вершину переднего угла
Вычисление горизонтальных углов
При выполнении условия расхождения в значениях угла, полученных за два полуприёма, средний горизонтальный угол рассчитывают по формуле: βср = (βКЛ + βКП) /2.
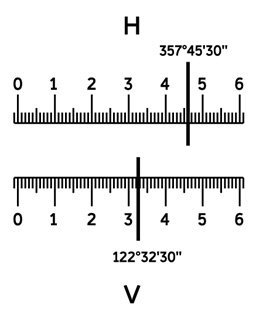
Лимб горизонтального угломерного круга оцифрован всегда от нуля до 360? через 1?, слева направо.
Отсчёт по горизонтальному кругу берут следующим образом:
- считывают по шкале алидады количество градусов отсчётного штриха (по рисунку – 125°);
- считывают минуты слева направо от нуля, учитывая, что цена деления на шкале ГУ – 5´ (по рисунку – 07´).
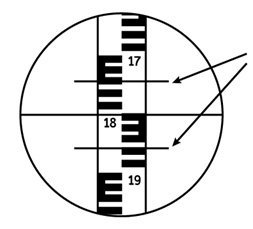
Отсчётный микроскоп теодолита RGK TO-15:
отсчёт по ГУК – “125°07´”
отсчёт по ВУК – “-0°35´”
Измерение вертикального угла теодолитом
Измеренный угол наклона может иметь как положительное, так и отрицательное значение, изменяясь от -90° до 90°.
Работа с теодолитом требует проводить горизонтирование алидады каждый раз при отсчёте. Горизонтальным считается положение, когда пузырёк цилиндрического уровня алидады или трубы расположен посередине ампулы. Однако, даже при нахождении пузырька в центре ампулы линия нулей отсчётного устройства может находиться под небольшим углом по отношению к линии горизонта, который называется место нуля вертикального круга (М0). Важной чертой измерения вертикальных углов является необходимость учёта места нуля вертикального круга. Для этого при создании съёмочного обоснования снимают отсчёты по вертикальному угломерному кругу (ВУК) при КЛ и КП, а при тахеометрической съёмке – на каждой станции перед началом работы определяют место нуля.
При измерении вертикальных углов теодолитом центр сетки нитей переводят на высоту инструмента, ранее отмеченную на рейке. Высоту инструмента определяют с помощью листа белой бумаги и рейки, приставляя её почти вплотную к окуляру. Пользователь при этом должен вести наблюдение в объектив. Лист передвигают по рейке, пока он не закроет ровно ½ поля зрения. Высоту инструмента на рейке удобно отмечать тонкой круглой резинкой.
Сначала снимают отсчёт, визируя при круге лево. Затем, переведя трубу через зенит, визируют и снимают отсчёт при круге права.
Существует несколько способов оцифровки лимба вертикального угломерного круга (ВУК). У теодолита RGK TO-15 (TO-05) оцифровка секторная, при которой ВУК разбит на 4 сектора по 90°, из которых два сектора имеют положительную оцифровку, а два других – отрицательную. Для взятия отсчёта:
- считывают количество градусов отсчётного штриха (по рисунку – “-0°”);
- считывают минуты – если вверху стоит “-0” – по отрицательной шкале от нуля до отсчётного штриха, если вверху стоит “+0” – по положительной шкале от нуля до отсчётного штриха (по рисунку – “-35?”).
Далее проводят вычисление вертикального угла. При этом отсчёты от 0° до 90° соответствуют измеряемому положительному вертикальному углу.
Вычисление вертикальных углов
После снятия отсчётов рассчитывают вертикальный угол через М0, либо по результатам двух отсчётов, полученных при визировании на цель в двух положениях зрительной трубы (КЛ и КП).
Расчётные формулы для секторной оцифровке лимба вертикального круга от нуля в обе стороны – по ходу и против хода часовой стрелки (RGK TO-05 и TO-15):
М0 = (КП + КЛ)/2; v = МО-КП; ν=КЛ−М0
При расчёте по этим формулам не обязательно добавлять 360°.
Измерение расстояний теодолитом
В этом разделе рассмотрим, как работать с теодолитом для измерения расстояний. В сетке нитей зрительной трубы теодолита имеются два дополнительных горизонтальных дальномерных штриха, расположенных по обе стороны от центра сетки нитей на равных расстояниях. Наличие этих штрихов позволяет производить измерение теодолитом расстояния D от прибора до рейки.
Для этого по рейке определяют величину дальномерного интервала n в сантиметрах, умножая полученное число на 100, затем полученное значение из сантиметров переводят в метры (дальномерный коэффициент зрительной трубы, как правило, равен 100) , т. е.
D = K*n =100*n
В случае, приведенном на рисунке:
- отчет по верхнему дальномерному штриху – 1747 мм;
- отчет по нижнему дальномерному штриху – 1856 мм.
Дальномерный интервал n равен разности отчетов по нижнему и верхнему дальномерным штрихам.
n = 1856-1747=109 мм = 10,9 см.
По формуле вычисляем расстояние: D = 100*10,9 см=1090 см = 10,9 м
Для измерения теодолитом расстояний при помощи нитяного дальномера относительная ошибка обычно составляет от 1/100 до 1/300.
Измерение теодолитом расстояния по дальномерным штрихам