Преобразование Лапласа и его свойства
Основные определения
1. Оригинал — это комплекснозначная функция действительного аргумента
, которая удовлетворяет следующим условиям:
а) при
;
б) на любом конечном отрезке функция
имеет не более чем конечное число точек разрыва первого рода;
в) имеет ограниченный рост, т.е. возрастает не быстрее показательной функции: существуют такие постоянные
и
, что
при
.
Замечания 5.1
1. Величина называется показателем роста функции
. Для любой ограниченной функции, являющейся оригиналом, можно принять
.
2. Обозначим , если пределы существуют и конечны.
3. Совокупность всех оригиналов называется пространством оригиналов.
4. В точке разрыва первого рода функция имеет конечные односторонние пределы:
.
Пример 5.1
2. Изображение функции — функция
комплексного переменного
, определяемая равенством
(5.1)
Область существования этой функции определяется областью сходимости интеграла Лапласа, стоящего в правой части равенства (5.1). Исследование интeгpaлa позволяет определить эту область и установить свойства функции . Имеет место следующее утверждение.
Утверждение 5.1. Если функция , является оригиналом, то интеграл Лапласа сходится абсолютно в области
(рис. 5.1) , где
— показатель роста оригинала. Внутри этой области, т.е. на любом замкнутом подмножестве
, интеграл сходится равномерно и определяет аналитическую функцию
.
Замечания 5.2
1. Утверждение 5.1 аналогично свойствам степенных рядов, сходящихся в круге и равномерно сходящихся внутри этого круга, где сумма ряда является аналитической функцией.
2. Свойство аналитичности изображения имеет важное значение в теории и практике применения преобразования Лапласа, так как позволяет использовать в пространстве изображений методы теории аналитических функций, в частности разложения функций в ряды и теорию вычетов.
3. Совокупность всех изображений называется пространством изображений.
4. Переход, определяющий изображение по оригиналу
, называется преобразованием Лапласа:
(5.2)
Запись означает, что оригиналу
соответствует изображение
.
5. Оригинал по изображению находится с помощью обратного преобразования Лапласа по формуле обращения
(5.3)
где путь интегрирования — любая прямая , параллельная мнимой оси и лежащая правее прямой
(рис. 5.1).
Непосредственное применение формулы обращения часто затруднительно. Поэтому на практике пользуются методами, изложенными ранее.
Замечания 5.3
1. Для преобразования Лапласа используются различные обозначения, на пример и
, что означает: оригиналу
соответствует изображение
и изображению
соответствует оригинал
. В некоторых учебниках вместо аргумента
применяется
, то есть
и
.
2. Для компактной записи оригиналов используется единичная ступенчатая функция
(5.4)
где — точка приложения (рис. 5.2). Так как во многих практических задачах аргумент
имеет смысл текущего времени, то
также называется моментом приложения единичной ступенчатой функции. В системах автоматического регулирования и управления функция
рассматривается как типовой входной сигнал.
При функция
является функцией Хевисайда:
(5.5)
Тогда, если функция удовлетворяет условиям “б”, “в” в определении оригинала (п. 1), но не удовлетворяет условию “а”, то функция
будет оригиналом, так как
Далее под заданной с помощью аналитической формулы функцией , там, где это не вызывает недоразумений, будем понимать произведение этой функции на функцию Хевисайда, а множитель
опускать.
3. Функции , являющиеся изображениями, удовлетворяют необходимому условию: если
есть изображение, то
при
. Поэтому функции
не являются изображениями. Однако в практических задачах функции типа
и другие встречаются. Это требует расширения понятий оригинала и изображения.
Класс оригиналов можно расширить, включив в него функции, которые могут быть не ограничены в окрестности некоторых конечных точек, но такие, что интеграл Лапласа от них, тем не менее, сходится абсолютно в некоторой полуплоскости . К числу таких обобщенных оригиналов относятся степенная функция
при
и некоторые другие.
4. Во всякой точке , являющейся точкой разрыва функции
, правая часть формулы (5.3) равна
.
Примеры 5.2-5.3
Пример 5.2. Найти изображение единичной функции Хевисайда .
Решение. Так как функция ограничена, то в качестве показателя роста можно положить
. По формуле (5.2) имеем
так как из равенства следует, что
при
.
Пример 5.3. Найти изображение функции , где
— действительное число.
Решение. Показателем роста можно считать . По формуле (5.2)
так как из равенства следует, что
при
.
Свойства преобразования Лапласа
Будем предполагать, что рассматриваемые далее функции являются оригиналами. Соответствующие им изображения (при
) обозначим
.
1. Линейность. Если — оригиналы, то для любых комплексных чисел
, функция
также является оригиналом и справедливо равенство
(5.6)
Заметим, что для функции существенно, что все слагаемыс являются оригиналами, так как, например, функция
является оригиналом, а слагаемые
и
не являются.
Справедливо и обратное утверждение: если — изображения, то
Здесь также важно, что слагаемые функции являются изображениями, поскольку из того, что
— изображение, не следует, что
— изображения. Например, функция
является изображением, а слагаемые
и
не являются.
Примеры 5.4-5.5
Пример 5.4. Найти изображение функции .
Решение. Из примера 5.2 имеем , а из примера 5.3 при
имеем
. Тогда согласно свойству линейности для оригинала
получаем
.
Пример 5.5. Найти изображение функции .
Решение. Используя формулу Эйлера (2.11), получаем .
Из примера 5.3 при и
следует:
. Тогда по свойству линейности
2. Подобие (теорема подобия). Для любого из
следует
(5.7)
и обратно: .
Пример 5.6
Найти изображение функции .
Решение. Из примера 5.5 следует, что . Тогда по теореме подобия
3. Смещение (теорема смещения). При любом комплексном из
следует
(5.8)
то есть умножению оригинала на соответствует смещение изображения на
.
Пример 5.7
Найти изображение функции .
Решение. Из примера 5.6 следует . Тогда по теореме смещения
.
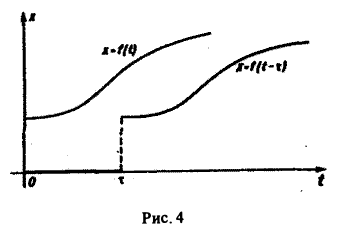
Запаздывание оригинала
4. Запаздывание (теорема запаздывания). Для любого из
следует
(5.9)
где (рис. 5.3), т.е. запаздыванию оригинала на
соответствует умножение изображения на
.
Примеры 5.8-5.10
Пример 5.8. Найти изображение функции .
Решение. В примере 5.5 получено . По теореме запаздывания при
имеем
.
Пример 5.9. Найти оригиналы по изображениям: a) ; б)
.
а) Из примера 5.7 следует, что при изображению
соответствует оригинал
. Тогда по теореме запаздывания при
имеем
б) По формуле 3 из табл. 5.1 .По теореме запаздывания при
получаем
. Заметим, что для похожего, но отличного от полученного, оригинала
(его можно записать в виде
) изображение имеет вид
.
Пример 5.10. Найти изображение функции , график которой представлен на рис. 5.4.
С учетом (5.4) представим функцию в виде
.
Из примера 5.2 имеем . Применяя свойства линейности и запаздывания, получаем
Заметим, что, находя предел при в последнем выражении, можно получить изображение δ-функции
Замечание 5.4. Дельта-функция часто встречается в инженерных приложениях как идеализация импульса конечной длительности. В теории автоматического регулирования и управления δ-функция вместе с единичной ступенчатой являются типовыми входными воздействиями.
Очевидно, изображение дельта-функции не удовлетворяет необходимому условию (п.2 замечаний 5.3). Этот факт свидетельствует о практическом требовании расширения понятия оригинала. Дельта-функция относится к обобщенным функциям и задается соотношением
(5.10)
Дифференцирование оригинала
5. Если функции являются оригиналами и
, то
(5.11)
где .
Примеры 5.11-5.12
Пример 5.11. Найти изображение , если
.
Решение. Из примера 5.7 следует, что при имеем
.
Найдем . Согласно (5.11)
.
Пример 5.12. Найти изображение выражения с начальными условиями
.
Решение. Пусть , тогда
. В примере 5.2 получено
. Используя свойство линейности, имеем
Интегрирование оригинала
Если функция является оригиналом и
, то
(5.12)
т.е. интегрированию оригинала соответствует деление изображения на .
Пример 5.13
Найти изображение интеграла от функции
.
Решение. Из примера 5.6 следует, что . Тогда
, то есть
.
Дифференцирование изображения
Если функция является оригиналом и
. то
(5.13)
Примеры 5.14-5.15
Интегрирование изображения
Если функция является оригиналом, то из
следует
(5.14)
Пример 5.16
Найти изображение функции .
Решение. Функция является оригиналом, так как
(условие “в”) и точка
является точкой разрыва первого рода (условие “б”). Из примера 5.13 следует
.
Отсюда .
Умножение изображений (теорема Бореля)
Из и
следует
(5.15)
т.е. свертке оригиналов соответствует произведение изображений. Функция определяется формулой
(5.16)
и называется сверткой оригиналов и
.
Пример 5.17
Найти оригинал, соответствующий изображению .
Решение. Представим в виде произведения изображений:
.
Из примеров 5.6 и 5.13 следует .
Согласно (5.15),(5.16) получаем искомый оригинал:
Дифференцирование свертки (интеграл Дюамеля)
10. Согласно свойствам 9 и 5 найдем преобразование Лапласа от производной свертки двух функций:
С другой стороны,
или, применяя правило дифференцирования интеграла, зависящего от параметра, имеем
Здесь при дифференцировании интеграла, зависящего от параметра, применялась формула Лейбница, которая для общего случая имеет вид
Объединяя полученные результаты, можно записать:
(5.17)
Формула (5.17) называется интегралом Дюамеля. Интеграл Дюамеля применяется для решения дифференциальных уравнений.
Пример 5.18
Найти оригиналы, соответствующие изображениям: a) ; б)
.
Решение. а) Заметим, что здесь нельзя непосредственно воспользоваться теоре мой Бореля, так как в произведении множитель
не является изображением (не выполняется необходимое условие).
Представим изображение в виде произведения . Из примера 5.3 вытекает
Тогда по формуле (5.17) имеем
Можно решить этот пример с помощью теоремы Бореля, представив изображение в виде
Тогда, используя свойство линейности и теорему Бореля, получаем
б) Представим изображение в виде произведения:
Из примера 5.6 при и
следует
Тогда по формуле (5.17) получаем
Теорема о связи “начальных” и “конечных” значений оригинала и изображения
Начальное значение оригинала находится по формуле
(5.18)
Если существует конечный предел , то
(5.19)
Из соотношений (5.18),(5.19) следует, что для нахождения начальных и конечных значений оригинала не требуется знания оригинала, а достаточно иметь соответствующее изображение. На практике соотношение (5.19) применяется, например, для нахождения установившегося значения выходного сигнала в системах автоматического регулирования.
Пример 5.19
Найти начальное и конечное значения оригинала, которому соответствует изображение .
Решение. Согласно (5.18) и (5.19) имеем
С другой стороны, из примера 5.7 следует, что
поэтому легко убедиться в правильности полученного результата.
Полученные решения примеров 5.2–5.17 позволяют сформировать таблицу преобразования Лапласа. Табл. 5.1 является фрагментом более полных таблиц, используемых далее при решении примеров и задач.
Нахождение изображения по оригиналу
Для нахождения изображения требуется применить свойства преобразования Лапласа Так, чтобы к функции или ее составляющим можно было применить результаты, содержащиеся в табл. 5.1.
Таблица 5.1. Таблица основных преобразований Лапласа
Посмотреть
Пример 5.21
Найти изображения функций:
a) ; б)
;
в) ; г)
;
д) ; е)
;
ж) ; з)
.
Решение
а) Согласно формуле 12 из табл. 5.1 . По свойству дифференцирования изображения (формула (5.13) при
):
или
.
Поэтому .
Можно решать иначе, используя формулу 10 из табл. 5.1 при а = 3 и свойство смещения при
и
.
б) Применим свойства линейности и интегрирования изображения. Так как в силу формул 1 и 9 из табл. 5.1 , то согласно (5.14)
в) По формуле 9 из табл. 5.1 . Функцию fit) можно записать, используя единичную ступенчатую функцию:
. Поэтому для нахождения изображения следует применить теорему запаздывания (5.9) к оригиналу
при
г) Согласно теореме смещения (5.8) и с учетом результата п. “в” имеем
, так как
.
д) По теореме запаздывания (5.9) при и по формуле 7 из табл. 5.1 при
получаем
е) Используя свойства линейности, запаздывания и формулы 6,1,8 из табл. 5.1, получаем
ж) По формуле 19 из табл. 5.1 находим . По свойству интегрирования изображения (формула (5.14)):
По свойству интегрирования оригинала (5.12): .
з) Используем формулу косинуса разности и запишем оригинал в виде суммы:
По свойству линейности получаем:
Заметим, что здесь и результаты пп. “в” и “з” различны так как оригиналами являются разные функции.
Нахождение изображений функций, заданных графиком
При решении прикладных задач оригинал часто задан графиком. Это может быть, например, входной сигнал, действующий на систему автоматической регулирования. В этом случае рекомендуется сначала записать аналитическое выражение оригинала с помощью единичной ступенчатой функции (5.4), привести полученное выражение к виду, удобному для применения табл. 5.1 и свойстве преобразования Лапласа.
Пример 5.22
Найти изображения функций, заданных графиками на рис. 5.5.
Решение.
а) Представим функцию в виде .
По формуле 3 из табл.5.1 и теореме запаздывания (формула (5.9) при )
б) Запишем функцию в виде .
По формулам 1,3 из табл. 5.1 и (5.6), (5.9) имеем .
в) Запишем изображенную функцию в виде .
По формулам 1,3 из табл. 5.1 и (5.6), (5.9) имеем .
г) Представим функцию в виде
По формулам 3 из табл. 5.1 и (5.6), (5.9) имеем .
д) Запишем функцию в форме
По формулам З из табл. 5.1 и (5.6), (5.9) .
е) Представим изображенную функцию в виде
По формулам 1,3 из табл. 5.1 и (5.6), (5.9) .
ж) Запишем функцию в форме .
По формуле 8 из табл. 5.1 и по теореме запаздывания .
з) Представим функцию в виде .
По формуле 6 из табл. 5.1 при и (5.9) при
имеем
и) Представим функцию в виде .
Используя формулы 2 из табл. 5.1 и (5.6), (5.9), получаем .
Нахождение изображений периодических функций
Во многих приложениях используются оригиналы, являющиеся периодическими функциями.
Пусть — оригинал с периодом
(рис. 5.6,в), образованный повторением функции
(рис. 5.6,б):
Для нахождения изображения периодической функции
следует:
1. Найти изображение функции .
2. Найти изображение по формуле
(5.20)
Пример 5.23.
Найти изображения функций, представленных на рис. 5.7.
Решение
а) По графику (рис. 5.7,в) получаем
Поэтому .
Поскольку , по формуле (5.20) находим
б) По графику (рис. 5.7,б) имеем , тогда
. По формуле (5.20) при
имеем
в) Функция, изображенная на рис. 5.7,в , имеет период . Запишем аналитическое выражение для
и соответствующее изображение
По формуле (5.20) получаем .
г) Для функции, изображенной на рис. 5.7,г, изображением для является
(см. пример 5.22 п.”ж”). Тогда по формуле (5.20) при
получаем
.
Нахождение оригинала по изображению
Непосредственное применение формулы обращения (5.3) затруднительно, поэтому для нахождения оригинала применяются теоремы разложения и правила преобразования изображения к виду, представленному в табл. 5.1.
Применение теорем разложения
Теорема 5.1 (первая теорема разложения). Если функция аналитична в некоторой окрестности бесконечно удаленной точки и ее разложение в ряд по степеням
имеет вид
, то функция (5.21) является оригиналом, соответствующим изображению
.
(5.21)
Теорема 5.2 (вторая теорема разложения). Если изображение является однозначной функцией и имеет лишь конечное число особых точек
лежащих в конечной части плоскости, то
(5.22)
Замечания 5.5
1. Формула (5.21) может быть записана в виде . Задача нахождения оригинала при выполнении условий теоремы сводится к нахождению коэффициентов разложения функции в ряд Лорана в окрестности бесконечно удаленной точки.
2. Формула (5.22) принимает наиболее простой вид в случае — рационального изображения, т.е.
, где
— многочлены степеней /пил соответственно, не имеющие общих корней. Если все полюсы
функции
простые, то по формуле (4.24) получаем
, а формула (5.22) принимает вид
(5.23)
3. Если при выполнении условий п.2 коэффициенты многочлена — лействительные числа, то его комплексные корни, как известно, являются по парно сопряженными. Нахождение суммы вычетов в таких точках можно заме нить нахождением действительной части вычета в одной из них. Действительио, вычет в точке
, используя свойства сопряженных чисел, можно записать следующим образом:
Это означает, что вычет в точке есть число, сопряженное вычету в точке
, а сумма таких чисел равна их удвоенной действительной части:
Пример 5.24
Найти оригиналы для функций:
a) ;
б) .
Решение. В случае “а” для решения задачи используем теорему 5.1, а в случае “б” — теорему 5.2.
а) Используем типовые разложения
Для заданных изображений получаем:
Согласно первой теореме разложения
б) Представим в виде
где — простые полюсы функции
. По второй теореме разложения
Тот же результат можно получить, пользуясь пп. 2 и 3 замечаний 5.5:
Функция имеет четыре простых полюса:
.
Так как вычет в простом полюсе находится по формуле , то по второй теореме разложения
Функция имеет два полюса: простой
и полюс второго порядка
.
По второй теореме разложения . Находим вычеты
получаем окончательный ответ .
Применение таблицы и свойств преобразования Лапласа
Приведем ряд известных приемов нахождения оригинала.
1. Если изображение отличается от табличного на постоянный множитель, то его следует умножить и одновременно поделить на этот множитель, а затем воспользоваться свойством линейности.
Пример 5.25
2. Изображение, заданное в виде дроби , разлагается на сумму дробей.
Пример 5.26
Найти оригинал для функций: а) ; б)
; в)
.
Решение. Представим дроби в виде суммы двух слагаемых, а затем воспользуемся свойством линейности и формулами из табл. 5.1:
а) ;
б) .
в) представим в виде
. По формулам 4,6 из табл. 5.1 находим
.
3. Если знаменатель дроби содержит квадратный трехчлен, то в нем выде ляется полный квадрат: . При этом числитель дроби представляется в виде многочлена от
.
Пример 5.27
Найти оригиналы для функций: a) ; б)
.
Решение. а) Выделим полный квадрат в знаменателе дроби и воспользуемся табл. 5.1 (по формуле 12 из табл. 5.1 при ):
б) Используем представление
По формулам 19,20 из табл. 5.1 и по теореме смещения (формула (5.8))
Можно решить эту задачу иначе, используя вторую теорему разложения (см. п. “б” примера 5.24):
4. Если оригинал представляет собой правильную рациональную дробь, то следует разложить ее на простейшие дроби и для каждой из полученных дробей найти оригинал.
Примеры 5.28-5.29
Пример 5.28. Найти оригиналы для функций:
а) ; б)
; в)
; г)
.
Решение. а) Представим в виде
, где
— неопределенные коэффициенты.
Отсюда следует равенство .
Приравнивая коэффициенты при одинаковых степенях , получаем систему уравнений для нахождения неопределенных коэффициентов:
Решая ее, получаем
и
По формулам 1,12,13 из табл. 5.1 .
б) Представим в виде
, где
— неопределенные коэффициенты.
Отсюда .
Подставляя последовательно , получаем
и поэтому
По формулам 6,7 из табл. 5.1 находим .
в) Представим изображение в виде . Отсюда
При получаем
, поэтому
По свойству линейности и по формуле 6 из табл. 5.1 получаем
Можно решить эту задачу иначе, используя вторую теорему разложения (см. п. “б” примера 5.24):
г) Представим в виде
, где
— неопределенные коэффициенты.
Из равенства при
получаем
, поэтому
.
По формуле 6 из табл. 5.1 имеем .
Можно также решить эту задачу иначе, используя вторую теорему разложения (см. п. “б” примера 5.24 и п. “в” данного примера):
Пример 5.29. Найти оригиналы для функций: a) ; б)
.
Решение. а) Решим пример различными способами.
Первый способ. Воспользуемся разложением дроби на элементарные:
По формулам 2,3,6,7 из табл. 5.1 получаем .
Второй способ. Применим вторую теорему разложения, учитывая, что и
— полюсы второго порядка функции
Третий способ. Обозначим . Тогда
. Рассмотрим функцию
. По свойству интегрирования оригинала (формула (5.12)) получаем
Заметим, что . Применяя еще раз свойство интегрирования оригинала, имеем
Четвертый способ. Представим изображение в виде произведения
, где
.
По формулам 3 и 7 из табл. 5.1 . Далее по теореме Бореля (формула (5.15))
б) Решим пример также несколькими способами.
Первый способ. Воспользуемся разложением дроби на элементарные:
По формуле 9 из табл. 5.1 получаем .
Второй способ. Применим вторую теорему разложения с учетом пп. 2,3 замечаний 5.5:
Третий способ. Представим изображение в виде произведения:
Отсюда . По теореме Бореля
Четвертый способ. Используем формулу 37 из табл. 5.1. При получаем
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Интегральное преобразование Лапласа онлайн, калькулятор изображения функций.
Теория функций комплексного переменного.

 : x^a
: x^a
модуль x: abs(x)
 : Sqrt[x]
: Sqrt[x]![sqrt[n]{x}](https://upload.wikimedia.org/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) : x^(1/n)
: x^(1/n) : a^x
: a^x : Log[a, x]
: Log[a, x] : Log[x]
: Log[x] : cos[x] или Cos[x]
: cos[x] или Cos[x]
 : sin[x] или Sin[x]
: sin[x] или Sin[x] : tan[x] или Tan[x]
: tan[x] или Tan[x] : cot[x] или Cot[x]
: cot[x] или Cot[x] : sec[x] или Sec[x]
: sec[x] или Sec[x] : csc[x] или Csc[x]
: csc[x] или Csc[x] : ArcCos[x]
: ArcCos[x] : ArcSin[x]
: ArcSin[x] : ArcTan[x]
: ArcTan[x] : ArcCot[x]
: ArcCot[x] : ArcSec[x]
: ArcSec[x] : ArcCsc[x]
: ArcCsc[x] : cosh[x] или Cosh[x]
: cosh[x] или Cosh[x] : sinh[x] или Sinh[x]
: sinh[x] или Sinh[x] : tanh[x] или Tanh[x]
: tanh[x] или Tanh[x] : coth[x] или Coth[x]
: coth[x] или Coth[x] : sech[x] или Sech[x]
: sech[x] или Sech[x] : csch[x] или Csch[е]
: csch[x] или Csch[е] : ArcCosh[x]
: ArcCosh[x] : ArcSinh[x]
: ArcSinh[x] : ArcTanh[x]
: ArcTanh[x] : ArcCoth[x]
: ArcCoth[x] : ArcSech[x]
: ArcSech[x] : ArcCsch[x]
: ArcCsch[x]101
функция F(p) комплексного аргумента p, определяемая согласно
(5.1), называется изображением по Лапласу функции f(t) или просто изображением.
Символически соответствие между оригиналом и изображением записывается обычно так:
f (t) • =• F( p) или F( p) • =• f (t).
Совокупность всех оригиналов f(t) называется пространством оригиналов, а совокупность всех изображений F(p) – пространством изображений.
Можно показать, что справедлива следующая теорема существования изображения: для всякого оригинала f (t) инте-
грал Лапласа F( p) = ∞∫ f (t)e−pt dt абсолютно сходится в полуплос-
0
кости Re p >α (α – показатель роста функции f (t) ) и определяет изображение F( p) , которое является аналитической функцией в
этой полуплоскости.
Эффективность преобразования Лапласа обусловлена тем, что оно имеет характер отображения, а именно, оно позволяет заменить функции и производимые над ними операции в пространстве оригиналов более простыми функциями и операциями над ними в пространстве изображений.
При этом изображения, получаемые в результате преобразования Лапласа, представляют собой аналитические функции, к которым применимы мощные методы теории функций комплексной переменной.
Изображения простейших функций
|
1. Пусть оригинал имеет вид: |
|||
|
0 |
при |
t < 0, |
(5.2) |
|
η(t) = |
при |
t > 0. |
|
|
1 |
Эта функция широко применяется в приложениях и называется единичной функцией или функцией Хевисайда (рис. 33).
Очевидно, функция η(t) удовлетворяет всем условиям, налагаемым на оригиналы. Функция η(t) ограниченная, поэтому для неë показатель роста α = 0. Следовательно, изображение еди-

102
ничной функции будет существовать и будет аналитической функцией при всех p =σ +is , при которых Re p =σ > 0.
Рис. 33 Изображение этой функции найдем, вычисляя интеграл Ла-
пласа (5.1):
|
∞ |
1 |
∞ |
1 |
|||||||
|
F( p) = ∫e−pt dt = − |
e−p t |
= |
. |
|||||||
|
0 |
p |
0 |
p |
|||||||
|
Учитывая, что всякий оригинал при t < 0 |
равен нулю, запишем |
|||||||||
|
единичную функцию просто в виде η(t) =1. Тогда получаем |
||||||||||
|
η(t) =1• =• |
1 |
. |
(5.3) |
|||||||
p
2. Изображение показательной функции. Пусть f (t) = ea t ,
тогда
|
∞ |
∞ |
1 |
∞ |
||||||
|
F( p) = ∫eat e−p t dt = ∫e−( p−a)t dt = − |
e−( p−a)t |
||||||||
|
p − a |
|||||||||
|
0 |
0 |
0 |
|||||||
|
Следовательно, |
1 |
||||||||
|
eat |
• =• |
. |
|||||||
|
p −a |
|||||||||
Нахождение изображений непосредственно по формуле (5.1) обычно затруднительно. Во многих случаях изображения по Лапласу могут быть найдены значительно проще, если воспользоваться свойствами преобразования Лапласа.
5.2. Свойства преобразования Лапласа
Для практического применения преобразования Лапласа необходимо знать не только изображения отдельных функций, но и правила отображения выполняемых над ними операций. Эти правила формулируются в виде многочисленных теорем, объединяемых общим названием “свойства преобразования Лапласа”. Каждая из этих теорем позволяет найти изображения тех или
103
иных функций – оригиналов. Рассмотрим некоторые основные из них.
|
1. Теорема линейности. Если f (t) |
• |
=• F ( p) , |
|||
|
1 |
1 |
||||
|
f |
2 |
(t) |
• |
=• F ( p), то для любых постоянных α и β линейной ком- |
|
|
2 |
бинации оригиналов соответствует такая же линейная комбинация изображений, то есть
|
α f (t) + β f |
(t) |
• |
=• α F ( p) + β F ( p) . |
(5.5) |
|
|
1 |
2 |
1 |
2 |
Это следует непосредственно из свойств определенных интегралов:
|
∞ |
∞ |
∞ |
|
∫[αf1 (t) + βf2 (t)]e−pt dt =α∫ f1 (t)e−pt dt + β∫ f2 (t)e−pt dt = |
||
|
0 |
0 |
0 |
=αF1 ( p) + βF2 ( p).
Пример. Найти изображения функций cost и sin t. Согласно формулам (2.11)
|
cos t = |
eit + e−it |
, |
sin t = |
eit −e−it |
. |
|
|
2 |
2i |
|||||
Учитывая соотношение (5.4) и применяя теорему линейности, получим
|
cos t = |
1 |
eit + |
1 |
e−it |
• =• |
1 |
1 |
+ |
1 |
1 |
= |
p |
. |
(5.6) |
|||||||||||||||
|
2 |
2 p −i |
2 p +i |
p |
2 +1 |
|||||||||||||||||||||||||
|
Аналогично |
2 |
||||||||||||||||||||||||||||
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||||||||||||||||
|
sin t = |
eit − |
e−it |
• =• |
− |
= |
. |
(5.7) |
||||||||||||||||||||||
|
2i |
p −i |
p +i |
p2 +1 |
||||||||||||||||||||||||||
|
2i |
2i |
2i |
|||||||||||||||||||||||||||
|
2. Теорема подобия. |
Если |
f (t) • =• |
F( p) , то |
||||||||||||||||||||||||||
|
f (a t) |
• = |
• |
1 |
F |
p |
(5.8) |
|||||||||||||||||||||||
|
a |
, |
||||||||||||||||||||||||||||
|
a |
то есть умножение аргумента оригинала на некоторое положительное число a приводит к делению аргумента изображения и самого изображения на то же число (к подобному изменению изображения).
Действительно, рассмотрим ∞∫ f (at)e−pt dt. Положим at = u. Тогда
0
t = u / a, dt = du / a. Пределы интегрирования при такой замене
104
переменной не меняются. Поэтому
|
∞ |
−pt |
1 |
∞ |
− |
p |
u |
1 |
p |
||||||||||||||||||||||||||||
|
∫ f (at)e |
∫ f (u)e |
|||||||||||||||||||||||||||||||||||
|
dt |
= |
a |
a |
du |
= |
F |
. |
|||||||||||||||||||||||||||||
|
0 |
0 |
a |
a |
|||||||||||||||||||||||||||||||||
|
Пример. Найти |
изображения |
функций |
cos ωt и |
sin ωt . |
||||||||||||||||||||||||||||||||
|
Учитывая изображения (5.6) и (5.7) |
и применяя |
теорему |
подо- |
|||||||||||||||||||||||||||||||||
|
бия, получим |
p |
|||||||||||||||||||||||||||||||||||
|
1 |
p |
|||||||||||||||||||||||||||||||||||
|
cos ωt • = |
• |
ω |
= |
. |
(5.9) |
|||||||||||||||||||||||||||||||
|
ω |
p 2 |
p2 |
+ω2 |
|||||||||||||||||||||||||||||||||
|
+1 |
||||||||||||||||||||||||||||||||||||
|
Аналогично |
ω |
|||||||||||||||||||||||||||||||||||
|
1 |
1 |
ω |
||||||||||||||||||||||||||||||||||
|
sin ωt |
=• |
= |
. |
(5.10) |
||||||||||||||||||||||||||||||||
|
• |
ω p 2 |
p2 |
+ω2 |
|||||||||||||||||||||||||||||||||
|
+1 |
||||||||||||||||||||||||||||||||||||
|
ω |
||||||||||||||||||||||||||||||||||||
|
3. Теорема смещения изображения. Если |
f (t) • =• F( p) , то |
для любого числа a (действительного или комплексного)
|
eat f (t) • =• F( p − a), |
(5.11) |
то есть умножение оригинала на eat приводит к смещению аргумента изображения на a.
Действительно, по определению преобразования Лапласа изображение функции eat f (t) будет
|
∞ |
∞ |
|
∫eat f (t)e−pt dt =∫ f (t)e−( p−a)t dt =F( p − a). |
|
|
0 |
0 |
Пример. Найти изображения функций e−a t cosωt и e−a t sin ωt .
Учитывая формулы (5.9) и (5.10) и применяя теорему смещения изображения, находим
|
e−at cosωt • =• |
p + a |
. |
(5.12) |
|||
|
( p + a)2 +ω |
2 |
|||||
|
Аналогично |
||||||
|
ω |
||||||
|
e−at sin ωt • =• |
. |
(5.13) |
||||
|
( p + a)2 +ω2 |
||||||

|
105 |
|
|
4. Теорема запаздывания. Если f (t) • =• F( p) , |
то для лю- |
|
бого постоянного τ > 0 |
|
|
f (t −τ) • =• e− pτ F( p) , |
(5.14) |
то есть “включение” оригинала с запаздыванием на время τ рав-
|
носильно умножению изображения на e− pτ . |
||||
|
Для доказательства теоремы учтем, |
что при t <τ |
аргумент |
||
|
t −τ < 0, поэтому |
функция f (t −τ) = 0. |
Тогда можно записать |
||
|
f (t −τ) •=• |
∞∫ f (t −τ)e−pt dt =∞∫ f (t −τ)e−pt dt , |
так как на |
интервале |
|
|
0 |
τ |
(0,τ) подынтегральная функция равна нулю. Выполняя замену
|
переменной: |
t −τ = t1, |
dt = dt1 и учитывая, что при этом |
|
нижний предел интегрирования будет равен нулю, получим |
||
|
∞∫ f (t −τ)e−pt dt = ∞∫ f (t1 )e−p(t1+τ )dt1 =e−pτ ∞∫ f (t1 )e−pt1 dt1 =e−pτ F( p). |
||
|
τ |
0 |
0 |
|
Следовательно, f (t −τ) • =• |
e− pτ F ( p) . |
График функции с запаздывающим аргументом f (t −τ) получается смещением графика функции f (t) вправо на расстояние τ
(см. рис. 34)
Рис. 34
Эта теорема позволяет находить изображения многих импульсных функций. Например, пусть требуется найти изображение единичного прямоугольного импульса
|
0 |
при |
t < 0, |
|
|
при |
0 < t <τ, |
(5.15) |
|
|
f (t) = 1 |
|||
|
при |
t >τ. |
||
|
0, |
График этой функции можно рассматривать как разность двух оригиналов: единичной функции (5.2), рис. 35а) и единичной функции, сдвинутой на τ ( рис. 35б):

106
Рис. 35
Изображение единичной функции определяется равенством (5.3), а изображение функции η(t −τ) по теореме запаздывания
будет 1p e−pτ . Применяя теорему линейности изображения, полу-
чим
f (t) •=• 1p − 1p e−pτ = 1p (1−e−pτ ).
Пример. Найти изображение функции f(at – b), если
f (t) • =• F( p) . Применяя теоремы подобия и запаздывания, нахо-
дим
f (at −b) • =• 1a F ap e(− p / a)b = 1a e(−b / a) p F ap .
В частности,
cos(ωt −α) • =• sin(ωt −α) • =•
|
p |
e |
−a |
p |
|||
|
ω , |
||||||
|
p2 +ω2 |
||||||
|
ω |
e−α |
p |
||||
|
ω |
. |
|||||
|
p2 +ω2 |
||||||
|
5. Теорема дифференцирования оригинала. |
Если |
|
f (t) • =• F ( p) , то |
|
|
f ′(t) • =• pF( p) − f (+0) , |
(5.18) |
то есть дифференцирование оригинала сводится к умножению
его изображения на p и вычитанию начального значения функции.
В (5.16) f (+0) = lim f (t) – правосторонний предел функции f(t).
t→+0
107
Действительно, преобразование Лапласа для производной
|
f ′(t) запишется в виде |
f ′(t) • =• |
∞∫ f ′(t)e−pt dt. |
||||||||||||
|
′ |
0 |
|||||||||||||
|
Полагая u = e |
− pt |
, dv = f |
du = −pe |
− pt |
dt , |
v = f (t) и при- |
||||||||
|
(t)dt, |
||||||||||||||
|
меняя формулу интегрирования по частям, находим |
||||||||||||||
|
∞∫ f ′(t)e−pt dt = f (t)e−pt |
0∞ + p∞∫ f (t)e−pt dt. |
|||||||||||||
|
0 |
0 |
|||||||||||||
|
Так как функция f (t) при t = 0 может иметь разрыв первого |
||||||||||||||
|
рода и учитывая третье условие роста оригинала ( |
f (t) |
< M eα t ), |
||||||||||||
|
получим: |
lim[ f (t)e− pt ] = 0, а lim[ f (t)e− pt ] = f (+0). Поэтому окон- |
|||||||||||||
|
t→−0 |
t→+0 |
|||||||||||||
|
чательно: |
f ′(t) • =• pF( p) − f (+0) . |
|||||||||||||
|
Если же функция f (t) непрерывна в точке t = 0, то |
||||||||||||||
|
lim f (t) = lim f (t) = f (0) = 0, тогда f ′(t) • =• |
pF( p). |
|||||||||||||
|
t→+0 |
t→−0 |
|||||||||||||
|
′ |
как оригинал, которому |
соответствует |
||||||||||||
|
Рассматривая f (t) |
изображение, определяемое по формуле (5.18), и применяя теорему дифференцирования повторно, получим изображение второй производной функции f(t):
f ′′(t) • =• p[ pF ( p) − f (+0)] − f ′(+0) = p2 F( p) − pf (+0) − f ′(+0),
(5.19)
…………………………………………………………………….
Продолжая этот процесс, найдем изображение n-ой производной:
|
f |
(n) |
(t) • = |
• |
p |
n |
F( p) − p |
n−1 |
f (+0) − p |
n−2 |
′ |
(n−2) |
(+0) |
− f |
(n−1) |
(+0). |
|
f (+0) −…pf |
|||||||||||||||
|
(5.20) |
|||||||||||||||
|
В частности, если все начальные значения функции и её |
|||||||||||||||
|
производных равны нулю, то |
|||||||||||||||
|
f (n) (t) • =• |
pn F( p). |
(5.21) |
Для практических приложений эта теорема является самой важной. Из неё следует, что дифференцирование в пространстве оригиналов заменяется существенно более простой операцией – умножением изображения на степень аргумента (с одновременным добавлением многочлена, коэффициентами которого являются начальные условия оригинала). Эта теорема лежит в основе операционного метода решения дифференциальных уравнений.
108
6. Теорема дифференцирования изображения. Если
f (t) • =• F ( p) , то
−tf (t) • =• F′( p),
то есть умножение оригинала на (−t) сводится к дифференциро-
ванию его изображения.
Действительно, как отмечалось, изображение является в области Re p >α аналитической функцией, поэтому обладает про-
изводными всех порядков. Дифференцируя интеграл в равенстве (5.1) по параметру p под знаком интеграла, получим
|
d |
F( p) = |
d |
∞∫ f (t)e−pt dt =∞∫ |
d |
[e−pt |
f (t)]dt =∞∫[−tf (t)e−pt ]dt •=• −tf (t). |
||||
|
dp |
||||||||||
|
dp 0 |
0 |
dp |
0 |
|||||||
|
Применяя теорему повторно, находим |
||||||||||
|
t |
2 |
f (t) • = |
• |
′′ |
||||||
|
F ( p), |
……………………
(−1)n tn f (t) • =• F (n) ( p).
Теорема дифференцирования изображения противоречит идее операционного исчисления, так как операция умножения оригинала на −t заменяется в пространстве изображений более сложной операцией дифференцирования, но она позволяет найти изображения очень распространенных степенных функций. Учи-
тывая, что 1• =• 1/ p и применяя последовательно теорему дифференцирования изображения, найдем:
|
t • =• |
1 |
, |
t2 |
• =• |
2 |
, |
K |
tn • =• |
n! |
. |
(5.22) |
|
p2 |
pn+1 |
||||||||||
|
p3 |
|||||||||||
|
7. Теорема интегрирования оригинала. Если |
f (t) • =• F ( p), |
||||||||||
|
то |
∫τ |
||||||||||
|
f (t)dt • =• |
F( p), |
(5.23) |
|||||||||
|
0 |
p |
то есть интегрированию оригинала соответствует деление его изображения на p.
Соответствие между некоторыми наиболее распространенными оригиналами и их изображениями указано в Приложении 1.
Примеры нахождения изображений сложных функций
1. f1 (t) = t sht .

109
Так как
sh t • =• p21−1,
то применяя теорему дифференцирования изображения, найдём
|
−t sh t • = |
• |
d |
1 |
= |
− |
2 p |
. |
|||
|
p2 −1 |
( p2 −1)2 |
|||||||||
|
dp |
Следовательно,
t sh t • =• ( p22−p1)2 .
2.f2 (t) = t5 sh t.
Применять теорему дифференцирования пять раз, конечно, неудобно. Представим f2 (t) в виде
|
t5 sh t = t5 |
et −e−t |
= |
1 t5 et |
− 1 t5 |
e−t . |
|||||
|
Так как t5 |
•=• 5!/ p6 , |
2 |
2 |
2 |
||||||
|
то по теореме смещения изображения |
||||||||||
|
et t5 • =• |
5! |
, |
e−t t5 • =• |
5! |
. |
|||||
|
( p −1)6 |
( p +1)6 |
|||||||||
Теперь по теореме линейности находим
|
1 |
5 |
t |
1 |
5 |
−t |
• 1 |
5! |
5! |
1 |
||||||||||||||||
|
f2 |
(t) = |
t |
e |
− |
t |
e |
• = |
− |
= 60 |
− |
|||||||||||||||
|
2 |
2 |
2 |
( p −1) |
6 |
( p +1) |
6 |
( p − |
1) |
6 |
||||||||||||||||
|
3. f3 (t) = e−2t t cos3t. |
||||
|
Представим f3 (t) в виде |
f3 (t) = tϕ(t). Для функции |
|||
|
ϕ(t) = e−2t cos3t изображение известно: |
||||
|
e−2t cos3t • |
=• |
p + 2 |
. |
|
|
( p + 2)2 +9 |
||||
По теореме дифференцирования изображения −t ϕ(t) • =• Следовательно,
|
t e |
−2t |
cos3t • = |
• |
− |
d |
p + 2 |
= |
( p + 2)2 −9 |
|||||||
|
2 . |
|||||||||||||||
|
+ 2) |
2 |
+9 |
|||||||||||||
|
dp ( p |
[( p + 2)2 +9] |
||||||||||||||
|
4. |
f4 (t) = e−3t (0,5 + cos2 2t). |
||||||||||||||
|
Так как |
cos2 2t = |
1 + cos 4t |
, то |
||||||||||||
|
2 |

|
110 |
||||||||||||||||||
|
f4 (t) =e−3t + |
1 |
e−3t cos 4t |
• =• |
1 |
+ |
p +3 |
. |
|||||||||||
|
p +3 |
2[( p +3)2 +16] |
|||||||||||||||||
|
2 |
||||||||||||||||||
|
5. |
f5 (t) = 2cos 4t cos 2t. |
|||||||||||||||||
|
Так как |
cosα cos β = 0,5[cos(α − β) +cos(α + β)], |
то |
||||||||||||||||
|
2cos 4t cos 2t = cos 2t + cos6t. |
||||||||||||||||||
|
Учитывая, что cosωt • =• |
p |
, |
по теоремам подобия и ли- |
|||||||||||||||
|
p2 +ω2 |
||||||||||||||||||
|
нейности получим |
||||||||||||||||||
|
p |
p |
2 p( p2 + |
20) |
|||||||||||||||
|
f5 (t) = cos 2t + cos 6t • = |
• |
+ |
= |
. |
||||||||||||||
|
p2 + 4 |
p2 +36 |
( p2 |
+ 4)( p2 |
+36) |
||||||||||||||
Замечания.
1. Грубой ошибкой будет представление изображения произведения функций-оригиналов в виде произведения изображений, соответствующих каждому из сомножителей, так как умножению оригиналов соответствует другая операция в пространстве изображений [6].
2. Решение приведенных задач возможно различными способами. В пособии указан лишь один из возможных способов решения.
5.3. Обратное преобразование Лапласа
При практическом применении преобразования Лапласа всегда приходится решать обратную задачу – построение оригинала по его изображению. Общий метод построения оригинала f(t) по заданному изображению F(p) базируется на теореме об-
ращения ( формуле Меллина23 ):
|
1 |
γ +i∞ |
|||
|
f (t) = |
∫F( p)e pt dp, |
γ >α, t > 0, (5.24) |
||
|
2π i |
||||
|
γ −i∞ |
где интегрирование проводится по любой бесконечной прямой Re p = γ, лежащей в полуплоскости абсолютной сходимости ин-
теграла Лапласа (см. рис. 36).
Непосредственно формулой (5.24) для нахождения оригинала по известному изображению пользуются редко. Но так как в ней рассматривается интеграл от аналитической функции, взятый
23 Меллин Р.Х. (1854 – 1933) – финский математик.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ранее мы рассмотрели интегральное преобразование Фурье
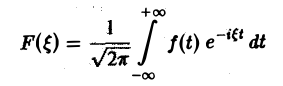
с ядром K(t, ξ) = 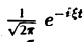 .
.
Преобразование Фурье неудобно тем, что должно быть выполнено условие абсолютной интегрируемости функции f(t) на всей оси t,
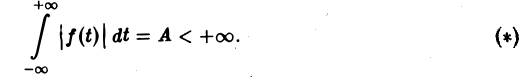
Преобразование Лапласа позволяет освободиться от этого ограничения.
Определение:
Функцией-оригиналом будем называть всякую комплекснозначную функцию f(t) действительного аргумента t, удовлетворяющую следующим условиям:
- f(t) непрерывна на всей оси t, кроме отдельных точек, в которых f(t) имеет разрыв 1-го рода, причем на каждом конечном интервале оси t таких точек может быть лишь конечное число;
- функция f(t) равна нулю при отрицательных значениях t, f(t) = 0 при t < 0;
- при возрастании t модуль f(t) возрастает не быстрее показательной функции, т. е. существуют числа М > 0 и з такие, что для всех t

Ясно, что если неравенство (1) выполняется при некотором s = s1, то оно будет выполнятся при всяком s2 > s1.
Точная нижняя грань sо всех чисел s, so = infs, для которых выполняется неравенство (1), называется показателем роста функции f(t).
Замечание:
В общем случае неравенство
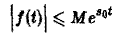
не имеет места, но справедлива оценка
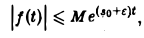
где ε > 0 — любое. Так, функция f(t) = t, t ≥ 0, имеет показатель роста so =0. Для нее неравенство |t| ≤ М ∀t ≥ 0 не выполняется, но ∀ε > О, ∀t > 0 верно неравенство 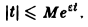
Условие (1) гораздо менее ограничительное, чем условие (*).
Пример:
Функция
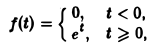
не удовлетворяет условию (*), но условие (1) выполнено при любом s ≥ 1 и М ≥ 1; показатель роста so = 1. Так что f(t) является функцией-оригиналом. С другой стороны, функция
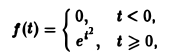
не является функцией-оригиналом: она имеет бесконечный порядок роста, sо = +∞. Простейшей функцией-оригиналом является
так называемая единичная функция
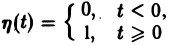
Если некоторая функция φ(t) удовлетворяет условиям 1 и 3 определения 1, но не удовлетворяет условию 2, то произведение f(t) = φ(t) η(t) уже является функцией-оригиналом.
Для простоты записи мы будем, как правило, множитель η(t) опускать, условившись, что все функции, которые мы будем рассматривать, равны нулю для отрицательных t, так что если речь идет о какой-то функции f(t) например, о sin t, cos t, et и т. д., то всегда подразумеваются следующие функции (рис. 2):
Определение:
Пусть f(t) есть функция-оригинал. Изображением функции f(t) по Лапласу называется функция F(p) комплексного переменного р = s + iσ, определяемая формулой

где интеграл берется по положительной полуоси t. Функцию F(p) называют также преобразованием Лапласа функции f(t); ядро преобразования K(t, р) = e-pt.
Тот факт, что функция f(x) имеет своим изображением F(p), будем записывать так:
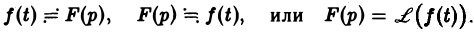
Пример:
Найти изображение единичной функции η(t).
Функция 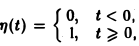 является функцией-оригиналом с показателем роста s0 = 0. В силу формулы (2) изображением функции η(t) будет функция
является функцией-оригиналом с показателем роста s0 = 0. В силу формулы (2) изображением функции η(t) будет функция
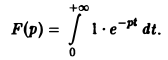
Если р = s + iσ, то при s > 0 интеграл в правой части последнего равенства будет сходящимся, и мы получим
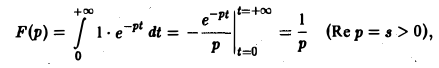
так что изображением функции η(t) будет функция 1/p. Как мы условились, будем писать, что η(t) = 1, и тогда полученный результат запишется так:
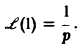
Теорема:
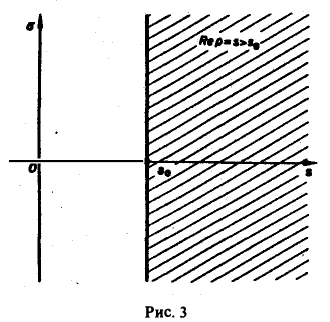
Для всякой функции-оригинала f(t) с показателем роста sо изображение F(p) определено в полуплоскости Re p = s > So и является в этой полуплоскости аналитической функцией (рис. 3).
Пусть
Для доказательства существования изображения F(p) в указанной полуплоскости достаточно установить, что несобственный интеграл (2) абсолютно сходится при s > so. Используя (3), получаем
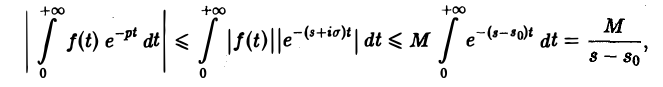
что и доказывает абсолютную сходимость интеграла (2). Одновременно мы получили оценку преобразования Лапласа F(p) в полуплоскости сходимости Re р = s > so
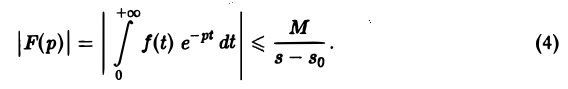
Дифференцируя выражение (2) формально под знаком интеграла по р, находим
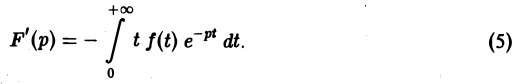
Существование интеграла (5) устанавливается так же, как было установлено существование интеграла (2).
Применяя для F'(p) интегрирование по частям, получаем оценку
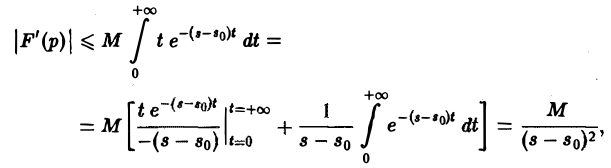
откуда следует абсолютная сходимость интеграла (5). (Внеинтегральное слагаемое 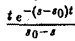 — при t → + ∞ имеет предел, равный нулю). В любой полуплоскости Re р ≥ S1 > So интеграл (5) сходится равномерно относительно р, поскольку он мажорируется сходящимся интегралом
— при t → + ∞ имеет предел, равный нулю). В любой полуплоскости Re р ≥ S1 > So интеграл (5) сходится равномерно относительно р, поскольку он мажорируется сходящимся интегралом
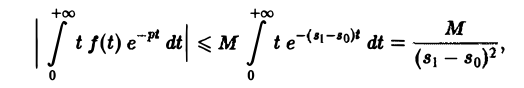
не зависящим от р. Следовательно, дифференцированиепо р законно и равенство (5) справедливо.
Поскольку производная F'(p) существует, преобразование Лапласа F(p) всюду в полуплоскости Re p = s > sо является аналитической функцией.
Из неравенства (4) вытекает
Следствие:
Если точка р стремится к бесконечности так, что Re р = s неограниченно возрастает, то
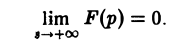
Пример:
Найдем еще изображение функции f(t) =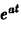 , где а = а + iβ — любое комплексное число.
, где а = а + iβ — любое комплексное число.
Показатель роста sо функции f(t) равен а.
Считая Rep = s> а, получим
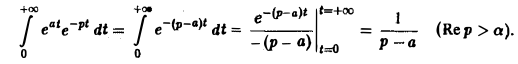
Таким образом,
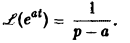
При а = 0 вновь получаем формулу
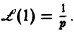
Обратим внимание на то, что изображение функции 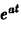 является аналитической функцией аргумента р не только в полуплоскости Re p > а, но и во всех точках р, кроме точки р = а, где это изображение имеет простой полюс. В дальнейшем мы не раз встретимся с подобной ситуацией, когда изображение F(p) будет аналитической функцией во всей плоскости комплексного переменного р, за исключением изолированных особых точек. Противоречия с теоремой 1 нет. Последняя утверждает лишь, что в полуплоскости Re p > So функция F(p) не имеет особых точек: все они оказываются лежащими или левее прямой Re p = So, или на самой этой прямой.
является аналитической функцией аргумента р не только в полуплоскости Re p > а, но и во всех точках р, кроме точки р = а, где это изображение имеет простой полюс. В дальнейшем мы не раз встретимся с подобной ситуацией, когда изображение F(p) будет аналитической функцией во всей плоскости комплексного переменного р, за исключением изолированных особых точек. Противоречия с теоремой 1 нет. Последняя утверждает лишь, что в полуплоскости Re p > So функция F(p) не имеет особых точек: все они оказываются лежащими или левее прямой Re p = So, или на самой этой прямой.
Замечание:
В операционном исчислении иногда пользуются изображением функции f(t) по Хевисайду, определяемым равенством
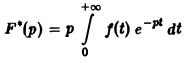
и отличаюикмся от шоСражения по Лапласу множителем р.

Свойства преобразования Лапласа
В дальнейшем через f(t), φ(t), … будем обозначать функции-оригиналы, а через F(p), Ф(р), … — их изображения по Лапласу,
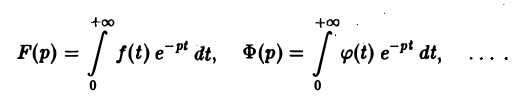
Из определения изображения следует, что если f(t) = 9 ∀t, то F(p) = 0.
Теорема единственности:
Если две непрерывные функции f(t) и φ{t) имеют одно и тоже изображение F(p), то они тождественно равны.
Теорема:
Линейность преобразования Лапласа. Если f{t) и φ{t) — функции-оригиналы, то для любых комплексных постоянных а и β
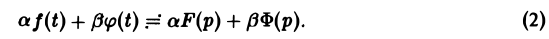
Справедливость утверждения вытекает из свойства линейности интеграла, определяющего изображение:
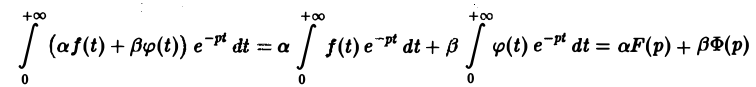
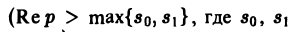 — показатели роста функций f(t) и φ(t) соответственно).
— показатели роста функций f(t) и φ(t) соответственно).
На основании этого свойства получаем
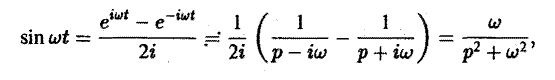
т. е. (3)
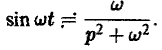
Аналогично находим, что
(4)
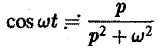
и, далее,
(5) (6)
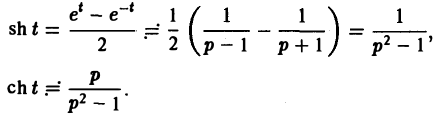
Теорема подобия:
Если f(t) — функция-оригинал и F(p) — ее изображение по Лапласу, то для любого постоянного а > 0
Полагая at = т, имеем
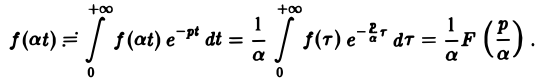
Пользуясь этой теоремой, из формул (5) и (6) получаем
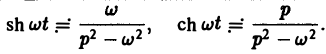
Теорема:
О дифференцировании оригинала. Пусть f(t) является функцией-оригиналом с изображением F(p) и пусть 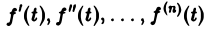 — также функции-оригиналы,
— также функции-оригиналы,  — показатель роста функции
— показатель роста функции 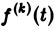 (k = 0, 1,…, п). Тогда
(k = 0, 1,…, п). Тогда
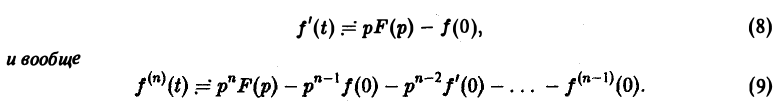
Здесь под fk(0) (k = 0,1,… , п — 1) понимается правое предельное значение 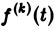 .
.
Пусть f(t) = F(p). Найдем изображение f'(t). Имеем
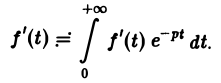
Интегрируя по частям, получаем
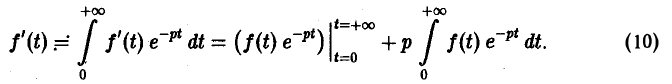
Внеинтегральное слагаемое в правой части (10) обращается в нуль при t → + ∞, т. к. при Re р = s > 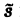 имеем
имеем
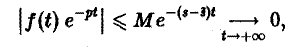
подстановка t = 0 дает -f(0).
Второе слагаемое справа в (10) равно pF(p). Таким образом, соотношение (10) принимаетвид
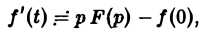
и формула (8) доказана. В частности, если f(0) = 0, то f'(t) = pF(p). Для отыскания изображения 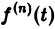 запишем
запишем
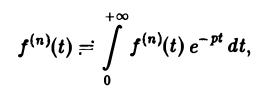
откуда, интегрируя п раз по частям, получим
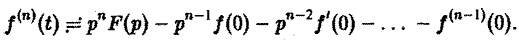
Пример:
Пользуясь теоремой о дифференцировании оригинала, найти изображение функции f(t) = sin2t.
Пусть f(t) = F(p). Тогда
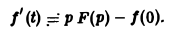
Но f(0) = О, а f'(0) = 2 sin t cos t = sin 2t = 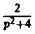 . Следовательно,
. Следовательно, 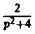 = pF(p), откуда F(p) =
= pF(p), откуда F(p) =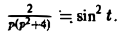
Теорема 5 устанавливает замечательное свойство интегрального преобразования Лапласа: оно (как и преобразование Фурье) переводит операцию дифференцирования в алгебраическую операцию умножения на р.
Формула включения. Если f(t) и f'(t) являются функциями-оригиналами, то (11)
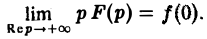
В самом деле, f'(<) = р F(p) — f(0). В силу следствия из теоремы 1, всякое изображение стремится к нулю при Rе р = s → + ∞. Значит, 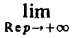 [pF(p) — f(0)] = 0, откуда вытекает формула включения (11).
[pF(p) — f(0)] = 0, откуда вытекает формула включения (11).
Теорема:
О дифференцировании изображения. Дифференцирование изображения сводится к умножению на (—t) оригинала,

Так как функция F(p) в полуплоскости Rep = s > so является аналитической, то ее можно дифференцировать по р. Имеем
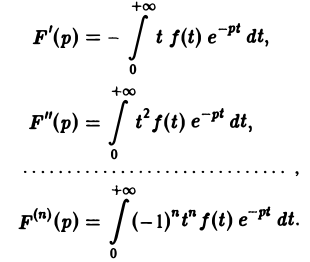
Последнее как раз и означает, что 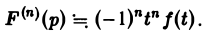
Пример:
Пользуясь теоремой 6, найти изображение функции 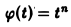 .
.
Как известно, 1 = 1/p. Здесь f(t) = 1, F(p) = 1/p. Отсюда (1/p)’= (-t) • 1, или 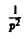 = t. Вновь применяя теорему 6, найдем
= t. Вновь применяя теорему 6, найдем
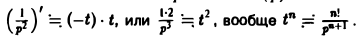
Теорема:
Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р: если f(t) = F(p), то

Положим

Нетрудно проверить, что если f(t) есть функция-оригинал, то и φ(t) будет функцией-оригиналом, причем φ(0) = 0. Пусть φ(t) = Ф(р). В силу (14)
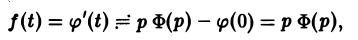
С другой стороны, f(t) =’ F(p), откуда F(p) = рФ(р), т.е. Ф(р) =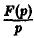 .
.
Последнее равносильно доказываемому соотношению (13).
Пример:
Найти изображение функции
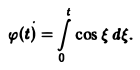
В данном случае f(t) = cos t, так что F(p) = 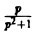 . Поэтому
. Поэтому
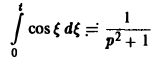
Теорема:
Интегрирование изображения. Если f(t) = F(p) и интеграл 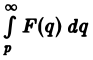 сходится, то он служит изображением функции
сходится, то он служит изображением функции 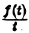

Действительно,
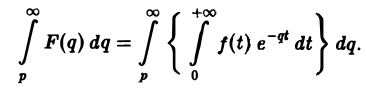
Предполагая, что путь интегрирования (р, ∞) лежит в полуплоскости Re p ≥ а> so, мы можем изменить порядок интегрирования (t > 0):
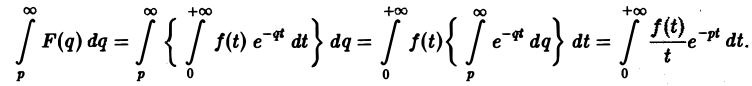
Последнее равенство означает, что 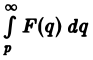 является изображением функции
является изображением функции 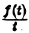 .
.
Пример:
Найти изображение функции 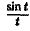 .
.
Как известно, sin t = 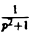 .
.
Поэтому
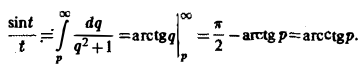
Теорема запаздывания:
Если f{t) = F(p), то для любого положительного τ («запаздывания»)
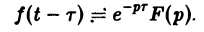
Так как
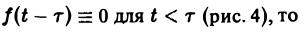
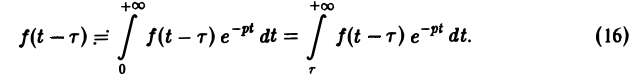
Положим ξ = t- τ. Тогда dt = d ξ. При t = τ получаем ξ = 0, при t = + ∞ имеем ξ = + ∞.
Поэтому соотношение (16) принимает вид
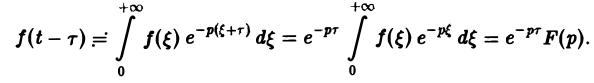
Пример:
Найти изображение функции f(t), заданной графически (рис. 5).
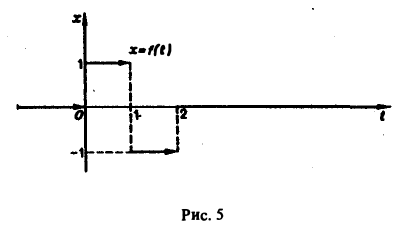
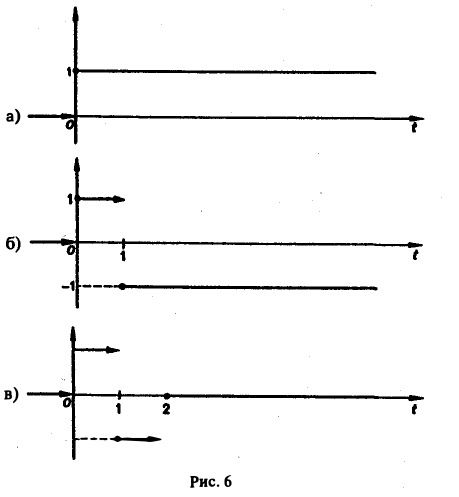
Запишем выражение для функции f(t) в следующем виде:
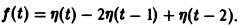
Это выражение можно получить так. Рассмотрим функцию f1(t) = η(t) для t ≥ 0 (рис. 6 а) и вычтем из нее функцию
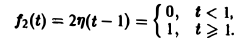
Разность f(t) — h(t) будет равна единице для t ∈ [0,1) и -1 для t ≥ 1 (рис. 6 b). К полученной разности прибавим функцию
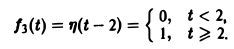
В результате получим функцию f(t) (рис. 6 в), так что
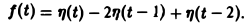
Отсюда, пользуясь теоремой запаздывания, найдем
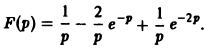
Теорема смещения:
Если f{t) = F(p) для любого комплексного числа ро
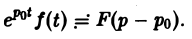
В самом деле,
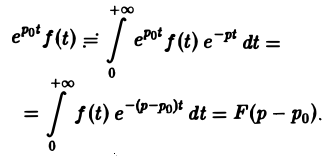
Теорема позволяет по известным изображениям функций находить изображения тех же функций, умноженных на показательную функцию 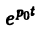 , например,
, например,
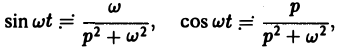
так что
Свертка функций. Теорема умножения
Пусть функции f(t) и φ(t) определены и непрерывны для всех t. Сверткой (f *φ)(t) этих функций называется новая функция от t, определяемая равенством
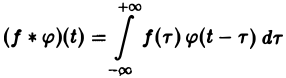
(если этот интеграл существует).
Для функций-оригиналов f(t) и φ(t) операция свертки всегда выполнима, причем
(17)
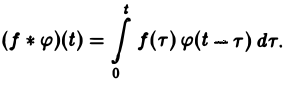
В самом деле, произведение функций-оригиналов f( τ ) φ(t — τ), как функция от τ, является финитной функцией, т.е. обращается в нуль вне некоторого конечного промежутка (в данном случае вне отрезка 0 ≤ τ ≤ t). Для финитных непрерывных функций операция свертки выполнима, и мы получаем формулу (17).
Нетрудно проверить, что операциясвертки коммутативна,
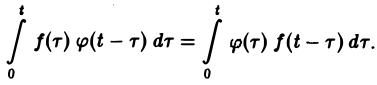
Теорема умножения:
Если f(t) = F(p), <p(t) =’Ф(р), то свертка (f * φ)(t) имеет изображение F(p) • Ф(р),
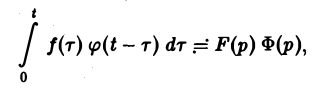
или
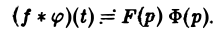
Нетрудно проверить, что свертка (f * φ)(t) функций-оригиналов есть функция-оригинал с показателем роста s* = mах{s1, s2}, где s1, s2 ~ показатели роста функций f(t) и φ(t) соответственно. Найдем изображение свертки,
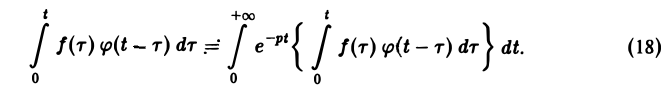
Воспользовавшись тем, что
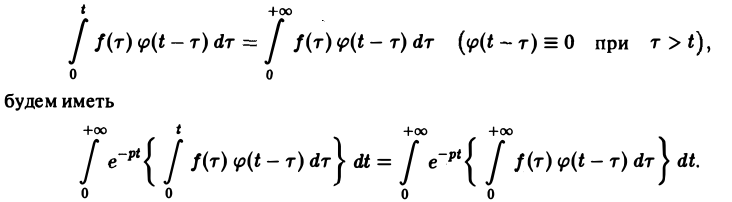
Меняя порядок интегрирования в интеграле справа (при Re р = s > s* такая операция законна) и применяя теорему запаздывания, получим
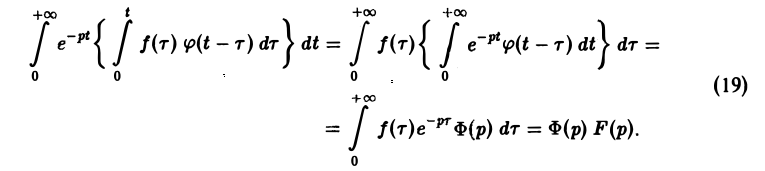
Таким образом, из (18) и (19) находим
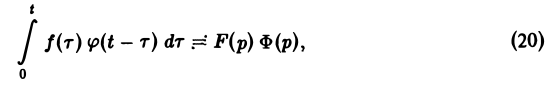
— умножению изображений отвечает свертывание оригиналов,
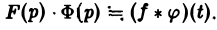
Пример:
Найти изображение функции
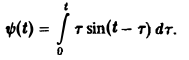
Функция ψ(t) есть свертка функций f(y) = t и φ(t) = sin t. В силу теоремы умножения
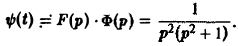
Задача:
Пусть функция f(t), периодическая с периодом Т, есть функция-оригинал. Показать, что ее изображение по Лапласу F[p) дается формулой
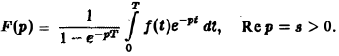
Отыскание оригинала по изображению
Задача ставится так: дана функция F(p), надо найти функцию f(t). изображением которой является F(p).
Сформулируем условия, достаточные для того, чтобы функция F(p) комплексного переменного р служила изображением.
Теорема:
Если аналитическая в полуплоскости Rep = s > so функция F(p)
1) стремится к нулю при |р| —» + ∞ в любой полуплоскости Re р = а > So равномерно относительно arg р;
2) интеграл
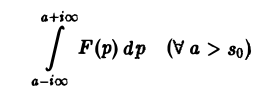
сходится абсолютно, то F(p) является изображением некоторой функции-оригинала f{t).
Задача:
Может ли функция F(p) = 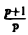 служить изображением некоторой функции-оригинала? Укажем некоторые способы отыскания оригинала по изображению.
служить изображением некоторой функции-оригинала? Укажем некоторые способы отыскания оригинала по изображению.
Отыскание оригинала с помощью таблиц изображений
Прежде всего стоит привести функцию F(p) к более простому, «табличному» виду. Например, в случае, когда F(p) — дробно-рациональная функция аргумента р,ее разлагают на элементарные дроби и пользуются подходящими свойствами преобразования Лапласа.
Пример:
Найти оригинал для
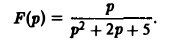
Запишем функцию F(p) в виде:
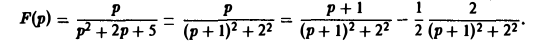
Пользуясь теоремой смещения и свойством линейности преобразования Лапласа, получаем
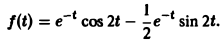
Пример:
Найти оригинал для функции
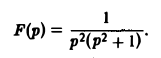
Запишем F(p) в виде
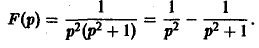
Отсюда f(t) = t — sin t.
Использование теоремы обращения и следствий из нее
Теорема обращения:
Если функция f(t) есть функция-оригинал с показателем роста so и F{p) — ее изображение, то в любой точке непрерывности функции f(t) выполняется соотношение
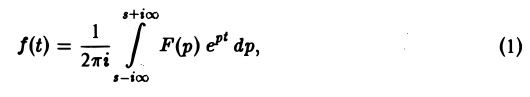
где интеграл берется вдоль любой прямой Re p = s > So и понимается в смысле главного значения, т. е. как
Формула (1) называется формулой обращения преобразования Лапласа, или формулой Меллина. В самом деле, пусть, например, f(t) — кусочно-гладкая на каждом конечном отрезке [0, а] функция-оригинал-с показателем роста so. Рассмотрим функцию φ(t) = 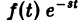 , где s>so — любое.
, где s>so — любое.
Функция φ(t) удовлетворяет условиям применимости интегральной формулы Фурье, и, следовательно, справедлива формула обращения преобразования Фурье,
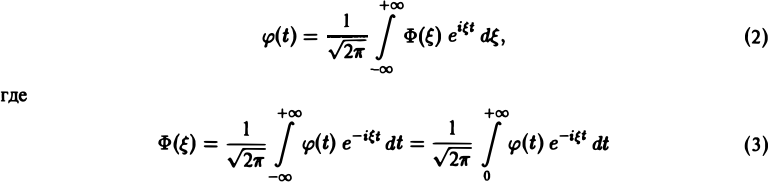
(φ(t) ≡ 0 при t < 0). Подставляя в (3) выражение φ(t) = f(t)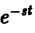 , найдем
, найдем
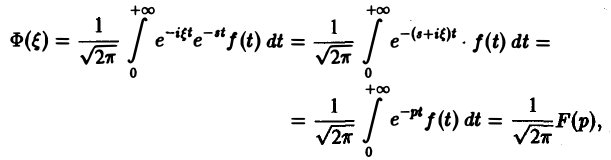
где F{p) — преобразование Лапласа функции f(t) при р = s + iξ. Формулу (2) можно переписать в виде
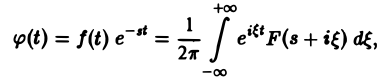
откуда получаем формулу обращения преобразования Лапласа
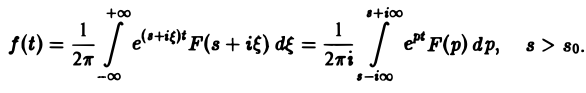
Как следствие из теоремы обращения получаем теорему единственности.
Теорема:
Две непрерывные функции f(t) и φ(t), имеющие одно и то же изображение F(p), тождественны.
Непосредственное вычисление интеграла обращения (1) обычно затруднительно. Отыскание оригинала по изображению упрощается при некоторых дополнительных ограничениях на F(p).
Теорема:
Пусть изображение F(p) — дробно-рациональная функция с полюсами р1, p2….pп. Тогда оригиналом для F(p) будет функция f(t) η(t), где
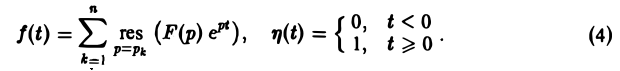
Пусть изображение F(p) — дробно-рациональная функция, F(p) = 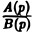 , где А(р), В(р) — многочлены относительно р (взаимно простые), причем степень числителя А(р) меньше степени знаменателя В(р), т. к. для всякого изображения должно выполняться предельное соотношение
, где А(р), В(р) — многочлены относительно р (взаимно простые), причем степень числителя А(р) меньше степени знаменателя В(р), т. к. для всякого изображения должно выполняться предельное соотношение
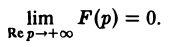
Пусть корни знаменателя В(р), являющиеся полюсами изображения F(p), суть р1, р2, …, рп, а их кратности равны r1, r2, …, rп соответственно.
Если число s, фигурирующее в формуле (1), взять большим всех Re pk (k = 1,2,…, п), то по формуле обращения, которая в этих условиях применима, получим
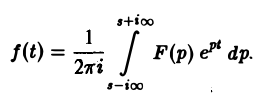
Рассмотрим замкнутый контур ГR (рис.7), состоящий из дуги CR окружности радиуса R с центром в начале координат и стягивающей ее хорды АВ (отрезка прямой Re р = s), и проходимый в положительном направлении, причем радиус R настолько велик, что все полюсы F(p) лежат внутри ГR.
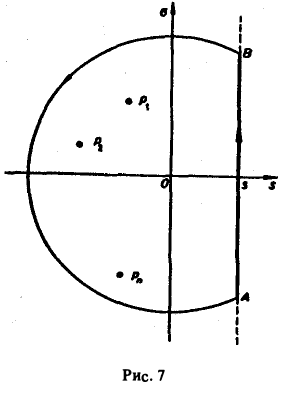
По теореме Коши о вычетах при любом R, удовлетворяющем указанному условию, будем иметь
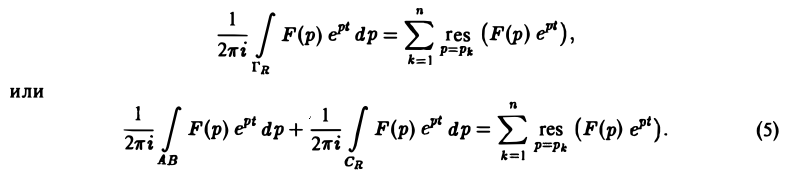
Второе слагаемое слева в равенстве (5) стремится к нулю при R → ∞. Это следует из леммы Жордана, если в ней заменить р на iz и учесть, что F(p) → 0 при Re p → + ∞. Переходя в равенстве (5) к пределу при R → ∞, мы получим слева
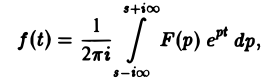
а справа — сумму вычетов по всем полюсам функции F(p)
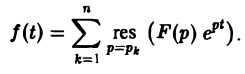
Замечание:
Воспользовавшись формулой для вычисления вычетов, найдем, что
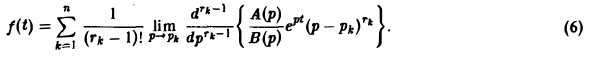
Если все полюсы p1, р2,…, рn — простые, то
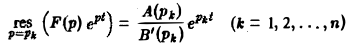
и формула (6) принимает вид

Пример:
Найти оригинал для функции
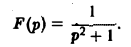
Функция F(p) имеет простые полюсы р1 = i. p2 = -i. Пользуясь формулой (7), находим
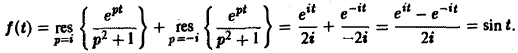
Теорема:
Пусть изображение F(p) является аналитической функцией в бесконечно удаленной точке р = ∞, причем ее разложение в окрестности |р| > R бесконечно удаленной точки имеет вид
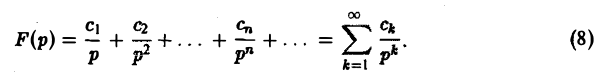
Тогда оригиналом для F(p) будет функция f(t) η{t), где
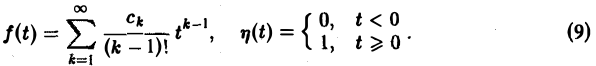
Пример:
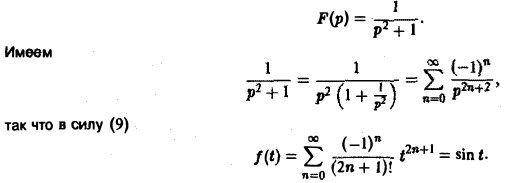
Приложения преобразования Лапласа (операционного исчисления)
Решение линейных дифференциальных уравнений с постоянными коэффициентами
Дано линейное дифференциальное уравнение второго порядка с постоянными коэффициентами
(1)
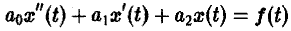
(ао, а1, а2 — действительные числа) и требуется найти решение уравнения (1) для t > 0, удовлетворяющее начальным условиям

Будем считать, что f(t) есть функция-оригинал. Тогда x(t) — также функция-оригинал. Пусть
f(t) = F(p), x(t) = X(p).
По теореме о дифференцировании оригинала имеем
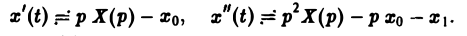
Перейдем в уравнении (1) от оригиналов к изображениям. Имеем
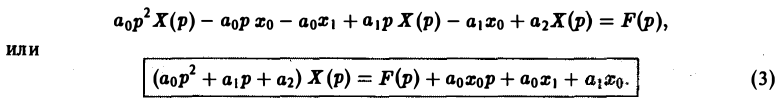
Это уже не дифференциальное, а алгебраическое уравнение относительно изображения Х(р) искомой функции. Его называют операторным уравнением. Решая его, найдем операторное решение задачи (1)-(2) —
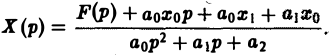
Оригинал для Х(р) будет искомым решением х(t) задачи (1)-(2).
Общий случай линейного дифференциального уравнения n-го порядка (n ≥ 1) с постоянными коэффициентами от случая п = 2 принципиально ничем не отличается.
Приведем общую схему решения задачи Коши
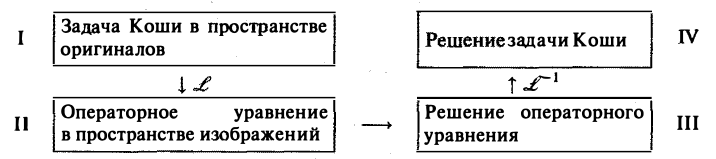
Здесь 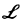 означает применение к 1 преобразование Лапласа,
означает применение к 1 преобразование Лапласа, 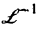 — применение к III обратного преобразования Лапласа.
— применение к III обратного преобразования Лапласа.
Пример:
Решить задачу Коши
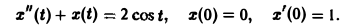
Здесь
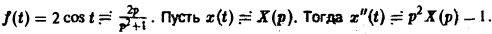
Операторное уравнение
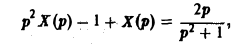
Откуда
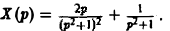
По теореме о дифференцировании изображения
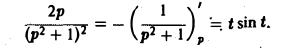
Поэтому
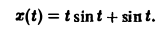
Формула Дюамеля
В приложениях операционного исчисления к решению дифференциальных уравнений часто пользуются следствием из теоремы умножения, известным под названием формулы Дюамеля.
Пусть f(t) и φt) — функции-оригиналы, причем функция f(t) непрерывна на [0, + ∞), a φ(t) — непрерывно дифференцируема на [0,+ ∞). Тогда если f(t) = F(p), φ{t) = Ф(р),то по теореме умножения получаем, что
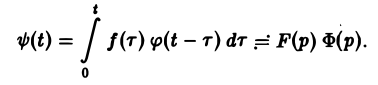
Нетрудно проверить, что функция ψ(t) непрерывно дифференцируема на [0, + ∞), причем
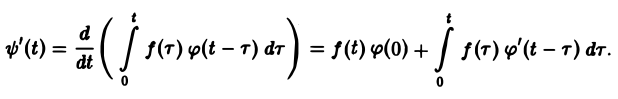
Отсюда, в силу правила дифференцирования оригиналов, учитывая, что ψ(0) = 0, получаем формулу Дюамеля
(4)
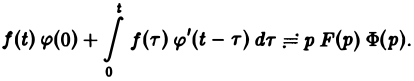
Покажем применение этой формулы.
Пусть требуется решить линейное дифференциальное уравнение n-го порядка (n ≥ 1) с постоянными коэффициентами

при нулевых начальных условиях
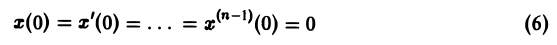
(последнее ограничение несущественно: задачу с ненулевыми начальными условиями можно свести к задаче с нулевыми условиями заменой искомой функции).
Если известно решение x(t) дифференциального уравнения с той же левой частью и правой частью, равной единице,
L[x(t)] = l (7)
при нулевых начальных условиях
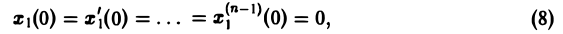
то формула Дюамеля (4) позволяет сразу получить решение исходной задачи (5)-(6).
В самом деле, операторные уравнения, отвечающие задачам (5)-(6) и (7)-(8), имеют соответственно вид

где F(p) — изображение функции f(t). Из (9) и (10) легко находи
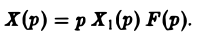
Отсюда по формуле Дюамеля
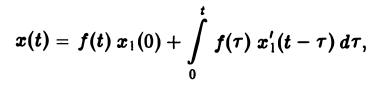
или, поскольку x1(0) = 0, (11)
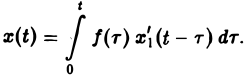
Пример:
Решить задачу Коши
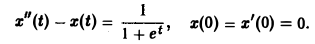
Рассмотрим вспомогательную задачу
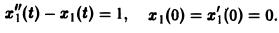
Применяя операционный метод, находим
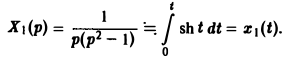
По формуле (11) получаем решение x(t) исходной задачи:
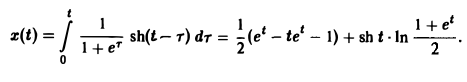
Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами
Интегрирование систем осуществляется так же, как и решение одного линейного дифференциального уравнения — путем перехода от системы дифференциальных уравнений к системе операторных уравнений. Решая последнюю как систему линейных алгебраических уравнений относительно изображений искомых функций, получаем операторное решение системы. Оригинал для негобудетрешением исходной системы дифференциальных уравнений.
Пример:
Найти решение линейной системы
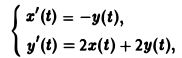
удовлетворяющее начальным условиям х(0) = у(0) = I.
Пусть х(<) = Х(р), y(t) = Y(p). Пользуясь свойством линейности преобразования Лапласа и теоремой о дифференцировании оригиналов, сводим исходную задачу Коши к операторной системе
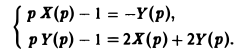
Решая последнюю относительно Х(р) и У(р), получаем
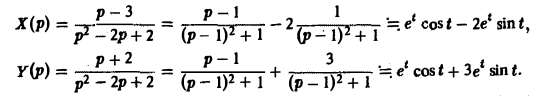
Решение исходной задачи Коши
Решение интегральных уравнений
Напомним, что интегральным уравнением называют уравнение, в котором неизвестная функция входит под знак интеграла. Мы рассмотрим лишь уравнение вида (12)
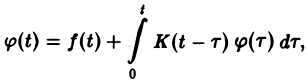
называемое линейным интегральным уравнением Вольтерра второго рода с ядром K(t — т), зависящим от разности аргументов (уравнение типа свертки). Здесь φ(t) — искомая функция, f(t) и K(t) — заданные функции.
Пусть f(t) и K(t) есть функции-оригиналы, f(t) =’ F(p), K(t) =’ K(p).
Применяя к обеим частям (12) преобразование Лапласа и, пользуясь теоремой умножения, получим
(13)
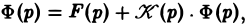
где Ф(р) = φ(t). Из (13)
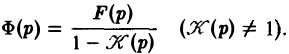
Оригинал для Ф(р) будет решением интегрального уравнения (12).
Пример:
Решить интегральное уравнение
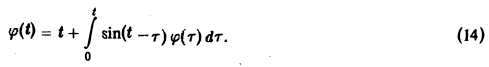
Применяя преобразование Лапласа к обеим частям (14), получим
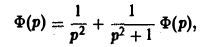
откуда
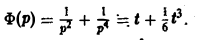
Функция 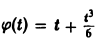 является решением уравнения (14) (подстановка
является решением уравнения (14) (подстановка 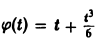 в уравнение (14) обращает последнее в тождество по t).
в уравнение (14) обращает последнее в тождество по t).
Замечание:
Преобразование Лапласа может быть использовано также при решении некоторых задач для уравнений математической физики.
Таблица преобразования Лапласа

Дополнение к преобразованию Лапласа


Смотрите также:
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

