Изоморфизм групп — взаимно-однозначное соответствие между элементами двух групп, сохраняющее групповые операции.
Если существует изоморфизм между двумя группами, группы называются изоморфными. С точки зрения теории групп изоморфные группы имеют одни и те же свойства и их можно не различать.
Определение[править | править код]
Если заданы две группы (G, ∗) и (H, 
Изоморфизм групп из (G, ∗) в (H, 
Другими словами, изоморфизм групп — это биекция 
.
Замечания[править | править код]
- Часто используется более короткая и простая запись. Если групповые операции не приводят к двусмысленности, их опускают:
- (Иногда даже пишут просто G = H. Не приведёт ли такая запись к путанице и двусмысленности, зависит от контекста. Например, употребление знака равно не очень подходит в случае, когда две группы являются подгруппами одной и той же группы.)
- Если H = G и
= ∗, биекция является автоморфизмом[⇨].
- Изоморфизм групп можно определить как двусторонний обратимый морфизм в категории групп.
Примеры[править | править код]
-
- посредством изоморфизма
- (смотрите экспонента).
-
- Изоморфизм задаётся выражением
- для любого x из
.
- Обобщая, для всех нечётных n, группа Dih2n изоморфна прямому произведению Dihn и Z2.
Для некоторых групп можно доказать изоморфизм, исходя из аксиомы выбора, но такое доказательство не показывает, каким образом сконструировать конкретный изоморфизм. Примеры:
Циклические группы[править | править код]
Если (G, ∗) является бесконечной циклической группой, то (G, ∗) изоморфна целым числам (по сложению). С алгебраической точки зрения это означает, что множество всех целых чисел (по сложению) является единственной бесконечной циклической группой.
Все конечные циклические группы заданного порядка изоморфны 
Пусть G — циклическая группа и n — порядок группы G. G является группой, порождённой элементом 
Мы покажем, что
Определим
, так что
. Ясно, что
биективно.
Таким образом,
, что доказывает, что
.
Свойства[править | править код]
- Ядро изоморфизма из (G, ∗) в (H,
) всегда равно {eG}, где eG — нейтральный элемент группы (G, ∗)
- Если (G, ∗) изоморфна (H,
) и если G абелева, то H тоже абелева.
- Если f — изоморфизм между (G, *) и (H,
), тогда, если a принадлежит G и имеет порядок n, то такой же порядок имеет f(a).
Следствия[править | править код]
Из определения следует, что любой изоморфизм 
,
откуда следует, что обратные отображаются в обратные,
и n-е степени в n-е степени,
для всех u из G,
а также что обратное отображение 
Отношение «изоморфно» удовлетворяет всем аксиомам отношения эквивалентности. Если f является изоморфизмом двух групп G и H, то все утверждения, верные для G, связанные со структурой группы, можно перенести посредством f на такие же утверждения в H, и наоборот.
Автоморфизмы[править | править код]
Изоморфизм из группы (G, ∗) в себя называется автоморфизмом этой группы. Так как изомофизм 
.
Автоморфизм всегда отображает нейтральный элемент в себя. Образ класса сопряжённости всегда является классом сопряжённости (тем же самым или другим). Образ элемента имеет тот же порядок, что и сам элемент.
Композиция двух автоморфизмов снова является автоморфизмом, и эта операция с множеством всех автоморфизмов группы G, обозначаемая Aut(G), образует группу, группу автоморфизмов G.
Для всех абелевых групп имеется, по меньшей мере, автоморфизм, переводящий элементы группы в их обратные. Однако в группах, где все элементы равны своим обратным, этот автоморфизм является тривиальным, например, в четверной группе Клейна (для этой группы все перестановки трёх, не являющихся нейтральными, элементов группы являются автоморфизмами, так что группа изоморфизмов изоморфна S3 и Dih3).
В Zp для простого числа p, один, не являющийся нейтральным, элемент может быть заменён другим, с соответствующими изменениями в других элементах. Группа автоморфизмов изоморфна Zp − 1. Например, для n = 7, умножение всех элементов Z7 на 3 (по модулю 7), является автоморфизмом порядка 6 в группе автоморфизмов, поскольку 36 ≡ 1 (по модулю 7), а меньшие степени 1 не дают. Таким образом, этот автоморфизм порождает Z6. Имеется ещё один автоморфизм с этим свойством — умножение всех элементов Z7 на 5 (по модулю 7). Таким образом, эти два автоморфизма соответствуют элементам 1 и 5 Z6, в этом порядке или обратном.
Группа автоморфизмов Z6 изоморфна Z2, поскольку только эти два элемента 1 и 5 порождают Z6.
Группа автоморфизмов Z2 × Z2 × Z2 = Dih2 × Z2 имеет порядок 168, что можно показать следующим образом. Все 7 элементов, не являющихся нейтральными, играют одну и ту же роль, так что мы можем выбрать, который играет роль (1,0,0). Любой из оставшихся шести может быть выбран для роли (0,1,0). Эти два определяют, что соответствует (1,1,0). (0,0,1) мы можем выбрать из четырёх, и этот выбор определяет оставшиеся элементы. Таким образом, получим 7 × 6 × 4 = 168 автоморфизмов. Они соответствуют автоморфизмам плоскости Фано, 7 точек которой соответствуют 7 элементам, не являющихся нейтральными. Прямые, соединяющие три точки, соответствуют операции группы: a, b, и c на прямой означают a + b = c, a + c = b, и b + c = a. См. также Полная линейная группа над конечным полем.
Для абелевых групп все автоморфизмы, за исключением тривиального, называются внешними автоморфизмами[en].
Неабелевы группы имеют нетривиальные внутренние автоморфизмы, и, возможно, внешние автоморфизмы.
Примечания[править | править код]
- ↑ Ash. A Consequence of the Axiom of Choice // Journal of the Australian Mathematical Society. — 1973. — Т. 19. — С. 306—308.
Ссылки[править | править код]
Herstein, I. N. Topics in Algebra. — 2 edition. — Wiley, 1975. — ISBN 0-471-01090-1..
Приветствую Вас, уважаемые Читатели! Продолжаю раскладывать некоторые основания теории групп. Сегодня мы перейдем от геометрической интерпретации к комбинаторной в том виде, в которой нам её дал великий Эварист Галуа. Поехали!
НАСТОЯТЕЛЬНО рекомендую перед прочтением данного материала ознакомиться с его первой частью и второй частью. Не лишним для понимания будет эта и эта статьи.
Итак, для удобства повторю рисунок из прошлого материала:
Давайте уйдем от треугольников, симметрий и поворотов, ведь теория групп, потому и прекрасна, что не привязана к физической среде. Обратите внимание, что симметрии на рисунке выше мы можем записать как переходы, если будем считать вершины, например, с верхней и далее против часовой стрелки.
Тогда симметрия S будет соответствовать переходу [1,2,3 ——>1,3,2]. Запишем все известные нам преобразования треугольника в таком виде:
Таким образом в математике записываются подстановки, которые определяют, новое расположение перестановок элементов множества. Как известно из той же комбинаторики, количество перестановок элементов равно факториалу от количества элементов, что в данном случае даёт 3! = 6 – столько же, сколько инвариантов у треугольника! Совпадение? Не думаю! Проверим еще вот что:
Как видно из рисунков, применение групповых операций даёт тот же результат, разве что записанный по другому. Чувствуется, что эти группы практически идентичны друг другу.
Впрочем, математика была бы не математикой, если бы не дала звучное название этой “идентичности”.
Проверим выполнение 3 свойств для некоторой функции f:
Если существует такая функция f (а она существует – обычная биекция, устанавливающая взаимно-однозначное соответствие между элементами G и H, мы на отдельных примерах это показали), то группы G и H называются изоморфными, а сама функция f – изоморфизмом. С точки зрения теории групп такие группы имеют абсолютно одинаковые свойства, и их нет необходимости различать. И это один из важнейших инструментов!
Изоморфизм – это частный случай гомоморфизма, а есть еще автоморфизмы, эпифорфизмы, диффеоморфизмы, гомеоморфизмы…, но это уже совсем другая история.
Проще всего понять, что такое “изоморфизм” можно на примере числовых групп и я расскажу об этом в одном из следующих материалов. Кстати, мы еще не закончили с треугольниками, ждите статью с подробным анализом таблицы, которую мы составили для инвариантов треугольника. Спасибо за внимание!
Читайте также:
Определение.
Пусть
![]()
и
![]()
– группы. Отображение
![]()
называется гомоморфизмом, если для
любых
![]()
![]()
.
Определение.
Изоморфизмом
групп
называется гомоморфизм, который является
взаимно однозначным отображением. Если
группы
и
изоморфны,
то принято обозначать
![]()
.
При гомоморфизме
единица группы всегда переходит в
единицу. Действительно, если
![]()
и
![]()
– единицы групп
и
соответственно,
то
![]()
.
Умножив это равенство на
![]()
,
получим
![]()
.
Далее, при
гомоморфизме обратный к элементу
![]()
элемент переходит в обратный к
![]()
.
Действительно,
![]()
.
Аналогично,
![]()
Это и означает, что
![]()
Определение.
Пусть G
– группа с единицей e
и элемент
![]()
Наименьшее натуральное n,
для которого
![]()
называется
порядком элемента g
и обозначается o(g).
Если такого n
не существует, то считается, что
![]()
Если
–
гомоморфизм
групп, то порядки элементов
g
и f(g)
связаны, а
именно, если
![]()
то
n
делится на
m.
Действительно,
![]()
,
поэтому элемент f(g)
имеет конечный
порядок. Допустим, что n
не делится на m.
Тогда
![]()
,
где
![]()
В этом случае
![]()
что противоречит тому, что m
– наименьшая степень такая, что
![]()
Задача 1.4.1.
Определите
порядки всех элементов в следующих
группах а)
![]()
б)
![]()
в)
![]()
а)
В
группе
![]()
единицей
является элемент
![]()
Групповая операция – это сложение по
модулю 12. Порядок элемента x
это наименьшее натуральное n
такое, что
![]()
Например,
![]()
Поэтому порядок элемента
![]()
обзначаемый
![]()
равен
2. Порядки элементов
![]()
и
![]()
равны 3. Элементы
![]()
и
![]()
имеют четвертый порядок,
![]()
и
![]()
– шестой. Наконец, элементы
![]()
имеют двенадцатый порядок. Сам элемент
![]()
как и единица любой группы, имеет первый
порядок.
б), в) Решите
самостоятельно.
Пример 1. Покажем,
что
![]()
Каждому преобразованию группы
можно сопоставить перестановку –
перестановку вершин треугольника ABC.
Действительно,
занумеруем вершины: A
– 1, B
– 2, C
– 3. Тогда отображение
![]()
при котором
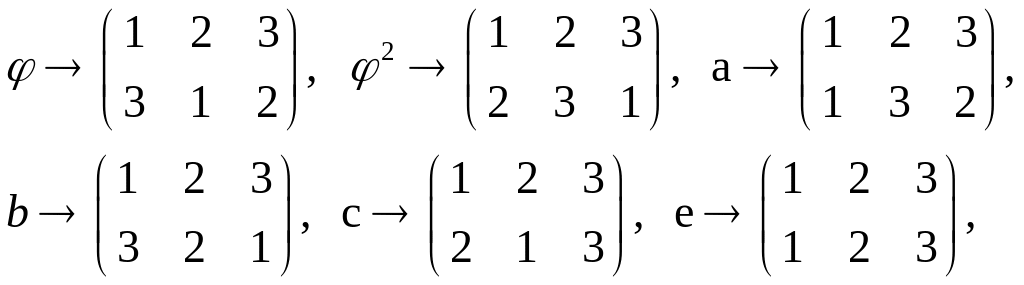
является изоморфизмом.
Пример 2.
Отображение
![]()
при котором каждому целому
![]()
ставится в соответствие его остаток
![]()
при делении на n
, является
гомоморфизмом групп, но не изоморфизмом.
Например, если
![]()
то
![]()
т.к.
![]()
Пример 3. Пусть
![]()
– группа всех действительных чисел
отличных от нуля с обычной операцией
умножения. Отображение
![]()
сопоставляет
каждой матрице ее определитель. Тогда
f
– гомоморфизм групп, т.к. определитель
произведения матриц равен произведению
определителей. Гомоморфизм f
не является
изоморфизмом, т.к. разные матрицы могут
иметь одинаковые определители.
Пример 4. Пусть
– группа всех действительных чисел с
операцией сложения, а
– группа всех положительных действительных
чисел с операцией умножения. Гомоморфизм
![]()
– определен формулой
![]()
Это действительно гомоморфизм, т.к.
![]()
Более того, этот гомоморфизм является
изоморфизмом.
Определение.
Пусть G
– группа. Нетрудно убедиться, что
множество всех изоморфизмов
![]()
также образует группу, которая называется
группой автоморфизмов группы G
и обозначается Aut
G.
Пример 5. Найдем
группу
![]()
Заметим, что в группе
![]()
каждый элемент
является суммой нескольких единиц:
![]()
Поэтому, чтобы задать гомоморфизм
![]()
достаточно задать
![]()
Действительно, если
![]()
то
![]()
и т.д.. Чтобы гомоморфизм был взаимно
однозначным отображением,
![]()
может равняться либо
![]()
либо
![]()
Обозначим первый автоморфизм
![]()
а второй –
![]()
Тогда
![]()
Поэтому
![]()
Ответы
1.4.1.б) Элементы
![]()
и
имеют
третий порядок, элементы a,b,c
– второй и
e
– первый;
в) элементы
![]()
имеют четвертый порядок, элемент (-1) –
второй и 1 – первый.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic. From the standpoint of group theory, isomorphic groups have the same properties and need not be distinguished.[1]
Definition and notation[edit]
Given two groups 









The two groups 

Often shorter and simpler notations can be used. When the relevant group operations are understood, they are omitted and one writes
Sometimes one can even simply write 
Conversely, given a group 




If 

Intuitively, group theorists view two isomorphic groups as follows: For every element 











An isomorphism of groups may equivalently be defined as an invertible group homomorphism (the inverse function of a bijective group homomorphism is also a group homomorphism).
Examples[edit]
In this section some notable examples of isomorphic groups are listed.
Some groups can be proven to be isomorphic, relying on the axiom of choice, but the proof does not indicate how to construct a concrete isomorphism. Examples:
Properties[edit]
The kernel of an isomorphism from 


If 



If 





If 



The number of distinct groups (up to isomorphism) of order 
Cyclic groups[edit]
All cyclic groups of a given order are isomorphic to 


Let 





We will show that
Define
so that
Clearly, 
which proves that
Consequences[edit]
From the definition, it follows that any isomorphism 


that it will map inverses to inverses,
and more generally, 

and that the inverse map 
The relation “being isomorphic” satisfies is an equivalence relation. If 





Automorphisms[edit]
An isomorphism from a group 

The image under an automorphism of a conjugacy class is always a conjugacy class (the same or another).
The composition of two automorphisms is again an automorphism, and with this operation the set of all automorphisms of a group 


For all abelian groups there is at least the automorphism that replaces the group elements by their inverses. However, in groups where all elements are equal to their inverses this is the trivial automorphism, e.g. in the Klein four-group. For that group all permutations of the three non-identity elements are automorphisms, so the automorphism group is isomorphic to 

In 








The automorphism group of 


The automorphism group of 









For abelian groups, all non-trivial automorphisms are outer automorphisms.
Non-abelian groups have a non-trivial inner automorphism group, and possibly also outer automorphisms.
See also[edit]
- Group isomorphism problem
- Bijection – One-to-one correspondence
References[edit]
- Herstein, I. N. (1975). Topics in Algebra (2nd ed.). New York: John Wiley & Sons. ISBN 0471010901.
- ^ a b Barnard, Tony & Neil, Hugh (2017). Discovering Group Theory: A Transition to Advanced Mathematics. Boca Ratan: CRC Press. p. 94. ISBN 9781138030169.
- ^ Budden, F. J. (1972). The Fascination of Groups (PDF). Cambridge: Cambridge University Press. p. 142. ISBN 0521080169. Retrieved 12 October 2022 – via VDOC.PUB.
- ^ Ash (1973). “A Consequence of the Axiom of Choice”. Journal of the Australian Mathematical Society. 19 (3): 306–308. doi:10.1017/S1446788700031505. Retrieved 21 September 2013.

Изоморфизм и гомоморфизм групп Определение. Группы G 1 и G 2 называются гомоморфными, если существует отображение : G 1 G 2, сохраняющее операции, определенные в G 1 и G 2. Т. е. , для и имеем: a, b G 1, (a b) = (a)○ (b). Обозн. : ~ . Если – взаимно-однозначное отображение, то группы называются изоморфными. Обозн. :

Примеры. 1) G 1 = , G 2 = <{ 1}, > : G 1 G 2 так, что (2 n) = 1; (2 n+1) = -1. Проверим сохранение операции: (2 n+2 k) = (2(n+k)) = 1 (2 n) (2 k) = 1 1=1 ((2 n+1)+(2 k+1)) = (2(n+k+1)) = 1 (2 n+1) (2 k+1) = (-1) = 1 1=1 (2 n+(2 k+1)) = (2(n+k)+1) = -1 (2 n) (2 k+1) = 1 (-1) = -1 – гомоморфизм. -1 = -1
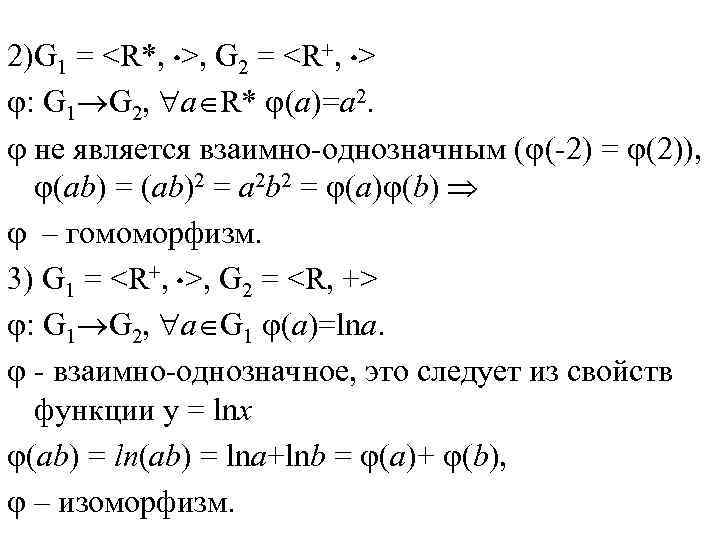
2)G 1 = , G 2 = : G 1 G 2, a R* (a)=a 2. не является взаимно-однозначным ( (-2) = (2)), (ab) = (ab)2 = a 2 b 2 = (a) (b) – гомоморфизм. 3) G 1 = , G 2 = : G 1 G 2, a G 1 (a)=lna. – взаимно-однозначное, это следует из свойств функции y = lnx (ab) = lna+lnb = (a)+ (b), – изоморфизм.

Свойства изоморфизма Т 1. Изоморфный образ группы является группой. Дано: , G 1 – группа. Доказать: G 2 – группа. Доказательство: 1) Выполнимость: Пусть : G 1 G 2 – изоморфизм, b 1, b 2 G 2. Докажем, что b 1○b 2 G 2. Т. к. – изоморфизм, то a 1, a 2 G 1, (a 1) = b 1, (a 2) = b 2. a 1 a 2 G 1; (a 1 a 2) G 2. (a 1 a 2) = (a 1)○ (a 2) = b 1○b 2 G 2. 2) Ассоциативность: b 1, b 2, b 3 G 2, докажем, что (b 1○b 2)○b 3 = b 1○(b 2○b 3). (b 1○b 2)○b 3 = ( (a 1)○ (a 2))○ (a 3) = -изом. (a 1 a 2)○ (a 3) = -изом. ((a 1 a 2) a 3) =G 1–гр. (a 1 (a 2 a 3)) = -изом. (a 1)○ (a 2 a 3)= -изом. = (a )○( (a )○ (a )) = b ○(b ○b ). 1 2 3

3) Существование нейтрального элемента. Пусть e – нейтральный элемент из G 1. Покажем, что (e) – нейтральный элемент G 2. Т. е. b G 2 b○ (e) = (e)○b = b. Т. к. – изоморфизм, то a G 1, (a) = b. b○ (e) = (a)○ (e) = (a) = b (e)○b = (e)○ (a) = (e a) = (a) = b b○ (e) = (e)○b = b, следовательно (e) – нейтральный элемент G 2. 4) Нейтрализующий элемент. b G 2 b-1 G 2, b○b-1 = e’, e’ = (e) – нейтральный элемент G 2. (a) = b. Покажем, что (a-1) = b-1. b○b-1 = (a)○ (a-1) = (a a-1) = (e) = e’ G 2, b-1○b = (a-1)○ (a) = (a-1 a) = (e) = e’.

1) Взаимная однозначность. а) Пусть am 1 = am 2 am 1 -m 2 =e св-ва порядка m 1 = m 2 + nt, t Z. (am 1) = (am 2). б) Пусть (am 1) = (am 2), т. е. тогда

2) Сохранение операций: (am 1 am 2) = (am 1+m 2) =

Т 5 (Кэли). Любая конечная группа порядка n изоморфна некоторой подгруппе подстановок n -ой степени. Дано: G – группа; |G| = n. Доказать: Н Sn такая, что G H. Доказательство: G = {a 1, a 2, …, an, } ai G рассмотрим произведения a 1 ai, a 2 ai, …, an ai G. Все эти произведения будут различными Обозначим: a 1 ai = a 1, a 2 ai = a 2, … an ai = a n. 1, 2, …, n – некоторый набор чисел от 1 до n. Рассмотрим отображение Покажем, что – изоморфизм.

1) Взаимная однозначность. а) Пусть ai = aj из однозначности произведения (ai) = (aj) б) Пусть (ai) = (aj). Тогда k, k=1, 2, …, n ak ai = ak aj ai = aj. 2) Для доказательства сохранения операции будем использовать подстановку: Тогда
![Ядро гомоморфизма (kernel ['kə: nəl]) Пусть : G 1 G 2; –гомоморфизм. Определение. Ядром Ядро гомоморфизма (kernel ['kə: nəl]) Пусть : G 1 G 2; –гомоморфизм. Определение. Ядром](https://present5.com/presentation/3/154154717_166247568.pdf-img/154154717_166247568.pdf-13.jpg)
Ядро гомоморфизма (kernel [‘kə: nəl]) Пусть : G 1 G 2; –гомоморфизм. Определение. Ядром гомоморфизма называется множество элементов группы G 1, которые отображаются в нейтральный элемент группы G 2. G 1 G 2 e´ Обозн. : Ker = {a G 1 / (a) =e’, e’ G 2}.

Т 1. Ядро гомоморфизма является нормальным делителем группы. Дано: G – группа, H = Ker . Доказать: H G. Доказательство: 1) Покажем, что H G а) a, b H ab H. Пусть a, b H, тогда (a) = (b) = e’. (ab) = – гомоморфизм (a) (b) = e’ e’ = e’ ab H. б) Пусть a H, тогда (a) = e’. Найдем (a-1) = ( (a))-1 = (e’)-1 = e’ a-1 H. 2) Покажем, что H G, т. е. a G a. H = Ha. Пусть ah a. H, покажем, что h 1 a Ha, такой, что ah=h 1 a. Рассмотрим aha-1 и найдем его образ: (aha-1) = (a) (h) (a-1) = (a) e (a-1) = (a a-1) = (e) = e’. Тогда aha-1 H или aha-1=h 1 ah=h 1 a.

Т 2. Любая нормальная подгруппа группы G является ядром некоторого гомоморфизма. Дано: H G Доказать: H – ядро некоторого гомоморфизма. Доказательство: G/H={H, g 1 H, g 2 H, …}. : G G/H g G (g) = g H. Покажем, что – гомоморфизм ( – сохраняет операцию). g 1, g 2 G (g 1 g 2) = (g 1 g 2) H = (g 1 g 2)H H = g 1 H g 2 H = (g 1) (g 2) – гомоморфизм. Покажем, что H = Ker . Пусть h H (h) = h H = H – нейтральный элемент G/H. Следовательно, h Ker и H Ker (1) Пусть h 1 Ker (h 1) = H или h 1 H = H h 1 H Ker H (2). Из (1) и (2) следует ч. т. д. Определение. Гомоморфизм группы G на факторгруппу G/H называется естественным гомоморфизмом группы G.

Т 3. Гомоморфный образ группы изоморфен факторгруппе по ядру этого гомоморфизма. Дано: : G 1 G 2; – гомоморфизм, H = Ker . Доказать: G 1/H G 2. Доказательство: Рассмотрим отображение : G 1/H G 2 такое, что g H G 1/H (g H) = (g); g G 1; (g) G 2. Покажем, что – изоморфизм. 1. Взаимная однозначность. Пусть g 1 H = g 2 H (g 2 -1 g 1)H = H g 2 -1 g 1 H, т. е. g 2 -1 g 1 Ker (g 2 -1 g 1) = e’ G 2. Т. к. – гомоморфизм, (g 2 -1) (g 1) = e’ или ( (g 2))-1 (g 1) = e’ (g 1) = (g 2) (g 1 H) = (g 2 H). Обратно, пусть (g 1 H) = (g 2 H), или (g 1) = (g 2), ( (g 2))-1 (g 1) = e’ G 2 (g 2 -1 g 1) = e’. Тогда g 2 -1 g 1 Ker = H или (g 2 -1 g 1)H = H g 1 H = g 2 H. 2. Сохранение операции. (g 1 H g 2 H) = ((g 1 g 2)H) = (g 1 g 2) = (g 1) (g 2) = (g 1 H) (g 2 H).





![f(u^{{-1}})=left[f(u)right]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1e1fbe22b073103c1a948972449f92413e0bb46)
![f(u^{n})=left[f(u)right]^{n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f48b11cde66496951fb09d74eddfef5a0626afba)













