Как найти изотерму адсорбции

Адсорбция. Изотерма адсорбции. Уравнение Гиббса.

ПН
растворов обычно отличается от ПН
растворителя.

Растворенное вещество может не изменять

,
повышать и понижать его.

Поверхностная свободная энергия
стремится к минимуму, поэтому при
повышении

вещество будет удаляться с поверхности
внутрь жидкости. Полному удалению
молекул растворенного вещества с
поверхности препятствует тепловое
движение, под действием которого вещество
стремится к равномерному распределению
в объеме.

Под влиянием этих двух факторов
устанавливается равновесие, в результате
которого концентрация вещества в
поверхностном слое уменьшается по
сравнению с концентрацией в объеме.

Если растворенное вещество снижает

,
то концентрация его в поверхностном
слое увеличивается.

Самопроизвольное изменение концентрации
вещества в поверхностном слое, отнесенное
к единице поверхности, называется
адсорбцией, обозначается через Г и
выражается в кмоль/м², или моль/см².

Если Г0 адсорбцию
называют положительной, если Г0
– отрицательной.

Если растворенное вещество не изменяет

,
адсорбция Г=0 и вещество равномерно
распределено между поверхностным слоем
и объемом.

Простое термодинамическое соотношение
между поверхностной концентрацией Г и
изменением ПН с активной концентрацией
растворяемого вещества

было выведено Гиббсом:

где

– активность раствора;

– универсальная газовая постоянная;

–
абсолютная температура.

Для
разбавленных растворов активность
заменяют концентрацией С:

Из уравнения следует, что только те
вещества показывают положительную
адсорбцию, с повышением концентрации
которых ПН понижается,

0.

Если

0,
концентрация растворенного вещества
в поверхностном слое будет уменьшаться:
Г0.

Вещества, повышающие ПН, называются
отрицательно поверхностно-активными
веществами (инактивными, ими являются
неорганические соли).

Вещества, понижающие ПН называют
поверхностно-активными (ПАВ) (см. стр.
98-102).

К ПАВ относятся органические вещества,
молекулы которых построены из участков
с резко различающимися свойствами. Одна
часть молекулы полярная, другая –
неполярная (углеводородный радикал).

Полярная: -OH, -COOH,
-SO₃Na,
-SO₃H,
-NH₂, -SO₂H.

Полярная часть гидрофильна, неполярная
– гидрофобна.

ПАВ характеризуются величиной ГЛБ
(гидрофильно-липофильного баланса).

Величина

,
согласно Ребиндеру, является мерой
способности вещества понижать
поверхностную энергию, она называется
поверхностной активностью и обозначается

.
Ее размерность – Н/м.

В
гомологическом ряду жирных кислот,
спиртов и аминов понижение

тем больше, чем длиннее цепь.

Согласно правилу Дюкло-Траубе, при
удлинении цепи на группу СН₂
поверхностная активность

возрастает на границе раствор-воздух
в 3-3,5 раз.

Для определения этой характеристики
строят зависимость

.
Используя уравнение Гиббса, строят
зависимость

.

Построение изотермы адсорбции и нахождение величин .

Изотерма адсорбции описывается уравнением
Ленгмюра:

где

–
предельная концентрация вещества,
адсорбиро-

ванного на 1 м² поверхности,
кмоль/м²;

–
константа равновесия, равная отношению
констант скоростей процессов десорбции
и адсорбции.

Зная
Г можно рассчитать площадь S,
приходящуюся на 1 молекулу.

Число адсорбированных молекул на 1 м²
составляет:

Отсюда:

С увеличением Г величина S
уменьшается и при

достигает минимального значения

:

Пользуясь

вычисляют толщину

насыщенного поверхностного слоя:

–
молекулярная масса;

–
плотность адсорбированного вещества.

Строят изотерму ПН (зависимость

от концентрации ПАВ).

По изотерме ПН рассчитывают Г по
уравнению Гиббса.

Для
этого к кривой

в нескольких точках проводят касательные
до пересечения их с осью ординат, проводя
также параллельные прямые до пересечения
с осью ординат (рис. 6.5). Из треугольника
АВD находят

или

.
Находят несколько значений

для C₁, C₂,
C₃,…и строят
зависимость
.

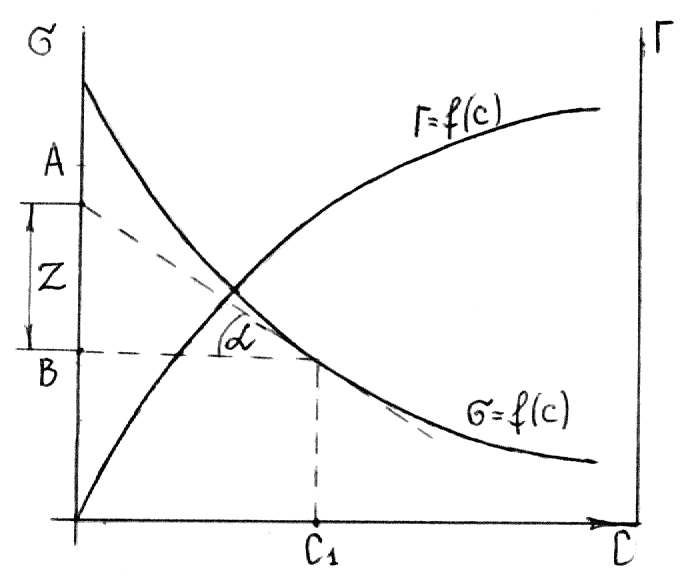
Рис.
6.5. Построение изотермы адсорбции по
изотерме

поверхностного
натяжения.

Каждой концентрации С соответствует
отрезок Z на оси ординат.

Длина отрезка, выраженная в единицах
ПН равна:

,
так как согласно построению

.

Подставив полученные значения Z
в уравнение:

получим:

Используя Z для ряда
концентраций, рассчитывают адсорбцию
Г.

Строят изотерму адсорбции, откладывая
по оси абсцисс С, а по оси ординат Г.

Где сложно провести касательную (в
интервале концентраций 0,2-0,15 моль/л)
рассчитывают изменение:

и

и определяют

для средней концентрации
0,1.

Данные заносят в таблицу:

Значение

определяют
графически по уравнению Лэнгмюра,
преобразовав его в уравнение прямой
линии (рис. 6.6):

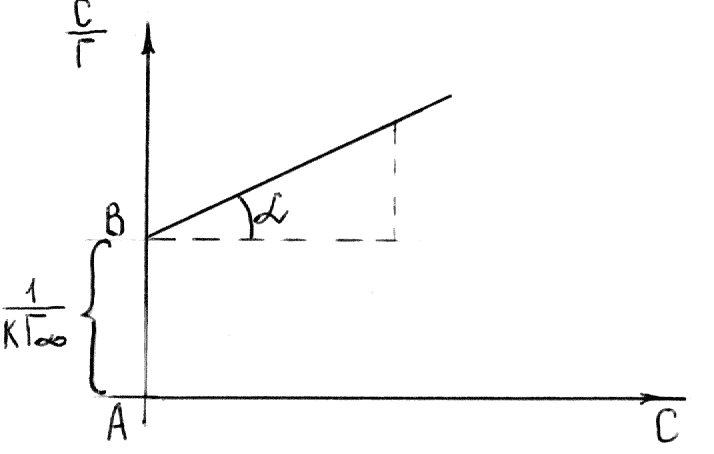
Рис. 6.6. График уравнения Ленгмюра в
прямолинейных координатах.

Угол

на рис. 6.6 позволяет определить

:

.

Отрезок

.

Из этого уравнения определяем

.

Из уравнения

вычисляем

и

из
уравнения

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 апреля 2020 года; проверки требует 1 правка.

Изоте́рма адсо́рбции, изоте́рма со́рбции — зависимость количества адсорбированного вещества (величины адсорбции) от парциального давления этого вещества в газовой фазе (или концентрации раствора) при постоянной температуре.

Описание[править | править код]

Экспериментальные изотермы адсорбции являются наиболее распространенным способом описания адсорбционных явлений. Методы получения адсорбционных данных для построения изотерм адсорбции основаны на измерении количества газа (жидкости), удаленного из газовой (жидкой) фазы при адсорбции, а также на различных способах определения количества адсорбата (адсорбированное вещество) на поверхности адсорбента (адсорбирующее вещество), например, волюметрический метод, гравиметрический метод и др.

Различают шесть основных типов изотерм адсорбции (см. рисунок). Тип I характерен для микропористых твёрдых тел с относительно малой долей внешней поверхности. Тип II указывает на полимолекулярную адсорбцию на непористых или макропористых адсорбентах. Тип III характерен для непористых сорбентов с малой энергией взаимодействия адсорбент-адсорбат. Типы IV и V аналогичны типам II и III, но для пористых адсорбентов. Изотермы типа VI характерны для непористых адсорбентов с однородной поверхностью.

Изотермы адсорбции используются для расчета удельной поверхности материалов, среднего размера пор или среднего размера нанесённых частиц, распределения пор или частиц по размерам.

Существует несколько методов математического выражения изотерм адсорбции, различающихся моделями, использованными для описания процесса адсорбции. При малых степенях покрытия поверхности адсорбатом для однородной поверхности уравнение изотермы адсорбции имеет вид уравнения Генри: a=Kp, где a — величина адсорбции, p — давление газа, K — константа. При средних степенях покрытия может быть применено эмпирическое уравнение Фрейндлиха: a = kp^1/n, где k и 1/n — константы.

Строгая теория изотермы адсорбции была предложена Ирвингом Ленгмюром для модели монослойной адсорбции на однородной поверхности, в которой можно пренебречь силами притяжения между молекулами адсорбата и их подвижностью вдоль поверхности. Уравнение изотермы Ленгмюра имеет вид: a=ambp/(1 + bp), где b — адсорбционный коэффициент, зависящий от энергии адсорбции и температуры; am — ёмкость монослоя.

Дальнейшее развитие теории состояло в исключении того или иного допущения, использованного Ленгмюром. Так, С. Брунауэром, П. Эмметом и Э. Теллером была предложена теория полимолекулярной адсорбции (метод БЭТ); Т. Хилл и Я. де Бур разработали теорию, учитывающую взаимодействие между адсорбированными молекулами (изотерма Хилла-де-Бура), и т. д.

См. также[править | править код]

• Метод BJH

Литература[править | править код]

• Полторак О. М.: Термодинамика в физической химии. — М.: Высшая школа, 1991. — 319 с.  (рус.)
• Sing K. S.W. et al.: Reporting physisorption data for gas/solid systems with special reference to the determination of surface area and porosity (recommendations) // Pure Appl. Chem. 1985. V. 57, № 4. P. 603—619.  (англ.)
• Карнаухов А. П.: Адсорбция. Текстура дисперсных и пористых материалов. — Новосибирск: Наука, 1999. — 470 с.  (рус.)

Ссылки[править | править код]

72,7% бесплатных материалов

964 руб. средняя цена курсовой работы

351 руб. средняя цена домашнего задания

119 руб. средняя цена решённой задачи

160 руб. средняя цена лабораторной работы

174 руб. средняя цена реферата

168 руб. средняя цена доклада

1610 руб. средняя цена ВКР

664 руб. средняя цена диссертации

596 руб. средняя цена НИР

357 руб. средняя цена отчёта по практике

276 руб. средняя цена ответов (шпаргалок)

201 руб. средняя цена лекций

222 руб. средняя цена семинаров

280 руб. средняя цена рабочей тетради

188 руб. средняя цена презентации

67 руб. средняя цена перевода

137 руб. средняя цена изложения

150 руб. средняя цена сочинения

308 руб. средняя цена статьи

Гарантия возврата средств