Если посмотреть на числовую окружность , то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).
Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций .
Например, для любого угла из второй четверти – синус положителен, а косинус , тангенс и котангенс отрицательны. А для любого угла из первой четверти – все четыре функции будут положительны.
Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.
Нам известен косинус, а найти нужно синус того же угла. Какая тригонометрическая формула связывает синус и косинус того же угла?
Основное тригонометрическое тождество. Запишем его.
Подставим известное, и проведем вычисления.
Важно понимать, что, например, первой четверти принадлежат не только углы от (0) до (frac<π><2>) , но и углы от (2π) до (frac<5π><2>) , и от (4π) до (frac<9π><2>) , и от (6π) до (frac<13π><2>) и так далее. Ведь как только мы заканчиваем полный оборот – кончается четвертая четверть и опять начинается первая.
Кроме того, нужно помнить, что углы могут откладываться в отрицательную сторону (по часовой стрелке), и тогда мы попадем в первую четверть только в конце круга. Ведь сначала мы пройдем четвертую четверть, потом в третью и т.д.
((0;-) (frac<π><2>) ()) – четвертая четверть
Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную.
Как определить какой четверти числовой окружности принадлежит точка
Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.
Единичной окружностью называют окружность радиуса 1.
Общий вид числовой окружности.
1) Ее радиус принимается за единицу измерения.
2) Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти (см.рисунок). Их соответственно называют первой, второй, третьей и четвертой четвертью.
3) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка.
Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.
Соответственно:
первая четверть – это дуга AB
вторая четверть – дуга BC
третья четверть – дуга CD
четвертая четверть – дуга DA
4) Начальная точка числовой окружности – точка А.
Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки.
Отсчет от точки А против часовой стрелки называется положительным направлением.
Отсчет от точки А по часовой стрелке называется отрицательным направлением.
Числовая окружность на координатной плоскости.
Центр радиуса числовой окружности соответствует началу координат (числу 0).
Горизонтальный диаметр соответствует оси x, вертикальный – оси y.
Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).
Значения x и y в четвертях числовой окружности:
x 0, y Основные величины числовой окружности:
Величина
в радианах
Величина
в радиусах
Имена и местонахождение основных точек числовой окружности:
Как запомнить имена числовой окружности.
Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности.
Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2π) против часовой стрелки.
1) Начнем с крайних точек на осях координат.
Начальная точка – это 2π (крайняя правая точка на оси х, равная 1).
Как вы знаете, 2π – это длина окружности. Значит, половина окружности – это 1π или π. Ось х делит окружность как раз пополам. Соответственно, крайняя левая точка на оси х, равная -1, называется π.
Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность – это π, то половина полуокружности – это π/2.
Одновременно π/2 – это и четверть окружности. Отсчитаем три таких четверти от первой до третьей – и мы придем в крайнюю нижнюю точку на оси у, равной -1. Но если она включает три четверти – значит имя ей 3π/2.
2) Теперь перейдем к остальным точкам. Обратите внимание: все противоположные точки имеют одинаковый числитель – причем это противоположные точки и относительно оси у, и относительно центра осей, и относительно оси х. Это нам и поможет знать их значения точек без зубрежки.
Надо запомнить лишь значение точек первой четверти: π/6, π/4 и π/3. И тогда мы «увидим» некоторые закономерности:
– Относительно оси у в точках второй четверти, противоположных точкам первой четверти, числа в числителях на 1 меньше величины знаменателей. К примеру, возьмем точку π/6. Противоположная ей точка относительно оси у тоже в знаменателе имеет 6, а в числителе 5 (на 1 меньше). То есть имя этой точки: 5π/6. Точка, противоположная π/4, тоже имеет в знаменателе 4, а в числителе 3 (на 1 меньше, чем 4) – то есть это точка 3π/4.
Точка, противоположная π/3, тоже имеет в знаменателе 3, а в числителе на 1 меньше: 2π/3.
– Относительно центра осей координат все наоборот: числа в числителях противоположных точек (в третьей четверти) на 1 больше значения знаменателей. Возьмем опять точку π/6. Противоположная ей относительно центра точка тоже имеет в знаменателе 6, а в числителе число на 1 больше – то есть это 7π/6.
Точка, противоположная точке π/4, тоже имеет в знаменателе 4, а в числителе число на 1 больше: 5π/4.
Точка, противоположная точке π/3, тоже имеет в знаменателе 3, а в числителе число на 1 больше: 4π/3.
– Относительно оси х (четвертая четверть) дело посложнее. Здесь надо к величине знаменателя прибавить число, которое на 1 меньше – эта сумма и будет равна числовой части числителя противоположной точки. Начнем опять с π/6. Прибавим к величине знаменателя, равной 6, число, которое на 1 меньше этого числа – то есть 5. Получаем: 6 + 5 = 11. Значит, противоположная ей относительно оси х точка будет иметь в знаменателе 6, а в числителе 11 – то есть 11π/6.
Точка π/4. Прибавляем к величине знаменателя число на 1 меньше: 4 + 3 = 7. Значит, противоположная ей относительно оси х точка имеет в знаменателе 4, а в числителе 7 – то есть 7π/4.
Точка π/3. Знаменатель равен 3. Прибавляем к 3 на единицу меньшее число – то есть 2. Получаем 5. Значит, противоположная ей точка имеет в числителе 5 – и это точка 5π/3.
3) Еще одна закономерность для точек середин четвертей. Понятно, что их знаменатель равен 4. Обратим внимание на числители. Числитель середины первой четверти – это 1π (но 1 не принято писать). Числитель середины второй четверти – это 3π. Числитель середины третьей четверти – это 5π. Числитель середины четвертой четверти – это 7π. Получается, что в числителях середин четвертей – четыре первых нечетных числа в порядке их возрастания:
(1)π, 3π, 5π, 7π.
Это тоже очень просто. Поскольку середины всех четвертей имеют в знаменателе 4, то мы уже знаем их полные имена: π/4, 3π/4, 5π/4, 7π/4.
Особенности числовой окружности. Сравнение с числовой прямой.
Как вы знаете, на числовой прямой каждая точка соответствует единственному числу. К примеру, если точка А на прямой равна 3, то она уже не может равняться никакому другому числу.
На числовой окружности все иначе, поскольку это окружность. К примеру, чтобы из точки А окружности прийти к точке M, можно сделать это, как на прямой (только пройдя дугу), а можно и обогнуть целый круг, а потом уже прийти к точке M. Вывод:
Пусть точка M равна какому-то числу t. Как мы знаем, длина окружности равна 2π. Значит, точку окружности t мы можем записать двояко: t или t + 2π. Это равнозначные величины.
То есть t = t + 2π. Разница лишь в том, что в первом случае вы пришли к точке M сразу, не делая круга, а во втором случае вы совершили круг, но в итоге оказались в той же точке M. Таких кругов можно сделать и два, и три, и двести. Если обозначить количество кругов буквой k, то получим новое выражение:
t = t + 2πk.
Отсюда формула:
Если точка M числовой окружности равна числу t, то она равна и числу вида t + 2πk, где k – любое целое число:
M(t) = M(t + 2πk),
где k ∈ Z.
Число k называется параметром.
Уравнение числовой окружности
(второе уравнение – в разделе «Синус, косинус, тангенс, котангенс»):
Помогите определить точку. № 4.17 ГДЗ Алгебра 10-11 класс Мордкович.
Какой четверти числовой окружности принадлежит точка, соответствующая числу:
а) 6; б) 2; в) 3; г) 4.
а) 6; IV; б) 2; II; в) 3; II; г) 4; III.








10. При каких значениях р уравнение -х 2 + 6х – 2 = р:
а) не имеет корней;
б) имеет один корень; ( Подробнее. )
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения ( Подробнее. )
Читали новость про 10 классника который растрелял ? как вы к этому относитесь
[spoiler title=”источники:”]
http://raal100.narod.ru/index/0-287
http://class.rambler.ru/temy-gdz/pomogite-opredelit-tochku-4-17-gdz-algebra-10-11-klass-mordkovich-34739.htm
[/spoiler]
Перейти к содержанию
Какой координатной четверти принадлежит точка?
Просмотров 30.1к. Обновлено 29 октября 2021
- Если у точки обе координаты (x и y) положительны, то она принадлежит первой четверти.
- Если координата x отрицательна, а y положительна, то точка находится во второй четверти.
- Если обе координаты отрицательны, то точка принадлежит третьей координатной четверти.
- Если x положительна, а y отрицательна, то точка находится в IV четверти.
Следует иметь в виду, что использовать в программе четыре отдельные инструкции if не совсем правильно. Хотя такое решение даст верный результат, программу нельзя будет назвать эффективной, т.к. даже если первая проверка дала «правду», дальнейшие проверки будут продолжены, хотя в них нет никакого смысла. Поэтому правильным решением будет использование вложенных конструкций if-else. Это замечание не касается языка Python, т.к. в нем есть конструкция множественного ветвления (if-elif-else).
Поскольку точка может лежать на одной из двух координатных осей или находиться в начале координат, то значит могут быть ситуации, когда точка не принадлежит ни одной из четвертей. Эти случаи обрабатываются в отдельных ветках, либо опускаются. Из этого также следует, что если первые три проверки не сработали, то нельзя делать однозначный вывод, что точка принадлежит оставшейся четверти. Поэтому в программе сообщение о том, в какой четверти находится точка может быть только в теле if, но не else.
Pascal
var x,y: integer;
begin
readln(x,y);
if (x>0) and (y>0) then
writeln('I quadrant')
else
if (x<0) and (y>0) then
writeln('II quadrant')
else
if (x<0) and (y<0) then
writeln('III quadrant')
else
if (x>0) and (y<0) then
writeln('IV quadrant');
end.
-5 3
II quadrant
Язык Си
#includemain() {
int x,y;
scanf("%d%d",&x,&y);
if (x>0 && y>0) printf("I");
else
if (x<0 && y>0) printf("II");
else
if (x<0 && y<0) printf("III");
else
if (x>0 && y<0) printf("IV");
printf("n");
}
Python
x = int(input("x="))
y = int(input("y="))
if x>0 and y>0:
print('I')
elif x<0 and y>0:
print('II')
elif x<0 and y<0:
print('III')
elif x>0 and y<0:
print('IV')
x=-3
y=-2
III
КуМир
алг координатная четверть
нач
цел x,y
ввод x,y
если x>0 и y>0 то вывод "I"
иначе
если x<0 и y>0 то вывод "II"
иначе
если x<0 и y<0 то вывод "III"
иначе
если x>0 и y<0 то вывод "IV" все
все
все
все
кон
Basic-256
input x
input y
if x>0 and y>0 then
print "I четверть"
else
if x<0 and y>0 then
print "II четверть"
else
if x<0 and y<0 then
print "III четверть"
else
if x>0 and y<0 then print "IV четверть"
endif
endif
endif
7
-2
IV четверть
Какой координатной четверти принадлежит точка?
Определить четверть координатной плоскости, которой принадлежит точка. Координаты точки ввести с клавиатуры.
- Если у точки обе координаты ( x и y ) положительны, то она принадлежит первой четверти.
- Если координата x отрицательна, а y положительна, то точка находится во второй четверти.
- Если обе координаты отрицательны, то точка принадлежит третьей координатной четверти.
- Если x положительна, а y отрицательна, то точка находится в IV четверти.
Следует иметь в виду, что использовать в программе четыре отдельные инструкции if не совсем правильно. Хотя такое решение даст верный результат, программу нельзя будет назвать эффективной, т.к. даже если первая проверка дала «правду», дальнейшие проверки будут продолжены, хотя в них нет никакого смысла. Поэтому правильным решением будет использование вложенных конструкций if-else. Это замечание не касается языка Python, т.к. в нем есть конструкция множественного ветвления (if-elif-else).
Поскольку точка может лежать на одной из двух координатных осей или находиться в начале координат, то значит могут быть ситуации, когда точка не принадлежит ни одной из четвертей. Эти случаи обрабатываются в отдельных ветках, либо опускаются. Из этого также следует, что если первые три проверки не сработали, то нельзя делать однозначный вывод, что точка принадлежит оставшейся четверти. Поэтому в программе сообщение о том, в какой четверти находится точка может быть только в теле if, но не else.
Как найти координаты точки?

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
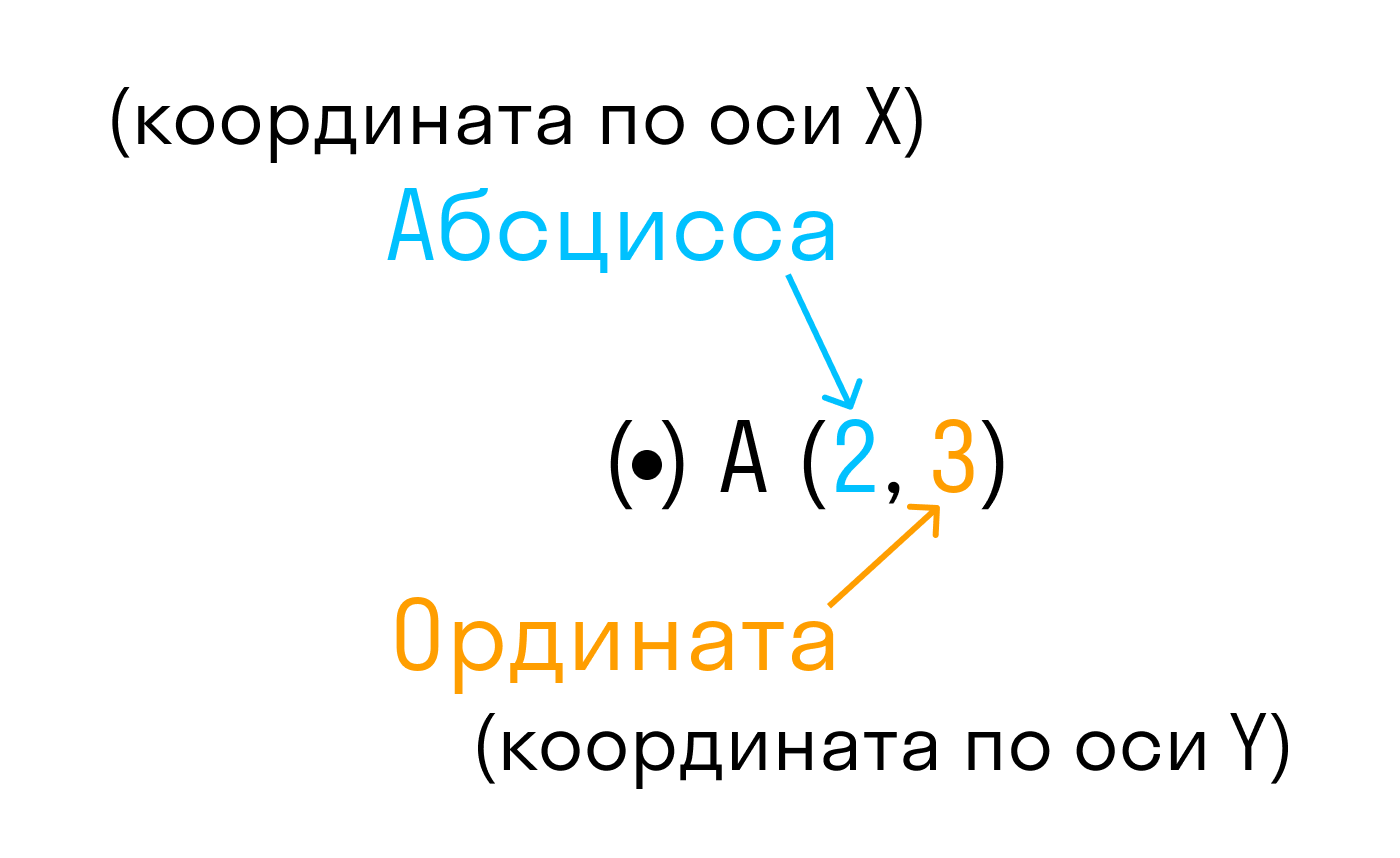
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
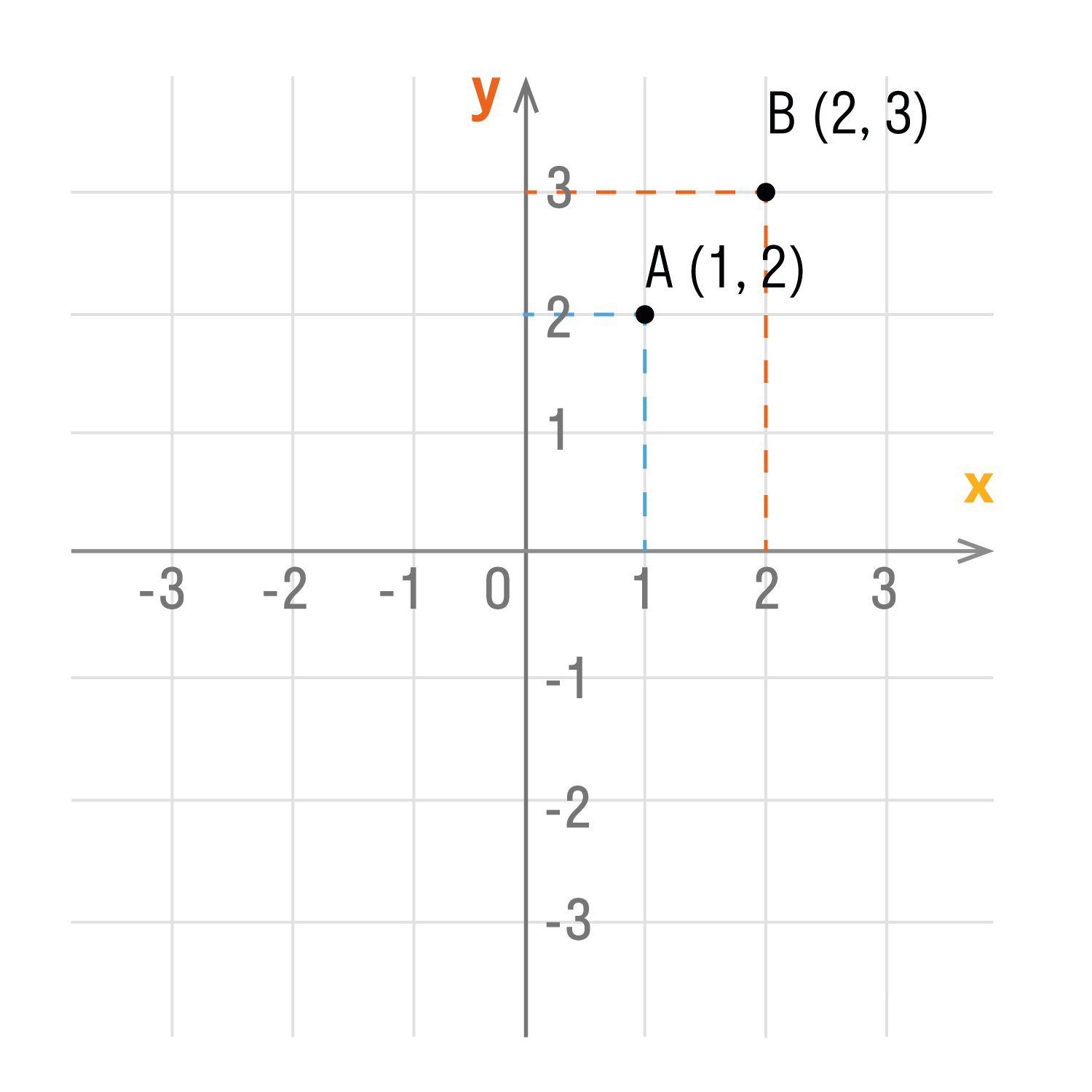
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
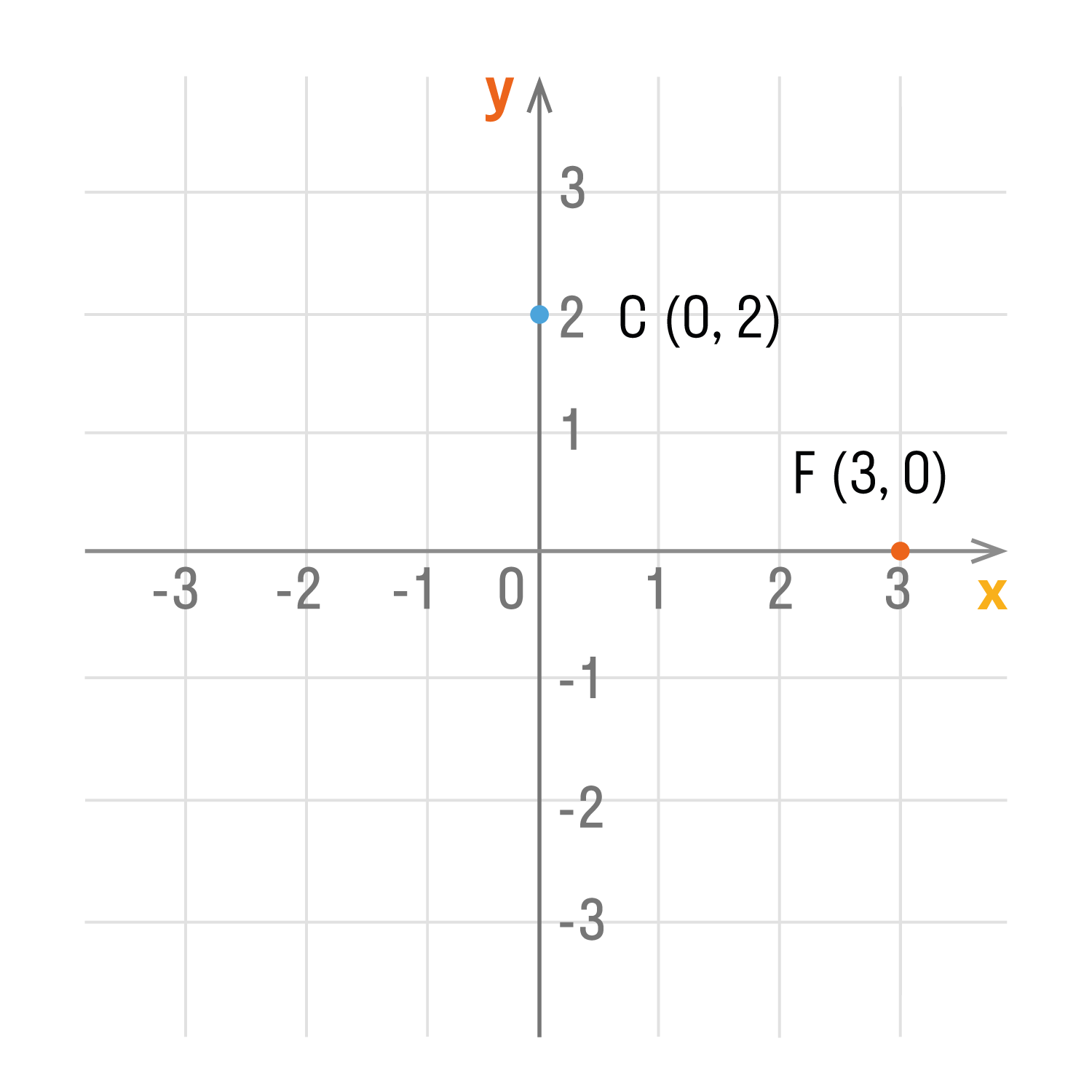
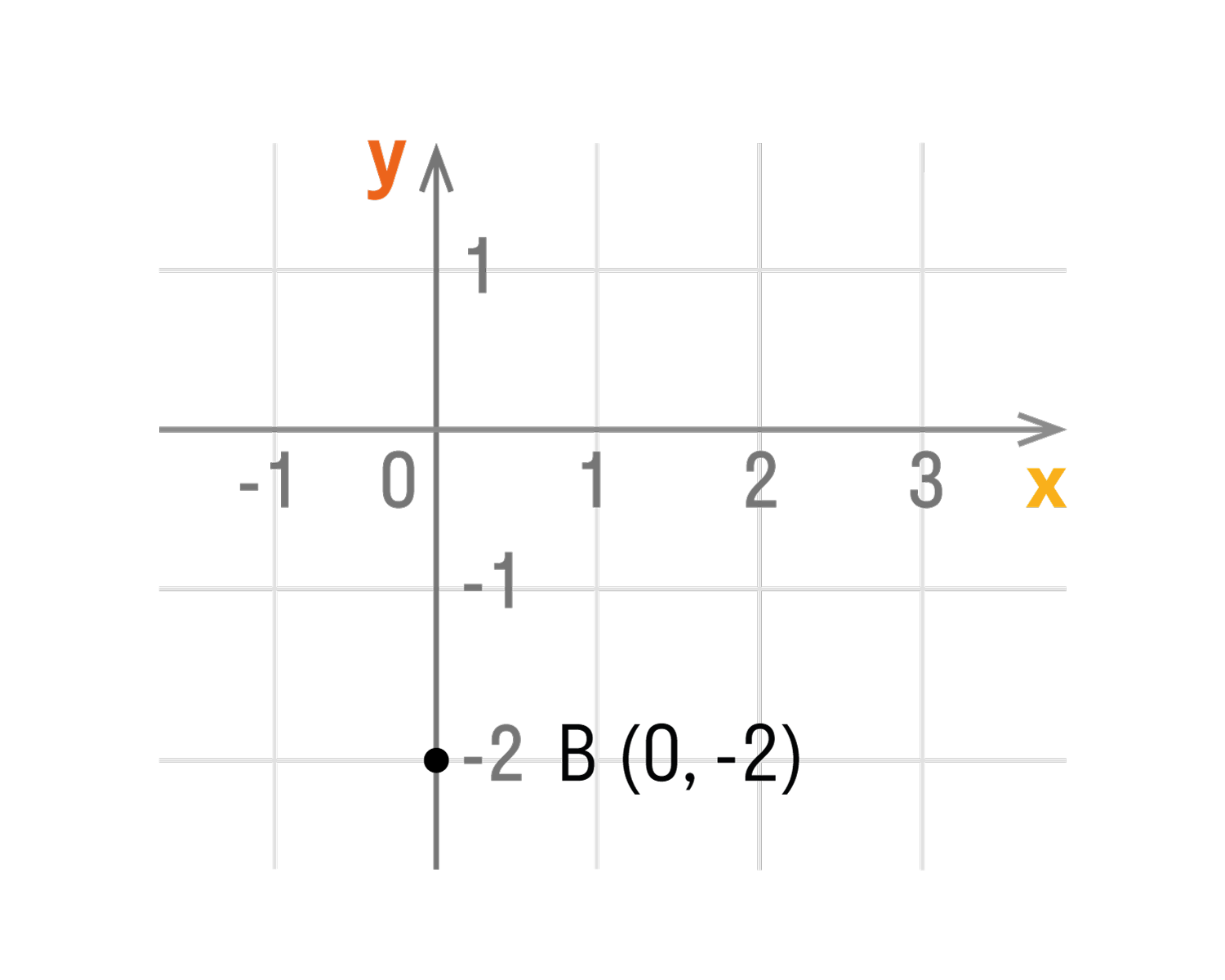
- Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0). - Начало координат — точка O. Ее координаты равны нулю: O (0,0).
- Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
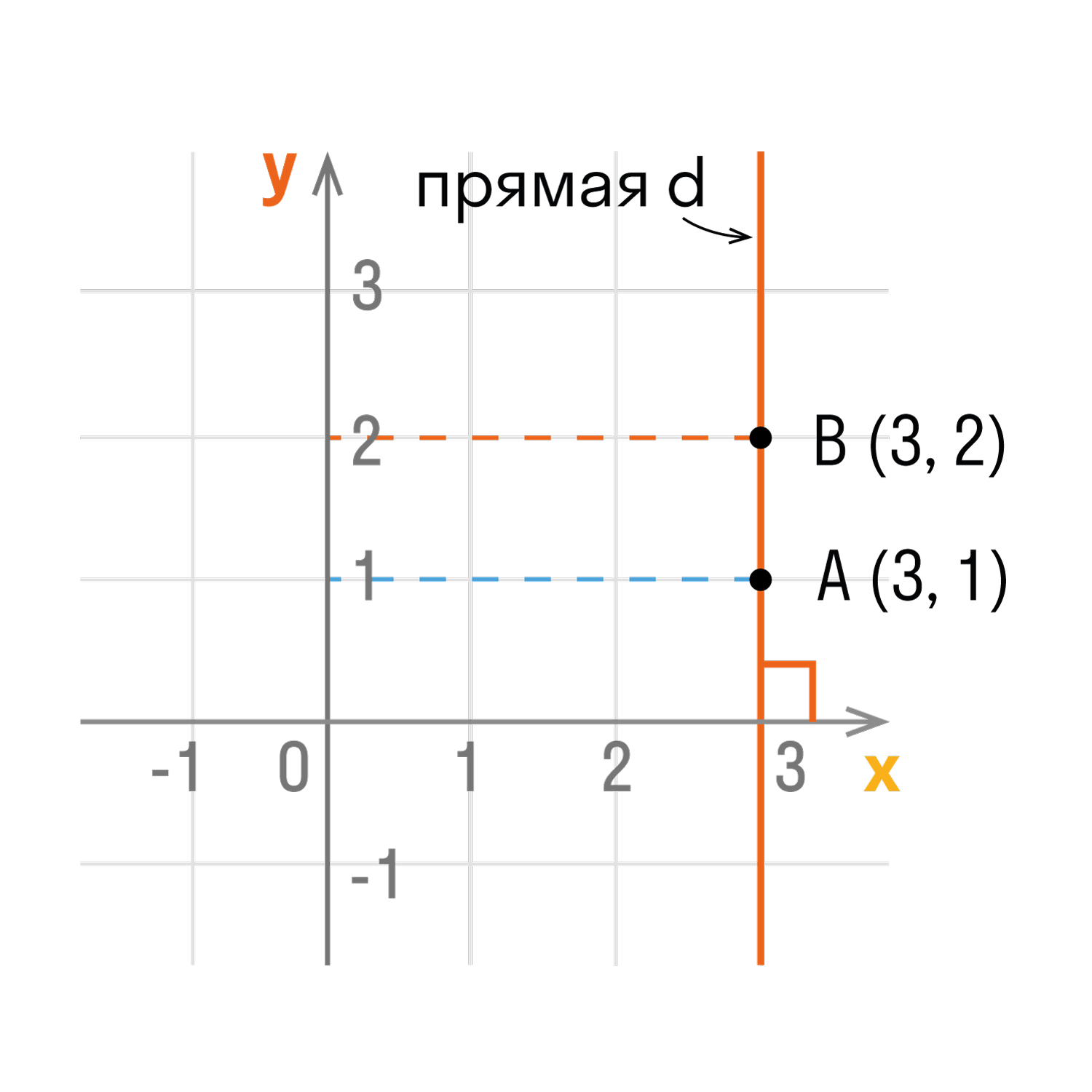
- Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
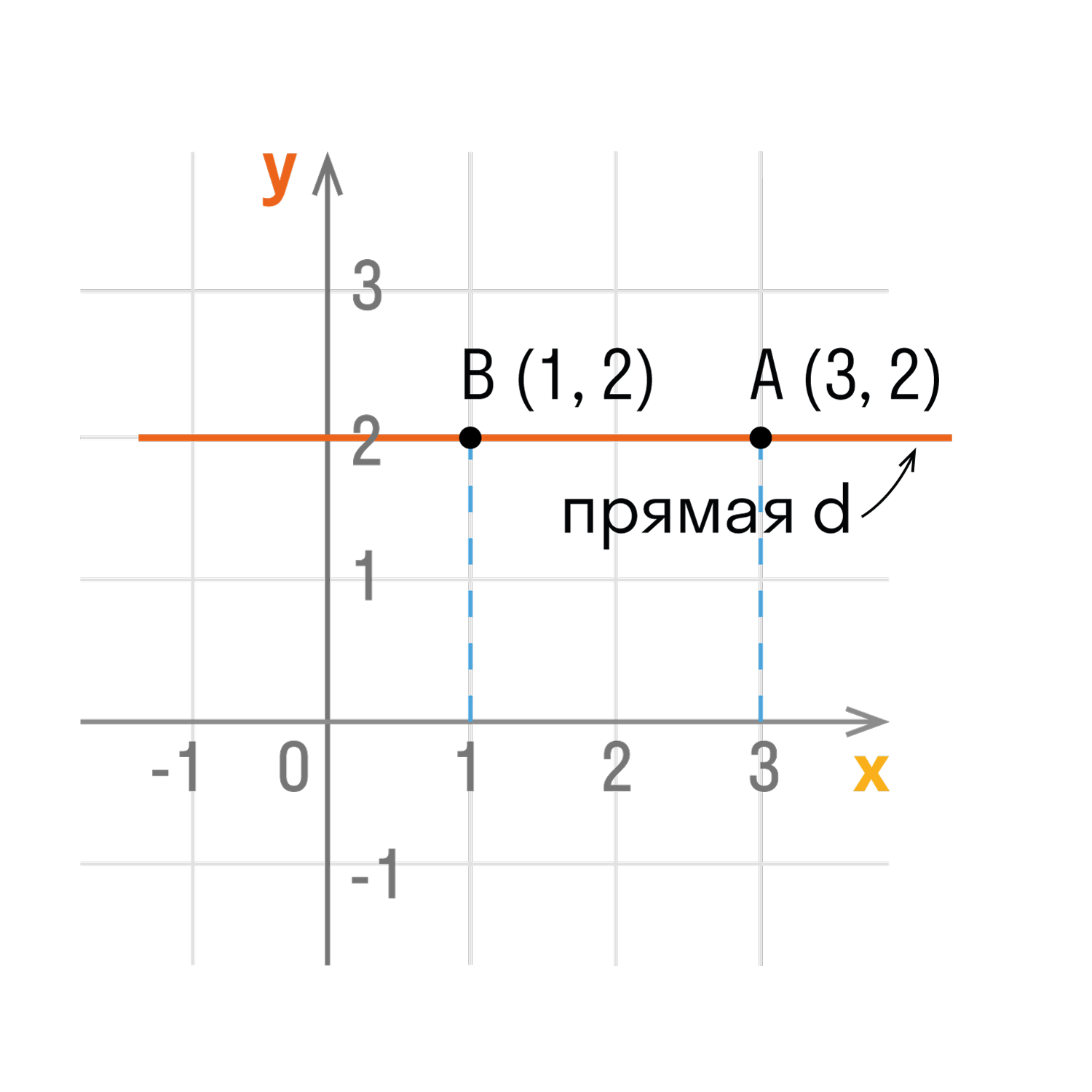
- Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).

- Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
Способ первый. Как определить положение точки D по её координатам (-4, 2):
- Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
- Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
- Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
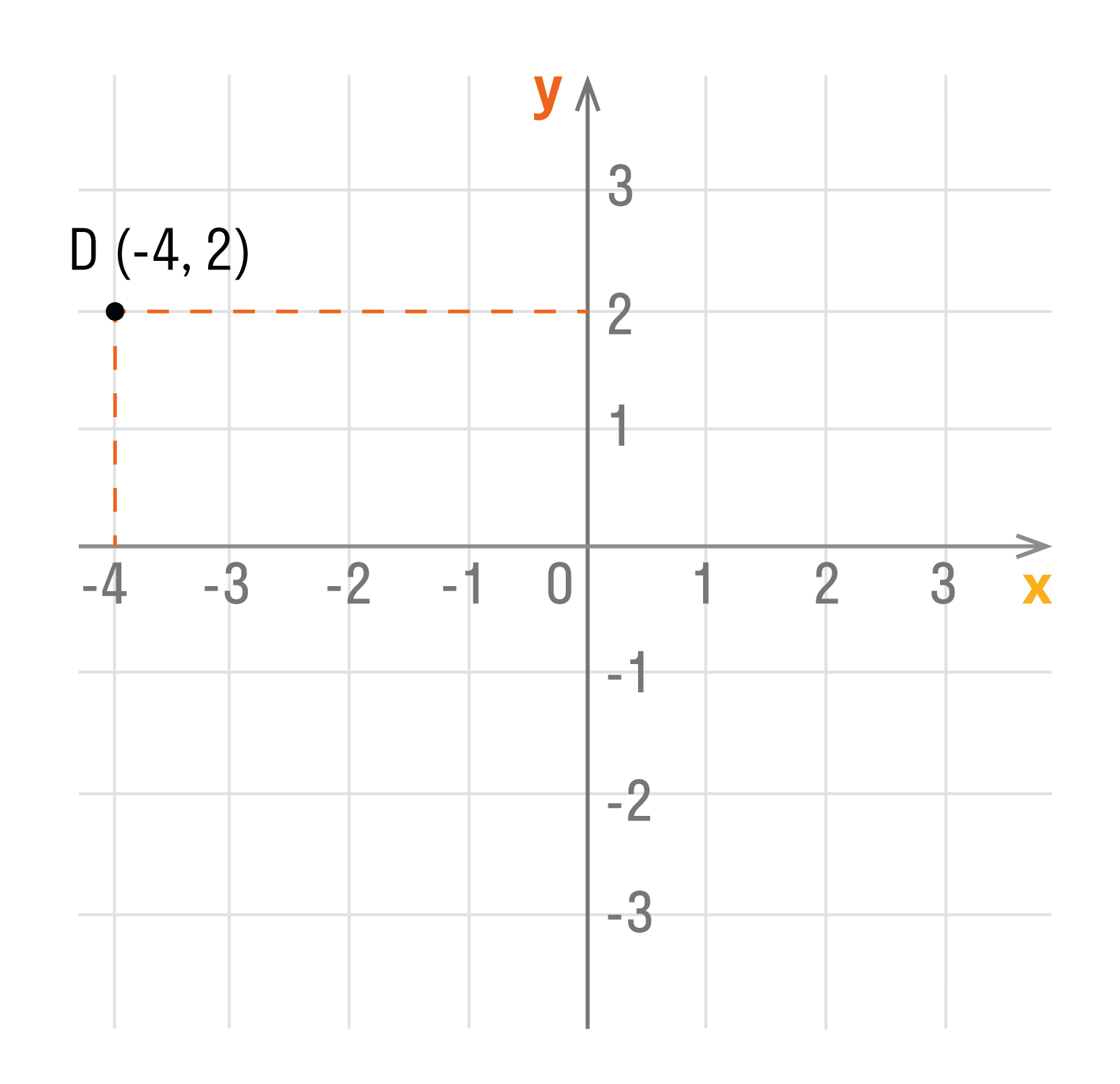
Способ второй. Как определить положение точки D (-4, 2):
- Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус. - Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
Люди добрые помогите с математикой. ПОЖАЛУЙСТА, УМОЛЯЮ.
1.Определи ординату данной точки: C(−3;−1).
Даны координаты точки. Определи, на которой координатной оси находится данная точка.
Точка P(0;18) находится на оси ординат или абсцисс.
2.Даны координаты точки. Определи, в какой координатной четверти находится данная точка.
Точка E(20;−12) находится в 1,2,3 или 4 четверти.
Определи, которая из данных точек находится в I квадранте координатной плоскости:
4.На координатной плоскости дана точка с координатами (5;5) .
Которые из данных координат являются координатами точки, симметричной данной точке относительно начальной точки системы координат?
1.Определи ординату данной точки: C(−3;−1). y=-1
Даны координаты точки. Определи, на которой координатной оси находится данная точка.
Точка P(0;18) находится на оси ординат
2.Даны координаты точки. Определи, в какой координатной четверти находится данная точка.
Точка E(20;−12) находится в 4 четверти.
Определи, которая из данных точек находится в I квадранте координатной плоскости:
4.На координатной плоскости дана точка с координатами (5;5) .
Которые из данных координат являются координатами точки, симметричной данной точке относительно начальной точки системы координат?
Объясните мне затупку, как определять на числовом круге в какой четверти находится точка
Профи
(952),
закрыт
2 года назад
Дармштадтий
Гуру
(3178)
2 года назад
в первой четверти-от 0 до 90
во второй-от 90 до 180
в третьей- от 180 до 270
и в четвёртой-от 270 до 360
Разобрались, но если цифра дана не в градусах?
Например, 19пи/6, вместо пи подставляем 180, получаем простой пример 19*180/6, производим простые арифметические действия и получаем 570. Хм, это число больше, чем те, которые есть на окружности, значит просто вычтем 360(полный оборот) и получим 210, и понимаем, что это третья четверть.
Константин ККК
Мудрец
(10421)
2 года назад
Отсчёт начинается от нуля – это луч от точки О в направлении оси икс, направо. Направление вращения – против часовой стрелки. Первая четверть – от трёх до 12 часов на циферблате. Вторая – от 12 часов до 9 часов. Третья – от 9 до 6, четвёртая – от 6 до 3 часов.
Константин КККМудрец (10421)
2 года назад
Полная окружность – это 2Пи, 3Пи/11=0,11Пи, первая четверть – это от нуля до Пи/2, то есть от нуля до 0,5Пи, точка 3Пи/11=0,11Пи, это меньше, чем 0,5Пи, поэтому эта точка (3Пи/11) лежит в первой четверти.
Координатные четверти


4.6
Средняя оценка: 4.6
Всего получено оценок: 123.
4.6
Средняя оценка: 4.6
Всего получено оценок: 123.
Человечество с самого начала своего существования нуждалось в определении своего места положения. Как узнать конкретное расположение точки с точностью до миллиметра? Только с помощью системы координат, об особенностях которой и пойдет речь сегодня.
Что такое система координат?
Система координат это комплекс мер, которые позволяют определить положение точки в пространстве или на плоскости.
В физике помимо комплекса определения положения точки используется еще и прибор для определения времени. В математике достаточно определить положение точки в один момент времени.
Существует две разновидности систем координат:
- Прямоугольная система координат. Это система координат, которая была изобретена английским математиком Декартом, потому второе название системы координат: декартова. Система представляет собой два взаимно перпендикулярных луча. Началом отсчета является точка пересечения лучей, на лучах отмечают единичные отрезки.
- Полярная система координат. Эта система куда более древняя. Она использовалась еще мореплавателями в древней Греции. В качестве координат используется еще и угол. Число откладывается на луче, от точки поднимается перпендикуляр. После из начала координат проводится прямая под заданным углом. Точка пересечения проведенной прямой и перпендикуляра и есть искомое положение точки.
Полярная система в современности используется крайне редко, она сложнее декартовой системы, а потому утратила свою популярность.
Координатные четверти
Два взаимно перпендикулярных луча образуют четыре координатные четверти. Горизонтальная ось называется осью абсцисс или осью Ох, вертикальная оси называется осью ординат или осью Оу. Начало координат рассекает оси на положительную и отрицательную часть.
Каждая из координатных четвертей имеет свой номер и обозначение в виде римской цифры. Сначала нумеруют верхние четверти, так верхняя правая четверть зовется первой, верхняя левая второй, нижняя левая третье, а нижняя правая четвертой.
Для того, чтобы узнать координаты точки в прямоугольной системе координат, следует опустить от точки перпендикуляры на оси и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты прописываются в скобочках, первой идет координата по оси Ох, второй по Оу.
Разберемся, какие координаты могут быть в осях:
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательна, а координата у положительна, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительна, а координата у отрицательна, то точка лежит в четвертой четверти.

Что мы узнали?
Мы поговорили о системах координат. Выделили две системы координат. Поговорили о координатных четвертях, а также сказали, как определить расположение точки в зависимости от ее координат.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 123.
А какая ваша оценка?
