Площадь квадрата можно найти с помощью двух основных формул:
1) Через сторону.
2) Через диагональ.
Как найти площадь квадрата, если известна его сторона.
Как известно, квадрат – это частный случай прямоугольника, у которого все стороны равны.
Площадь прямоугольника равна произведению 2 его сторон:
Sпр = a * b, a и b – стороны прямоугольника.
В случае с квадратом a = b.
Таким образом, площадь квадрата будет находиться по формуле:
Sкв = a².
Например, если сторона квадрата равна 10 см., то его площадь = 10 * 10 = 100 см².
Как найти площадь квадрата, если известна его диагональ.
Диагональ делит квадрат на 2 прямоугольных треугольника. При этом диагональ является гипотенузой, а стороны квадрата – катетами.
Нам нужно выразить квадрат стороны через теорему Пифагора. Согласно данной теореме:
a*a + b*b = c*c.
a и b – катеты, c – гипотенуза.
В нашем случае a = b, а гипотенуза – это диагональ d.
Перепишем формулу в виде:
2a² = d².
a² = d² / 2.
Таким образом, если известна диагональ квадрата, то его площадь равна половине квадрата этой диагонали.
Например, если диагональ равна 10 см., то площадь квадрата = 10 * 10 / 2 = 50 см².


{S = a ^2}
На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.
Квадрат – четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.
Содержание:
- калькулятор площади квадрата
- формула площади квадрата через сторону
- формула площади квадрата через диагональ
- формула площади квадрата через радиус вписанной окружности
- формула площади квадрата через радиус описанной окружности
- формула площади квадрата через периметр
- примеры задач
Формула площади квадрата через сторону

S = a ^2
a – сторона квадрата
Формула площади квадрата через диагональ

S=dfrac{d^2}{2}
d – диагональ квадрата
Формула площади квадрата через радиус вписанной окружности

S = 4r^2
r – радиус вписанной окружности
Формула площади квадрата через радиус описанной окружности

S = 2R^2
R – радиус описанной окружности
Формула площади квадрата через периметр

S = dfrac{P^2}{16}
P – периметр квадрата
Примеры задач на нахождение площади квадрата
Задача 1
Найдите площадь квадрата если его диагональ равна 1.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2
Ответ: 0.5 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение
Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.
S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2
Ответ: 13778 см²
Проверим ответ с помощью калькулятора .
Задача 3
Найдите площадь квадрата если его сторона равна 8 см.
Решение
Используем первую формулу.
S = a ^2 = 8 ^2 = 64 : см^2
Ответ: 64 см²
Проверим результат на калькуляторе .
Задача 4
Найдите площадь квадрата периметр которого равен 456 см.
Решение
Используем формулу для площади квадрата через периметр.
S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2
Ответ: 12996 см²
Проверка .
Задача 5
Найдите площадь квадрата со стороной 15 см.
Решение
Воспользуемся формулой площади квадрата через сторону.
S = a ^2 = 15 ^2 = 225 : см^2
Ответ: 225 см²
Проверка .
Как рассчитать площадь квадрата
На данной странице калькулятор поможет рассчитать площадь квадрата онлайн. Для расчета задайте длину стороны или диагональ.
Квадрат — это правильный четырёхугольник. У него все стороны и углы равны между собой. Квадрат есть частный вид прямоугольника, а также частный вид ромба.
Через сторону
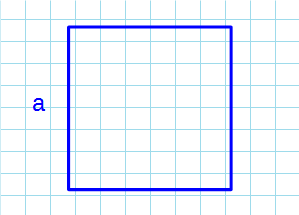
Формула для нахождения площади квадрата через сторону:
a – сторона квадрата.
Через диагональ
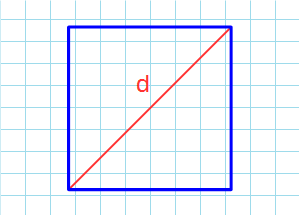
Формула для нахождения площади квадрата через диагональ:
d – диагональ квадрата.
Что такое квадрат и понятие его площади
Квадрат — простейшая плоская геометрическая фигура. Является одновременно правильным четырёхугольником и прямоугольником, все стороны которого равны.
Состоит соответственно из четырёх равных сторон, четырёх вершин ABCD и прямых углов 90°.
Под площадью квадрата подразумевается пространство, ограниченное его сторонами (та часть плоскости, что внутри). Способов расчёта существует немного, а формулы для вычисления площади весьма простые.
Как найти площадь квадрата через сторону
Данный способ и калькулятор позволит найти площадь квадрата через значение длины его сторон — введите его в соответствующее поле. В зелёном поле автоматически выведется результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через периметр
Данный способ и калькулятор позволит найти площадь квадрата через значение его периметра — введите его в соответствующее поле. В зелёном поле выведется результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через диагональ
Данный способ и калькулятор позволит найти площадь квадрата через значение длины его диагонали — введите его в соответствующее поле. В зелёном поле получите результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через радиус вписанной окружности
Данный способ и калькулятор позволит найти площадь квадрата через значение радиуса вписанной окружности — введите его в соответствующее поле. В зелёном поле выведется результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через радиус описанной окружности
Данный способ и калькулятор позволит найти площадь квадрата через значение радиуса описанной окружности — введите его в соответствующее поле. В зелёном поле выведется результат автоматически.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Ваша оценка?
[Оценок: 5 / Средняя: 4.6]
