Как найти какая часть квадрата закрашена

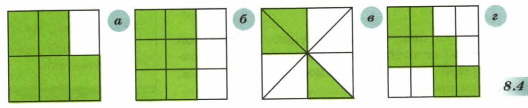
Определите а сколько равных частей разделен квадрат и какая его часть закрашена (рис. 8.4, а−г). Запишите соответствующую дробь, назовите ее числитель и знаменатель. Какая часть квадрата осталась незакрашенной?

Давайте я вам расскажу про замечательные задачки от Катрионы Ширер?

Они замечательны тем, что не громоздкие, красивые, “легкоусвояемые” как в виде условий так и на стадии анализа решения, ну если сам решить не смог. Да и очень увлекательны в процессе решения – там надо всегда пытаться увидеть красивое решение.

Я поняла, что это идеально для подготовки моих школьников к ЕГЭ. Они не навороченные, но вдумываться надо, да и без формул не обойтись, и интригуют – а это самое главное.

Короче, ловите!

Задача 1. Квадраты одинакового цвета равны. Найдите закрашенную площадь

СМОТРЕТЬ РЕШЕНИЕ

Задача 2. Точками отмечены середины сторон. Какая часть квадрата закрашена?

СМОТРЕТЬ РЕШЕНИЕ

Задача 3. Красный треугольник занимает четверть квадрата. Какую часть занимает желтый равнобедренный треугольник?

СМОТРЕТЬ РЕШЕНИЕ

Задача 4. Все треугольники правильные. Какая часть прямоугольника закрашена?

СМОТРЕТЬ РЕШЕНИЕ

Задача 5. Квадрат разделён на равные по площади части. Найдите длину синего отрезка.

СМОТРЕТЬ РЕШЕНИЕ

Задача 6. Линии соединяют вершины и середины сторон квадрата. Какая часть закрашена?

СМОТРЕТЬ РЕШЕНИЕ

Задача 7. Все точки расположены равномерно по периметру. Какая часть квадрата закрашена?

СМОТРЕТЬ РЕШЕНИЕ

Я очарована этими задачками и надеюсь, что понравится и вам!

У меня есть ещё=)

А вы знали, что если подписаться на канал, то будет меньше рекламы?
Я – нет.
А оно оказывается так 😉

Я опишу одну возможную схему решения этой задачки. Мой подход заключается в предварительной декомпозиции задачи на более простые однотипные. В этом смысле, надо сразу предупредить, “чистого” символьного решения у меня нет — лень было возиться с аккуратным выписыванием формул для площадей составляющих картинку треугольников. Причем я попробовал и вычисление площадей по координатам вершин и с использованием принципа включений-исключений, но в обоих случаях не было сразу видно, получится ли впоследствии объединить формулы в одну с более компактной записью.

Поэтому, вместо чистого решения, я решил вычислить площади в виде чисел, а не в символьно-формульном виде. Да, не шибко-то красиво, но что-то долго эта задача висит здесь без ответа и должного внимания.

Итак. Сначала, чтобы зафиксировать обозначения, я попробую ещё раз изложить своё понимание условия. На следующем рисунке изображёт единичный квадрат (т.е. квадрат со стороной 1), обозначены оси координат, начало координат (вершина 0 справа-сверху) и ключевые точки в вершинах и серединах сторон этого единичного квадрата:

Середины двух сторон, а именно точки A и F я уже соединил отрезком. (Далее, для упрощения, я не буду рисовать оси координат.) Но продолжая строить отрезки можно получить следующую последовательность фигур:

Далее я собираюсь изолировать восьмую часть (“сектор”) большого квадрата и закрасить треугольники только в нём:

Идея в том, что я могу вычислить процентное отношение суммарной площади этих маленьких треугольников к этой одной восьмой квадрата, а в силу симметрии картинки, это число и будет ответом.

Два из этих маленьких треугольников образуются ранее проведёнными отрезками так:

Обозначим площади этих треугольников как S_0 и S_1, соответственно.

(Обратите внимание, что я показал только существенные отрезки и скрыл остальные.)

Но отрезки 0C, AF и 0D дают ещё один треугольник с площадью S_2:

Промежуточные итоги:

• S_0 — площадь треугольника, образованного отрезками AF, AE, C0;
• S_1 — то же, но для отрезков AE, BF, C0;
• S_2 — то же, для AF, 0C, 0D.

Приведённый ранее рисунок с пересечением восьмой части квадрата и объединения этих треугольников, содержал, однако, лишь половину площади S_2, т.к. соответствующий треугольник разбивался на две части биссектрисой угла A0F. Поэтому для суммарной площади закрашенных треугольников во всём квадрате справедлива очевидная формула S=8(S_0+S_1+S_2/2). А 100*S даст ответ задачи в процентах.

Чтобы найти площади S_i я решил, вместо использования каких-нибудь хитрых соображений симметрии или принципа включения-исключения, искать площади этих треугольников по координатам их вершин. Конкретно, мне было удобно воспользоваться методом трапеций, натягивая прямоугольные трапеции на стороны треугольника и находя модуль суммы ориентированных площадей таких трапеций. Для нахождения же координат, мне было удобно сначала преобразовать отрезки в уравнения прямых вида ax+b=y (точки пересечения легко находятся решением систем уравнений такого вида).

Ну раз квадрат единичный и A, C, F, D делят стороны пополам, то можно сразу выписать координаты этих контрольных точек: A(1/2,0), B(1,0), C(1,1/2), D(1/2,1), E(0,1), F(0,1/2); У вершины 0 координаты, естественно (0,0). Также мне понадобится словарь из пяти прямых:

• прямая a содержит отрезок AF;
• b — AE;
• c — 0C;
• d — 0D;
• e — BF.

Пусть для прямых g и h точка их пересечения обозначается g*h, и пусть S(K, L, M) — площадь треугольника с вершинами K, L, M. Тогда,

• S_0=S(a*c, b*c, A);
• S_1=S(b*c, e*c, b*e);
• S_2=S(0, a*c, a*d).

Полезные факты:

• Если дан некоторый отрезок с концами (x_0, y_0) и (x_1, y_1), то в уравнении ax+b=y прямой, содержащей этот отрезок, коэффициент a равен a=(y_1-y_0)/(x_1-x_0); свободное слагаемое равно b=-ax_0+y_0.
• Для прямых a_0x+b_0=y и a_1x+b_1=y точка их пересечения (x,y) может быть найдена решением системы из этих двух уравнений; конкретно, x=(b_0-b_1)/(a_1-a_0), y=a_0 x + b_0; надеюсь, я ничего не напутал. 🙂

Например для прямых, содержащих отрезки AF и 0С, т.е. для прямых a и с имеем уравнения -1x+1/2=y и (1/2)x+0=y. Точка пересечения: x~0.(3), y~0.166667. (Видите? А я предупреждал, вместо того, что построить красивое символьное решения я вот так приблизительно вычислял координаты; ужас.)

Треугольник с площадью S_0 оказался натянут на вершины (1/2,0)=A, (0,333333, 0.166667), (0.4, 0.2). То же я проделал для других треугольников. Далее, методом трапеций (не вижу смысла показывать здесь промежуточные выкладки, тем более что я немного автоматизировал расчёты короткой программулькой на C) я получил:

• S_0 ~ 0.008333;
• S_1 ~ 0.008333, причем, из-за приблизительных вычислений я даже не могу сказать, действительно ли S_0=S_1 — этот впрос я оставляю читателю в качестве упражнения; 🙂
• S_2 ~ 0.041667.

По ранее выведенной формуле для суммарной площади теперь легко получается ответ 100*S=100*8(S_0+S_1+­S_2/2) ~ 29.9%.

Для проверки, я взял следующую картинку с изолированными маленькими треугольниками внутри восьмой части квадрата:

И просто посчитал процентное отношение красных пикселей к количеству пикселей в нечёрном треугольном “секторе” и получил величину ~ 47.464%.

Как видите, что-то пошло не так… 🙁 Но потом я обратил внимание, на то, что картинка имеет разрешение всего 48×48. Я сгенерировал ещё одну с разрешением 100×100 и получил результат ~39.6%. Увеличил до 277×277 и тем снизил результат до 33.55%. Ну, в общем, вы поняли — оценка площади заливки по картинке вносит существенную ошибку и требует изображения большого размера. При разрешении 986×986 результат подсчёта был уже 31.03%, но до 30% так и не дошёл. 🙁

В любом случае, писанину я выбрасывать не стал и выложил её здесь, чтобы “поднять” этот незаслуженно лишённый внимания вопрос. Может быть кто-то воспользуется идеей декомпозиции на площади S_0, S_1, S_2 и решит задачу, так сказать, аналитически. (И всё-равно есть какое-то подозрение, что за симметричностью исходной картинки кроется какая-то хитрость, могущая позволить приблизиться к решению реорганизацией структуры этого построения.)