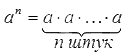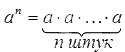Как найти какое число возвели в степень - Сайт, где вы сможете решить свои вопросы

Как узнать, в какую степень возведено число при наличии результата возведения?

Лови Бабло

Ученик

(123),
закрыт

9 лет назад

Здравствуйте, расскажите пожалуйста, как решаются задачи вроде такой:
(1 известное число) ^(неизвестное) =(2 известное)
Как узнать эту степень?
Конкретный пример: 10^(А) =316. Надо найти “А”. Знаю, что “А” должно быть 2.5, а вот как его находят?
_______________________
И ещё вопрос (возник в процессе выбора категории и подкатегории для этого топика) : математика – это естественная или гуманитарная наука? Чуем чую, что ни гуманитарная, но и к естественным вроде тоже не относится, какую же подкатегорию выбирать? =)

Дополнен 9 лет назад

вспомнил – это ТОЧНАЯ наука =) вот только категории такой тут нет =)

.

Оракул

(77956)

9 лет назад

Конкретный пример: 10^(А) =316. Надо найти “А”. Знаю, что “А” должно быть 2.5, а вот как его находят?
Неправильно! Никак не два с половиной.
Логарифм надо брать. По основанию десять. Вот так вот: lg(316).

Источник

Степень числа

Степень числа — это выражение, обозначающее краткую запись произведения одинаковых сомножителей.

Рассмотрим умножение одинаковых чисел, например:

Произведение 5 · 5 · 5 можно записать так: 5 3 (пять в третьей степени). Выражение 5 3 — это степень. Следовательно,

5 · 5 · 5 = 5 3 = 125.

Рассмотрим выражение 5 3 . В этом выражении число 5 — основание степени, а число 3 — показатель степени.

Основание степени — это повторяющийся множитель. Показатель степени — это число, указывающее количество повторений, то есть показатель степени показывает сколько одинаковых множителей содержится в произведении.

Степень числа: определения, обозначение, примеры

В рамках этого материала мы разберем, что такое степень числа. Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.

Степени с натуральными показателями: понятие квадрата и куба числа

Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a ), а в качестве показателя – натуральное (обозначим буквой n ).

Степень числа a с натуральным показателем n – это произведение n -ного числа множителей, каждый из которых равен числу а . Записывается степень так: a n , а в виде формулы ее состав можно представить следующим образом:

Например, если показатель степени равен 1 , а основание – a , то первая степень числа a записывается как a 1 . Учитывая, что a – это значение множителя, а 1 – число множителей, мы можем сделать вывод, что a 1 = a .

В целом можно сказать, что степень – это удобная форма записи большого количества равных множителей. Так, запись вида 8 · 8 · 8 · 8 можно сократить до 8 4 . Примерно так же произведение помогает нам избежать записи большого числа слагаемых ( 8 + 8 + 8 + 8 = 8 · 4 ) ; мы это уже разбирали в статье, посвященной умножению натуральных чисел.

Как же верно прочесть запись степени? Общепринятый вариант – « a в степени n ». Или можно сказать « n -ная степень a » либо « a n -ной степени». Если, скажем, в примере встретилась запись 8 12 , мы можем прочесть « 8 в 12 -й степени», « 8 в степени 12 » или « 12 -я степень 8 -ми».

Вторая и третья степени числа имеют свои устоявшиеся названия: квадрат и куб. Если мы видим вторую степень, например, числа 7 ( 7 2 ) , то мы можем сказать « 7 в квадрате» или «квадрат числа 7 ». Аналогично третья степень читается так: 5 3 – это «куб числа 5 » или « 5 в кубе». Впрочем, употреблять стандартную формулировку «во второй/третьей степени» тоже можно, это не будет ошибкой.

Разберем пример степени с натуральным показателем: для 5 7 пятерка будет основанием, а семерка – показателем.

В основании не обязательно должно стоять целое число: для степени ( 4 , 32 ) 9 основанием будет дробь 4 , 32 , а показателем – девятка. Обратите внимание на скобки: такая запись делается для всех степеней, основания которых отличаются от натуральных чисел.

Например: 1 2 3 , ( — 3 ) 12 , — 2 3 5 2 , 2 , 4 35 5 , 7 3 .

Для чего нужны скобки? Они помогают избежать ошибок в расчетах. Скажем, у нас есть две записи: ( − 2 ) 3 и − 2 3 . Первая из них означает отрицательное число минус два, возведенное в степень с натуральным показателем три; вторая – число, соответствующее противоположному значению степени 2 3 .

Иногда в книгах можно встретить немного другое написание степени числа – a ^ n (где а – основание, а n — показатель). То есть 4 ^ 9 – это то же самое, что и 4 9 . В случае, если n представляет собой многозначное число, оно берется в скобки. Например, 15 ^ ( 21 ) , ( − 3 , 1 ) ^ ( 156 ) . Но мы будем использовать обозначение a n как более употребительное.

О том, как вычислить значение степени с натуральным показателем, легко догадаться из ее определения: нужно просто перемножить a n -ное число раз. Подробнее об этом мы писали в другой статье.

Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала.

Что такое степени с целым показателем

В показателях степени могут стоять не только натуральные числа, но и вообще любые целые значения, в том числе отрицательные и нули, ведь они тоже принадлежат к множеству целых чисел.

Степень числа с целым положительным показателем можно отобразить в виде формулы: .

При этом n – любое целое положительное число.

Разберемся с понятием нулевой степени. Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так:

Равенство a m : a n = a m − n будет верно при условиях: m и n – натуральные числа, m < n , a ≠ 0 .

Последнее условие важно, поскольку позволяет избежать деления на ноль. Если значения m и n равны, то мы получим следующий результат: a n : a n = a n − n = a 0

Но при этом a n : a n = 1 — частное равных чисел a n и a . Выходит, что нулевая степень любого отличного от нуля числа равна единице.

Однако такое доказательство не подходит для нуля в нулевой степени. Для этого нам нужно другое свойство степеней – свойство произведений степеней с равными основаниями. Оно выглядит так: a m · a n = a m + n .

Если n у нас равен 0 , то a m · a 0 = a m (такое равенство также доказывает нам, что a 0 = 1 ). Но если а также равно нулю, наше равенство приобретает вид 0 m · 0 0 = 0 m , Оно будет верным при любом натуральном значении n , и неважно при этом, чему именно равно значение степени 0 0 , то есть оно может быть равно любому числу, и на верность равенства это не повлияет. Следовательно, запись вида 0 0 своего особенного смысла не имеет, и мы не будем ему его приписывать.

При желании легко проверить, что a 0 = 1 сходится со свойством степени ( a m ) n = a m · n при условии, что основание степени не равно нулю. Таким образом, степень любого отличного от нуля числа с нулевым показателем равна единице.

Разберем пример с конкретными числами: Так, 5 0 — единица, ( 33 , 3 ) 0 = 1 , — 4 5 9 0 = 1 , а значение 0 0 не определено.

После нулевой степени нам осталось разобраться, что из себя представляет степень отрицательная. Для этого нам понадобится то же свойство произведения степеней с равными основаниями, которое мы уже использовали выше: a m · a n = a m + n .

Введем условие: m = − n , тогда a не должно быть равно нулю. Из этого следует, что a − n · a n = a − n + n = a 0 = 1 . Выходит, что a n и a − n у нас являются взаимно обратными числами.

В итоге a в целой отрицательной степени есть не что иное, как дробь 1 a n .

Такая формулировка подтверждает, что для степени с целым отрицательным показателем действительны все те же свойства, которыми обладает степень с натуральным показателем (при условии, что основание не равно нулю).

Степень a с целым отрицательным показателем n можно представить в виде дроби 1 a n . Таким образом, a — n = 1 a n при условии a ≠ 0 и n – любое натуральное число.

Проиллюстрируем нашу мысль конкретными примерами:

3 — 2 = 1 3 2 , ( — 4 . 2 ) — 5 = 1 ( — 4 . 2 ) 5 , 11 37 — 1 = 1 11 37 1

В последней части параграфа попробуем изобразить все сказанное наглядно в одной формуле:

Степень числа a с натуральным показателем z – это: a z = a z , e с л и z — ц е л о е п о л о ж и т е л ь н о е ч и с л о 1 , z = 0 и a ≠ 0 , ( п р и z = 0 и a = 0 п о л у ч а е т с я 0 0 , з н а ч е н и я в ы р а ж е н и я 0 0 н е о п р е д е л я е т с я ) 1 a z , е с л и z — ц е л о е о т р и ц а т е л ь н о е ч и с л о и a ≠ 0 ( е с л и z — ц е л о е о т р и ц а т е л ь н о е ч и с л о и a = 0 п о л у ч а е т с я 0 z , е г о з н а ч е н и е н е о п р е д е л я е т с я )

Что такое степени с рациональным показателем

Мы разобрали случаи, когда в показателе степени стоит целое число. Однако возвести число в степень можно и тогда, когда в ее показателе стоит дробное число. Это называется степенью с рациональным показателем. В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.

Что такое рациональные числа? В их множество входят как целые, так и дробные числа, при этом дробные числа можно представить в виде обыкновенных дробей (как положительных, так и отрицательных). Сформулируем определение степени числа a с дробным показателем m / n , где n – натуральное число, а m – целое.

У нас есть некоторая степень с дробным показателем a m n . Для того, чтобы свойство степени в степени выполнялось, равенство a m n n = a m n · n = a m должно быть верным.

Учитывая определение корня n -ной степени и что a m n n = a m , мы можем принять условие a m n = a m n , если a m n имеет смысл при данных значениях m , n и a .

Приведенные выше свойства степени с целым показателем будут верными при условии a m n = a m n .

Основной вывод из наших рассуждений таков: степень некоторого числа a с дробным показателем m / n – это корень n -ой степени из числа a в степени m . Это справедливо в том случае, если при данных значениях m , n и a выражение a m n сохраняет смысл.

Далее нам необходимо определить, какие именно ограничения на значения переменных накладывает такое условие. Есть два подхода к решению этой проблемы.

1. Мы можем ограничить значение основания степени: возьмем a , которое при положительных значениях m будет больше или равно 0 , а для отрицательных – строго меньше (поскольку при m ≤ 0 мы получаем 0 m , а такая степень не определена). В таком случае определение степени с дробным показателем будет выглядеть следующим образом:

Степень с дробным показателем m / n для некоторого положительного числа a есть корень n -ной степени из a, возведенного в степень m . В виде формулы это можно изобразить так:

Для степени с нулевым основанием это положение также подходит, но только в том случае, если ее показатель – положительное число.

Степень с нулевым основанием и дробным положительным показателем m / n можно выразить как

0 m n = 0 m n = 0 при условии целого положительного m и натурального n .

При отрицательном отношении m n < 0 степень не определяется, т.е. такая запись смысла не имеет.

Отметим один момент. Поскольку мы ввели условие, что a больше или равно нулю, то у нас оказались отброшены некоторые случаи.

Выражение a m n иногда все же имеет смысл при некоторых отрицательных значениях a и некоторых m . Так, верны записи ( — 5 ) 2 3 , ( — 1 , 2 ) 5 7 , — 1 2 — 8 4 , в которых основание отрицательно.

2. Второй подход – это рассмотреть отдельно корень a m n с четными и нечетными показателями. Тогда нам потребуется ввести еще одно условие: степень a , в показателе которой стоит сократимая обыкновенная дробь, считается степенью a , в показателе которой стоит соответствующая ей несократимая дробь. Позже мы объясним, для чего нам это условие и почему оно так важно. Таким образом, если у нас есть запись a m · k n · k , то мы можем свести ее к a m n и упростить расчеты.

Если n – нечетное число, а значение m – положительно, a – любое неотрицательное число, то a m n имеет смысл. Условие неотрицательного a нужно, поскольку корень четной степени из отрицательного числа не извлекают. Если же значение m положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа.

Объединим все данные выше определения в одной записи:

Здесь m/n означает несократимую дробь, m – любое целое число, а n – любое натуральное число.

Для любой обыкновенной сократимой дроби m · k n · k степень можно заменить на a m n .

Степень числа a с несократимым дробным показателем m / n – можно выразить в виде a m n в следующих случаях: — для любых действительных a , целых положительных значений m и нечетных натуральных значений n . Пример: 2 5 3 = 2 5 3 , ( — 5 , 1 ) 2 7 = ( — 5 , 1 ) — 2 7 , 0 5 19 = 0 5 19 .

— для любых отличных от нуля действительных a , целых отрицательных значений m и нечетных значений n , например, 2 — 5 3 = 2 — 5 3 , ( — 5 , 1 ) — 2 7 = ( — 5 , 1 ) — 2 7

— для любых неотрицательных a , целых положительных значений m и четных n , например, 2 1 4 = 2 1 4 , ( 5 , 1 ) 3 2 = ( 5 , 1 ) 3 , 0 7 18 = 0 7 18 .

— для любых положительных a , целых отрицательных m и четных n , например, 2 — 1 4 = 2 — 1 4 , ( 5 , 1 ) — 3 2 = ( 5 , 1 ) — 3 , .

В случае других значений степень с дробным показателем не определяется. Примеры таких степеней: — 2 11 6 , — 2 1 2 3 2 , 0 — 2 5 .

Теперь объясним важность условия, о котором говорили выше: зачем заменять дробь с сократимым показателем на дробь с несократимым. Если бы мы этого не сделали бы, то получились бы такие ситуации, скажем, 6 / 10 = 3 / 5 . Тогда должно быть верным ( — 1 ) 6 10 = — 1 3 5 , но — 1 6 10 = ( — 1 ) 6 10 = 1 10 = 1 10 10 = 1 , а ( — 1 ) 3 5 = ( — 1 ) 3 5 = — 1 5 = — 1 5 5 = — 1 .

Определение степени с дробным показателем, которое мы привели первым, удобнее применять на практике, чем второе, поэтому мы будем далее пользоваться именно им.

Таким образом, степень положительного числа a с дробным показателем m / n определяется как 0 m n = 0 m n = 0 . В случае отрицательных a запись a m n не имеет смысла. Степень нуля для положительных дробных показателей m / n определяется как 0 m n = 0 m n = 0 , для отрицательных дробных показателей мы степень нуля не определяем.

В выводах отметим, что можно записать любой дробный показатель как в виде смешанного числа, так и в виде десятичной дроби: 5 1 , 7 , 3 2 5 — 2 3 7 .

При вычислении же лучше заменять показатель степени обыкновенной дробью и далее пользоваться определением степени с дробным показателем. Для примеров выше у нас получится:

5 1 , 7 = 5 17 10 = 5 7 10 3 2 5 — 2 3 7 = 3 2 5 — 17 7 = 3 2 5 — 17 7

Что такое степени с иррациональным и действительным показателем

Что такое действительные числа? В их множество входят как рациональные, так и иррациональные числа. Поэтому для того, чтобы понять, что такое степень с действительным показателем, нам надо определить степени с рациональными и иррациональными показателями. Про рациональные мы уже упоминали выше. Разберемся с иррациональными показателями пошагово.

Допустим, что у нас есть иррациональное число a и последовательность его десятичных приближений a 0 , a 1 , a 2 , . . . . Например, возьмем значение a = 1 , 67175331 . . . , тогда

a 0 = 1 , 6 , a 1 = 1 , 67 , a 2 = 1 , 671 , . . . , a 0 = 1 , 67 , a 1 = 1 , 6717 , a 2 = 1 , 671753 , . . .

и так далее (при этом сами приближения являются рациональными числами).

Последовательности приближений мы можем поставить в соответствие последовательность степеней a a 0 , a a 1 , a a 2 , . . . . Если вспомнить, что мы рассказывали ранее о возведении чисел в рациональную степень, то мы можем сами подсчитать значения этих степеней.

Возьмем для примера a = 3 , тогда a a 0 = 3 1 , 67 , a a 1 = 3 1 , 6717 , a a 2 = 3 1 , 671753 , . . . и т.д.

Последовательность степеней можно свести к числу, которое и будет значением степени c основанием a и иррациональным показателем a . В итоге : степень с иррациональным показателем вида 3 1 , 67175331 . . можно свести к числу 6 , 27 .

Степень положительного числа a с иррациональным показателем a записывается как a a . Его значение – это предел последовательности a a 0 , a a 1 , a a 2 , . . . , где a 0 , a 1 , a 2 , . . . являются последовательными десятичными приближениями иррационального числа a . Степень с нулевым основанием можно определить и для положительных иррациональных показателей, при этом 0 a = 0 Так, 0 6 = 0 , 0 21 3 3 = 0 . А для отрицательных этого сделать нельзя, поскольку, например, значение 0 — 5 , 0 — 2 π не определено. Единица, возведенная в любую иррациональную степень, остается единицей, например, и 1 2 , 1 5 в 2 и 1 — 5 будут равны 1 .

Как узнать степень числа?

Самое разумное разложить число на простые множители, тогда можно найти и основание и показатель степени.
Если известно основание, то показатель можно найти логарифмированием, например,
2^x=8
Чтобы найти x нужно прологарифмировать обе части по основанию 2
x = log по основанию 2 от 8 = ln 8 / ln 2 (так можно на калькуляторе посчитать) = 3
Если известен показатель, то основание находится извлечением корня, например,
x^3=8
извлекаем корень кубический из обоих частей
x=корень кубический из 8 = 2

Если же неизвестно ни то ни другое разложи число на простые множители, это делается последовательным делением числа на простые множители
614656 / 2 = 307328
307328 / 2 = 153664
153664 / 2 = 76832
76832 / 2 = 38416
38416 / 2 = 19208
19208 / 2 = 9604
9604 / 2 = 4802
4802 / 2 = 2401
2401 не делится на 2, на 3, на 5 (последовательно перебираем простые числа)
2407 / 7 = 343
343 / 7 = 49
49 / 7 = 7
7 / 7 = 1
Итого мы делили на 2 восемь раз и на 7 четыре раза, следовательно
614656 = 2^8 * 7^4
Если мы хотим найти представление в виде a^b с натуральными a и b и b должно быть максимальным, то в качестве b нужно брать НОД степеней полученных в разложении на простые множители, то есть в данном случае b=НОД (8,4)=4
основанием степени a будет служить 2^(8/b) * 7^(4/b) = 2^2 * 7^1 = 4*7=28

Аналитического способа не существует. То бишь формулы для нахождения степени и числа, которое возводят в эту степень — нет.

Так для общего развития скажу, что даже нахождение достаточно больших простых чисел — занятие затруднительное и очень хорошо оплачиваемое. А для решения вашей задачи (как минимум) нужно знать что это число уже не простое. :)))

Здравствуйте, уважаемый Максим Сальников !

Общей методики для задач такого типа, как мне известно, нет .

Самый простой способ — разложить данное число на простые множители .

В приведённом Вами примере это будет выглядеть так :

614656 = ( 2 x 2 x2 x 2 x 2 x 2 x 2 x 2 ) x ( 7 x 7 x 7 x 7 )

Из 7 x 7 x 7 x 7 следует, что » вероятная степень » равна 4 : 7 x 7 x 7 x 7 = 7 ^ 4 ( 1 )

Тогда из 2 x 2 x2 x 2 x 2 x 2 x 2 x 2 образуем ( 2 x 2 ) x ( 2 x 2 ) x( 2 x 2 ) x ( 2 x 2 ) = 4 ^ 4 ( 2 )

Согласно ( 1 ) и ( 2 ) можем записать : 614656 = ( 4 ^ 4 ) x ( 7 ^ 4 ) = ( 4 x 7 ) ^ 4 = 28 ^ 4 !

Источник

До сих пор примеры реальных задач, для решения которых может понадобиться математика, были если не совсем уж фантастическими, то, по крайней мере, не затрагивали тех приятных тем, от которых в нижней части живота распространяется приятная судорога. Мы, конечно, имеем в виду деньги. И не просто деньги сами по себе, а деньги всё возрастающие, увеличивающиеся, позволяющие сформировать стабильный пассивный доход и купить пожизненный абонемент в местную сеть стейк-хаусов.

Как такого дохода достичь? Если отвлечься от всяких «бинарных опционов», «уникальных рекламных предложений», «командного сетевого бизнеса без начальных вложений» и тому подобного, проверенным веками методом оказывается размещение денег в банке под определённый процент. Разве ещё не говорили о процентах? Вроде как нет… Ну ничего, сейчас исправимся.

Ранее мы подметили, что любое рациональное число со знаменателем, делящимся на , может быть представлено в виде десятичной дроби. Например, $frac{2}{10}=0.2, frac{3}{100}=0.03, frac{5}{1000}=0.005$ . «Процент» это просто название для одной сотой. Иначе говоря, у нас есть изначальное число, которое мы делим на равных частей, каждая из которых и равна одному проценту. Записывается это как , и так далее.

Как вообще искать процент от числа? Самый простой способ это разделить на и умножить на то количество процентов, которое нам нужно найти. К примеру, найдём от . Делим на , получаем , которые затем умножаем на , имея в итоге . Неплохо, но мы были вынуждены выполнить целых два действия вместо одного. А как сделать это одним? Для начала запишем всё, что проделали: $frac{251}{100} cdot 23$ . Как мы знаем, в случае умножения у нас свободный порядок операций, поэтому вполне можно написать $frac{251}{100} cdot 23 = 251 cdot frac{23}{100}$ . Но ведь двадцать три сотых это есть , следовательно, для нахождения процента нам нужно лишь умножить их на исходное число и дело в шляпе.

А если нам нужно найти, скажем, от числа, имея в виду, что это сумма самого числа и его пятипроцентной доли? Логика ровно такая же, если один процент это , то это уже , на которые мы исходное число и умножаем. Понятно? Не совсем?

Начнём с каких-то более приземлённых ситуаций. У вас есть рублей и вы мечтаете ровно о том, о чём все амбициозные предприниматели в начале карьерного пути — закупиться на полгода вперёд дошираком (стейки будут уже потом). Одна проблема — для этого вам необходимо рублей. Как человек дела, вы направляете свой капитал на самые социально полезные цели — начинаете выдавать микро-кредиты под ежемесячно, при этом проценты считаются от уже полученной суммы. То есть, спустя один месяц вам должны отдать , а по итогам следующего месяца новый процент будет исчисляться как раз от , а не начальных десяти тысяч. Оно и правильно, пусть банки подавятся своими жалкими в год.

Такой расклад вас устраивает, но для пущей убедительности хорошо бы иметь конкретный бизнес-план. Как никак, вам предстоит заработать целых рублей! Таким образом, вам нужно узнать, когда ваша десятка себя удвоит, иначе говоря, когда начисление процентов доведёт её до .

Давайте думать, как это вычислить. После одного месяца, как было замечено, у вас станет . Сколько будет через два месяца? А будет . Порядок действий при умножении не важен, поэтому мы имеем . Таким образом, через месяцев у вас окажется . Приятные бухгалтерские хлопоты… Но как найти само значение ? Неужели надо заниматься скучным подбором вариантов?

Выпишем итоговое задание:

Обе стороны равенства мы можем разделить на , получив , что и станет предметом нашего пристального внимания. Вдумайтесь — нам нужно узнать, в какую степень возвести одно число, чтобы получить другое. Необычно, согласитесь. До этого мы только вычисляли сами числа, а степени нам были даны, а тут, совершенно внезапно, от нас требуется нечто обратное.

Что поделать? Обратиться к очередному неизведанному понятию математики — логарифму. Что такое логарифм? Это… степень. Правда, не совсем в таком виде, как корни. Разъясним на примере.

Как-как? «Логарифм»? Это про деньги? Нет? А про что? Про рост денег? Про рост выражения где одна переменная связана с другой при помощи степени? Помедленнее давайте, я записываю, в таких вопросах очень внимательным надо быть, всё по папочкам раскладывать.

Имеется запись вида , которая читается как «логарифм по основанию . Означает это ту степень, в которую надо возвести , чтобы получить . Скажем, и так далее. Запись не сильно интуитивная, но можно прибегнуть к небольшой хитрости — посмотрите на то, что располагается под , то есть на основание. Мы привыкли, что степени пишутся сверху, поэтому можно взять за привычку считать, что в степень возводится именно то, что снизу. Так вы не запутаетесь, что на что умножать и где тут вообще основание, потому что основание всегда снизу. Почти как фундамент.

Из нашего определения логарифма следует, что $2^{log_2 8}=8$ . Почему? Смотрите, сам логарифм даёт нам степень, в которую нужно возвести двойку, чтобы получить восьмёрку, эта степень равна тройке. Двойка в этой степени и даёт нам искомую восьмёрку. В общем виде это выглядит так:

$[a^{log_a x}=x]$

Опять же, в указанном свойстве нет ровным счётом ничего необычного. Это даже не свойство само по себе, а просто прямое следствие из самого определения логарифма в том виде, в котором мы его записали. А вот дальше начинаются свойства, которые следует доказать. Пожалуй, это первый раз в нашем курсе, когда мы не будем заходить издалека, показывать, как эти свойства вытекают из бытовых рассуждений. Вообще обойдёмся без предварительных ласк и, к сожалению, геометрических иллюстраций — их сделать в принципе возможно, но по своему виду они будут даже менее наделены смыслом, чем замысловатые формулы.

Только не подумайте чего дурного, все доказываемые свойства всё так же вытекают из операций со степенями, увидеть это можно всего за несколько шагов, просто это не такое тавтологическое следствие, как в случае с корнями. Подсчёт логарифма это как-никак другая, противоположная возведению в степень операция. Ну и да, доказывать мы сейчас будем только несколько основных свойств, которые имеют множество более частных следствий, но это всё будет уже в практическом приложении.

Итак, поехали. Первое свойство утверждает, что:

Несмотря на наши угрозы, для его доказательства почти не нужны формулы, хватит и простых слов. Итак, смотрите, это по определению степень, в которую нужно возвести , чтобы получить некоторое . Для простоты можно назвать эту степень , и тогда . Однако нам нужно узнать, как возведением в степень получить не просто , а , т.е. , которое раз умножили само на себя. В который раз нас выручает глубокое понимание того, как ведут себя степени при умножении. Ведь если мы договорились, что и, следовательно, , то чему тогда равен ? Он равен , так как это просто ещё один способ записать этот же самый . При возведении одной степени в другую, они перемножаются, получаем $(a^m)^n=a^{mn}=x^n$ .

Так… и что? А то, что это и есть значение нашего логарифма! Следите за пальцами:

$[x^n=a^{mn}]$

Теперь пришло время для обратной замены, т.е. вместо мы опять записываем наш логарифм:

$[x^n=a^{n cdot log_a x}]$

В этом равенстве во всей красе представлен ответ на наш исходный вопрос — «в какую степень нужно возвести , чтобы получить ? Эта самая степень указана у нас во всём гнетущем безобразии, нужно возвести в степень .

С практической точки зрения это может прийтись кстати, если нет желания заучивать по или значений степеней для самых популярных в этом контексте чисел. Допустим, как узнать ? Если что, , то есть, вы совершенно точно не хотите это считать вручную. Какое счастье, что ! Ведь нам всего лишь следует воспользоваться доказанным свойством:

Ясное дело, что в этом частном случае нам хватило бы и знания об умножении степеней, однако поверьте, логарифмы в течение веков использовались для дичайшего ускорения монотонных операций по умножению и делению больших чисел не просто потому, что никому не было известно про степени. Как вообще эта мешанина из букв и цифр кому-то может помочь? Для ответа на этот вопрос нам предстоит доказать ещё одно свойство:

Представив на секунду, что мы оказались на кушетке в кабинете психоаналитика, будем проговаривать все проблемы, которые перед нами встали, да причём в самом явном виде. О тяжёлых отношениях с отцом и играх в доктора в детском садике упоминать не будем, опишем самую актуальную проблему. Итак, от нас требуется узнать, как ещё можно выразить , то есть как узнать, в какую степень нужно возвести , чтобы получить , используя тот факт, что число само является произведением каких-то и .

Опять будем вводить условности. Предположим, что и , т.е. что и . То есть, мы знаем, как из получить как , так и . Чему в таком случае равно произведение ? Судя по всему, $xy=a^m cdot a^n=a^{m+n}$ . Выразим это ещё раз, но теперь вместо и вернём логарифмы:

$[xy=a^{m+n}=a^{log_a x+log_a y}]$

В какую степень надо возвести , чтобы получить число ? Основание нужно возвести в степень , как и утверждается в основном свойстве.

— Братишка… Ты это, погоди… А как это считать помогает?

Помогает, поверьте, причём значительно. Видите-ли, если вы живёте в 17-м веке, то у вас, наверное, рабов, как у греков, уже нет, но свободного времени всё равно хватает. Да и не сказать, что за окном движуха круглосуточная. Как бороться с давящей скукой серых будней? Можно взять какое-то число за основание и пересчитать все значения для тысяч его степеней. На всякий случай повторим, что в 17-м веке у творческих людей представления об увлекательном досуге были весьма своеобразными.

И если вы думаете, что подсчёты состояли в вычислении $10^2, 10^3, 10^{23}$ и т.п., то вы сильно заблуждаетесь. Тотальному вычислению подлежали значения $10^{0.32453}, 10^{2.28594}$ и тому подобное. Адски трудоёмко? — Да. Кошмарно долго? — Да. Вместо этого лучше пересмотреть все сезоны Breaking Bad? — Да. Однако как только эта работа оказывается завершена, последующие арифметические операции можно выполнять с невиданной до тех пор скоростью.

Скажем, вам нужно умножить на , а калькулятора с собой рядом нет. Кстати говоря, калькуляторов рядом не было ещё каких-то 40 лет назад, поэтому в любой уважающей себя организации можно было найти толстенные книги, в которых указаны значения великого множества логарифмов по любым основаниям (чаще всего это было и ).

Имея под рукой пару таких томиков, любое умножение на раз-два превращалось в простейшее сложение. Достаточно было найти $log_{10} 2345=3.370142$ и $log_{10} 1488=3.172602$ . Далее эти значения складывались, получалось что-то вроде . Наконец, пару минут листания справочников, и вот находится заветное число, для которого $log_{10} x =6.542744$ . Числом этим оказывается .

Зафиксируем всю цепочку действий:

$[log_{10} x = log_{10} (2345 cdot 1488) = log_{10} 2345 + log_{10} 1488]$

Узнаёте наше свежедоказанное свойство в боевых условиях??

Дотошный читатель сейчас наверняка скажет «секунду… это почему такое получается после умножения? мой калькулятор утверждает, что , а он никогда не ошибается!».

Это будет верно. Дело в том, что логарифмы дают лишь приблизительное значение выражений, чем точнее вам нужен результат, тем больше знаков после запятой в степени логарифма будьте добры указать. Другое дело, что для практических целей вам хватит и первых знаков, если не меньше.

Очень смешно, когда вещи и явления превращаются в свою противоположность. Родоначальник логарифмов в их современном понимании Джон Непер писал: «Я всегда старался, насколько позволяли мои силы и способности, освободить людей от трудности и скуки вычислений, докучливость которых обыкновенно отпугивает очень многих от изучения математики.». Откуда ему было знать, что сегодня выражения с логарифмами будут наводить ужас на тысячи людей именно своей непонятностью и проблемами с точным подсчётом. Хорошо, что Джон до этих дней не дожил.

Что-то мы увлеклись сторонними рассуждениями, а у нас ведь ещё целое свойство осталось:

$[log_a frac{x}{y}=log_a x - log_a y]$

Посмотрим, сработает ли с ним уже взятая на вооружение логика. Итак, нам нужно найти степень, в которую мы возведём , чтобы в итоге получить $frac{x}{y}$ . Дробное число тут как-то не очень к месту, поэтому давайте применим новейшее правило и представим $log_a frac{x}{y}$ как $log_a (x cdot y^{-1})$ . Тогда искомая степень найдётся по формуле $log_a (x cdot y^{-1}) = log_a x + log_a y^{-1}$ .

Обратим внимание, что ещё на пару абзацев выше мы доказали, что при нахождении логарифма от какого-то элемента в степени, саму степень можно вынести и представить как ещё один множитель. Но наша-то степень это , поэтому получается, что $log_a x+log_a y^{-1}=log_a x + (-1 cdot log_a y) = log_a x - log_a y$ .

Теперь можно триумфально завершить достаточно скучное сегодняшнее путешествие, расчленив ещё одну формулу, известную как «формулу замены основания»:

$[log_a x =frac{log_b x}{log_b a}]$

Как вы уже, наверное, догадываетесь, здесь тоже не обойтись без замен. Предположим, что , т.е. . Предположили? В таком случае сосредоточьтесь, ибо сейчас мы возьмём логарифм по основанию и от левой, и от правой части равенства. Почему это можем сделать? Ну, если и это одно и то же, то и нахождение логарифмов от них по любому основанию должно дать одно и то же, смекаете?

Славненько, самое время воспользоваться правилом о выносе степени, которое с первого взгляда показалось нам таким пустяковым:

Сделали? А теперь избавимся от логарифма , поделив обе части равенства на него же:

$[frac{f log_b a}{log_b a}=frac{log_b x}{log_b a}]$

$[f=log_a x=frac{log_b x}{log_b a} ]$

Спрашивается, к чему мы пришли? К очень удобному способу переходить от одних оснований к другим — отвечаем мы. По жизни никаких ситуаций исключать нельзя, тем более живя в России. Кто знает, вдруг вам придётся «упростить выражение , и что вы делать будете? А-а-а, не знаете… Ну ладно, расскажем. Хотя на самом деле вы всё уже знаете.

Для начала будет полезно заметить, что уж точно не может являться никакой степенью пятёрки. Значит, надо перейти к другому основанию. Как это сделать? А по нашей сладенькой формуле.

$[log_5 256=frac{log_2 256}{log_2 5}= frac{8}{log_2 5}]$

Знаменатель мы не упростили, так как там наверняка что-то кошмарное должно стоять, уж лучше глаз порадуется.

Проведённое доказательство формулы для смены основания помимо своей полезности обладает ещё одним важным качеством. Это очень плохое математическое доказательство. Оно не отвечает в интуитивно понятном виде на вопрос «что происходит?», не даёт иллюстраций и безусловно понятных схем. По мере его развития мы просто видим, что одни операции приводят к возможностям сделать какие-то другие, а уже эти, третьи, двигают нас к итоговым выводам. К превеликому сожалению, в математике хватает и таких, чисто описательных доказательств, от которых никуда не деться, сколько бы мы ни старались подобрать им внятные альтернативы. Придётся смириться и страдать. Обещаем, что в следующих статьях опять вернёмся к ярким рисункам, цветастым квадратикам и той атмосфере непринуждённости, с которой наш учебник и начинался.

Ой, кстати, а что с бизнесом? Ну, тем самым, который позволит каждый день обедать сочной яичной лапшой с улыбающейся корейской девушкой на этикетке? Бизнес идёт в гору! Мы остановились на записи , где и было наше заветное число периодов. Теперь-то мы знаем, что $n=log_{1.06}2$ , а таблица логарифмов (обманываем, само собой, обычный калькулятор) говорит, что в данном случае . Получается, всего-лишь месяцев и ваша предпринимательская мечта исполнится. Что дальше? Решать только вам! Кто знает, может, пройдёт всего несколько лет и вы станете одалживать совсем другие суммы. Такие, которые позволят утолять голод исключительно тройными инфаркт-чизбургерами с шоколадным беконом. Но это будет совсем другая история…

Источник

Мы все еще со школы знаем как осуществлять действия с вещественными числами. Без труда можем выяснить чему равняется корень из какого либо числа, или как возводить числа в степень. Но как быть с комплексными?

Недавно я выпустил несколько статей, посвященных комплексному анализу. Рекомендую вам прочесть их, если пропустили. Или освежить свои воспоминания, если думаете, что забыли что-то. (Мнимая единица. Случай, когда можно поделить на 0)

Обычные действия

Для начала я предлагаю вам разобрать некоторые обычные действия. В общем, они практически ни как не отличаются от привычных нам. Для удобства мы будем пользоваться алгебраической формой представления числа. (Z = a + ib , Y = c +id). Итак:

Сложение/вычитание : Z+Y = (a+c) +i(b+d).
Инверсия числа: !Z = a – ib.
Модуль числа: |Z| = √ (a^2+b^2).
Умножение: Z*Y = (a + ib)*(c + id) = (ac-bd) + i(bc+ad).
Деление: Z/Y = (a+ib)/(c+id) = (Z*!Y)/(|Y|^2.)

Как быть со степенью?

Но как быть с действиями возведения в степень? Мы знаем, что возведение в степень – это сокращенное умножение: 2^3 = 2*2*2 = 8. Но как быть с возведением в мнимую степень?

Тут нам нужно воспользоваться другой формой записи: показательной. В этом случае число представляется в следующем виде:

И вот здесь мы видим, что возведение в мнимую степень подобно вращению числа. Подробнее об этом нам говорит формула Эйлера:

e^(i⋅x) = cos(x) + i⋅sin(x) , где r = 1. (доказательство этого тождества не такое сложное, но оно лежит за рамками данной статьи)

То есть показатель поле i говорит нам то, на какой угол нам следует повернуть вектор. Если угол равен 0, то мы очевидно попадет в 1, или что означает, что e^0 = 1.

“Главный гвоздь программы”

Но так что. Чему же будет равно выражение i^i ? То есть, мы полностью мнимое число возводим в мнимую степень, что же мы ожидаем получить? Давайте посмотрим:

Здесь мы воспользовались замечательным свойством экспоненты и натурального логарифма. В показателе получился логарифм комплексного числа, чему же он равен? Для этого вернемся на комплексную плоскость и посмотрим, на одно равенство. Нам нужно найти, где е в какой-то степени дает нам i. Самое первое на картинке. Давайте возьмем логарифм от обеих частей:

Вот мы и выяснили, чему равняется этот логарифм. Теперь давайте подставим все обратно:

Таким образом мы получили, что это абсолютно вещественное число и равняется оно примерно 0,208.

Ну хорошо, с первым персонажем мы разобрались. А что насчет следующего:

Если мы вооружимся знаниями полученными в предыдущей части статьи, то все пойдет гораздо легче. Нам необходимо просто воспользоваться свойством корня.

Ну и здесь мы уже знаем ответ. Получается, что это равняется:

Как то так. Надеюсь, что эта статья была для вас интересной и вы получили много нового из нее. Не забывайте ставить лайки, если считаете, что такой контент нужен для моей аудитории. Подписывайтесь на канал, если вам интересна тема математики, физики и технологий.

Всего вам доброго и до скорых встреч!

Источник

Действия, обратные возведению в степень

7. В виду последней особенности действий возведения в степень для него можно составить 2 обратных задачи. Напр.:

1) Я задумал число, возвел его в третью степень (или: в куб), получилось 64; какое число я задумал?

Эту задачу можно записать в виде

(?)³ = 64

2) Я взял число 3, возвел его в некоторую степень, – получилось 81. В какую степень было возведено число 3.

Эту задачу можно записать в виде:

3^? = 81

Теперь уже, так как возведение в степень не обладает переместительным законом, эти две задачи следует считать совершенно различными.

Сначала решать их можно подбором: попробуем число 1, 1³ = 1, а не 64, след., 1 не годится; 2³ = 8, а не 64, след., 2 не годится, 3³ = 27, а не 64, след., 3 не годится; 4³ = 64, след., в 1 задаче было задумано число 4. Также выясним, что во второй задаче число 3 было возведено в 4-ую степень.

Так как таких задач можно составить очень много, то для их решения необходимо изобрести новые действия. Эти действия обратны возведению в степень. Итак, для возведения в степень существуют два обратных действия: первое из них называется извлечением корня и служит для решения вопросов, подобных первой из наших задач; второе называется нахождением логарифма и служит для решения вопросов, подобных второй задаче.

Если мы обратим внимание на то, что в первой задаче нам даны степень 64 и показатель степени 3, то мы установим определение:

Извлечением корня называется действие, обратное возведению в степень, при помощи которого по данной степени и по данному показателю находят основание степени.

Также точно: во второй задаче даны степень (81) и основание степени (3), а надо найти показателя степени. Поэтому

нахождением логарифма называется действие, обратное возведению в степень, при помощи которого по данной степени и по данному основанию находится показатель степени.

Источник

Как узнать, в какую степень возведено число при наличии результата возведения?

Степень числа

Степень числа: определения, обозначение, примеры

Степени с натуральными показателями: понятие квадрата и куба числа

Что такое степени с целым показателем

Что такое степени с рациональным показателем

Что такое степени с иррациональным и действительным показателем

Как узнать степень числа?

Обычные действия

Как быть со степенью?

“Главный гвоздь программы”

Всего вам доброго и до скорых встреч!

Действия, обратные возведению в степень

Вам также может понравиться

Как найти файл word по дате

Как найти идентификационный номер сбербанка

Как составить сводный сметный расчет в двух уровнях цен

Добавить комментарий Отменить ответ