Точка, которая лежит на прямой, разделяет прямую на две части, каждая из которых называется лучом, исходящим из этой точки, а саму точку называют началом каждого из лучей.
Точка (A) разделяет прямую (a) на два луча. Так как в задании важно понять, который из лучей рассматривать,
поставим на прямой ещё две точки (B) и (C) и назовём лучи:
луч (AB) и луч (AC).
Обрати внимание!
Первой точкой всегда называют начальную точку луча.
На этом рисунке любая из точек может быть начальной точкой некоторого луча, который нарисован. Из каждой точки исходят два луча в противоположных направлениях и так же, как прямая, продолжаются бесконечно.
Обрати внимание!
Луч (BC) — тот же луч (BA), но луч (BC) oтличается от луча (AC). Эти лучи имеют некоторую общую часть.
Угол — геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Эти лучи называют сторонами угла, а их общее начало — вершиной угла.
Угол обозначают большими латинскими буквами
∠KMN
или малыми греческими буквами, например,
α
.
Обрати внимание!
Угол
∠KMN
можно назвать также
∠NMK
, но буква вершины всегда пишется посередине.
Иногда угол можно обозначить только одной большой латинской буквой вершины,
цифрой или названиями лучей — малыми латинскими буквами, например,
∠M
,
∠1
или
∠mn
.
Лучи (n) и (m) с общим началом в точке (M) делят плоскость на две части — внутреннюю область угла и внешнюю область угла.
Углом можно называть также лучи с общим началом вместе с внутренней областью. Тогда точки (A) и (B) не принадлежат углу
∠M
, а точки (C), (D) и (E) принадлежат углу
∠M
.
Если нарисовать два луча, исходящих из одной точки, то получим два угла.
Если обе стороны угла являются дополнительными полупрямыми, угол называют развёрнутым.
В этом случае получаем два развёрнутых угла.
Если во внутренней области угла провести луч с началом в вершине данного угла, то этот луч делит данный угол на два угла.
В таком случае очень важно следить за названиями углов, так как мы имеем данный угол и две его части. Например, не совсем понятно, какой угол мы подразумеваем, если пишем
∠A
. Лучше использовать три большие буквы, тогда названия углов будут понятны:
∠CAB
,
∠CAD
,
∠DAB
.
Содержание:
Определение: Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, и частью плоскости, которую они ограничивают.
Два угла называются равными, если их можно совместить наложением.
Биссектрисой угла называется луч, который выходит из вершины угла и делит его на два равных угла.
Определение. Развернутым углом называется угол, стороны которого являются дополнительными лучами.
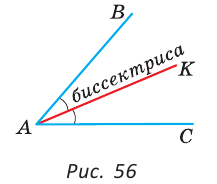
На рисунке 56 луч АК — биссектриса угла ВАС и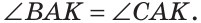 
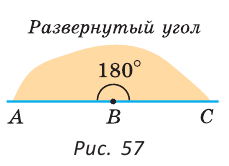
На рисунке 57 угол ABC — развернутый, лучи ВА и ВС — дополнительные. Другая (незакрашенная) полуплоскость относительно прямой АС также задает развернутый угол ABC.
Углы измеряются в градусах, минутах, секундах.
Развернутый угол равен 180°;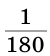 
часть развернутого угла называется градусом и обозначается 1°; 
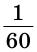часть одного градуса называется минутой и обозначается 1′; 
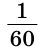часть минуты называется секундой и обозначается 1″.
Угол, равный 5 градусов 20 минут и 35 секунд, записывается так: 5°20’35”.
Вместо «градусная мера угла равна 20°» часто говорят «угол равен 20°», вместо найти «градусную меру угла» говорят «найти угол».
Определения
Определение: Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, и частью плоскости, которую они ограничивают.
Определение: Угол, равный 90°, называется прямым; угол, меньший 90°, — острым; угол, больший 90°, но меньший 180°, — тупым; угол, равный 360°, называется полным (его стороны совпадают).
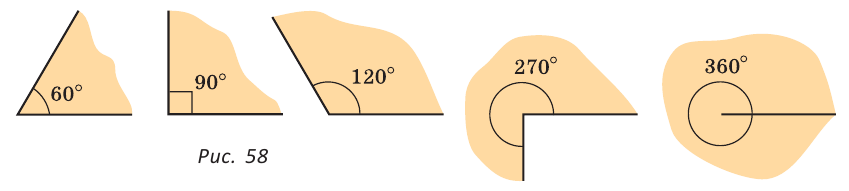
На рисунке 58 последовательно изображены: острый угол, равный 60°; прямой угол, равный 90°; тупой угол, равный 120°; угол, равный 270°; и полный угол, равный 360°.
Градусная мера угла является его важной характеристикой. Свойства градусной меры угла: любой угол имеет градусную меру, выраженную некоторым положительным числом; равным углам соответствуют равные градусные меры, а большему углу — большая градусная мера. И наоборот.
Аксиомы
Аксиома измерения углов. Если внутри угла из его вершины провести луч, то он разобьет данный угол на два угла, сумма градусных мер которых равна градусной мере данного угла.
Аксиома откладывания углов. От любого луча в данную полуплоскость можно отложить угол данной градусной меры, и притом только один.
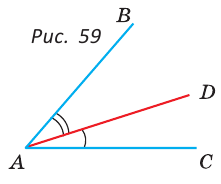
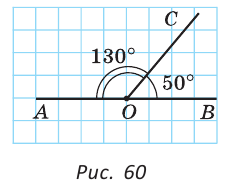
На рисунке 59 луч AD проходит внутри угла ВАС. По аксиоме измерения углов 
Например, если из вершины развернутого угла АОВ (рис. 60) провести ЛУЧ ОС, который составит со стороной ОВ угол 50°, то со стороной OA луч ОС составит 180° – 50° = 130°.
Два луча с общим началом задают на плоскости два угла. В дальнейшем будем рассматривать меньший из этих двух углов (если они неразвернутые). Такой угол меньше 180°.
Пример №1
Внутри угла ВАС, равного 114°, из его вершины проведен луч АЕ. Угол ВАЕ в 2 раза больше угла ЕАС. Найти величину угла ВАЕ.
Решение:
Пусть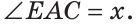 
Тогда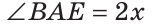 
(рис. 61).
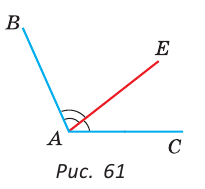
По аксиоме измерения углов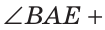 
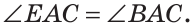
Тогда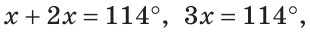 
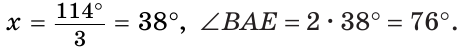
Ответ: 76о
Замечания. 1. Возможен другой способ записи решения, когда рядом с буквой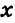 
пишут знак градуса: 
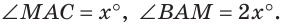Тогда в уравнении знак градуса писать не нужно: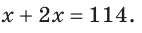 
2. В дальнейшем при решении задач не будем ссылаться на аксиому измерения углов.
Пример №2
Внутри угла проведены лучи BD и BF (рис. 62).
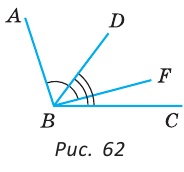
Найти величину угла DBF, если:
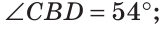
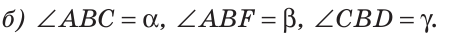
Решение:
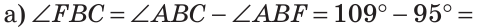
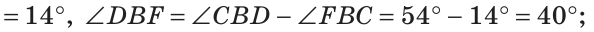
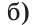Если сложить углы ABF и CBD, то получим угол ABC плюс угол DBF.
Отсюда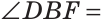 
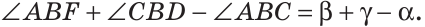
Ответ: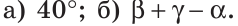 
Пример №3
Луч AD делит угол ВАС на два угла BAD и CAD. Доказать, что угол между биссектрисами АК и АЕ углов BAD и CAD равен половине угла ВАС (рис. 63).
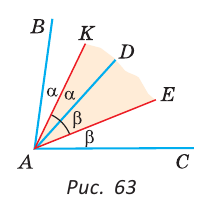
Доказательство:
Так как АК иАЕ — биссектрисы, то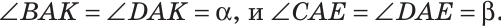 
Тогда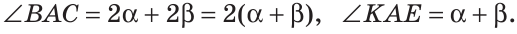 
Следовательно,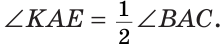 
Что и требовалось доказать.
Замечание. В данной задаче мы доказали свойство: «Если внутри угла из его вершины провести луч, то угол между биссектрисами полученных углов равен половине данного угла».
Геометрия 3D
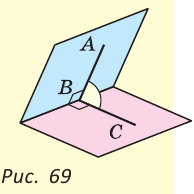
В пространстве при пересечении двух плоскостей образуются двугранные углы. Две полуплоскости с общей границей являются гранями такого двугранного угла, а их граница — его ребром. Измеряется двугранный угол величиной линейного угла, образованного двумя лучами, проведенными в каждой из полуплоскостей из точки на ребре двугранного угла перпендикулярно этому ребру. На рисунке 69 ZABC — линейный угол изображенного двугранного угла.
Геометрия 3D
В пространстве при пересечении двух плоскостей образуются двугранные углы. Две полуплоскости с общей границей являются гранями такого двугранного угла, а их граница — его ребром. Измеряется двугранный угол величиной линейного угла, образованного двумя лучами, проведенными в каждой из полуплоскостей из точки на ребре двугранного угла перпендикулярно этому ребру. На рисунке 69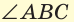 
— линейный угол изображенного двугранного угла.
Смежные углы. Вертикальные углы
Определение. Два угла называются смежными, если у них одна сторона общая, а две другие являются дополнительными лучами.
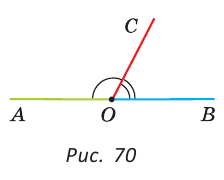
Если на рисунке 70 лучи OA и ОВ дополнительные, то углы АОС и ВОС — смежные.
Теорема (свойство смежных углов). Сумма смежных углов равна 180°.
Дано: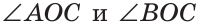 
— смежные.
Доказать: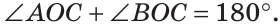 
Доказательство:
Из определения смежных углов следует, что лучи OA и ОВ являются дополнительными и поэтому образуют развернутый угол АОВ, равный 180°. Луч ОС проходит между сторонами этого угла, и по аксиоме измерения углов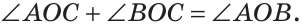 
Поэтому 
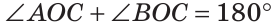. Теорема доказана.
Следствия.
- Если смежные углы равны, то каждый из них прямой.
- Если два угла равны, то равны и смежные с ними углы.
Замечание. Все теоремы курса геометрии 7—9 классов описывают свойства фигур на плоскости.
Определение. Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами к сторонам другого.
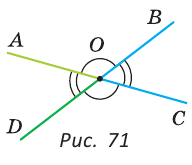
При пересечении двух прямых АС и DB в точке О (рис. 71) получим, что лучи OA и ОС, О В и OD — дополнительные. Поэтому углы AOD и BОС — вертикальные. Углы АОВ и DOC также вертикальные.
Теорема (свойство вертикальных углов). Вертикальные углы равны.
Дано: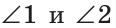 
— вертикальные (рис. 72).
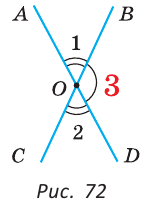
Доказать: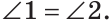 
Доказательство:
Углы 1 и 3 смежные, так как лучи OA и OD — дополнительные по определению вертикальных углов. По свойству смежных углов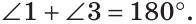 
Углы 2 и 3 также смежные,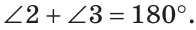 
Так как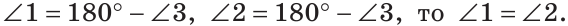 
Теорема доказана.
Углом между двумя пересекающимися прямыми называется меньший из образованных ими углов. Если при пересечении прямых АВ и CD (рис. 73)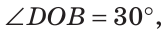 
то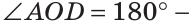 
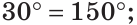
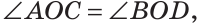
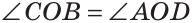как вертикальные. Угол между прямыми АВ и CD равен 30°. Говорят, что прямые пересекаются под углом 30°.
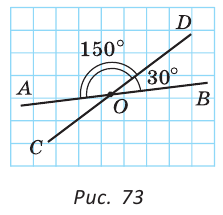
При пересечении двух прямых образуются четыре угла (не считая развернутых). Если один из них 90°, то и остальные по 90° (докажите самостоятельно). Говорят, что прямые пересекаются под прямым углом.
Угол между параллельными прямыми считается равным 0°.
Пример №4
Смежные углы относятся как 2:3. а) Найти величину каждого из углов, б) Определить, сколько процентов развернутого угла составляет меньший угол.
Решение:
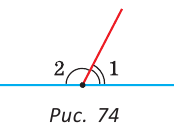
а) Пусть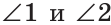 
— данные смежные углы (рис. 74). Согласно условию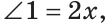 
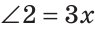(градусную меру одной части принимаем за 
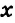). По свойству смежных углов
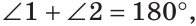то есть 
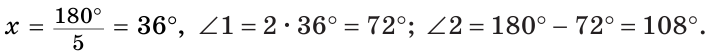
б) Меньшим является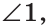 
а 72° от 180° составляют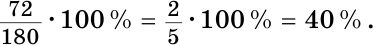 
Ответ: 72°, 108°; 40 %.
Пример №5
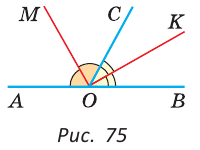
а) Найти угол между биссектрисами ОК и ОМ смежных углов ВОС и АОС (рис. 75), если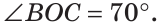 
б) Доказать, что биссектрисы смежных углов образуют прямой угол.
Решение:
а) Если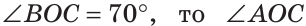 
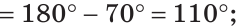
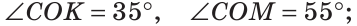
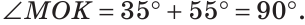
б) Так как ОМ и ОК — биссектрисы, то
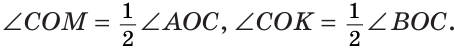Найдем градусную меру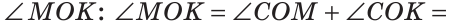 
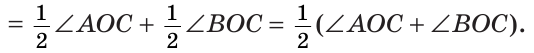По свойству смежных углов 
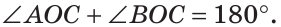Тогда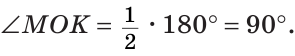 
. Что и требовалось доказать.
Замечание. Можно было сослаться на ключевую задачу 3* к § 5.
Пример №6
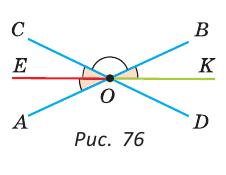
Доказать, что биссектрисы вертикальных углов образуют развернутый угол.
Решение:
а) Пусть ОЕ и ОК — биссектрисы вертикальных углов АОС и BOD (рис. 76). Докажем, что 
— развернутый. Известно, что биссектриса делит угол пополам. Так как вертикальные углы равны, то равны и их половины. Поэтому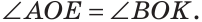 
б)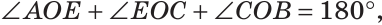 
так как лучи OA и ОВ дополнительные, и поэтому 
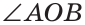— развернутый. Заменив в последнем равенстве 
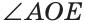на равный ему 
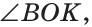получим 
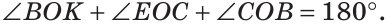Отсюда следует, что — развернутый.
Замечание. Из решения задачи следует свойство: если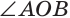 
— развернутый и 
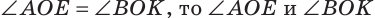— вертикальные.
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
- Свойства прямоугольного треугольника
- Расстояние между параллельными прямыми
- Задачи на построение циркулем и линейкой
- Задачи на построение по геометрии
Содержание:
- Определение развернутого угла
- Примеры решения задач с развернутыми углами
Определение развернутого угла
Определение
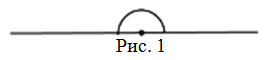
Развернутый угол – это угол,
стороны которого составляют прямую (рис. 1).
Градусная мера развернутого угла равна $180^{circ}$.
Любой луч, проведенный из вершины развернутого угла, делит его на два угла. Полученные в результате углы имеют
одну общую сторону, а две другие составляют прямую. Такие углы называются смежными.
Биссектриса развернутого угла делит его на два
прямых угла.
Если произвольный луч, проведенный из вершины развернутого угла, не является биссектрисой,
то он делит развернутый угол на два, один из которых острый (меньше прямого), а другой – тупой (больше прямого)
Примеры решения задач с развернутыми углами
Пример
Задание. Развернутый угол разделен лучом на два угла,
градусные меры которых относятся как 1:4.
Найдите полученные углы.
Решение. Обозначим искомые углы как
$alpha$ и
$beta$ . Пусть
$x$ – коэффициент пропорциональности, тогда
$alpha = x$, а соответственно
$beta = 4x$ . Так как градусная мера развернутого угла равна
$180^{circ}$ и согласно свойствам угла, что градусная мера
угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами, то делаем вывод, что
$$x+4 x=180^{circ} Rightarrow 5 x=180^{circ}$$
Отсюда находим:
$x=alpha=36^{circ}$ и $beta=4 x=4 cdot 36^{circ}=144^{circ}$
Ответ. $36^{circ}$ и $144^{circ}$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Луч
$OC$ делит развернутый угол
$AOB$ на два угла
$AOC$ и
$BOC$ так, что угол
$AOC$ на
$30^{circ}$ больше угла
$BOC$ . Найти углы
$AOC$ и
$BOC$ .
Решение. Изобразим заданный развернутый угол и проведем луч
$OC$ (рис. 2).
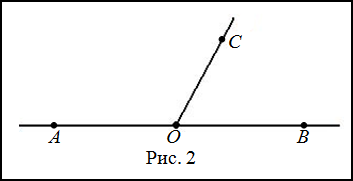
Пусть $angle B O C=x^{circ}$, тогда из условия получаем, что
$angle A O C=(x+30)^{circ}$. Так как эти углы являются
смежными, то их сумма равна
$180^{circ}$, то есть
$$angle A O C+angle B O C=180^{circ}$$
а тогда
$$x+x+30=180 Rightarrow 2 x=150 Rightarrow x^{circ}=angle B O C=75^{circ}$$
Отсюда
$$angle A O C=(x+30)^{circ}=105^{circ}$$
Ответ. $angle A O C=105^{circ}, angle B O C=75^{circ}$
Читать дальше: что такое вертикальные углы.
Содержание
- – Как луч называется биссектрисой угла?
- – Какой луч называется биссектрисой угла если он исходит из?
- – Как доказать что луч является биссектрисой угла?
- – Какой луч называют?
- – Что такое луч и что такое угол?
- – Что такое отрезок объясните?
- – Как построить биссектрису угла с помощью циркуля?
- – Как найти угол с биссектрисой?
- – Как доказать что это биссектриса угла?
- – Чему равна биссектриса угла?
- – Что такое луч Математика 2 класс?
- – Что такое луч в геометрии как обозначаются лучи?
- – Как начертить луч и обозначить его?
Биссектрисой (от лат. bi – “двойное”, и sectio – “разрезание”) угла называется луч, который исходит из вершины угла и делить угол на две равные части (пополам) (рис. … Мнемоническое правило: биссектриса это крыса, которая бегает по углам и делит угол пополам.
Как луч называется биссектрисой угла?
Ответ: Биссектрисой угла называется луч, исходящий из вершины угла и делящий его на два равных угла.
Какой луч называется биссектрисой угла если он исходит из?
Биссектри́са (от лат. bi- «двойное», и sectio «разрезание») угла — луч, исходящий из вершины угла и делящий этот угол на два равных угла.
Как доказать что луч является биссектрисой угла?
Основное свойство биссектрисы угла
- Всякая точка, лежащая на биссектрисе некого угла, находится на одинаковом расстоянии от сторон этого угла.
- И наоборот: если точка лежит на одинаковом расстоянии от сторон данного угла, то она гарантированно лежит на биссектрисе этого угла.
2 июн. 2018 г.
Какой луч называют?
Луч (в геометрии) или полупрямая — линия, имеющая начало, но не имеющая конца или часть прямой, состоящая из данной точки и всех точек, лежащих по одну сторону от неё. Любая точка на прямой разделяет прямую на два луча.
Что такое луч и что такое угол?
Луч – часть прямой, состоящая из всех точек, лежащих по одну сторону от заданной точки и той точки, которая является началом луча. Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Угол также рассматривается как часть плоскости, ограниченная двумя лучами с общим началом.
Что такое отрезок объясните?
Ответ: Отрезок это часть прямой, ограниченная двумя точками.
Как построить биссектрису угла с помощью циркуля?
Например, если Вам нужно построить биссектрису угла, равного 78 градусов, то нужно приложить транспортир к одной из сторон этого угла, отметить точку возле метки 78 / 2 = 39 градусов и провести луч из вершины заданного угла через полученную точку. Это и будет биссектриса угла 78 градусов.
Как найти угол с биссектрисой?
Разделите величину угла пополам.
Биссектриса делит угол на две равные части. Поэтому, чтобы найти угол, под которым проходит биссектриса, разделите величину угла (в градусах) на 2. . Таким образом, биссектриса проходит под углом 80 градусов.
Как доказать что это биссектриса угла?
Руководствуясь теоремой о параллельных прямых, которые пересекают стороны угла, вы получите равенство: АК/КС=АВ/ВМ=АВ/ВС. Таким образом, биссектриса внутреннего угла делит противоположную сторону треугольника на пропорциональные его прилежащим сторонам части и является отрезком, что и требовалось доказать.
Чему равна биссектриса угла?
Биссектрисой (от лат. bi – “двойное”, и sectio – “разрезание”) угла называется луч, который исходит из вершины угла и делить угол на две равные части (пополам) (рис. 1). Мнемоническое правило: биссектриса это крыса, которая бегает по углам и делит угол пополам.
Что такое луч Математика 2 класс?
Луч — это часть прямой, ограниченная одной точкой. Луч имеет начало, но не имеет конца. … Точка, которая лежит на прямой, разделяет прямую на две части, каждая из которых называется лучом, исходящим из этой точки. Точка A разделяет прямую a на два луча.
Что такое луч в геометрии как обозначаются лучи?
Для обозначения луча используют две точки, первой называют начало луча, а второй – любую другую точку, принадлежащую этому лучу. Например, луч с началом в точке О можно обозначить OК или OВ (луч ОК; луч ОВ).
Как начертить луч и обозначить его?
При обозначении луча двумя точками, на первом месте ставится буква, обозначающая начало луча, а на втором — буква, обозначающая какую-либо другую его точку: луч BC. Посмотрим на следующий пример: Луч с началом в точке A можно обозначить как AB или AC.
Интересные материалы:
Какой падеж чаще?
Какой падеж на дереве?
Какой палец развит у непарнокопытных?
Какой параллели Солнце бывает в зените 22 июня?
Какой парогенератор лучше Tefal или Philips?
Какой пароль у root?
Какой Патронус у Седрика Диггори?
Какой период относится к средне каменному веку?
Какой песок используют в бетоне?
Какой Петлюра умер?
Начальные геометрические сведения
Луч и угол
13. Проведите лучи h и p с началом в точке О так, чтобы угол kp был развёрнутым. Запишите обозначения всех получившихся углов.
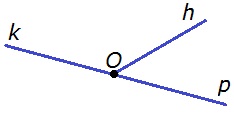
О т в е т.
∠kp, ∠kh, ∠hp.
14. а) Закрасьте цветным карандашом внутреннюю область угла М.
б) Какие точки лежат на сторонах угла М; внутри угла М; вне угла М?
а)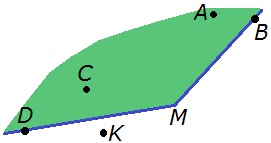 
О т в е т.
На сторонах угла М лежат точки D и B; внутри угла М лежат точки С и А; вне угла М лежит точка К.
15. Какой луч на рисунке делит угол АВС на два угла? Объясните ответ.
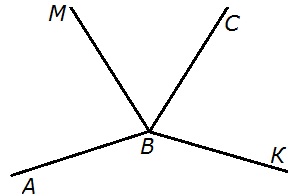
Р е ш е н и е. Луч делит угол на два угла, если он:
1) исходит из вершины угла;
2) проходит внутри угла.
Луч ВМ делит угол АВС на два угла, так как он исходит из вершины угла АВС и проходит внутри угла АВС.
Луч ВК не делит угол АВС на два угла, так как он исходит из вершины угла АВС, но не проходит внутри угла АВС.
О т в е т.
Луч ВМ делит угол АВС на два угла.
ГДЗ. Ответы по геометрии. Рабочая тетрадь. 7 класс. Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А., Юдина И.И.
Геометрия. 7 класс
