Алгоритм решения задач вида: найти “наибольшую площадь“, “наибольший объем“.
Данный вид задач подразумевает нахождение точек максимума площади (объема) в зависимости от длин сторон фигуры.
- шаг – записываем формулу площади (объема) (S=a*b).
- шаг – выражаем одну сторону фигуры через другую. Например в задаче “Проволока длинной 76 см согнута в прямоугольник , найдите длину сторон, при которых площадь прямоугольника наибольшая” была указана связь между сторонами прямоугольника – известный периметр, что позволило выразить одну сторону через другую и периметр (b = frac{P}{2}-a)), аналогично и в задаче Периметр основания прямоугольного параллелепипеда .
- шаг – подставляем подученную формулу в формулу порщади (объема)(например для прямоугольника (S=a*b = a*(frac{P}{2}-a) = a*frac{P}{2}-a^2).
- шаг – находим первую производную и приравниваем ее к нулю (S’= (a*frac{P}{2}-a^2)` = frac{P}{2}-2*a = 0)
- шаг – решаем полученное уравнение и находим корни уравнения (т.е. значения неизвестного при котором значение функции (производной) равно 0). Это и будет ответ, т.е. длина стороны при которой площадь будет наибольшей (аналогично и с объемом) (frac{P}{2}-2*a = 0 => a = frac{P}{4}).
- шаг – желательно проверить истинность полученного решения – подставить найденное значение в функцию (площади или объема) и рассчитать ее, а для сравнения взять соседнее значение стороны (больше или меньше) и так же подставить. Если площадь получится меньше, значит задача решена верно, если нет, то нужно искать ошибку.
P.S. вопросы и пожелания пишите в личку.
Для того, чтобы определить, поместятся ли предметы в коробку нужно выполнить предварительный расчёт с двумя условиями: 1) максимальная длина одного предмета должна быть меньше стороны коробки; 2) сумма объёмов предметов должна быть меньше объёма коробки.
Наибольшая длина каждого предмета – это 40 см, это меньше чем 60 см, то есть первое условие выполняется.
Проверка выполнения второго условия.
Объём коробки: V=60*60*60=216000 cм^3.
Объём первого предмета: V1=40*10*10=4000 cм^3.
Объём второго предмета: V2=10*40*40=16000 cм^3.
Один предмет положили на другой предмет, они занимают суммарный объём:
Ve=V1+V2=4000+16000=20000 cм^3.
Второе условие выполняется: Ve<V, 20000<216000.
Первый предмет – это прямоугольный параллелепипед с малым квадратом.
Второй предмет – это прямоугольный параллелепипед с большим квадратом.
Значит в коробке удобно сначала положить второй предмет, а затем первый предмет.
При этом необходимо составить трёхмерный чертёж, как предметы будут лежать в коробке.
Если бы предметы имели другую форму, то вместимость коробки определятся по максимальной длине большего предмета, а суммарный объём предметов надо определить по объёмам кубов или параллелепипедов, куда бы поместился каждый предмет.
Skip to content
В этой статье объясняется функция МАКС с множеством примеров формул, которые показывают, как найти наибольшее значение в Excel и выделить наибольшее число на листе.
МАКС – одна из самых простых и простых в использовании функций Excel. Тем не менее, у нее есть несколько хитростей, которые дадут вам большие возможности. Скажите, как вы используете функцию МАКС с условиями? Или знаете, как извлечь абсолютное наибольшее значение? Мы предложим несколько решений для этих и других аналогичных задач.
- Функция МАКС — основные сведения
- Найти максимальное в группе чисел
- Вычисляем максимум в несмежных диапазонах
- Как получить максимальную (последнюю) дату
- Максимальное значение с условиями
- Наибольшее число без учёта нулей
- Как найти максимальное число игнорируя ошибки
- Определяем абсолютное максимальное значение
- Максимум применительно к тексту
- Вычисление наибольшей разницы
- Выводим адрес ячейки с максимальным значением
- Как выделить цветом самое большое число
- Почему не получается?
Функция МАКС
Функция МАКС в Excel возвращает наибольшее значение в указанном вами наборе данных.
Синтаксис у неё следующий:
МАКС(число1; [число2];…)
Где число может быть представлено числовым значением, массивом, именованным диапазоном, ссылкой на ячейку или диапазоном, содержащим числа.
Число1 является обязательным, число2 и последующие аргументы необязательны.
Чтобы создать самую простую формулу, чтобы выбрать максимальное значение в таблице Excel, вы можете вводить числа непосредственно в список аргументов, например:
=МАКС(1; 2; 3)
На практике это – очень редкий случай. По большей части вы будете иметь дело с диапазонами и ячейками.
Самый быстрый способ найти наибольшее значение в диапазоне, – это:
- В ячейке введите = МАКС(
- Выберите диапазон чисел с помощью мыши.
- Введите закрывающую скобку.
- Жмём Enter для завершения.
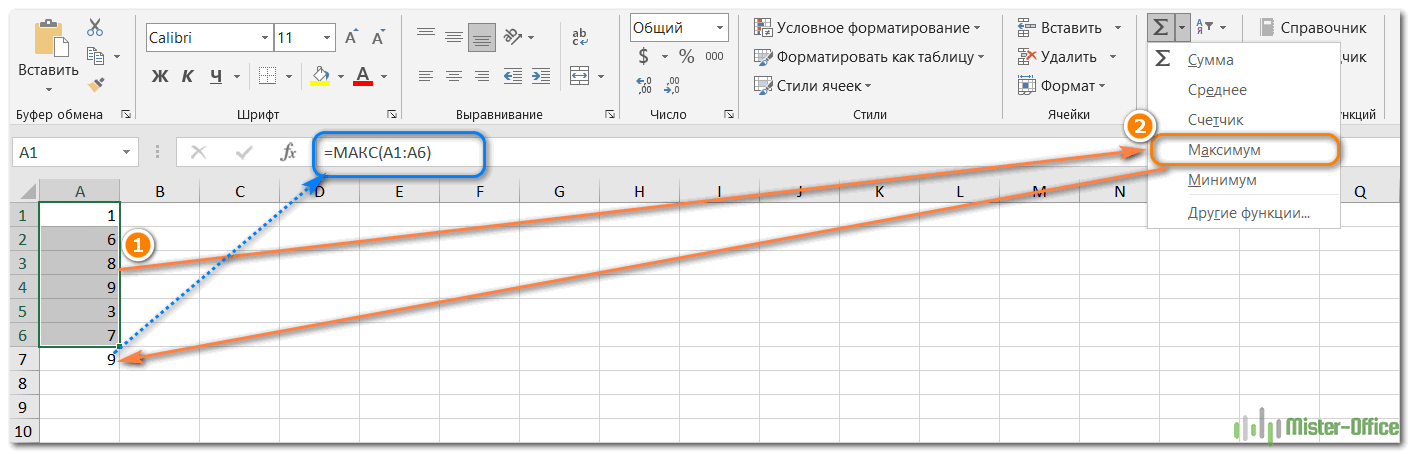
Например, чтобы найти максимальное значение в диапазоне A1: A6, формула будет выглядеть следующим образом:
=МАКС(A1:A6)
Если ваши числа находятся в непрерывном диапазоне (как в этом примере), вы можете заставить Excel автоматически создать формулу МАКС. Вот как:
- Выделите ячейки со своими числами.
- На вкладке «Главная» в группе «Форматы» нажмите «Автосумма» и выберите «Максимум» из раскрывающегося списка.
5 фактов, которые нужно знать о функции МАКС –
- В текущих версиях Excel она может обрабатывать до 255 аргументов.
- Если аргументы не содержат ни одного числа, возвращается ноль.
- Если аргументы содержат одно или несколько значений ошибки, возвращается ошибка.
- Пустые ячейки игнорируются.
- Обрабатываются логические значения и текстовые представления чисел, предоставленные непосредственно в списке аргументов (ИСТИНА приравнивается к 1, ЛОЖЬ – к 0). Если используется ссылка на ячейку с логическим или текстовым значением, то они игнорируются.
Как найти в Excel наибольшее число – примеры.
Ниже мы покажем несколько стандартных вариантов использования функции МАКС.
Во многих случаях существует несколько различных решений для одной и той же задачи, поэтому я рекомендую вам протестировать все варианты, чтобы выбрать наиболее подходящий.
Как выбрать максимальное значение в группе чисел.
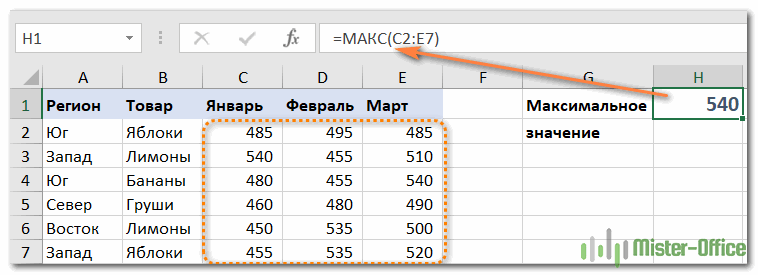
Чтобы в Excel извлечь наибольшее число в группе чисел, передайте эту группу функции МАКС в качестве ссылки на диапазон. Диапазон может содержать любое количество строк и столбцов. Например, чтобы получить максимальное значение из C2: E7, используйте эту простую формулу:
=МАКС(C2:E7)
Предположим, у нас есть сведения об учениках с их оценкой, но некоторые из значений оценки являются логическими, текстовыми, а некоторые пока вовсе не имеют оценки.
Применим функцию:
= МАКС(B2:B10)
Как видите, игнорируются ячейки с текстом, а также пустые, логические значения приравниваются к нулю, а затем вычисляется максимальное число, как показано в таблице Excel выше.
Наибольшее значение в несмежных ячейках или диапазонах Excel
Чтобы осуществить поиск в несмежных ячейках и диапазонах, необходимо включить в формулу ссылку на каждый отдельный адрес. Рассмотрим пошагово:
- Начните вводить функцию МАКС в ячейку.
- После того, как вы ввели открывающую скобку, нажмите и удерживайте Ctrl и выберите мышкой нужные ячейки и диапазоны.
- Отпустите
Ctrlи введите закрывающую круглую скобку. - Нажмите
Enter.
Вы получите формулу максимального числа в Excel, подобную этому:
=МАКС(C2:E2;C7:E7)
Как получить наибольшую (последнюю) дату в Excel
Во внутренней системе Excel даты – это не что иное, как порядковые номера дней, поэтому функция МАКС обрабатывает их без проблем.
Например, чтобы найти последнюю дату доставки из C2: C7, запишите обычную формулу, которую вы использовали бы для чисел:
=МАКС(C2:C7)
Поскольку дата – это также число, всё работает замечательно.
Максимальное значение с условиями.
Довольно часто случается, что из большого объёма данных Excel нужно выбрать максимальное значение из какой-то его части. К примеру, найти самую большую партию какого-то определённого товара в огромном списке продаж. Или же найти наивысшую оценку по какому-то предмету среди большого набора данных оценок, набранных учащимися определенного класса по нескольким предметам в школе.
Если вы хотите получить максимальное значение Excel с учётом каких-то условий, то вы можете выбрать из нескольких предложенных ниже формул. Чтобы убедиться, что все они возвращают одинаковый результат, мы протестируем их на одном и том же наборе данных.
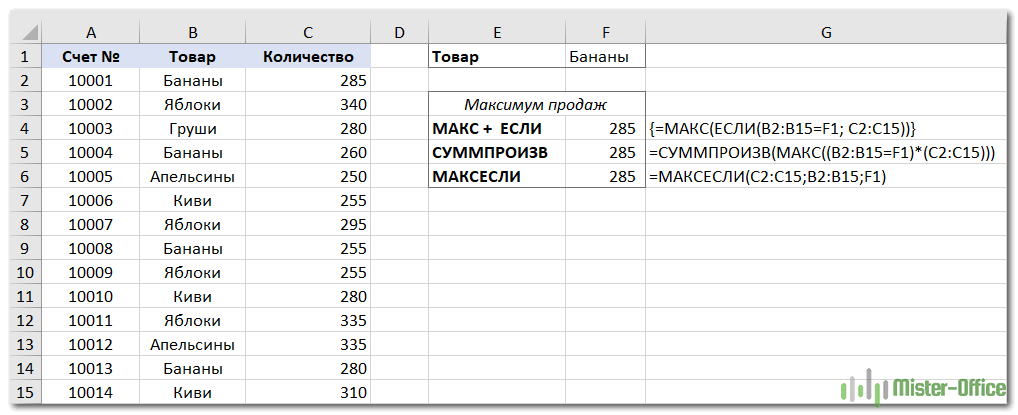
Задача: мы хотим найти самую большую продажу для определенного товара, указанного в F1.
МАКС + ЕСЛИ
Если вы ищете решение, которое работает во всех версиях Excel, используйте функцию ЕСЛИ для проверки условия, а затем передайте полученный массив в функцию:
=МАКС(ЕСЛИ(B2:B15=F1; C2:C15))
Чтобы это работало, необходимо нажать Ctrl + Shift + Enter одновременно, чтобы ввести как формулу массива. Если все сделано правильно, Excel заключит ваше выражение в {фигурные скобки}, что является визуальным указанием на формулу массива.
Также можно оценить несколько условий одновременно, о чем мы поговорим далее.
МАКС + СУММПРОИЗВ
Если вам не нравится использовать формулы массива в ваших листах, объедините МАКС с функцией СУММПРОИЗВ, которая умеет работать с массивами:
=СУММПРОИЗВ(МАКС((B2:B15=F1)*(C2:C15)))
МАКСЕСЛИ
В Excel 2019 и Office 365 есть специальная функция МАКСЕСЛИ, которая предназначена для поиска наибольшего значения по 126 критериям.
В нашем случае используется только одно условие, поэтому формула очень проста:
=МАКСЕСЛИ(C2:C15;B2:B15;F1)
На приведенном ниже скриншоте показаны все 3 формулы в действии:
Выбираем максимальное значение в Excel без учета нулей
Фактически, это разновидность условного МАКС, рассмотренного в предыдущем примере. Чтобы исключить нули, используйте логический оператор «не равно» и поместите выражение «<> 0» либо в критерий функции МАКСЕСЛИ, либо в конструкцию МАКС + ЕСЛИ.
Как вы понимаете, проверка этого условия имеет смысл только в случае наличия отрицательных чисел. Для положительных чисел эта проверка излишняя, потому что любое положительное число больше нуля.
Чтобы попробовать, давайте найдем самую маленькую скидку в диапазоне C2:C7. Поскольку все скидки представлены отрицательными числами, наименьшая скидка фактически является наибольшим значением.
Обязательно нажмите Ctrl + Shift + Enter, чтобы правильно заполнить эту формулу массива:
=МАКС(ЕСЛИ(C2:C7<>0; C2:C7))
А это обычная формула –
=МАКСЕСЛИ(C2:C7;C2:C7;”<>0″)
И вот что у нас получилось:
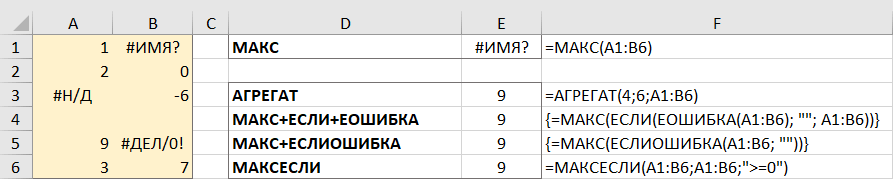
Как найти максимальное значение, игнорируя ошибки
Когда вы работаете с большим объемом данных, управляемых различными формулами, есть вероятность, что некоторые из них приведут к ошибкам. Соответственно, функция МАКС тоже вернет ошибку.
В качестве обходного пути можно использовать МАКС вместе с ЕОШИБКА. Учитывая, что вы ищете в диапазоне A1: B5, формула принимает следующую форму:
=МАКС(ЕСЛИ(ЕОШИБКА(A1:B6); “”; A1:B6))
Чтобы упростить формулу, используйте функцию ЕСЛИОШИБКА вместо комбинации ЕСЛИ + ЕОШИБКА. Это также сделает логику более очевидной – если есть ошибка в A1:B6, замените ее пустой строкой (”), а затем вычислите самое большое значение в диапазоне:
=МАКС(ЕСЛИОШИБКА(A1:B6; “”))
Неудобство состоит в том, что нужно не забывать нажимать Ctrl + Shift + Enter, потому что это работает только как формула массива.
В Excel 2019 и Office 365 функция МАКСЕСЛИ может быть хорошим решением при условии, что ваш набор данных содержит хотя бы одно положительное число или нулевое значение:
=МАКСЕСЛИ(A1:B6;A1:B6;”>=0″)
Поскольку формула выполняет поиск максимального значения с условием «больше или равно 0», она не будет работать для набора данных, состоящего исключительно из отрицательных чисел.
Также идеально подходит функция АГРЕГАТ, которая может выполнять ряд операций и игнорировать значения ошибок:
=АГРЕГАТ(4;6;A1:B6)
Число 4 в первом аргументе предписывает выполнить поиск максимального числа, шестёрка во втором аргументе – это параметр «игнорировать ошибки», а A1: B6 – ваш целевой диапазон.
Все формулы возвращают одинаковый результат:
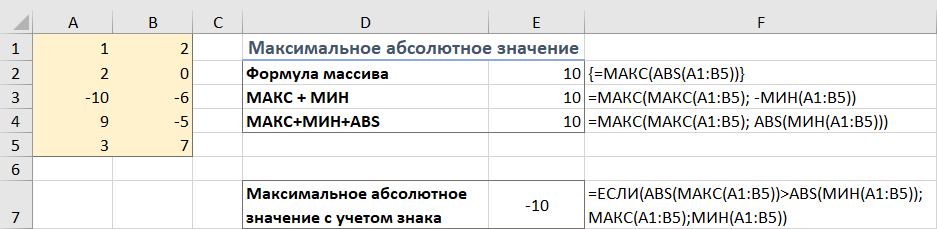
Как найти абсолютное наибольшее значение в Excel
При работе с диапазоном положительных и отрицательных чисел иногда может потребоваться найти максимальное абсолютное значение независимо от знака.
Первая идея, которая приходит в голову, – получить абсолютные значения всех чисел в диапазоне с помощью функции ABS и передать их в МАКС:
{= МАКС(ABS( диапазон ))}
Это формула массива, поэтому не забудьте подтвердить ее с помощью Ctrl + Shift + Enter. Еще одно предостережение: он работает только с числами и приводит к ошибке в случае нечисловых данных.
Не нравится это решение? Тогда давайте построим что-нибудь более жизнеспособное 🙂
Что, если мы найдем минимальное значение, изменим или проигнорируем его знак, а затем вычислим вместе со всеми другими числами? Да, это будет отлично работать как обычная формула. В качестве дополнительного бонуса это отлично обрабатывает текстовые записи и ошибки.
С исходными данными в A1: B5 расчёты выглядят следующим образом.
Формула массива (заполняется с помощью Ctrl + Shift + Enter):
=МАКС(ABS(A1:B5))
Обычная формула (заполняется клавишей Enter):
=МАКС(МАКС(A1:B5); -МИН(A1:B5))
или же
=МАКС(МАКС(A1:B5); ABS(МИН(A1:B5)))
На скриншоте ниже показаны результаты:
Вернуть максимальное абсолютное значение с сохранением знака
В некоторых ситуациях может потребоваться найти наибольшее абсолютное значение в таблице Excel, но вернуть число с исходным знаком, а не его абсолютное значение.
Предполагая, что числа находятся в ячейках A1: B5, вот выражение, которое следует использовать:
=ЕСЛИ(ABS(МАКС(A1:B5))>ABS(МИН(A1:B5)); МАКС(A1:B5);МИН(A1:B5))
Сложная на первый взгляд логика довольно проста. Сначала вы находите наибольшее и наименьшее числа в диапазоне и сравниваете их абсолютные значения. Если абсолютное (без учёта знака) максимальное значение больше абсолютного минимального значения, возвращается это наиболшее число, иначе – наименьшее число.
Поскольку формула возвращает исходное, а не абсолютное значение, информация о знаке сохраняется (см. скриншот выше).
Максимальное значение применительно к тексту.
Предположим, у нас есть список имен, и нам нужно вычислить их максимальную длину, то есть найти наибольшее количество символов в ячейке Excel.
Здесь мы должны применить функцию ДЛСТР для вычисления длины имени.
=ДЛСТР(А2)
А затем применим функцию МАКС, чтобы узнать максимальную длину ФИО.
=МАКС(B2;B13)
А можно обойтись без дополнительного столбца и вычислить максимальную длину текстового значения в одной ячейке. Для этого нужно объединить эти формулы, вложив ДЛСТР в МАКС:
=МАКС(ДЛСТР(A2:A13))
Учтите, что это формула массива. Ведь можно работать не только с диапазоном, но и с массивом числовых значений, который формируется другой функцией.
Вычислить наибольшую разницу в сумме.
Предположим, нам нужно вычислить наибольшую разницу в сумме за любой смежный месяц для каждого товара. Или, выражаясь иначе, найти максимальное изменение продаж за месяц.
Ниже представлена таблица Excel с небольшой выборкой данных за 4 месяца.
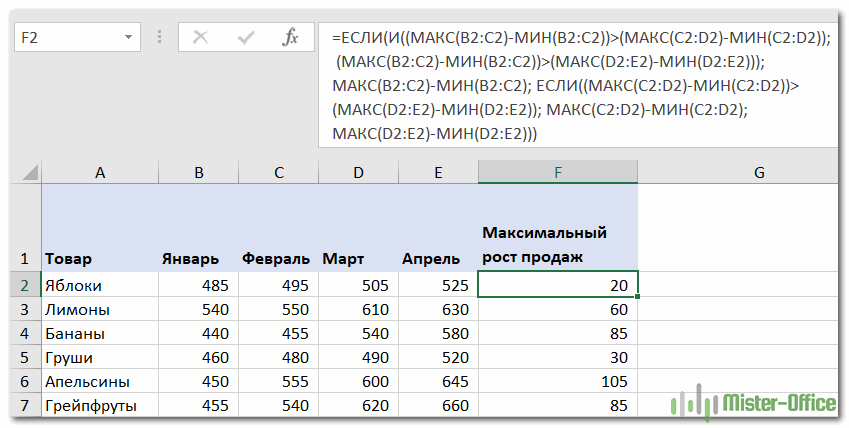
Если решать проблему «в лоб», то можно использовать функцию ЕСЛИ со множеством условий:
=ЕСЛИ(И((МАКС(B2:C2)-МИН(B2:C2))>(МАКС(C2:D2)-МИН(C2:D2)), (МАКС(B2:C2)-МИН(B2:C2))>(МАКС(D2:E2)-МИН(D2:E2))), МАКС(B2:C2)-МИН(B2:C2), ЕСЛИ((МАКС(C2:D2)-МИН(C2:D2))>(МАКС(D2:E2)-МИН(D2:E2)), МАКС(C2:D2)-МИН(C2:D2),МАКС(D2:E2)-МИН(D2:E2)))
Но при помощи функции МАКС можно значительно упростить расчет и не пользоваться такой длинной и сложной конструкцией.
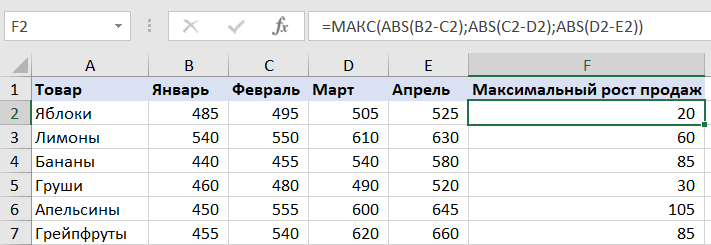
Используя функцию ABS, мы будем искать максимальное изменение вне зависимости от знака. Попробуйте заменить большую формулу этой:
=МАКС(ABS(B2-C2);ABS(C2-D2);ABS(D2-E2))
Как вы можете видеть в таблице ниже, этот вариант намного проще и возвращает те же результаты.
Как найти адрес ячейки Excel с максимальным числом.
Есть ли решение, которое сообщит адрес ячейки с наибольшим числом, а не само число? То есть, если A4 равно 9 и это значение является самым большим, как мне составить формулу, которая возвратит координаты A4 вместо 9?
Вы можете использовать функции ЯЧЕЙКА , ИНДЕКС и ПОИСКПОЗ в сочетании с функцией МАКС, чтобы вернуть адрес ячейки с наибольшим значением.
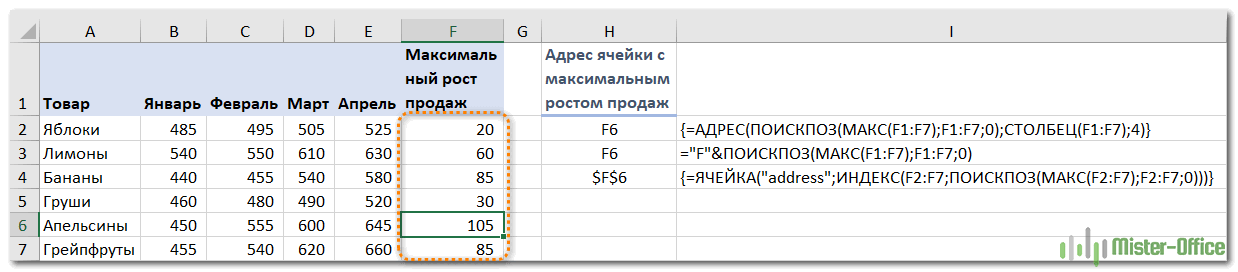
Например, если вы хотите найти ячейку с наивысшим значением в столбце от А1 до А7, вы можете использовать следующий расчёт:
=ЯЧЕЙКА(“адрес”;ИНДЕКС(A1:A7;ПОИСКПОЗ(МАКС(A1:A7);A1:A7;0)))
Получаем результат в виде абсолютной ссылки $А$4, которая указывает на самое большое число из этого диапазона.
Однако учтите, что это выражение работает только с одним столбцом.
А вот еще альтернативные варианты поиска адреса наибольшего числа по столбцу, из которых вы можете выбрать наиболее подходящий для себя:
Формула массива –
{=АДРЕС(ПОИСКПОЗ(МАКС(F1:F7);F1:F7;0);СТОЛБЕЦ(F1:F7);4)}
Обычная формула, в которой явным образом нужно указать столбец:
=”F”&ПОИСКПОЗ(МАКС(F1:F7);F1:F7;0)
Ещё одна формула массива –
{=ЯЧЕЙКА(“address”;ИНДЕКС(F2:F7;ПОИСКПОЗ(МАКС(F2:F7);F2:F7;0)))}
На скриншоте вы видите, что все они возвращают один и тот же адрес:
И ещё одна формула массива для вывода адреса, которая работает с диапазоном из нескольких строк и столбцов:
{=АДРЕС(МАКС(ЕСЛИ((C2:E7=МАКС(C2:E7));СТРОКА(C2:E7))); МАКС(ЕСЛИ((C2:E7=МАКС(C2:E7));СТОЛБЕЦ(C2:E7))))}
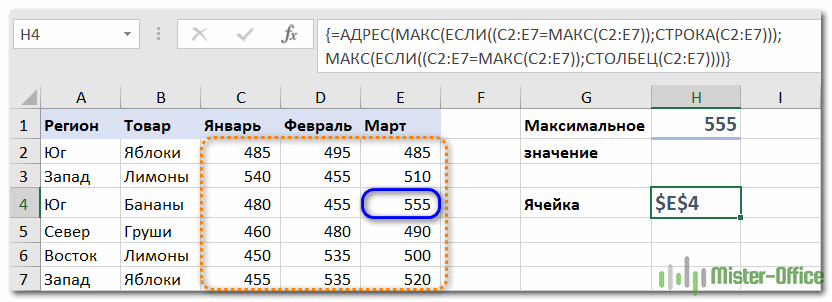
В данном случае, как видите, мы ищем адрес наибольшего числа в двумерном диапазоне C2:E7.
Напомню, что формула массива вводится с использованием комбинации клавиш Ctrl + Shift + Enter.
Как выделить наибольшее значение в Excel
В ситуации, когда вы хотите определить самое большое число в исходном наборе данных, самый быстрый способ – выделить его с помощью условного форматирования Excel. Приведенные ниже примеры покажут вам два разных варианта действий.
Выделите максимальное число в диапазоне Excel
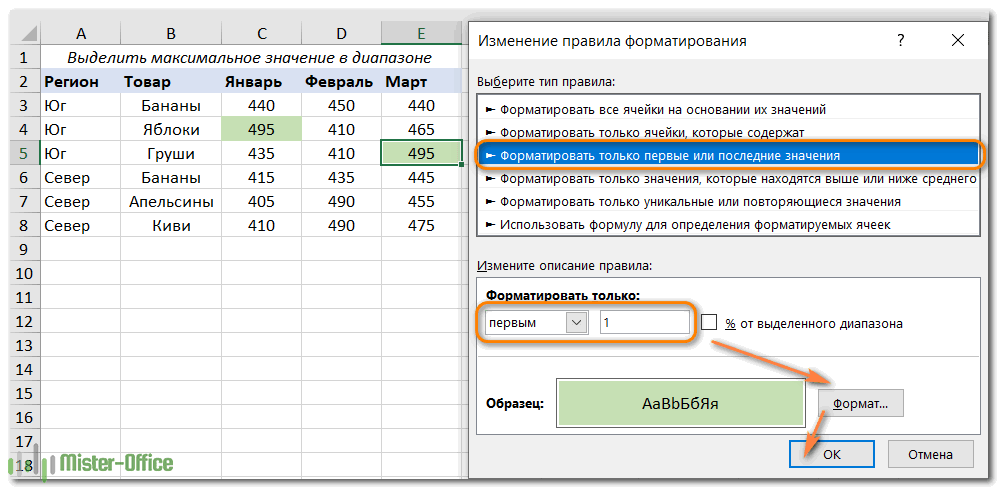
В Microsoft Excel есть встроенное правило для форматирования максимальных чисел в диапазоне, которое идеально соответствует нашим потребностям. Вот как можно применить его:
- Выберите диапазон чисел (в нашем случае C2: E8).
- На вкладке «Главная» в группе «Стили» щелкните «Условное форматирование»> «Новое правило».
- В диалоговом окне «Новое правило форматирования» выберите «Форматировать только первые или последние значения».
- На нижней панели выберите «первым» из раскрывающегося списка и введите 1 в поле рядом с ним (это означает, что вы хотите выделить только одну ячейку, содержащую наибольшее значение).
- Нажмите кнопку «Формат» и выберите стиль оформления.
- Дважды щелкните OK, чтобы закрыть оба окна.
Как выделить цветом максимальное число в каждой строке
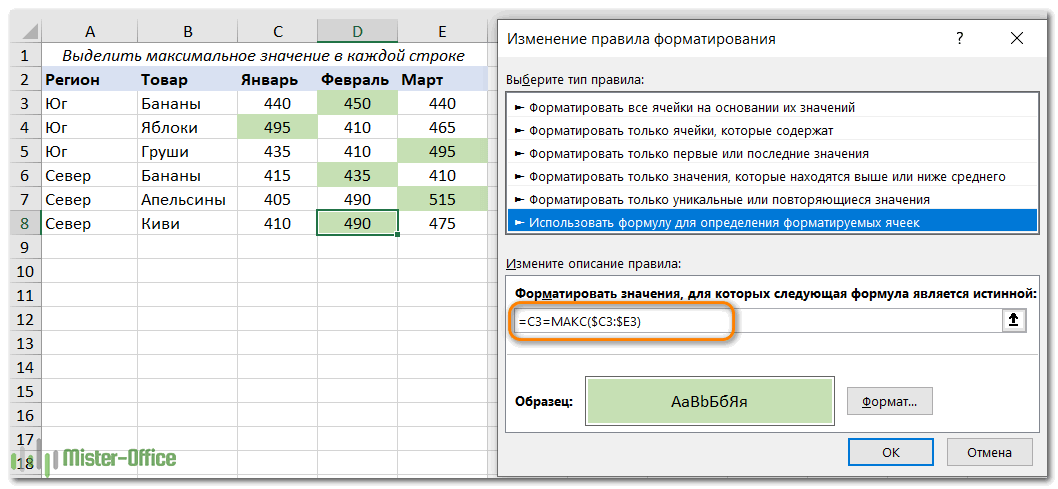
Поскольку нет встроенного правила, чтобы выделить наибольшее значение из каждой строки таблицы Excel, вам придется настроить собственное на основе функции МАКС. Вот как:
- Выберите все строки, которые вы хотите проверить (C3:E8).
- Кликните Новое правило > Использовать формулу.
- В поле Форматировать значения, запишите:
=C3=МАКС($C3:$E3)
Где C3 – крайняя верхняя левая ячейка, а $C3:$E3 – координаты первой строки. Чтобы правило работало, обязательно зафиксируйте координаты столбца в диапазоне знаком $.
- Нажмите кнопку «Формат» и выберите нужный формат.
- Дважды щелкните ОК.
Кончик. Таким же образом вы можете выделить максимальное значение в каждом столбце. Шаги в точности такие же, за исключением того, что вы пишете условие для диапазона первого столбца и фиксируете координаты строки:
=C2=МАКС(C$2:C$7)
Дополнительные сведения см. в статье « Как создать правило условного форматирования на основе формул» .
Почему не получается найти наибольшее число?
МАКС – одна из самых простых в использовании функций Excel. Если вопреки всем ожиданиям она не работает, то, скорее всего, это одна из следующих проблем:
МАКС возвращает ноль
Если обычная формула МАКС возвращает 0, даже если в указанном диапазоне есть числа явно большие, скорее всего, эти числа отформатированы как текст.
Это особенно актуально, когда вы запускаете функцию МАКС для данных, получаемых другими формулами или же импортированных из других программ.
Вы можете проверить это с помощью функции ЕЧИСЛО, например:
=ЕЧИСЛО(A1)
Если приведенная выше формула возвращает ЛОЖЬ, то значение в A1 не является числовым. Это означает, что вы должны устранять неполадки с исходными данными, а не с формулой.
МАКС возвращает значение #Н/Д, #ЗНАЧ или другую ошибку.
Пожалуйста, внимательно проверьте указанные ячейки. Если какая-либо из указанных ячеек содержит ошибку, поиск максимума приведет к той же ошибке. Чтобы обойти это, посмотрите, как получить максимальное значение, игнорируя все ошибки .
Вот как можно найти максимальное значение в Excel. Благодарю вас за чтение!
Функция ЕСЛИОШИБКА – примеры формул – В статье описано, как использовать функцию ЕСЛИОШИБКА в Excel для обнаружения ошибок и замены их пустой ячейкой, другим значением или определённым сообщением. Покажем примеры, как использовать функцию ЕСЛИОШИБКА с функциями визуального… 
Сравнение ячеек в Excel – Вы узнаете, как сравнивать значения в ячейках Excel на предмет точного совпадения или без учета регистра. Мы предложим вам несколько формул для сопоставления двух ячеек по их значениям, длине или количеству…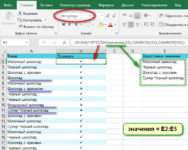 
Как проверить правильность ввода данных в Excel? – Подтверждаем правильность ввода галочкой. Задача: При ручном вводе данных в ячейки таблицы проверять правильность ввода в соответствии с имеющимся списком допустимых значений. В случае правильного ввода в отдельном столбце ставить… 
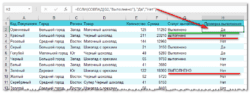Функция ЕСЛИ: проверяем условия с текстом – Рассмотрим использование функции ЕСЛИ в Excel в том случае, если в ячейке находится текст. СодержаниеПроверяем условие для полного совпадения текста.ЕСЛИ + СОВПАДИспользование функции ЕСЛИ с частичным совпадением текста.ЕСЛИ + ПОИСКЕСЛИ… 
Визуализация данных при помощи функции ЕСЛИ – Функцию ЕСЛИ можно использовать для вставки в таблицу символов, которые наглядно показывают происходящие с данными изменения. К примеру, мы хотим показать в отдельной колонке таблицы, происходит рост или снижение продаж.…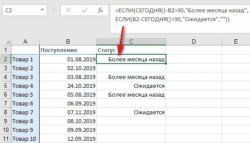 
3 примера, как функция ЕСЛИ работает с датами. – На первый взгляд может показаться, что функцию ЕСЛИ для работы с датами можно применять так же, как для числовых и текстовых значений, которые мы только что обсудили. К сожалению, это…
План урока:
Понятие объема
Свойства объема
Объем куба и прямоугольного параллелепипеда
Объем прямой призмы
Объем цилиндра
Понятие объема
Понятие объема появилось у человечества задолго до того, как геометрия оформилась как строгая наука. Многие вещества и товары, такие как зерно, рис и вода, необходимо хранить и транспортировать в различных упаковках (сосуды, бочки, ящики, контейнеры). При этом разные емкости могут вместить разное количество товаров. Например, пусть есть бочка, имеющая форму цилиндра, и контейнер, выглядящий как прямоугольный параллелепипед:
Предположим, что в бочку можно поместить 5 кг пшеницы, а в контейнер помещается уже 15 кг пшеницы, то есть в контейнер можно положить в 3 раза больше пшеницы, чем в бочку. Можно сказать, что вместимость контейнера втрое больше вместимости бочки. Однако измерять вместимость емкости с помощью массы пшеницы, помещаемой в него, неудобно, ведь в них можно класть и другие вещества. Мы можем положить в емкости что-нибудь более тяжелое, например сухой песок. Тогда в бочку может влезть уже 10 кг песка, а в контейнер – 30 кг. И снова получается, что вместимость контейнера втрое больше, хотя масса вещества увеличилась.
Именно для измерения вместимости и было введено понятие объема. Если в одну упаковку помещается вдвое больше товаров, чем во вторую упаковку, то и объем у нее будет вдвое больше. С древнейших времен замечено, что отношение объемов двух сосудов не зависит от того вещества, которое в них хранят. Например, если в один сосуд помещается в 5 раз больше риса, чем в другой сосуд, то в него также будет помещаться в 5 раз больше воды, в 5 раз больше песка, в 5 раз больше нефти и т. д. Таким образом, в практическом смысле объем – это количественная характеристика вместимости тех или иных упаковок.
В рамках стереометрии изучаются не реальные сосуды, а абстрактные тела. Каждое из них занимает определенную часть пространства, большую или меньшую. Объем используется для измерения этих частей пространства. Для обозначения объема используется латинская буква V.
Для измерения объема необходима единица измерения. Условно принимается, что куб, чьим ребром является единичный отрезок, имеет объем, равный единице. Такой куб именуется единичным. Заметим, что грани единичного куба – это единичные квадраты.
В случае, когда длина ребра куба является безразмерной величиной, то объем также будет безразмерной величиной. Если же указана единица измерения длины, то объем куба будет измеряться этой же единицей, к которой приписано слово «кубический». Например, если ребро куба равно 1 м, то объем куба будет равен 1 кубическому метру, или 1 м3. Объем куба с ребром 1 мм будет составлять 1 мм3 и т. д.
,
Свойства объема
Свойства объема во многом совпадают со свойствами площади. Ясно, что у равных тел будут одинаковы и объемы.
Второе свойство объема связано с тем, что он является аддитивной величиной. Это значит, что если тело можно разбить на несколько тел, то его объем будет равен сумме объемов этих тел.
Это свойство аддитивности объема уже позволяет решать некоторые стереометрические задачи.
Задание. Тело состоит из цилиндра объемом 12 см3 и конуса объемом 4 см3. Каков объем этого тела?
Решение. Здесь надо просто сложить объемы цилиндра и конуса, чтобы найти общий объем всей фигуры:
Ответ: 16 см3.
Задание. Найдите объем фигуры, показанной на рисунке:
Решение. Данную фигуру несложно разбить на три единичных куба:
Тогда объем тела будет равен сумме объемов трех единичных кубов, то есть трем:
Ответ: 3.
Задание. Вычислите объем фигуры, получающейся при рассечении куба плоскостью, проходящей через два его ребра.
Решение. Ясно, что такая секущая плоскость будет делить куб на две равные фигуры (иначе просто не удастся провести плоскость через два ребра):
Также понятно, что два получившихся многогранника равны друг другу. Обозначим объем каждого из них как V. Тогда в сумме их объем должен быть равен 1, ведь вместе эти фигуры образуют единичный куб. Это позволяет составить уравнение, из которого можно вычислить величину V:
Объем куба и прямоугольного параллелепипеда
Докажем важную вспомогательную теорему:
Действительно, пусть у двух параллелепипедов одинаковы основания. Тогда их можно совместить. Пусть общим основанием будет АВСD, а высотами параллелепипедов будут отрезки АР и АК, причем АР <АК. Объем меньшего параллелепипеда с высотой АР обозначим как VР, а большего – как VK:
Нам надо доказать, что объемы фигур пропорциональны их высотам:
Для начала рассмотрим случай, когда отношение высот является рациональным числом. Это означает, что существует некоторая дробь m/n, такая, что
где m и n – натуральные числа. Тогда разобьем отрезок АК как раз на n равных отрезков. В этом случае отрезок АР будет состоять в точности из m таких отрезков. Далее через концы отрезков проведем плоскости, параллельные основанию:
В результате мы получили n равных параллелепипедов («пластин»), которые все вместе образуют большой параллелепипед объемом VK. Поэтому объем одной такой пластины равен величине VK/n:
Итак, мы доказали теорему для случая, когда отношение высот является рациональным числом. Теперь перейдем к более сложному случаю, когда это отношение представляет собой иррациональное число. Здесь можно рассуждать от противного. Предположим, что теорема ошибочна, тогда для каких-нибудь двух параллелепипедов отношение их объемов будет равно не отношению их высот, а какому-то другому числу k:
Это значит, что k либо меньше, либо больше, чем отношение АР/АК. Рассмотрим случай, когда k< АР/АК (случай, когда k> АР/АК, рассматривается аналогичным образом). Тогда возьмем какое-нибудь рациональное число R, находящееся между числами k и АР/АК:
(Примечание. Здесь мы неявно используем утверждение, которое можно доказать в рамках алгебры – между любыми двумя различными действительными числами располагается хотя бы одно рациональное число).
Умножим это неравенство на длину АК:
Построим параллелепипеды с общим основанием АВСD и высотами АК и АР, а также с высотой АЕ = R•АК. Так как R•АК < АР, то точка Е будет лежать между А и Р:
Объем параллелепипеда с высотой АЕ обозначим как VЕ. Ясно, что
ведь число k не может быть одновременно и больше, и меньше R. Полученное противоречие означает, что исходное предположение об ошибочности теоремы неверно, и на самом деле она справедлива, ч. т. д.
Теперь с помощью доказанной теоремы можно вывести известную ещё из младших классов формулу для расчета объема прямоугольного параллелепипеда.Пусть измерения прямоугольного параллелепипеда являются числами а, b и c. Построим:
- единичный куб;
- параллелепипед с габаритами а, 1, 1 с объемом V1;
- параллелепипед с габаритами а, b, 1 с объемом V2;
- параллелепипед с габаритами а, b, c с объемом V.
Тогда можно последовательно вычислить их объемы. Объем первого параллелепипеда будет в а раз больше объема единичного куба, то есть он будет равен а. Объем второго параллелепипеда будет больше ещё в bраз, а третьего – ещё в с раз:
Соответственно, для расчета объема параллелепипеда используется формула
Иногда эту формулу формулируют несколько иначе: объем параллелепипеда – это произведение площади его основания на длину высоты, перпендикулярной этому основанию.
Задание. Три смежных ребра прямоугольного параллелепипеда имеют длины 9, 4 и 7 см. Каков объем параллелепипеда?
Решение. Здесь надо просто перемножить габариты параллелепипеда:
Ответ: 252 см3.
Куб можно рассматривать как прямоугольный параллелепипед с одинаковыми измерениями. Поэтому для вычисления его объема надо умножить ребро куба само на себя дважды, то есть возвести его в куб.
Задание. Вычислите объем куба с ребром 8 метров.
Решение. Просто возводим сторону ребро куба в третью степень:
Задание. Если ребро куба увеличить на 2 дм, то его объем вырастет на 98 дм3. Какова длина ребра этого куба?
Решение. Обозначим длину ребра буквой х. Тогда объем куба будет составлять х3 дм. Если ребро увеличить на 2 дм, то оно будет иметь длину х + 2 дм, и тогда объем куба будет равен уже (х + 2)3 дм. Условие задачи можно записать в виде уравнения:
Это квадратное уравнение имеет два корня, 3 и (– 5), что можно проверить с помощью теоремы Виета. Корень х = – 5 не имеет геометрического смысла, поэтому остается ответ х = 3.
Ответ: 3 дм.
Далее рассмотрим перевод единиц измерения объема. Например, как перевести 1 м3 в кубические сантиметры? Рассмотрим куб с ребром 1 м. Ясно, что его объем будет равен 1 м3. С другой стороны, можно сказать, что длина ребра этого куба составляет 100 см:
Тогда объем этого куба можно посчитать так:
Аналогично можно переводить и другие единицы измерения.
Объем прямой призмы
Рассмотрим сначала прямую призму, в чьем основании располагается прямоугольный треугольник. Ее можно достроить до прямоугольного параллелепипеда:
Ясно, что объем параллелепипеда будет вдвое больше объема исходной призмы, ведь он состоит из двух таких призм. Аналогично и площадь основания у параллелепипеда будет вдвое больше. Обозначим площадь основания призмы буквой S, а ее высоту как h, тогда площадь основания параллелепипеда будет 2S, а его объем составит 2S•h. Тогда объем призмы будет вдвое меньше, то есть он окажется равным S•h.
Далее рассмотрим прямую призму, в основании которой лежит уже произвольный треугольник. Проведем в этом треугольнике высоту, которая упадет на противоположную сторону (такую высоту всегда можно провести). Далее через эту высоту проведем плоскость, перпендикулярную основанию. В результате мы разделим призму на две прямых призмы, в основании каждой из которых будет лежать прямоугольный треугольник:
Пусть площади получившихся прямоугольных треугольников обозначены как S1и S2, а общая площадь основания исходной призмы – это S. Мы можем вычислить объемы этих призм:
Теперь, наконец, рассмотрим прямую призму, чье основание – произвольный многоугольник. Этот многоугольник можно разбить на несколько треугольников с площадями S1, S2, S3…, а призма соответственно будет разбита на несколько треугольных призм с объемами V1, V2, V3 и. т. д.
Объем каждой треугольный призмы мы можем рассчитать:
Задание. Все ребра правильной шестиугольной призмы одинаковы, их длина обозначена буквой а. Найдите объем такой призмы.
Решение. Сначала необходимо найти площадь основания призмы, то есть площадь правильного шестиугольника. Напомним формулы для правильных многоугольников, изученные ещё в девятом классе:
Для вычисления объема надо лишь умножить полученную площадь на высоту призмы, а она также равна а:
Задание. В кубе АВСDА1В1С1D1 через середины ребер СD и BC проведено сечение, параллельное ребру СС1. Это сечение отсекает от куба треугольную призму, чей объем равен 19. Найдите объем куба.
Решение. Ясно, что и куб, и треугольная призма будут прямыми призмами, причем у них одинаковая высота СС1. Тогда можно утверждать, что отношение их объемов равно отношению площадей их оснований:
Пусть сторона АВ имеет длину а. Тогда площадь квадрата АВСD будет составлять а2. Отрезки ЕС и FC будут вдвое короче АВ, то есть их длина составляет a/2. ∆EFC – прямоугольный, и его площадь может быть рассчитана как половина произведения его катетов:
Объем цилиндра
Цилиндр не получится разбить на несколько призм, поэтому для вычисления его объема используется другой метод. Впишем цилиндр в правильную n-угольную призму. Одновременно построим и другую правильную n-угольную призму, которая сама будет вписана в цилиндр. Объем вписанной призмы обозначим как Vв, а объем описанной призмы как Vо. Объем самого цилиндра – это Vц. При этом высоты всех трех фигур одинаковы:
Ясно, что объем вписанной призмы меньше объема цилиндра, а тот в свою очередь меньше объема описанной призмы:
Теперь будем неограниченно увеличивать число n. При этом площади Sв и Sо будут стремиться к площади основания цилиндра, равной величине πr2, где r– радиус основания цилиндра. Это возможно лишь в том случае, если справедливо равенство
Задание. Найдите объем цилиндра с высотой 5 см и радиусом 6 см.
Решение. Сначала находим площадь основания:
Задание. Известно, что высота цилиндра вдвое больше его радиуса, а объем цилиндра равен 54π. Найдите радиус цилиндра.
Решение. Обозначим радиус цилиндра буквой х. Тогда по условию высота будет вдвое больше, то есть она составит 2х. Вычислим объем цилиндра:
Ответ: 3.
Задание. Труба изготовлена из металла с плотностью 11,4 г/см3. Внутренний диаметр трубы равен 13 мм, а ее стенка имеет толщину 4 мм. Длина трубы – 25 метров. Какова ее масса?
Решение. Для расчета массы необходимо сперва вычислить объем трубы. Ясно, что если к объему трубы прибавить объем внутреннего отверстия, то в итоге получится объем большого цилиндра, чей диаметр равен наружному диаметру трубы:
Легко найти объем отверстия, ведь оно имеет форму цилиндра. Его радиус вдвое меньше диаметра, то есть он равен 13/2 = 6,5 мм. При расчете важно не забыть перевести высоту в миллиметры:
Сегодня мы узнали о такой характеристике тел, как объем. Если объем куба и прямоугольного параллелепипеда мы умели находить ещё в средней школе, то определять объем цилиндра и прямой призмы мы научились только сейчас. Однако все эти случаи по сути одинаковы – надо перемножить высоту фигуры и площадь ее основания. В будущем мы научимся вычислять объемы более сложных фигур – пирамиды, конуса, шара.
Основные формулы для решения задач по химии
05-Авг-2012 | комментариев 450 | Лолита Окольнова
Все, все основные задачи по химии решаются с помощью
нескольких основных понятий и формул.
У всех веществ разная масса, плотность и объем. Кусочек металла одного элемента может весить во много раз больше, чем точно такого же размера кусочек другого металла.
Моль (количество моль)
обозначение: моль, международное: mol — единица измерения количества вещества. Соответствует количеству вещества, в котором содержится NA частиц (молекул, атомов, ионов). Поэтому была введена универсальная величина — количество моль. Часто встречающаяся фраза в задачах — «было получено… моль вещества»
NA = 6,02 · 1023
NA — число Авогадро. Тоже «число по договоренности». Сколько атомов содержится в стержне кончика карандаша? Несколько миллионов. Оперировать такими величинами не удобно. Поэтому химики и физики всего мира договорились — обозначим 6,02 · 1023 частиц (атомов, молекул, ионов) как 1 моль вещества.
1 моль = 6,02 · 1023 частиц
Это была первая из основных формул для решения задач.
Молярная масса вещества
Молярная масса вещества — это масса одного моль вещества. Обозначается как M
Есть еще молекулярная масса — Mr
Находится по таблице Менделеева — это просто сумма атомных масс вещества.
Например, нам дана серная кислота — H2SO4. Давайте посчитаем молярную массу вещества: атомная масса H =1, S-32, O-16.
Mr(H2SO4)=1•2+32+16•4=98 гмоль.
Вторая необходимая формула для решения задач —
формула массы вещества:
Т.е., чтобы найти массу вещества, необходимо знать количество моль (n), а молярную массу мы находим из Периодической системы.
Закон сохранения массы — масса веществ, вступивших в химическую реакцию, всегда равна массе образовавшихся веществ.
Если мы знаем массу (массы) веществ, вступивших в реакцию, мы можем найти массу (массы) продуктов этой реакции. И наоборот.
Третья формула для решения задач по химии —
объем вещества:
Откуда взялось число 22.4? Из закона Авогадро:
в равных объёмах различных газов, взятых при одинаковых температуре и давлении, содержится одно и то же число молекул.
Согласно закону Авогадро, 1 моль идеального газа при нормальных условиях (н.у.) имеет один и тот же объём Vm = 22,413 996(39) л
Т.е., если в задаче нам даны нормальные условия, то, зная количество моль (n), мы можем найти объем вещества.
Итак, основные формулы для решения задач по химии
Число Авогадро NA
6,02 · 1023 частиц
Количество вещества n (моль)
n=mM
n=V22.4 (лмоль)
Масса вещества m (г)
m=n•Mr
Объем вещества V(л)
V=n•22.4 (лмоль)
или вот еще удобная табличка:
Это формулы. Часто для решения задач нужно сначала написать уравнение реакции и (обязательно!) расставить коэффициенты — их соотношение определяет соотношение молей в процессе.
В ОГЭ и ЕГЭ по химии задач , в которых нужно было бы найти только объем массу кол-во моль нет — это обычно ЧАСТЬ решения задачи. Однако, чтобы легко решать более сложные задачи, нужно тренироваться на таких вот небольших упражнениях.
Находим количество вещества по массе
1 Какое количество вещества алюминия содержится в образце металла массой 10.8 г?2 Какое количество вещества содержится в оксиде серы (VI) массой 12 г?
3 Определите количество моль брома, содержащееся в массе 12.8 г.
Находим массу по количеству вещества:
4. Определите массу карбоната натрия количеством вещества 0.25 моль.Объем по количеству вещества:
5. Какой объем будет иметь азот при н.у., если его количество вещества 1.34 моль?6. Какой объем занимают при н.у. 2 моль любого газа?
Ответы:/p>
- 0.4 моль
- 0.15 моль
- 0.08 моль
- 26.5 г
- 30 л
- 44.8 л
Категории:
|
Обсуждение: “Основные формулы для решения задач по химии”
(Правила комментирования)
