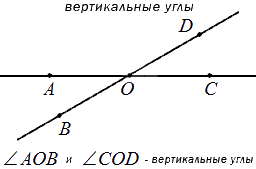
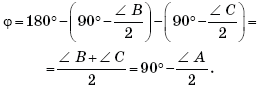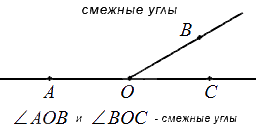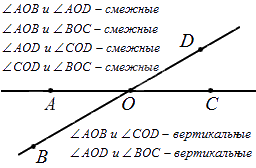Вопрос: Как определить наибольший угол треугольника?
Как найти наибольший угол в треугольнике?
сначала используйте Закон косинусов, чтобы вычислить наибольший угол. затем используйте Закон синусов, чтобы найти другой угол. и, наконец, добавьте углы треугольника к 180 °, чтобы найти последний угол.
Как узнать, какой угол больше?
Сможете определить, какой угол самый большой? Как вы могли догадаться, наибольший угол будет противоположным 18, потому что это самая длинная сторона. Точно так же наименьший угол будет противоположен самой короткой стороне, 7. Следовательно, размер угла в середине будет противоположным 13.
Какой угол у треугольника самый большой?
Наибольший угол в 5 раз меньше наименьшего, поэтому наибольший угол равен 5 градусам. Таким образом, наименьший угол составляет 24 градуса.
.
| слова | проверка |
|---|---|
| Наибольший угол треугольника в 5 раз больше наименьшего. | 120 в пять раз больше 24? Да! |
Как найти угол треугольника от наименьшего к наибольшему?
В любом треугольнике наименьший угол всегда поперек самой короткой стороны, а наибольший угол всегда поперек самой длинной стороны. В приведенном выше треугольнике ABC, поскольку угол A является наименьшим углом, сторона BC должна быть самой короткой стороной.
Как найти угол треугольника с двумя сторонами?
- Шаг 1 Две известные нам стороны – Противоположная (300) и Соседняя (400).
- Шаг 2 SOHCAHTOA сообщает нам, что мы должны использовать Tangent.
- Шаг 3 Вычислить напротив / рядом = 300/400 = 0.75.
- Шаг 4 Найдите угол на калькуляторе с помощью tan-1.
Какая сторона в прямоугольном треугольнике самая короткая?
В любом треугольнике самая длинная сторона противоположна наибольшему углу, а самая короткая сторона противоположна наименьшему углу. Таким образом, в прямоугольном треугольнике гипотенуза всегда является самой длинной стороной.
Какое правило поиска недостающей стороны треугольника?
Найти недостающую сторону прямоугольного треугольника довольно просто, если известны две стороны. Одна из наиболее известных математических формул – a2 + b2 = c2 a 2 + b 2 = c 2, известная как теорема Пифагора.
Какой угол противоположен самой длинной стороне?
Концепции. Самая длинная сторона треугольника противоположна наибольшему углу, а самая короткая сторона противоположна наименьшему углу. Неравенство треугольника: В любом треугольнике сумма длин любых двух сторон больше, чем длина третьей стороны. Теорема Пифагора: в прямоугольном треугольнике с гипотенузой c, a2 + b2 = c2.
Становится ли угол больше, если его линии длиннее?
Острые углы часто переоцениваются, что объясняется латеральными тормозными механизмами. … Однако в экспериментах 1 и 2 было обнаружено, что углы с более длинными плечами считаются большими.
Все ли треугольники равны 180 градусам?
Ответ положительный! Чтобы математически доказать, что сумма углов треугольника всегда равна 180 градусам, нам нужно установить некоторые основные факты об углах. Первый факт, который нам нужно рассмотреть, – это определение прямого угла: прямой угол – это просто прямая линия, отсюда и название.
Какое наибольшее количество тупых углов может содержать треугольник?
Джонсон З. Треугольник может иметь максимум 1 тупой угол.
Какая сторона треугольника самая длинная?
В прямоугольном треугольнике гипотенуза – это самая длинная сторона, «противоположная» сторона – это сторона, лежащая напротив заданного угла, а «смежная» сторона находится рядом с заданным углом.
Как определить угол?
Лучший способ измерить угол – использовать транспортир. Для этого вы начнете с выстраивания одного луча вдоль линии под углом 0 градусов на транспортире. Затем совместите вершину с серединой транспортира. Следуйте по второму лучу, чтобы определить угол с точностью до градуса.
Возможен ли треугольник со следующими углами и сторонами?
Нет, невозможно, чтобы сумма угла треугольника составляла 180 градусов.
Треугольник. Формулы и свойства треугольников.
Типы треугольников
По величине углов
По числу равных сторон
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 – 2 bc · cos α
b 2 = a 2 + c 2 – 2 ac · cos β
c 2 = a 2 + b 2 – 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 – a 2
mb = 1 2 √ 2 a 2 +2 c 2 – b 2
mc = 1 2 √ 2 a 2 +2 b 2 – c 2
Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p – a ) b + c
lb = 2√ acp ( p – b ) a + c
lc = 2√ abp ( p – c ) a + b
где p = a + b + c 2 – полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b – c )( b + c – a )( c + a – b ) 4( a + b + c )
Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Связь между вписанной и описанной окружностями треугольника
Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы площади треугольника
Формула Герона
Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
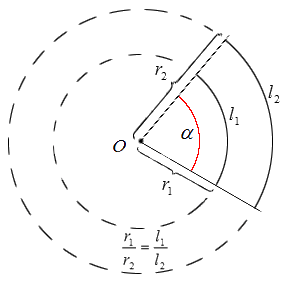
Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k – коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
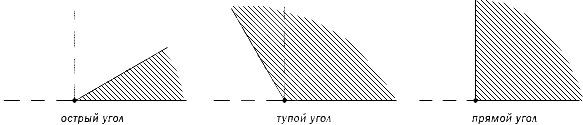
Остроугольный, прямоугольный и тупоугольный треугольники.
Виды треугольников
Остроугольный треугольник — это треугольник,
в котором все углы острые.
Прямоугольный треугольник — это треугольник,
в котором один из углов прямой.
Тупоугольный треугольник — это треугольник,
в котором один из углов тупой.
Как определить вид треугольника
Для того, чтобы понять какой треугольник — остроугольный, прямоугольный или тупоугольный
нужно знать какая градусная мера у углов в треугольнике.
Если один из углов в треугольнике прямой, значит треугольник прямоугольный. Все углы острые в треугольнике — значит треугольник остроугольный. Если в треугольнике один из углов тупой, значит треугольник тупоугольный.
В произвольном треугольнике все углы острые, или два угла острые, а третий прямой или тупой. Если в треугольнике вам известно, что один углов тупой или прямой, значит сумма двух других углов не больше 90 градусов.
В прямоугольном треугольнике стороны напротив острых углов называются катетами, а сторона напротив прямого угла называется гипотенузой.
Градусные меры острого, тупого, прямого углов в треугольниках
Чтобы понять как называется угол и как называется треугольник с этими углами — надо знать его градусную меру:
- Острый угол в любом из треугольников не больше 90 градусов.
- Прямой угол в любом из треугольников равен 90 градусам.
- Тупой угол в любом из треугольников больше 90 градусов, но меньше 180 градусов.
[spoiler title=”источники:”]
http://ru.onlinemschool.com/math/formula/triangle/
http://colibrus.ru/ostrougolnyy-pryamougolnyy-i-tupougolnyy-treugolniki/
[/spoiler]
Сравнение углов
- Сравнение наложением
- Сравнение измерением
Сравнить два угла — это значить узнать, какой из углов больше, какой меньше, или определить, что углы равны.
Сравнить углы можно двумя способами: наложением или измерением их величин.
Сравнение наложением
Рассмотрим, как сравнивать углы путём наложения. Дано два угла, ∠BOA и ∠COA:
Чтобы выяснить, равны они или нет, наложим один угол на другой так, чтобы вершина одного угла совпала с вершиной другого угла и сторона одного угла совместилась со стороной другого:
Мы видим, что ∠СOA составляет часть ∠BOA, поэтому ∠СOA меньше ∠BOA, это записывают так:
∠COA < ∠BOA или ∠BOA > ∠COA.
Если при наложении углов обе их стороны совмещаются, то углы равны.
Сравнение измерением
При сравнении углов путём измерения их величин больше будет тот угол, у которого больше величина.
Пример. Сравнить два угла: ∠BOC и ∠MON.
Так как величина ∠BOC (60°) меньше, чем величина ∠MON (70°), то
∠BOC < ∠MON.
Какой угол больше?
В геометрии сравнение величин играет существенную роль. Даже
если в явном виде вопрос о сравнении величин в задаче не ставится, то по ходу
решения часто приходится это делать или учитывать.
В предлагаемой коллекции задач речь идет о сравнении углов. Умение ответить
на вопрос: «Какой угол больше?», представляется важным для более глубокого и
тонкого понимания ряда геометрических фактов. Такого рода задачи особенно
полезны на начальном этапе изучения геометрии, в 7–9-х классах. Опыт решения
таких задач весьма ценен в последующих «поединках» с куда более трудными
конкурсными и олимпиадными задачами.
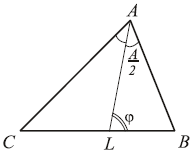
1. В треугольнике ABC AL — биссектриса угла A.
Угол ALB равен ϕ
.
Что больше: или ϕ?
Решение. Поскольку угол
ϕ — внешний для треугольника ALC, то поэтому
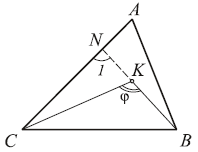
2. Внутри треугольника ABC взята точка K.
Угол BKC равен ϕ>.
Что больше: ϕ или
A?
Решение. Продлим BK до пересечения с AC в
точке N. Очевидно, 1
> A (он
является внешним для треугольника ABN). Но
ϕ >
1 (так как
ϕ — внешний угол для
треугольника CNK). Следовательно, ϕ > A.
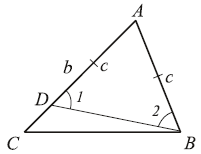
3. В треугольнике ABC сторона AC = b,
сторона AB = c. Известно, что b > c. Какой из углов
больше: B или
C?
Статья опубликована при поддержке школы “Классический пансион МГУ имени М.В.
Ломоносова”. Лучшая частная школа Москвы – общеобразовательное учреждение
универсального образования повышенного уровня, образовательный комплекс
универсального развития, индивидуальный подход к каждому учащемуся,
высококвалифицированные педагоги. Узнать подробнее о школе и предоставляемом
образовании, контакты Вы сможете на сайте, который располагается по адресу: http://www.pansionmsu.ru/pre-school/.
Решение. Поскольку b > c, отложим на
отрезке AC = b отрезок AD, равный c.
Тогда
1 =
2 и
C <
1, так как
1 — внешний для
треугольника BDC.
В то же время B >
2, так как
2 составляет
лишь часть угла B. Значит, B
> C.
Вывод. В треугольнике против большей стороны лежит
больший угол.
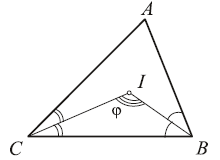
4. Биссектрисы углов B и C треугольника
ABC пересекаются в точке I. Пусть
BIC =
ϕ. Что больше:
ϕ или 90°?
Решение. Из треугольника BIC находим
ϕ:
Таким образом, ϕ > 90°.
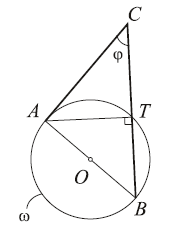
5. AB — диаметр окружности. Точка C
находится вне окружности. ACB
= ϕ. Сравнить угол
ϕ с углом 90°.
Решение . Пусть BC пересекает окружность в точке
T. Соединим точки A и T.
ATB = 90°
(вписанный, опирается на диаметр). Поскольку угол ATB является внешним
для треугольника ACT, то ϕ< 90°. (Если точка
C окажется на прямой AB, то ϕ= 0.)
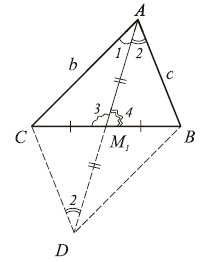
6. AM1 — медиана треугольника ABC,
в котором b > c. Какой из углов больше:
1 или
2?
3 или
4?
Решение. Удвоив медиану AM1, получим
параллелограмм ABDC. При этом
CD = AB = c,
CDA =
2
(внутренние накрест лежащие). В треугольнике ACD
против стороны b лежит угол 2, а против стороны c лежит угол 1.
Следовательно, 2
> 1 (так как
b > c).
Кроме того, 3
= 2 +
B как внешний
угол треугольника ABM1, а
4 =
1 +
C как внешний
угол треугольника ACM1. Поскольку
2 >
1 и
B >
C, то
3 >
4.
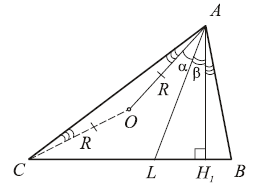
7. В треугольнике ABC AH1 и AL —
соответственно высота и биссектриса. O — центр описанной около этого
треугольника окружности. OAL
= α, LAH1
= β. Что больше: α или β?
Решение . Угол AOC и угол B — соответственно
центральный и вписанный углы, опирающиеся на одну дугу окружности, поэтому
AOC = 2
B
(центральный угол).
Тогда OAC =
OCA = 90°
– B.
Из треугольника ABH1 находим:
BAH1
= 90° –
B.
Так как AL —
биссектриса угла A и OAC
= H1AB,
то α = β (если от равных углов
отнять равные, то останутся равные углы).
Замечание . Покажите, что в случае тупоугольного
треугольника все остается в силе.
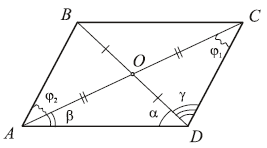
8. В параллелограмме против большей диагонали лежит
больший угол. Докажите!
Решение. Пусть в параллелограмме ABCD диагональ
AC больше диагонали BD. Покажем, что
ADC >
BAD. Так как
AO > OD (половины соответствующих диагоналей), то α > β
(из треугольника AOD). Аналогично из треугольника COD:
γ >
ϕ1 (CO >
DO). Однако ϕ1
= ϕ2
(внутренние накрест лежащие). Тогда α + γ > β +
ϕ2,
или ADC >
BAD.
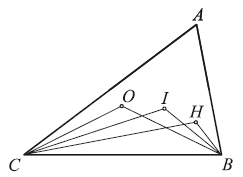
9. В остроугольном треугольнике ABC точки O,
I, H — соответственно центр описанной окружности, центр вписанной
окружности и ортоцентр (точка пересечения высот). Сравните углы BOC,
BIC, BHC.
Решение. Нетрудно показать, что каждый из указанных углов
можно выразить через угол A:
BOC = 2
A,
(покажите!),
BHC = 180°
– A.
Тогда очевидно, что при 0 < A < 60°:
BHC >
BIC >
BOC.
В случае, если A
= 60°:
BHC =
BIC =
BOC.
При 60°
< A < 90°
верно следующее двойное неравенство:
BOC >
BIC >
BHC.
Замечание. 1. Отметим, что если
A = 60°,
то BOC =
BHC =
BIC = 120°.
При этом точки B, H, I, O, C лежат на одной
окружности.
2. Сравните углы BOC, BIC, BHC в случае, когда
треугольник ABC — тупоугольный.
10. Сравните углы B и C треугольника ABC,
в котором hb и hc — высоты к сторонам b
и с соответственно, и hb < hc.
Решение. Поскольку высоты треугольника обратно
пропорциональны его сторонам то, очевидно, b > c, а значит и
B >
C.
11. В треугольнике ABC mb и mc —
медианы к соответствующим сторонам и mb < mc.
Что больше: B
или С?
По формуле медианы
Так как mb < mc, то,
очевидно, b > c, и B
> C.
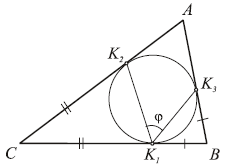
12. Окружность, вписанная в остроугольный треугольник
ABC, касается его сторон в точках K1, K2,
K3. Пусть j
= K2K1K3.
Сравните ϕ и
A.
Решение . Найдем величину угла
j. Треугольник BK1K3 —
равнобедренный (BK1 = BK3 — касательные к
окружности, проведенные из одной точки) и
Аналогично рассуждая, получим
Тогда
Следовательно:
если 0 < A
< 60°, то
ϕ >
A;
если A
= 60°, то
ϕ =
A;
если 60°
< A < 90°,
то ϕ <
A.
Понятно, что в случае тупоугольного треугольника ABC:
ϕ <
A.
13. В остроугольном треугольнике ABC:
A >
B >
C. H
и M — соответственно ортоцентр и центроид (точка пересечения медиан)
этого треугольника. Сравните углы: AHB и AMB; BHC и BMC.
Решение. Проведем в треугольнике ABC высоты AH1 и CH3 и медианы AM1 и CM3.
Поскольку C <
B, то
точка M1 находится между точками C и H1.
То есть высота AH1 проходит внутри треугольника ABM1.
Аналогично, M3 находится между B и H3 (так как B <
A), и
высота CH3 расположена внутри треугольника ACM3.
Таким образом, ортоцентр H находится внутри треугольника AMM3.
Теперь очевидно, что AHB >
AMB,
так как точка H — внутри треугольника AMB (задача 2). А BMC >
BHC, поскольку
центроид M — внутри треугольника BHC.
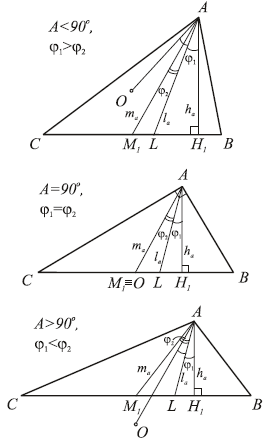
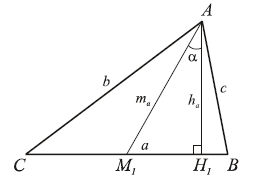
14. Из вершины A треугольника ABC выходят
высота ha, биссектриса la и медиана ma.
Какой угол больше: между высотой и биссектрисой или между биссектрисой и
медианой?
Решение. Пусть ϕj1 —
угол между высотой и биссектрисой, ϕ2 —
угол между биссектрисой и медианой. По задаче 7 биссектриса угла A
является также биссектрисой угла OAH1. Тогда дополнительные
комментарии к рисункам представляются излишними. Таким образом,
если A —
острый угол, то угол между высотой и биссектрисой больше;
если A
= 90°, то они равны;
если A
> 90°, то больше угол
между биссектрисой и медианой.
15. Дан остроугольный треугольник ABC, в котором
A >
B >
C. Пусть:
α =
(ha;
ma), β = (hb;
mb), γ
= (hc;
mc).
Какой из углов α,
β и
γ является наибольшим?
Поскольку A
> B >
C, то и
a > b > c.
Сравним
b2(2(a2 + c2)
– b2) a2(2(b2 + c2) – a2);
2a2b2 + 2b2c2
– b4 2a2b2 + 2a2c2
– a4;
a4 – b4
2c2(a2
– b2); a2 + b2
2c2.
Но a2 + b2 > 2c2
(так как a > c и b > c). Следовательно, cos α > cos β и
α <
β. Сравнив аналогичным
образом cos β и cos γ,
убеждаемся: cos β <
cos γ и
β >
γ. Удивительно, что хотя
B —
средний из углов треугольника ABC, именно угол
β =
(hb;
mb) оказался наибольшим!
Задачи для самостоятельного решения
16. Дан равнобедренный треугольник
ABC
(b = c). На прямой CB за точку B взята точка D.
Что больше: ACB
или ADB?
17. В вершине A треугольника ABC проведена
касательная AQ к описанной около него окружности. Сравните углы ACB
и QAB.
18. В четырехугольнике ABCD углы B и C
равны. Известно, что CD > AB. Какой угол больше: A или D?
19. На медиане AM1 треугольника ABC
взята точка K (произвольно). Известно, что b > c. Сравните
углы ACK и ABK.
20. Биссектрисы углов A, B, C треугольника ABC
пересекают описанную около него окружность соответственно в точках W1,
W2, W3. Пусть
W2W1W3
= ϕ.
Что больше:
ϕ или
A?
21. Сравните углы B и C треугольника ABC,
в котором lb < lc (lb и
lc — биссектрисы углов B и C
соответственно).
Указание. Воспользуйтесь формулой биссектрисы
22. Известно, что в треугольнике ABC с ортоцентром
H выполняется неравенство BH>CH. Что больше:
B или
C?
23. Q — точка, симметричная ортоцентру H
относительно середины стороны BC треугольника ABC. Пусть
ϕ =
BQC. Сравните
ϕ и
A.
24. M — центроид треугольника ABC, в
котором b > c. Что больше:
AMB или
AMC?
25. Из медиан треугольника ABC составлен треугольник с углами
α,
β,
γ (α —
против стороны, равной медиане AM1;
β — против BM2;
γ — против CM3).
Известно, что в треугольнике ABCA >
B >
C.
Сравните углы: A и α,
B и β, C
и γ.
Ануфриева Н., Филипповский Г.
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
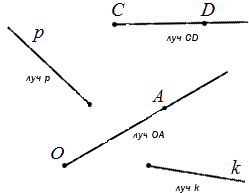
Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
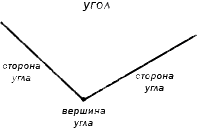
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.
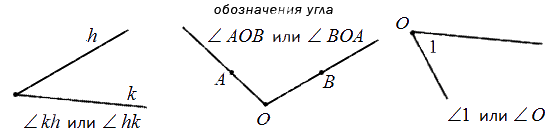
Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной – ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
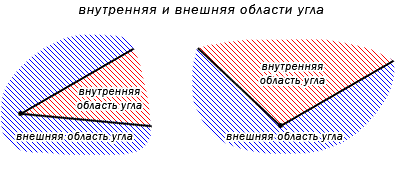
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Сравнение углов
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
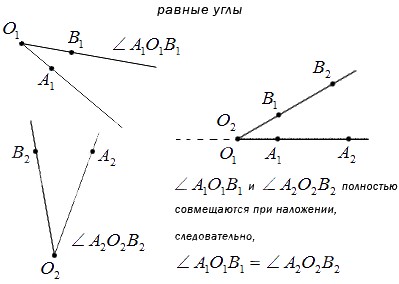
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
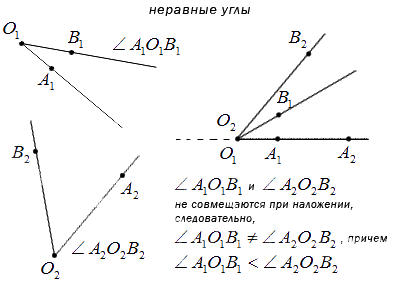
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Минутой называют одну шестидесятую часть градуса.
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «”». Имеет место обозначение:
1°=60’=3600”, 1’=(160)°, 1’=60”, 1”=(160)’=(13600)° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59” .
Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Приведем пример обозначения градусной меры угла равного 17°3’59” . Запись имеет еще один вид 17+360+593600=172393600.
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам».
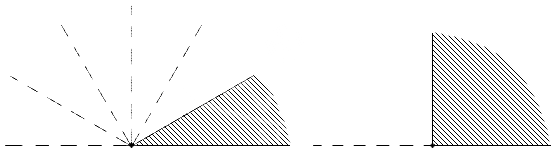
В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов.
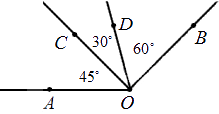
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
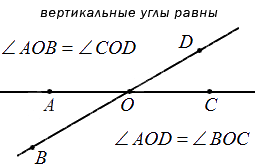
Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
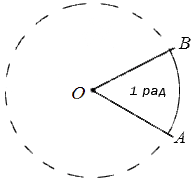
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
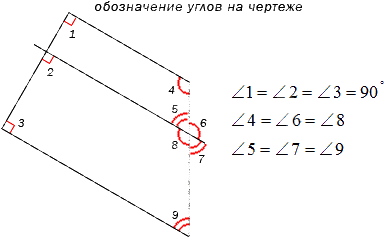
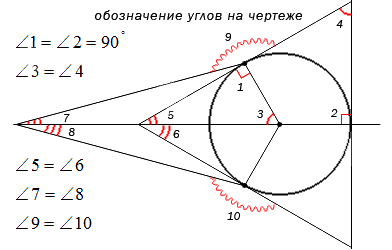
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
|
Сравнить два угла на глаз невозможно, ведь отличаться они могут совсем на немного и тогда нам будет казаться, что углы равные, хотя на самом деле один больше другого. Поэтому обычно сравнивают углы либо измерением с помощью например транспортира, или наложением если такое возможно. И тот и другой вариант имеют свою погрешность, но если абсолютная точность не требуется, то они вполне годятся. При наложении углы просто накладываются друг на друга, чтобы совместились вершина угла и одна сторона обоих углов. Тогда по взаимоположению второй стороны этих углов можно сделать вывод о равенстве или неравенстве углов. автор вопроса выбрал этот ответ лучшим Вили Борисович 6 лет назад В повседневной жизни обычно уроки геометрии не всегда вам пригодятся. Однако если вы например начинаете свой бизнес к примеру производство мебели, то уроки геометрии вам просто необходимы. Поэтому жизнь большая и учится всему лучше уж в школе. Как сравнить углы. Nelli4ka 5 лет назад Углы часто можно сравнить визуально. Если же это не представляется возможным, тогда один угол необходимо наложить на другой. Делается это так: одна сторона любая сторона одного угла накладывается на одну сторону другого угла. Если второй угол перекрывает первый, при этом отчетливо видно, что одна его сторона уходит в сторону, значит, он больше. Он может и “вписываться” в первый угол, тогда он меньше. А может быть, перед вами два одинаковых угла, тогда обе стороны обоих углов совпадут. Но в случае, если они изображены у вас, скажем, в ученической тетради или учебнике, удобнее всего сравнивать углы при помощи транспортира. Сначала замерить один угол, затем второй. У какого угла значение по транспортиру превышает значение другого угла, тот и является большим. Evaina 2 года назад Сравнить углы – это значит узнать какой из углов больше, какой угол меньше, или же , что углы равны. На глаз сравнить углы конечно же невозможно, поэтому есть два способа измерения углов, это наложение одного угла на другой и измерение их величин с помощью транспортира. На рисунке мы видим: А вот как произвести сравнение углов с помощью измерения их величин: Shipo3 5 лет назад Углы могут быть равными или один из них может быть больше другого, второй, соответственно, окажется меньше. Самый надёжный способ – это измерение каждого угла в градусах (например, с помощью линейки транспортёра). Тот угол, который в градусах будет больше, и в реальности будет больше. Если есть возможность, то угол сравнивают наложением. При этом совмещают их вершины и один из лучей (сторон, если это фигура и луч ограничен). mercupit 6 лет назад Можно так: если отрезки прямых, образующие один угол, соответственно параллельны отрезкам прямых, образующие другой угол, то эти углы равны между собой. Знаете ответ? |