
Господин Экзамен
Другие калькуляторы
- График неявной функции
- Поверхность, заданная уравнением
Канонический вид/
Уравнение эллипса
Каноническое уравнение эллипса
⚟
График:
x: [,
]
y: [,
]
z: [,
]
Качество:
(Кол-во точек на оси)
Тип построения:
© Господин Экзамен
Каноническое уравнение эллипса по двум точкам
| Две точки с координатами |
|
Первая координата |
|
Вторая координата |
| Каноническое уравнение эллипса |
| Большая полуось эллипса |
| Малая полуось эллипса |
| Эксцентриситет эллипса |
| Фокусное/фокальное расстояние |
| Коэффициент сжатия |
| Координаты первого фокуса F1(x1:y1) |
| Координаты второго фокуса F2(x2:y2) |
| Фокальный параметр |
| Перифокусное расстояние |
| Апофокусное расстояние |
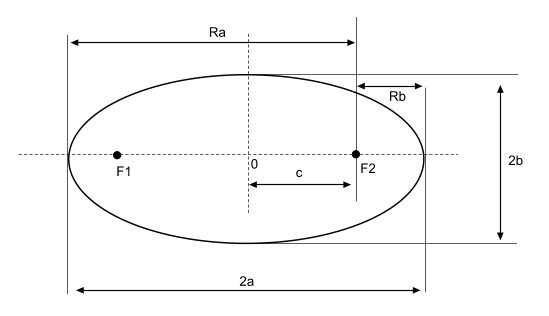
Уравнение эллипса в каноническом виде имеет вот такой вид.
Так как тут всего две переменных, то логично предположить, что по двум заданным точкам мы всегда сможем построить формулу эллипса.
Для расчета поставленной задачи воспользуемся материалом расчет кривой второго порядка на плоскости, который и позволит легко и быстро получить результат.
Кроме этого, на этой странице мы получим следующую информацию.
Фокальный параметр – половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса
Значение полуосей – большая полуось 

Эксцентриситет – коэффициент, показывающий насколько его фигура отличается от окружности
Фокальное расстояние
Коэффициент сжатия – отношение длин малой и большой полуосей
Перифокусное расстояние
Апофокусное расстояние
Примеры задач
Cоставить каноническое уравнение эллипса по двум точкам
Ввводим данные в калькулятор, не забывая что квадратный корень у нас обозначается sqrt
и получаем результат
| Каноническое уравнение эллипса |
 |
| Большая полуось эллипса |
|
8.48528137423857 |
| Малая полуось эллипса |
|
5.656854249492381 |
| Эксцентриситет эллипса |
|
0.8958064164776166 |
| Фокусное/фокальное расстояние |
|
32.2490309931942 |
| Коэффициент сжатия |
|
0.4444444444444444 |
| Координаты первого фокуса F1(x1:y1) |
|
-16.1245154965971 : 0 |
| Координаты второго фокуса F2(x2:y2) |
|
16.1245154965971 : 0 |
| Фокальный параметр |
|
3.5555555555555554 |
| Перифокусное расстояние |
|
1.875484503402901 |
| Апофокусное расстояние |
|
34.1245154965971 |
И еще один пример
Даны две точки с координатами (3:2) и (4:-9) построить каноническое уравнение эллипса.
Если мы введем данные в калькулятор получим
 |
| Большая полуось эллипса |
|
5.877538136328849 |
| Малая полуось эллипса |
|
NaN |
Как видно, одна из осей не может быть определена, так как нам придется брать корень квадратный из отрицательного числа, а следовательно одна из осей будет комплексным числом, что быть не может.
Таким образом по этим двум точкам, нельзя построить эллипс.
А что же можно построить? Перейдя по ссылке данной в начале статьи, мы можем увидеть что это каноническое уравнение гиперболы.
Более подробно, про гиперболу есть отдельный калькулятор Каноническое уравнение гиперболы по двум точкам
Удачных расчетов!
| Equation | Canonical form | Type | Measurement |
|---|---|---|---|
| 9x^2+12xy+4y^2-24x-16y+3=0 | x^2=1 | Two parallel straight lines | Line |
| x^2-2xy+y^2-10x-6y+25=0 | y^2=4*sqrt(2)*x | Parabola | Line |
| 5x^2+4xy+y^2-6x-2y+2=0 | x^2/(1/sqrt(2*sqrt(2)+3))^2 + y^2/(1/sqrt(-2*sqrt(2)+3))^2=0 | Degenerate Ellipse | Line |
| 5*x^2+4*x*y+8*y^2+8*x+14*y+5=0 | x^2/(3/4)^2+y^2/(1/2)^2=1 | Ellipse | Line |
| 2*x^2+4*y^2+z^2-4*x*y-4*y-2*z+5=0 | z^2/(2/sqrt(2)/sqrt(3-sqrt(5)))^2+x^2/(2/sqrt(2)/sqrt(3+sqrt(5)))^2+y^2/(2/sqrt(2))^2=-1 | Imaginary Ellipsoid | Surface |
| x^2+y^2-z^2-2*x-2*y+2*z+2=0 | x^2/1^2+y^2-z^2=-1 | Double Hyperboloid | Surface |
| x^2+y^2-6*x+6*y-4*z+18=0 | x^2/2+y^2-2*z=0 or x^2/2+y^2+2*z=0 | Elliptical Paraboloid | Surface |
| x^2+4*y^2+9*z^2+4*x*y+12*y*z+6*x*z-4*x-8*y-12*z+3=0 | x^2/=1/14 | Two Parallel Planes | Surface |
Here is a simple calculator to solve ellipse equation and calculate the elliptical co-ordinates such as center, foci, vertices, eccentricity and area and axis lengths such as Major, Semi Major and Minor, Semi Minor axis lengths from the given ellipse expression. An ellipse is a figure consisting of all points for which the sum of their distances to two fixed points, (foci) is a constant.
Solve Ellipse Equation
Here is a simple calculator to solve ellipse equation and calculate the elliptical co-ordinates such as center, foci, vertices, eccentricity and area and axis lengths such as Major, Semi Major and Minor, Semi Minor axis lengths from the given ellipse expression. An ellipse is a figure consisting of all points for which the sum of their distances to two fixed points, (foci) is a constant.
Code to add this calci to your website 

Solving Ellipse Equation is just the inverse of finding the ellipse expression from the given elliptical co-ordinates such as center, foci, vertices, eccentricity and area.
| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки

Примеры
-
9x^2+4y^2=36
-
центр:9x^2+4y^2=1
-
ось:16x^2+25y^2=100
-
площадь:25x^2+4y^2+100x-40y=400
-
фокусы:frac{(x-1)^2}{9}+frac{y^2}{5}=100
-
вершины:9x^2+4y^2=36
-
эксцентриситет:16x^2+25y^2=100
- Показать больше
Описание
Рассчитать площадь эллипса, центр, радиус, фокусы, вершины и эксцентриситет шаг за шагом
ellipse-function-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Practice Makes Perfect
Learning math takes practice, lots of practice. Just like running, it takes practice and dedication. If you want…
Read More
Введите Задачу
Сохранить в блокнот!
Войти




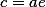


;M_2(3sqrt{1.5}:sqrt{2}))


