Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.
Прямая – это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.
Уравнения прямой, проходящей через две точки могут быть следующих видов:
- каноническое уравнение,
- параметрическое уравнение,
- общее уравнение прямой,
- уравнение прямой с угловым коэффициентом,
- уравнение прямой в полярных координатах и другие.
Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.
Каноническое уравнение прямой на плоскости
{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}
xa и ya – координаты первой точки A,
xb и yb – координаты второй точки B
Параметрическое уравнение прямой на плоскости
{begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases}}
xa, ya – координаты точки, лежащей на прямой,
{l;m} – координаты направляющего вектора прямой,
t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.
Каноническое уравнение прямой в пространстве
{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a} = dfrac{z-z_a}{z_b-z_a}}
xa, ya и za – координаты первой точки A,
xb, yb и zb – координаты второй точки B
Параметрическое уравнение прямой в пространстве
{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a \ z=n cdot t + z_a end{cases} }
xa, ya и za – координаты точки, лежащей на прямой,
{l;m;n} – координаты направляющего вектора прямой,
t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.
Пример нахождения уравнения прямой, проходящей через две точки
Найдем уравнения прямой, проходящей через точки A(1,2) и B(3,8).
Каноническое уравнение прямой
Каноническое уравнение прямой, проходящей через две точки имеет вид {dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}
Подставим в формулу координаты точек A и B: {dfrac{x-1}{3-1} = dfrac{y-2}{8-2}}
Получаем каноническое уравнение прямой: {dfrac{x-1}{2} = dfrac{y-2}{4}}
Уравнение прямой с угловым коэффициентом
Из канонического уравнения получаем уравнение прямой с угловым коэффициентом: {y=3x-1}
Параметрическое уравнение прямой
Параметрическое уравнение прямой имеет вид:
{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases} }
где {x_a, y_b} – координаты точки, лежащей на прямой, {{l;m}} – координаты направляющего вектора прямой, t – произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении. В качестве координат используем координаты точки {A(x_a, y_b)}.
Найдем координаты направляющего вектора:
overline{AB} = {x_b – x_a; y_b – y_a} = {3-1; 8-2} = {2; 6}
Получаем параметрическое уравнение:
begin{cases} x=2 t + 1 \ y=6 t + 2 end{cases}
Используем калькулятор для проверки полученного ответа.
Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.
Уравнение прямой, проходящей через две заданные точки на плоскости
Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.
Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.
Рассмотрим на примере решения подобной задачи. Необходимо составить уравнение прямой a, проходящей через две несовпадающие точки M1(x1, y1) и M2(x2, y2), находящиеся в декартовой системе координат.
В каноническом уравнении прямой на плоскости, имеющего вид x-x1ax=y-y1ay, задается прямоугольная система координат Оху с прямой, которая пересекается с ней в точке с координатами M1(x1, y1) с направляющим вектором a→=(ax, ay).
Необходимо составить каноническое уравнение прямой a, которая пройдет через две точки с координатами M1(x1, y1) и M2(x2, y2).
Прямая а имеет направляющий вектор M1M2→ с координатами(x2-x1, y2-y1), так как пересекает точки М1 и М2. Мы получили необходимые данные для того, чтобы преобразовать каноническое уравнение с координатами направляющего вектора M1M2→=(x2-x1, y2-y1) и координатами лежащих на них точках M1(x1, y1) и M2(x2, y2). Получим уравнение вида x-x1x2-x1=y-y1y2-y1 или x-x2x2-x1=y-y2y2-y1.
Рассмотрим рисунок, приведенный ниже.
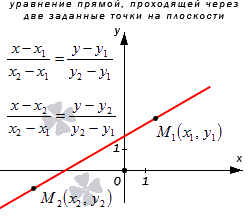
Следуя по вычислениям, запишем параметрические уравнения прямой на плоскости, которое проходит через две точки с координатами M1(x1, y1) и M2(x2, y2). Получим уравнение вида x=x1+(x2-x1)·λy=y1+(y2-y1)·λ или x=x2+(x2-x1)·λy=y2+(y2-y1)·λ.
Рассмотрим подробней на решении нескольких примеров.
Записать уравнение прямой, проходящей через 2 заданные точки с координатами M1-5, 23, M21, -16.
Решение
Каноническим уравнением для прямой, пересекающейся в двух точках с координатами x1, y1 и x2, y2 принимает вид x-x1x2-x1=y-y1y2-y1. По условию задачи имеем, что x1=-5, y1=23, x2=1, y2=-16. Необходимо подставить числовые значения в уравнение x-x1x2-x1=y-y1y2-y1. Отсюда получим, что каноническое уравнение примет вид x-(-5)1-(-5)=y-23-16-23⇔x+56=y-23-56.
Ответ: x+56=y-23-56.
При необходимости решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.
Составить общее уравнение прямой, проходящей через точки с координатами M1(1, 1) и M2(4, 2) в системе координат Оху.
Решение
Для начала необходимо записать каноническое уравнение заданной прямой, которая проходит через заданные две точки. Получим уравнение вида x-14-1=y-12-1⇔x-13=y-11.
Приведем каноническое уравнение к искомому виду, тогда получим:
x-13=y-11⇔1·x-1=3·y-1⇔x-3y+2=0
Ответ: x-3y+2=0.
Примеры таких заданий были рассмотрены в школьных учебниках на уроках алгебры. Школьные задачи отличались тем, что известным было уравнение прямой с угловым коэффициентом, имеющее вид y=kx+b. Если необходимо найти значение углового коэффициента k и числа b, при которых уравнение y=kx+b определяет линию в системе Оху, которая проходит через точки M1(x1, y1) и M2(x2, y2), где x1≠x2. Когда x1=x2 , тогда угловой коэффициент принимает значение бесконечности, а прямая М1М2 определена общим неполным уравнением вида x-x1=0.
Потому как точки М1 и М2 находятся на прямой, тогда их координаты удовлетворяют уравнению y1=kx1+bи y2=kx2+b. Следует решить систему уравнений y1=kx1+by2=kx2+b относительно k и b.
Для этого найдем k=y2-y1x2-x1b=y1-y2-y1x2-x1·x1 или k=y2-y1x2-x1b=y2-y2-y1x2-x1·x2.
С такими значениями k и b уравнение прямой, проходящее через заданные две точки, принимает следующий вид y=y2-y1x2-x1·x+y2-y2-y1x2-x1·x1 или y=y2-y1x2-x1·x+y2-y2-y1x2-x1·x2.
Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.
Записать уравнение прямой с угловым коэффициентом, проходящей через точки с координатами M2(2, 1) и y=kx+b.
Решение
Для решения задачи применяем формулу с угловым коэффициентом, имеющую вид y=kx+b. Коэффициенты k и b должны принимать такое значение, чтобы данное уравнение соответствовало прямой, проходящей через две точки с координатами M1(-7, -5) и M2(2, 1).
Точки М1 и М2 располагаются на прямой, тогда их координаты должны обращать уравнение y=kx+b верное равенство. Отсюда получаем, что -5=k·(-7)+b и 1=k·2+b. Объединим уравнение в систему -5=k·-7+b1=k·2+bи решим.
При подстановке получаем, что
-5=k·-7+b1=k·2+b⇔b=-5+7k2k+b=1⇔b=-5+7k2k-5+7k=1⇔⇔b=-5+7kk=23⇔b=-5+7·23k=23⇔b=-13k=23
Теперь значения k=23 и b=-13 подвергаются подстановке в уравнение y=kx+b. Получаем, что искомым уравнением, проходящим через заданные точки, будет уравнение, имеющее вид y=23x-13.
Такой способ решения предопределяет траты большого количества времени. Существует способ, при котором задание решается буквально в два действия.
Запишем каноническое уравнение прямой, проходящей через M2(2, 1) и M1(-7, -5), имеющее вид x-(-7)2-(-7)=y-(-5)1-(-5)⇔x+79=y+56.
Теперь переходим к уравнению в угловым коэффициентом. Получаем, что: x+79=y+56⇔6·(x+7)=9·(y+5)⇔y=23x-13.
Ответ: y=23x-13.
Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве
Если в трехмерном пространстве имеется прямоугольная система координат Охуz с двумя заданными несовпадающими точками с координатами M1(x1, y1, z1) и M2(x2, y2, z2), проходящая через них прямая M1M2, необходимо получить уравнение этой прямой.
Имеем, что канонические уравнения вида x-x1ax=y-y1ay=z-z1az и параметрические вида x=x1+ax·λy=y1+ay·λz=z1+az·λспособны задать линию в системе координат Охуz, проходящую через точки, имеющие координаты (x1, y1, z1) с направляющим вектором a→=(ax, ay, az).
Прямая M1M2 имеет направляющий вектор вида M1M2→=(x2-x1, y2-y1, z2-z1), где прямая проходит через точку M1(x1, y1, z1) и M2(x2, y2, z2), отсюда каноническое уравнение может быть вида x-x1x2-x1=y-y1y2-y1=z-z1z2-z1 или x-x2x2-x1=y-y2y2-y1=z-z2z2-z1, в свою очередь параметрические x=x1+(x2-x1)·λy=y1+(y2-y1)·λz=z1+(z2-z1)·λ или x=x2+(x2-x1)·λy=y2+(y2-y1)·λz=z2+(z2-z1)·λ.
Рассмотрим рисунок, на котором изображены 2 заданные точки в пространстве и уравнение прямой.
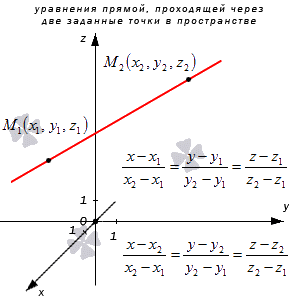
Написать уравнение прямой, определенной в прямоугольной системе координат Охуz трехмерного пространства, проходящей через заданные две точки с координатами M1(2, -3, 0) и M2(1, -3, -5).
Решение
Необходимо найти каноническое уравнение. Так как речь идет о трехмерном пространстве, значит при прохождении прямой через заданные точки, искомое каноническое уравнение примет вид x-x1x2-x1=y-y1y2-y1=z-z1z2-z1.
По условию имеем, что x1=2, y1=-3, z1=0, x2=1, y2=-3, z2=-5. Отсюда следует, что необходимые уравнения запишутся таким образом:
x-21-2=y-(-3)-3-(-3)=z-0-5-0⇔x-2-1=y+30=z-5
Ответ: x-2-1=y+30=z-5.
3.1. Канонические
уравнения прямой.
Пусть в системе
координат Oxyz
дана прямая, которая проходит через
точку
![]()
 (см. рис.18).Обозначим через
(см. рис.18).Обозначим через
![]() вектор, параллельный данной прямой.
вектор, параллельный данной прямой.
Вектор![]() называетсянаправляющим
называетсянаправляющим
вектором прямой.
Возьмем на прямой точку ![]() и рассмотрим вектор
и рассмотрим вектор
![]() Векторы
Векторы![]() коллинеарны, следовательно, их
коллинеарны, следовательно, их
соответствующие координаты пропорциональны:
![]() (3.3.1)
(3.3.1)
Эти уравнения
называются каноническими
уравнениями прямой.
 Пример: Написать
Пример: Написать
уравнения прямой, проходящей через
точку M(1,
2, –1) параллельно вектору
![]()
Решение:
Вектор
![]() является направляющим вектором искомой
является направляющим вектором искомой
прямой. Применяя формулы (3.1.1), получим:
![]()
Это канонические
уравнения прямой.
Замечание:
Обращение в нуль одного из знаменателей
означает обращение в нуль соответствующего
числителя, то есть y
– 2 = 0; y
= 2. Данная прямая лежит в плоскости y
= 2, параллельной плоскости Oxz.
3.2.
Параметрические
уравнения прямой.
Пусть прямая
задана каноническими уравнениями
![]()
Обозначим ![]() тогда
тогда![]() Величина t
Величина t
называется параметром и может принимать
любые значения:
![]() .
.
Выразим x,
y
и z
через t
:
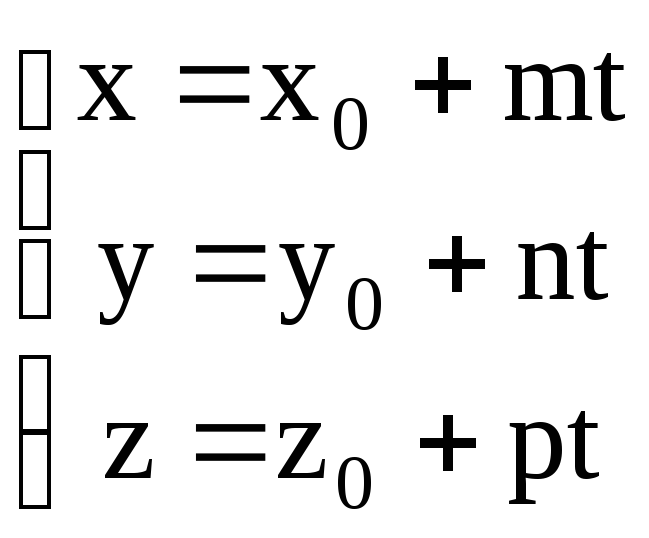 (3.2.1)
(3.2.1)
Полученные уравнения
называются параметрическими
уравнениями прямой.
Пример 1:
Составить
параметрические уравнения прямой,
проходящей через точку M
(1, 2, –1) параллельно вектору ![]()
Решение:
Канонические уравнения этой прямой
получены в примере пункта 3.1:
![]()
Для нахождения
параметрических уравнений прямой
применим вывод формул (3.2.1):
![]()
![]()
Итак,
 – параметрические уравнения данной
– параметрические уравнения данной
прямой.
Ответ:

Пример 2.
Составить
параметрические уравнения прямой,
проходящей через точку M
(–1, 0, 1) параллельно вектору
![]() гдеA
гдеA
(2, 1, –1), B
(–1, 3, 2).
Решение:
Вектор ![]() является направляющим
является направляющим
вектором искомой прямой.
Найдем вектор ![]() .
.![]()
= (–3; 2; 3). По формулам
(3.2.1) запишем уравнения прямой:
 – это искомые
– это искомые
параметрические уравнения прямой.
3.3. Уравнения
прямой, проходящей через две заданные
точки.
Через две заданные
точки в пространстве проходит единственная
прямая (см. рис.20). Пусть даны точки
![]() Вектор
Вектор![]() можно принять за направляющий вектор
можно принять за направляющий вектор
данной прямой. Тогда уравнения прямой
наход им
им
по формулам (3.1.1):![]()
![]() ).
).
![]()
![]() (3.3.1)
(3.3.1)
Пример 1.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки
![]()
Решение:
Применяем
формулу (3.3.1)
![]()
Получили канонические
уравнения прямой. Для получения
параметрических уравнений применим
вывод формул (3.2.1). Получим
![]()
 – это параметрические
– это параметрические
уравнения прямой.
Пример 2.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки ![]()
Решение:
По формулам
(3.3.1) получим:

![]() Это канонические
Это канонические
уравнения.
Переходим к
параметрическим уравнениям:
![]()
 – параметрические
– параметрические
уравнения.
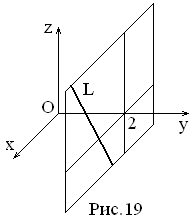
Полученная прямая
параллельна оси oz
(см. рис.21).
3.4. Прямая как
линия пересечения двух плоскостей.
Пусть в
пространстве даны две плоскости
![]() и
и ![]()
Если эти плоскости
не совпадают и не параллельны, то они
пересекаются по прямой:

Эта система двух
линейных уравнений задает прямую как
линию пересечения двух плоскостей. От
уравнений (3.4.1) можно перейти к каноническим
уравнениям (3.1.1) или параметрическим
уравнениям (3.2.1). Для этого необходимо
найти точку
![]() лежащую на прямой, и направляющий вектор
лежащую на прямой, и направляющий вектор![]() Координаты точки
Координаты точки![]() получим из системы (3.4.1), придав одной
получим из системы (3.4.1), придав одной
из координат произвольное значение
(например,z
= 0). За направляющий вектор
![]() можно взять векторное произведение
можно взять векторное произведение
векторов![]() то есть
то есть

Пример 1.
Составить
канонические уравнения прямой
![]()
Решение: Пусть
z
= 0. Решим систему
![]()
Сложив эти уравнения,
получим: 3x
+ 6 = 0
![]() x
x
= –2. Подставим найденное значение x
= –2 в первое уравнение системы и получим:
–2 + y
+ 1 = 0
![]()
![]() y
y
= 1.
Итак, точка
![]() лежит на искомой прямой.
лежит на искомой прямой.
Для нахождения
направляющего вектора прямой запишем
нормальные векторы плоскостей:
![]() и найдем их векторное произведение:
и найдем их векторное произведение:
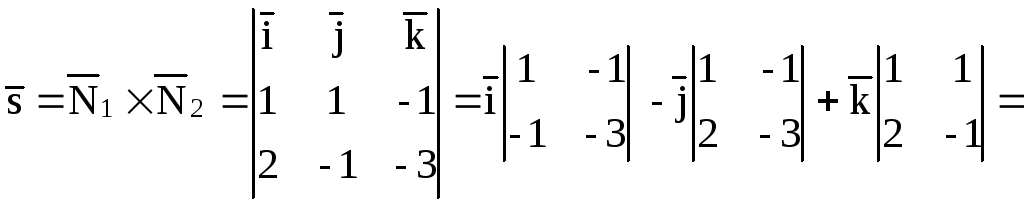
![]()
Уравнения прямой
находим по формулам (3.1.1):
![]()
Ответ: ![]() .
.
Другой способ:
Канонические и параметрические
уравнения прямой (3.4.1) легко получить,
найдя две различные точки на прямой из
системы (3.4.1), а затем применив формулы
(3.3.1) и вывод формул (3.2.1).
Пример 2.
Составить канонические и параметрические
уравнения прямой
![]()
Решение:
Пусть y
= 0. Тогда система примет вид: ![]()
Сложив уравнения,
получим: 2x
+ 4 = 0; x
= –2. Подставим x
= –2 во второе уравнение системы и
получим: –2 –z
+1 = 0
![]() z
z
= –1. Итак, нашли точку
![]()
Для нахождения
второй точки положим x
= 0. Будем иметь: ![]()
![]() То есть
То есть
![]()
Далее применяем
формулы (3.3.1):
![]()
Получили канонические
уравнения прямой.
Составим
параметрические уравнения прямой:
![]()

Ответ:
![]()
;  .
.
3.5. Взаимное
расположение двух прямых в пространстве.
Пусть прямые
![]() заданы уравнениями:
заданы уравнениями:
![]()
 :
:
![]() ;
;![]() :
: ![]()
![]() .
.
Под углом между
этими прямыми понимают угол между их
направляющими векторами
![]() (см. рис.22). Этот угол
(см. рис.22). Этот угол![]() находим по формуле из векторной алгебры:
находим по формуле из векторной алгебры:
![]()
или
![]() (3.5.1)
(3.5.1)
Если прямые ![]() перпендикулярны
перпендикулярны
(![]() ),то
),то
![]() Следовательно,
Следовательно,
![]() (3.5.2)
(3.5.2)
Это условие
перпендикулярности двух прямых в
пространстве.
Если прямые ![]()
параллельны (![]() ),то их направляющие
),то их направляющие
векторы коллинеарны (![]() ),
),
то есть
![]() (3.5.3)
(3.5.3)
Это условие
параллельности двух прямых в пространстве.
Пример 1. Найти
угол между прямыми:
![]() а).
а). ![]()
и ![]()
б). ![]() и
и ![]()
Решение:
а). Запишем направляющий вектор прямой
![]() Найдем направляющий вектор
Найдем направляющий вектор![]() второй прямой. Для этого находим
второй прямой. Для этого находим
нормальные векторы![]() плоскостей, входящих в систему
плоскостей, входящих в систему
![]()
Затем найдем их векторное произведение:
![]()
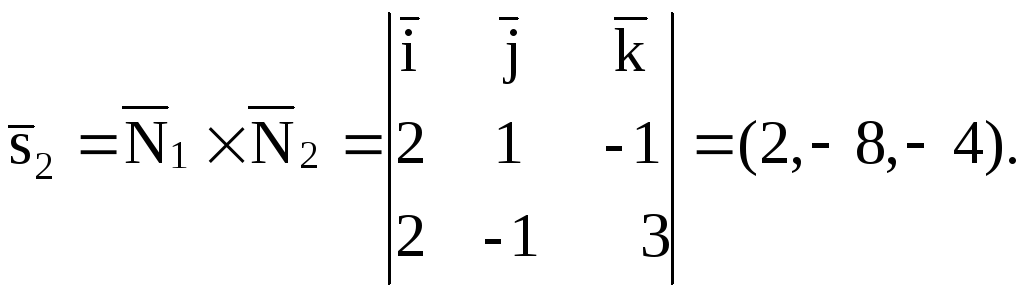 (см. пример 1
(см. пример 1
пункта 3.4).
По формуле (3.5.1)
получим:
![]()
Следовательно,
![]()
б). Запишем
направляющие векторы данных прямых:
![]() Векторы
Векторы![]() коллинеарны, так как их соответствующие
коллинеарны, так как их соответствующие
координаты пропорциональны:
![]() Значит прямые
Значит прямые
![]() параллельны (
параллельны (![]() ),
),
то есть
![]()
Ответ: а).
![]() б).
б). ![]()
Пример 2. Доказать
перпендикулярность прямых:
![]() и
и ![]()
Решение:
Запишем направляющий вектор первой
прямой
![]()
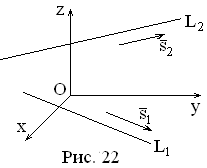
Найдем направляющий
вектор
![]() второй прямой. Для этого находим
второй прямой. Для этого находим
нормальные векторы![]() плоскостей, входящих в систему:
плоскостей, входящих в систему:
![]()
Вычислим их векторное произведение:
![]()
 (См. пример 1пункта 3.4).
(См. пример 1пункта 3.4).
Применим условие
перпендикулярности прямых (3.5.2):
![]()
Условие выполнено;
следовательно, прямые перпендикулярны
(![]() ).
).
Соседние файлы в предмете Математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.20154.96 Кб8Содержание OneNote.onetoc2
- #
Понятие канонического уравнения прямой
Чтобы разобраться, что такое каноническое уравнение, нужно рассмотреть следующий пример. Дана прямоугольная система координат, в которой задана некая произвольная прямая. Известны координаты произвольной точки на отрезке [M_{1}left(x_{1}, y_{1}right)] и координаты направляющего вектора [bar{a}=left(a_{x^{prime}} a_{y}right)]. Используя все имеющиеся данные составим и запишем уравнение, которое будет описывать данную заданную прямую.
Рассмотрим точку [mathrm{M}(x, y)]. Вектор [overline{M_{1} M}] можно отнести к направляющим исходной линии в координатной плоскости. Координатами вектора будут точки [left(x-x_{1}, y-y_{1}right)]. Чтобы правильно определить векторные координаты, необходимо вспомнить основное правило решения векторов.
Произвольные точки [M(x, y)] будут являться основой для необходимой прямой с направляющим вектором [bar{a}=left(a_{x}, a_{y}right)], только тогда, когда вектора [overline{M_{1} M}] и [bar{a}=left(a_{x}, a_{y}right)] будут являться коллинеарными по отношению друг к другу.
Исходя из этого можно составить формулу коллинеарности двух векторов.
Формула
[overline{M_{1} M}=lambda cdot overline{mathrm{a}}, lambda in R]
Где:
После преобразования данного равенства в координатную форму, можно получить следующее уравнение:
[begin{aligned}
&x-x_{1}=lambda cdot a_{x} \
&y-y_{1}=lambda cdot a_{y}
end{aligned}]
Однако, обязательно выполнение главных условий: [a_{x} neq 0] и [a_{y} neq 0].
При выполнении вышеперечисленных условий, получаем следующие равенства:
[begin{aligned}
&x-x_{1}=lambda cdot a_{x} Rightarrow lambda=frac{x-x_{1}}{a_{x}} \
&y-y_{1}=lambda cdot a_{y} Rightarrow lambda=frac{x-x_{1}}{a_{x}} \
&Leftrightarrow frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}
end{aligned}]
Все выполненные преобразования привели к тому, что мы получили окончательную формулу канонического уравнения на плоскости [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}].
Иначе такое равенство, еще называют уравнением прямой канонического вида.
Используя данную запись [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}], можно в прямоугольной системе координат задать прямую, которой будет характерен направляющий вектор [bar{a}=left(a_{x}, a_{y}right)]. Также данная линия будет проходить через заданную точку [M_{1}left(x_{1}, y_{1}right)].
Например: задано уравнение [frac{x-2}{sqrt{3}}=frac{y-3}{1}]. Задается линия, которая будет проходить через точки [M_{1}(2,3)]. Ее направляющий вектор имеет координатные точки: [bar{a}=(sqrt{3}, 1)].
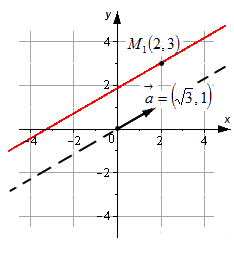
Когда любая прямая в системе координат проходит через две любые точки [M_{1}left(x_{1}, y_{1}right)] и [M_{2}left(x_{2}, y_{2}right)] и имеет направляющий вектор [bar{a}=left(a_{x}, a_{y}right)], множество всех векторов можно записать как [mu cdot overline{mathrm{a}}=left(mu cdot mathrm{a}{x^{prime}} mu cdot a{y}right), mu in R, mu neq 0].
Таким образом, каждое уравнение прямой канонического вида [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}], будет соответствовать заданной прямой на плоскости.
Пример 1
В системе координат задана прямая, которая проходит через точки [M_{1}(2,4)], и имеет направляющий вектор [bar{a}=(1,-3)].
Решение задачи:
Составим и запишем общий вид канонического уравнения [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}].
Далее подставим в него заданные значения [x_{1}=2, y_{1}=-4, a_{x}=1, a_{y}=-3].
Проведем необходимый расчет и получим следующую запись:
[frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}} Leftrightarrow frac{x-2}{1}=frac{y-(-4)}{-2} Leftrightarrow frac{x-2}{1}=frac{y+4}{-3}].
Ответ: [frac{x-2}{1}=frac{y+4}{-3}]
Каноническое уравнение на плоскости с точками ax и ay равными нулевому значению
При условии, что одно из значений переменной является нулю, будет использоваться первоначальный вид уравнения. Две переменные нулевыми быть не могут, так как это невозможно по определению. Направляющий вектор не может быть нулевым.
В такой ситуации выражение [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}] считается условным, и его нужно понимать как равенство [a_{y}left(x-x_{1}right)=a_{x}left(y-y_{1}right)].
Если [frac{x-x_{1}}{0}=frac{y-y_{1}}{a_{y}}] при [a_{x}=0], а заданная прямая проходит через точки [M_{1}left(x_{1}, y_{1}right)]. В данном случае она является параллельной относительно оси ординат. Если [x_{1}=0], то прямая будет совпадать с осью координат.
Утверждение необходимо доказать. Для заданной прямой вектор [bar{a}=left(a_{x}, a_{y}right)] является направляющим. Также данный вектор будет являться коллинеарным по отношению к координатному вектору [bar{j}=(0.1)].
Если второй параметр является нулевым значением, то [a_{y}=0] и мы получим равенство [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{0}]. Данное уравнение характеризует прямую, которая проходит через точку [M_{1}left(x_{1}, y_{1}right)] и располагается параллельно оси абсцисс. Это утверждение будет правдивым, так как [bar{a}=left(a_{x^{prime}} 0right)], и является для прямой направляющим вектором. А вектор, в свою очередь, коллинеарен по отношению к вектору координат [bar{j}=(0.1)].
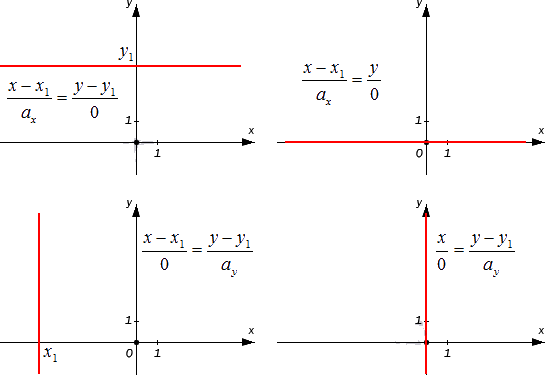
Примеры 2 — 3
На координатной плоскости задана прямая, которая расположена параллельно оси Oy. Она проходит через точку
[M_{1}left(sqrt[3]{2},-frac{1}{7}right)].
Необходимо составить каноническое уравнение для заданной прямой, используя исходные данные.
Решение:
Так как прямая по отношению к координатной оси является параллельной, можно использовать координатный вектор
[bar{j}=(0.1)]. Данный вектор будет служить, как направляющий.
Искомое уравнение будет выглядеть в следующем виде:
[frac{x-sqrt[3]{2}}{0}=frac{y-left(-frac{1}{7}right)}{1} Leftrightarrow
frac{x-sqrt[3]{2}}{0}=frac{y+frac{1}{7}}{1}].
Ответ: [frac{x-sqrt[3]{2}}{0}=frac{y+frac{1}{7}}{1}].
Согласно графику, нужно составить каноническое уравнение прямой.
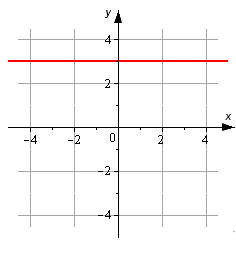
Решение:
Исходя из графика можно сказать, что линия параллельна оси Ox и проходит через точку [M_{1}(0,3)].
Используем координатный вектор как направляющий.
Записываем каноническое уравнение: [frac{x-0}{1}=frac{y-3}{0} Leftrightarrow
frac{x}{1}=frac{y-3}{0}].
Ответ: [frac{x}{1}=frac{y-3}{0}].
Преобразование канонического уравнения прямой в уравнение другого вида
Стандартную форму канонического уравнения [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}] можно поставить в систему параметрических уравнений для плоскости.
Для преобразования одного вида уравнения в другой необходимо одну часть уравнения приравнять к другой.
[begin{aligned}
&frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}} Leftrightarrow frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}=lambda Leftrightarrow frac{x-x_{1}}{a_{y}}=lambda Rightarrow \
&frac{y-y_{1}}{a_{y}}=lambda Leftrightarrow x=x_{1}+a_{x} cdot lambda Rightarrow y=y_{1}+a_{y} cdot lambda
end{aligned}]
Примеры 4 — 5
Задана прямая на плоскости в виде канонического уравнения [frac{x+2}{3}=frac{y-1}{11}].
Необходимо записать параметрическое уравнение для прямой.
Принцип решения задачи:
Нужно поставить знак равенства между отдельными частями уравнения и переменной [lambda]. Получается
следующий вид уравнения: [frac{x+2}{3}=lambda] и [frac{y-1}{11}=lambda].
Далее можно записать необходимы уравнения параметрического вида:
[frac{x+2}{3}=lambda] и [frac{y-1}{11}=lambda.].
[Leftrightarrow x+2=3 cdot lambda] и
[y-1=11 cdot lambda Leftrightarrow x=-2+3 cdot lambda] и [y=1+11 cdot lambda]
Ответ: [x=-2+3 cdot lambda] и [y=1+11 cdot lambda].
Задана на плоскости прямая при помощи канонического уравнения [frac{x-1}{2}=frac{y+4}{0}].
Необходимо составить общей вид канонического уравнения для данной прямой.
Решение:
Аналогичным образом решаем задачу, как в предыдущем примере:
[frac{x-1}{2}=lambda] и [frac{y+4}{0}=lambda].
[Leftrightarrow x-1=2 cdot lambda] и [y+4=0
cdot lambda Leftrightarrow x=-2+1 cdot lambda] и [y=-4+0 cdot lambda]
[Leftrightarrow 0
cdot(x-1)=2 cdot(y+4) Leftrightarrow y+4=0]
Ответ: [y+4=0].
Нет времени решать самому?
Наши эксперты помогут!
Принцип решения задач на составление канонических уравнений
Первым делом канонические уравнения применяется для тех задач, где необходимо вычислить принадлежность точки к заданному отрезку на плоскости.
Рассмотрим несколько вариантов задач, и подробно опишем их решение.
Примеры 6 — 8
Задана линия, каноническое уравнение которой выглядит следующим образом:
[frac{x-1}{2}=frac{y+frac{1}{2}}{-3}].
Нужно определить принадлежат ли две точки [M_{1}left(3,-3 frac{1}{2}right)] и [M_{2}(5,-4)]
прямой.
Решение:
Для того чтобы проверить принадлежность прямой, нужно подставить заданные координаты точек в каноническое
уравнение.
Выполнив данное действие получим верное равенство: [frac{3-1}{2}=frac{-3 frac{1}{2}+frac{1}{2}}{-2}
Leftrightarrow 1=1].
Согласно результату, можно сказать что точка [M_{1}left(3,-3 frac{1}{2}right)] принадлежит заданному
отрезку.
Аналогичным образом нужно поступить и с другой точкой.
[frac{5-1}{2}=frac{-4 frac{1}{2}+frac{1}{2}}{-3} Leftrightarrow 2=frac{7}{6}]
Полученное в ходе решения равенство не является верным, следовательно, точка [M_{2}(5,-4)] не будет ей
принадлежать.
Ответ: прямой принадлежат координаты точки [M_{1}left(3,-3 frac{1}{2}right)], координаты точки
[M_{2}(5,-4)] нет.
Заданы координаты двух точек [M_{1}(2,4)] и [M_{2}(-1,3)]. Нужно определить, будет ли заданная прямая на
плоскости с помощью уравнения [frac{x-2}{0}=frac{y-3}{2}], проходить через заданные координаты.
Решение:
Уравнение [frac{x-2}{0}=frac{y-3}{2}] можно преобразовать, и записать как [2 cdot(x-2)=0 cdot(y-3)
Leftrightarrow x-2=0].
Заданные координаты точек подставим преобразованное уравнение, и произведем проверку.
Для точки [M_{1}(2,4) 2-2=0 Leftrightarrow 0=0].
Так как равенство верное, можно сделать вывод, что точка принадлежит прямой.
Аналогичным образом проводится проверка второй точки: [M_{2}(-1,3)]
[-1-2=0 Leftrightarrow-3=0].
Равенство неверное, поэтому точка [M_{2}(-1,3)] не принадлежит прямой.
Ответ: через точку [M_{1}(2,4)] прямая будет проходить, так как равенство верное, через точку
[M_{2}(-1,3)] нет.
Задачи, в которых заданы точки с координатами, будут являться наиболее простыми по отношению нахождения
канонического уравнения прямой.
Наиболее сложнее решаются задачи, когда предварительно необходимо определить координаты точек, через которые
проходит прямая.
Наиболее распространенной является тип задач, где нужно доказать прохождение прямой, через заданные точки.
Задана прямая, которая проходит через точки [M_{1}(0,-3)] и [M_{2}(2,-2)] в прямоугольной системе координат. Согласно условию задачи, необходимо составить каноническое уравнение.
Решение:
Вычислим координаты вектора [overline{M_{1} M_{2}}=(2.1)], по уже известной методике решения, используя заданные точки. По отношению к прямой данный вектор будет направляющим.
[frac{x-0}{2}=frac{y-(-3)}{1} Leftrightarrow frac{x}{2}=frac{y+3}{1}]
Ответ: [frac{x-0}{2}=frac{y-(-3)}{1} Leftrightarrow frac{x}{2}=frac{y+3}{1}].
Уравнение прямой, проходящей через две точки онлайн
С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через две точки. Дается подробное решение с пояснениями. Для построения уравнения прямой задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точек в ячейки и нажимайте на кнопку “Решить”.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение прямой, проходящей через две точки − примеры и решения
Пример 1. Построить прямую, проходящую через точки A(2, 1, 1), B(3, 1, -2).
 |
(1) |
Подставив координаты точек A и B в уравнение (1), получим:

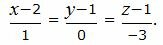
(Здесь 0 в знаменателе не означает деление на 0).
Составим параметрическое уравнение прямой:
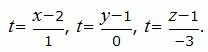
Выразим переменные x, y, z через параметр t :
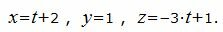
Каноническое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:
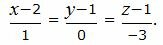
Параметрическое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:
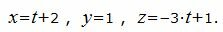
Пример 2. Построить прямую, проходящую через точки A(1, 1/5, 1) и B(−2, 1/2, −2).
 |
(2) |
Подставив координаты точек A и B в уравнение (2), получим:
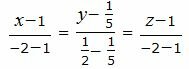
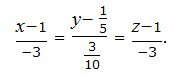
Составим параметрическое уравнение прямой:

Выразим переменные x, y, z через параметр t :
Каноническое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:
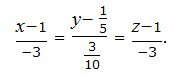
Параметрическое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:
Уравнение прямой, которая проходит через две заданные точки: примеры, решения
Данная статья раскрывает получение уравнения прямой, проходящей через две заданные точки в прямоугольной системе координат, расположенной на плоскости. Выведем уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат. Наглядно покажем и решим несколько примеров, касающихся пройденного материала.
Уравнение прямой, проходящей через две заданные точки на плоскости
Перед получением уравнения прямой, проходящей через две заданные точки необходимо обратить внимание на некоторые факты. Существует аксиома, которая говорит о том, что через две несовпадающие точки на плоскости возможно провести прямую и только одну. Иначе говоря, две заданные точки плоскости определяются прямой линией, проходящей через эти точки.
Если плоскость задана прямоугольной системой координат Оху, то любая изображенная в нем прямая будет соответствовать уравнению прямой на плоскости. Также имеется связь с направляющим вектором прямой. Этих данных достаточно для того, чтобы произвести составление уравнения прямой, проходящей через две заданные точки.
Рассмотрим на примере решения подобной задачи. Необходимо составить уравнение прямой a , проходящей через две несовпадающие точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , находящиеся в декартовой системе координат.
В каноническом уравнении прямой на плоскости, имеющего вид x – x 1 a x = y – y 1 a y , задается прямоугольная система координат О х у с прямой, которая пересекается с ней в точке с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) .
Необходимо составить каноническое уравнение прямой a , которая пройдет через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) .
Прямая а имеет направляющий вектор M 1 M 2 → с координатами ( x 2 – x 1 , y 2 – y 1 ) , так как пересекает точки М 1 и М 2 . Мы получили необходимые данные для того, чтобы преобразовать каноническое уравнение с координатами направляющего вектора M 1 M 2 → = ( x 2 – x 1 , y 2 – y 1 ) и координатами лежащих на них точках M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x – x 1 x 2 – x 1 = y – y 1 y 2 – y 1 или x – x 2 x 2 – x 1 = y – y 2 y 2 – y 1 .
Рассмотрим рисунок, приведенный ниже.
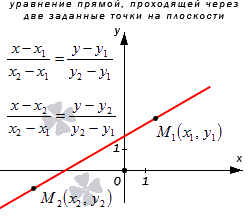
Следуя по вычислениям, запишем параметрические уравнения прямой на плоскости, которое проходит через две точки с координатами M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) . Получим уравнение вида x = x 1 + ( x 2 – x 1 ) · λ y = y 1 + ( y 2 – y 1 ) · λ или x = x 2 + ( x 2 – x 1 ) · λ y = y 2 + ( y 2 – y 1 ) · λ .
Рассмотрим подробней на решении нескольких примеров.
Записать уравнение прямой, проходящей через 2 заданные точки с координатами M 1 – 5 , 2 3 , M 2 1 , – 1 6 .
Каноническим уравнением для прямой, пересекающейся в двух точках с координатами x 1 , y 1 и x 2 , y 2 принимает вид x – x 1 x 2 – x 1 = y – y 1 y 2 – y 1 . По условию задачи имеем, что x 1 = – 5 , y 1 = 2 3 , x 2 = 1 , y 2 = – 1 6 . Необходимо подставить числовые значения в уравнение x – x 1 x 2 – x 1 = y – y 1 y 2 – y 1 . Отсюда получим, что каноническое уравнение примет вид x – ( – 5 ) 1 – ( – 5 ) = y – 2 3 – 1 6 – 2 3 ⇔ x + 5 6 = y – 2 3 – 5 6 .
Ответ: x + 5 6 = y – 2 3 – 5 6 .
При необходимости решения задачи с другим видом уравнения, то для начала можно перейти к каноническому, так как из него проще прийти к любому другому.
Составить общее уравнение прямой, проходящей через точки с координатами M 1 ( 1 , 1 ) и M 2 ( 4 , 2 ) в системе координат О х у .
Для начала необходимо записать каноническое уравнение заданной прямой, которая проходит через заданные две точки. Получим уравнение вида x – 1 4 – 1 = y – 1 2 – 1 ⇔ x – 1 3 = y – 1 1 .
Приведем каноническое уравнение к искомому виду, тогда получим:
x – 1 3 = y – 1 1 ⇔ 1 · x – 1 = 3 · y – 1 ⇔ x – 3 y + 2 = 0
Ответ: x – 3 y + 2 = 0 .
Примеры таких заданий были рассмотрены в школьных учебниках на уроках алгебры. Школьные задачи отличались тем, что известным было уравнение прямой с угловым коэффициентом, имеющее вид y = k x + b . Если необходимо найти значение углового коэффициента k и числа b , при которых уравнение y = k x + b определяет линию в системе О х у , которая проходит через точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , где x 1 ≠ x 2 . Когда x 1 = x 2 , тогда угловой коэффициент принимает значение бесконечности, а прямая М 1 М 2 определена общим неполным уравнением вида x – x 1 = 0 .
Потому как точки М 1 и М 2 находятся на прямой, тогда их координаты удовлетворяют уравнению y 1 = k x 1 + b и y 2 = k x 2 + b . Следует решить систему уравнений y 1 = k x 1 + b y 2 = k x 2 + b относительно k и b .
Для этого найдем k = y 2 – y 1 x 2 – x 1 b = y 1 – y 2 – y 1 x 2 – x 1 · x 1 или k = y 2 – y 1 x 2 – x 1 b = y 2 – y 2 – y 1 x 2 – x 1 · x 2 .
С такими значениями k и b уравнение прямой, проходящее через заданные две точки, принимает следующий вид y = y 2 – y 1 x 2 – x 1 · x + y 2 – y 2 – y 1 x 2 – x 1 · x 1 или y = y 2 – y 1 x 2 – x 1 · x + y 2 – y 2 – y 1 x 2 – x 1 · x 2 .
Запомнить сразу такое огромное количество формул не получится. Для этого необходимо учащать количество повторений в решениях задач.
Записать уравнение прямой с угловым коэффициентом, проходящей через точки с координатами M 2 ( 2 , 1 ) и y = k x + b .
Для решения задачи применяем формулу с угловым коэффициентом, имеющую вид y = k x + b . Коэффициенты k и b должны принимать такое значение, чтобы данное уравнение соответствовало прямой, проходящей через две точки с координатами M 1 ( – 7 , – 5 ) и M 2 ( 2 , 1 ) .
Точки М 1 и М 2 располагаются на прямой, тогда их координаты должны обращать уравнение y = k x + b верное равенство. Отсюда получаем, что – 5 = k · ( – 7 ) + b и 1 = k · 2 + b . Объединим уравнение в систему – 5 = k · – 7 + b 1 = k · 2 + b и решим.
При подстановке получаем, что
– 5 = k · – 7 + b 1 = k · 2 + b ⇔ b = – 5 + 7 k 2 k + b = 1 ⇔ b = – 5 + 7 k 2 k – 5 + 7 k = 1 ⇔ ⇔ b = – 5 + 7 k k = 2 3 ⇔ b = – 5 + 7 · 2 3 k = 2 3 ⇔ b = – 1 3 k = 2 3
Теперь значения k = 2 3 и b = – 1 3 подвергаются подстановке в уравнение y = k x + b . Получаем, что искомым уравнением, проходящим через заданные точки, будет уравнение, имеющее вид y = 2 3 x – 1 3 .
Такой способ решения предопределяет траты большого количества времени. Существует способ, при котором задание решается буквально в два действия.
Запишем каноническое уравнение прямой, проходящей через M 2 ( 2 , 1 ) и M 1 ( – 7 , – 5 ) , имеющее вид x – ( – 7 ) 2 – ( – 7 ) = y – ( – 5 ) 1 – ( – 5 ) ⇔ x + 7 9 = y + 5 6 .
Теперь переходим к уравнению в угловым коэффициентом. Получаем, что: x + 7 9 = y + 5 6 ⇔ 6 · ( x + 7 ) = 9 · ( y + 5 ) ⇔ y = 2 3 x – 1 3 .
Ответ: y = 2 3 x – 1 3 .
Уравнения прямой, которая проходит через две заданные точки в трехмерном пространстве
Если в трехмерном пространстве имеется прямоугольная система координат О х у z с двумя заданными несовпадающими точками с координатами M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , проходящая через них прямая M 1 M 2 , необходимо получить уравнение этой прямой.
Имеем, что канонические уравнения вида x – x 1 a x = y – y 1 a y = z – z 1 a z и параметрические вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ способны задать линию в системе координат О х у z , проходящую через точки, имеющие координаты ( x 1 , y 1 , z 1 ) с направляющим вектором a → = ( a x , a y , a z ) .
Прямая M 1 M 2 имеет направляющий вектор вида M 1 M 2 → = ( x 2 – x 1 , y 2 – y 1 , z 2 – z 1 ) , где прямая проходит через точку M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , отсюда каноническое уравнение может быть вида x – x 1 x 2 – x 1 = y – y 1 y 2 – y 1 = z – z 1 z 2 – z 1 или x – x 2 x 2 – x 1 = y – y 2 y 2 – y 1 = z – z 2 z 2 – z 1 , в свою очередь параметрические x = x 1 + ( x 2 – x 1 ) · λ y = y 1 + ( y 2 – y 1 ) · λ z = z 1 + ( z 2 – z 1 ) · λ или x = x 2 + ( x 2 – x 1 ) · λ y = y 2 + ( y 2 – y 1 ) · λ z = z 2 + ( z 2 – z 1 ) · λ .
Рассмотрим рисунок, на котором изображены 2 заданные точки в пространстве и уравнение прямой.
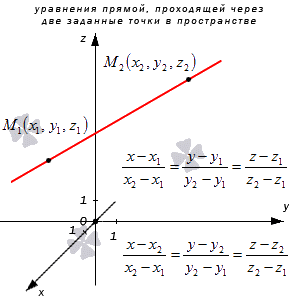
Написать уравнение прямой, определенной в прямоугольной системе координат О х у z трехмерного пространства, проходящей через заданные две точки с координатами M 1 ( 2 , – 3 , 0 ) и M 2 ( 1 , – 3 , – 5 ) .
Необходимо найти каноническое уравнение. Так как речь идет о трехмерном пространстве, значит при прохождении прямой через заданные точки, искомое каноническое уравнение примет вид x – x 1 x 2 – x 1 = y – y 1 y 2 – y 1 = z – z 1 z 2 – z 1 .
По условию имеем, что x 1 = 2 , y 1 = – 3 , z 1 = 0 , x 2 = 1 , y 2 = – 3 , z 2 = – 5 . Отсюда следует, что необходимые уравнения запишутся таким образом:
x – 2 1 – 2 = y – ( – 3 ) – 3 – ( – 3 ) = z – 0 – 5 – 0 ⇔ x – 2 – 1 = y + 3 0 = z – 5
Ответ: x – 2 – 1 = y + 3 0 = z – 5 .
Уравнение прямой проходящей через две точки
Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.
Прямая — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.
Уравнения прямой, проходящей через две точки могут быть следующих видов:
- каноническое уравнение,
- параметрическое уравнение,
- общее уравнение прямой,
- уравнение прямой с угловым коэффициентом,
- уравнение прямой в полярных координатах и другие.
Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-prjamoj-kotoraja-prohodit-cherez-dve-zad/
http://mnogoformul.ru/uravnenie-pryamoj-po-dvum-tochkam
[/spoiler]

