Приведение кривой второго порядка к каноническому виду
Пример №1 . Привести уравнение второго порядка к каноническому виду с помощью поворота и параллельного переноса осей координат. Построить кривую.
Пример №2 . Выполнив последовательно преобразования координат: поворот, а затем параллельный перенос координатных осей, преобразовать к каноническому виду уравнение кривой второго порядка и построить ее в исходной системе координат, а также найти параметры кривой.
Алгоритм перехода кривой второго порядка к каноническому виду
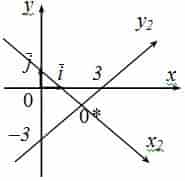
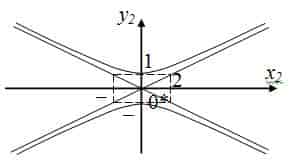
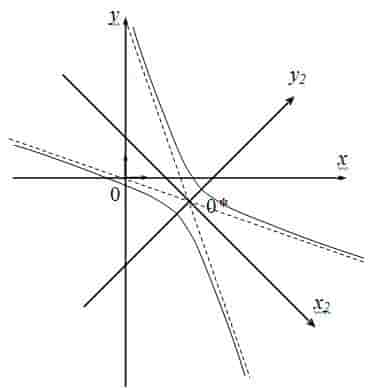
Пример №1 . 4y=-6-sqrt(4x-x 2 )
sqrt(4x-x 2 ) = -(4y+6)
Возведем в квадрат
4x-x 2 = (4y+6) 2
Раскрывая скобки, получаем:
16y 2 +48y + 36 +x 2 -4x = 0
Далее решается калькулятором. Если самостоятельно решать, то получим:
4x-x 2 = (4y+6) 2
-(x 2 – 4x) = 2(y+3/2) 2
-(x 2 – 4x + 4) = (y+3/2) 2
-(x – 2) 2 = (y+3/2) 2
(y+3/2) 2 + (x – 2) 2 = 0
Пример №2 . x=1-2/3 sqrt(y 2 -4y-5)
Здесь надо сначала привести к нормальному виду.
3/2(x-1)=sqrt(y 2 -4y-5)
Возводим в квадрат
9/4(x-1) 2 =y 2 -4y-5
9/4x 2 -9/4*2x+9/4-y 2 +4y+5=0
9/4x 2 -9/2x-y 2 +4y+29/4=0
Далее можно решать как с калькулятором, так и без него:
9/4(x-1) 2 =y 2 -4y-5
9/4(x-1) 2 =y 2 -4y+4-4-5
9/4(x-1) 2 =(y 2 -2)-9
9/4(x-1) 2 -(y 2 -2) = -9
-1/4(x-1) 2 +1/9(y 2 -2) = 1
Кривые второго порядка – определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру – значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде 
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения

- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение  называется уравнением фигуры, если
называется уравнением фигуры, если 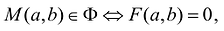 , то есть (а, b) – решение уравнения F(x,y) = 0.
, то есть (а, b) – решение уравнения F(x,y) = 0.
Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения  , т.е. уравнение фигуры задает эту фигуру.
, т.е. уравнение фигуры задает эту фигуру.
Возможны два вида задач:
- дано уравнение
 и надо построить фигуру Ф, уравнением которой является
и надо построить фигуру Ф, уравнением которой является  ;
; - дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения  и решается, чаще всего, методами математического анализа.
и решается, чаще всего, методами математического анализа.
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
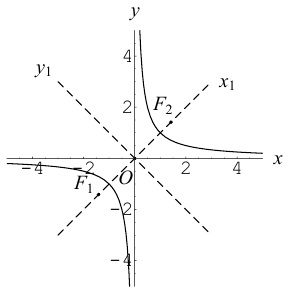
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 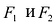 , есть величина постоянная (большая, чем расстояние между
, есть величина постоянная (большая, чем расстояние между 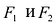 ).
).
Точки 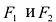 называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с b. В этом случае а называется большой полуосью, a b – малой.
называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с b. В этом случае а называется большой полуосью, a b – малой.
Если а =Ь, то уравнение (7.3) можно переписать в виде:
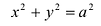 (7.5)
(7.5)
Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 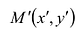 координаты которой задаются формулами
координаты которой задаются формулами 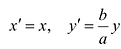 будет окружность (4) переводить в эллипс, заданный соотношением
будет окружность (4) переводить в эллипс, заданный соотношением 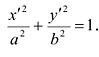
Число 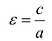 называется эксцентриситетом эллипса. Эксцентриситет
называется эксцентриситетом эллипса. Эксцентриситет 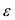 характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении
характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении 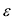 становится более вытянутым
становится более вытянутым
Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 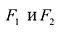 . Их длины
. Их длины 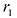 и
и 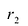 задаются формулами
задаются формулами 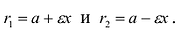 Прямые
Прямые 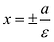 называются директрисами эллипса. Директриса
называются директрисами эллипса. Директриса 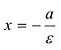 называется левой, а
называется левой, а 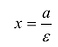 – правой. Так как для эллипса
– правой. Так как для эллипса 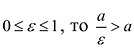 и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины.
и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины.
Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е. 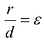
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 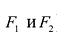 есть величина постоянная (не равная нулю и меньшая, чем расстояние между
есть величина постоянная (не равная нулю и меньшая, чем расстояние между 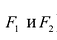 ).
).
Точки 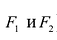 называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов
называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов 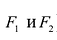 обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А – произвольная точка плоскости с координатами (х, у) и пусть
обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А – произвольная точка плоскости с координатами (х, у) и пусть 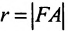 . Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты
. Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты 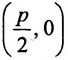 .
.
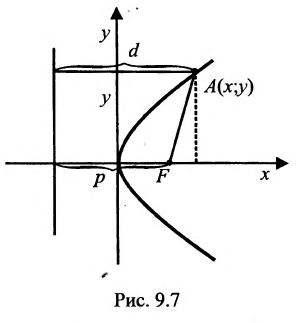
Тогда 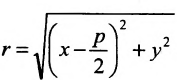 А расстояние
А расстояние 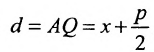 Подставив в формулу r=d, будем иметь
Подставив в формулу r=d, будем иметь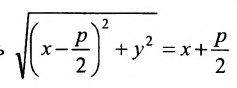 . Возведя обе части равенства в квадрат, получим
. Возведя обе части равенства в квадрат, получим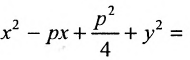
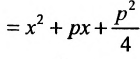 или
или
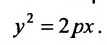 (9.4.1)
(9.4.1)
Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 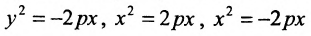 также определяют параболы.
также определяют параболы.
Легко показать, что уравнение 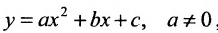 , определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а
, определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а 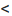 О. Для этого выделим полный квадрат:
О. Для этого выделим полный квадрат:
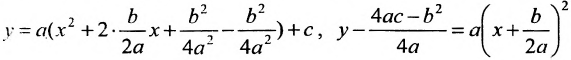
и сделаем параллельный перенос по формулам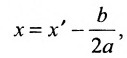
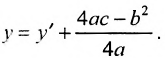
В новых координатах преобразуемое уравнение примет вид: 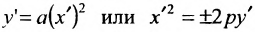 где р – положительное число, определяется равенством
где р – положительное число, определяется равенством 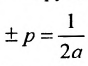 .
.
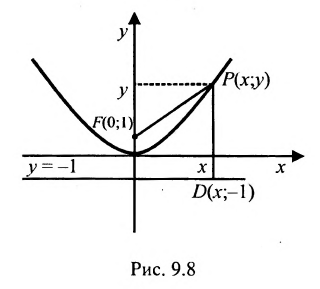
Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию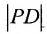 , называется параболой. Прямая у = -1 называется директрисой параболы, а точка F – фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию
, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F – фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию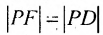 , запишем это равенство с помощью координат:
, запишем это равенство с помощью координат: 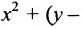
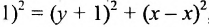 , или после упрощения
, или после упрощения 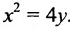 . Это уравнение геометрического места точек, образующих параболу (рис. 9.8).
. Это уравнение геометрического места точек, образующих параболу (рис. 9.8).
Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
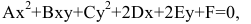
где коэффициенты А, В и С не равны одновременно нулю 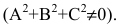
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению
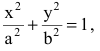 которое называют каноническим уравнением эллипса.
которое называют каноническим уравнением эллипса.
Число а называют большей полуосью эллипса, число 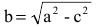 – мень-
– мень-
шей полуосью эллипса, 2а и 2b – соответственно большей и меньшей осями эллипса. Точки 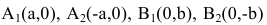 называют вершинами эллипса, а
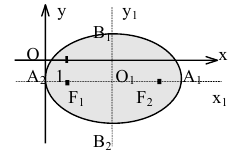
называют вершинами эллипса, а 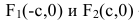 – его фокусами (рис. 12).
– его фокусами (рис. 12).
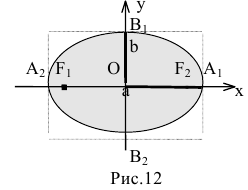
Координатные оси являются осями симметрии эллипса, а начало координат – его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 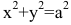 и определяет окружность радиуса а с центром в начале координат.
и определяет окружность радиуса а с центром в начале координат.
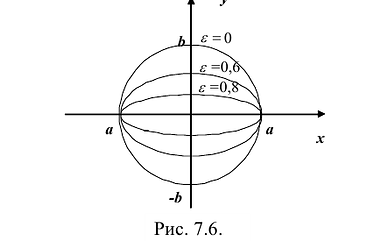
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
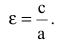
Эксцентриситет изменяется от нуля до единицы 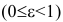 и характеризует форму эллипса. Для окружности
и характеризует форму эллипса. Для окружности 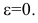 Чем больше эксцентриситет, тем более вытянут эллипс.
Чем больше эксцентриситет, тем более вытянут эллипс.
Пример:
Показать, что уравнение
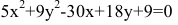
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:
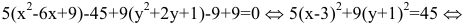
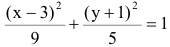 – каноническое уравнение эллипса с центром в точке
– каноническое уравнение эллипса с центром в точке 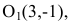 большей полуосью а=3 и меньшей полуосью
большей полуосью а=3 и меньшей полуосью 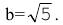
Найдем эксцентриситет эллипса:
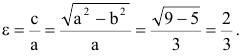
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 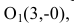 а оси
а оси 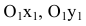 параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.
параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е. 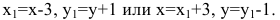
В новой системе координат координаты 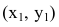 вершин и фокусов гиперболы будут следующими:
вершин и фокусов гиперболы будут следующими:
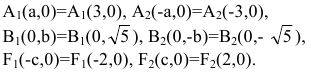
Переходя к старым координатам, получим:
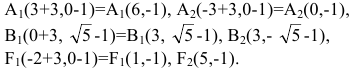
Построим график эллипса.
 Задача решена.
Задача решена.
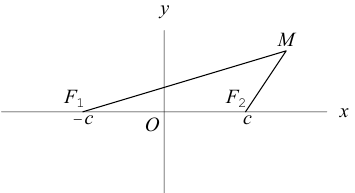
Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Канонические уравнения прямой в пространстве: теория, примеры, решение задач
Одним из видов уравнений прямой в пространстве является каноническое уравнение. Мы рассмотрим это понятие во всех подробностях, поскольку знать его необходимо для решения многих практических задач.
В первом пункте мы сформулируем основные уравнения прямой, расположенной в трехмерном пространстве, и приведем несколько примеров. Далее покажем способы вычисления координат направляющего вектора при заданных канонических уравнениях и решение обратной задачи. В третьей части мы расскажем, как составляется уравнение прямой, проходящей через 2 заданные точки в трехмерном пространстве, а в последнем пункте укажем на связи канонических уравнений с другими. Все рассуждения будут проиллюстрированы примерами решения задач.
Что такое каноническое уравнение прямой в пространстве
О том, что вообще из себя представляют канонические уравнения прямой, мы уже говорили в статье, посвященной уравнениям прямой на плоскости. Случай с трехмерным пространством мы разберем по аналогии.
Допустим, у нас есть прямоугольная система координат O x y z , в которой задана прямая. Как мы помним, задать прямую можно разными способами. Используем самый простой из них – зададим точку, через которую будет проходить прямая, и укажем направляющий вектор. Если обозначить прямую буквой a , а точку M , то можно записать, что M 1 ( x 1 , y 1 , z 1 ) лежит на прямой a и направляющим вектором этой прямой будет a → = ( a x , a y , a z ) . Чтобы множество точек M ( x , y , z ) определяло прямую a , векторы M 1 M → и a → должны быть коллинеарными,
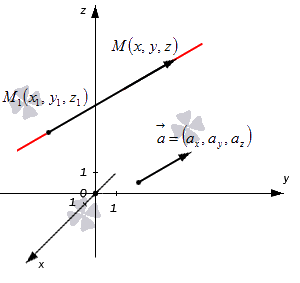
Если мы знаем координаты векторов M 1 M → и a → , то можем записать в координатной форме необходимое и достаточное условие их коллинеарности. Из первоначальных условий нам уже известны координаты a → . Для того чтобы получить координаты M 1 M → , нам необходимо вычислить разность между M ( x , y , z ) и M 1 ( x 1 , y 1 , z 1 ) . Запишем:
M 1 M → = x – x 1 , y – y 1 , z – z 1
После этого нужное нам условие мы можем сформулировать так: M 1 M → = x – x 1 , y – y 1 , z – z 1 и a → = ( a x , a y , a z ) : M 1 M → = λ · a → ⇔ x – x 1 = λ · a x y – y 1 = λ · a y z – z 1 = λ · a z
Здесь значением переменной λ может быть любое действительное число или ноль. Если λ = 0 , то M ( x , y , z ) и M 1 ( x 1 , y 1 , z 1 ) совпадут, что не противоречит нашим рассуждениям.
При значениях a x ≠ 0 , a y ≠ 0 , a z ≠ 0 мы можем разрешить относительно параметра λ все уравнения системы x – x 1 = λ · a x y – y 1 = λ · a y z – z 1 = λ · a z
Между правыми частями после этого можно будет поставить знак равенства:
x – x 1 = λ · a x y – y 1 = λ · a y z – z 1 = λ · a z ⇔ λ = x – x 1 a x λ = y – y 1 a y λ = z – z 1 a z ⇔ x – x 1 a x = y – y 1 a y = z – z 1 a z
В итоге у нас получились уравнения x – x 1 a x = y – y 1 a y = z – z 1 a z , с помощью которых можно определить искомую прямую в трехмерном пространстве. Это и есть нужные нам канонические уравнения.
Такая запись используется даже при нулевых значениях одного или двух параметров a x , a y , a z , поскольку она в этих случаях она также будет верна. Все три параметра не могут быть равны 0 , поскольку направляющий вектор a → = ( a x , a y , a z ) нулевым не бывает.
Если один-два параметра a равны 0 , то уравнение x – x 1 a x = y – y 1 a y = z – z 1 a z носит условный характер. Его следует считать равным следующей записи:
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , λ ∈ R .
Частные случаи канонических уравнений мы разберем в третьем пункте статьи.
Из определения канонического уравнения прямой в пространстве можно сделать несколько важных выводов. Рассмотрим их.
1) если исходная прямая будет проходить через две точки M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , то канонические уравнения примут следующий вид:
x – x 1 a x = y – y 1 a y = z – z 1 a z или x – x 2 a x = y – y 2 a y = z – z 2 a z .
2) поскольку a → = ( a x , a y , a z ) является направляющим вектором исходной прямой, то таковыми будут являться и все векторы μ · a → = μ · a x , μ · a y , μ · a z , μ ∈ R , μ ≠ 0 . Тогда прямая может быть определена с помощью уравнения x – x 1 a x = y – y 1 a y = z – z 1 a z или x – x 1 μ · a x = y – y 1 μ · a y = z – z 1 μ · a z .
Вот несколько примеров таких уравнений с заданными значениями:
x – 3 2 = y + 1 – 1 2 = z ln 7
Тут x 1 = 3 , y 1 = – 1 , z 1 = 0 , a x = 2 , a y = – 1 2 , a z = ln 7 .
x – 4 0 = y + 2 1 = z + 1 0
Тут M 1 ( 4 , – 2 , – 1 ) , a → = ( 0 , 1 , 0 ) .
Как составить каноническое уравнение прямой в пространстве
Мы выяснили, что канонические уравнения вида x – x 1 a x = y – y 1 a y = z – z 1 a z будут соответствовать прямой, проходящей через точку M 1 ( x 1 , y 1 , z 1 ) , а вектор a → = ( a x , a y , a z ) будет для нее направляющим. Значит, если мы знаем уравнение прямой, то можем вычислить координаты ее направляющего вектора, а при условии заданных координат вектора и некоторой точки, расположенной на прямой, мы можем записать ее канонические уравнения.
Разберем пару конкретных задач.
У нас есть прямая, заданная в трехмерном пространстве с помощью уравнения x + 1 4 = y 2 = z – 3 – 5 . Запишите координаты всех направляющих векторов для нее.
Решение
Чтобы получить координаты направляющего вектора, нам надо просто взять значения знаменателей из уравнения. Мы получим, что одним из направляющих векторов будет a → = ( 4 , 2 , – 5 ) , а множество всех подобных векторов можно сформулировать как μ · a → = 4 · μ , 2 · μ , – 5 · μ . Здесь параметр μ – любое действительное число (за исключением нуля).
Ответ: 4 · μ , 2 · μ , – 5 · μ , μ ∈ R , μ ≠ 0
Запишите канонические уравнения, если прямая в пространстве проходит через M 1 ( 0 , – 3 , 2 ) и имеет направляющий вектор с координатами – 1 , 0 , 5 .
Решение
У нас есть данные, что x 1 = 0 , y 1 = – 3 , z 1 = 2 , a x = – 1 , a y = 0 , a z = 5 . Этого вполне достаточно, чтобы сразу перейти к записи канонических уравнений.
x – x 1 a x = y – y 1 a y = z – z 1 a z ⇔ x – 0 – 1 = y – ( – 3 ) 0 = z – 2 5 ⇔ ⇔ x – 1 = y + 3 0 = z – 2 5
Ответ: x – 1 = y + 3 0 = z – 2 5
Эти задачи – самые простые, потому что в них есть все или почти все исходные данные для записи уравнения или координат вектора. На практике чаще можно встретить те, в которых сначала нужно находить нужные координаты, а потом записывать канонические уравнения. Примеры таких задач мы разбирали в статьях, посвященных нахождению уравнений прямой, проходящей через точку пространства параллельно заданной, а также прямой, проходящей через некоторую точку пространства перпендикулярно плоскости.
Канонические уравнения с одним или двумя a, равными нулю
Ранее мы уже говорили, что одно-два значения параметров a x , a y , a z в уравнениях могут иметь нулевые значения. При этом запись x – x 1 a x = y – y 1 a y = z – z 1 a z = λ приобретает формальный характер, поскольку мы получаем одну или две дроби с нулевыми знаменателями. Ее можно переписать в следующем виде (при λ ∈ R ):
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ
Рассмотрим эти случаи подробнее. Допустим, что a x = 0 , a y ≠ 0 , a z ≠ 0 , a x ≠ 0 , a y = 0 , a z ≠ 0 , либо a x ≠ 0 , a y ≠ 0 , a z = 0 . В таком случае нужные уравнения мы можем записать так:
-
В первом случае:
x – x 1 0 = y – y 1 a y = z – z 1 a z = λ ⇔ x – x 1 = 0 y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x – x 1 = 0 y – y 1 a y = z – z 1 a z = λ
Во втором случае:
x – x 1 a x = y – y 1 0 = z – z 1 a z = λ ⇔ x = x 1 + a x · λ y – y 1 = 0 z = z 1 + a z · λ ⇔ y – y 1 = 0 x – x 1 a x = z – z 1 a z = λ
В третьем случае:
x – x 1 a x = y – y 1 a y = z – z 1 0 = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ z – z 1 = 0 ⇔ z – z 1 = 0 x – x 1 a x = y – y 1 a y = λ
Получается, что при таком значении параметров нужные прямые находятся в плоскостях x – x 1 = 0 , y – y 1 = 0 или z – z 1 = 0 , которые располагаются параллельно координатным плоскостям (если x 1 = 0 , y 1 = 0 либо z 1 = 0 ). Примеры таких прямых показаны на иллюстрации.
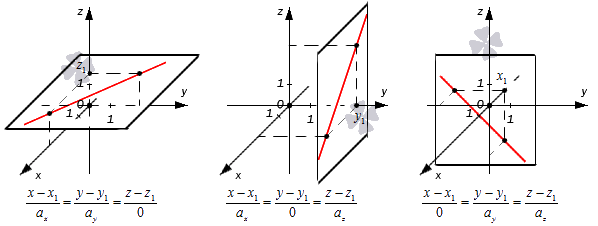
Следовательно, мы сможем записать канонические уравнения немного иначе.
- В первом случае: x – x 1 0 = y – y 1 0 = z – z 1 a z = λ ⇔ x – x 1 = 0 y – y 1 = 0 z = z 1 + a z · λ , λ ∈ R
- Во втором: x – x 1 0 = y – y 1 a y = z – z 1 0 = λ ⇔ x – x 1 = 0 y = y 1 + a y · λ , λ ∈ R z – z 1 = 0
- В третьем: x – x 1 a x = y – y 1 0 = z – z 1 0 = λ ⇔ x = x 1 + a x · λ , λ ∈ R y = y 1 = 0 z – z 1 = 0
Во всех трех случаях исходные прямые будут совпадать с координатными осями или окажутся параллельными им: x 1 = 0 y 1 = 0 , x 1 = 0 z 1 = 0 , y 1 = 0 z 1 = 0 . Их направляющие векторы имеют координаты 0 , 0 , a z , 0 , a y , 0 , a x , 0 , 0 . Если обозначить направляющие векторы координатных прямых как i → , j → , k → , то направляющие векторы заданных прямых будут коллинеарными по отношению к ним. На рисунке показаны эти случаи:
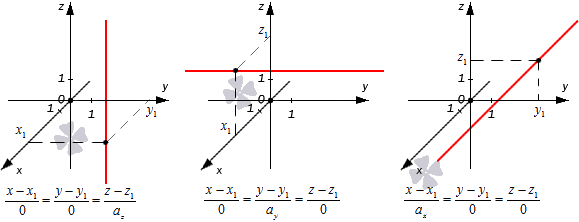
Покажем на примерах, как применяются эти правила.
Найдите канонические уравнения, с помощью которых можно определить в пространстве координатные прямые O z , O x , O y .
Решение
Координатные векторы i → = ( 1 , 0 , 0 ) , j → = 0 , 1 , 0 , k → = ( 0 , 0 , 1 ) будут для исходных прямых направляющими. Также мы знаем, что наши прямые будут обязательно проходить через точку O ( 0 , 0 , 0 ) , поскольку она является началом координат. Теперь у нас есть все данные, чтобы записать нужные канонические уравнения.
Для прямой O x : x 1 = y 0 = z 0
Для прямой O y : x 0 = y 1 = z 0
Для прямой O z : x 0 = y 0 = z 1
Ответ: x 1 = y 0 = z 0 , x 0 = y 1 = z 0 , x 0 = y 0 = z 1 .
В пространстве задана прямая, которая проходит через точку M 1 ( 3 , – 1 , 12 ) . Также известно, что она расположена параллельно оси ординат. Запишите канонические уравнения этой прямой.
Решение
Учитывая условие параллельности, мы можем сказать, что вектор j → = 0 , 1 , 0 будет для нужной прямой направляющим. Следовательно, искомые уравнения будут иметь вид:
x – 3 0 = y – ( – 1 ) 1 = z – 12 0 ⇔ x – 3 0 = y + 1 1 = z – 12 0
Ответ: x – 3 0 = y + 1 1 = z – 12 0
Как записать каноническое уравнение прямой, которая проходит через две заданные точки
Допустим, что у нас есть две несовпадающие точки M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , через которые проходит прямая. Как в таком случае мы можем сформулировать для нее каноническое уравнение?
Для начала примем вектор M 1 M 2 → (или M 2 M 1 → ) за направляющий вектор данной прямой. Поскольку у нас есть координаты нужных точек, сразу вычисляем координаты вектора:
M 1 M 2 → = x 2 – x 1 , y 2 – y 1 , z 2 – z 1
Далее переходим непосредственно к записи канонического уравнения, ведь все нужные данные у нас уже есть. Исходная прямая будет определяться записями следующего вида:
x – x 1 x 2 – x 1 = y – y 1 y 2 – y 1 = z – z 1 z 2 – z 1 x – x 2 x 2 – x 1 = y – y 2 y 2 – y 1 = z – z 2 z 2 – z 1
Получившиеся равенства – это и есть канонические уравнения прямой, проходящей через две заданные точки. Взгляните на иллюстрацию:
Приведем пример решения задачи.
в пространстве есть две точки с координатами M 1 ( – 2 , 4 , 1 ) и M 2 ( – 3 , 2 , – 5 ) , через которые проходит прямая. Запишите канонические уравнения для нее.
Решение
Согласно условиям, x 1 = – 2 , y 1 = – 4 , z 1 = 1 , x 2 = – 3 , y 2 = 2 , z 2 = – 5 . Нам требуется подставить эти значения в каноническое уравнение:
x – ( – 2 ) – 3 – ( – 2 ) = y – ( – 4 ) 2 – ( – 4 ) = z – 1 – 5 – 1 ⇔ x + 2 – 1 = y + 4 6 = z – 1 – 6
Если мы возьмем уравнения вида x – x 2 x 2 – x 1 = y – y 2 y 2 – y 1 = z – z 2 z 2 – z 1 , то у нас получится: x – ( – 3 ) – 3 – ( – 2 ) = y – 2 2 – ( – 4 ) = z – ( – 5 ) – 5 – 1 ⇔ x + 3 – 1 = y – 2 6 = z + 5 – 6
Ответ: x + 3 – 1 = y – 2 6 = z + 5 – 6 либо x + 3 – 1 = y – 2 6 = z + 5 – 6 .
Преобразование канонических уравнений прямой в пространстве в другие виды уравнений
Иногда пользоваться каноническими уравнениями вида x – x 1 a x = y – y 1 a y = z – z 1 a z не очень удобно. Для решения некоторых задач лучше использовать запись x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ . В некоторых случаях более предпочтительно определить нужную прямую с помощью уравнений двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 . Поэтому в данном пункте мы разберем, как можно перейти от канонических уравнений к другим видам, если это требуется нам по условиям задачи.
Понять правила перехода к параметрическим уравнениям несложно. Сначала приравняем каждую часть уравнения к параметру λ и разрешим эти уравнения относительно других переменных. В итоге получим:
x – x 1 a x = y – y 1 a y = z – z 1 a z ⇔ x – x 1 a x = y – y 1 a y = z – z 1 a z ⇔ ⇔ x – x 1 a x = λ y – y 1 a y = λ z – z 1 a z = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ
Значение параметра λ может быть любым действительным числом, ведь и x , y , z могут принимать любые действительные значения.
В прямоугольной системе координат в трехмерном пространстве задана прямая, которая определена уравнением x – 2 3 = y – 2 = z + 7 0 . Запишите каноническое уравнение в параметрическом виде.
Решение
Сначала приравниваем каждую часть дроби к λ .
x – 2 3 = y – 2 = z + 7 0 ⇔ x – 2 3 = λ y – 2 = λ z + 7 0 = λ
Теперь разрешаем первую часть относительно x , вторую – относительно y , третью – относительно z . У нас получится:
x – 2 3 = λ y – 2 = λ z + 7 0 = λ ⇔ x = 2 + 3 · λ y = – 2 · λ z = – 7 + 0 · λ ⇔ x = 2 + 3 · λ y = – 2 · λ z = – 7
Ответ: x = 2 + 3 · λ y = – 2 · λ z = – 7
Следующим нашим шагом будет преобразование канонических уравнений в уравнение двух пересекающихся плоскостей (для одной и той же прямой).
Равенство x – x 1 a x = y – y 1 a y = z – z 1 a z нужно для начала представить в виде системы уравнений:
x – x 1 a x = y – y 1 a y x – x 1 a x = z – z 1 a x y – y 1 a y = z – z 1 a z
Поскольку p q = r s мы понимаем как p · s = q · r , то можно записать:
x – x 1 a x = y – y 1 a y x – x 1 a x = z – z 1 a z y – y 1 a y = z – z 1 a z ⇔ a y · ( x – x 1 ) = a x · ( y – y 1 ) a z · ( x – x 1 ) = a x · ( z – z 1 ) a z · ( y – y 1 ) = a y · ( z – z 1 ) ⇔ ⇔ a y · x – a x · y + a x · y 1 – a y · x 1 = 0 a z · x – a x · z + a x · z 1 – a z · x 1 = 0 a z · y – a y · z + a y · z 1 – a z · y 1 = 0
В итоге у нас вышло, что:
x – x 1 a x = y – y 1 a y = z – z 1 a z ⇔ a y · x – a x · y + a x · y 1 – a y · x 1 = 0 a z · x – a x · z + a x · z 1 – a z · x 1 = 0 a z · y – a y · z + a y · z 1 – a z · y 1 = 0
Выше мы отмечали, что все три параметра a не могут одновременно быть нулевыми. Значит, ранг основной матрицы системы будет равен 2 , поскольку a y – a x 0 a z 0 – a x 0 a z – a y = 0 и один из определителей второго порядка не равен 0 :
a y – a x a z 0 = a x · a z , a y 0 a z – a x = a x · a y , – a x 0 0 – a x = a x 2 a y – a x 0 a z = a y · a z , a y 0 0 – a y = – a y 2 , – a x 0 a z – a y = a x · a y a z 0 0 a z = a z 2 , a z – a x 0 – a y = – a y · a z , 0 – a x a z – a y = a x · a z
Это дает нам возможность исключить одно уравнение из наших расчетов. Таким образом, канонические уравнения прямой можно преобразовать в систему из двух линейных уравнений, которые будут содержать 3 неизвестных. Они и будут нужными нам уравнениями двух пересекающихся плоскостей.
Рассуждение выглядит довольно сложным, однако на практике все делается довольно быстро. Продемонстрируем это на примере.
Прямая задана каноническим уравнением x – 1 2 = y 0 = z + 2 0 . Напишите для нее уравнение пересекающихся плоскостей.
Решение
Начнем с попарного приравнивания дробей.
x – 1 2 = y 0 = z + 2 0 ⇔ x – 1 2 = y 0 x – 1 2 = z + 2 0 y 0 = z + 2 0 ⇔ ⇔ 0 · ( x – 1 ) = 2 y 0 · ( x – 1 ) = 2 · ( z + 2 ) 0 · y = 0 · ( z + 2 ) ⇔ y = 0 z + 2 = 0 0 = 0
Теперь исключаем из расчетов последнее уравнение, потому что оно будет верным при любых x , y и z . В таком случае x – 1 2 = y 0 = z + 2 0 ⇔ y = 0 z + 2 = 0 .
Это и есть уравнения двух пересекающихся плоскостей, которые при пересечении образуют прямую, заданную с помощью уравнения x – 1 2 = y 0 = z + 2 0
Ответ: y = 0 z + 2 = 0
Прямая задана уравнениями x + 1 2 = y – 2 1 = z – 5 – 3 , найдите уравнение двух плоскостей, пересекающихся по данной прямой.
Решение
Приравниваем дроби попарно.
x + 1 2 = y – 2 1 = z – 5 – 3 ⇔ x + 1 2 = y – 2 1 x + 1 2 = z – 5 – 3 y – 2 1 = z – 5 – 3 ⇔ ⇔ 1 · ( x + 1 ) = 2 · ( y – 2 ) – 3 · ( x + 1 ) = 2 · ( z – 5 ) – 3 · ( y – 2 ) = 1 · ( z – 5 ) ⇔ x – 2 y + 5 = 0 3 x + 2 z – 7 = 0 3 y + 7 – 11 = 0
Получаем, что определитель основной матрицы полученной системы будет равен 0 :
1 – 2 0 3 0 2 0 3 1 = 1 · 0 · 1 + ( – 2 ) · 2 · 0 + 0 · 3 · 3 – 0 · 0 · 0 – 1 · 2 · 3 – ( – 2 ) · 3 · 1 = 0
Минор второго порядка нулевым при этом не будет: 1 – 2 3 0 = 1 · 0 – ( – 2 ) · 3 = 6 . Тогда мы можем принять его в качестве базисного минора.
В итоге мы можем вычислить ранг основной матрицы системы x – 2 y + 5 = 0 3 x + 2 z – 7 = 0 3 y + z – 11 = 0 . Это будет 2. Третье уравнение исключаем из расчета и получаем:
x – 2 y + 5 = 0 3 x + 2 z – 7 = 0 3 y + z – 11 = 0 ⇔ x – 2 y + 5 = 0 3 x + 2 z – 7 = 0
Ответ: x – 2 y + 5 = 0 3 x + 2 z – 7 = 0
[spoiler title=”источники:”]
http://www.evkova.org/krivyie-vtorogo-poryadka
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/kanonicheskie-uravnenija-prjamoj-v-prostranstve/
[/spoiler]
Канонические уравнения линий второго порядка
Рассмотрим задачу приведения уравнения линии второго порядка к наиболее простому (каноническому) виду.
Напомним, что алгебраической линией второго порядка называется геометрическое место точек плоскости, которое в какой-либо аффинной системе координат может быть задано уравнением вида
где
— многочлен второй степени двух переменных
. Требуется найти прямоугольную систему координат, в которой уравнение линии приняло бы наиболее простой вид.
Результатом решения поставленной задачи является следующая основная теорема (3.3)
Классификация алгебраических линий второго порядка (теорема 3.3)
Для любой алгебраической линии второго порядка существует прямоугольная система координат , в которой уравнение этой линии принимает один из следующих девяти канонических видов:
Теорема 3.3 дает аналитические определения линий второго порядка. Согласно пункту 2 замечаний 3.1, линии (1), (4), (5), (6), (7), (9) называются вещественными (действительными), а линии (2), (3), (8) — мнимыми.
Приведем доказательство теоремы, поскольку оно фактически содержит алгоритм решения поставленной задачи.
Без ограничения общности можно предполагать, что уравнение линии второго порядка задано в прямоугольной системе координат . В противном случае можно перейти от непрямоугольной системы координат
к прямоугольной
, при этом уравнение линии будет иметь тот же вид и ту же степень согласно теореме 3.1 об инвариантности порядка алгебраической линии.
Пусть в прямоугольной системе координат алгебраическая линия второго порядка задана уравнением
(3.34)
в котором хотя бы один из старших коэффициентов отличен от нуля, т.е. левая часть (3.34) — многочлен двух переменных
второй степени. Коэффициенты при первых степенях переменных
и
, а также при их произведении
взяты удвоенными просто для удобства дальнейших преобразований.
Для приведения уравнения (3.34) к каноническому виду используются следующие преобразования прямоугольных координат:
– поворот на угол
(3.35)
– параллельный перенос
(3.36)
– изменение направлений координатных осей (отражения в координатных осях):
оси ординат оси абсцисс
обеих осей
– переименование координатных осей (отражение в прямой )
(3.38)
где и
— координаты произвольной точки в старой
и новой
системах координат соответственно.
Кроме преобразования координат обе части уравнения можно умножать на отличное от нуля число.
Рассмотрим сначала частные случаи, когда уравнение (3.34) имеет вид:
Эти уравнения (также многочлены в левых частях) называются приведенными. Покажем, что приведенные уравнения (I), (II), (III) сводятся к каноническим (1)–(9).
Уравнение (I). Если в уравнении (I) свободный член равен нулю , то, разделив обе части уравнения
на старший коэффициент
, получим
— уравнение двух совпадающих прямых (9), содержащих ось абсцисс
. Если же свободный член отличен от нуля
, то разделим обе части уравнения (I) на старший коэффициент
. Если величина
отрицательная, то, обозначив ее через
, где
, получаем
— уравнение пары параллельных прямых (7):
или
. Если же величина
положительная, то, обозначив ее через
, где
, получаем
— уравнение пары мнимых параллельных прямых (8). Это уравнение не имеет действительных решений, поэтому на координатной плоскости нет точек, отвечающих этому уравнению. Однако в области комплексных чисел уравнение
имеет два сопряженных решения
, которые иллюстрируются штриховыми линиями (см. пункт 8 теоремы 3.3).
Уравнение (II). Разделим уравнение на старший коэффициент и перенесем линейный член в правую часть:
. Если величина
отрицательная, то, обозначая
, получаем
— уравнение параболы (6). Если величина
положительная, то, изменяя направление оси абсцисс, т.е. выполняя второе преобразование в (3.37), получаем уравнение
или
, где
. Это уравнение параболы в новой системе координат
.
Уравнение (III). Возможны два случая: либо старшие коэффициенты одного знака (эллиптический случай), либо противоположных знаков (гиперболический случай).
В эллиптическом случае при
переносим свободный член в правую часть и делим обе части на
:
Если знак старших коэффициентов противоположен знаку
, то, обозначая положительные величины
и
через
и
, получаем
— уравнение эллипса (1).
Если знак старших коэффициентов совпадает со знаком
, то, обозначая положительные величины
и
через
и
, получаем
— уравнение мнимого эллипса (2). Это уравнение не имеет действительных решений. Однако оно имеет решения в области комплексных чисел, которые иллюстрируются штриховой линией (см. пункт 2 теоремы 3.3).
Можно считать, что в уравнениях эллипса (действительного или мнимого) коэффициенты удовлетворяют неравенству , в противном случае этого можно добиться, переименовывая координатные оси, т.е. делая преобразование (3.38) системы координат.
Если свободный член уравнения (III) равен нулю , то, обозначая положительные величины
и
через
и
, получаем
— уравнение пары мнимых пересекающихся прямых (3). Этому уравнению удовлетворяет только точка с координатами
и
, т.е. точка
— начало координат. Однако в области комплексных чисел левую часть уравнения можно разложить на множители
, поэтому уравнение имеет сопряженные решения
, которые иллюстрируются штриховыми линиями, пересекающимися в начале координат (см. пункт 3 теоремы 3.3).
В гиперболическом случае при
переносим свободный член в правую часть и делим обе части на
:
Величины и
имеют противоположные знаки. Без ограничения общности считаем, что знак
совпадает со знаком свободного члена
, т.е.
. В противном случае нужно переименовать координатные оси, т.е. сделать преобразование (3.38) системы координат. Обозначая положительные величины
и
через
и
, получаем
— уравнение гиперболы (4).
Пусть в уравнении (III) свободный член равен нулю . Тогда можно считать, что
, а
(в противном случае обе части уравнения умножим на –1) . Обозначая положительные величины
и
через
и
, получаем
— уравнение пары пересекающихся прямых (5). Уравнения прямых находятся в результате разложения на множители левой части уравнения
, то есть
Таким образом, приведенные уравнения (I),(II),(III) алгебраической линии второго порядка сводятся к одному из канонических видов (1)–(9), перечисленных в теореме 3.3.
Осталось показать, что общее уравнение (3.34) можно свести к приведенным при помощи преобразований прямоугольной системы координат.
Упрощение общего уравнения (3.34) производится в два этапа. На первом этапе при помощи поворота системы координат “уничтожается” член с произведением неизвестных. Если произведения неизвестных нет , то поворот делать не надо (в этом случае переходим сразу ко второму этапу). На втором этапе при помощи параллельного переноса “уничтожаются” один или оба члена первой степени. В результате получаются приведенные уравнения (I),(II),(III).
Первый этап: преобразование уравнения линии второго порядка при повороте прямоугольной системы координат.
Если коэффициент , выполним поворот системы координат на угол
. Подставляя выражения (3.35) в уравнение (3.34), получаем:
Приводя подобные члены, приходим к уравнению вида (3.34):
(3.39)
где
Определим угол так, чтобы
. Преобразуем выражение для
, переходя к двойному углу:
Угол должен удовлетворять однородному тригонометрическому уравнению
, которое равносильно уравнению
(3.40)
поскольку . Это уравнение имеет бесконечное количество корней
Выберем любой из них, например, угол из интервала
. Тогда в уравнении (3.39) исчезнет член
, поскольку
.
Обозначив оставшиеся старшие коэффициенты через и
, получим уравнение
(3.41)
Согласно теореме 3.1, уравнение (3.41) является уравнением второй степени (при преобразовании (3.35) порядок линии сохраняется), т.е. хотя бы один из старших коэффициентов или
отличен от нуля. Далее будем считать, что именно коэффициент при
не равен нулю
. В противном случае (при
и
) следует сделать поворот системы координат на угол
, который также удовлетворяет условию (3.40). Тогда вместо координат
в (3.41) получим
соответственно, т.е. отличный от нуля коэффициент
будет при
.
Второй этап: преобразование уравнения линии второго порядка при параллельном переносе прямоугольной системы координат.
Уравнение (3.41) можно упростить, выделяя полные квадраты. Нужно рассмотреть два случая: или
(согласно предположению
), которые называются центральный (включающий эллиптический и гиперболический случаи) или параболический соответственно. Геометрический смысл этих названий раскрывается в дальнейшем.
Центральный случай: и
. Выделяя полные квадраты по переменным
, получаем
После замены переменных
(3.42)
получаем уравнение
(3.43)
где .
Параболический случай: и
. Выделяя полный квадрат по переменной
, получаем
(3.44)
Если , то последнее уравнение приводится к виду
Сделав замену переменных
(3.45)
получим, где
(3.46)
Если , то уравнение (3.44) приводится к виду, где
,
(3.47)
(3.48)
Замены переменных (3.42), (3.45), (3.48) соответствуют параллельному переносу системы координат (см. пункт 1″a” замечаний 2.3).
Таким образом, при помощи параллельного переноса системы координат получаем новую систему координат
, в которой уравнение линии второго порядка принимает вид (3.43), или (3.46), или (3.47). Эти уравнения являются приведенными (вида (III),(II) или (I) соответственно).
Основная теорема 3.3 о приведении уравнения алгебраической линии второго порядка к каноническому виду доказана.
Замечания 3.8
1. Система координат, в которой уравнение алгебраической линии второго порядка имеет канонический вид, называется канонической. Каноническая система координат определяется неоднозначно. Например, изменяя направление оси ординат на противоположное, снова получаем каноническую систему координат, так как замена переменной на
не изменяет уравнений (1)–(9). Поэтому ориентация канонической системы координат не имеет принципиального значения, ее всегда можно сделать правой, изменив при необходимости направление оси ординат.
2. Ранее показано, что преобразования прямоугольных систем координат на плоскости сводятся к одному из преобразований (2.9) или (2.10):
Поэтому задача приведения уравнения линии второго порядка к каноническому виду сводится к нахождению начала канонической системы координат
и угла
наклона ее оси абсцисс
к оси абсцисс
исходной системы координат
.
3. В случаях (3),(5),(7),(8),(9) линии называются распадающимися, поскольку соответствующие им многочлены второй степени разлагаются в произведение многочленов первой степени.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Содержание:
Аналитическая геометрия
В этой главе все геометрические объекты мы будем определять и изучать с помощью соответствующих уравнений этих объектов и, следовательно, в принципе геометрия может быть изложена без единого чертежа. И, действительно, все чертежи, которые мы будем использовать, будут служить лишь для визуальной иллюстрации наших рассуждений.
Уравнение поверхности в выбранной декартовой системе координат 
т. е. в виде связи или зависимости между координатами х, у, z произвольной точки поверхно-аналогично, уравнение
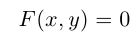
определяет некоторую линию (кривую) в системе координат 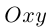 на плоскости.
на плоскости.
Кривая в пространстве может быть задана как пересечение двух поверхностей и, следовательно, она определяется системой из уравнений этих поверхностей:
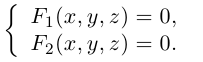
Кроме того, кривую на плоскости или в пространстве можно также задать с помощью зависимостей координат произвольной то’жи этой кривой от некоторого параметра, т. е. с помощью параметрических уравнений:

где t – действительный параметр.
Плоскость в пространстве. Различные виды уравнения плоскости
Найдем уравнение плоскости в пространстве с выбранной в нем декартовой системой координат 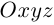 . Будем исходить из того, что положение этой плоскости полностью определяется точкой
. Будем исходить из того, что положение этой плоскости полностью определяется точкой 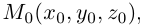 . через которую проходит плоскость и ненулевым вектором
. через которую проходит плоскость и ненулевым вектором 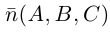 . ей перпендикулярным. Вектор
. ей перпендикулярным. Вектор 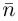 называется нормальным вектором плоскости.
называется нормальным вектором плоскости.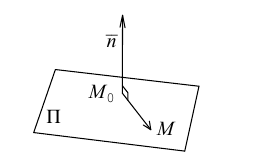
Пусть 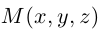 — произвольная точка плоскости П. Тогда вектор
— произвольная точка плоскости П. Тогда вектор 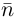 ортогонален вектору
ортогонален вектору 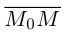 и, следовательно,
и, следовательно,
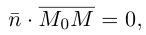
или, учитывая, что 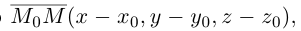 запишем в координатах уравнение плоскости П :
запишем в координатах уравнение плоскости П :
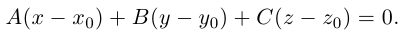
Преобразовав полученное уравнение к виду
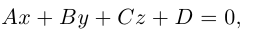
мы получим тем самым общее уравнение плоскости.
Рассмотрим теперь некоторые частные случаи общего уравнения плоскости. Если в общем уравнении плоскости отсутствует, одна из координат, то нормальный вектор  этой плоскости перпендикулярен соответствующей координатной оси и, следовательно, плоскость расположена параллельно этой координатной оси.
этой плоскости перпендикулярен соответствующей координатной оси и, следовательно, плоскость расположена параллельно этой координатной оси.
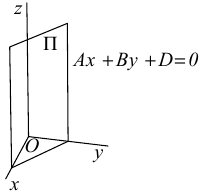
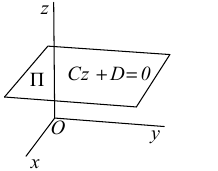
Аналогично, если в общем уравнении плоскости отсутствуют две координаты, то нормальный вектор данной плоскости перпендикулярен соответствующей координатной плоскости и, значит, плоскость расположена параллельно этой координатной плоскости.
Научимся теперь находить уравнение плоскости по трем элементам.
1) Плоскость, проходящая через точку, параллельно двум векторам.
Пусть плоскость 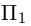 проходит через точку
проходит через точку 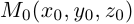 параллельно неколлинеарным векторам
параллельно неколлинеарным векторам 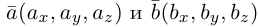 .
.
Обозначим через  произвольную точку плоскости
произвольную точку плоскости  Для точек данной плоскости и только для них три вектора
Для точек данной плоскости и только для них три вектора 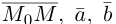 компланарны и, следовательно (глава II, §5, теорема), их смешанное произведение равно нулю, т. е.
компланарны и, следовательно (глава II, §5, теорема), их смешанное произведение равно нулю, т. е.
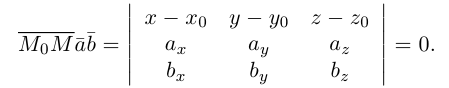
Раскрыв определитель (проще всего, разлагая его по первой строке), получим общее уравнение плоскости 
2)Плоскость, проходящая через две точки, параллельно вектору.
Найдем уравнение плоскости  , проходящей через две точки
, проходящей через две точки 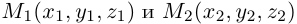 , параллельно ненулевому вектору
, параллельно ненулевому вектору 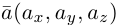 . Задача сводится к предыдущей, если положить, например,
. Задача сводится к предыдущей, если положить, например, 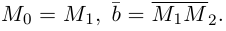 Тогда
Тогда
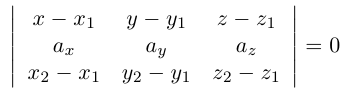
– искомое уравнение плоскости 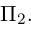
3)Плоскость, проходящая через три точки.
Если плоскость 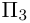 проходит через три точки
проходит через три точки 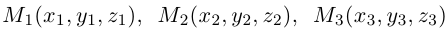 , не лежащие на одной прямой, то ее уравнение можно найти, как и в случае 1). положив например,
, не лежащие на одной прямой, то ее уравнение можно найти, как и в случае 1). положив например, 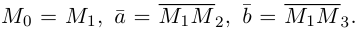 Следовательно, уравнение плоскости
Следовательно, уравнение плоскости 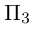 записать в виде:
записать в виде:
Замечание. Во всех трех случаях уравнение плоскости можно найти, вычислив предварительно ее нормальный вектор. Например, в первом случае в качестве нормального вектора можно взять векторное произведение 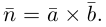 Тогда
Тогда 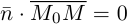 — уравнение плоскости.
— уравнение плоскости.
Пример №1
Найти уравнение плоскости 11 ^ – перпендикулярной плоскости
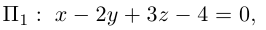
параллельной вектору 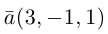 и проходящей через точку пересечения плоскости
и проходящей через точку пересечения плоскости 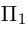 с координатного осью
с координатного осью 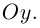
Решение. Из уравнения плоскости 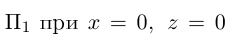 находим у = — 2. Следовательно, плоскость
находим у = — 2. Следовательно, плоскость 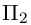 проходит через точку
проходит через точку 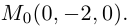 Кроме того,
Кроме того, 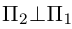 , поэтому нормальный вектор
, поэтому нормальный вектор 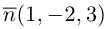 плоскости
плоскости 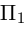 параллелен плоскости
параллелен плоскости 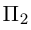 . Осталось записать искомое уравнение по трем элементам: точке
. Осталось записать искомое уравнение по трем элементам: точке 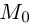 и векторам
и векторам 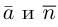 . Имеем:
. Имеем:
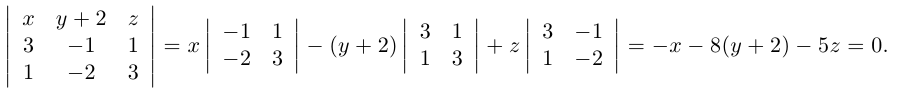
Таким образом, общее уравнение плоскости  имеет вид:
имеет вид:
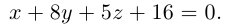
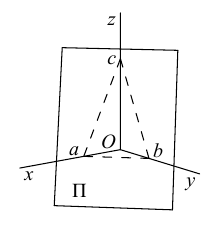
Пусть плоскость 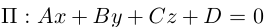 не проходит через начало координат и не параллельна ни одной из координатных осей. Тогда, очевидно, все числа A, В, С, D отличны от нуля.
не проходит через начало координат и не параллельна ни одной из координатных осей. Тогда, очевидно, все числа A, В, С, D отличны от нуля.
Разделив обе части уравнения плоскости на число D. мы можем записать его в виде:
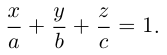
Числа а, b, с представляют собой величины отрезков, которые плоскость П отсекает на координатных осях. Полученное уравнение называется уравнением плоскости в отрезках.
Найдем теперь формулу для вычисления расстояния от точки 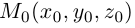 до плоскости
до плоскости 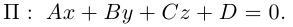
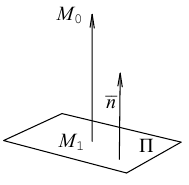
Обозначим искомое расстояние через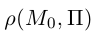 . Очевидно.
. Очевидно.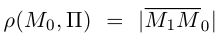 , где точка
, где точка 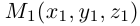 — основание перпендикуляра, опущенного из точки
— основание перпендикуляра, опущенного из точки 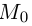 на плоскость П. Вычислим скалярное произведение коллинеарных векторов
на плоскость П. Вычислим скалярное произведение коллинеарных векторов 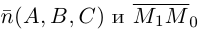 . С одной стороны,
. С одной стороны,
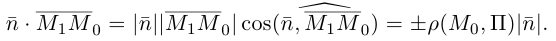
С другой,
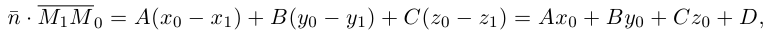
так как 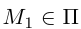 и поэтому
и поэтому 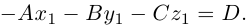 Следовательно, расстояние от точки
Следовательно, расстояние от точки 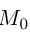 до плоскости П вычисляется по формуле:
до плоскости П вычисляется по формуле:
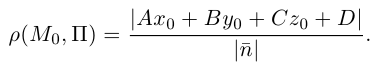
В заключение этого параграфа выясним характер взаимного расположения двух плоскостей. Пусть плоскости заданы своими общими уравнениями:
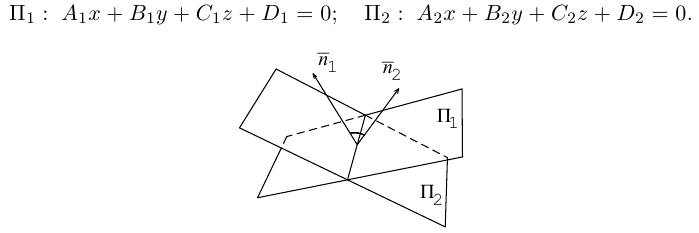
Очевидно, что угол 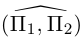 между этими плоскостями равен углу между их нормальными векторами
между этими плоскостями равен углу между их нормальными векторами 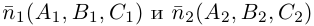 и, следовательно,
и, следовательно,
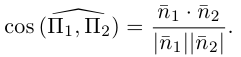
В частности,
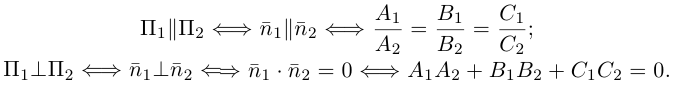
Пример №2
Убедиться в том, что плоскость отсекающая на координатных осях
отсекающая на координатных осях  отрезки величиной 2, —1, 2 соответственно и плоскость
отрезки величиной 2, —1, 2 соответственно и плоскость
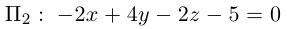
параллельны и найти расстояние между ними.
Решение. Запишем уравнение плоскости II| в отрезках:
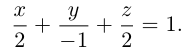
Преобразовав его к общему виду, получим:
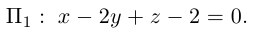
Так как нормальные векторы 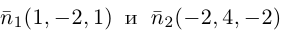 плоскостей
плоскостей  коллинеарны. то эти плоскости параллельны. Возьмем какую-нибудь точку в плоскости
коллинеарны. то эти плоскости параллельны. Возьмем какую-нибудь точку в плоскости  например,
например, 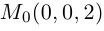 . Тогда
. Тогда
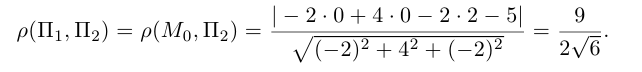
Уравнения прямой в пространстве
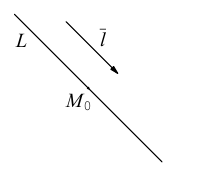
Пусть прямая L в пространстве с декартовой системой координат  проходит через точку
проходит через точку 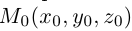 и параллельна ненулевому вектору
и параллельна ненулевому вектору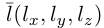 , который называется направляющим вектором прямой.
, который называется направляющим вектором прямой.
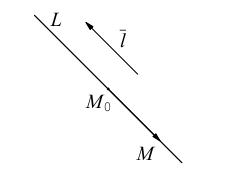
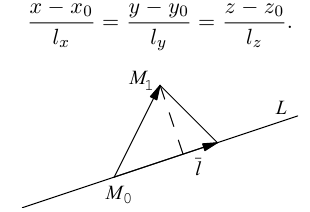
Обозначим через 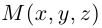 произвольную точку прямой L. Вектор
произвольную точку прямой L. Вектор 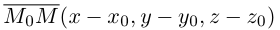 коллинеарен вектору
коллинеарен вектору  и, следовательно, их координаты пропорциональны, т. е.
и, следовательно, их координаты пропорциональны, т. е.
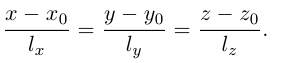
Эта двойная пропорция представляет собой канонические уравнения прямой в пространстве.
Заметим, что в канонических уравнениях прямой формально допускается запись нулей в знаменателях, это означает лишь то, что прямая перпендикулярна соответствующей координатной оси или координатной плоскости.
Если прямая проходит через две точки 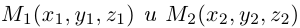 , то в качестве ее направляющего вектора можно взять вектор
, то в качестве ее направляющего вектора можно взять вектор 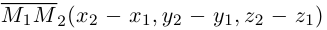 и, следовательно, канонические уравнения этой прямой имеют вид:
и, следовательно, канонические уравнения этой прямой имеют вид:
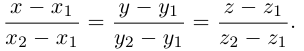
Коллинеарные векторы 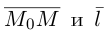 линейно связаны (глава II. §1), т.е. существует действительный параметр t такой, что
линейно связаны (глава II. §1), т.е. существует действительный параметр t такой, что
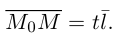
Если точка М перемещается вдоль прямой, параметр t изменяется в пределах от 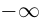 до
до 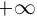 . Так как
. Так как 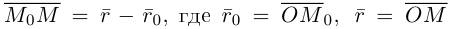 – радиусы-векторы точек
– радиусы-векторы точек 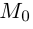 и М соответственно, то последнее уравнение мы можем переписать в виде
и М соответственно, то последнее уравнение мы можем переписать в виде
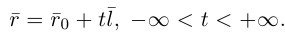
Это уравнение называется векторным уравнением прямой.
Переходя в полученном векторном уравнении к координатам, запишем параметрические уравнения прямой:
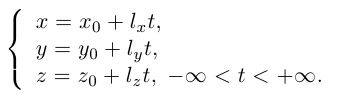
Прямую в пространстве можно задать также как пересечение двух плоскостей.
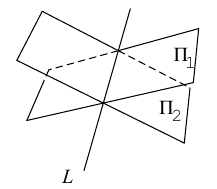
Система
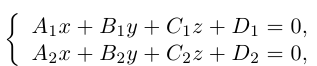
составленная из уравнений этих плоскостей, дает нам общие уравнения прямой в пространстве. Для перехода от общих к каноническим уравнениям прямой, достаточно найти какую-нибудь точку на ней, решив при фиксированном значении одной из координат систему уравнений плоскостей, а также определить направляющий вектор прямой, которым может служить векторное произведение нормальных векторов 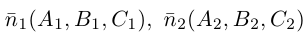 плоскостей. т. е. вектор
плоскостей. т. е. вектор 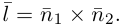
Пример №3
Найти канонические уравнения прямой
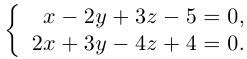
Решение. Полагая в данной системе z = 0, получим
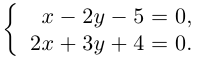
Решив эту систему, найдем х = 1, у = —2. Таким образом, мы получили точку 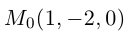 на прямой. Найдем ее направляющий вектор:
на прямой. Найдем ее направляющий вектор:
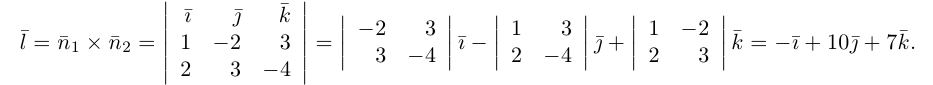
Осталось записать канонические уравнения данной прямой:
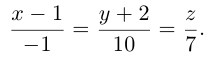
Научимся теперь вычислять расстояние от точки до прямой в пространстве. Пусть задана точка 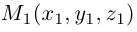 и прямая L своими каноническими уравнениями
и прямая L своими каноническими уравнениями
Искомое расстояние 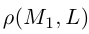 равно, очевидно, высоте треугольника, построенного, на векторах
равно, очевидно, высоте треугольника, построенного, на векторах 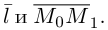 Воспользовавшись геометрическим смыслом длины векторного произведения (глава II. §4), найдем:
Воспользовавшись геометрическим смыслом длины векторного произведения (глава II. §4), найдем:
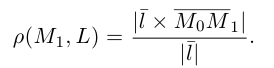
Пусть нам известны канонические уравнения двух прямых в пространстве:
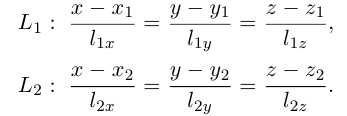
Очевидно, 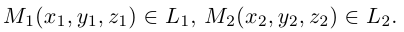
Один из углов между этими прямыми равен углу между их направляющими векторами 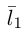 и
и 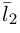 и, следовательно.
и, следовательно.
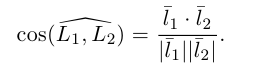
Изучим взаимное расположение прямых  . Если направляющие векторы
. Если направляющие векторы  коллинеарны, то данные прямые параллельны или совпадают. Совпадать они будут в том случае, когда
коллинеарны, то данные прямые параллельны или совпадают. Совпадать они будут в том случае, когда 
В случае, когда 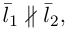 , прямые пересекаются или являются скрещивающимися.
, прямые пересекаются или являются скрещивающимися.
Прямые пересекаются, очевидно, тогда и только тогда, когда векторы  компланарны. В противном случае данные прямые являются скрещивающимися. Таким образом, для того, чтобы выяснить, являются ли две данные непараллельные прямые пересекающимися или скрещивающимися, достаточно вычислить смешанное произведение
компланарны. В противном случае данные прямые являются скрещивающимися. Таким образом, для того, чтобы выяснить, являются ли две данные непараллельные прямые пересекающимися или скрещивающимися, достаточно вычислить смешанное произведение 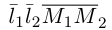 и, если оно окажется равным нулю, то прямые пересекаются, иначе – скрещиваются.
и, если оно окажется равным нулю, то прямые пересекаются, иначе – скрещиваются.
Расстояние 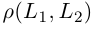 между двумя скрещивающимися прямыми равно, очевидно, расстоянию между параллельными плоскостями, в которых расположены эти прямые и, следовательно, равно высоте параллелепипеда, построенного на векторах
между двумя скрещивающимися прямыми равно, очевидно, расстоянию между параллельными плоскостями, в которых расположены эти прямые и, следовательно, равно высоте параллелепипеда, построенного на векторах 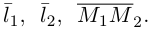 Отсюда, использовав геометрический смысл смешанного произведения (глава II. §5), мы и найдем искомое расстояние:
Отсюда, использовав геометрический смысл смешанного произведения (глава II. §5), мы и найдем искомое расстояние:
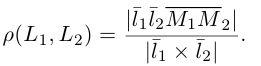
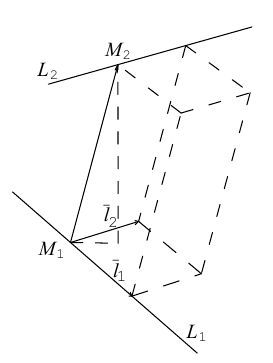
Пример №4
Убедиться в том, что прямые
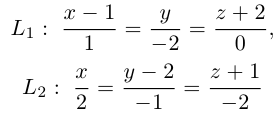
являются скрещивающимися. Найти расстояние между ними и уравнение общего перпендикуляра к ним.
Решение. Первая прямая проходит через точку 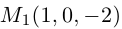 параллельно вектору
параллельно вектору 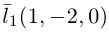 . а вторая – через точку
. а вторая – через точку 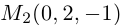 параллельно вектору
параллельно вектору 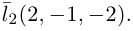 Вычислим смешанное произведение векторов
Вычислим смешанное произведение векторов 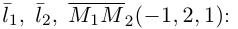
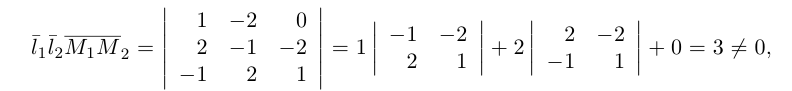
следовательно, прямые  являются скрещивающимися. Для вычисления расстояния между ними иенолтьзуем приведенную выше формулу. Так как
являются скрещивающимися. Для вычисления расстояния между ними иенолтьзуем приведенную выше формулу. Так как
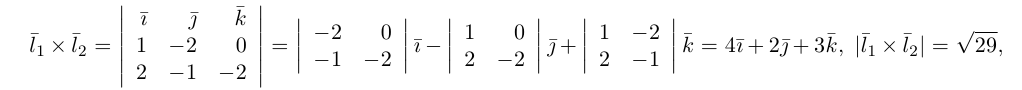
Осталось найти уравнение общего перпендикуляра к данным прямым. Заметим, прежде всего, что его направляющим вектором является уже вычисленный нами вектор 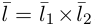 . Очевидно, указанный перпендикуляр расположен в пересечении двух плоскостей
. Очевидно, указанный перпендикуляр расположен в пересечении двух плоскостей 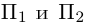 , проходящих через данные прямые параллельно вектору
, проходящих через данные прямые параллельно вектору  Найдем уравнения этих плоскостей по трем элементам. Первая из них проходит через точку
Найдем уравнения этих плоскостей по трем элементам. Первая из них проходит через точку  параллельно векторам
параллельно векторам  следовательно (§1),
следовательно (§1),
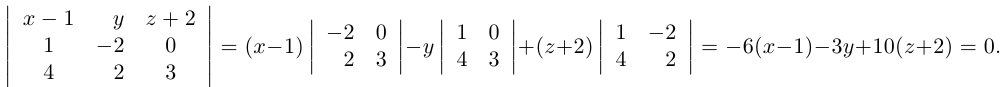
Таким образом, плоскость  имеет уравнение
имеет уравнение 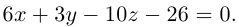 Аналогично, плоскость
Аналогично, плоскость  содержит точку
содержит точку 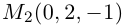 и расположена параллельно векторам
и расположена параллельно векторам  поэтому
поэтому
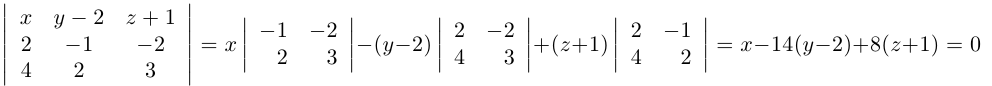
и, стало быть, 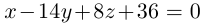 – уравнение плоскости
– уравнение плоскости  . Система из уравнений плоскостей
. Система из уравнений плоскостей  и даст нам общие уравнения перпендикуляра к прямым
и даст нам общие уравнения перпендикуляра к прямым 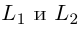 :
:
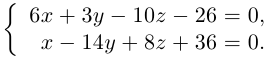
В заключение этого параграфа вычислим угол между прямой L, заданной каноническими уравнениями
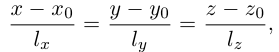
и плоскостью П, для которой известно ее общее уравнение
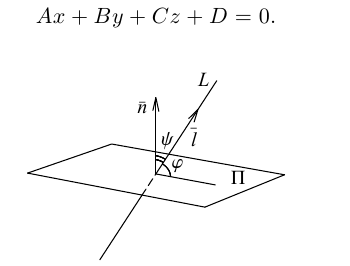
Очевидно, искомый угол 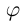 связан с углом
связан с углом 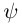 между направляющим вектором
между направляющим вектором 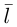 прямой и нормальным вектором
прямой и нормальным вектором 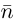 плоскости соотношением
плоскости соотношением 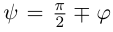 следовательно,
следовательно, 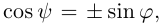 откуда,
откуда,
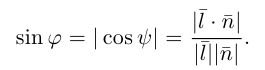
В частности, если 
Прямая на плоскости
Для прямой на плоскости наблюдается большее разнообразие ее уравнений, так как на плоскости прямая фиксируется точкой, через которую она проходит и, либо вектором ей перпендикулярным (нормальным вектором), либо вектором ей параллельным (направляющим вектором) и, следовательно, для прямой на плоскости можно записывать как уравнения, характерные для плоскости в пространстве (§1), так и аналоги уравнений прямой в пространстве (§2). Перечислим, не повторяя деталей, изложенных в предыдущих двух параграфах, основные уравнения прямой на плоскости и связанные с ними формулы.
Пусть прямая L на плоскости с выбранной в ней системой координат  проходит через точку
проходит через точку 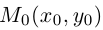 перпендикулярно ненулевому вектору
перпендикулярно ненулевому вектору 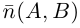 .
.
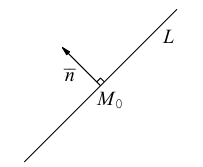
Уравнение такой прямой имеет вид:
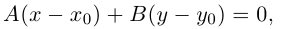
откуда после очевидных преобразований получим уравнение
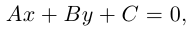
которое представляет собой общее уравнение прямой на плоскости.
Пусть прямая L отсекает на координатных осях 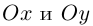 отрезки величиной а и Ь соответственно.
отрезки величиной а и Ь соответственно.
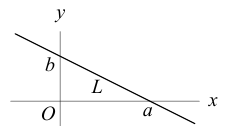
Тогда, как и для плоскости, мы можем записать уравнение прямой в отрезках:
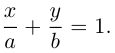
Если прямая L содержит точку 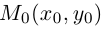 и расположена параллельно ненулевому вектору
и расположена параллельно ненулевому вектору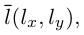
то ее каноническое уравнение имеет вид:
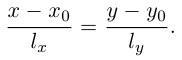
По аналогии с прямой в пространстве, прямая на плоскости может быть задана также векторным уравнением
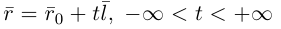
и параметрическими уравнениями
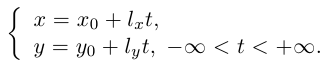
Расстояние от точки 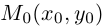 прямой L на плоскости, заданной общим уравнением
прямой L на плоскости, заданной общим уравнением 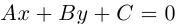 , может быть вычислено по формуле:
, может быть вычислено по формуле:
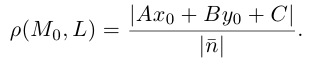
Найдем еще одно уравнение прямой на плоскости, характерное для этого геометрического объекта. Пусть прямая L, заданная своим каноническим уравнением 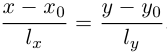 , непараллельна оси
, непараллельна оси 
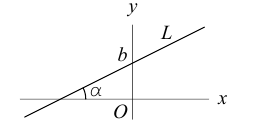
Тогда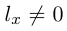 и мы можем записать уравнение прямой L с угловым коэффициентом:
и мы можем записать уравнение прямой L с угловым коэффициентом:
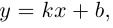
где 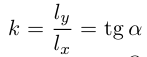 – угловой коэффициент прямой, b – величина отрезка, который отсекает эта прямая на оси
– угловой коэффициент прямой, b – величина отрезка, который отсекает эта прямая на оси 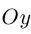 . В частности,
. В частности,
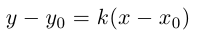
представляет собой уравнение прямой с угловым коэффициентом, которая проходит через точку 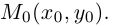
Если две прямые на плоскости заданы общими или каноническими уравнениями, то их взаимное расположение исследуется по аналогии с плоскостями или прямыми, заданными такими же уравнениями (§1 или §2). Изучим поэтому взаимное расположение двух прямых, которые заданы уравнениями с угловым коэффициентом. Итак, рассмотрим две прямые
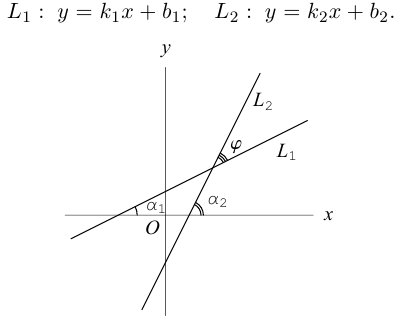
Предположим сначала, что прямые не являются перпендикулярными, обозначим через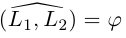 острый угол между ними. Тогда, очевидно,
острый угол между ними. Тогда, очевидно, 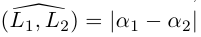 и, следовательно,
и, следовательно,
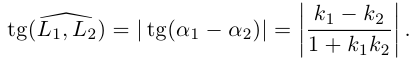
Если же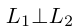 , то нормальные векторы
, то нормальные векторы 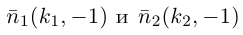 этих прямых ортогональны, следовательно,
этих прямых ортогональны, следовательно,
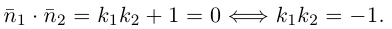
Таким образом, для перпендикулярности прямых 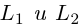 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 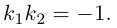
Очевидно. прямые 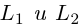 параллельны в том и только в том случае, когда равны углы, которые они образуют с осью Ох. Следовательно, для параллельности прямых
параллельны в том и только в том случае, когда равны углы, которые они образуют с осью Ох. Следовательно, для параллельности прямых 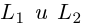 необходимо и достаточно, чтобы совпадали их угловые коэффициенты, т. е.
необходимо и достаточно, чтобы совпадали их угловые коэффициенты, т. е. 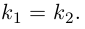
Пример №5
Даны прямая 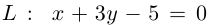 и точка А(—2, 1). Найти уравнения прямых
и точка А(—2, 1). Найти уравнения прямых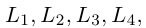 проходящих через точку А и таких, что
проходящих через точку А и таких, что 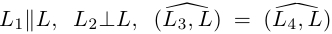
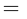
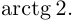
Решение. Прямые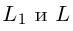 имеют общий нормальный вектор
имеют общий нормальный вектор 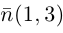 , поэтому,
, поэтому,
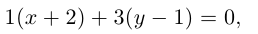
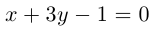 – общее уравнение прямой
– общее уравнение прямой 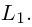
Так как 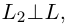 то направляющим вектором прямой
то направляющим вектором прямой 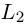 является нормальный вектор прямой L, следовательно,
является нормальный вектор прямой L, следовательно,
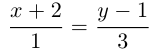 каноническое уравнение прямой
каноническое уравнение прямой 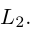
Из уравнения прямой L находим 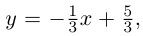 следовательно,
следовательно, 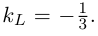 Тогда угловые коэффициенты прямых
Тогда угловые коэффициенты прямых 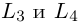 удовлетворяют уравнению
удовлетворяют уравнению
откуда,  Осталось записать уравнения прямых
Осталось записать уравнения прямых 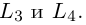
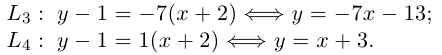
Кривые второго порядка на плоскости
В предыдущих трех параграфах нами были изучены линейные геометрические объекты -плоскость и прямая в пространстве и на плоскости. Мы показали, что в декартовой системе координат они определяются алгебраическими уравнениями первой степени, т. е. линейными уравнениями. Предметом нашего исследования в этом параграфе будут являться кривые второго порядка, т. е. линии на плоскости, уравнения которых в декартовой системе координат Оху имеют вид:
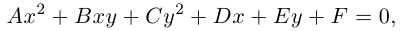
где А, В, С, D, Е, F – действительные числа. Мы убедимся в том, что, за исключением случаев вырождения данное уравнение определяет одну из трех замечательных линий — эллипс, гиперболу или параболу. Приведем сначала геометрическое определение каждой из этих линий и найдем их канонические уравнения.
Эллипс
Определение: Эллипсом называется множество точек на плоскости, для каждой из которых сумма расстояний до двух фиксированных точек (фокусов эллипса) есть величина постоянная.
Найдем каноническое уравнение эллипса. Обозначим через 2с фокусное расстояние, т. е. расстояние между фокусами, а через 2а — постоянную сумму расстояний от точек эллипса до фокусов. Из неравенства треугольника следует, что 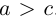 . Выберем декартову систему координат на плоскости следующим образом: ось Ох направим через фокусы, а начало координат выберем посередине между ними.
. Выберем декартову систему координат на плоскости следующим образом: ось Ох направим через фокусы, а начало координат выберем посередине между ними.
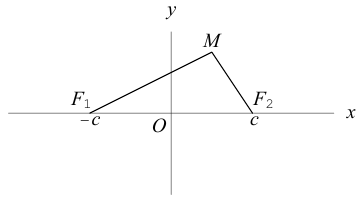
Пусть М(х, у) — произвольная точка эллипса. По определению этой линии,
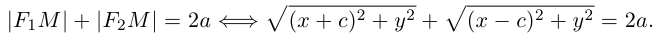
Упростим последнее уравнение:
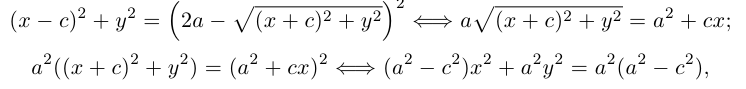
откуда, использовав обозначение 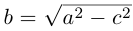 , мы и получим каноническое уравнение эллипса :
, мы и получим каноническое уравнение эллипса :
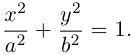
Построим эту линию. Для этого прежде всего заметим, что она симметрична относительно координатных осей и начала координат, так как переменные x и у входят в каноническое уравнение в квадратах. Отсюда следует, что эллипс достаточно построить в первой координатной четверти и затем отразить его относительно координатных осей. Из канонического уравнения эллипса находим:
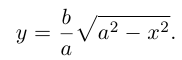
Очевидно, эта функция определена и убывает при 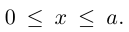 Кроме того, ее график располагается выше прямой
Кроме того, ее график располагается выше прямой 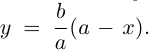 Из приведенных рассуждений следует, что эллипс представляет собой следующую замкнутую линию на плоскости:
Из приведенных рассуждений следует, что эллипс представляет собой следующую замкнутую линию на плоскости:
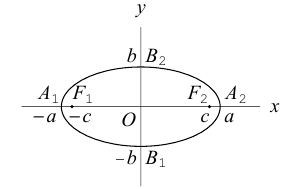
Числа а и b называются соответственно большой и малой полуосями эллипса. Точка O(0,0) -центр эллипса, точки 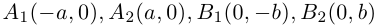 – вершины эллипса, отрезок
– вершины эллипса, отрезок 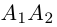 — большая,
— большая, 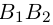 — малая оси эллипса.
— малая оси эллипса.
Форму эллипса характеризует величина 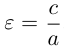 . равная отношению фокусного расстояния к длине большой оси. Это число называется эксцентриситетом эллипса. Очевидно,
. равная отношению фокусного расстояния к длине большой оси. Это число называется эксцентриситетом эллипса. Очевидно, 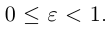 Так как
Так как
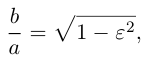
то при 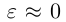 мы имеем
мы имеем 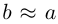 , и, следовательно, эллипс по форме мало отличается от окружности. В предельном случае, когда
, и, следовательно, эллипс по форме мало отличается от окружности. В предельном случае, когда 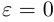 . полуоси совпадают и эллипс превращается в окружность. Если же
. полуоси совпадают и эллипс превращается в окружность. Если же 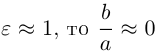 и эллипс является вытянутым вдоль оси Ох.
и эллипс является вытянутым вдоль оси Ох.
Замечание. В уравнении эллипса может оказаться, что 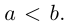 Тогда фокусы эллипса находятся на оси
Тогда фокусы эллипса находятся на оси 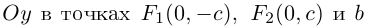 — большая,
— большая, 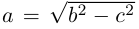 — малая полуоси эллипса.
— малая полуоси эллипса.
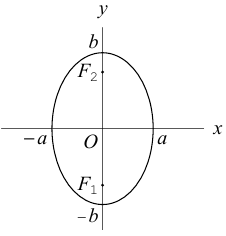
Гипербола
Определение: Гипербола представляет собой линию на плоскости, для каждой точки которой абсолютная величина разности расстояний до двух фиксированных точек (фокусов гиперболы) есть величина постоянная.
Обозначим и здесь фокусное расстояние через 2с. а через 2а — постоянную абсолютную величину разности расстояний от точек гиперболы до фокусов. Для гиперболы а < с, что следует из неравенства треугольника. Выберем декартову систему координат на плоскости точно также, как и при выводе канонического уравнения эллипса.
По определению гиперболы для произвольной точки М(х, у) этой линии
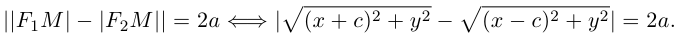
Избавляясь от корней в этом уравнении, получим:
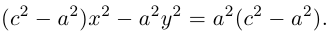
Обозначая здесь 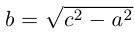 , получим каноническое уравнение гиперболы:
, получим каноническое уравнение гиперболы:
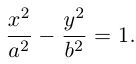
Как видно из ее уравнения, гипербола симметрична относительно координатных осей и начала координат. Из канонического уравнения гиперболы следует, что в первой четверти
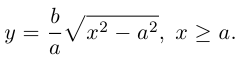
Эта функция возрастает, 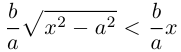 при всех
при всех 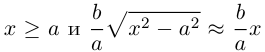 при больших х.
при больших х.
а а а а
Это означает, что в первой четверти гипербола, выходя из точки (а, 0) на оси Ох, приближается
затем при больших значениях х к прямой 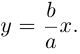 Следовательно, гипербола выглядит следующим образом:
Следовательно, гипербола выглядит следующим образом:
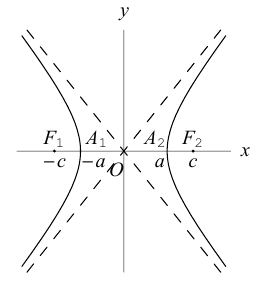
Прямые  называются асимптотами гиперболы. Точка O(0,0) – центр гиперболы. Точки
называются асимптотами гиперболы. Точка O(0,0) – центр гиперболы. Точки 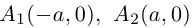 называются вершинами гиперболы. Ось симметрии гиперболы, пересекающая ее в вершинах, называется действительной осью. Вторая ось симметрии, не имеющая с гиперболой общих точек, называется мнимой осью гиперболы. Числа а и Ь называются соответственно действительной и мнимой полуосями гиперболы. Если полуоси равны, то гипербола называется равносторонней (равнобочной).
называются вершинами гиперболы. Ось симметрии гиперболы, пересекающая ее в вершинах, называется действительной осью. Вторая ось симметрии, не имеющая с гиперболой общих точек, называется мнимой осью гиперболы. Числа а и Ь называются соответственно действительной и мнимой полуосями гиперболы. Если полуоси равны, то гипербола называется равносторонней (равнобочной).
Как и для эллипса, определим эксцентриситет гиперболы как отношение половины фокусного расстояния к действительной полуоси:
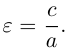
Так как
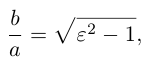
то эксцентриситет гиперболы характеризует величину угла, в котором она располагается. При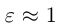 угол мал и, наоборот, если эксцентриситет велик, то и угол. в котором находится гипербола, близок к развернутому.
угол мал и, наоборот, если эксцентриситет велик, то и угол. в котором находится гипербола, близок к развернутому.
Замечание. В каноническом уравнении гиперболы знаки перед квадратами могут располагаться и в обратном порядке:
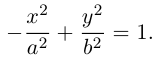
В этом случае фокусы и вершины находятся на оси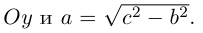
Парабола
Определение: Параболой называется множество точек плоскости, равноудаленных от. фиксированной точки (фокуса параболы) и фиксированной прямой (директрисы параболы).
Обозначим расстояние от фокуса до директрисы через р. Число р > 0 называется параметром параболы. Выберем удобную систему координат на плоскости: ось Ох направим через фокус F перпендикулярно директрисе D, а начало координат возьмем посередине между директрисой и фокусом.
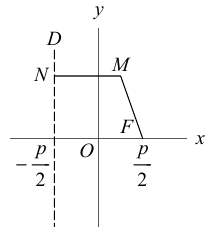
Если М(х,у) – произвольная точка параболы, то по определению этой кривой
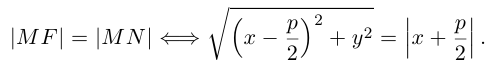
После возведения в квадрат и очевидных преобразований, получим каноническое уравнение параболы:
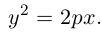
Очевидно, парабола проходит через начало координат и симметрична относительно оси Ох. Точка O(0,0) называется вершиной параболы, ось Ох – осью параболы.
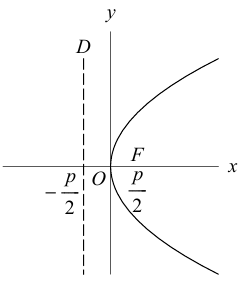
Замечание. Если бы при выборе системы координат мы направили ее оси в противоположные стороны, то каноническое уравнение параболы приняло бы вид:
Аналогично, уравнения
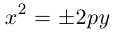
также определяют параболы, фокусы которых расположены на оси Оу. а директрисы параллельны оси Ох.
Приведение уравнения кривой второго порядка к каноническому виду
Покажем, что общее уравнение кривой второго порядка на плоскости, кроме случаев вырождения, определяет одну из линий — эллипс, гиперболу или параболу.
Выясним сначала, как преобразуются координаты точки на плоскости при параллельном переносе системы координат. Предположим, что осуществлен параллельный перенос системы координат Оху в точку 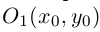 . Пусть
. Пусть 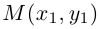 — координаты точки М в старой Оху, а
— координаты точки М в старой Оху, а 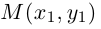 — координаты той же точки в новой
— координаты той же точки в новой  системе координат.
системе координат.
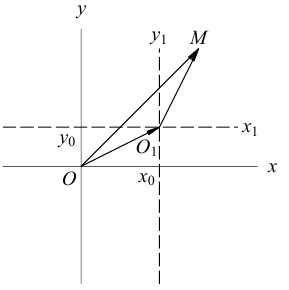
Так как 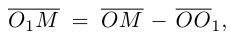 то новые и старые точки координаты на плоскости связаны линейными соотношениями:
то новые и старые точки координаты на плоскости связаны линейными соотношениями:
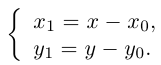
Рассмотрим теперь уравнение второго порядка на плоскости в частном случае, когда оно не содержит произведения координат ху :
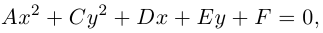
причем коэффициенты А и С не равны одновременно нулю. Здесь возможны три случая.
а) АС > 0. Очевидно, всегда можно считать, тгго А > 0, С > 0. Выделяя в уравнении второго порядка полные квадраты по переменным х и у, получим:
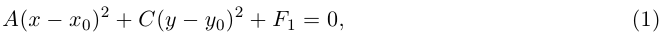
где 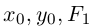 — некоторые действительные числа. Ясно, что при
— некоторые действительные числа. Ясно, что при 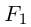 > 0 ни одна из точек плоскости не удовлетворяет этому уравнению. Если
> 0 ни одна из точек плоскости не удовлетворяет этому уравнению. Если 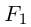 = 0, то единственным решением полученного уравнения является точка
= 0, то единственным решением полученного уравнения является точка 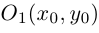 . Наконец, при
. Наконец, при 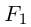 < 0 уравнение приводится к виду
< 0 уравнение приводится к виду
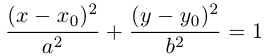
и, следовательно, в смещенной с помощью параллельного переноса в точку 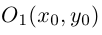 системе координат оно является каноническим уравнением эллипса:
системе координат оно является каноническим уравнением эллипса:
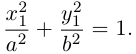
b) АС < 0. Будем считать для определенности, что А > 0. С < 0.
В этом случае исходное уравнение второго порядка также приводится к виду (1). При F = 0 оно определяет пару прямых, проходящих, через точку 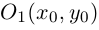 :
:
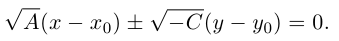
Если же 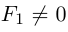 , то полученное уравнение мы можем преобразовать к виду
, то полученное уравнение мы можем преобразовать к виду
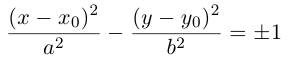
и, стало быть, после параллельного переноса системы координат в точку 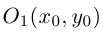 последнее уравнение является каноническим уравнением гиперболы:
последнее уравнение является каноническим уравнением гиперболы:
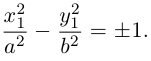
c) АС = 0. Предположим, например, что 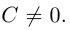
Выделяя в данном уравнении второго порядка полный квадрат по переменной у, получим:
С {у ~ Уо)2 + Dx + F1=0.
Если в этом уравнении D = 0, то при 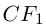 > 0 множество решений этого уравнения пусто, а при
> 0 множество решений этого уравнения пусто, а при 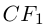 < 0 полученное уравнение определяет пару прямых, параллельных оси Ох :
< 0 полученное уравнение определяет пару прямых, параллельных оси Ох :
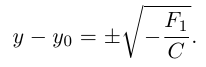
Если же 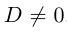 , то мы можем привести уравнение к виду:
, то мы можем привести уравнение к виду:
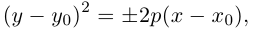
т.е. после параллельного переноса системы координат в точку 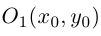 , мы получим тем самым каноническое уравнение параболы:
, мы получим тем самым каноническое уравнение параболы:
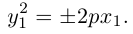
Аналогично. если в исходном уравнении второго порядка 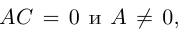 то, не принимая во внимание вырожденные случаи, это уравнение мы также можем привести к каноническому уравнению параболы:
то, не принимая во внимание вырожденные случаи, это уравнение мы также можем привести к каноническому уравнению параболы:
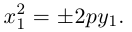
Пример №6
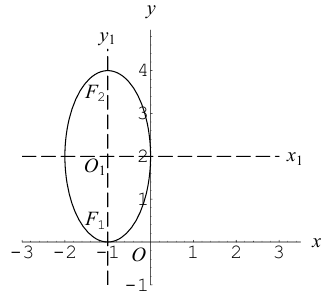
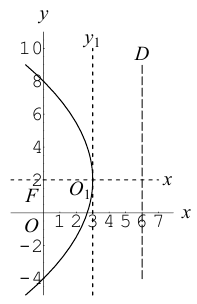
Привести уравнение второго порядка к каноническому виду, назвать и построить кривую:
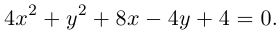
Решение. Выделяя полные квадраты по обеим переменным, получим:
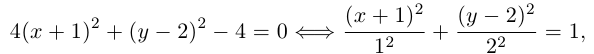
что представляет собой каноническое уравнение эллипса в смещенной в точку 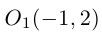 системе координат. Для этого эллипса
системе координат. Для этого эллипса 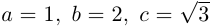 и, следовательно, фокусы находятся в точках
и, следовательно, фокусы находятся в точках 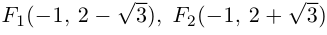 . Эксцентриситет эллипса равен
. Эксцентриситет эллипса равен 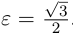
Пример №7
Найти каноническое уравнение параболы с вершиной в точке 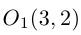 , осью симметрии, параллельной координатной оси Ох и фокусом на оси Оу. Построить параболу.
, осью симметрии, параллельной координатной оси Ох и фокусом на оси Оу. Построить параболу.
Решение. Фокус параболы находится в точке F(0 , 2), следовательно, уравнение параболы с учетом смещения имеет вид:
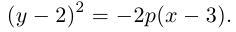
Здесь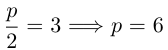 и, стало быть.
и, стало быть.
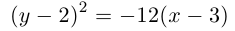
каноническое уравнение параболы.
Замечание. Для приведения к каноническому виду уравнения второго порядка, содержащего произведение координат ху, необходимо кроме параллельного переноса выполнить еще и поворот системы координат на определенный угол. Например, для равносторонней гиперболы ху = 1 следует повернуть систему координат Оху вокруг ее начала на угол 45° против часовой стрелки. Поскольку вершины гиперболы находятся на расстоянии 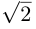 от начала координат. то в новой системе координат
от начала координат. то в новой системе координат 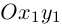 каноническое уравнение гиперболы имеет вид:
каноническое уравнение гиперболы имеет вид:
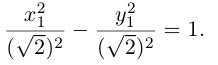
Поверхности второго порядка в пространстве
В заключение этой главы мы изучим поверхности в пространстве, которые в декартовой системе координат задаются алгебраическими уравнениями второй степени. Существуют пять видов таких поверхностей: эллипсоид, гиперболоиды, параболоиды, цилиндры второго порядка и конус второго порядка.
Поверхность вращения
Найдем уравнение поверхности, которая получается вращением некоторой линии вокруг одной из координатных осей. Пусть линия L, которая в координатной плоскости Oyz задается уравнением F(y, z) = 0. вращается вокруг оси Oz.
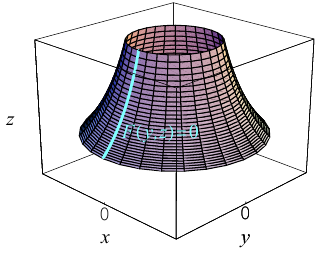
Пусть M(x,y,z) – произвольная точка на поверхности вращения. Перегоним ее по окружности, расположенной в сечении поверхности плоскостью, проходящей через данную точку перпендикулярно оси Oz, в точку N на линии L. Поскольку расстояние от точки М до оси Oz равно 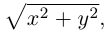 то точка N имеет координаты
то точка N имеет координаты 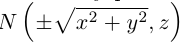 . Подставив координаты точки N в уравнение линии L. мы и получим тем самым уравнение поверхности вращения:
. Подставив координаты точки N в уравнение линии L. мы и получим тем самым уравнение поверхности вращения:
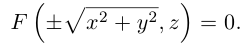
Найдем теперь уравнения поверхностей, которые получаются вращением кривых второго порядка с последующей линейной деформацией этих поверхностей.
Эллипсоид
Возьмем в плоскости Oyz эллипс
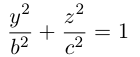
и будем вращать его вокруг оси Oz. В результате, как следует из предыдущего пункта, мы получим поверхность с уравнением
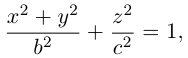
которая называется эллипсоидом вращения. Заменив в найденном уравнении координату х на —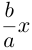 , т. е. линейно деформируя поверхность вдоль оси Ох с коэффициентом
, т. е. линейно деформируя поверхность вдоль оси Ох с коэффициентом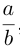 —, мы получим тем самым уравнение эллипсоида общего вида:
—, мы получим тем самым уравнение эллипсоида общего вида:
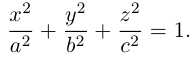
Положительные числа а, b, с называются полуосями эллипсоида.
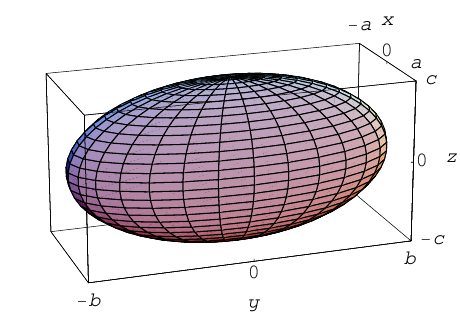
Очевидно, сечениями эллипсоида плоскостями параллельными координатным, являются эллипсы.
Замечание. В частном случае, когда а = b = с = R эллипсоид превращается в сферу
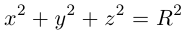
радиуса R с центром в начале координат.
Гиперболоиды
а) Однополостный гиперболоид.
Вращая гиперболу
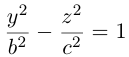
вокруг оси Oz, получим однополостный гиперболоид вращения с уравнением
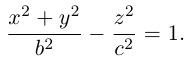
После линейной деформации вдоль оси Ох эта поверхность превращается в однополостный гиперболоид общего вида с осью Oz :
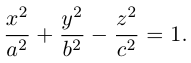
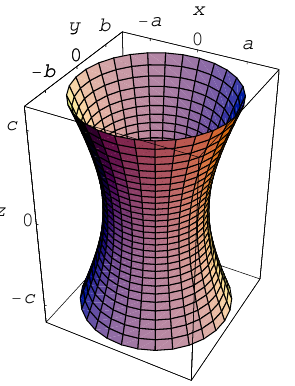
Аналогично, уравнения однополостных гиперболоидов с осями Ох и Оу имеют, соответственно, вид:
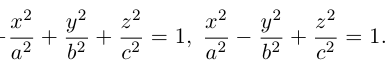
Сечениями однополостного гиперболоида плоскостями, перпендикулярными его оси, являются эллипсы, а в сечениях плоскостями, перпендикулярными другим координатным осям, располагаются гиперболы.
Двухполостный гиперболоид
Поверхность, полученная вращением вокруг оси Оz гиперболы
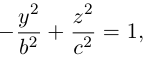
вершины которой расположены на оси вращения, называется двухполостным гиперболоидом вращения. Запишем уравнение двухполостного гиперболоида:
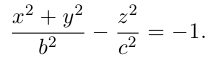
Линейная деформация двухполостного гиперболоида вращения вдоль оси Ох прообразует его в двухполостный гиперболоид общего вида с осью Oz. Уравнение этой поверхности имеет вид:
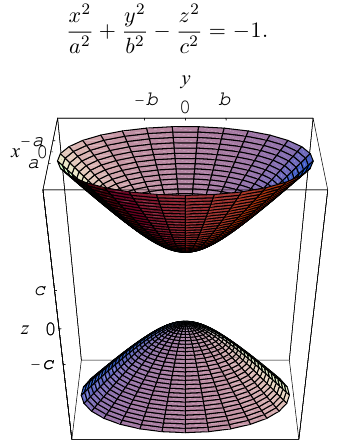
Двухполостные гиперболоиды с осями Ох и Оу имеют, соответственно, уравнения:
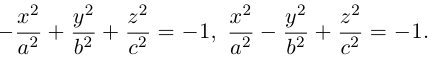
Как и в случае однополостного гиперболоида, сечениями двухполостного гиперболоида плоскостями, параллельными координатным, являются эллипсы и гиперболы.
Параболоиды
а) Эллиптический параболоид
Вращение параболы вокруг ее оси приводит к поверхности, которая называется параболоидом вращения. В частности, если параболу с каноническим уравнением 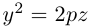 вращать вокруг оси Oz, то, как следует из пункта 0, уравнение полученного параболоида вращения имеет вид:
вращать вокруг оси Oz, то, как следует из пункта 0, уравнение полученного параболоида вращения имеет вид:
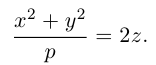
Линейная деформация параболоида вращения вдоль оси Оу превращает его в эллиптический параболоид с уравнением:
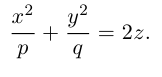
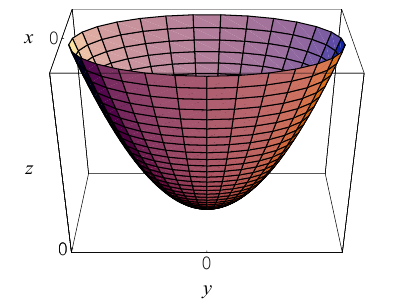
Положительные числа p, q называются параметрами параболоида, точка O(0,0) – вершина, ось Oz – ось эллиптического параболоида.
Уравнения эллиптических параболоидов с осями Ох и Оу имеют, соответственно, вид:
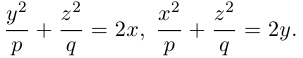
Как следует из уравнения эллиптического параболоида, плоскости, перпендикулярные его оси, пересекают эту поверхность по эллипсам, а в сечениях плоскостями, параллельными другим координатным, находятся параболы.
Замечание. Изменение знака в правой части уравнения эллиптического параболоида приводит к отражению этой поверхности относительно координатной плоскости, перпендикулярной оси параболоида.
b) Гиперболический параболоид.
Будем поступательно перемещать образующую параболу
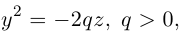
расположенную в плоскости Oyz, параллельно самой себе вдоль направляющей параболы
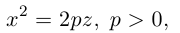
находящейся в плоскости Oxz. Полученная таким образом поверхность называется гиперболическим параболоидом или седловидной поверхностью.
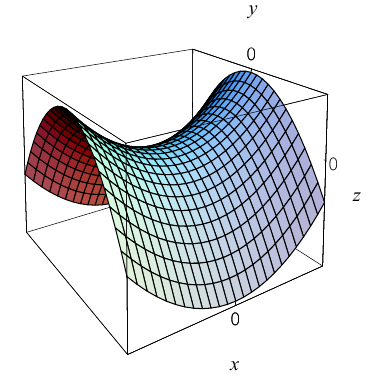
Найдем уравнение этой поверхности. Пусть М(х. у, z) – произвольная точка гиперболического параболоида. По его построению точка М принадлежит параболе с вершиной в точке 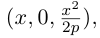 , параллельной параболе
, параллельной параболе 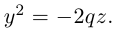 Так как координаты произвольной точки
Так как координаты произвольной точки  этой параболы удовлетворяют уравнению
этой параболы удовлетворяют уравнению
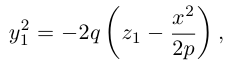
то, подставив в него координаты точки М, мы и получим после несложных преобразований уравнение гиперболического параболоида:
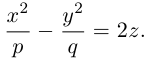
Здесь, как и для эллиптического параболоида, числа р, q – параметры гиперболического параболоида, точка O(0,0) и ось Oz – соответственно вершина и ось гиперболического параболоида.
Замечание 1. Седловидная поверхность может быть также получена перемещением параболы 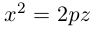 параллельно самой себе вдоль параболы
параллельно самой себе вдоль параболы 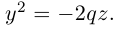
Судя по уравнению гиперболического параболоида, в сечениях этой поверхности плоскостями z = h > 0 находятся гиперболы, действительные оси которых параллельны координатной оси Ох. Аналогично, плоскости z = h < 0 пересекают данную поверхность по гиперболам с действительными осями, параллельными оси Оу. Наконец, плоскость Оху пересекает гиперболический параболоид по двум прямым 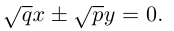
Гиперболические параболоиды, осями которых служат координатные оси Ох и Оу, имеют, соответственно, уравнения:
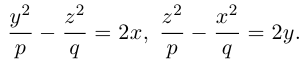
Замечание 2. Отразив седловидную поверхность относительно координатной плоскости, перпендикулярной ее оси, получим гиперболический параболоид, уравнение которого отличается знаком правой части от уравнения исходной поверхности.
Цилиндры второго порядка
Цилиндром второго порядка называется поверхность, полученная перемещением некоторой прямой (образующей) вдоль кривой второго порядка (направляющей), расположенной в плоскости, не содержащей образующую, параллельно фиксированному ненулевому вектору в пространстве.
Ограничимся случаем, когда направляющая расположена в одной из координатных плоскостей, а образующая перпендикулярна этой плоскости. Возьмем для определенности в плоскости Оху кривую второго порядка и будем перемещать прямую, параллельную оси Oz, вдоль этой кривой. Так как проекцией любой точки M(x,y,z) полученного таким образом цилиндра на плоскость Оху является точка N(x,y), принадлежащая кривой второго порядка, то координаты точки М удовлетворяют уравнению этой кривой. Следовательно, уравнением построенного цилиндра является уравнение его направляющей.
Перечислим теперь цилиндры второго порядка.
1) 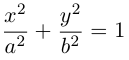 – эллиптический цилиндр.
– эллиптический цилиндр.
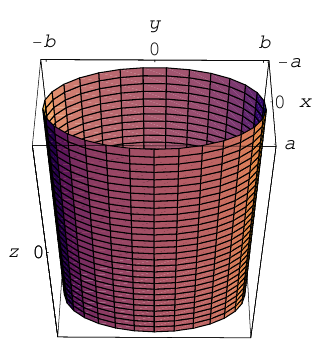
В частности, при а = b мы получим круговой цилиндр.
2 2 X у
2) 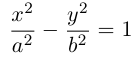 – гиперболический цилиндр.
– гиперболический цилиндр.
3) 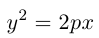 – параболический цилиндр.
– параболический цилиндр.
Аналогичные уравнения имеют цилиндры второго порядка, образующие которых параллельны осям Ох и Оу, а направляющие расположены в координатных плоскостях Oyz и Oxz, соответственно.
Конус второго порядка
Конус второго порядка представляет собой поверхность, которая может быть получена перемещением прямой (образующей), имеющей неподвижную точку, которая называется вершиной конуса, вдоль кривой второго порядка (направляющей), расположенной в плоскости, не содержащей вершину.
Найдем уравнение конуса, вершина которого совпадает с началом координат, а направляющей служит эллипс с уравнением
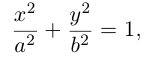
расположенный в плоскости z = с, с > 0.
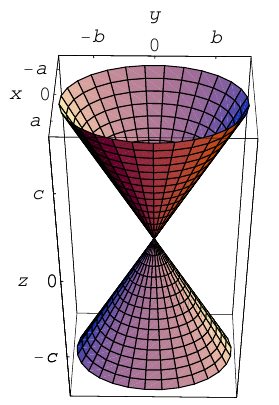
Пусть M(x,y,z) – произвольная точка конуса. Обозначим через  точку перс-сечения образующей, проходящей через точку М, с направляющей. Координаты точки
точку перс-сечения образующей, проходящей через точку М, с направляющей. Координаты точки  удовлетворяют уравнениям
удовлетворяют уравнениям
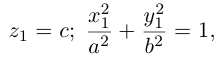
а точки M – уравнениям
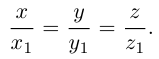
Из последних уравнений мы находим:
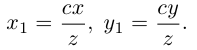
Подставив найденные выражения для в уравнение эллипса, получим после несложных преобразований уравнение конуса второго порядка:
в уравнение эллипса, получим после несложных преобразований уравнение конуса второго порядка:
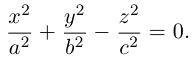
Координатная ось Oz называется осью конуса. Если а = b, то конус является круговым.
Конусы второго порядка с осями Ох и Оу имеют, соответственно, уравнения:
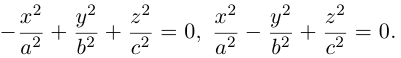
Покажем, что вид конуса второго порядка не зависит от выбора направляющей. Действительно, если в качестве направляющей взять гиперболу
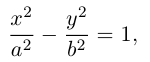
находящегося в плоскости 2 = с, то после рассуждений, аналогичных предыдущим, получим поверхность с уравнением
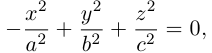
т. е. конус с осью Ох. Если же за направляющую мы выберем в плоскости z = с параболу с уравнением
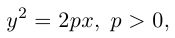
то построенный таким образом конус имеет уравнение
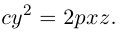
Наблюдая со стороны положительной полуоси Оу, повернем систему координат Oxz вокруг оси Оу на угол 45° против часовой стрелки. Тогда произведение xz в системе координат 
запишется как  (§4, пункт 4, замечание). Следовательно, в новой системе координат Oxyz найденное уравнение поверхности приобретает вид
(§4, пункт 4, замечание). Следовательно, в новой системе координат Oxyz найденное уравнение поверхности приобретает вид
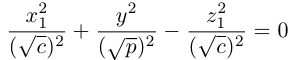
и, стало быть, эта поверхность является конусом с осью 
Как следует из уравнения конуса и его построения, плоскости, перпендикулярные его оси, пересекают эту поверхность по эллипсам, сечениями конуса плоскостями, параллельными его оси, являются гиперболы, и, наконец, в сечениях конуса плоскостями, параллельными образующей, располагаются параболы.
Приведение уравнения поверхности второго порядка к каноническому виду
По аналогии с уравнением кривой второго порядка (§4, пункт 4), уравнение поверхности второго порядка, не содержащее произведений координат, мы можем за счет выделения полных квадратов привести к уравнению одной из рассмотренных в пунктах 1—5 поверхностей. Следовательно, мы получим одну из поверхностей второго порядка в смещенной с помощью параллельного переноса системе координат. Исключение, правда, составляет случай, когда уравнение поверхности содержит полный квадрат и два линейных слагаемых относительно других координат. Такая поверхность представляет собой параболический цилиндр в смещенной с помощью параллельного переноса и повернутой затем вокруг одной из координатных осей системе координат.
Пример №8
Привести уравнение второго порядка
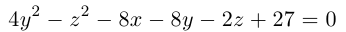
к каноническому виду, назвать и построить поверхность.
Решение. После выделения полных квадратов по переменным у, z получим:
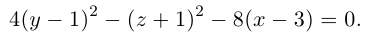
Переписав это уравнение в виде
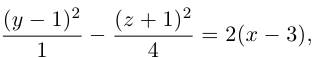
мы замечаем, что в смещенной с помощью параллельного переноса в точку 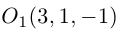 системе координат, эта поверхность представляет собой гиперболический параболоид с параметрами р = 1, q = 4.
системе координат, эта поверхность представляет собой гиперболический параболоид с параметрами р = 1, q = 4.
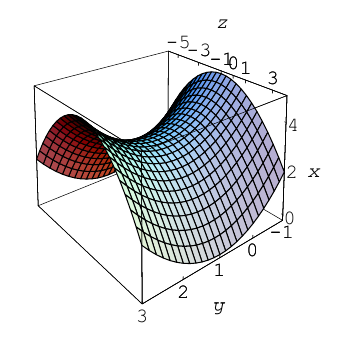
Прямая на плоскости. Общее уравнение прямой на плоскости
Докажем, что всякая прямая на плоскости задается в любой пдск уравнением первой степени относительно двух переменных.
Если A – некоторая точка на прямой  – вектор, перпендикулярный ей, то, во-первых, через A перпендикулярно
– вектор, перпендикулярный ей, то, во-первых, через A перпендикулярно 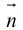 проходит единственная прямая на плоскости, а, во-вторых, для любой точки
проходит единственная прямая на плоскости, а, во-вторых, для любой точки 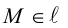 вектор
вектор 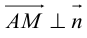 . Таким свойством обладают только точки, лежащие на
. Таким свойством обладают только точки, лежащие на .
.
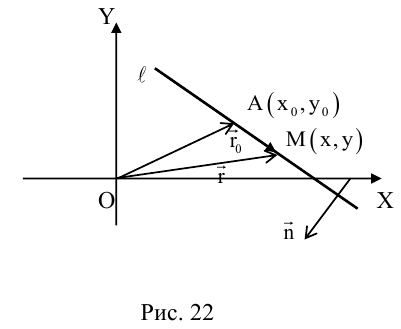
Чтобы вывести уравнение прямой, зададим на плоскости пдск XOY .
В этой системе координат 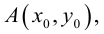
Пусть M (x, y) – произвольная точка
на  . Тогда (рис. 22 )
. Тогда (рис. 22 )  . Так как
. Так как 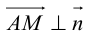 , то по свойству 5 скалярного произведения
, то по свойству 5 скалярного произведения 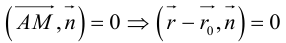 – векторное уравнение прямой
– векторное уравнение прямой  .
.
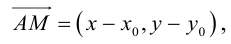 поэтому по формуле (2.5) получим
поэтому по формуле (2.5) получим

Координаты точек, лежащих на прямой , связаны соотношением (3.1). Если же
, связаны соотношением (3.1). Если же 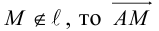 не перпендикулярен
не перпендикулярен 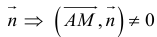 значит, координаты M не будут удовлетворять полученному уравнению. Поэтому (3.1) – уравнение прямой, проходящей через заданную точку, перпендикулярно заданному вектору. Заметим, что это уравнение линейно относительно переменных x и y .
значит, координаты M не будут удовлетворять полученному уравнению. Поэтому (3.1) – уравнение прямой, проходящей через заданную точку, перпендикулярно заданному вектору. Заметим, что это уравнение линейно относительно переменных x и y .
Определение: Любой ненулевой вектор  , перпендикулярный прямой
, перпендикулярный прямой  , называется ее нормальным вектором, или нормалью.
, называется ее нормальным вектором, или нормалью.
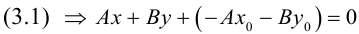 . Обозначая
. Обозначая 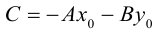 , получим
, получим

(3.2) – общее уравнение прямой на плоскости, 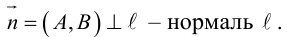
Уравнение прямой с направляющим вектором
Определение: Любой ненулевой вектор  , параллельный прямой, называется ее направляющим вектором.
, параллельный прямой, называется ее направляющим вектором.
Если A – некоторая точка на прямой 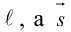 – вектор, параллельный ей, то, во-первых, через A параллельно
– вектор, параллельный ей, то, во-первых, через A параллельно  проходит единственная прямая, а, во-вторых, для любой точки
проходит единственная прямая, а, во-вторых, для любой точки 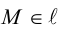 вектор
вектор 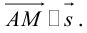 Таким свойством обладают только точки, лежащие на
Таким свойством обладают только точки, лежащие на  .
.
Чтобы вывести уравнение прямой, зададим на плоскости пдск XOY . В этой системе координат 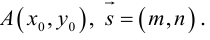
Пусть M (x, y) – произвольная точка на . Тогда 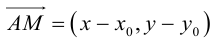 и
и 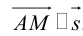 . Запишем условие коллинеарности векторов:
. Запишем условие коллинеарности векторов:

(3.3) – уравнение прямой на плоскости с направляющим вектором.
Если 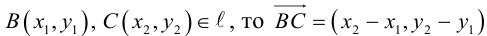 – направляющий вектор прямой , поэтому уравнение прямой, проходящей через две точки имеет вид:
– направляющий вектор прямой , поэтому уравнение прямой, проходящей через две точки имеет вид:

Уравнение прямой с угловым коэффициентом
Пусть 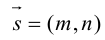 – направляющий вектор прямой
– направляющий вектор прямой не параллельна оси OY , тогда
не параллельна оси OY , тогда 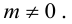
Определение: Угловым коэффициентом прямой  называется число
называется число
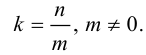
Очевидно, что если  – угол между прямой
– угол между прямой 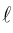 и положительным направлением оси ОХ, то
и положительным направлением оси ОХ, то 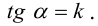
Рассмотрим уравнение (3.3) прямой с направляющим вектором 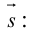
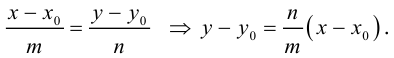
Отсюда следует (3.5) – уравнение прямой с заданным угловым коэффициентом, проходящей через заданную точку 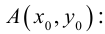

Из (3.5) получим 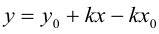 . Обозначим
. Обозначим 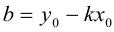 , тогда
, тогда

(3.6) – уравнение прямой с угловым коэффициентом.
Угол между прямыми на плоскости
Определение: Углом между двумя прямыми на плоскости называется любой из двух смежных углов, образованных ими при пересечении. Если прямые параллельны, то угол между ними равен 0 или радиан.
радиан.
Пусть прямые заданы общими уравнениями.
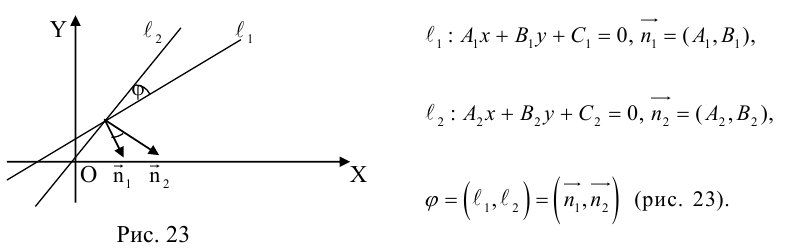
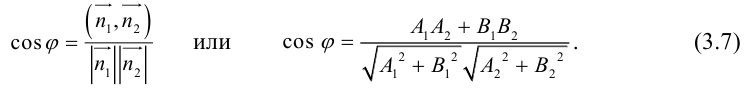
Условие параллельности прямых:
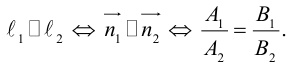
Условие перпендикулярности прямых:
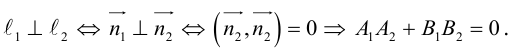
Рассмотрим случай, когда прямые заданы уравнениями с угловым коэффициентом.
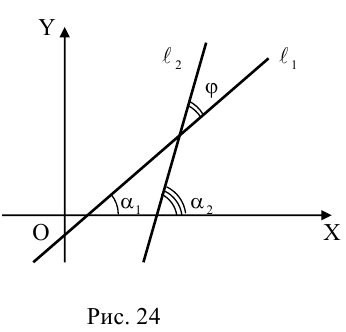
Так как  (рис. 24 ), то
(рис. 24 ), то
Условие параллельности прямых:
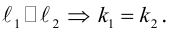
Условие перпендикулярности:
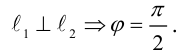 Так как
Так как 
не существует, то 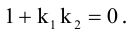
Пример №9
Даны вершины треугольника: 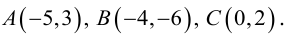
Написать:
а) уравнение медианы AM , б) высоты AH , в) найти угол между AM и AH
(рис. 25).

Перепишем уравнение медианы в общем виде:
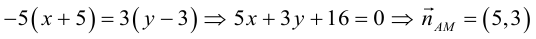 – нормаль АМ.
– нормаль АМ.
б)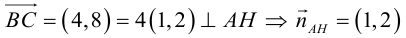 – нормаль AH . Уравнение прямой (3.1), проходящей через точку A перпендикулярно вектору
– нормаль AH . Уравнение прямой (3.1), проходящей через точку A перпендикулярно вектору  :
:
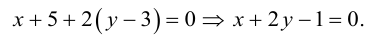
в)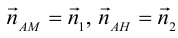 . По формуле (3.7)
. По формуле (3.7) 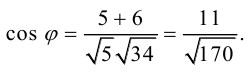
Расстояние от точки до прямой на плоскости
Пусть в некоторой пдск XOY задана прямая 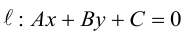 и точка
и точка 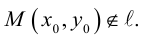 Найдем расстояние от точки M до прямой .
Найдем расстояние от точки M до прямой .
Пусть  – проекция точки M на
– проекция точки M на  (рис. 26), тогда
(рис. 26), тогда 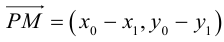 .
.
Нормаль
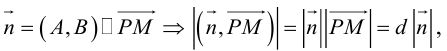
где d – искомое расстояние,  – скалярное произведение.
– скалярное произведение.
Следовательно,
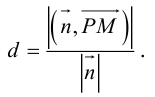
Так как 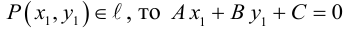 . Поэтому
. Поэтому
Отсюда 
(3.8) – формула для вычисления расстояния от точки до прямой на плоскости.
Пример №10
Найти длину высоты 
Уравнение  –
–
искомая длина высоты АН.
Кривые второго порядка
Окружность
Определение: Кривые второго порядка – плоские линии, которые в пдск XOY задаются уравнениями второй степени относительно двух переменных x,y.
Определение: Окружностью называется совокупность точек плоскости, равноудаленных от фиксированной точки, называемой ее центром.
Выведем уравнение окружности. Зададим пдск XOY . Пусть 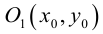 – фиксированная точка (центр окружности), а R – расстояние от точек окружности до ее центра (радиус окружности). Если
– фиксированная точка (центр окружности), а R – расстояние от точек окружности до ее центра (радиус окружности). Если 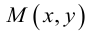 – произвольная точка окружности, то длина
– произвольная точка окружности, то длина 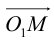 равна R .
равна R . 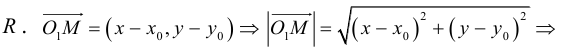

Если точка M (x, y) не лежит на окружности, то 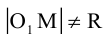 и ее координаты уравнению (3.9) не удовлетворяют, поэтому, (3.9) – уравнение окружности с центром
и ее координаты уравнению (3.9) не удовлетворяют, поэтому, (3.9) – уравнение окружности с центром 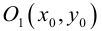 радиуса R .
радиуса R .
Если  , то уравнение окружности примет вид:
, то уравнение окружности примет вид:

(3.10) – каноническое уравнение окружности.
Пример №11
Показать, что уравнение 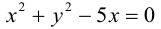 задает окружность (то есть найти ее центр и радиус).
задает окружность (то есть найти ее центр и радиус).
Приведем данное уравнение к виду (3.9), выделив полный квадрат по переменной x :
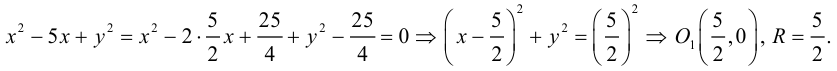
Пример №12
Написать уравнение линии центров окружностей
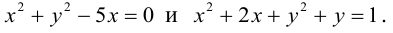
Найдем центр второй окружности:
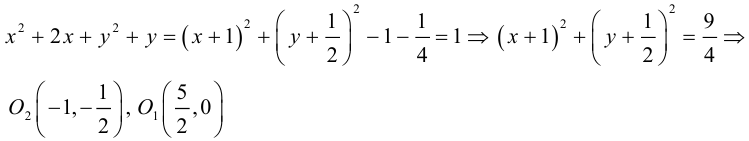
Уравнение прямой (3.4), проходящей через две точки:
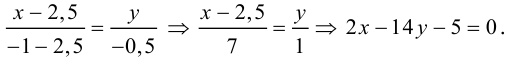
Эллипс
Определение: Эллипс – совокупность точек плоскости, сумма расстояний от которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.
Чтобы вывести уравнение эллипса, выберем пдск следующим образом: ось абсцисс проведем через фокусы 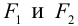 , а ось ординат – посередине отрезка
, а ось ординат – посередине отрезка 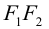 перпендикулярно оси абсцисс. Обозначим расстояние между фокусами
перпендикулярно оси абсцисс. Обозначим расстояние между фокусами 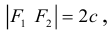 тогда
тогда 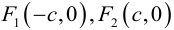 . Пусть M(x, y) – произвольная точка, лежащая на эллипсе, а 2a – сумма расстояний от точек на эллипсе до
. Пусть M(x, y) – произвольная точка, лежащая на эллипсе, а 2a – сумма расстояний от точек на эллипсе до  ,
,
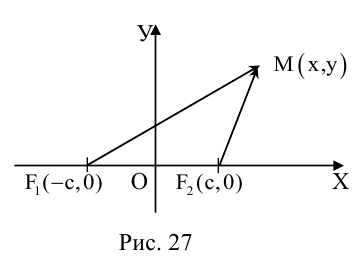
2a>2c определению эллипса.
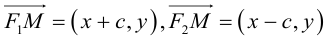 (рис. 27).
(рис. 27).
Запишем в виде уравнения свойство точек, принадлежащих эллипсу, сформулированное в определении:
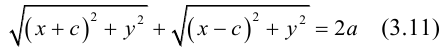
(3.11) – уравнение эллипса в выбранной системе координат. Преобразуем его к
более простому (каноническому) виду. Для этого умножим (3.11) на сопряженное выражение:
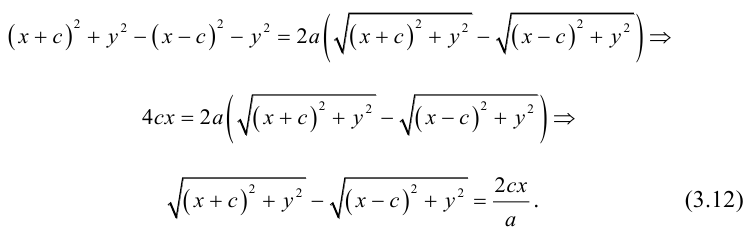
Сложим (3.11) и (3.12) и результат возведем в квадрат:
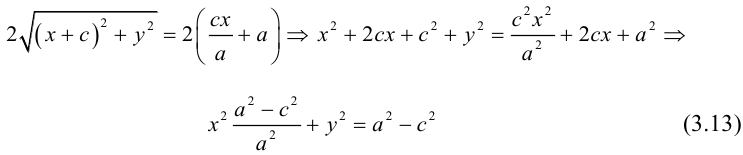
Так как по определению a>c, то есть  , то обозначим
, то обозначим  .
.
Тогда из (3.13) получим:

(3.14) – каноническое уравнение эллипса.
Исследуем форму эллипса по его каноническому уравнению. Найдем точки пересечения с осями координат:
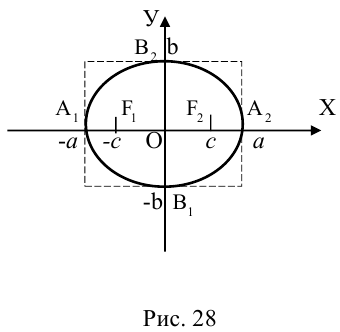
Из (3.14) следует, что
Значит, эллипс расположен в прямоугольнике со сторонами  .
.
Кроме того, из уравнения следует, что он симметричен относительно OX и OY . O(0,0) – точка пересечения осей симметрии – центр симметрии эллипса.
Ось, на которой лежат фокусы, называется фокальной осью эллипса. Точки пересечения эллипса с осями симметрии называются его вершинами.
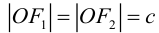 – полуфокусное расстояние,
– полуфокусное расстояние, 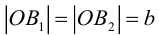 – малая полуось,
– малая полуось,
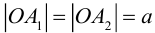 – большая полуось эллипса и
– большая полуось эллипса и 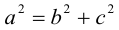 (рис. 28).
(рис. 28).
Отношение полуфокусного расстояния к длине большой полуоси 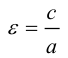 называется эсцентриситетом эллипса. Он характеризует форму эллипса.
называется эсцентриситетом эллипса. Он характеризует форму эллипса.
Так как 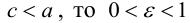 , и чем меньше
, и чем меньше  , тем больше эллипс похож на окружность. Для окружности
, тем больше эллипс похож на окружность. Для окружности  .
.
ЗАМЕЧАНИЕ 1. Уравнение эллипса, центр которого 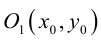 , а оси симметрии параллельны координатным осям, имеет вид:
, а оси симметрии параллельны координатным осям, имеет вид:

ЗАМЕЧАНИЕ 2. К кривым второго порядка эллиптического типа относятся также мнимый эллипс
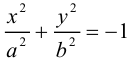 и точка
и точка 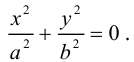
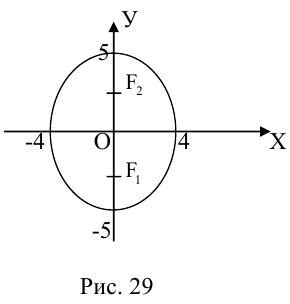
Пример №13
Найти эксцентриситет эллипса 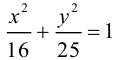 (рис. 29).
(рис. 29).
Так как  , то фокусы лежат на оси OY и поэтому
, то фокусы лежат на оси OY и поэтому 
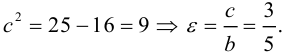
Гипербола
Определение: Гипербола – совокупность точек плоскости, модуль разности расстояний от которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная, не равная нулю и меньшая, чем расстояние между фокусами.
Чтобы вывести уравнение гиперболы, выберем пдск следующим образом:
ось абсцисс проведем через фокусы  , а ось ординат – посередине отрез-
, а ось ординат – посередине отрез-
ка  перпендикулярно оси абсцисс. Тогда
перпендикулярно оси абсцисс. Тогда 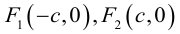 – фокусы гиперболы (рис. 30). Пусть M(x, y) – произвольная точка, лежащая на гиперболе.
– фокусы гиперболы (рис. 30). Пусть M(x, y) – произвольная точка, лежащая на гиперболе.
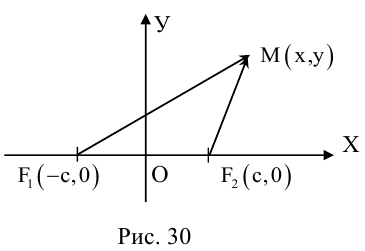
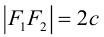 – расстояние между фокусами, 2a – модуль разности расстояний от точек на гиперболе до
– расстояние между фокусами, 2a – модуль разности расстояний от точек на гиперболе до 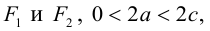
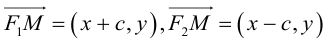 (рис. 30).
(рис. 30).
Запишем свойство точек, принадлежащих гиперболе, сформулированное в определении:
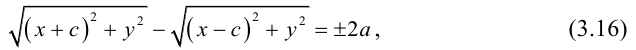
(3.16) – уравнение гиперболы в выбранной системе координат ( «+» – если разность расстояний положительна, и «–» – если отрицательна). Чтобы привести это уравнение к более простому виду, умножим (3.16) на сопряженное выражение и выполним такие же действия, как при упрощении уравнения эллипса, после чего получим:

По определению 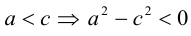 . Обозначим
. Обозначим 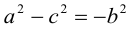 , тогда (3.17) перепишется в виде:
, тогда (3.17) перепишется в виде:

(3.18) – каноническое уравнение гиперболы.
Исследуем форму гиперболы по ее каноническому уравнению.
Из (3.18) следует, что гипербола симметрична относительно осей координат. Если x=0, 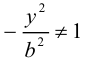 , значит, точек пересечения с OY нет; если y = 0 , то
, значит, точек пересечения с OY нет; если y = 0 , то 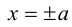 . Точки пересечения с осями симметрии называются вершинами гиперболы. Кроме того, из (3.18) следует, что
. Точки пересечения с осями симметрии называются вершинами гиперболы. Кроме того, из (3.18) следует, что 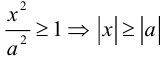 . Точка пересечения осей симметрии называется центром гиперболы. Ось симметрии, на которой расположены фокусы, называется фокальной осью. При этом фокальная ось также называется действительной (с ней гипербола пересекается), а ось симметрии, с которой гипербола не пересекается, называется ее мнимой осью.
. Точка пересечения осей симметрии называется центром гиперболы. Ось симметрии, на которой расположены фокусы, называется фокальной осью. При этом фокальная ось также называется действительной (с ней гипербола пересекается), а ось симметрии, с которой гипербола не пересекается, называется ее мнимой осью.
c – полуфокусное расстояние, a – действительная полуось, b – мнимая полуось. Отношение полуфокусного расстояния к длине действительной полуоси называется эксцентриситетом гиперболы: 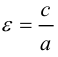 . Так как по определению
. Так как по определению 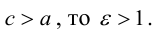
Считая, что 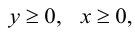 из (3.18) получим, что
из (3.18) получим, что 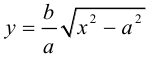 – уравнение части гиперболы, расположенной в первой четверти. Заметим, что при неограниченном возрастании
– уравнение части гиперболы, расположенной в первой четверти. Заметим, что при неограниченном возрастании 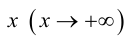 разность
разность 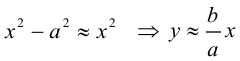 , то есть при достаточно больших x гипербола приближается к прямой
, то есть при достаточно больших x гипербола приближается к прямой 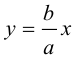 ,
,
причем ординаты точек на ней меньше соответствующих ординат точек на этой
прямой: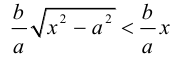 . Прямая
. Прямая 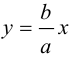 называется асимптотой гиперболы.
называется асимптотой гиперболы.
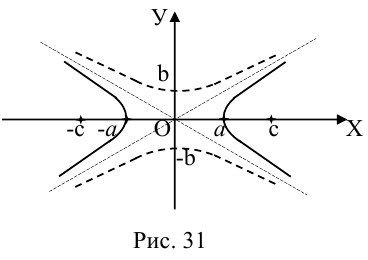
Из симметрии гиперболы следует, что то же самое происходит во второй, третьей и четвертой четвертях. Поэтому 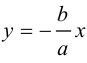 – также асимптота.
– также асимптота.
Итак, прямые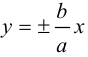 – асимптоты гиперболы (3.18), а гипербола – кривая, состоящая из двух ветвей (рис. 31).
– асимптоты гиперболы (3.18), а гипербола – кривая, состоящая из двух ветвей (рис. 31).
Если фокусы гиперболы лежат на OY , то ее уравнение имеет вид:

Гиперболы (3.18) и (3.19) называются сопряженными (рис. 31). Уравнения асимптот (3.19) такие же, как и для (3.18), но действительной является ось OY .
Если a = b, то гипербола называется равносторонней: 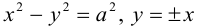 – уравнения ее асимптот (рис. 32 ).
– уравнения ее асимптот (рис. 32 ).
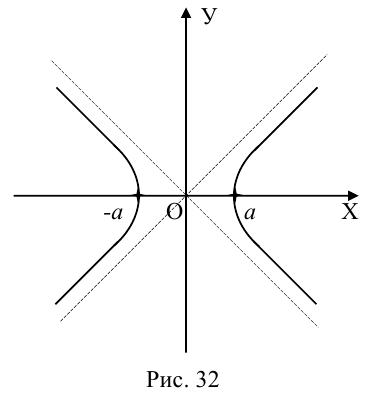
Очевидно, в этом случае асимптоты перпендикулярны. После поворота осей координат на  против часовой стрелки, получим гиперболу, задаваемую уравнением
против часовой стрелки, получим гиперболу, задаваемую уравнением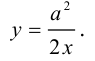
ЗАМЕЧАНИЕ 1. Если центр гиперболы в точке 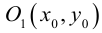 , а оси симметрии параллельны координатным осям, то уравнение гиперболы имеет вид
, а оси симметрии параллельны координатным осям, то уравнение гиперболы имеет вид
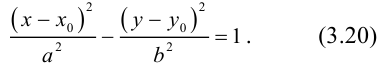
ЗАМЕЧАНИЕ 2. К кривым второго порядка гиперболического типа относится также пара пересекающихся прямых: 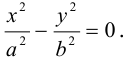
Пример №14
Найти координаты центра и написать уравнения асимптот гиперболы 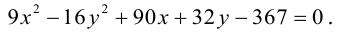
Приведем данное уравнение к виду (3.20):
Таким образом,  – центр,
– центр,  – уравнения асимптот данной гиперболы.
– уравнения асимптот данной гиперболы.
Парабола
Определение: Парабола – совокупность точек плоскости, равноудаленных от фиксированной точки этой плоскости, называемой фокусом, и фиксированной прямой, не проходящей через эту точку, называемой директрисой. Чтобы вывести уравнение параболы, выберем пдск следующим образом: ось абсцисс проведем через фокус перпендикулярно директрисе, а ось ординат посередине между фокусом и директрисой (рис. 33).
Пусть расстояние между фокусом F и директрисой DK равно p . Тогда 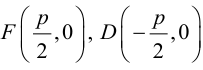 . Если M(x, y) – произвольная точка на параболе, то по определению
. Если M(x, y) – произвольная точка на параболе, то по определению
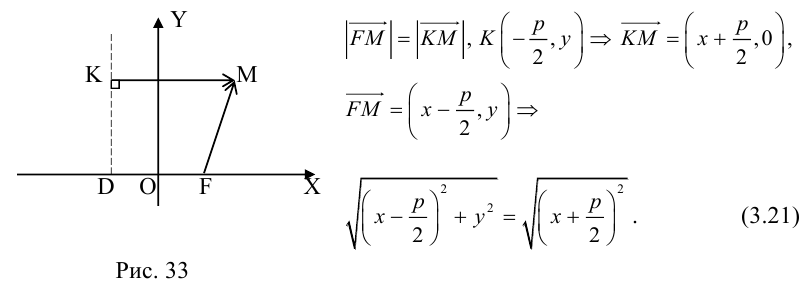
(3.21) – уравнение параболы в выбранной системе координат.
Упростим его:
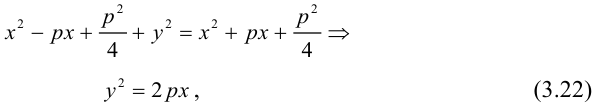
(3.22) – каноническое уравнение параболы; p называется ее параметром.
Из уравнения следует, что парабола симметрична относительно OX и проходит через начало координат. Кроме того, если 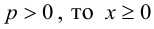 , поэтому кривая лежит в правой полуплоскости и с ростом величины
, поэтому кривая лежит в правой полуплоскости и с ростом величины 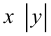 также растет. Точка пересечения параболы с осью симметрии называется ее вершиной (рис. 34).
также растет. Точка пересечения параболы с осью симметрии называется ее вершиной (рис. 34).
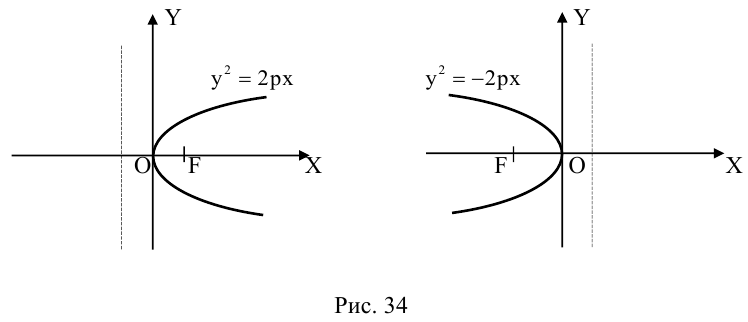
Если фокус параболы на оси ОУ (рис. 35), то ее каноническое уравнение имеет вид 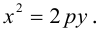
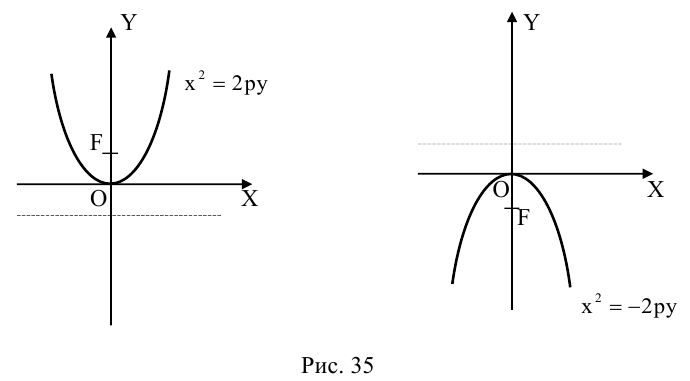
ЗАМЕЧАНИЕ 1. Если вершина параболы в точке 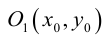 и ось симметрии параллельна OX , то ее уравнение имеет вид
и ось симметрии параллельна OX , то ее уравнение имеет вид 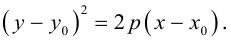
ЗАМЕЧАНИЕ 2. К кривым второго порядка параболического типа относятся также 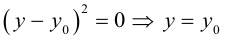 – пара совпадающих прямых;
– пара совпадающих прямых;
 – пара параллельных прямых;
– пара параллельных прямых; 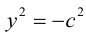 пара мнимых параллельных прямых.
пара мнимых параллельных прямых.
Пример №15
Написать уравнение геометрического места точек, равноудаленных от прямой x + y – 1 = 0 и точки F(-3,2).
По определению множество точек, равноудаленных от данных точки и прямой, является параболой. Пусть M (x, y) – произвольная точка искомой параболы, тогда 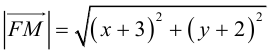 . Расстояние от точки M до прямой x + y – 1 = 0 вычисляется по формуле (3.8):
. Расстояние от точки M до прямой x + y – 1 = 0 вычисляется по формуле (3.8): 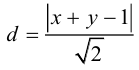 . Из условия следует, что
. Из условия следует, что
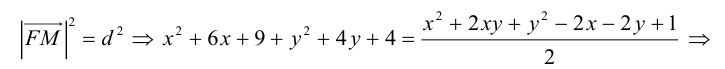 – уравнение искомого геометрического места точек.
– уравнение искомого геометрического места точек.
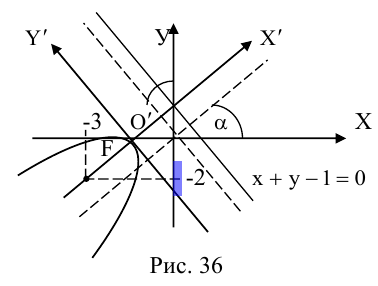
Если оси координат системы XOY повернуть на угол  так, чтобы одна из них стала параллельна директрисе, а затем перенести начало координат в точку
так, чтобы одна из них стала параллельна директрисе, а затем перенести начало координат в точку  – вершину параболы, то в новой системе
– вершину параболы, то в новой системе  уравнение параболы будет каноническим
уравнение параболы будет каноническим 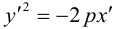 (рис. 36).
(рис. 36).
ЗАМЕЧАНИЕ. Можно показать, что, кроме окружности, эллипса, гиперболы, параболы и вырожденных случаев, указанных в замечаниях, других кривых второго порядка не существует.
Преобразования координат на плоскости
Преобразование координат — замена системы координат на плоскости, в пространстве или, в самом общем случае, на заданном n-мерном многообразии.
Параллельный перенос координатных осей
Пусть на плоскости задана пдск ХОУ. Будем называть ее “старой”. “Новая” система координат  получена из “старой” параллельным переносом осей в точку
получена из “старой” параллельным переносом осей в точку  . Выясним, как связаны координаты
. Выясним, как связаны координаты 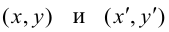 одной и той же точки М в этих системах координат.
одной и той же точки М в этих системах координат.
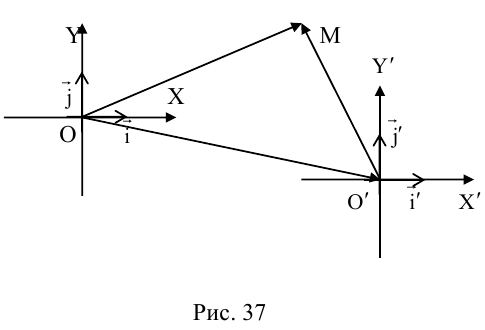
Пусть  – орты координатных осей системы ХОУ, а
– орты координатных осей системы ХОУ, а  – системы
– системы 
Тогда 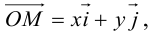
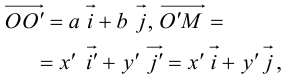
так как 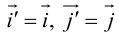 по определению равенства векторов (рис. 37).
по определению равенства векторов (рис. 37).
Так как 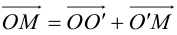 , то
, то
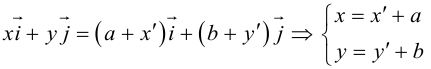
или

(3.23) – формулы параллельного переноса осей пдск.
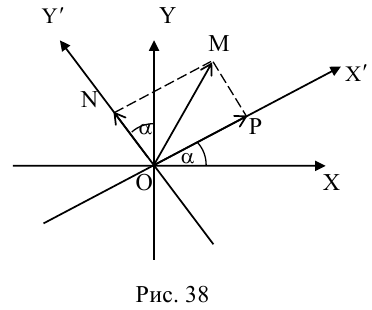
Поворот координатных осей на угол α
Поворот координатных осей на угол  .
.
Пусть “новая” пдск  получена из “старой” системы координат XOY поворотом осей ОХ и ОУ на угол
получена из “старой” системы координат XOY поворотом осей ОХ и ОУ на угол 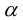 (рис. 38) и М(х, у) – произвольная точка в системе XOY . Выясним, какими станут ее координаты в “новой” пдск.
(рис. 38) и М(х, у) – произвольная точка в системе XOY . Выясним, какими станут ее координаты в “новой” пдск.
Из рис. 38 очевидно, что

Так как 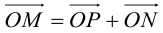 , то
, то
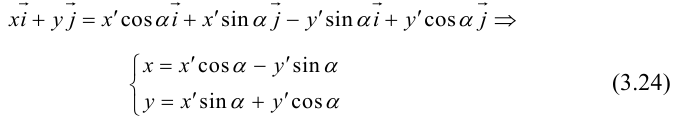
(3.24) – формулы поворота координатных осей на угол , выражающие старые координаты точки через новые.
Если обозначить 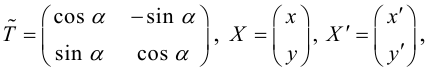 , то (3.24) можно переписать:
, то (3.24) можно переписать: 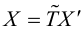 . Так как
. Так как 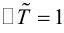 , то существует
, то существует 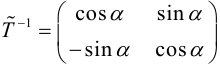 и
и
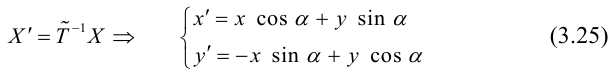
(3.25) – формулы поворота координатных осей на угол 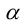 , выражающие новые координаты точки через старые.
, выражающие новые координаты точки через старые.
Пример №16
Каким будет уравнение прямой x + y – 1 = 0 после поворота координатных осей на угол 
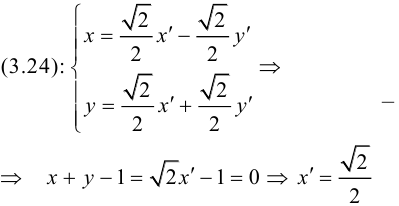
новое уравнение прямой (рис. 39).
Линейные преобразования на плоскости
Рассмотрим систему линейных уравнений:

Каждой точке плоскости M(x, y) по формулам (3.26) можно поставить в соответствие единственную точку 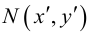 той же плоскости. При этом точка N называется образом точки M , а точка M – прообразом точки N . Кроме того,уравнения (3.26) линейны относительно x и y , поэтому будем говорить, что (3.26) определяют линейное преобразование плоскости в себя.
той же плоскости. При этом точка N называется образом точки M , а точка M – прообразом точки N . Кроме того,уравнения (3.26) линейны относительно x и y , поэтому будем говорить, что (3.26) определяют линейное преобразование плоскости в себя.
Преобразование (3.26) определяется матрицей 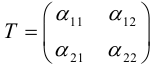 , которая называется матрицей линейного преобразования. Обозначая ,
, которая называется матрицей линейного преобразования. Обозначая ,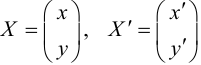
(3.26) можно переписать в виде 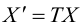 . Можно показать, что определитель
. Можно показать, что определитель 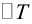 равен коэффициенту изменения площадей при линейном преобразовании (3.26). При этом
равен коэффициенту изменения площадей при линейном преобразовании (3.26). При этом  , если в результате преобразования направление обхода некоторого контура не меняется, и
, если в результате преобразования направление обхода некоторого контура не меняется, и  , если оно меняется на противоположное. Поясним это на примерах.
, если оно меняется на противоположное. Поясним это на примерах.
Пример №17
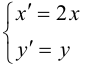 – растяжение вдоль
– растяжение вдоль
оси OX в 2 раза. 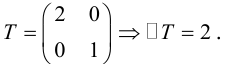
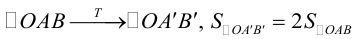 (рис. 40).
(рис. 40).
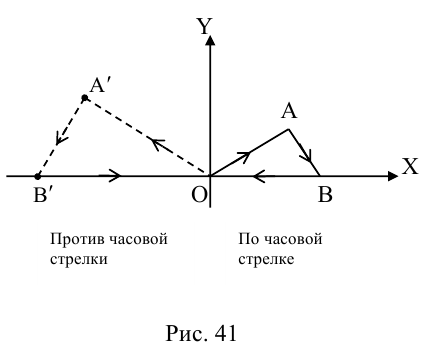
Пример №18
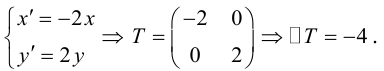
при этом направление обхода  от O к A , затем к B – по часовой стрелке, а соответствующее направление обхода
от O к A , затем к B – по часовой стрелке, а соответствующее направление обхода  – против часовой стрелки. Геометрически данное преобразование – растяжение вдоль OX и OY в 2 раза и отражение симметрично относительно оси OY (рис. 41).
– против часовой стрелки. Геометрически данное преобразование – растяжение вдоль OX и OY в 2 раза и отражение симметрично относительно оси OY (рис. 41).
Определение: Линейное преобразование (3.26) называется невырожденным, если 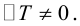
В этом случае существует обратная матрица 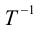 и можно найти
и можно найти 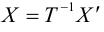 . То есть, если
. То есть, если 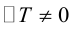 , то не только у каждого прообраза существует единственный образ, но и наоборот: для каждого образа существует единственный прообраз. В этом случае говорят, что (3.26) устанавливает взаимно однозначное соответствие между точками плоскости, или линейное преобразование плоскости на себя.
, то не только у каждого прообраза существует единственный образ, но и наоборот: для каждого образа существует единственный прообраз. В этом случае говорят, что (3.26) устанавливает взаимно однозначное соответствие между точками плоскости, или линейное преобразование плоскости на себя.
Можно показать, что невырожденное линейное преобразование переводит прямую в прямую, а кривую второго порядка – в кривую второго порядка.
Пример №19
Пусть 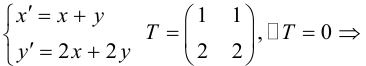 преобразование вырожденное.
преобразование вырожденное.
Какими будут образы точек, лежащих, например, на прямой x + y – 1 = 0
(рис. 42)?
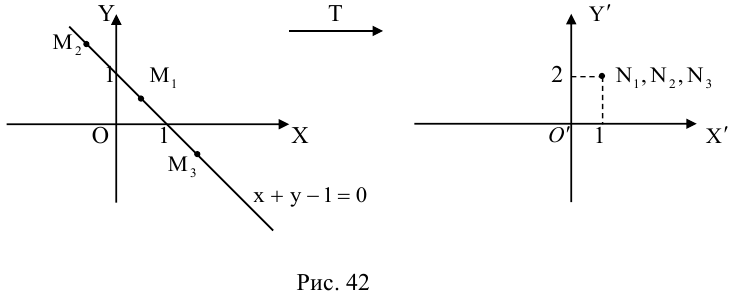
Очевидно, что если 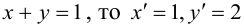 , то есть у точки N(1,2) существует бесконечное множество прообразов: все они лежат на прямой x + y – 1 = 0. Потому данное вырожденное линейное преобразование не устанавливает взаимно-однозначного соответствия между точками плоскости.
, то есть у точки N(1,2) существует бесконечное множество прообразов: все они лежат на прямой x + y – 1 = 0. Потому данное вырожденное линейное преобразование не устанавливает взаимно-однозначного соответствия между точками плоскости.
Пример №20
Рассмотрим формулы (3.25):
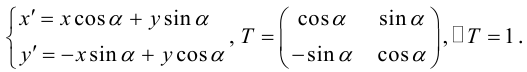
Очевидно, что поворот осей пдск на угол 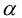 – линейное преобразование.
– линейное преобразование.
Так как это линейное преобразование невырожденное, то существует
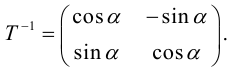
Заметим, что в этом случае 
Определение: Матрица A называется ортогональной, если  .
.
Линейное преобразование, матрица которого ортогональна, называется ортогональным.
Таким образом, поворот координатных осей – ортогональное линейное преобразование.
Можно показать, что если A – ортогональная матрица, то 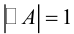 (доказать самостоятельно). Таким образом, в результате ортогональных линейных преобразований на плоскости площади фигур остаются неизменными.
(доказать самостоятельно). Таким образом, в результате ортогональных линейных преобразований на плоскости площади фигур остаются неизменными.
Произведение линейных преобразований
Рассмотрим матрицы 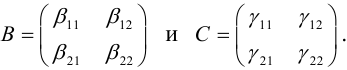 Каждая из них определяет линейное преобразование плоскости. Если M(x, y) – некоторая точка плоскости, то под действием линейного преобразования
Каждая из них определяет линейное преобразование плоскости. Если M(x, y) – некоторая точка плоскости, то под действием линейного преобразования 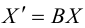 с матрицей B она перейдет в точку
с матрицей B она перейдет в точку 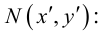

В свою очередь точка N под действием линейного преобразования 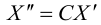 с матрицей C перейдет в точку
с матрицей C перейдет в точку 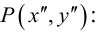

Такое последовательное выполнение линейных преобразований называется их произведением: 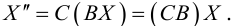
Покажем, что произведение линейных преобразований также линейное преобразование, и найдем его матрицу. Подставим (3.27) в (3.28):
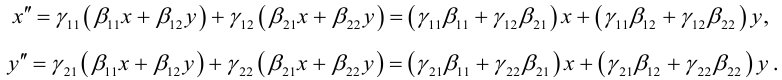
То есть
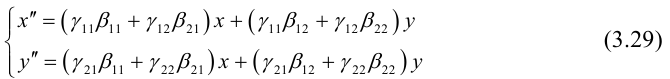
(3.29) – система линейных уравнений, а потому произведение линейных преобразований линейно. Матрица (3.29) имеет вид:
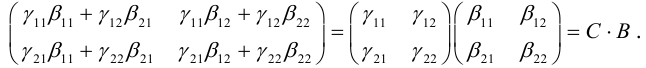
Таким образом, матрица произведения линейных преобразований равна произведению их матриц. Само же правило умножения матриц, сформулированное в гл.1, находит объяснение в этом выводе.
Приведение квадратичной формы к каноническому виду
Определение: Квадратичной формой относительно двух переменных x и y называется однородный многочлен второй степени:
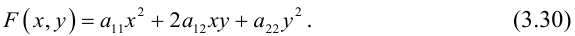
Уравнение 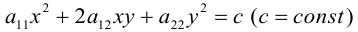 задает на плоскости кривую второго порядка, причем, так как вместе с точкой M(x, y) , лежащей на этой кривой, ей принадлежит и точка
задает на плоскости кривую второго порядка, причем, так как вместе с точкой M(x, y) , лежащей на этой кривой, ей принадлежит и точка 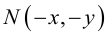 , кривая симметрична относительно
, кривая симметрична относительно
начала координат, то есть является центральной кривой (эллиптического или гиперболического типа).
Предположим, что уравнение 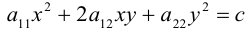 задает в пдск ХОУ эллипс. Если
задает в пдск ХОУ эллипс. Если 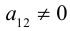 , то это уравнение не является каноническим уравнением эллипса, а потому, хотя О(0, 0) – его центр, оси симметрии не совпадают с ОХ и ОУ (рис. 43). Тем не менее, заметим, что если оси системы XOY повернуть на
, то это уравнение не является каноническим уравнением эллипса, а потому, хотя О(0, 0) – его центр, оси симметрии не совпадают с ОХ и ОУ (рис. 43). Тем не менее, заметим, что если оси системы XOY повернуть на
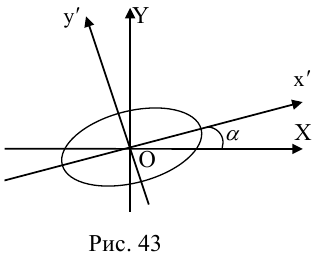
угол 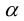 , то в системе
, то в системе 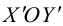 эллипс будет задаваться каноническим уравнением: кривая симметрична относительно
эллипс будет задаваться каноническим уравнением: кривая симметрична относительно  . Найдем линейное преобразование, соответствующее этому повороту.
. Найдем линейное преобразование, соответствующее этому повороту.
Матрица 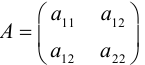 называется матрицей квадратичной формы (3.30).
называется матрицей квадратичной формы (3.30).
Пусть 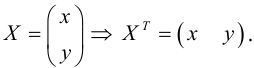
Вычислим 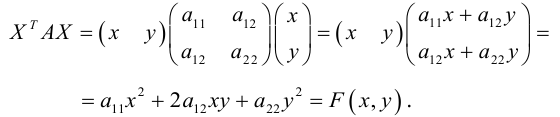
Таким образом, квадратичная форма может быть записана в матричном виде:

Пусть x, y – координаты точек плоскости в системе XOY , а  – координаты точек плоскости в новой системе
– координаты точек плоскости в новой системе  , где кривая задается каноническим уравнением. Переход от “старых” координат к “новым” будем искать в виде
, где кривая задается каноническим уравнением. Переход от “старых” координат к “новым” будем искать в виде
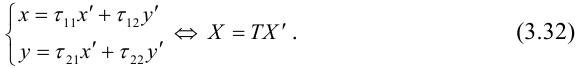
(3.32) – ортогональное линейное преобразование с матрицей
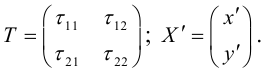
По определению ортогональной матрицы

(В результате ортогонального преобразования не происходит изменение площадей фигур, то есть фигуры не деформируются.)
Чтобы узнать, как изменится матрица квадратичной формы в результате линейного преобразования (3.32), подставим (3.32) в (3.31): 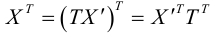 (свойство 5 умножения матриц)
(свойство 5 умножения матриц)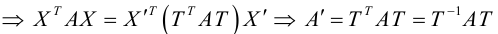
(свойство 2 умножения матриц и равенство (3.33)) – матрица новой квадратичной формы.
Так как в “новой” системе координат кривая должна задаваться каноническим уравнением, то есть в нем должно отсутствовать произведение координат xy, то  имеет вид:
имеет вид: 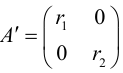
, где  – неизвестные числа. Умножим равенство
– неизвестные числа. Умножим равенство 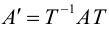 на матрицу T слева. Так как
на матрицу T слева. Так как 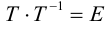 , то получим:
, то получим:
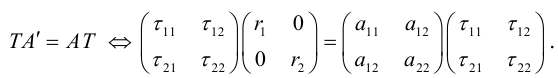
По определению равных матриц имеем:
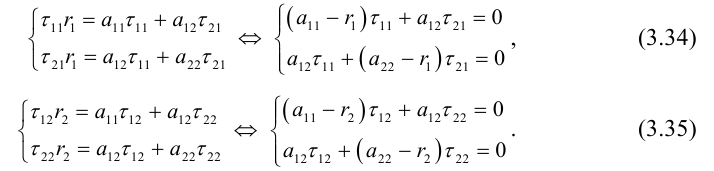
Системы уравнений (3.34), (3.35) – линейные и однородные. Они имеют нетривиальное решение, если их определители равны 0.
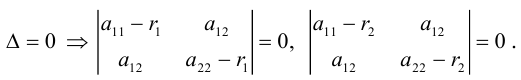
Это означает, что 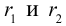 являются решениями уравнения
являются решениями уравнения
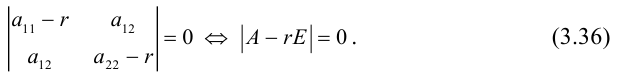
Уравнение (3.36) называется характеристическим уравнением матрицы A (характеристическим уравнением квадратичной формы). Его решения 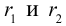 называются собственными значениями матрицы A (квадратичной формы).
называются собственными значениями матрицы A (квадратичной формы).
Покажем, что дискриминант квадратного уравнения (3.36) положителен, то есть любая квадратичная форма двух переменных имеет 2 различных собственных значения.
Вычислим определитель (3.36):
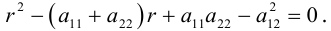
Дискриминант 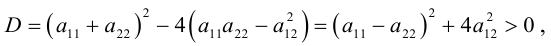
так как 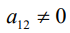 (иначе квадратичная форма будет канонической).
(иначе квадратичная форма будет канонической).
Таким образом, коэффициентами при 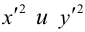 в каноническом виде квадратичной формы являются ее собственные значения, то есть решения уравнения (3.36).
в каноническом виде квадратичной формы являются ее собственные значения, то есть решения уравнения (3.36).
Решим (3.36) и подставим 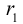 в (3.34). Система имеет бесконечное множество решений и пусть
в (3.34). Система имеет бесконечное множество решений и пусть 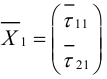 – одно их них. Так как система (3.34) однородная, то
– одно их них. Так как система (3.34) однородная, то 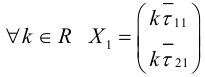 – тоже решение. Подберем k так, чтобы вектор
– тоже решение. Подберем k так, чтобы вектор
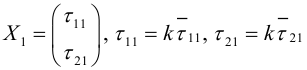 был единичным:
был единичным: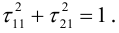
Векторы 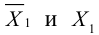 называется собственными векторами квадратичной формы, соответствующими собственному значению
называется собственными векторами квадратичной формы, соответствующими собственному значению  , или первыми собственными векторами. Их направление называется первым главным направлением квадратичной формы. Таким образом, первым собственным вектором квадратичной формы называется любое ненулевое решение системы (3.34).
, или первыми собственными векторами. Их направление называется первым главным направлением квадратичной формы. Таким образом, первым собственным вектором квадратичной формы называется любое ненулевое решение системы (3.34).
Аналогично подставим  в (3.35) и найдем
в (3.35) и найдем 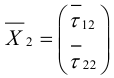 – второй собственный вектор, соответствующий собственному значению r2 . Его направление называется вторым главным направлением квадратичной формы.
– второй собственный вектор, соответствующий собственному значению r2 . Его направление называется вторым главным направлением квадратичной формы. 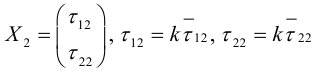 – второй единичный собственный вектор, то есть
– второй единичный собственный вектор, то есть 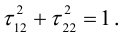
Можно показать, что  . Кроме того,
. Кроме того, 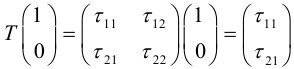 – первый собственный вектор, а
– первый собственный вектор, а 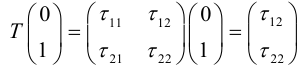 – второй собственный
– второй собственный
вектор, поэтому ортами “новой” системы координат  , к которой мы перейдем в результате линейного преобразования с матрицей T , являются единичные собственные векторы квадратичной формы, найденные как решения систем (3.34), (3.35). Направив оси “новой” системы координат вдоль собственных векторов
, к которой мы перейдем в результате линейного преобразования с матрицей T , являются единичные собственные векторы квадратичной формы, найденные как решения систем (3.34), (3.35). Направив оси “новой” системы координат вдоль собственных векторов  , получим систему координат, в которой квадратичная форма будет иметь канонический вид
, получим систему координат, в которой квадратичная форма будет иметь канонический вид 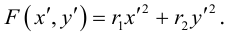
ВЫВОД.
Чтобы привести квадратичную форму к каноническому виду, надо:
- Составить и решить характеристическое уравнение (3.36); его решения – собственные значения – являются коэффициентами при
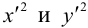 в каноническом виде квадратичной формы.
в каноническом виде квадратичной формы. - Найти единичные собственные векторы, решив (3.34) и (3.35); они будут ортами новой системы координат
 .При этом если ось
.При этом если ось сонаправлена с
сонаправлена с 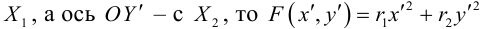 – канонический вид, который квадратичная форма имеет в системе
– канонический вид, который квадратичная форма имеет в системе  .
.
Приведение общего уравнения кривой второго порядка к каноническому виду
Общее уравнение кривой второго порядка имеет вид:
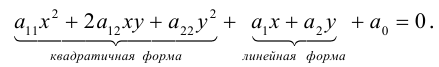
В результате невырожденного линейного преобразования с матрицей T квадратичная форма перейдет в квадратичную форму, линейная – в линейную, а свободный член  не изменится. Каждую группу слагаемых будем преобразовывать отдельно, а именно: найдем ортогональное преобразование, приводящее квадратичную форму к каноническому виду, затем посмотрим, как в результате этого преобразования изменится линейная форма (ортогональное преобразование в нашем случае – это поворот осей).
не изменится. Каждую группу слагаемых будем преобразовывать отдельно, а именно: найдем ортогональное преобразование, приводящее квадратичную форму к каноническому виду, затем посмотрим, как в результате этого преобразования изменится линейная форма (ортогональное преобразование в нашем случае – это поворот осей).
После поворота осей подберем параллельный перенос новой системы  так, чтобы после него уравнение кривой стало каноническим.
так, чтобы после него уравнение кривой стало каноническим.
Пример №21
Привести к каноническому виду ранее полученное уравнение параболы (стр. 58) и построить ее:
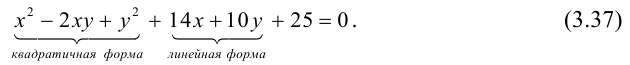
1) Составим матрицу квадратичной формы: 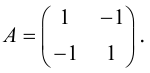
2) Составим и решим характеристическое уравнение (3.36):
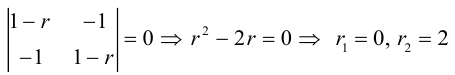 – собственные значения.
– собственные значения.
3) Найдем первый единичный собственный вектор, то есть решим систему (3.34):
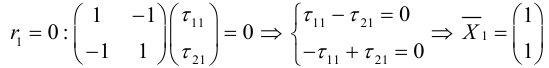 – первый собственный вектор.
– первый собственный вектор.
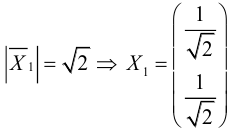 – первый единичный собственный вектор (орт оси
– первый единичный собственный вектор (орт оси  ).
).
4) Найдем второй единичный собственный вектор, то есть решим (3.35):
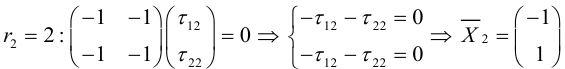 – второй собственный вектор.
– второй собственный вектор.
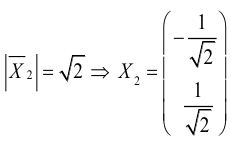 – второй единичный собственный вектор (орт оси
– второй единичный собственный вектор (орт оси 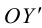 ) .
) .
Заметим, что 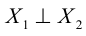 ,так как скалярное произведение
,так как скалярное произведение 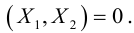
В полученной таким образом системе координат 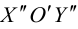 , взяв несколько контрольных точек, нарисуем параболу
, взяв несколько контрольных точек, нарисуем параболу 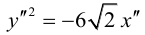 (рxис. 44).
(рxис. 44).
Сравните эскиз (рис. 36) и данный рисунок, являющийся результатом точных расчетов.
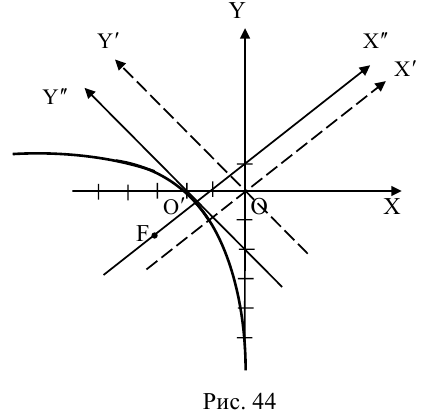
Плоскость
Покажем, что плоскость в пространстве задается в любой пдск линейным уравнением относительно трех переменных x, y, z.
Если A – некоторая точка на плоскости  – вектор, перпендикулярный ей, то, во-первых, через A перпендикулярно
– вектор, перпендикулярный ей, то, во-первых, через A перпендикулярно  проходит единственная плоскость, а, во-вторых, для любой точки
проходит единственная плоскость, а, во-вторых, для любой точки 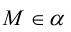 вектор
вектор 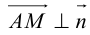 . Таким свойством обладают только точки, лежащие на
. Таким свойством обладают только точки, лежащие на  .
.
Чтобы вывести уравнение плоскости, зададим в пространстве пдск OXYZ . В этой системе координат 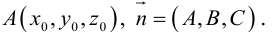
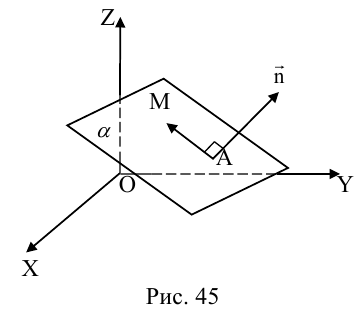
Пусть M(x,y,z) – произвольная точка на плоскости  .
.
Тогда  и
и  (рис. 45).
(рис. 45).
Вычислив скалярное произведение, получим:
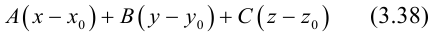
Координаты точек, лежащих в плоскости  , связаны соотношением (3.38). Если же
, связаны соотношением (3.38). Если же 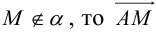 не перпендикулярен
не перпендикулярен 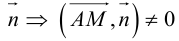 ,значит, координаты такой точки не удовлетворяют полученному уравнению. Поэтому (3.38) – уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору. Заметим, что это уравнение линейно относительно x, y, z.
,значит, координаты такой точки не удовлетворяют полученному уравнению. Поэтому (3.38) – уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору. Заметим, что это уравнение линейно относительно x, y, z.
Раскрыв скобки в (3.38), получим 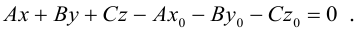
Обозначим 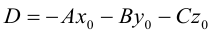 , тогда уравнение (3.38) примет вид:
, тогда уравнение (3.38) примет вид:

(3.39) – общее уравнение плоскости в пространстве,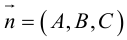 – ее нормаль.
– ее нормаль.
Определение: Любой ненулевой вектор  , перпендикулярный плоскости
, перпендикулярный плоскости 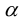 , называется ее нормальным вектором, или нормалью.
, называется ее нормальным вектором, или нормалью.
Особые случаи расположения плоскости
Выясним, какие особенности в расположении плоскости влечет за собой равенство нулю одного или нескольких коэффициентов в уравнении (3.39).
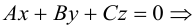 координаты точки O(0,0,0) удовлетворяют уравнению, значит, плоскость проходит через начало координат.
координаты точки O(0,0,0) удовлетворяют уравнению, значит, плоскость проходит через начало координат. 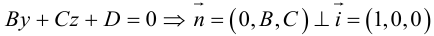 , так как
, так как 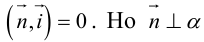 , значит, плоскость
, значит, плоскость  .
. 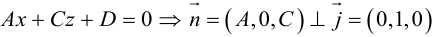 , так как
, так как 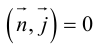 .Значит, плоскость
.Значит, плоскость  .
.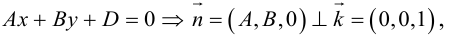 так как
так как 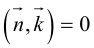 . Значит, плоскость
. Значит, плоскость  .
. 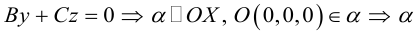 проходит через OX .
проходит через OX . 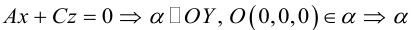 проходит через OY .
проходит через OY . 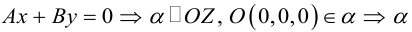 проходит через OZ .
проходит через OZ . -
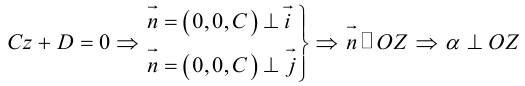 или
или 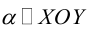 .
. 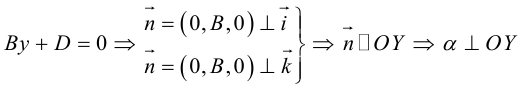 или
или 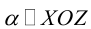 .
. -
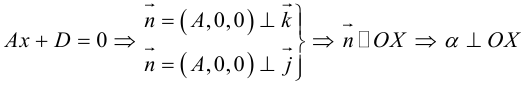 или
или 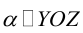 .
. 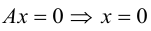 – плоскость YOZ .
– плоскость YOZ . 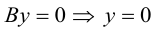 – плоскость XOZ .
– плоскость XOZ . 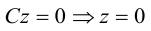 – плоскость XOY .
– плоскость XOY .
Уравнение плоскости в отрезках
Пусть плоскость 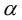 не параллельна ни одной из координатных осей и не проходит через начало координат. Тогда она отсекает на координатных осях отрезки a,b,c (рис. 46). Выведем уравнение такой плоскости.
не параллельна ни одной из координатных осей и не проходит через начало координат. Тогда она отсекает на координатных осях отрезки a,b,c (рис. 46). Выведем уравнение такой плоскости.
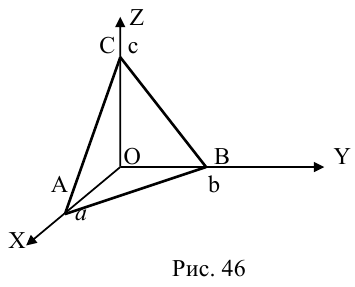
Рассмотрим 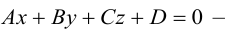 общее уравнение плоскости. Так как
общее уравнение плоскости. Так как  , то
, то 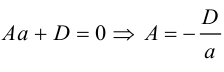 .
.
Аналогично 
Подставив А, В, С в общее уравнение, получим
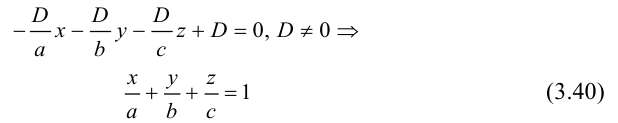
(3.40) – уравнение плоскости в отрезках.
Пример №22
Вычислить объем тетраэдра, образованного плоскостями
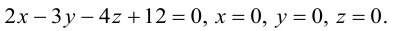
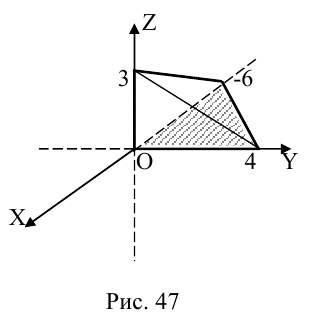
Перепишем уравнение плоскости в виде (3.40):
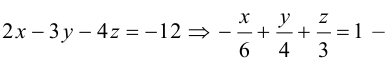
уравнение данной плоскости в отрезках. Поэтому (рис. 47)
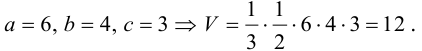
Уравнение плоскости, проходящей через три точки
Пусть в некоторой пдск заданы три точки, не лежащие на одной прямой:
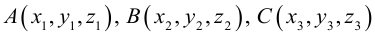 . Известно, что через них проходит единственная плоскость
. Известно, что через них проходит единственная плоскость  .
.
Чтобы вывести ее уравнение, рассмотрим произвольную точку этой плоскости M(x,y,z) . Тогда 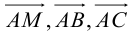 – компланарные векторы, и их смешанное произведение равно нулю:
– компланарные векторы, и их смешанное произведение равно нулю: 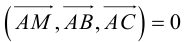 . Тогда по формуле (2.9) получим
. Тогда по формуле (2.9) получим
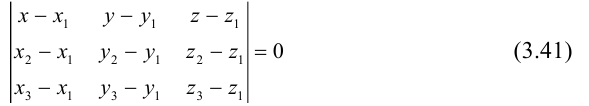
(3.41) – уравнение плоскости, проходящей через три точки.
ЗАМЕЧАНИЕ. Если точки лежат на одной прямой, то векторы  коллинеарны и их соответствующие координаты пропорциональны. Поэтому в определителе (3.41) две строки пропорциональны и по свойству 6 определителей он тождественно равен нулю, что означает, что координаты любой точки M(x,y,z) удовлетворяют уравнению (3.41). Это иллюстрация того факта, что через прямую и любую точку можно провести плоскость.
коллинеарны и их соответствующие координаты пропорциональны. Поэтому в определителе (3.41) две строки пропорциональны и по свойству 6 определителей он тождественно равен нулю, что означает, что координаты любой точки M(x,y,z) удовлетворяют уравнению (3.41). Это иллюстрация того факта, что через прямую и любую точку можно провести плоскость.
Пример №23
Написать уравнение плоскости, проходящей через точки
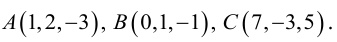
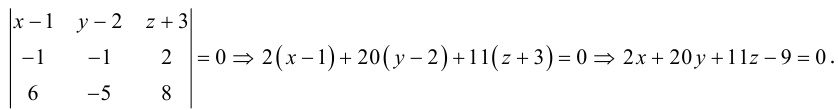
Угол между плоскостями
Определение: Углом между плоскостями называется любой из двух смежных двугранных углов, образованных плоскостями при их пересечении.
Если плоскости параллельны, то угол между ними равен 0 или  радиан.
радиан.
Рассмотрим плоскости 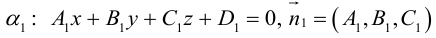 и
и
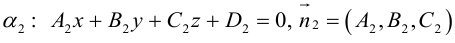 .
.
Очевидно, 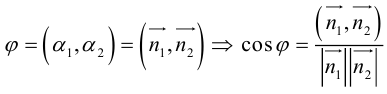
или 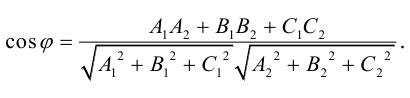
Если 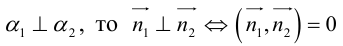 –0 условие перпендикулярности плоскостей.
–0 условие перпендикулярности плоскостей.
Если 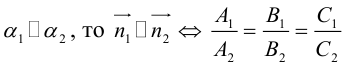 – условие параллельности плоскостей.
– условие параллельности плоскостей.
Пример №24
Найти угол между плоскостями
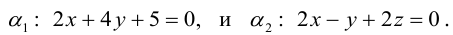
 плоскости перпендикулярны.
плоскости перпендикулярны.
Прямая линия в пространстве
Всякая линия в пространстве есть результат пересечения двух поверхностей. В частности прямую линию можно рассматривать как результат пересечения двух плоскостей
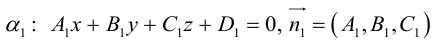
и
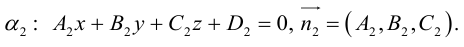
Если 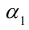 не параллельна
не параллельна 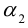 , то есть
, то есть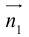 не коллинеарен
не коллинеарен 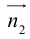 , то система уравнений
, то система уравнений
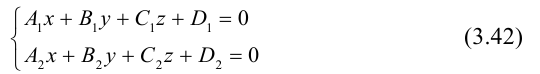
определяет прямую линию в пространстве.
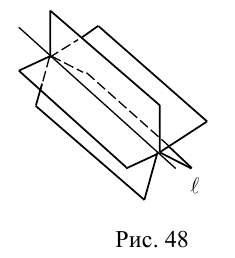
Уравнения (3.42) называются общими уравнениями прямой в пространстве.
Очевидно, одна и та же прямая может быть результатом пересечения разных пар плоскостей (рис. 48), поэтому прямую в пространстве можно задать различными способами.
Уравнения (3.42) неудобны в использовании, так как не дают представления о расположении прямой относительно выбранной системы координат.
Поэтому выведем более удобные уравнения, эквивалентные (3.42), то есть из бесконечного множества плоскостей, проходящих через данную прямую, выберем в некотором смысле более заметную пару.
Канонические уравнения прямой в пространстве
Пусть в некоторой пдск задана прямая  , проходящая через точку
, проходящая через точку 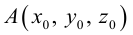 параллельно ненулевому вектору
параллельно ненулевому вектору 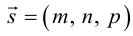 . Такой вектор называется направляющим вектором этой прямой.
. Такой вектор называется направляющим вектором этой прямой.
Для произвольной точки  вектор
вектор 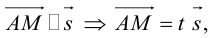 где t – не-который числовой множитель. Кроме того,
где t – не-который числовой множитель. Кроме того, 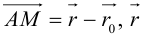 – радиус-вектор точки M ,
– радиус-вектор точки M ,  – радиус вектор точки A
– радиус вектор точки A
(рис. 49).
Отсюда 
(3.43) – векторное уравнение прямой в пространстве. Из (3.43) получаем:

(3.44) – параметрические уравнения прямой в пространстве,  – параметр.
– параметр.
Выразим из каждого уравнения (3.44) параметр:
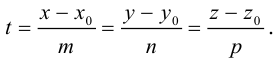
Тогда 
(3.45) – канонические уравнения прямой в пространстве, то есть уравнения прямой, проходящей через точку 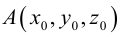 параллельно вектору
параллельно вектору 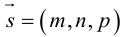 .
.
Заметим, что уравнения (3.45) задают прямую как результат пересечения плоскостей
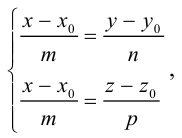
одна из которых параллельна OZ , а вторая – OY или как
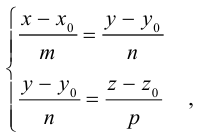
где первая плоскость параллельна OZ , а вторая – OX .
Если прямая 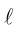 проходит через две заданные точки
проходит через две заданные точки 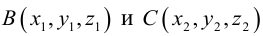 , то
, то 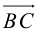 направляющий вектор этой прямой, поэтому из (3.45) получим:
направляющий вектор этой прямой, поэтому из (3.45) получим:

(3.46) – уравнения пространственной прямой, проходящей через две заданные точки.
Угол между прямыми в пространстве
Рассмотрим прямые, заданные в некоторой пдск каноническими уравнениями:
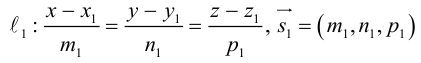
и
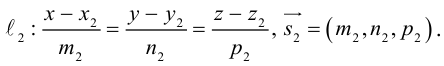
Определение: Углом между прямыми в пространстве называется угол между двумя пересекающимися прямыми, проходящими через произвольную точку пространства параллельно данным.
Из определения следует, что 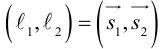 . Если
. Если  , то
, то
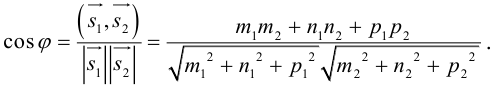
1)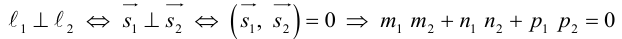 – условие перпендикулярности прямых.
– условие перпендикулярности прямых.
2)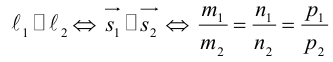 – условие параллельности прямых в пространстве.
– условие параллельности прямых в пространстве.
Пример №25
Найти угол между прямой 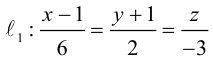 и прямой
и прямой  , проходящей через точки
, проходящей через точки 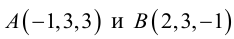 .
.
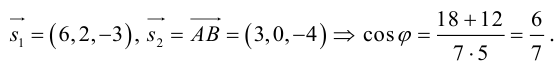
Заметим, что уравнение прямой  имеет вид:
имеет вид: 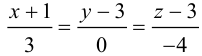 . В данном случае ноль в знаменателе писать принято: он означает, что направляющий вектор прямой (и сама прямая) параллелен плоскости XOZ . Эта прямая является результатом пересечения плоскостей
. В данном случае ноль в знаменателе писать принято: он означает, что направляющий вектор прямой (и сама прямая) параллелен плоскости XOZ . Эта прямая является результатом пересечения плоскостей 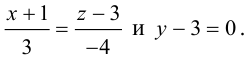
Приведение общих уравнений прямой в пространстве к каноническому виду
Рассмотрим прямую  , заданную общими уравнениями (3.42) в пространстве:
, заданную общими уравнениями (3.42) в пространстве:
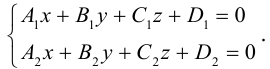
Привести эти уравнения к каноническому виду можно двумя способами:
- найти координаты какой-либо точки
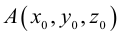 , лежащей на
, лежащей на 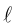 , ее направляющий вектор s и написать уравнения (3.45);
, ее направляющий вектор s и написать уравнения (3.45); - найти координаты двух точек, лежащих на
 , и воспользоваться уравнениями (3.46).
, и воспользоваться уравнениями (3.46).
1 способ.
Координаты точки A – любое частное решение системы линейных уравнений (3.42). Эта система имеет бесконечное множество решений, так как ранги основной и расширенной матриц 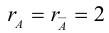 , а число неизвестных
, а число неизвестных 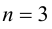 .
.
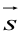 – направляющий вектор прямой
– направляющий вектор прямой  , поэтому
, поэтому 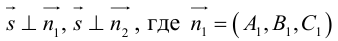 – нормаль плоскости
– нормаль плоскости 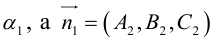 – нормаль плоскости
– нормаль плоскости 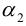 . Из определения векторного произведения векторов следует, что тогда
. Из определения векторного произведения векторов следует, что тогда 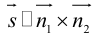 . Так как
. Так как 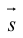 – произвольный вектор, параллельный
– произвольный вектор, параллельный 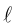 , то будем считать, что
, то будем считать, что 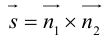 .
.
Пример №26
Привести уравнения прямой 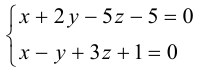 к каноническому виду.
к каноническому виду.
Найдем какое-нибудь частное решение этой системы: пусть, например,
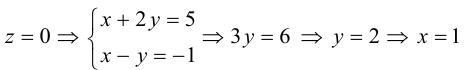 , то есть точка A(1,2,0) лежит на прямой.
, то есть точка A(1,2,0) лежит на прямой.
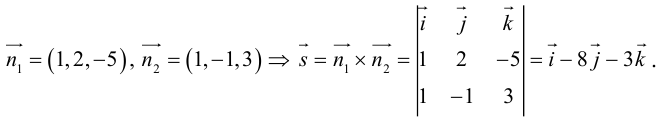
Таким образом, 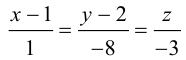 – канонические уравнения данной прямой.
– канонические уравнения данной прямой.
2 способ.
Найдем два произвольных частных решения системы уравнений, задающей прямую.
В рассмотренном примере  . Пусть теперь
. Пусть теперь
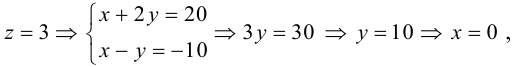
тогда 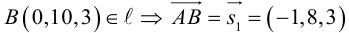 – направляющий вектор прямой, который отличается от найденного ранее только знаком. Поэтому уравнения
– направляющий вектор прямой, который отличается от найденного ранее только знаком. Поэтому уравнения 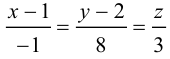 совпадают (с точностью до знака) с уже найденными.
совпадают (с точностью до знака) с уже найденными.
Угол между прямой и плоскостью
Определение: Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость.
Пусть в некоторой пдск заданы плоскость
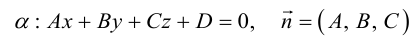
и прямая
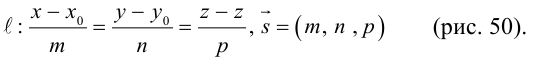
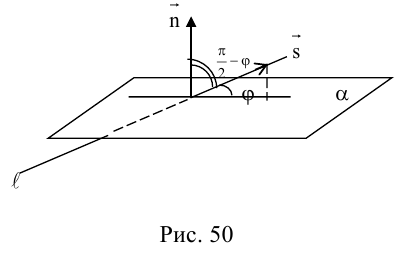
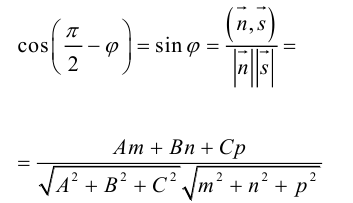


Определение общих точек прямой и плоскости
Чтобы найти общие точки прямой : 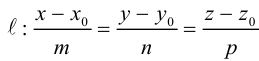 и плоскости
и плоскости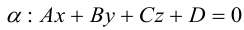 , надо решить систему линейных уравнений:
, надо решить систему линейных уравнений:
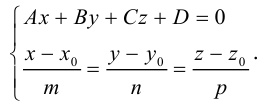
Решение этой системы будет наименее трудоемким, если перейти к параметрическим уравнениям прямой (3.44):
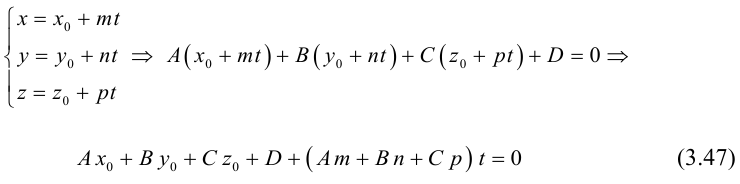
1) Пусть 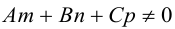 . Это значит, что прямая не параллельна плоскости, а потому они имеют одну общую точку. Из (3.47) найдем
. Это значит, что прямая не параллельна плоскости, а потому они имеют одну общую точку. Из (3.47) найдем
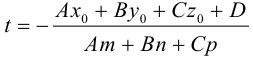
и по формулам (3.44) M(x,y,z) – их точку пересечения.
2) Пусть 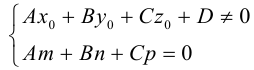 . Это означает, что в (3.47) решений нет: выполнено условие параллельности прямой и плоскости, при этом точка
. Это означает, что в (3.47) решений нет: выполнено условие параллельности прямой и плоскости, при этом точка 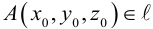 , но не лежит в плоскости
, но не лежит в плоскости  , значит, прямая и плоскость общих точек не имеют.
, значит, прямая и плоскость общих точек не имеют.
3) Пусть 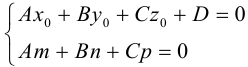 . Тогда любое
. Тогда любое 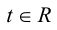 – решение (3.47) и система имеет бесконечно много решений: выполнено условие параллельности прямой и плоскости и точка
– решение (3.47) и система имеет бесконечно много решений: выполнено условие параллельности прямой и плоскости и точка 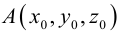 , лежащая на прямой, лежит в плоскости. Это значит, что прямая лежит в плоскости, то есть имеет с ней бесконечное множество общих точек.
, лежащая на прямой, лежит в плоскости. Это значит, что прямая лежит в плоскости, то есть имеет с ней бесконечное множество общих точек.
Пример №27
Найти проекцию точки 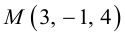 на плоскость
на плоскость 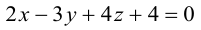 (рис. 53).
(рис. 53).
Пусть прямая 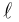 проходит через точку М перпендикулярно плоскости
проходит через точку М перпендикулярно плоскости  . Точка ее пересечения с плоскостью и будет искомой проекцией. В качестве направляющего вектора
. Точка ее пересечения с плоскостью и будет искомой проекцией. В качестве направляющего вектора 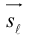 можно взять нормаль к плоскости
можно взять нормаль к плоскости 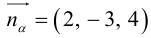 .
.
Напишем канонические уравнения прямой (3.45):

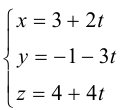 Подставим x,y,z в уравнение плоскости:
Подставим x,y,z в уравнение плоскости:
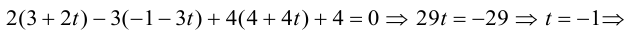
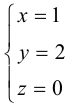 , то есть P 1,2,0 – искомая проекция.
, то есть P 1,2,0 – искомая проекция.
Цилиндрические поверхности
Уравнение F(x, y, z)=0 задает в пространстве некоторую поверхность.
Пусть уравнение содержит только две переменные, например, F(x,y)=0.Рассмотренное в плоскости XOY , оно задает некоторую кривую. Но ему будут удовлетворять и все точки пространства, которые проецируются в точки этой кривой, так как в уравнении отсутствует z , то есть все точки M(x,y,z) у которых х и у связаны соотношением 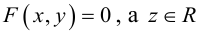 – произвольно.
– произвольно.
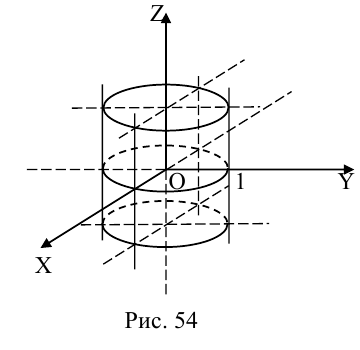
Пример №28
Построить поверхность 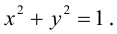
На плоскости это уравнение задает окружность с центром О(0, 0) и R=1.
В пространстве ему удовлетворяют координаты всех точек, проекция которых на плоскость ХОУ лежит на этой окружности. Очевидно, что эта поверхность – круговой цилиндр
(рис. 54).
Цилиндрические поверхности бывают не только круговыми.
Определение: Цилиндрической называется поверхность, полученная движением прямой, параллельной некоторому вектору, и пересекающей при движении некоторую кривую. При этом движущаяся прямая называется образующей, а кривая, которую она пересекает, называется направляющей цилиндрической поверхности.
Для поверхности 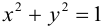 образующая параллельна оси OZ (так как в уравнении z отсутствует), а направляющей является окружность в плоскости XOY .
образующая параллельна оси OZ (так как в уравнении z отсутствует), а направляющей является окружность в плоскости XOY .
ВЫВОД. Если уравнение поверхности содержит только две переменные, то оно задает цилиндрическую поверхность. У поверхности F(y,z) ,образующая параллельна OX , а направляющая лежит в плоскости YOZ . Для поверхности F(x,z) ,образующая параллельна OY , направляющая в плоскости XOZ .
Пример №29
Построить и назвать поверхности  Эти уравнения задают цилиндрические поверхности. В первом случае направляющей является парабола в плоскости YOZ , а образующая параллельна OX (рис. 55). Во втором – образующая синусоида в плоскости XOZ , образующая параллельна OY (рис. 56).
Эти уравнения задают цилиндрические поверхности. В первом случае направляющей является парабола в плоскости YOZ , а образующая параллельна OX (рис. 55). Во втором – образующая синусоида в плоскости XOZ , образующая параллельна OY (рис. 56).
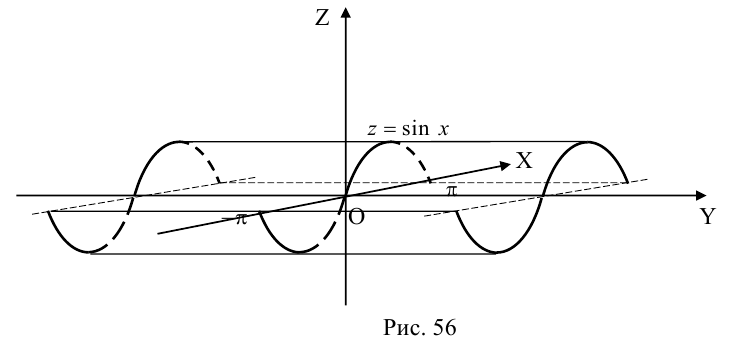
Поверхности вращения
Определение: Поверхностью вращения называется поверхность, полученная в результате вращения плоской кривой вокруг оси, лежащей в ее
плоскости.
Из определения следует, что сечением такой поверхности любой плоскостью, перпендикулярной оси вращения, является окружность.
Пусть в плоскости YOZ задана кривая  – координаты точки в плоской системе координат YOZ . Эта кривая вращается вокруг оси OZ . Выведем уравнение поверхности вращения.
– координаты точки в плоской системе координат YOZ . Эта кривая вращается вокруг оси OZ . Выведем уравнение поверхности вращения.
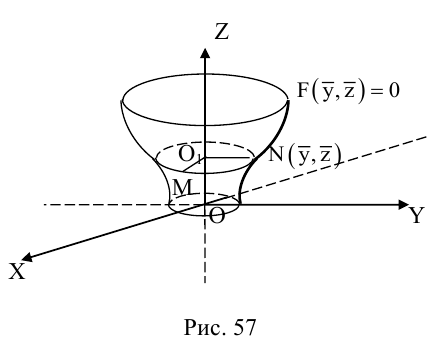
Пусть M(x,y,z) – произвольная точка на поверхности,  , z– центр окружности сечения, проходящего через точку M , а
, z– центр окружности сечения, проходящего через точку M , а 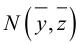 – точка, лежащая на кривой и одновременно в рассматриваемом сечении (рис. 57).
– точка, лежащая на кривой и одновременно в рассматриваемом сечении (рис. 57).
Тогда 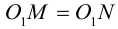 – радиусы сечения.
– радиусы сечения.
Но 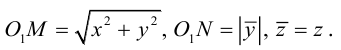
Таким образом, уравнение поверхности вращения получим, если в уравнении кривой  заменим на
заменим на 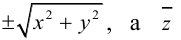 – на z. Тогда получим:
– на z. Тогда получим:
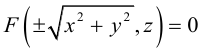 – уравнение поверхности вращения (OZ – ось вращения).
– уравнение поверхности вращения (OZ – ось вращения).
Очевидно, что если кривая F(y,z)=0 вращается вокруг OY , то уравнение
поверхности вращения имеет вид: 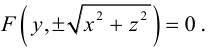
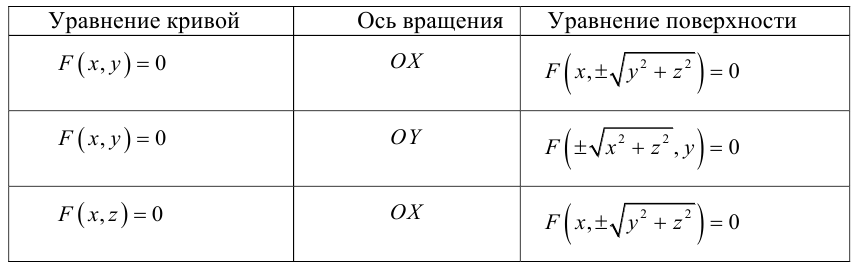
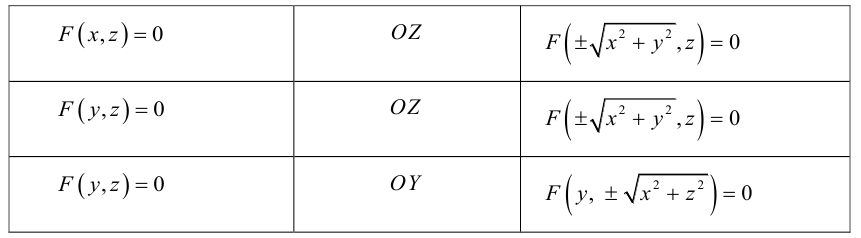
Некоторые поверхности второго порядка
1. Пусть эллипс 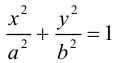 вращается вокруг оси OY .
вращается вокруг оси OY .
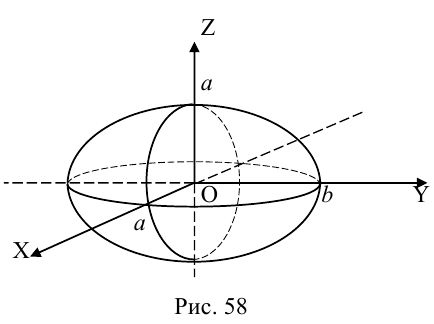
Полученная поверхность является поверхностью второго порядка, так ее уравнение 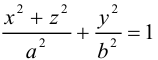 – второй степени относительно переменных x,y,z . Она называется эллипсоидом вращения (рис. 58).
– второй степени относительно переменных x,y,z . Она называется эллипсоидом вращения (рис. 58).
Поверхность, задаваемая уравнением 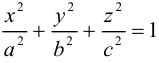 , называется трехосным эллипсоидом.
, называется трехосным эллипсоидом.
2. Если гипербола 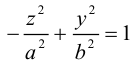 вращается вокруг оси OZ , то уравнение
вращается вокруг оси OZ , то уравнение
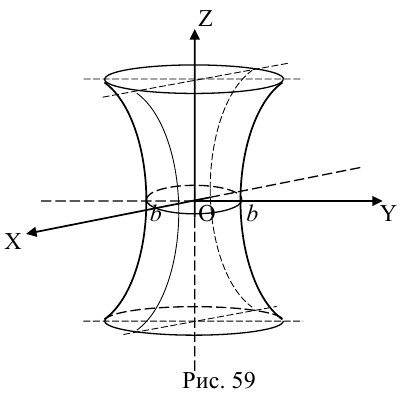
поверхности вращения имеет вид
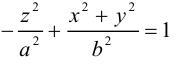
или
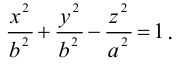
Такая поверхность называется однополостным гиперболоидом вращения (рис. 59).
3. Если гипербола 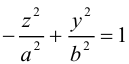 вращается вокруг оси OY , то уравнение поверхности имеет вид
вращается вокруг оси OY , то уравнение поверхности имеет вид 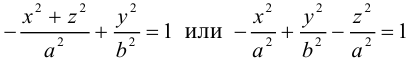 . Такая поверхность называется двуполостным гиперболоидом вращения (рис. 60).
. Такая поверхность называется двуполостным гиперболоидом вращения (рис. 60).
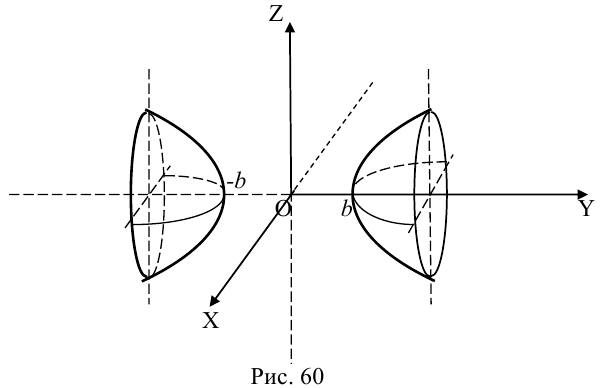
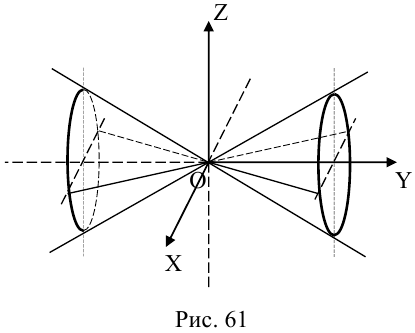
4. Если пара пересекающихся прямых 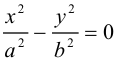 вращается вокруг оси OY , то получается конус вращения с уравнением
вращается вокруг оси OY , то получается конус вращения с уравнением 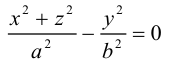 или
или 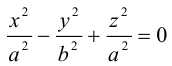 (рис. 61).
(рис. 61).
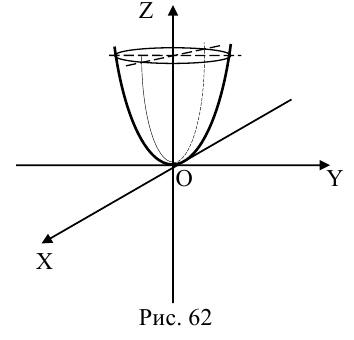
5. При вращении параболы  вокруг оси OZ получается поверхность
вокруг оси OZ получается поверхность  , которая называется эллиптическим параболоидом вращения (рис. 62).
, которая называется эллиптическим параболоидом вращения (рис. 62).
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Векторная алгебра
- Геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика
Прямую линию в прямоугольной системе координат можно задать с помощью канонического уравнения. В этой статье мы расскажем, что это такое, приведем примеры, рассмотрим связи канонических уравнений с другими типами уравнений для этой прямой. В последнем пункте мы разберем несколько задач на закрепление темы.
Понятие канонического уравнения прямой
Допустим, что у нас есть декартова (прямоугольная) система координат, в которой задана прямая. Нам известны координаты произвольно взятой точки этой прямой M1(x1, y1), а также ее направляющего вектора a→=(ax, ay). Попробуем составить уравнение, которое описывало бы эту прямую.
Возьмем плавающую точку M(x, y). Тогда вектор M1M→ можно считать направляющим для исходной прямой. Его координаты будут равны x-x1, y-y1 (если нужно, повторите материал о том, как правильно вычислять координаты вектора с помощью координат отдельных его точек).
Множество произвольно взятых точек M(x, y) будут определять нужную нам прямую с направляющим вектором a→=(ax, ay) только в одном случае – если векторы M1M→ и a→=(ax, ay) будут коллинеарны по отношению друг к другу. Посмотрите на картинку:
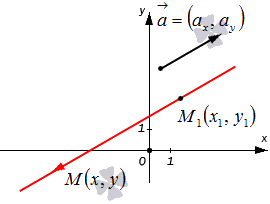
Таким образом, мы можем сформулировать необходимое и достаточное коллинеарности этих двух векторов:
M1M→=λ·a→, λ∈R
Если преобразовать полученное равенство в координатную форму, то мы получим:
x-x1=λ·axy-y1=λ·ay
При условии, что ax≠0 и ay≠0, получим:
x-x1=λ·axy-y1=λ·ay⇔λ=x-x1axλ=y-y1ay⇔x-x1ax=y-y1ay
Итог наших преобразований и будет каноническим уравнением прямой на плоскости. Запись вида x-x1ax=y-y1ay также называют уравнением прямой в каноническом виде.
Таким образом, с помощью уравнения x-x1ax=y-y1ay можно задать в прямоугольной системе координат на плоскости прямую, которая имеет направляющий вектор a→=(ax, ay) и проходит через точку M1(x1, y1).
Примером уравнения подобного типа является, например, x-23=y-31. Прямая, которая задана с его помощью, проходит через M1(2, 3) и имеет направляющий вектор a→=3, 1. Ее можно увидеть на рисунке:
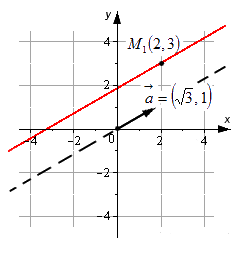
Из определения канонического уравнения нужно сделать несколько важных выводов. Вот они:
1. Если прямая, имеющая направляющий вектор a→=(ax, ay), проходит через две точки – M1(x1, y1) и M2(x2, y2), то уравнение для нее может быть записано как в виде x-x1ax=y-y1ay, так и x-x2ax=y-y2ay.
2. Если заданная прямая имеет направляющий вектор с координатами a→=(ax, ay), то множество всех ее векторов можно обозначить как μ·a→=(μ·ax, μ·ay), μ∈R, μ≠0. Таким образом, любое уравнение прямой в каноническом виде x-x1μ·ax=y-y1μ·ay будет соответствовать этой прямой.
Разберем важный пример задачи на нахождение канонического уравнения.
В прямоугольной системе координат на плоскости задана прямая, которая проходит через точку M1(2, -4) и имеет направляющий вектор с координатами a→=(1, -3). Запишите каноническое уравнение, описывающее данную прямую.
Решение
Для начала вспомним общий вид нужного нам канонического уравнения – x-x1ax=y-y1ay. Подставим в него имеющиеся значения x1=2, y1=-4, ax=1, ay=-3 и подсчитаем:
x-x1ax=y-y1ay⇔x-21=y-(-4)-3⇔x-21=y+4-3
Получившееся в итоге равенство и будет нужным ответом.
Ответ: x-21=y+4-3
Канонические уравнения прямой на плоскости с ax или ay, равными нулю
Если значение хотя бы одной переменной a является нулевым, то уравнение плоскости используют в первоначальном виде. Сразу две переменные нулевыми не могут быть по определению, поскольку нулевой вектор не бывает направляющим. В таком случае мы можем считать запись x-x1ax=y-y1ay условной и понимать ее как равенство ay(x-x1)=ax(y-y1).
Разберем случаи канонических уравнений на плоскости с одним нулевым a более подробно. Допустим, что x-x10=y-y1ay при ax=0, а исходная прямая будет проходить через M1(x1, y1). В таком случае она является параллельной оси ординат (если x1=0, то она будет с ней совпадать). Докажем это утверждение.
Для этой прямой вектор a→=(0, ay) будет считаться направляющим. Этот вектор является коллинеарным по отношению к координатному вектору j→=(0,1).
Если же нулевым является значение второго параметра, то есть ay=0, то мы получаем равенство вида x-x1ax=y-y10. Это уравнение описывает прямую, проходящую через M1(x1, y1), которая расположена параллельно оси абсцисс. Это утверждение верно, поскольку a→=(ax, 0) является для этой прямой направляющим вектором, а он в свою очередь является коллинеарным по отношению к координатному вектору i→=(1, 0).
Проиллюстрируем два частных случая канонического уравнения, описанные выше:
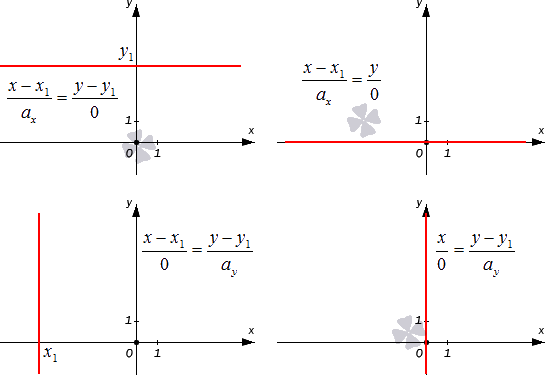
На плоскости задана прямая, параллельная оси Oy. Известно, что она проходит через точку M123, -17. Запишите каноническое уравнение для нее.
Решение
Если прямая по отношению оси ординат является параллельной, то мы можем взять координатный вектор j→=(0, 1) в качестве направляющего для нее. В таком случае искомое уравнение выглядит следующим образом:
x-230=y–171⇔x-230=y+171
Ответ: x-230=y+171
На рисунке изображена прямая. Запишите ее каноническое уравнение.
Решение
Мы видим, что исходная прямая проходит параллельно оси Ox через точку M1(0, 3). Мы берем координатный вектор i→=(1, 0) в качестве направляющего. Теперь у нас есть все данные, чтобы записать нужное уравнение.
x-01=y-30⇔x1=y-30
Ответ: x1=y-30
Преобразование канонического уравнения прямой в другие виды уравнений
Мы уже выяснили, что в прямоугольной системе координат на плоскости заданную прямую можно описать с помощью канонического уравнения. Оно удобно для решения многих задач, однако иногда лучше производить вычисления с помощью другого типа уравнений. Сейчас мы покажем, как преобразовать каноническое уравнение в другие виды, если это требуется по ходу решения.
Стандартной форме записи канонического уравнения x-x1ax=y-y1ay можно поставить в соответствие систему параметрических уравнений на плоскости x=x1+ax·λy=y1+ay·λ. Чтобы преобразовать один вид уравнения в другой, нам надо приравнять правую и левую часть исходного равенства к параметру λ. После этого надо выполнить разрешение получившихся равенств относительно переменных x и y:
x-x1ax=y-y1ay⇔x-x1ax=y-y1ay=λ⇔⇔x-x1ax=λy-y1ay=λ⇔x=x1+ax·λy=y1+ay·λ
Покажем на примере, как именно выполняется это действие с конкретными числами.
У нас есть прямая, заданная на плоскости с помощью канонического уравнения x+23=y-111. Запишите параметрические уравнения исходной прямой.
Решение
Сначала поставим знак равенства между отдельными частями уравнения и переменной λ и получим x+23=λy-111=λ.
Далее можно перейти к формулированию необходимых параметрических уравнений:
x+23=λy-111=λ⇔x+2=3·λy-1=11·λ⇔x=-2+3·λy=1+11·λ
Ответ: x=-2+3·λy=1+11·λ
Из канонического уравнения можно получить не только параметрические, но и общие уравнения прямой. Вспомним понятие пропорции: запись ab=cd можно представить в виде a·d=b·c с сохранением смысла. Значит, что x-x1ax=y-y1ay⇔ay(x-x1)=ax(y-y1)⇔ayx-axy-ayx1+axy1=0.
Это и есть общее уравнение прямой. Это станет более очевидно, если мы добавим в него значения параметров ay=A, -ax=B, -ayx1+axy1=C.
Прямая на плоскости описана с помощью канонического уравнения x-12=y+40. Вычислите общее уравнение этой прямой.
Решение
Делаем указанные выше действия по порядку.
x-12=y+40⇔0·(x-1)=2·(y+4)⇔y+4=0
Ответ: y+4=0 .
Также из канонического уравнения мы можем получить уравнение прямой в отрезках, прямой с угловым коэффициентом или нормальное уравнение прямой, но это действие выполняется в два шага: первым делом мы получаем общее уравнение прямой, а вторым – преобразуем его в уравнение указанного типа. Разберем пример такой задачи.
На плоскости задана прямая с помощью уравнения x+33=y-22. Запишите уравнение этой же прямой в отрезках.
Решение
Для начала преобразуем исходное каноническое уравнение в общее уравнение прямой.
x+33=y-22⇔2·(x+3)=3·(y-2)⇔2x-3y+6+23=0
Далее переходим к формулировке уравнения прямой в отрезках.
2x-3y+6+23=0⇔2x-3y=-6+23⇔⇔2-(6+23)x-3-(6+23)y=1⇔x-6+232+y6+233=1⇔x-3+3+y33+2=1
Ответ: x-3+3+y33+2=1
Достаточно легко решить и задачу, обратную этой, т.е. привести уравнение прямой на плоскости обратно к каноническому. Допустим, у нас есть общее уравнение прямой в стандартной формулировке – Ax+By+C=0. При условии A≠0 мы можем перенести By вправо с противоположным знаком. Получим Ax+C=-By. Теперь выносим A за скобки и преобразуем равенство так:
Ax+CA=-By
Получившееся уравнение мы записываем в виде пропорции: x+CA-B=yA.
У нас получилось нужное нам каноническое уравнение прямой на плоскости.
А как сделать преобразование, если B≠0? Переносим все слагаемые, кроме Ax, вправо с противоположными знаками. Получаем, что Ax=-By-C. Выносим -B за скобки:
Ax=-By+CB
Формируем пропорцию: x-B=y+CBA
Есть общее уравнение прямой x+3y-1=0. Перепишите его в каноническом виде.
Решение
Оставим с левой стороны только одну переменную x. Получим:
x=-3y+1
Теперь вынесем -3 за скобки: x=-3y-13. Преобразуем равенство в пропорцию и получим необходимый ответ:
x-3=y-131
Ответ: x-3=y-131
Таким же образом мы поступаем, если нам нужно привести к каноническому виду уравнение прямой в отрезках и уравнение прямой с угловым коэффициентом.
Наиболее простая задача – переход от параметрических уравнений к каноническим. Нужно просто выразить параметр λ в системе уравнений x=x1+ax·λy=y1+ay·λ и приравнять обе части равенств. Схема решения выглядит так:
x=x1+ax·λy=y1+ay·λ⇔λ=x-x1axλ=y-y1ay⇔x-x1ax=y-y1ay
Если значение одного из параметров a будет нулевым, мы поступаем точно таким же образом.
Прямая на плоскости описана с помощью системы параметрических уравнений x=3+0·λy=-2-4·λ. Запишите каноническое уравнение для этой прямой.
Решение
Для начала преобразуем исходные уравнения в систему x=3+0·λy=-2-4·λ. Следующим шагом будет выражение параметра в каждом уравнении:
x=3+0·λy=-2-4·λ⇔λ=x-30λ=y+2-4
Ставим знак равенства между получившимися частями и получаем нужное нам каноническое уравнение: x-30=y+2-4
Ответ: x-30=y+2-4
Как решать задачи на составление канонических уравнений
В первую очередь канонические уравнения используются для тех задач, где нужно выяснить, принадлежит ли некоторая точка заданной прямой или нет. Вспомним, что в случае, если точка лежит на прямой, ее координаты будут удовлетворять уравнению этой прямой.
На плоскости задана прямая, каноническое уравнение которой имеет вид x-12=y+12-3. Выясните, лежат ли на ней точки M13, -312 и M2(5, -4).
Решение
Для проверки принадлежности необходимо подставить координаты точки в исходное уравнение и проверить, получим ли мы в итоге верное равенство.
3-12=-312+12-2⇔1=1
Результат говорит нам, что точка M13, -312 принадлежит исходной прямой.
Точно так же поступим и с координатами второй точки:
5-12=-4+12-3⇔2=76
Получившееся в итоге равенство не является верным, значит, эта точка заданной прямой не принадлежит.
Ответ: первая точка лежит на заданной прямой, а вторая нет.
Есть две точки M1(2, 4) и M2(-1, 3). Будет ли прямая, которая задана в той же плоскости с помощью уравнения x-20=y-32, проходить через них?
Решение
Вспомним, что запись x-20=y-32 можно понимать как 2·(x-2)=0·(y-3)⇔x-2=0. Подставим координаты заданных точек в это равенство и проверим.
Начнем с первой точки M1(2, 4) : 2-2=0⇔0=0
Равенство верное, значит, эта точка расположена на заданной прямой.
Подставляем данные второй точки: -1-2=0⇔-3=0.
Равенство неверное, значит, точка M2(-1, 3) не лежит на исходной прямой.
Ответ: через точку M1(2, 4) прямая проходит, а через M2(-1, 3) нет.
Далее мы посмотрим, какие еще типичные задачи на нахождение канонического уравнения можно встретить. Возьмем примеры с разными условиями.
Наиболее простыми являются задачи на нахождение канонического уравнения прямой на плоскости, в которых уже заданы координаты некой точки, лежащей на прямой. В первой части материала мы уже приводили пример решения такой задачи.
Чуть сложнее будет найти нужное уравнение, если нам предварительно нужно будет вычислить координаты направляющего вектора исходной прямой. Чаще всего встречаются задачи, в которой нужная прямая проходит через две точки с известными координатами.
Прямая на плоскости проходит через точку M1(0, -3) и через точку M2(2, -2). Сформулируйте для этой прямой канонической уравнение.
Решение
Eсли у нас есть координаты двух точек, то мы можем вычислить по ним координаты вектора M1M2→=2, 1. По отношению к прямой, чье уравнение мы составляем, он будет направляющим вектором. После этого мы можем записать следующее:
x-02=y-(-3)1⇔x2=y+31
Также можно использовать координаты второй точки. Тогда мы получим: x-22=y-(-2)1⇔x-22=y+21
Ответ: x2=y+31
Посмотрим, как нужно составлять канонические уравнения прямой на плоскости в том случае, если направляющий вектор этой прямой нужно вычислять исходя из параллельных или перпендикулярных ей прямых.
Известно, что точка M1(1, 3) принадлежит некоторой прямой, которая параллельна второй прямой, заданной с помощью уравнения x2=y-5. Запишите каноническое уравнение первой прямой.
Решение
Для первой прямой можно определить направляющий вектор a→=2, -5. Его можно рассматривать и в качестве направляющего для второй прямой, что следует из самого определения направляющих векторов. Это позволяет нам получить всю информацию, нужную для записи искомого уравнения: x-12=y-3-5
Ответ: x-12=y-3-5
Через точку M1(-1, 6) проходит прямая, которая является перпендикулярной другой прямой, определенной на плоскости с помощью уравнения 2x-4y-7=0. Запишите каноническое уравнение первой прямой.
Решение
Из данного уравнения мы можем взять координаты нормального вектора второй прямой – 2, 4. Мы знаем, что этот вектор является направляющим по отношению к первой. Тогда мы можем записать искомое уравнение:
x-(-1)2=y-64⇔x+11=y-62
Ответ: x+11=y-62
Каноническое уравнение прямой
Определение.
Любой вектор, отличный от нулевого,
параллельный заданной прямой, называется
направляющим
вектором
этой прямой.
Пусть
на прямой
![]() задана точка
задана точка![]() ,
,
а вектор![]() – направляющий вектор прямой
– направляющий вектор прямой![]() .
.
Точка![]() принадлежит прямой, если вектор
принадлежит прямой, если вектор![]() параллелен вектору
параллелен вектору![]() :
:
![]() .
.
(12)
Уравнение
(12) называется каноническим
уравнением прямой
на плоскости.
Угол
между прямыми, заданными каноническими
уравнениями,
определяется как угол между направляющими
векторами этих прямых:
![]() .
.
Условием
параллельности прямых будет условие
коллинеарности их направляющих векторов:
![]() ||
||![]() .
.
Условие
перпендикулярности прямых равносильно
условию равенства нулю скалярного
произведения их направляющих векторов:
![]()
![]() .
.
Параметрические уравнения прямой
Пусть
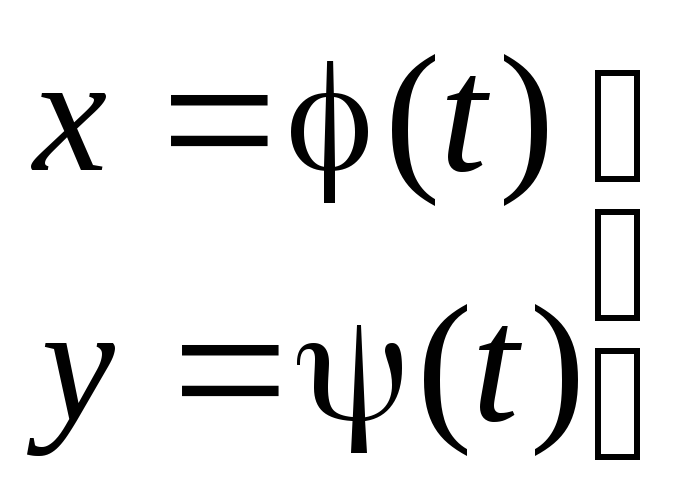 .
.
Если
величины х
и у
рассматривать как координаты точки М
при каждом значении t,
то такие уравнения называются
параметрическими уравнениями траектории
точки М.
Аргумент t
– переменный параметр.
В
каноническом уравнении прямой (12) примем
одну из величин (правую или левую часть
равенства) за параметр t.
Получим два уравнения
![]() или
или
![]() . (13)
. (13)
Уравнения
(13) – это параметрические уравнения
прямой на плоскости. Если принять, что
параметр t
– время, то параметрические уравнения
приобретают физический смысл. Они
определяют закон движения точки по
прямой L.
Нормальное (нормированное) уравнение прямой
П усть
усть
существует прямаяL.
Проведем вектор
![]() ,
,
перпендикулярный![]() ,
,
через начало координат.Р
– точка пересечения прямой и нормали.
На
нормали введем положительное направление
от О к Р.
Пусть
![]()
![]() – полярный угол нормали,
– полярный угол нормали,
![]() –полярный
–полярный
угол вектора
![]() .
.
Обозначим |ОР|
= р.
Выберем на прямой
![]() точкуМ(х,у).
точкуМ(х,у).
Проекция вектора
![]() на
на
нормаль определяется как
npn![]() =
=
p (14)
Найдем
выражение npn![]()
через координаты точки М.
Пусть
![]() – полярные координаты точки М.
– полярные координаты точки М.
npn![]()
![]() =
=
![]() .
.
npn![]() =
=![]() (15)
(15)
Из
(1) и (2) =>
![]() или
или
![]() (16)
(16)
Уравнение
(16) – это нормальное
уравнение
прямой.
Расстояние от точки до прямой

Пусть
М*
– любая точка плоскости, d
– её расстояние от данной прямой.
Определение.
Отклонением точки М*
от данной прямой называется число (+d),
если М*
лежит по ту сторону от прямой, куда
указывает положительное направление
нормали, и (–d)
– в обратном случае.
![]() =
=
±d
Теорема.
Пусть точка М* (х*, у*)произвольная точка
плоскости, L
– прямая, заданная уравнением xcosα
+ ysinα
– р =
0. Отклонение точки М* от этой прямой
задается формулой
![]() . (17)
. (17)
Доказательство.
Проекция точки М*
на нормаль – точка
![]() .
.
Отклонение точкиМ*
от прямой
δ=
PQ
= OQ
– OP.
Но
OQ
= npn![]() ,
,
а ОР = р
![]() δ =npn
δ =npn![]() *
*
– р
npn![]() =
=
![]()
![]()
![]() .
.
Таким образом,
отклонение точки М* от прямой легко
вычисляется, если прямая задана нормальным
уравнением. Достаточно лишь подставить
в нормальное уравнение прямой координаты
точки.
Пусть
прямая задана общим уравнением: Ах
+ Ву + С = 0, а
x
cosα
+ y
sinα
– р =
0 – её нормальное уравнение .
Поскольку два
уравнения определяют одну прямую, их
коэффициенты должны быть пропорциональны.
Уравнение
![]() (18)
(18)
совпадает с
нормальным уравнением. Тогда
![]() ;
;
![]() .
.
Отсюда
можно найти
![]() :
:
![]() –нормирующий
–нормирующий
множитель уравнения прямой.
Определим знак
нормирующего множителя:
µС
= – р < 0.
Следовательно,
знак µ противоположен знаку С
в уравнении. (Если С
= 0 – знак µ произвольный).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
