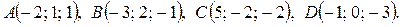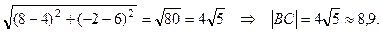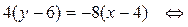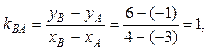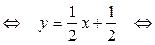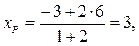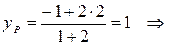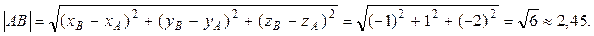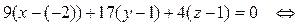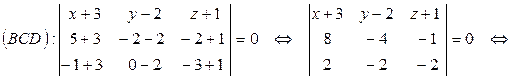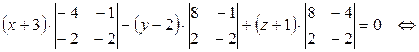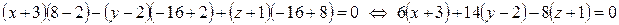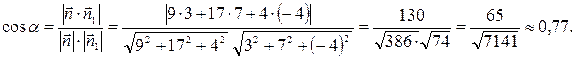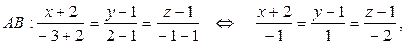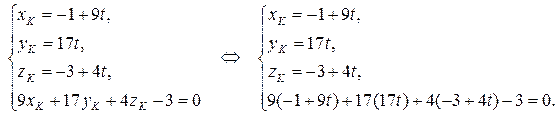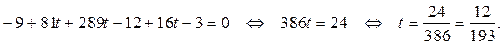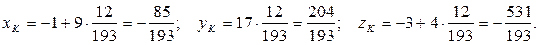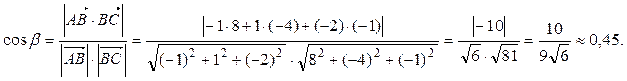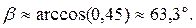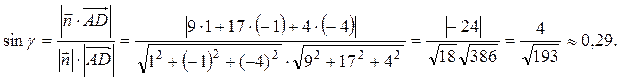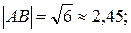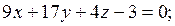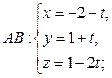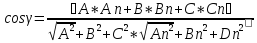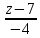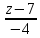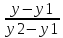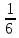Как найти каноническое уравнение высоты пирамиды

1.Определяем уравнение плоскости, проходящей через грань А1А2А3
$$begin{vmatrix}x-x_1 & y-y_1 & z-z_1\
x_2-x_1 & y_2-y_1 & z_2-z_1\
x_3-x_1 & y_3-y_1 & z_3-z_1end{vmatrix} = 0 ;$$

$$begin{vmatrix}x-8 & y-6 & z-4\
10-8 & 5-6 & 5-4\
5-8 & 6-6 & 8-4end{vmatrix} =
begin{vmatrix}x-8 & y-6 & z-4\
2 & -1 & 1\
-3 & 0 & 4end{vmatrix} = $$
$$=(x-8)(-1times4-1times0)-(y-6)(2times4-1(-3))+(z-4)(2times0-(-1)(-3))=$$
$$= -4(x-8)-11(y-6)-3(z-4) = -4x+32-11y+66-3z+12=$$ $$=-4x-11y-3z+110 = 0$$

Уравнение плоскости: $%-4x-11y-3z+110=0$%
или, если умножить на -1: $%4x+11y+3z-110=0$%

2.Получаем уравнение прямой, перпендикулярной плоскости А1А2А3 и проходящей через точку A4 (т.е. высоту пирамиды)

Из уравнения плоскости $%4x+11y+3z-110=0$% берем коэффициенты при x,y,z и получаем нормальный вектор: {4,11,3}.
Параметрическое уравнение прямой с заданным направляющим вектором {A,B,C} и проходящей через данную точку (x0,y0,z0):

$$left{begin{array}{l}x=x_0+At\y=y_0+Bt\z=z_0+Ctend{array}right.$$

Подставляем нормальный вектор плоскости и точку A4:

$$left{begin{array}{l}x=8+4t\y=10+11t\z=7+3tend{array}right.$$

Получили параметрическое уравнение высоты пирамиды.
Если нужно каноническое уравнение, в каждом уравнении выражаем параметр t, а потом приравниваем:

$$left{begin{array}{l}t=frac{x-8}4\t=frac{y-10}{11}\t=frac{z-7}3end{array}right.$$

$$frac{x-8}4 = frac{y-10}{11} = frac{z-7}3$$

Уравнение высоты: $%frac{x-8}4 = frac{y-10}{11} = frac{z-7}3$%

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Составить каноническое уравнение высоты пирамиды проведенной из вершины

Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет – тут

Неправильный логин или пароль.

Укажите электронный адрес и пароль.

Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.

Инструкция по изменению пароля отправлена на почту.

Чтобы зарегистрироваться, укажите ваш email и пароль

Нажимая кнопку “Зарегистрироваться” вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.

Уравнения прямой в пространстве

Параметрические уравнения прямой l в пространстве:

(15)

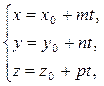
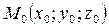
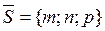
где – фиксированная точка прямой;

– направляющий вектор прямой l, т.е. любой вектор, параллельный l;

t – числовой параметр.

Каждому значению параметра 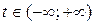соответствует единственная точка прямой l.

Канонические уравнения прямой:

. (16)

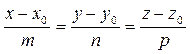
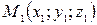
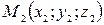
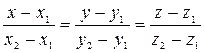
Уравнения прямой, проходящей через две данные точки и :

. (17)

Углом между прямыми называют угол между их направляющими векторами =<m₁; n₁; p₁> и =<m₂; n₂; p₂>, или дополнительный к нему (обычно берется острый угол), то есть

. (18)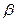

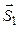
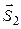
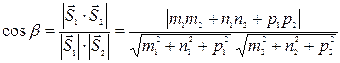
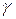
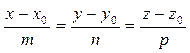
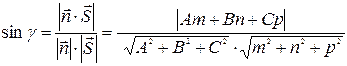
Углом между плоскостью и прямой l (в случае их пересечения) называется угол между прямой и её проекцией на плоскость. Синус угла между плоскостью и прямой определяется по формуле:

. (19)

Примерный вариант и образец выполнения

РГЗ №1

Задача 1. Даны координаты вершин треугольника АВС:

Требуется: 1) вычислить длину стороны ВС;

2) составить уравнение стороны ВС;

3) найти внутренний угол треугольника при вершине В;

4) составить уравнение высоты АК, проведенной из вершины А;

5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан);

6) сделать чертеж в системе координат.

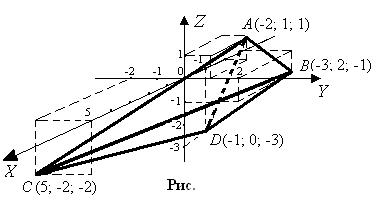
Задача 2.Даны координаты точек – вершин пирамиды ABCD:

1) вычислить длину ребра AB;

2) найти уравнение плоскости грани ABC;

3) найти угол между гранями ABC и BCD;

4) составить параметрические уравнения прямой AB;

5) составить канонические уравнения высоты пирамиды DK, проведенной из вершины D;

6) найти координаты точки пересечения DK и грани ABC;

7) найти угол между ребрами AB и BC;

8) найти угол 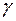между ребром AD и гранью ABC;

9) сделать чертеж пирамиды в системе координат.

Решение задачи 1.

1) Вычислим длину стороны ВС по формуле (1):

|BС|= =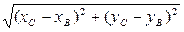

2) Составим уравнение стороны ВС, используя формулу (8):

y = –2x + 14 – уравнение ВС.

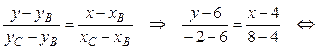
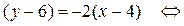
3) Внутренний угол треугольника при вершине В найдем как угол между прямыми ВА и ВС. Для этого сначала вычислим угловой коэффициент прямой ВА по формуле (7):

и возьмем из уравнения ВС угловой коэффициент прямой ВС: .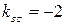

Из расположения точек A, B, C на координатной плоскости видно, что угол В в треугольнике ABC – острый, поэтому по формуле (11) вычислим

.

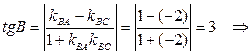
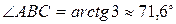
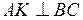
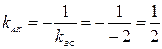
4) Для получения уравнения высоты АK, проведенной из вершины А, используем уравнение пучка прямых (6) и условие перпендикулярности прямых (10). Сначала вычислим угловой коэффициент прямой АK . Так как , то .

Уравнение AK получим по формуле (6):

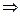
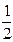
у – у_А = k_AK(x– x_A) у – (–1) = (x– (–3))

5) Для определения координат центра тяжести треугольника используем свойство точки пересечения его медиан: если AМ – медиана треугольника и P – точка пересечения его медиан, то P делит AМ в отношении 2 : 1, начиная от точки А, т.е. .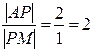

Основание медианы AМ – точка М является серединой отрезка ВС. Найдем координаты точки М по формулам (3):

М(6; 2).

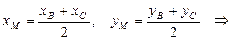
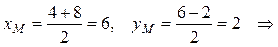
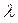
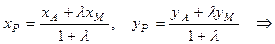
Теперь, когда координаты концов отрезка AМ известны, найдем координаты точки P, которая делит AМ в отношении = 2, начиная от точки А, по формулам деления отрезка в заданном отношении (2):

P(3; 1) – центр тяжести треугольника АВС.

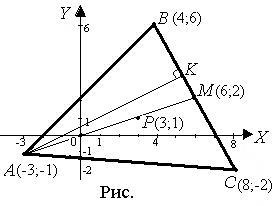
6) Построим чертеж к задаче в системе координат ХОY (рис. 3). Полученные при решении задачи результаты не противоречат чертежу.

1) длина стороны |BС| = ;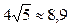

2) уравнение стороны ВС: y = –2x + 14;

3) угол при вершине В: ;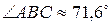

4) уравнение высоты АK: x –2y + 1 = 0;

5) координаты центра тяжести треугольника P(3; 1);

6) чертеж на рис. 3.

Решение задачи 2.

1) Длину ребра 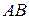найдем по формуле:

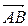
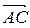
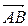
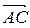
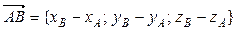
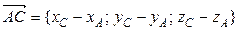
2) Чтобы получить уравнение плоскости грани ABC, необходимо найти вектор, перпендикулярный плоскости ABC, т.е. вектор, перпендикулярный векторам и . Одним из таких векторов является векторное произведение на . Для того, чтобы найти его, сначала вычислим координаты векторов по формулам:

= <–3–(–2); 2–1; –1–1>= <–1; 1; –2>,

=<7; –3; –3>.

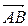
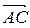
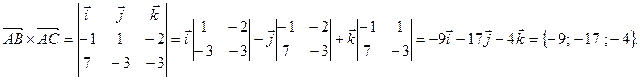
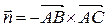
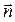
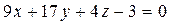
Найдем векторное произведение и :

В качестве вектора нормали к плоскости ABC можно взять любой вектор, коллинеарный полученному, например, = <9; 17; 4>. Используем уравнение плоскости, проходящей через точку перпендикулярно вектору (формула (12):

– уравнение плоскости грани ABC.

3) Прежде, чем найти угол между гранями ABC и BCD, получим уравнение грани BCD, используя уравнение плоскости, проходящей через три заданные точки (формула (13):

– уравнение грани BCD.

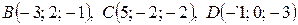
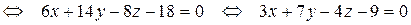
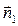
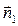
Из уравнения плоскости BCD возьмем координаты вектора нормали , перпендикулярного этой плоскости: =<3; 7; –4>.

Косинус угла между плоскостями (гранями) ABC и BCD найдем по формуле(14):

Отсюда .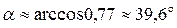

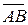
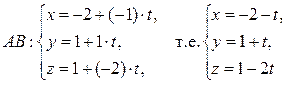
4) Уравнения ребра AB можно записать как параметрические уравнения прямой, проходящей через точку A(–2;1;1) и имеющей направляющий вектор = <–1; 1; –2>(формулы (15)):

– параметрические уравнения AB.

Другой способ: можно использовать уравнения прямой, проходящей через две точки 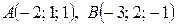(формулы (17)):

откуда, обозначив каждую из дробей буквой t, получаем:

– параметрические уравнения AB.

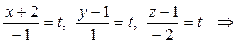
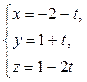
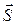
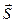
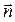
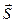
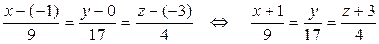
5) Высота пирамиды DK – это прямая, проведенная из вершины D перпендикулярно грани ABC. Она имеет направляющий вектор , коллинеарный вектору нормали плоскости ABC. Можно взять, например, = = <9; 17; 4>. Запишем канонические уравнения высоты DK, используя точку D(–1; 0; –3) и вектор = <9; 17; 4>(формулы (16)):

– канонические уравнения DK.

6) Прежде, чем найти точку пересечения DK и грани ABC, получим параметрические уравнения прямой DK.Обозначив каждую из дробей в канонических уравнениях буквой t, получаем:

– параметрические уравнения DK.

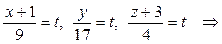
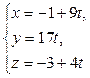
Точка пересечения DK и грани ABC (точка К) лежит на прямой, а значит, имеет координаты 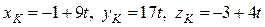, и принадлежит плоскости, т.е. ее координаты удовлетворяют уравнению плоскости ABC. Поэтому координаты точки K найдем, решив систему:

Решим последнее уравнение относительно t:

Вычислим координаты точки K, подставив найденное значениепараметра t в первые три уравнения системы:

Итак, точка пересечения DK и грани ABC: .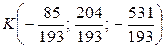

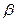
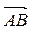
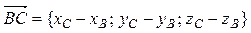
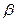
7) Угол между ребрами AB и BC найдем, как угол между направляющими векторами прямых AB и BC: = <–1; 1; –2>и =<8; –4; –1>. Вычислим косинус угла по формуле (18):

Тогда угол между ребрами AB и BC:

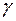
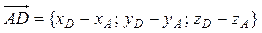
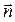
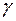
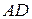
8) Чтобы определить угол между ребром AD и гранью ABC, найдем направляющий вектор прямой: =<1; –1; –4>. Плоскость ABC имеет вектор нормали = <9; 17; 4>. Синус угла между прямой и плоскостью ABC можно вычислить по формуле (19):

Тогда угол между ребром AD и гранью ABC:

9) Выполним чертеж пирамиды в системе координат (рис.4).

1)

2) АВС:

3) ;

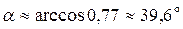
4)

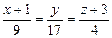
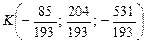
5) DK: ; 6) ;

7) ; 8) ;

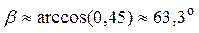
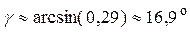
[spoiler title=”источники:”]

http://reshka.feniks.help/vysshaya-matematika/analiticheskaja-geometrija/dany-koordinaty-vershin-piramidy

http://lektsii.org/11-1720.html

[/spoiler]

0 Пользователей и 1 Гость просматривают эту тему.

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Раздел 1.5

Задача
1.6

Даны
вершины пирамиды A(x₁,y₁,z₁),
B(x₂,y₂,z₂),
C(x₃,y₃,z₃),
D(x₄,y₄,z₄).
Найти: а) угол между гранями АВС и ABD;

б)
каноническое и параметрические уравнения
прямой CD;

в)
уравнения плоскости параллельной
плоскости АВС, проходящую через точку
D;

г)
каноническое уравнение высоты пирамиды.

x₁=7
x₂=5
x₃=5
x₄=2

y₁=2
y₂=7
y₃=3
y₄=3

z₁=2
z₂=7
z₃=1
z₄=7

Вектор
АВ={xB-xA,
yB-yA, zB-zA}={-2, 5, 5}
Длина
ребра
АВ=7.3

Вектор
BC={xC-xB, yC-yB, zC-zB}={0, -4, -6}
Длина
ребра
ВC=7.2

Вектор
АC={xC-xA,
yC-yA, zC-zA}={-2, 1, -1}
Длина
ребра
АC=2.4

Вектор
АD={xD-xA,
yD-yA, zD-zA}={-5, 1, 5}
Длина
ребра
АD=7.1

Вектор
BD={xD-xB, yD-yB, zD-zB}={-3, -4, 0}
Длина
ребра
BD=5

Вектор
CD={xD-xC, yD-yC, zD-zC}={-3, 0, 6}
Длина
ребра
CD=6.7

А)
Угол между гранями ABC и ABD

Угол
между гранями равен углу между нормалями
к этим граням

Уравнение
плоскости ABC:
-5x – 6y + 4z + 39 = 0

Уравнение
плоскости ABD:
20x – 15y + 23z-156 = 0

γ
= arccos (0.27) = 74.338^o

Б)
Каноническое
и параметрические уравнения прямой CD

Вектор
CD={xD-xC, yD-yC, zD-zC}={-3, 0, 6}

С
(5; 3; 1) D
(2; 3; 7)

Решение.
Воспользуемся формулой для уравнения
прямой проходящей через две точки

=
==t

X
= 5 – 3t
Y
= 3 + t
Z
= 1 + 6t

В)
Уравнения плоскости параллельной
плоскости АВС, проходящую через точку
D

Решение:
Вектор n
( -5; -6; 4) есть нормальный вектор
плоскости ABC
= -5x
– 6y
+ 4z
+ 39 = 0.

Уравнение
плоскости, которая проходит через
точку D
(2; 3; 7) и имеет нормальный вектор n
= (-5; -6; 4), имеет вид 

-5
* (x
– 2) – 6 * (y
– 3) + 4 * (z
– 7) = 0 ↔ –5x
– 6y
– 4z
+ 51 = 0.

Это
искомое уравнение плоскости, проходящей
через заданную точку параллельно
заданной плоскости.

Г)
Каноническое уравнение высоты пирамиды.

Уравнение
плоскости ABC: −5x
− 6y + 4z + 39 = 0 или,
если умножить на -1: 5x
+ 6y – 4z – 39 = 0

Получаем
уравнение прямой, перпендикулярной
плоскости ABC
и проходящей через точку D (т.е. высоту
пирамиды)

Из
уравнения плоскости 5x
+ 6y – 4z – 39 = 0 берем
коэффициенты при x,y,z и получаем нормальный
вектор: {5, 6, -4}. Параметрическое уравнение
прямой с заданным направляющим вектором
(A,B,C) и проходящей через данную точку
(2, 3, 7):

x=
2+At y= 3+Bt z= 8+Ct

Подставляем
нормальный вектор плоскости и точку D:

x=
2+5t y= 3+6t z= 7-4t

Получили
параметрическое уравнение высоты
пирамиды. Если нужно каноническое
уравнение, в каждом уравнении выражаем
параметр t, а потом приравниваем:

t
=
t
=
t
=

Уравнение
высоты: t
=
t
=
t
=

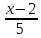
Задача
1. 7.

Даны
три точки на плоскости: A(0;2)
B(6;6)
С(-12;3)

Найти:

а)
уравнение стороны AB;

б)
уравнение высоты, опущенной из вершины
A;

в)
уравнение медианы, опущенной из вершины
B;

г)
уравнение прямой, параллельной прямой
BС, проходящей через точку

А;

д)
угол при вершине B.

А)
Уравнение стороны AB

Решение:
Даны
три вершины треугольника, поэтому
уравнения сторон будем искать ка
уравнение прямой, проходящей через две
заданные точки  =
Подставляем
координаты вершин: уравнение
стороны AB,
при известных координатах вершины
A(0;-2) и B(6;6

AB
=
=

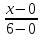
Б)
Уравнение высоты, опущенной из вершины
A

Решение:

Прямая,
проходящая через точку A(0;-2)
и перпендикулярная прямой Ax + By + C = 0
имеет направляющий вектор (A;B) и, значит,
представляется уравнениями:

Найдем
уравнение высоты через вершину Ay
= -6x -2 или y +6x + 2 = 0

В)
Уравнение медианы, опущенной из вершины
B

Решение:
Обозначим
середину стороны AC буквой М. Тогда
координаты точки M найдем по формулам
деления отрезка пополам.
M(-6;¹/₂)
Уравнение
медианы BM найдем, используя формулу для
уравнения прямой, проходящей через две
заданные точки. Медиана BМ проходит
через точки B(6;6) и М(-6;¹/₂),
поэтому:

Каноническое
уравнение прямой:
илиили
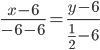
y =¹¹/₂₄x
+ ¹³/₄ или
24y -11x – 78 = 0

Найдем
длину медианы:
Расстояние между двумя
точками выражается через координаты
формулой:

ВМ
= √(-6-6)²
+ √(
-6)²
= √12²
+ ()²
= √=√697

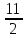
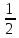
Г)
Уравнение прямой, параллельной прямой
BС, проходящей через точку А

Решение:
Прямая,
проходящая через точки В(6; 6) и С(-12; 3),
представляется уравнениями:

Уравнение
прямой BC
Каноническое уравнение
прямой:

y
= ¹/₆x
+ 5 или 6y -x – 30 = 0

Уравнение
прямой BC: y = ¹/₆x
+ 5
Уравнение AB
параллельно BC находится по формуле:
y
– y₀ =
k(x – x₀)
Подставляя
x₀ =
0, k = ¹/₆,
y₀ =
-2 получим:
y-(-2) = ¹/₆(x-0)
y
= ¹/₆x
-2 или 6y -x +12 = 0

Д)
Угол при вершине B.

Решение:
Найдем угол B как угол между двумя
прямыми.
Уравнение прямой AB: y = ⁴/₃x
-2
Уравнение прямой BC: y = ¹/₆x
+ 5
Угол φ между двумя прямыми, заданными
уравнениями с угловыми коэффициентами
y = k₁x
+ b₁ и
y₂ =
k₂x
+ b₂,
вычисляется по формуле:

Угловые
коэффициенты данных прямых равны ⁴/₃ и ¹/₆.
Воспользуемся формулой, причем ее правую
часть берем по модулю:

tg
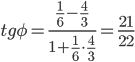
φ =²¹/₂₂
Ответ:
φ = arctg (²¹/₂₂)
= 43.67⁰

Задача
1.8

Перевести
уравнение кривой второго порядка а₁₁x²
+ a₂₂y²
+ 2a₁x
+ 2a₂y
+ a₀
= 0 к каноническому виду, выяснить, что
это за кривая. Найти координаты смещённого
центра. Построить кривую на плоскости.

а₁₁
=
3 а₂₂
= 2 а₁
= 3
а₂
= 4 а₀
= -45

Дано
уравнение кривой:
3x² +
2y² +
6x + 8y – 45 = 0
1. Определить тип кривой.
2.
Привести уравнение к каноническому
виду и построить кривую в исходной
системе координат.
3. Найти соответствующие
преобразования координат.

Решение:

Приводим
квадратичную форму B = 3x² +
2y²
к
главным осям, то есть к каноническому
виду. Матрица этой квадратичной формы:

B =

3 0 0 2

Находим
собственные числа и собственные векторы
этой матрицы:
(3 – λ)x₁ +
0y₁ =
0
0x₁ +
(2 – λ)y₁ =
0
Характеристическое уравнение:

3 – λ 0 0 2 – λ

= λ 2 – 5λ + 6 = 0

λ² -5
λ + 6 = 0
D = (-5)² –
4 • 1 • 6 = 1

Исходное
уравнение определяет эллипс (λ₁ >
0; λ₂ >
0)
Вид квадратичной формы:
3x² +
2y²
Выделяем
полные квадраты:
для x₁:
3(x₁²+2•1x₁ +
1) -3•1 = 3(x₁+1)²-3
для
y₁:
2(y₁²+2•2y₁ +
2²)
-2•2² =
2(y₁+2)²-8

В
итоге получаем:
3(x₁+1)²+2(y₁+2)² =
56
Разделим все выражение на 56
Полуоси
эллипса:Данное
уравнение определяет эллипс с центром
в точке:
C(-1; -2)
Найдем координаты
фокусов F₁(-c;0)
и F₂(c;0),
где c – половина расстояния между
фокусами
Итак,
фокусы эллипса:С
учетом центра, координаты фокусов
равны:Тогда
эксцентриситет будет равен: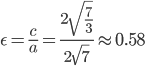Вследствие
неравенстваc
< a эксцентриситет
эллипса меньше 1.

Онлайн решение Пирамиды по координатам вершин

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

8) основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

Примечание: дробные числа записывайте
через точку, а не запятую.

Примеры решений по аналитической геометрии в пространстве

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии в пространстве, которые относятся к исследованию пирамиды. Обычно в такой задаче нужно найти длины ребер, углы между ребрами, уравнения граней пирамиды и их площади, объем пирамиды, угол между ребром и гранью, уравнение высоты, длину высоты пирамиды и т.д.

Решения задачи о пирамиде онлайн

Задача 1. Для пирамиды с вершинами в точках $A_1, A_2, A_3, A_4$ найти:
А) длину ребра $A_1A_2$;
Б) угол между ребрами $A_1A_2$ и $A_1A_4$;
В) уравнение плоскости $A_1A_2A_3$;
Г) площадь грани $A_1A_2A_3$;
Д) угол между ребрами $A_1A_4$ и плоскостью $A_1A_2A_3$;
Е) уравнение высоты, опущенной из точки $A_4$ на грань $A_1A_2A_3$;
Ж) объем пирамиды $A_1A_2A_3A_4$.

Задача 2. Даны координаты вершин пирамиды $$A(12;11;17), B(14;12;14), C(13;14;15), D(12;21;12).$$ Найти:
— объем пирамиды;
— площадь грани $ABC$;
— уравнение плоскости, проходящей через точки $B,C,D$;
— длину высоты пирамиды, опущенной на грань $ABC$.

Задача 3. Пирамида $АВСD$ задана координатами своих вершин: $$А(4, -1,0), B(2, 3, 4), C(-1, 4, 1), D(4, -3, 5).$$ Найдите:
1. угол между ребрами $АВ$ и $АС$,
2. уравнение ребра $АВ$,
3. уравнение грани $АВС$,
4. уравнение высоты, опущенной из вершины $D$, на грань $АВС$,
5. выясните, образуют ли векторы $АВ, АС, АD$ линейно независимую систему,
6. координаты вектора $MN$, если $М$ – середина ребра $AD$, $N$ – середина ребра $ВC$,
7. разложите вектор $MN$ по базису $AB, AC, AD$, если он таковым является.

A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; )

Примечание: дробные числа записывайте через точку, а не запятую. Округлять до -го знака после запятой. Как найти высоту пирамиды по векторам Инструкция . Для решения подобных задач в онлайн режиме заполните координаты вершин, нажмите Далее . см. также по координатам треугольника найти. Решение онлайн Видеоинструкция Оформление Word Пример №1 . В пирамиде SABC : треугольник ABC – основание пирамиды, точка S – ее вершина. Даны координаты точек A, B, C, S . Сделать чертеж. Решение: Координаты векторов находим по формуле: X = x2 – x1; Y = y2 – y1; Z = z2 – z1 Так, для вектора AB, это будут координаты: X = 0-2; Y = 3-0; Z = 0-0, или AB(-2;3;0). AC(-2;0;1); AD(-2;2;3); BC(0;-3;1); BD(0;-1;3); CD(0;2;2) . Длину вектора находим по формуле: Пример №2 . В тетраэдре ABCD вычислить: объем тетраэдра ABCD; высоту тетраэдра, опущенную из вершины D на грань ABC. A(2, 3, -2), B(3, 1, 0), C(-2, 2, 1), D(6, 1, -1) Ответ Проверено экспертом Даны вершины пирамиды A(3;-2;3)B(-1;0;2)C(-3;1;-1)D(-3;-3;1) . Находим векторы АВ, АС и АД. Вектор АВ = (-4; 2; -1 ), модуль равен √(16+4+1) = √21 ≈ 4,58258. Определяем векторное произведение АВ х АС. -6 3 -4 | -6 3 = -8i + 6j – 12k – 16j + 3i + 12k = -5i – 10j = (-5; -10; 0). Далее находим смешанное произведение (АВ х АС) х АД. (АВ х АС) = (-5; -10; 0), (АВ х АС) х АД = 30 + 10 + 0 = 40. Объем пирамиды равен (1/6) этого произведения: V = (1/6)*40 = (20/3) куб.ед. Высота h пирамиды ABCD, опущенная из вершины D на плоскость основания ABC, равна: h = 3V/S(ABC). Площадь основания АВС равна половине модуля векторного произведения АВ х АС. S(ABC) = (1/2)*√((-5)² + (-10)² + 0²) = (1/2)√(25 + 100) = (5/2)√5 кв.ед. h = (3*20/3)/((5/2)√5) = 8/√5 = 8√5/5 ≈ 3,5777. 1) чертёж пирамиды по координатам её вершин; 2) длины и уравнения рёбер, медиан, апофем, высот; 3) площади и уравнения граней; 4) система линейных неравенств, определяющих пирамиду; 5) основания и точка пересечения медиан (центроид); 6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням; 7) объём пирамиды; 8) основания, площади и уравнения биссекторов; 9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные; 10) параметры и уравнения вписанной и описанной сфер; Внимание! Этот сервис может не работать в браузере Internet Explorer. Запишите координаты вершин пирамиды и нажмите кнопку.

A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; )