

Калькулятор онлайн.
Уравнение прямой касательной к графику функции в заданной точке
Эта математическая программа находит уравнение касательной к графику функции ( f(x) ) в заданной пользователем
точке ( x_0 ).
Программа не только выводит уравнение касательной, но и отображает процесс решения задачи.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Статью из энциклопедии о касательной прямой вы можете посмотреть
здесь (статья из Википедии).
Если вам нужно найти производную функции, то для этого у нас есть задача Найти производную.
Примеры подробного решения >>
Введите выражение функции ( f(x)) и число (x_0) – абсциссу точки в которой нужно построить касательную
Наши игры, головоломки, эмуляторы:
Немного теории.
Угловой коэффициент прямой
Напомним, что графиком линейной функции ( y=kx+b) является прямая. Число (k=tg alpha ) называют угловым коэффициентом
прямой, а угол ( alpha ) – углом между этой прямой и осью Ox
Если ( k>0), то (0< alpha < frac{pi}{2} ), в этом случае функция ( y=kx+b) возрастает.
Если ( k<0), то (-frac{pi}{2}< alpha < 0 ), в этом случае функция ( y=kx+b) убывает.
Уравнение касательной к графику функции
Если точка М(а; f(a)) принадлежит графику функции у = f(x) и если в этой точке к графику функции можно
провести касательную, не перпендикулярную оси абсцисс, то из геометрического смысла производной следует, что угловой
коэффициент касательной равен f'(a). Далее мы выработаем алгоритм составления уравнения касательной к графику любой функции.
Пусть даны функция у = f(x) и точка М(а; f(a)) на графике этой функции; пусть известно, что существует f'(a). Составим уравнение
касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат,
имеет вид y = kx + b, поэтому задача состоит в нахождении значений коэффициентов k и b.
С угловым коэффициентом k все понятно: известно, что k = f'(a). Для вычисления значения b воспользуемся тем, что искомая прямая
проходит через точку М(а; f(a)). Это значит, что если подставить координаты точки М в уравнение прямой, получим верное
равенство: (f(a)=ka+b ), т.е. ( b = f(a) – ka ).
Осталось подставить найденные значения коэффициентов k и b в уравнение прямой:
$$ y=kx+b $$
$$ y=kx+ f(a) – ka $$
$$ y=f(a)+ k(x-a) $$
$$ y=f(a)+ f'(a)(x-a) $$
Нами получено уравнение касательной к графику функции ( y = f(x) ) в точке ( x=a ).
Алгоритм нахождения уравнения касательной к графику функции ( y=f(x) )
1. Обозначить абсциссу точки касания буквой ( a )
2. Вычислить ( f(a) )
3. Найти (f'(x) ) и вычислить (f'(a) )
4. Подставить найденные числа ( a, f(a), f'(a) ) в формулу ( y=f(a)+ f'(a)(x-a) )
Уравнение касательной онлайн
Уравнение касательной
к графику функции
в точке
имеет вид:
Уравнение касательной онлайн
Переменная функции:
Точка в которой необходимо найти касательную:
Написать уравнение касательной к функцииfxx24x7в точкеx00
Установить калькулятор на свой сайт
Другие полезные разделы:
Нахождение производной функции онлайн
Уравнение нормали к графику функции онлайн
Таблица производных
Оставить свой комментарий:
Примеры решений
Ранг матрицы
Умножение матриц
Метод Гаусса
Найти производную
Найти интеграл
Решение СЛАУ методом Крамера
Диф уравнения онлайн
Определитель матрицы
Точки разрыва функции
-
- Математика онлайн
- Линейная алгебра
- Вычислительная математика
- Теория вероятностей
- Математическая статистика
- Статистика онлайн
-
- Математический анализ
- Свойства функций y=f(x)
- Предел функции
- Точки разрыва функции
- Первый замечательный предел
- Второй замечательный предел
- Производная функции
- Уравнение касательной к кривой
- Дифференциал функции
- Правило Лопиталя
- Экстремумы функций одной переменной
- Асимптоты графика функции
- ✍ Помощь в решении контрольных
Уравнение касательной к кривой линии
Уравнение касательной в общем виде записывается как: yk=y0+y'(x0)(x-x0)
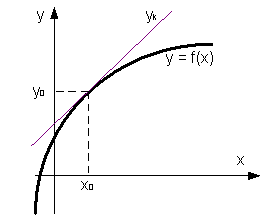
Назначение. Онлайн-калькулятор предназначен для нахождения уравнения касательной к графику функции. Решение оформляется в формате Word (см. пример).
- Шаг №1
- Шаг №2
- Видеоинструкция
Примеры:
Функция задана в явном виде, например y = 1/2*x3+5*x
Функция задана в неявном виде, например y2 – 1/2*x3 – 8
Функция задана в параметрическом виде, например x = 5*cos(t);y = 3*sin(t)
Функция задана в явном виде,
Функция задана в неявном виде
Функция задана в параметрическом виде
Алгоритм составления уравнения касательной к графику функции
- Вычисление значения функции y0 в точке x0:y0 = f(x0). Если исходное значение y0 задано, то переходим к п.2.
- Нахождение производной y'(x).
- Вычисление значения производной при x0.
- Запись уравнения касательной к кривой линии в форме: yk = y0 + y'(y0)(x – x0)
Касательные к кривым второго порядка
| Уравнение линии | Уравнение касательной | |
| Эллипс | 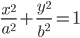 |
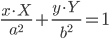 |
| Гипербола | 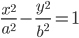 |
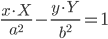 |
| Парабола | y2 = 2px | yY = p(X + x) |
см. также Касательная плоскость к поверхности.
Онлайн калькулятор для вычисления уравнения касательной к графику функции.
Ряд Маклорена (=Макларена) это ряд Тейлора в окрестности точки а=0.
Вычисление значения функции y0 в точке x0:y0 = f(x0). Если исходное значение y0
задано, то переходим к п.2.
Нахождение производной y'(x).
Вычисление значения производной при x0.
Запись уравнения касательной к кривой линии в форме: yk = y0 + y'(y0)(x – x0)
Калькулятор поможет составить и решить уравнение касательной к графику функции онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Инструкции:
Используйте этот калькулятор для вычисления касательной линии для заданной функции в заданной точке, показывая все шаги. Пожалуйста, введите функцию и соответствующую точку в поле формы ниже.
Об этом калькуляторе касательных линий
Этот калькулятор позволит вам легко провести вычисления, необходимые для получения касательной к линии функции в заданной точке, показывая все шаги.
Все, что вам нужно сделать, это задать действительную функцию f(x) и точку, в которой вы хотите провести касательную линию. Функцией может быть любая дифференцируемая функция, например f(x) = sin(x), или f(x) = x^2 – x + 1, и т.д. Точкой может быть любое допустимое числовое выражение, например, 1/2.
Затем, когда вся необходимая информация предоставлена и она достоверна, нужно нажать кнопку “Вычислить”, чтобы вам были показаны все шаги уравнения касательной линии.
Применения касательных линий в науке очень много. Также называется
первый порядок или линейная аппроксимация
но оно имеет действительно глубокий смысл в физике и инженерии, где идея основного вклада в изменение (часть первого порядка) является той, которая раскрывает много информации о процессе.
Что такое касательная линия
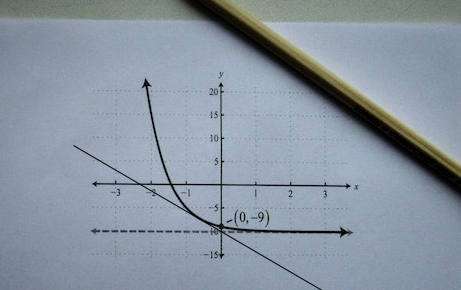
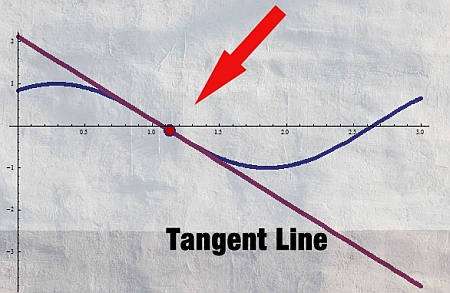
Проще говоря, касательная — это линия, которая пересекает кривую, но пересекает ее только в одной точке (по крайней мере, локально). Эта касательная строится путем фиксирования точки (x_0) и взятия другой точки (x_1).
Затем, построив линию, проходящую через точки ((x_0, f(x_0))) и ((x_1, f(x_1))), получим то, что называется
Секантная линия
как показано на графике ниже:
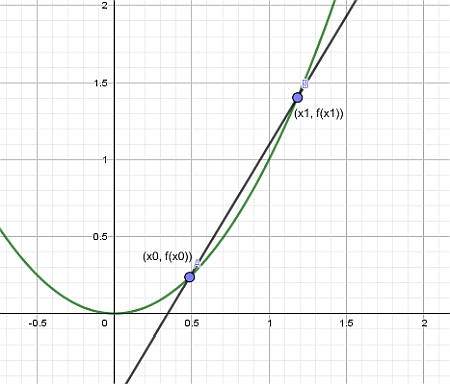
Наконец, мы приближаем точку (x_1) к (x_0), и мы получаем касательную:
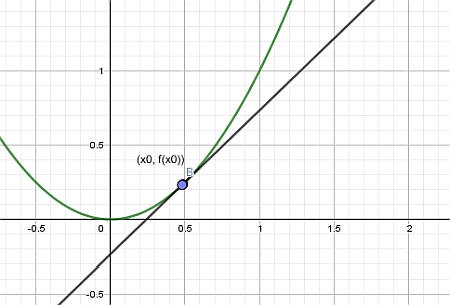
Шаги для геометрического нахождения касательной линии
-
Шаг 1:
Определите функцию f(x), с которой вы хотите работать, и точку x0. Вам нужны обе эти точки -
Шаг 2:
Точка (x0, f(x0)) будет лежать на кривой функции f(x). Постройте ее -
Шаг 3:
Выберите точку (x1, f(x1)) для x1, отличного от x0 (может быть слева или справа от x). Постройте график -
Шаг 4:
Проведите прямую, проходящую через точки (x0, f(x0)) и (x1, f(x1)) -
Шаг 5:
Выберите точку x2, которая находится на полпути между x0 и x1, и проведите прямую, проходящую через точки (x0, f(x0)) и (x2, f(x2)) -
Шаг 6:
Повторите этот процесс несколько раз
Этот графический метод поможет вам получить приблизительное представление о том, как выглядит линия касательной, но является приблизительным (если только функция f(x) не является линейной).
Формула касательной линии
Метод аппроксимации с использованием секущих может дать вам представление о том, что вы ищете, но, к счастью, существует точная формула для вычисления касательной к функции в точке (x_0). Формула касательной линии:
[displaystyle y = f(x_0) + f'(x_0) (x – x_0) ]
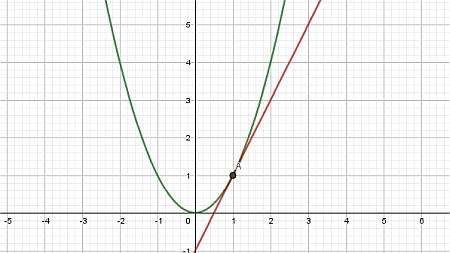
Просто, да? Проще говоря, эта формула говорит о том, что касательная линия – это
прямая, проходящая через точку
((x_0, f(x_0))) и имеет наклон (m = f'(x_0))
Тогда, говоря простым языком, наклон касательной в данной точке в точности является производной функции в этой точке.
Шаги для применения формулы касательной линии
-
Шаг 1:
Определите функцию f(x) и точку x0 -
Шаг 2:
Вычислите значение функции в точке x0, которое равно f(x0) -
Шаг 3:
Вычислите производную f(x) в точке x0, поэтому вам нужна f'(x0) -
Шаг 4:
Непосредственно применить формулу касательной линии (y = f(x_0) + f'(x_0) (x – x_0))
Как только вы получите
уравнение прямой
вы можете преобразовать его в формат, наиболее подходящий для конкретной ситуации.
Наклон касательной линии
Один из ключевых выводов заключается в том, что наклон касательной в точке (x_0) в точности равен (f'(x_0)), который является производной в точке (x_0). Это обеспечивает четкую и чрезвычайно полезную интерпретацию производной в геометрических терминах.
Эта связь позволяет найти уравнение касательной к данной кривой в данной точке, просто посмотрев на производную функции.
Когда у вас есть горизонтальная касательная?
Горизонтальная касательная появится, когда выбрана точка (x_0), когда соответствующая производная в этой точке равна нулю. В этом случае касательная (которая представляет собой линию, которая локально касается кривой в одной точке) будет параллельна оси y.
Итак, все, что вам нужно знать для определения горизонтальных касательных линий, — это найти точки, в которых производная функции равна нулю.
Когда у вас есть вертикальная касательная линия?
Вертикальная касательная появится, когда производная “бесконечна” в точке. Это простой способ сказать, что производная не определена в данной точке, но сходится к бесконечности по мере приближения к этой точке.
Например, можно сказать, что (f(x) = frac{1}{x}) имеет вертикальную касательную при x = 0. Хотя можно утверждать, что касательной нет, потому что производная при x = 0 определена некорректно.
Пример: касательная линия
Найдите уравнение касательной для (f(x) = x^2 – 2x + 1) в точке (x_0 = 2).
Отвечать:
Нам нужно работать со следующей функцией: (displaystyle f(x)=x^2-2x+1). Во-первых, нам нужно вычислить его производную.
Функция уже упрощена, поэтому мы можем перейти непосредственно к вычислению ее производной:
( displaystyle frac{d}{dx}left(x^2-2x+1right))
By linearity, we know (frac{d}{dx}left( x^2-2x+1 right) = frac{d}{dx}left(x^2right)-frac{d}{dx}left(2xright)+frac{d}{dx}left(1right)), so plugging that in:
( displaystyle = ,,)
(displaystyle frac{d}{dx}left(x^2right)-frac{d}{dx}left(2xright)+frac{d}{dx}left(1right))
Since the derivative of a constant is 0, we find that:
( displaystyle = ,,)
(displaystyle frac{d}{dx}left(x^2right)-frac{d}{dx}left(2xright))
Directly we get: (frac{d}{dx}left( 2x right) = 2) and using the Power Rule for polynomial terms: (frac{d}{dx}left( x^2 right) = 2x)
( displaystyle = ,,)
(displaystyle 2x-2)
Касательная Линия
: Уравнение касательной для функции (displaystyle f(x)=x^2-2x+1) в точке (x_0 = 2):
[y = y_0 + f'(x_0)(x – x_0) ]
В данном случае (displaystyle y_0 = f(x_0)), поэтому подстановка значения точки (x_0 = 2) в функцию приводит к:
[y_0 = f(x_0) = f(2) = 2^2-2cdot 2+1 = 1 ]
Кроме того, подстановка значения точки (x_0 = 2) в вычисляемую производную приводит к:
[f'(x_0) = f'(2) = 2cdot 2-2 = 2 ]
Теперь подставим эти значения в формулу касательной линии и получим:
[y = y_0 + f'(x_0)(x – x_0) ][Rightarrow y = 1+2left(x-2right) = 2x-3 ]
Заключение
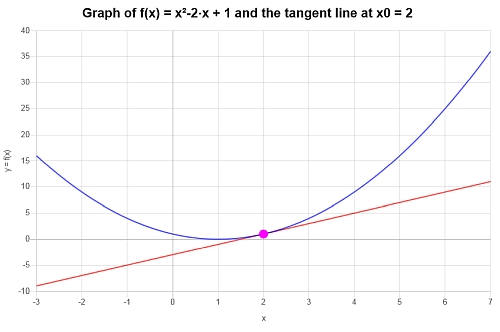
: Следовательно, установлено, что касательная для функции (displaystyle f(x)=x^2-2x+1) в точке (x_0 = 2) имеет вид:
[y = 2x-3 ]
Для данной функции и ее касательной в точке (x_0 = 2) получается следующий график:
Пример: уравнение касательной линии
Что такое касательная в точке x = 1/2 для функции (f(x) = sin(x) + 1)?
Решение:
Предусмотрена следующая функция: (displaystyle f(x)=sinleft(xright)+1), для которой нам нужно вычислить ее производную.
Функция уже упрощена, поэтому мы можем перейти непосредственно к вычислению ее производной:
( displaystyle frac{d}{dx}left(sinleft(xright)+1right))
By linearity, we know (frac{d}{dx}left( sin(x)+1 right) = frac{d}{dx}left(sin(x)right)+frac{d}{dx}left(1right)), so plugging that in:
( displaystyle = ,,)
(displaystyle frac{d}{dx}left(sinleft(xright)right)+frac{d}{dx}left(1right))
The derivative of a constant is 0, so then:
( displaystyle = ,,)
(displaystyle frac{d}{dx}left(sinleft(xright)right))
Directly differentiating: (frac{d}{dx}left( sinleft(xright) right) = cosleft(xright))
( displaystyle = ,,)
(displaystyle cosleft(xright))
Касательная Линия
: Мы находим, что соответствующее уравнение касательной в точке (x_0 = frac{1}{2}) имеет вид:
[y = y_0 + f'(x_0)(x – x_0) ]
Но в данном конкретном случае (displaystyle y_0 = f(x_0)), что означает, что нам нужно подставить значение точки (x_0 = frac{1}{2}) в функцию, поэтому мы получаем:
[y_0 = f(x_0) = fleft(frac{1}{2}right) = sinleft(frac{1}{2}right)+1]
Теперь, проделав то же самое с производной, для (x_0 = frac{1}{2}) находим
[f'(x_0) = f’left(frac{1}{2}right) = cosleft(frac{1}{2}right) ]
Теперь нам нужно просто вставить значения, и мы находим, что
[y = y_0 + f'(x_0)(x – x_0) ][Rightarrow y = sinleft(frac{1}{2}right)+1+cosleft(frac{1}{2}right)left(x-frac{1}{2}right) = xcosleft(frac{1}{2}right)-frac{1}{2}cosleft(frac{1}{2}right)+sinleft(frac{1}{2}right)+1 ]
Заключение
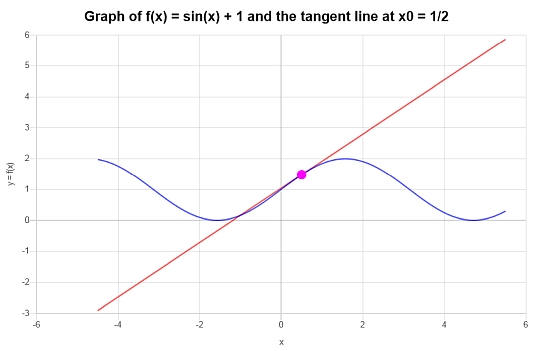
: Мы находим, что соответствующая касательная, которую мы ищем, в соответствующей точке (x_0 = frac{1}{2}) задается выражением
[y = xcosleft(frac{1}{2}right)-frac{1}{2}cosleft(frac{1}{2}right)+sinleft(frac{1}{2}right)+1 ]
Графически:
Пример: другая касательная линия
Что такое касательная в точке x = 0 для функции (f(x) = cos(x))? Имеет ли этот результат смысл?
Отвечать:
Обратите внимание, что (f'(x) = -sin(x)), а затем (f'(0) = -sin(0) = 0). То есть касательная имеет наклон m = 0 при x = 0, поэтому уравнение касательной имеет вид (y = y_0 = cos(0) = 1). Это имеет смысл, потому что в этом случае касательная является горизонтальной линией.
Больше калькуляторов дифференциации
Некоторые люди могут утверждать, что дифференцирование – это относительно простое упражнение, и что использование
производный калькулятор
может и не понадобиться, но на самом деле вычисление производных может быть довольно громоздким и потребовать длительного времени
алгебраические вычисления
.
Когда у вас есть выражение с более чем одной переменной, чтобы найти производную, вам нужно определить, являются ли переменные независимыми друг от друга, в этом случае вы используете
частные производные
или если есть уравнение, которое связывает переменные, в этом случае вам нужно использовать
неявное дифференцирование
.
Основными двумя направлениями в дифференциальном исчислении являются интегрирование и дифференцирование, и оба они находят широкое применение повсеместно.
частные производные
подробно описаны в инженерных и экономических приложениях.
С одной стороны, дифференцирование имеет дело с бесконечно малыми скоростями изменений, тогда как интегрирование – с суммированием бесконечно малых скоростей изменений
Фундаментальная теорема исчисления
.
