Касательная к окружности
О чем эта статья:
Касательная к окружности, секущая и хорда — в чем разница
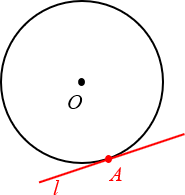
В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.
Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.
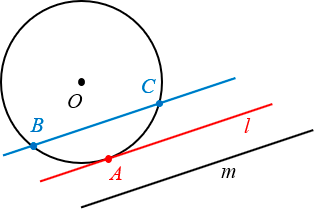
Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).
Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.
Свойства касательной к окружности
Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.
Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.
Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:
- окружность с центральной точкой А;
- прямая а — касательная к ней;
- радиус АВ, проведенный к касательной.
Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.
Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.
В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.
Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Задача
У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.
Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.
Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.
∠АОС = 180° – ∠САО – ∠АСО = 180° – 90° – 28° = 62°
Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.
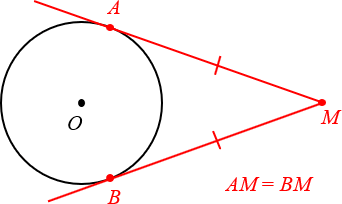
Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.
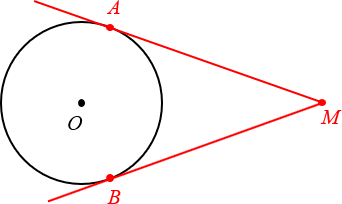
Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.
Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.
Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.
Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.
Задача 1
У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.
Решение
Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.
∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).
Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:
∠BDC = ∠BDA × 2 = 30° × 2 = 60°
Итак, угол между касательными составляет 60°.
Задача 2
К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.
Решение
Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.
Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.
∠МNК = (180° – ∠МКN) : 2 = (180° – 50°) : 2 = 65°
Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.
Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.
Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.
Задача 1
Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.
Решение
Исходя из соотношения касательной и секущей МА 2 = МВ × МС.
Найдем длину внешней части секущей:
МС = МВ – ВС = 16 – 12 = 4 (см)
МА 2 = МВ × МС = 16 х 4 = 64
Задача 2
Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.
Решение
Допустим, что МО = у, а радиус окружности обозначим как R.
В таком случае МВ = у + R, а МС = у – R.
Поскольку МВ = 2 МА, значит:
МА = МВ : 2 = (у + R) : 2
Согласно теореме о касательной и секущей, МА 2 = МВ × МС.
(у + R) 2 : 4 = (у + R) × (у – R)
Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:
Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).
Ответ: MO = 10 см.
Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.
Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.
Задача 1
Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.
Решение
Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.
АВ = ∠АВС × 2 = 32° × 2 = 64°
Задача 2
У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.
Решение
Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:
КМ = 2 ∠МКВ = 2 х 84° = 168°
Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.
∠ОКМ = ∠ОМК = (180° – ∠КОМ) : 2
Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:
∠ОМК = (180° – ∠КОМ) : 2 = (180° – 168°) : 2 = 6°
Определение формулы касательной к окружности
| Коэффициенты окружности |
| Точка на окружности, через которую надо провести касательную |
| Общая формула окружности |
| Уравнение касательной в указанной точке |
Касательная к окружности
Если не использовать понятие производной, и взять объяснение из учебников середины прошлого века, то “Касательная к окружности – это прямая пересекающая окружность в двух совпадающих точках”
Окружность на плоскости может быть представлена в виде нескольких исходных данных
1. В виде координат центра окружности (x0,y0) и её радиуса R.
2. В виде общего уравнения
В виде параметрического вида и в полярных координатах мы рассматривать не будем, так как там формулы тоже на базируются на координатах центра окружности и радиусе.
Наша задача, зная параметры окружности и точку принадлежащую этой окружности вычислить параметры касательной к этой окружности.
Эта задача, является частным решением более общего калькулятор касательная к кривой второго порядка
Итак, если окружность выражена формулой
Уравнение касательной к окружности если нам известны параметры общего уравнения таково:
Таким образом, зная все коэффициенты, мы очень легко найдем уравнение касательной в заданной точке.
ВАЖНО: При указании точки, она должна быть обязательно(!!) принадлежать окружности,
и не быть точкой в какой либо стороне. В противном случае, уравнение касательной будет неверным.
Примеры
Вычислить уравнение касательной в точке (13.8, 0) к окружности выраженной формулой
Теорема о секущей и касательной
Об этой теореме можно сказать: в учебнике нет, а на экзамене есть. Конечно, в учебнике она тоже есть – но никак не выделена и найти ее почти невозможно.
Множество задач ЕГЭ и ОГЭ решаются с помощью этой теоремы.
Если из одной точки к окружности проведены секущая и касательная, то произведение всей секущей на ее внешнюю часть равно квадрату отрезка касательной.
Пусть МС – касательная, МВ – секущая к окружности. Покажем, что
Как мы доказали , и это значит, что треугольники МСА и МВС подобны по двум углам.
Запишем соотношение сходственных сторон:
.
[spoiler title=”источники:”]
http://abakbot.ru/online-2/330-kasatelnaya-circle
[/spoiler]
Касательные, секущие, хорды.
Окружность – это фигура, которая состоит из множества точек плоскости, равноудаленных от данной точки (центра).
Отрезок, соединяющий любую точку на окружности с центром окружности, называется радиусом ($R$).
$ОС=OD=OE=R.$
Отрезок, соединяющий любые две точки на окружности, называется хордой, а хорда, проходящая через центр, – диаметром ($d$).
$ВС$ – хорда
$СЕ$ – диаметр
Свойства хорды и диаметра:
1. Диаметр равен двум радиусам $d=2R; СЕ=2СО$
2. Равные хорды стягивают равные дуги
Если $AB=CD$, то $∪AB=∪CD$.
3.Вся окружность составляет $360°$. Диаметр делит окружность на две полуокружности по $180°$.
4. Хорды окружности, удаленные от центра на равные расстояния, равны.
5. Из двух хорд больше та, которая менее отдалена от центра.
Касательные и секущие:
Прямая, имеющая с окружностью только одну общую точку, называется касательной. $АВ$ – касательная
Прямая, имеющая с окружностью две общие точки, называется секущей. $CD$ – секущая
Свойства:
1. Касательная перпендикулярна радиусу, проведенному в точку касания.
$ОА⊥АС; OB⊥BC$
2. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
$АС=ВС; ОС$ – биссектриса
3. Если хорды $АС$ и $BD$ пересекаются в некоторой точке $N$, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
$AN·NC=BN·ND$
Пример:
Хорды $АВ$ и $CD$ пересекаются в точке $Е$. Найдите $ЕD$, если $АЕ=16, ВЕ=9, СЕ=ED$.
Решение:
Если хорды $АВ$ и $СD$ пересекаются в некоторой точке $Е$, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
$AЕ·ЕВ=СЕ·ЕD$
Так как $СЕ=ED$, данное выражение можно записать в виде:
$ЕD^2=AЕ·ЕВ$
Подставим числовые значения
$ЕD^2=16·9$
$ЕD=√{16·9}=4·3=12$
Ответ: $12$
4. Если из одной точки к одной окружности проведены две секущие, то произведение первой секущей на ее внешнюю часть равно произведению второй секущей на свою внешнюю часть.
$АС·ВС=EC·DC$
5. Если из одной точки к окружности проведены секущая и касательная, то произведение секущей на ее внешнюю часть равно квадрату длины касательной.
$BD·СB=AB^2$
Углы в окружности:
1. Угол, образованный двумя радиусами, называется центральным. Центральный угол равен градусной мере дуги, на которую он опирается
$∠О=∪BmA$
2. Угол, вершина которого лежит на окружности, а стороны являются хордами, называется вписанным. Вписанный угол равен половине градусной меры дуги, на которую он опирается
$∠B={∪AmC}/{2}$
Пример:
Точки $A, B, C$, расположенные на окружности, делят её на три дуги, градусные меры которых относятся как $2:3:7$. Найдите больший угол треугольника $ABC$. Ответ дайте в градусах.
Решение:
Данное условие можно рассмотреть как задачу на части:
1) Найдем общее количество частей, на которые разделили окружность.
$2+3+7=12$ (всего частей)
2) Найдем, сколько градусов приходится на одну часть
$360:12=30°$
3) $∪АВ$ составляет две части, следовательно, $∪АВ=2·30=60°$
$∪АС=3·30=90°$
$∪СВ=7·30=210°$
4) В треугольнике $АВС$ самым большим углом является $∠А$, он вписанный, опирается на дугу $СВ$ и равен ее половине.
$∠А={∪СВ}/{2}={210}/{2}=105°$
Ответ: $105$
3. Угол между хордой и касательной равен половине дуги, отсекаемой хордой .
$∠B={∪BmC}/{2}$
1. Угол между хордами равен полусумме дуг, на которые этот угол опирается
$∠СND={∪CD+∪AB}/{2}$
2. Угол между двумя касательными равен полуразности дуг, заключенных внутри угла.
$∠В={∪АmC-∪AnC}/{2}$
3. Угол между двумя секущими равен полуразности дуг, заключенных внутри угла.
$∠С={∪AE-∪BD}/{2}$
4. Угол между касательной и секущей равен полуразности дуг, заключенных внутри угла.
$∠B={∪AD-∪AC}/{2}$
На этой странице вы узнаете
- Сколько вариантов “окружность + прямая” можно начертить на листе бумаги?
- Что такое сопряжение и с чем его едят?
- Какие окружности изображены на олимпийском флаге?
В жизни мы ежедневно сталкиваемся с касаниями. Касаемся предметов или друг друга. А может ли окружность, подобно человеку, чего-то касаться? Давайте узнаем в этой статье.
Взаимное расположение прямой и окружности
Перед нами стоит задача начертить прямую и окружность на бумаге. Задумайтесь на секунду: как бы вы сейчас выполнили эту задачу?
Поскольку их взаимное расположение не уточнено, то есть несколько вариантов, как их начертить.
1 случай. Прямая и окружность будут лежать в разных местах на листе и никак не пересекутся друг с другом.

2 случай. Прямая будет только касаться окружности.

3 случай. Прямая пересечет окружность.

Каждый человек изобразит эти элементы в разных положениях относительно друг друга. Но так ли много разнообразия будет? На самом деле, существует всего три варианта расположения фигур:
— Они не касаются и не пересекаются;
— Прямая касается окружности;
— Прямая пересекает окружность.
Оказывается, в математике существуют термины для второго и третьего случая. Начнем их рассматривать с касательной к окружности.
Касательная
Касательная – это прямая, которая имеет с окружностью только одну общую точку.
На рисунке АВ – касательная, которая касается окружности в точке А.
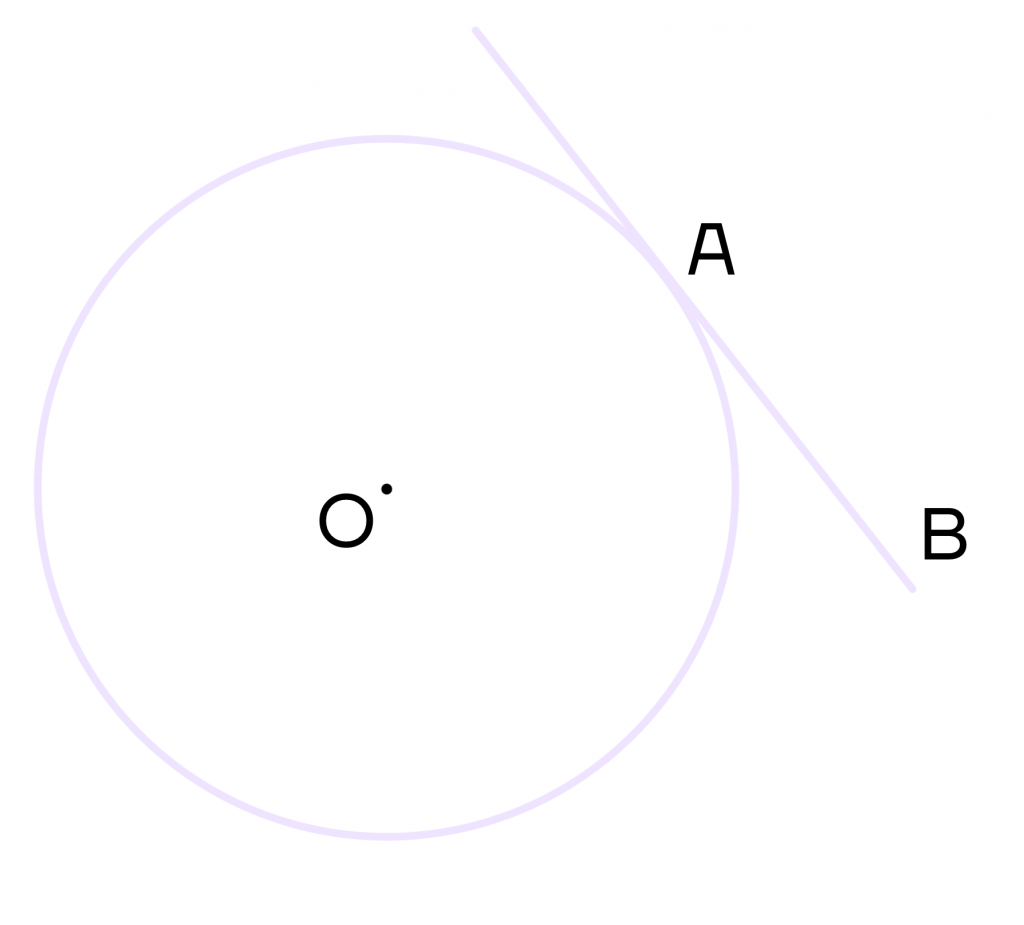
Многие вещи, которые нас окружают, имеют плавные формы. Например, если мы посмотрим на цепь велосипеда, она имеет изогнутую форму.
Все такие детали можно вычертить, а называться эти чертежи будут сопряжениями. Сопряжение в черчении – это плавный переход линии в окружность или окружности до окружности. Чтобы построить сопряжения, есть целые законы, которые основаны на касании к окружности.
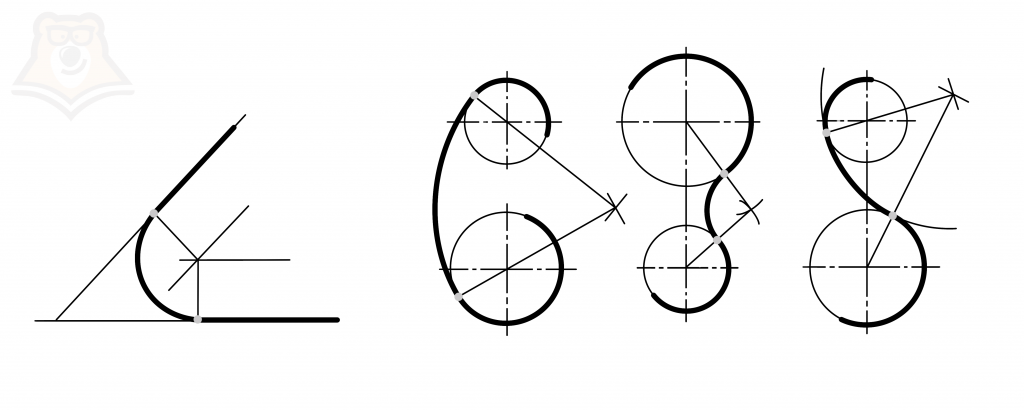
Свойства касательной
1 свойство. Касательная перпендикулярна радиусу, проведенному из центра окружности в точку касания.
Проведем радиус ОА, тогда ОА ⟂ АВ.
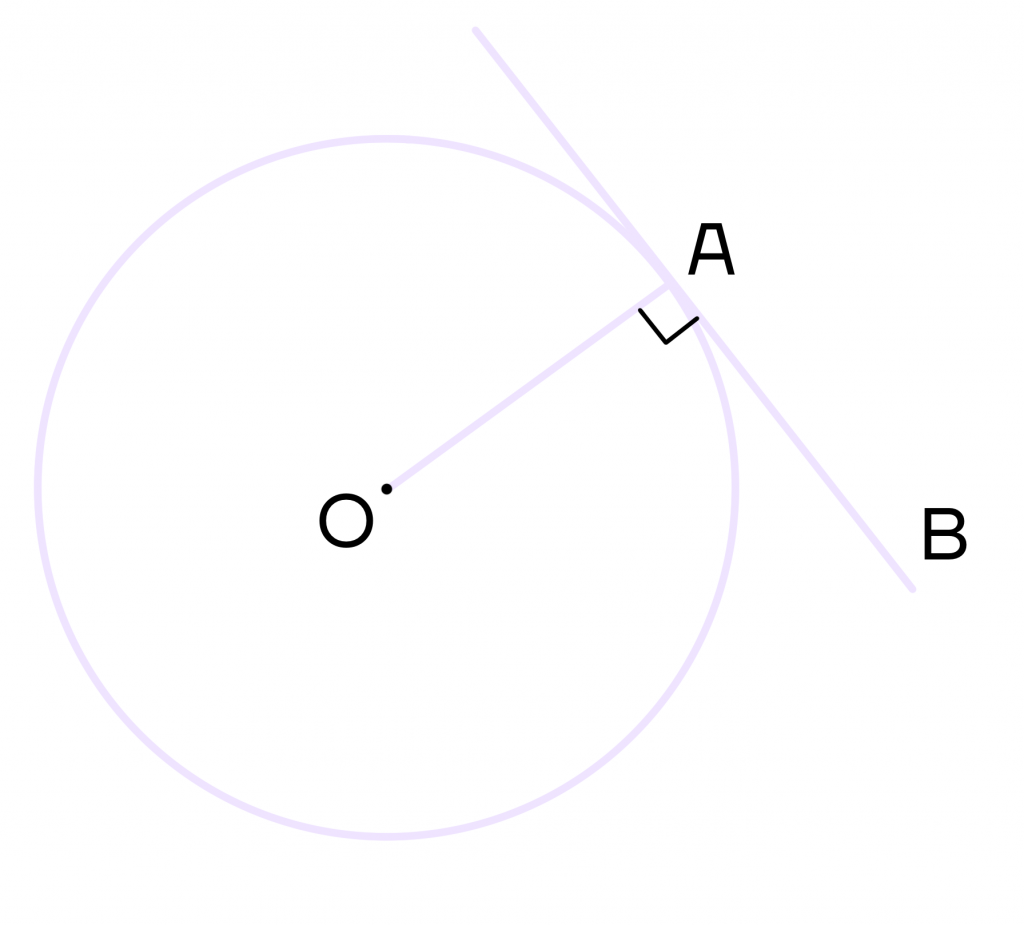
2 свойство. Если провести две касательных из одной точки, то их отрезки будут равны.
Проведем из точки В еще одну касательную ВС, тогда АВ = ВС.
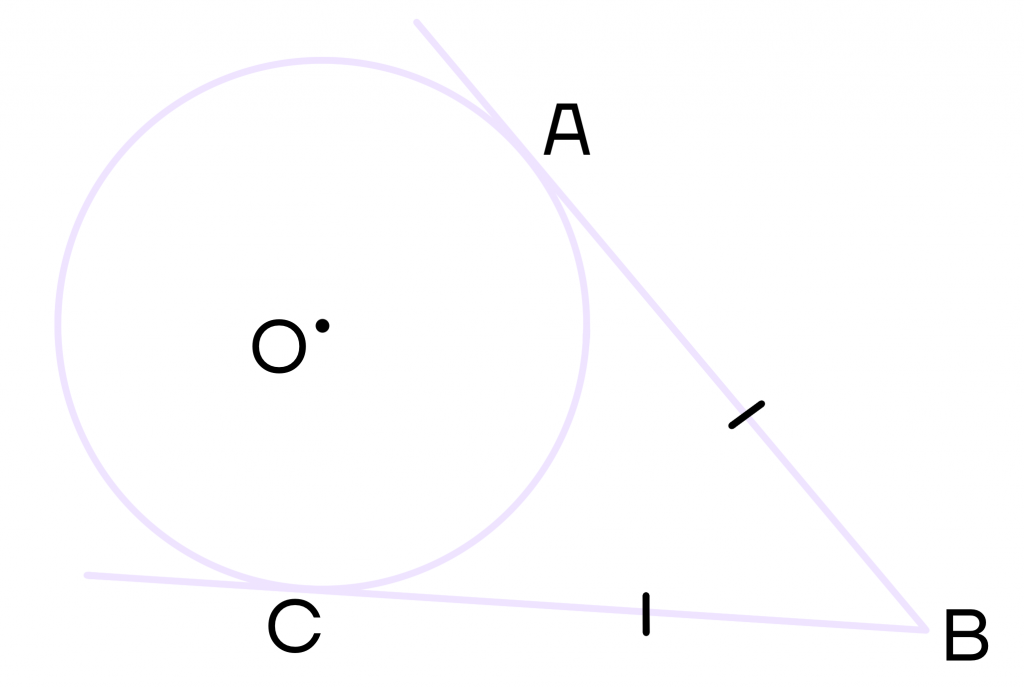
Если перевернуть рисунок, то можно заметить, что он отдаленно напоминает воздушный шар. А в воздушных шарах, также как и в свойстве касательных, используются равные по длине веревки.
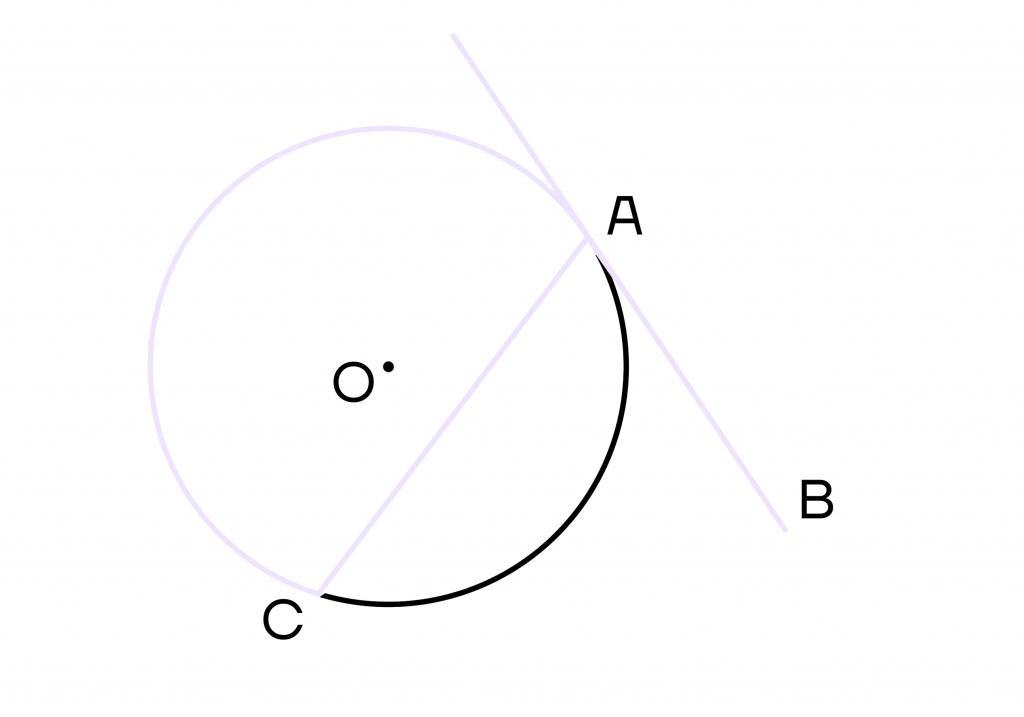
3 свойство. Угол между хордой и касательной равен половине дуги, которая заключена между этими касательной и хордой.
Проведем хорду АС, тогда угол САВ равен (frac{1}{2}⋃АС).
Секущая
Теперь обратим внимание на третий случай, когда прямая пересекает окружность. Такая прямая называется секущей.
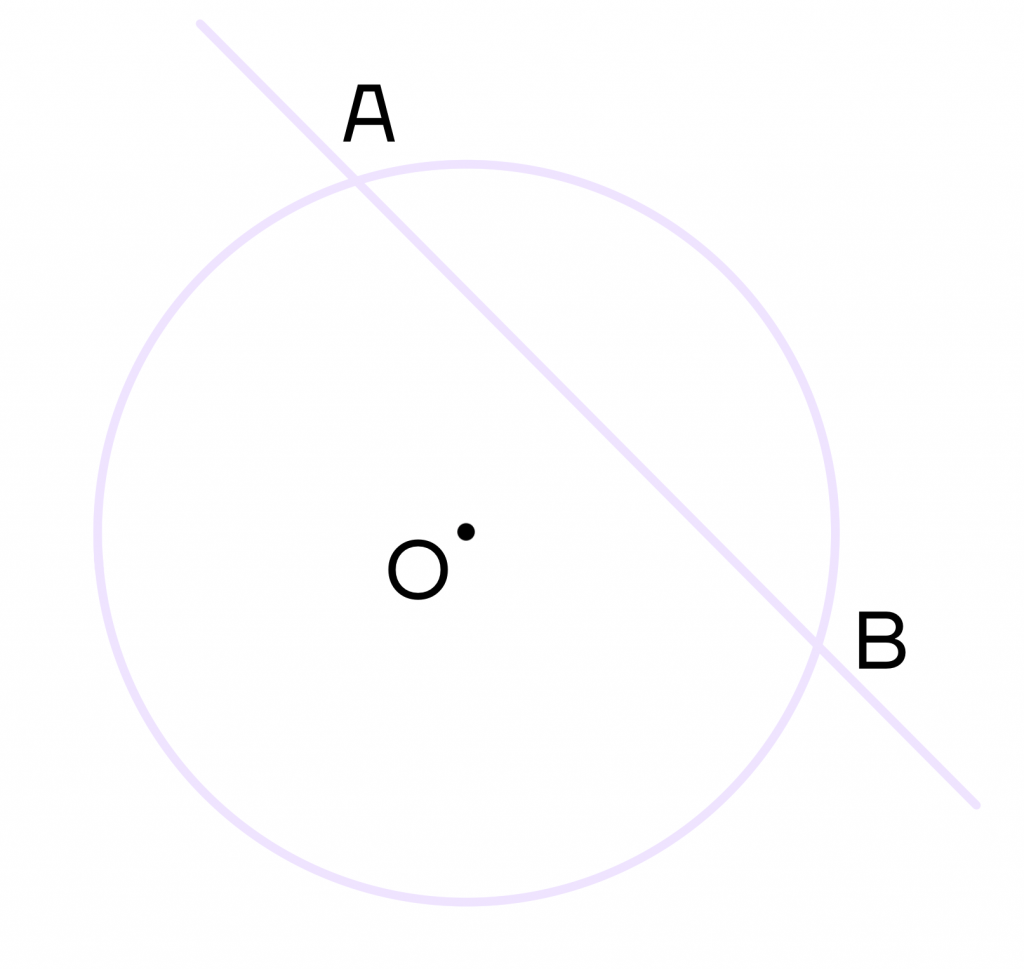
Секущая – это прямая, которая пересекает окружность в двух точках.
Пусть на рисунке АВ – секущая, тогда точки А и В – точки пересечения окружности и секущей.
Вспомни, как мы нарезаем пиццу или пирог. Каждый разрез будет секущей, то есть будет разделять круг на несколько частей.
Свойства секущей
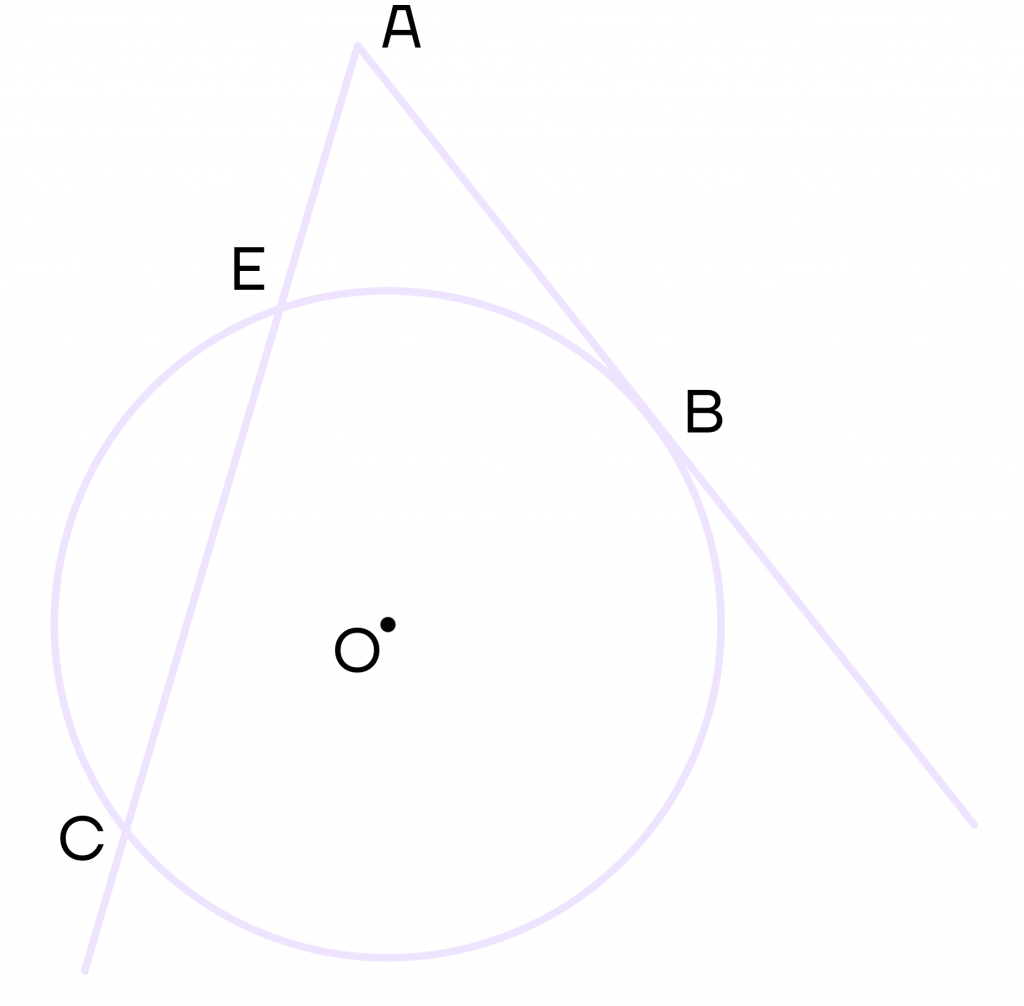
1 свойство. Если из одной точки провести секущую и касательную к окружности, то квадрат касательной равен произведению секущей на ее внешнюю часть.
Проведем из точки А касательную АВ и секущую АС. Пусть секущая будет пересекать окружность в точках С и Е. Тогда выполняется равенство АВ2 = АС * АЕ.
2 свойство. Если из одной точки провести две секущих к окружности, то произведение первой секущей на ее внешнюю часть равняется произведению второй секущей на ее внешнюю часть.
Проведем секущие АВ (пересекает окружность в точках Е и В) и АС (пересекает окружность в точках С и D). Тогда выполняется равенство АС * AD = АВ * АЕ.
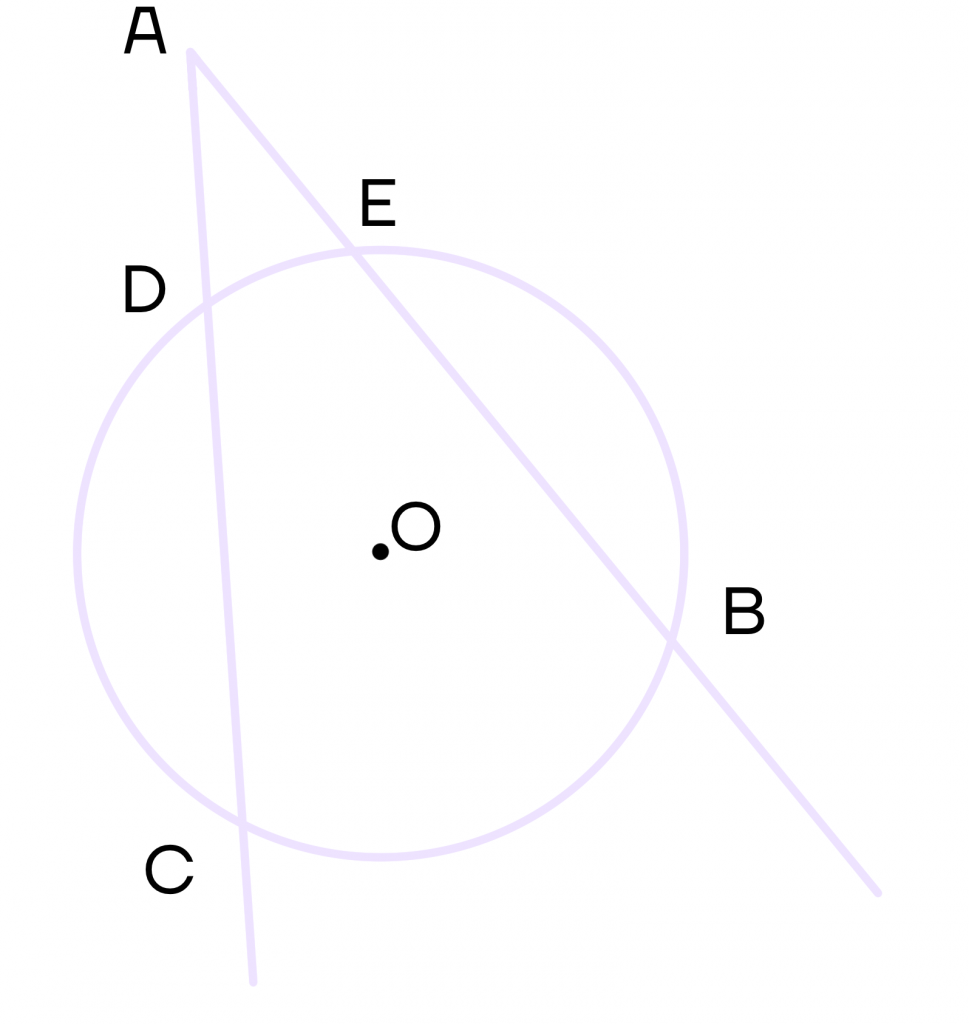
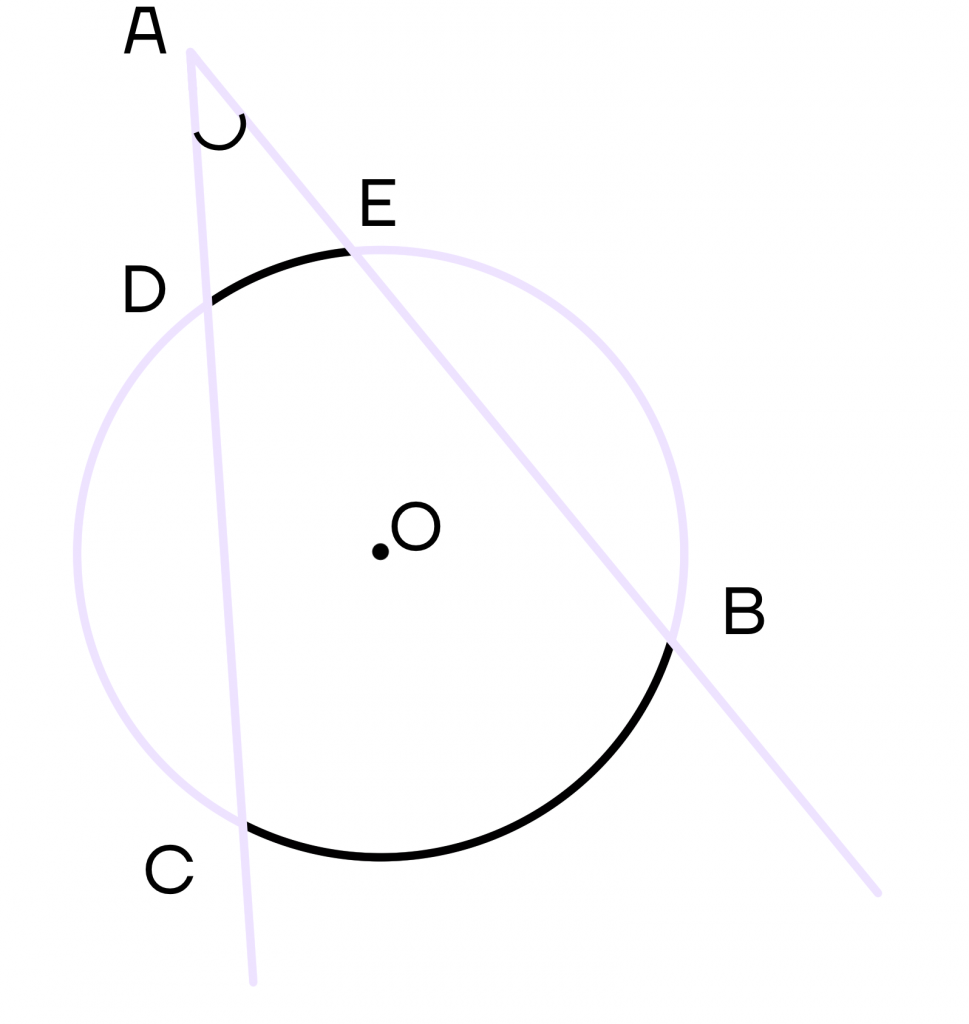
3 свойство. Угол между двумя секущими равен половине разности градусных мер большей и меньшей дуг, которые заключены между секущими.
Допустим, необходимо найти угол САВ. Тогда угол (CAB = frac{1}{2}(⋃CB-⋃DE)).
Не стоит пугаться знака “⋃” – в математике таким образом обозначают дугу окружности.
Касание окружностей
Мы рассмотрели касание прямой и окружности, но могут ли две окружности касаться друг друга? Если у окружностей одна общая точка, то они являются касающимися друг к другу.
И есть даже несколько вариантов такого касания:
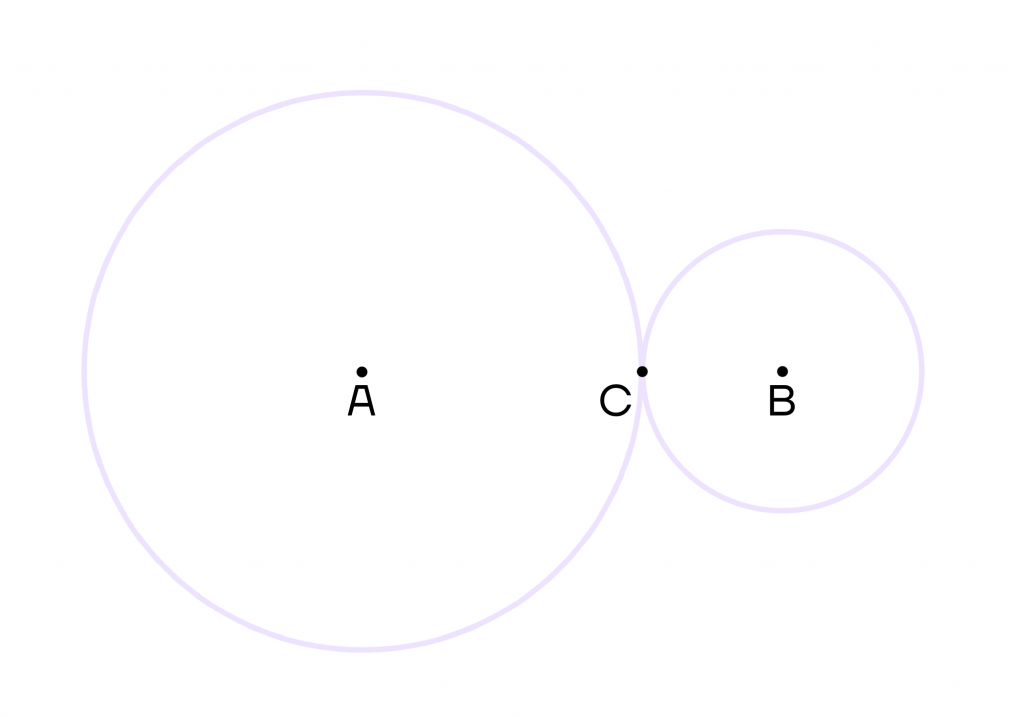
- Внешнее, когда окружности лежат по разные стороны от точки касания.
В данном случае точка С – точка касания.
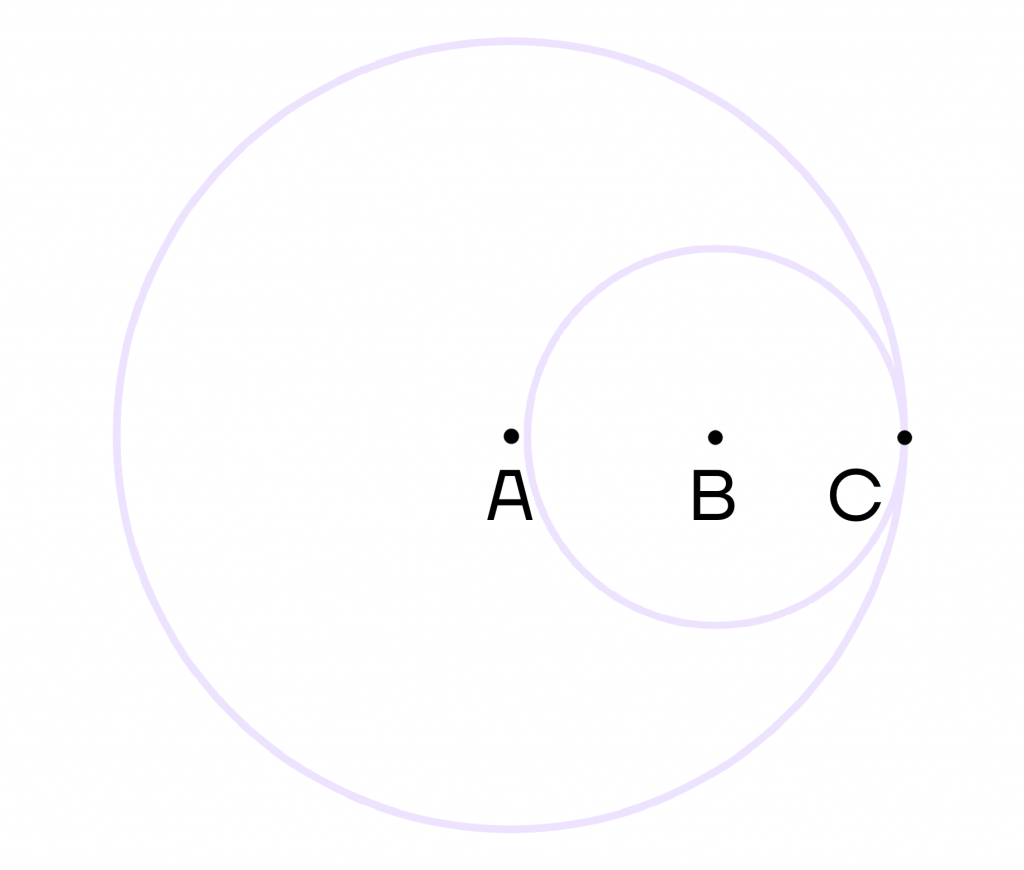
- Внутреннее, когда одна окружность как бы “лежит” в другой.
В данном случае точка С также является точкой касания.
Касание окружностей нередко применяется при создании ювелирных украшений. Такое решение создает неповторимые и очень красивые образы.

Как мы уже определили, окружности могут касаться друг друга. Но есть еще один вариант их взаимного расположения: окружности пересекаются друг с другом. В этом случае они будут иметь две общие точки.
Пересекающиеся окружности изображены на олимпийском флаге, их там целых 5. По одной из версий, они обозначают 5 частей света.

Рассмотрим свойство касающихся окружностей:
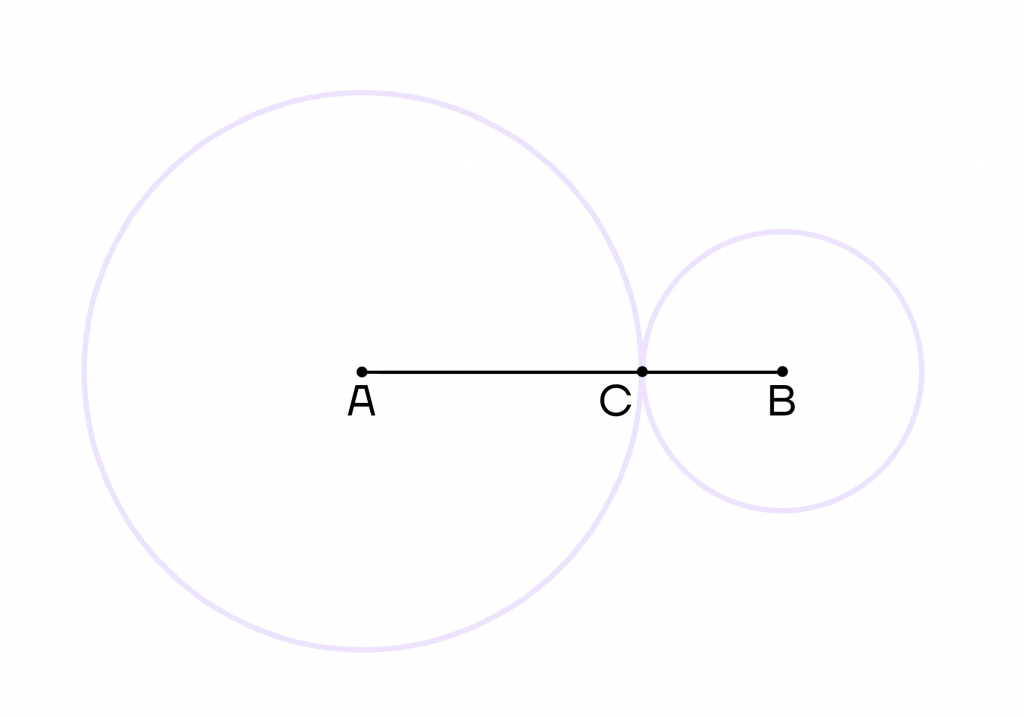
- Прямая, построенная через центры таких окружностей, включает точку касания.
Если мы построим прямую через центры окружностей А и В, то на этой же прямой будет лежать точка касания С.
Фактчек
- Прямая и окружность имеют три варианта взаимного расположения: не пересекаться, касаться или пересекать друг друга.
- Касательная – это прямая, которая проведена к окружности и имеет с ней только одну общую точку. Касательная перпендикулярна радиусу, который проведен в точку касания.
- Секущая – это прямая, которая проходит через окружность и имеет с ней две точки пересечения.
- Если провести из одной точки касательную и секущую, то квадрат касательной будет равен произведению секущей на ее внешнюю часть.
- Две окружности также могут касаться друг друга. Касание может быть как внешним, так и внутренним. При этом если соединить центры окружности прямой, то на этой же прямой будет лежать точка касания.
Проверь себя
Задание 1.
Как называется прямая, которая проведена к окружности и имеет с ней одну общую точку?
- Секущая;
- Хорда;
- Касательная;
- Диаметр.
Задание 2.
Дуга, заключенная между касательной и хордой, равняется 50(circ). Чему равен угол между касательной и хордой?
- 25(circ);
- 50(circ);
- 100(circ);
- 180(circ).
Задание 3.
Длина секущей равна 9, а ее внешняя часть равняется 4. Чему равна касательная к окружности, проведенная из той же точки, что и секущая?
- 36;
- 6;
- 9;
- 5.
Задание 4.
Между секущими заключены дуги окружности, которые равняются 70 и 30 градусам. Чему равен угол между секущими?
- 40;
- 10;
- 80;
- 20.
Задание 5.
Каким бывает касание двух окружностей?
- Только внешним;
- Только внутренним;
- Внешним и внутренним;
- Две окружности не могут касаться друг друга.
Ответы: 1. – 3 2. – 1 3. – 2 4. – 4 5. – 3
Теорема о пропорциональности отрезков секущей и касательной
(Свойство касательной и секущей, проведённых из одной точки)
Для касательной и секущей к окружности, проведённых из одной точки, квадрат расстояния от этой точки до точки касания равен произведению длины секущей на длину её внешней части.
Другими словами, квадрат расстояния от данной точки до точки касания равен произведению расстояний от этой точки до точек пересечения секущей с окружностью.
Дано: окр. (O;R), AK — касательная, AB — секущая,
окр. (O;R)∩AK=K, (O;R)∩AB=B, C
Доказать:
Доказательство:

Рассмотрим треугольники ABK и AKC.
У них ∠A — общий.
(как угол между хордой и касательной)
(как вписанный угол, опирающийся на дугу CK).
Следовательно, ∠ABK=∠AKC.
Значит, треугольники ABK и AKC подобны (по двум углам).
Из подобия треугольников следует пропорциональность их соответствующих сторон:
По основному свойству пропорции
Что и требовалось доказать.
Задача
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найти AC, если диаметр окружности равен 15, а AB=4.

∆ABC, B, C ∈ окр.(O;R) O∈AC, AB — касательная, AB=4, FC — диаметр, FС=15
Найти: AC
Решение:
По свойству касательной и секущей, проведённых из одной точки,
Пусть AF=x, тогда AC=x+15. Составим и решим уравнение:
Второй корень не подходит по смыслу задачи. Следовательно, AC=1+15=16.
Ответ: 16.
Что такое касательная к окружности
8 июля 2018
- Домашняя работа
- Ответы и решения
Определение. Касательная к окружности — это прямая на плоскости, имеющая ровно одну общую точку с окружностью.
Вот парочка примеров:
На этом можно было бы закончить, однако практика показывает, что недостаточно просто зазубрить определение — нужно научиться видеть касательные на чертежах, знать их свойства и вдобавок как следует попрактиковаться в применении этих свойств, решая реальные задачи. Всем этим всем мы сегодня и займёмся.
Основные свойства касательных
Для того, чтобы решать любые задачи, нужно знать четыре ключевых свойства. Два из них описаны в любом справочнике / учебнике, а вот последние два — про них как-то забывают, а зря.
1. Отрезки касательных, проведённых из одной точки, равны
Чуть выше мы уже говорили про две касательных, проведённых из одной точки M. Так вот:
Отрезки касательных к окружности, проведённых из одной точки, равны.
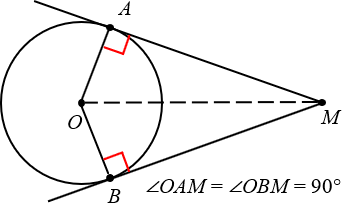
2. Касательная перпендикулярна радиусу, проведённому в точку касания
Ещё раз посмотрим на картинку, представленную выше. Проведём радиусы OAи OB, после чего обнаружим, что углы OAMи OBM — прямые.
Радиус, проведённый в точку касания, перпендикулярен касательной.
Этот факт можно использовать без доказательства в любой задаче:
Кстати, заметьте: если провести отрезок OM, то мы получим два равных треугольника: OAM и OBM.
3. Соотношение между касательной и секущей
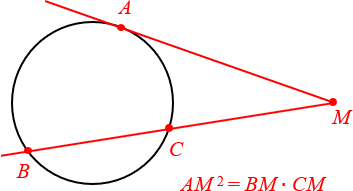
А вот это уже факт посерьёзнее, и большинство школьников его не знают. Рассмотрим касательную и секущую, которые проходят через одну и ту же общую точку M. Естественно, секущая даст нам два отрезка: внутри окружности (отрезок BC — его ещё называют хордой) и снаружи (его так и называют — внешняя часть MC).
Произведение всей секущей на её внешнюю часть равно квадрату отрезка касательной
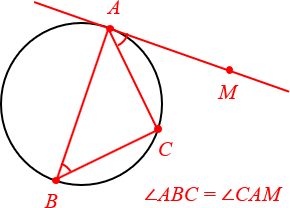
4. Угол между касательной и хордой
Ещё более продвинутый факт, который часто используется для решения сложных задач. Очень рекомендую взять на вооружение.
Угол между касательной и хордой равен вписанному углу, опирающемуся на эту хорду.
Откуда берётся точка B? В реальных задачах она обычно «всплывает» где-то в условии. Поэтому важно научиться распознавать данную конфигурацию на чертежах.
Смотрите также:
- Вписанный угол в геометрии
- Задачи B12, сводящиеся к линейным уравнениям
- Геометрическая вероятность
- Задача 18: метод симметричных корней
- Задача B2 про комиссию в терминале
- Значение тригонометрических функций