Рассмотрим два способа решения.
1) Прямые, параллельные указанным, задаются уравнениями вида $%2x-y+k=0$%, где $%k$% — параметр. Подставим $%y=2x+k$% в уравнение эллипса. Это даст квадратное уравнение относительно $%x$%. Далее надо будет выяснить, при каких значений параметра оно имеет ровно один корень. Это значит, что дискриминант надо приравнять к нулю. Эти значения $%k$% и дадут уравнения касательных.
У нас $%4x^2+5y^2=120$%, то есть $%4x^2+5(2x+k)^2=120$%, то есть $%24x^2+20kx+5k^2-120=0$%. Далее $%D/4=100k^2-24(5k^2-120)=20(144-k^2)=0$%, откуда $%k=pm12$%. Это значит, что уравнения касательных имеют вид $%2x-ypm12=0$%.
2) Вектор нормали к эллипсу в точке $%(x,y)$% находится через частные производные. Получается $%(frac{x}{15};frac{y}{12})$%, что пропорционально $%(4x;5y)$%. Он параллелен вектору нормали к прямой, то есть $%(2;-1)$%, откуда $%2x=-5y$%. Подстановка в уравнение эллипса, записанное в виде $%4x^2+5y^2=120$%, даёт $%y=pm2$%. Поэтому координаты точек касания равны $%(5;-2)$% и $%(-5;2)$%. Через первую из них проходит прямая $%2x-y=12$%, а через вторую $%2x-y=-12$%.
Эллипс
Определение эллипса.
Напомним, что мы назвали эллипсом линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
frac>>+frac>>=1label
$$
при условии (a geq b > 0).
Из уравнения eqref следует, что для всех точек эллипса (|x| leq a) и (|y| leq b). Значит, эллипс лежит в прямоугольнике со сторонами (2a) и (2b).
Точки пересечения эллипса с осями канонической системы координат, имеющие координаты ((a, 0)), ((-a, 0)), ((0, b)) и ((0, -b)), называются вершинами эллипса. Числа (a) и (b) называются соответственно большой и малой полуосями эллипса.
Рис. 8.1. Эллипс
В каноническое уравнение входят только квадраты координат. Поэтому, если координаты ((x, y)) какой-либо точки /(M) ему удовлетворяют, то ему удовлетворяют и координаты ((-x, y)), ((x, -y)) и ((-x, -y)) точек (M_<1>), (M_<2>) и (M_<3>) (рис. 8.1). Следовательно, справедливо следующее утверждение.
Оси канонической системы координат являются осями симметрии эллипса, а начало канонической системы — его центром симметрии.
Внешний вид эллипса проще всего описать сравнением с окружностью радиуса (a) с центром в центре эллипса: (x^<2>+y^<2>=a^<2>). При каждом (x) таком, что (|x| Рис. 8.2. Сжатие окружности к эллипсу. Ординаты всех точек уменьшаются в отношении (b/a).
Фокусы, эксценриситет и директрисы эллипса.
У эллипса есть две замечательные точки, которые называются его фокусами.
Фокусами называются точки (F_<1>) и (F_<2>) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат (рис. 8.3).
Рис. 8.3. Фокусы эллипса.
Для окружности (c=0), и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не является окружностью.
Отметим, что (varepsilon Утверждение 2.
Расстояние от произвольной точки (M(x, y)), лежащей на эллипсе, до каждого из фокусов (рис. 8.3) является линейной функцией от ее абсциссы (x):
$$
r_<1>=|F_<1>M|=a-varepsilon x, r_<2>=|F_<2>M|=a+varepsilon x.label
$$
Очевидно, что (r_<1>^<2>=(x-c)^<2>+y^<2>). Подставим сюда выражение для (y^<2>), найденное из уравнения эллипса. Мы получим
$$
r_<1>^<2>=x^<2>-2cx+c^<2>+b^<2>-fracx^<2>>>.nonumber
$$
Учитывая равенство eqref, это можно преобразовать к виду
$$
r_<1>^<2>=a^<2>-2cx+fracx^<2>>>=(a-varepsilon x)^<2>.nonumber
$$
Так как (x leq a) и (varepsilon Утверждение 3.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса (2a).
Необходимость. Если мы сложим равенства eqref почленно, то увидим, что
$$
r_<1>+r_<2>=2a.label
$$
Достаточность. Пусть для точки (M(x, y)) выполнено условие eqref, то есть
$$
sqrt<(x-c)^<2>+y^<2>>=2a-sqrt<(x+c)^<2>+y^<2>>.nonumber
$$
Возведем обе части равенства в квадрат и приведем подобные члены:
$$
xc+a^<2>=asqrt<(x+c)^<2>+y^<2>>.label
$$
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение eqref. Мы придем к (b^<2>x^<2>+a^<2>y^<2>=a^<2>b^<2>), равносильному уравнению эллипса eqref.
Рис. 8.4. Фокусы и директрисы эллипса.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса (varepsilon).
Уравнение касательной к эллипсу.
Выведем уравнение касательной к эллипсу, заданному каноническим уравнением. Пусть (M_<0>(x_<0>, y_<0>)) — точка на эллипсе и (y_ <0>neq 0). Через (M_<0>) проходит график некоторой функции (y=f(x)), который целиком лежит на эллипсе. (Для (y_ <0>> 0) это график (f_<1>(x)=bsqrt<1-x^<2>/a^<2>>), для (y_ <0>Утверждение 5.
Касательная к эллипсу в точке (M_<0>(x_<0>, y_<0>)) есть биссектриса угла, смежного с углом между отрезками, соединяющими эту точку с фокусами.
Рис. 8.5.
Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Определения и понятия
Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.
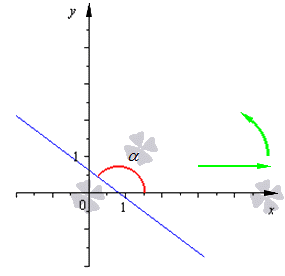
На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .
- Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
- Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 α π 2 или 0 ° α 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α > 0 , причем имеется возрастание графика.
- Если α = π 2 , тогда расположение прямой перпендикулярно о х . Равенство задается при помощи равенства x = c со значением с , являющимся действительным числом.
- Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2 α π или 90 ° α 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.
Определение 3
Секущей называют прямую, которая проходит через 2 точки функции f ( x ) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.
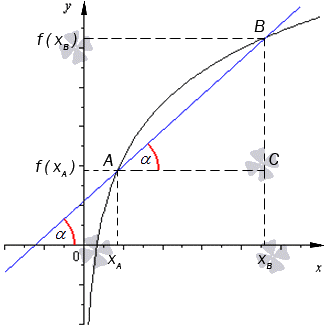
По рисунку видно, что А В является секущей, а f ( x ) – черная кривая, α – красная дуга, означающая угол наклона секущей.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.
Получаем формулу для нахождения секущей вида:
k = t g α = B C A C = f ( x B ) – f x A x B – x A , где абсциссами точек А и В являются значения x A , x B , а f ( x A ) , f ( x B ) – это значения функции в этих точках.
Очевидно, что угловой коэффициент секущей определен при помощи равенства k = f ( x B ) – f ( x A ) x B – x A или k = f ( x A ) – f ( x B ) x A – x B , причем уравнение необходимо записать как y = f ( x B ) – f ( x A ) x B – x A · x – x A + f ( x A ) или
y = f ( x A ) – f ( x B ) x A – x B · x – x B + f ( x B ) .
Секущая делит график визуально на 3 части: слева от точки А , от А до В , справа от В . На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.
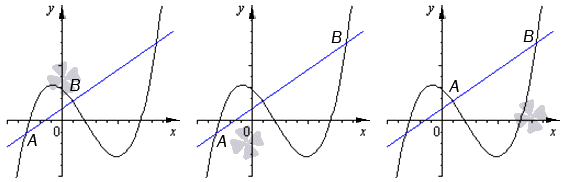
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Касательная к графику функции f ( x ) в точке x 0 ; f ( x 0 ) называется прямая, проходящая через заданную точку x 0 ; f ( x 0 ) , с наличием отрезка, который имеет множество значений х , близких к x 0 .
Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами ( 1 ; 2 ) . Для наглядности, необходимо рассмотреть графики с приближенными к ( 1 ; 2 ) значениями. Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.
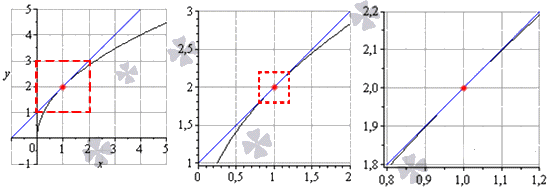
Очевидно, что y = 2 x сливается с прямой у = х + 1 .
Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А . Для наглядности приведем рисунок.
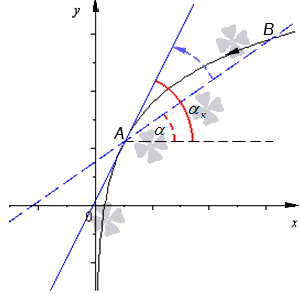
Секущая А В , обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .
Касательной к графику функции y = f ( x ) в точке А считается предельное положение секущей А В при В стремящейся к А , то есть B → A .
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Геометрический смысл производной функции в точке
Перейдем к рассмотрению секущей А В для функции f ( x ) , где А и В с координатами x 0 , f ( x 0 ) и x 0 + ∆ x , f ( x 0 + ∆ x ) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f ( x ) = f ( x 0 + ∆ x ) – f ( ∆ x ) . Для наглядности приведем в пример рисунок.
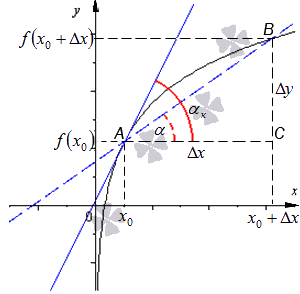
Рассмотрим полученный прямоугольный треугольник А В С . Используем определение тангенса для решения, то есть получим отношение ∆ y ∆ x = t g α . Из определения касательной следует, что lim ∆ x → 0 ∆ y ∆ x = t g α x . По правилу производной в точке имеем, что производную f ( x ) в точке x 0 называют пределом отношений приращения функции к приращению аргумента, где ∆ x → 0 , тогда обозначим как f ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x .
Отсюда следует, что f ‘ ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.
То есть получаем, что f ’ ( x ) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 ( x 0 ) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f ‘ ( x 0 ) .
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.
Уравнение касательной к графику функции y = f ( x ) в точке x 0 , f 0 ( x 0 ) принимает вид y = f ‘ ( x 0 ) · x – x 0 + f ( x 0 ) .
Имеется в виду, что конечным значением производной f ‘ ( x 0 ) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f ‘ ( x ) = ∞ и lim x → x 0 – 0 f ‘ ( x ) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f ‘ ( x ) ≠ lim x → x 0 – 0 f ‘ ( x ) .
Расположение касательной зависит от значения ее углового коэффициента k x = f ‘ ( x 0 ) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у – k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x 0 .
Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 – 6 – 3 3 x – 17 – 3 3 в точке с координатами ( 1 ; 3 ) с определением угла наклона.
Решение
По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, ( 1 ; 3 ) является точкой касания, тогда x 0 = – 1 , f ( x 0 ) = – 3 .
Необходимо найти производную в точке со значением – 1 . Получаем, что
y ‘ = e x + 1 + x 3 3 – 6 – 3 3 x – 17 – 3 3 ‘ = = e x + 1 ‘ + x 3 3 ‘ – 6 – 3 3 x ‘ – 17 – 3 3 ‘ = e x + 1 + x 2 – 6 – 3 3 y ‘ ( x 0 ) = y ‘ ( – 1 ) = e – 1 + 1 + – 1 2 – 6 – 3 3 = 3 3
Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3
Отсюда следует, что α x = a r c t g 3 3 = π 6
Ответ: уравнение касательной приобретает вид
y = f ‘ ( x 0 ) · x – x 0 + f ( x 0 ) y = 3 3 ( x + 1 ) – 3 y = 3 3 x – 9 – 3 3
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
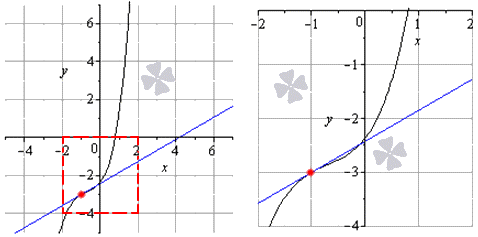
Выяснить наличие существования касательной к графику заданной функции
y = 3 · x – 1 5 + 1 в точке с координатами ( 1 ; 1 ) . Составить уравнение и определить угол наклона.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
y ‘ = 3 · x – 1 5 + 1 ‘ = 3 · 1 5 · ( x – 1 ) 1 5 – 1 = 3 5 · 1 ( x – 1 ) 4 5
Если x 0 = 1 , тогда f ’ ( x ) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 ( x – 1 ) 4 5 = 3 5 · 1 ( + 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 – 0 3 5 · 1 ( x – 1 ) 4 5 = 3 5 · 1 ( – 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке ( 1 ; 1 ) .
Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .
Для наглядности изобразим графически.
Найти точки графика функции y = 1 15 x + 2 3 – 4 5 x 2 – 16 5 x – 26 5 + 3 x + 2 , где
- Касательная не существует;
- Касательная располагается параллельно о х ;
- Касательная параллельна прямой y = 8 5 x + 4 .
Решение
Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ – ∞ ; 2 и [ – 2 ; + ∞ ) . Получаем, что
y = – 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ – ∞ ; – 2 1 15 x 3 – 6 x 2 + 9 x + 12 , x ∈ [ – 2 ; + ∞ )
Необходимо продифференцировать функцию. Имеем, что
y ‘ = – 1 15 x 3 + 18 x 2 + 105 x + 176 ‘ , x ∈ – ∞ ; – 2 1 15 x 3 – 6 x 2 + 9 x + 12 ‘ , x ∈ [ – 2 ; + ∞ ) ⇔ y ‘ = – 1 5 ( x 2 + 12 x + 35 ) , x ∈ – ∞ ; – 2 1 5 x 2 – 4 x + 3 , x ∈ [ – 2 ; + ∞ )
Когда х = – 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:
lim x → – 2 – 0 y ‘ ( x ) = lim x → – 2 – 0 – 1 5 ( x 2 + 12 x + 35 = – 1 5 ( – 2 ) 2 + 12 ( – 2 ) + 35 = – 3 lim x → – 2 + 0 y ‘ ( x ) = lim x → – 2 + 0 1 5 ( x 2 – 4 x + 3 ) = 1 5 – 2 2 – 4 – 2 + 3 = 3
Вычисляем значение функции в точке х = – 2 , где получаем, что
- y ( – 2 ) = 1 15 – 2 + 2 3 – 4 5 ( – 2 ) 2 – 16 5 ( – 2 ) – 26 5 + 3 – 2 + 2 = – 2 , то есть касательная в точке ( – 2 ; – 2 ) не будет существовать.
- Касательная параллельна о х , когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f ‘ ( x 0 ) . То есть необходимо найти значения таких х , когда производная функции обращает ее в ноль. То есть значения f ’ ( x ) и будут являться точками касания, где касательная является параллельной о х .
Когда x ∈ – ∞ ; – 2 , тогда – 1 5 ( x 2 + 12 x + 35 ) = 0 , а при x ∈ ( – 2 ; + ∞ ) получаем 1 5 ( x 2 – 4 x + 3 ) = 0 .
– 1 5 ( x 2 + 12 x + 35 ) = 0 D = 12 2 – 4 · 35 = 144 – 140 = 4 x 1 = – 12 + 4 2 = – 5 ∈ – ∞ ; – 2 x 2 = – 12 – 4 2 = – 7 ∈ – ∞ ; – 2 1 5 ( x 2 – 4 x + 3 ) = 0 D = 4 2 – 4 · 3 = 4 x 3 = 4 – 4 2 = 1 ∈ – 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ – 2 ; + ∞
Вычисляем соответствующие значения функции
y 1 = y – 5 = 1 15 – 5 + 2 3 – 4 5 – 5 2 – 16 5 – 5 – 26 5 + 3 – 5 + 2 = 8 5 y 2 = y ( – 7 ) = 1 15 – 7 + 2 3 – 4 5 ( – 7 ) 2 – 16 5 – 7 – 26 5 + 3 – 7 + 2 = 4 3 y 3 = y ( 1 ) = 1 15 1 + 2 3 – 4 5 · 1 2 – 16 5 · 1 – 26 5 + 3 1 + 2 = 8 5 y 4 = y ( 3 ) = 1 15 3 + 2 3 – 4 5 · 3 2 – 16 5 · 3 – 26 5 + 3 3 + 2 = 4 3
Отсюда – 5 ; 8 5 , – 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.
Рассмотрим графическое изображение решения.
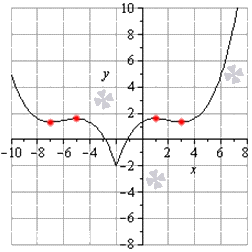
Черная линия – график функции, красные точки – точки касания.
- Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y ‘ ( x ) = 8 5 . Тогда, если x ∈ – ∞ ; – 2 , получаем, что – 1 5 ( x 2 + 12 x + 35 ) = 8 5 , а если x ∈ ( – 2 ; + ∞ ) , тогда 1 5 ( x 2 – 4 x + 3 ) = 8 5 .
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
– 1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 – 4 · 43 = – 28 0
Другое уравнение имеет два действительных корня, тогда
1 5 ( x 2 – 4 x + 3 ) = 8 5 x 2 – 4 x – 5 = 0 D = 4 2 – 4 · ( – 5 ) = 36 x 1 = 4 – 36 2 = – 1 ∈ – 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ – 2 ; + ∞
Перейдем к нахождению значений функции. Получаем, что
y 1 = y ( – 1 ) = 1 15 – 1 + 2 3 – 4 5 ( – 1 ) 2 – 16 5 ( – 1 ) – 26 5 + 3 – 1 + 2 = 4 15 y 2 = y ( 5 ) = 1 15 5 + 2 3 – 4 5 · 5 2 – 16 5 · 5 – 26 5 + 3 5 + 2 = 8 3
Точки со значениями – 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .
Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках – 1 ; 4 15 , 5 ; 8 3 .
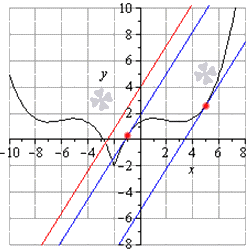
Возможно существование бесконечного количества касательных для заданных функций.
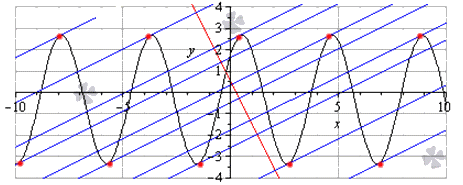
Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x – π 4 – 1 3 , которые располагаются перпендикулярно прямой y = – 2 x + 1 2 .
Решение
Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется – 1 , то есть записывается как k x · k ⊥ = – 1 . Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k ⊥ = – 2 , тогда k x = – 1 k ⊥ = – 1 – 2 = 1 2 .
Теперь необходимо найти координаты точек касания. Нужно найти х , после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y ‘ ( x 0 ) . Из данного равенства найдем значения х для точек касания.
y ‘ ( x 0 ) = 3 cos 3 2 x 0 – π 4 – 1 3 ‘ = 3 · – sin 3 2 x 0 – π 4 · 3 2 x 0 – π 4 ‘ = = – 3 · sin 3 2 x 0 – π 4 · 3 2 = – 9 2 · sin 3 2 x 0 – π 4 ⇒ k x = y ‘ ( x 0 ) ⇔ – 9 2 · sin 3 2 x 0 – π 4 = 1 2 ⇒ sin 3 2 x 0 – π 4 = – 1 9
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.
3 2 x 0 – π 4 = a r c sin – 1 9 + 2 πk или 3 2 x 0 – π 4 = π – a r c sin – 1 9 + 2 πk
3 2 x 0 – π 4 = – a r c sin 1 9 + 2 πk или 3 2 x 0 – π 4 = π + a r c sin 1 9 + 2 πk
x 0 = 2 3 π 4 – a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z
Z – множество целых чисел.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у :
y 0 = 3 cos 3 2 x 0 – π 4 – 1 3
y 0 = 3 · 1 – sin 2 3 2 x 0 – π 4 – 1 3 или y 0 = 3 · – 1 – sin 2 3 2 x 0 – π 4 – 1 3
y 0 = 3 · 1 – – 1 9 2 – 1 3 или y 0 = 3 · – 1 – – 1 9 2 – 1 3
y 0 = 4 5 – 1 3 или y 0 = – 4 5 + 1 3
Отсюда получаем, что 2 3 π 4 – a r c sin 1 9 + 2 πk ; 4 5 – 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; – 4 5 + 1 3 являются точками касания.
Ответ: необходимы уравнения запишутся как
y = 1 2 x – 2 3 π 4 – a r c sin 1 9 + 2 πk + 4 5 – 1 3 , y = 1 2 x – 2 3 5 π 4 + a r c sin 1 9 + 2 πk – 4 5 + 1 3 , k ∈ Z
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Рисунок показывает, что расположение функции идет на промежутке [ – 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = – 2 x + 1 2 . Красные точки – это точки касания.
Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
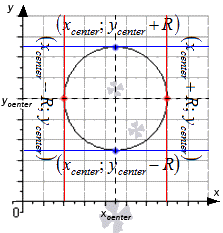
Для задания окружности с центром в точке x c e n t e r ; y c e n t e r и радиусом R применяется формула x – x c e n t e r 2 + y – y c e n t e r 2 = R 2 .
Данное равенство может быть записано как объединение двух функций:
y = R 2 – x – x c e n t e r 2 + y c e n t e r y = – R 2 – x – x c e n t e r 2 + y c e n t e r
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
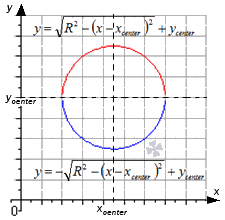
Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 – x – x c e n t e r 2 + y c e n t e r или y = – R 2 – x – x c e n t e r 2 + y c e n t e r в указанной точке.
Когда в точках x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r – R касательные могут быть заданы уравнениями y = y c e n t e r + R и y = y c e n t e r – R , а в точках x c e n t e r + R ; y c e n t e r и
x c e n t e r – R ; y c e n t e r будут являться параллельными о у , тогда получим уравнения вида x = x c e n t e r + R и x = x c e n t e r – R .
Касательная к эллипсу
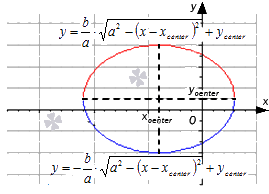
Когда эллипс имеет центр в точке x c e n t e r ; y c e n t e r с полуосями a и b , тогда он может быть задан при помощи уравнения x – x c e n t e r 2 a 2 + y – y c e n t e r 2 b 2 = 1 .
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
y = b a · a 2 – ( x – x c e n t e r ) 2 + y c e n t e r y = – b a · a 2 – ( x – x c e n t e r ) 2 + y c e n t e r
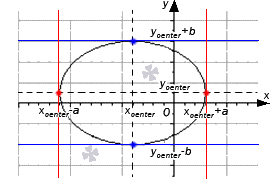
Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у . Ниже для наглядности рассмотрим рисунок.
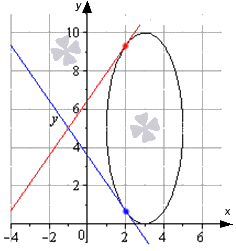
Написать уравнение касательной к эллипсу x – 3 2 4 + y – 5 2 25 = 1 в точках со значениями x равного х = 2 .
Решение
Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что
x – 3 2 4 x = 2 + y – 5 2 25 = 1 1 4 + y – 5 2 25 = 1 ⇒ y – 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5
Тогда 2 ; 5 3 2 + 5 и 2 ; – 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.
Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что
x – 3 2 4 + y – 5 2 25 = 1 y – 5 2 25 = 1 – x – 3 2 4 ( y – 5 ) 2 = 25 · 1 – x – 3 2 4 y – 5 = ± 5 · 1 – x – 3 2 4 y = 5 ± 5 2 4 – x – 3 2
Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 – x – 3 2 , а нижний y = 5 – 5 2 4 – x – 3 2 .
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид
y ‘ = 5 + 5 2 4 – x – 3 2 ‘ = 5 2 · 1 2 4 – ( x – 3 ) 2 · 4 – ( x – 3 ) 2 ‘ = = – 5 2 · x – 3 4 – ( x – 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = – 5 2 · 2 – 3 4 – ( 2 – 3 ) 2 = 5 2 3 ⇒ y = y ‘ ( x 0 ) · x – x 0 + y 0 ⇔ y = 5 2 3 ( x – 2 ) + 5 3 2 + 5
Получаем, что уравнение второй касательной со значением в точке
2 ; – 5 3 2 + 5 принимает вид
y ‘ = 5 – 5 2 4 – ( x – 3 ) 2 ‘ = – 5 2 · 1 2 4 – ( x – 3 ) 2 · 4 – ( x – 3 ) 2 ‘ = = 5 2 · x – 3 4 – ( x – 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = 5 2 · 2 – 3 4 – ( 2 – 3 ) 2 = – 5 2 3 ⇒ y = y ‘ ( x 0 ) · x – x 0 + y 0 ⇔ y = – 5 2 3 ( x – 2 ) – 5 3 2 + 5
Графически касательные обозначаются так:
Касательная к гиперболе
Когда гипербола имеет центр в точке x c e n t e r ; y c e n t e r и вершины x c e n t e r + α ; y c e n t e r и x c e n t e r – α ; y c e n t e r , имеет место задание неравенства x – x c e n t e r 2 α 2 – y – y c e n t e r 2 b 2 = 1 , если с вершинами x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r – b , тогда задается при помощи неравенства x – x c e n t e r 2 α 2 – y – y c e n t e r 2 b 2 = – 1 .
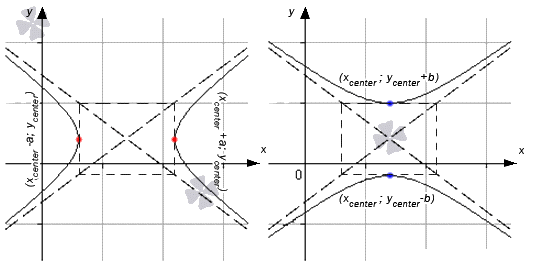
Гипербола может быть представлена в виде двух объединенных функций вида
y = b a · ( x – x c e n t e r ) 2 – a 2 + y c e n t e r y = – b a · ( x – x c e n t e r ) 2 – a 2 + y c e n t e r или y = b a · ( x – x c e n t e r ) 2 + a 2 + y c e n t e r y = – b a · ( x – x c e n t e r ) 2 + a 2 + y c e n t e r
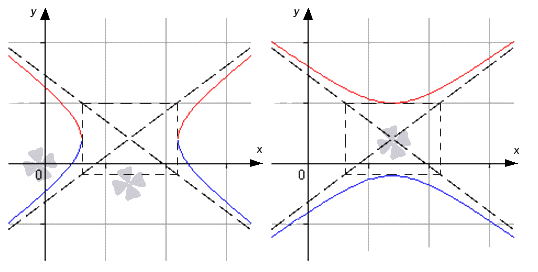
В первом случае имеем, что касательные параллельны о у , а во втором параллельны о х .
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
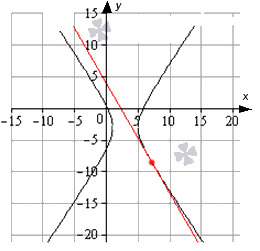
Составить уравнение касательной к гиперболе x – 3 2 4 – y + 3 2 9 = 1 в точке 7 ; – 3 3 – 3 .
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
x – 3 2 4 – y + 3 2 9 = 1 ⇒ y + 3 2 9 = x – 3 2 4 – 1 ⇒ y + 3 2 = 9 · x – 3 2 4 – 1 ⇒ y + 3 = 3 2 · x – 3 2 – 4 и л и y + 3 = – 3 2 · x – 3 2 – 4 ⇒ y = 3 2 · x – 3 2 – 4 – 3 y = – 3 2 · x – 3 2 – 4 – 3
Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; – 3 3 – 3 .
Очевидно, что для проверки первой функции необходимо y ( 7 ) = 3 2 · ( 7 – 3 ) 2 – 4 – 3 = 3 3 – 3 ≠ – 3 3 – 3 , тогда точка графику не принадлежит, так как равенство не выполняется.
Для второй функции имеем, что y ( 7 ) = – 3 2 · ( 7 – 3 ) 2 – 4 – 3 = – 3 3 – 3 ≠ – 3 3 – 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.
y ‘ = – 3 2 · ( x – 3 ) 2 – 4 – 3 ‘ = – 3 2 · x – 3 ( x – 3 ) 2 – 4 ⇒ k x = y ‘ ( x 0 ) = – 3 2 · x 0 – 3 x 0 – 3 2 – 4 x 0 = 7 = – 3 2 · 7 – 3 7 – 3 2 – 4 = – 3
Ответ: уравнение касательной можно представить как
y = – 3 · x – 7 – 3 3 – 3 = – 3 · x + 4 3 – 3
Наглядно изображается так:
Касательная к параболе
Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y ( x 0 ) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y ‘ ( x 0 ) · x – x 0 + y ( x 0 ) . Такая касательная в вершине параллельна о х .
Следует задать параболу x = a y 2 + b y + c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у . Получаем, что
x = a y 2 + b y + c ⇔ a y 2 + b y + c – x = 0 D = b 2 – 4 a ( c – x ) y = – b + b 2 – 4 a ( c – x ) 2 a y = – b – b 2 – 4 a ( c – x ) 2 a
Графически изобразим как:
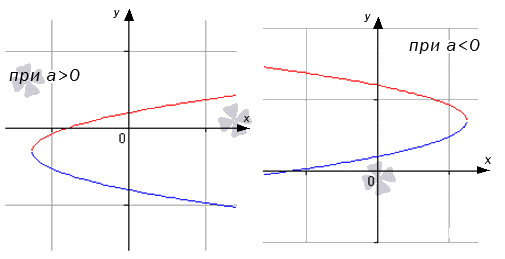
Для выяснения принадлежности точки x 0 , y ( x 0 ) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.
Написать уравнение касательной к графику x – 2 y 2 – 5 y + 3 , когда имеем угол наклона касательной 150 ° .
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
– 2 y 2 – 5 y + 3 – x = 0 D = ( – 5 ) 2 – 4 · ( – 2 ) · ( 3 – x ) = 49 – 8 x y = 5 + 49 – 8 x – 4 y = 5 – 49 – 8 x – 4
Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.
k x = y ‘ ( x 0 ) = t g α x = t g 150 ° = – 1 3
Отсюда определим значение х для точек касания.
Первая функция запишется как
y ‘ = 5 + 49 – 8 x – 4 ‘ = 1 49 – 8 x ⇒ y ‘ ( x 0 ) = 1 49 – 8 x 0 = – 1 3 ⇔ 49 – 8 x 0 = – 3
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.
Вторая функция запишется как
y ‘ = 5 – 49 – 8 x – 4 ‘ = – 1 49 – 8 x ⇒ y ‘ ( x 0 ) = – 1 49 – 8 x 0 = – 1 3 ⇔ 49 – 8 x 0 = – 3 x 0 = 23 4 ⇒ y ( x 0 ) = 5 – 49 – 8 · 23 4 – 4 = – 5 + 3 4
Имеем, что точки касания – 23 4 ; – 5 + 3 4 .
Ответ: уравнение касательной принимает вид
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/proizvodnye/kasatelnaja-k-grafiku-funktsii-v-tochke/
[/spoiler]
Директрисы
кривых второго порядка.
Все кривые 2-го порядка имеют директрису:
прямая, по отношению к которой эллипс,
гипербола и парабола имеют особые
свойства. Использование директрисы в
случае параболы мы видели в самом
определении параболы.
При
получении канонических уравнений
эллипса, гиперболы и параболы было
установлено понятие эксцентриситета
–
![]() ,
,
причём:
а).
![]() <
<
1 → для эллипса; б).
![]() =
=
1 → для параболы; в).
![]() >
>
1 → для гиперболы.
Общее
определение. Кривой второго порядка
называют геометрическое место точек
![]()
![]()
плоскости, обладающих свойством:
расстояние от точки
![]()
до точки
![]() ,
,
называемой фокусом,
равно расстоянию точки
![]()
до прямой
![]() ,
,
называемой директрисой,
умноженному на некоторое число
![]()
–
эксцентриситет.
Замечание:
Определение кривых 2-го порядка с
использованием директрисы не позволяет
принять
![]() =0,
=0,
хотя раньше такое значение эксцентриситета
выделяло частный случай эллипса –
окружность!
Из общего
определения кривых второго порядка с
использованием директрисы и эксцентриситета
следует: директриса и кривая второго
порядка не могут пересекаться!
О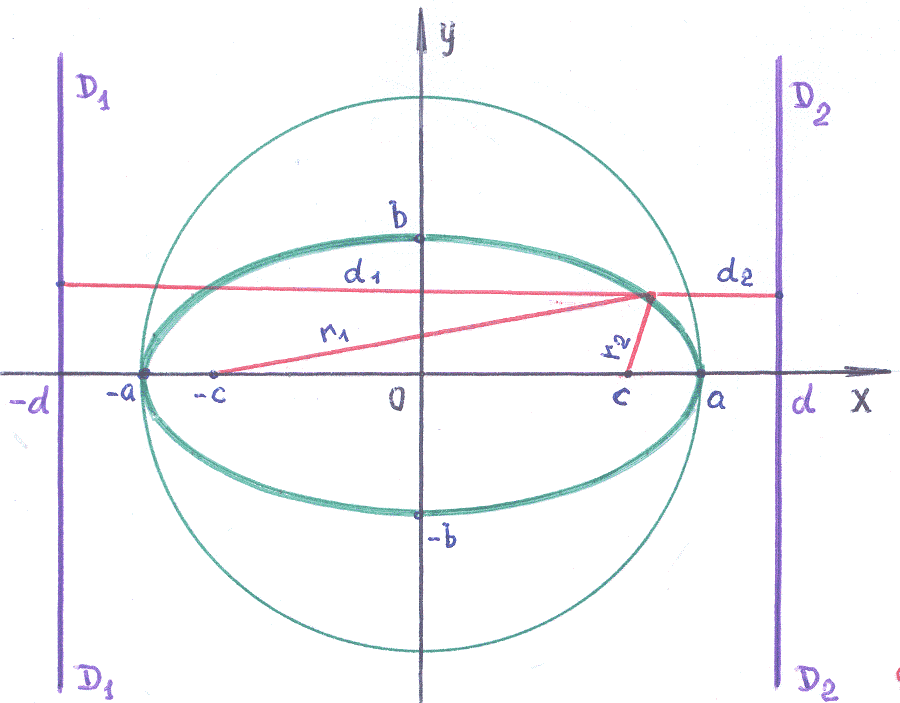 пределим
пределим
директрису для эллипса.
При
рассмотрении канонического уравнения
эллипса было установлено: кривая
симметрична относительно осей
![]()
и
![]() .
.
Это означает, что эллипс должен иметь
две, симметрично расположенные
относительно оси
![]() ,
,
директрисы. Обозначим эти директрисы,
как
![]()
и
![]() .
.
В
соответствии с определением, для левой
директрисы имеем:
![]() =
=![]() ·
·![]() .
.
Но, для эллипса:
![]() =
=![]()
и
![]() =
=![]() .
.
Легко видеть, что в этом случае:
![]() .
.
Это значит, что
![]()
и уравнение левой директрисы:
![]() .
.
Для
правой директрисы:
![]() =
=![]()
и
![]() =
=![]() .
.
Используя условие:
![]() =
=![]() ·
·![]() ,
,
получаем такое же значение параметра:
![]()
и уравнение правой директрисы:
![]() .
.
Если
учесть, что для эллипса
![]() <1,
<1,
то
![]() .
.
Это подтверждает предположение, что
кривая и директриса не пересекаются!
Определим
директрису для гиперболы.
П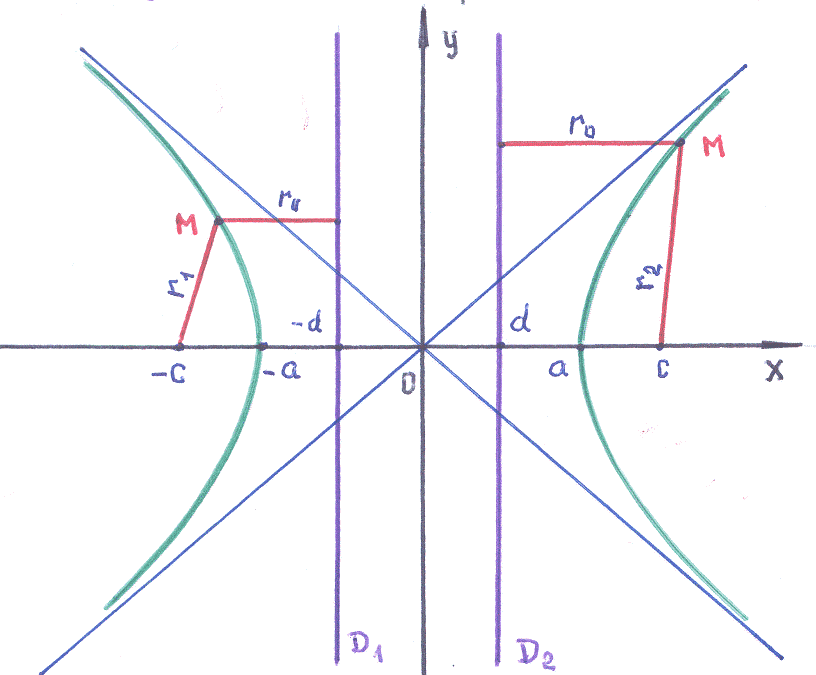 ри
ри
рассмотрении канонического уравнения
гиперболы было установлено: кривая
симметрична относительно осей
![]()
и
![]() .
.
Это означает, что гипербола должна иметь
две, симметрично расположенные
относительно оси
![]() ,
,
директрисы. Обозначим эти директрисы,
как
![]()
и
![]() .
.
В
соответствии с определением, для левой
директрисы имеем:
![]() =
=![]() ·
·![]() .
.
Но, для левой ветви гиперболы было
получено:
![]() =
=![]() ,
,
а
![]() =
=![]() .
.
Легко видеть, что в этом случае:
![]() .
.
Это значит, что
![]()
и уравнение левой директрисы:
![]() .
.
Для
правой директрисы:
![]() =
=![]()
и
![]() =
=![]() .
.
Используя условие:
![]() =
=![]() ·
·![]() ,
,
получаем такое же значение параметра:
![]()
и уравнение правой директрисы:
![]() .
.
Если
учесть, что для гиперболы
![]() >1,
>1,
то
![]() .
.
Это подтверждает предположение, что
кривая и директриса не пересекаются!
☺☺
Пример 5–09:
Дан эллипс:
![]() .
.
Определить его полуоси, фокусы,
эксцентриситет и директрисы.
Решение:
1).
Приведём заданное уравнение эллипса к
канонической форме:
![]() .
.
2). Тогда:
![]() =5,
=5,
![]() =3,
=3,
и можно вычислить:
![]() =4,
=4,
![]() =
=![]() =
=![]() ,
,
после чего:
![]() =
=![]() =
=![]() .
.
Ответ: полуоси:
![]() =5,
=5,
![]() =3,
=3,
фокусы:
![]() (–4,0)
(–4,0)
и
![]() (4,0),
(4,0),
![]() =
=![]() ,
,
директрисы:
![]() =
=![]() .
.
Пример 5–10:
Составить уравнение гиперболы, если её
фокусы лежат на оси
![]()
симметрично относительно начала
координат и заданы:
1) точки
![]() (6,–1)
(6,–1)
и
![]() (–8,2
(–8,2![]() ),
),
лежащие на гиперболе;
2) точка
![]() (–3,
(–3,
![]() )
)
и уравнения директрис: x=![]() .
.
Решение:
1).
Воспользуемся уравнением гиперболы:
![]()
и учтём, что точки
![]()
и
![]()
лежат на кривой. Для точки
![]() :
:
![]() ,
,
для точки
![]() :
:
![]() .
.
Решая полученную систему уравнений,
получаем:
![]() ,
,![]() .
.
Уравнение гиперболы:
![]() .
.
2).
Воспользуемся уравнением гиперболы
и учтём, что точка
![]()
лежит на гиперболе:
![]() .
.
Учитывая:
![]() =
=![]() ,
,
из уравнения директрисы получаем:
![]() =
=![]() ,
,
откуда:
![]()
=![]()
![]() .
.
3). Далее
воспользуемся выражением для гиперболы:
![]() ,
,
или
![]() .
.
Если подставить значения
![]()
и
![]()
в уравнение:
![]() ,
,
то получим уравнение
относительно
![]() :
:
 ,
,
из которого следует
![]() =3
=3
и
![]() =
=![]() .
.
4). Для
![]() =3
=3
вычисляем:
![]() =4
=4
и
![]() =5.
=5.
Тогда уравнение
гиперболы:
![]() .
.
5). Если
![]() =
=![]() ,
,
то:
![]() =
=![]()
и
![]() =
=![]() .
.
В этом случае
гипербола:
 .
.
Ответ: в случае 1)
![]() ;
;
в случае 2)
![]() ,
,
или
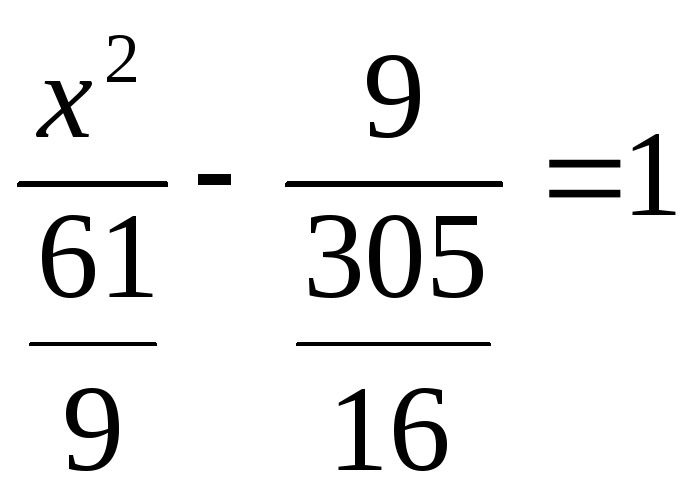 .
.
☻
Диаметры
кривых второго порядка.
Продолжим исследование кривых второго
порядка, используя общее для этих кривых
уравнение:
![]() .
.
Из этого уравнения получаем:
Окружность:
при
![]() =
=![]() =1,
=1,
![]() =0,
=0,
![]() =–
=–![]() ;
;
эллипс:
при
![]() =
=![]() ,
,
![]() =
=![]() ,
,
![]() =0,
=0,
![]() =–1.
=–1.
Гипербола:
при
![]() =
=![]() ,
,
![]() =–
=–![]() ,
,
![]() =0,
=0,
![]() =–1;
=–1;
парабола:
при
![]() =0,
=0,
![]() =1,
=1,
![]() =–
=–
p,
![]() =0.
=0.
У равнение
равнение
![]()
будем использовать для решения вопросов
о диаметрах и касательных для эллипса,
гиперболы и параболы.
Если
кривую 2-го порядка пересекать прямыми,
параллельными
![]() :
:![]() ,
,
то получим хорды с угловым коэффициентом
![]() .
.
Если на каждой хорде выделить середину,
то (оказывается!) все эти средние точки
лежат на одной прямой
![]() .
.
Эту прямую
![]()
называют диаметром
кривой второго порядка, сопряжённым
хордам направления k.
Обозначим
концы хорд:
![]()
![]()
и
![]()
![]() ,
,
а точка
![]()
![]()
–
середина хорды. Тогда, воспользовавшись
формулами для вычисления координат
середины отрезка, получим:
![]() =
=![]() ,
,
![]() =
=![]() . (19)
. (19)
Так как
точки
![]()
![]()
и
![]()
![]()
принадлежат кривой, то, используя общее
уравнение, можем записать: ![]()
и
![]() .
.
Составим разность последних равенств:
![]() . (20)
. (20)
Рассмотрим два
случая:
1). Пусть
![]()
![]() 0.
0.
Разделим равенство (20) на 2![]() :
:
![]() .
.
Учитывая, что
![]()
– угловой коэффициент прямой, получаем:
![]() .
.
Если параметр
![]()
![]() 0,
0,
то последнее равенство есть прямая.
Если
![]() =0,
=0,
но
![]()
![]() 0,
0,
то равенство
![]()
– тоже есть прямая, именно диаметр
кривой второго порядка.
2). Пусть
![]() =0:
=0:
это значит, что хорды параллельны оси
![]() .
.
В этом случае
![]()
![]() 0,
0,
и из уравнения (20) следует:
![]() =0
=0
– ось
![]() .
.
Применим
полученные результаты к окружности,
эллипсу, гиперболе и параболе, используя
их канонические уравнения.
О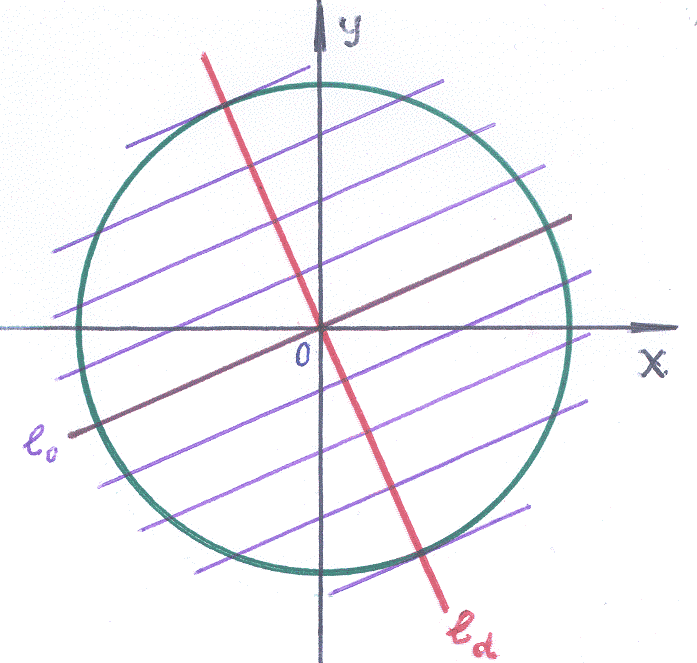 пределим
пределим
диаметры для окружности.
Пусть
![]()
определяет направления хорд окружности.
Учитывая, для окружности коэффициенты
общего уравнения кривой второго порядка:
![]() =
=![]() =1,
=1,
![]() =0,
=0,
![]() =–
=–![]() ,
,
уравнение диаметра окружности принимает
вид:
![]() ,
,
или
![]() =
=![]() =
=![]() .
.
Так как произведение:
![]() =–1,
=–1,
то у окружности хорды и соответствующий
им диаметр взаимно перпендикулярны.
Отметим также, что диаметр окружности
как геометрическое место середин
параллельных хорд проходит через начало
координат.
Полученный
для окружности результат можно было
предвидеть, так как в элементарной
геометрии было доказано: диаметр
окружности, проходящий через середину
хорды, ей перпендикулярен!
Определим
диаметры для эллипса.
Учитывая,
что эллипс – это сжатая окружность, из
геометрических соображений можем
предположить, что все диаметры эллипса
проходят через начало координат
![]() .
.
Пусть
![]()
определяет направления хорд эллипса.
Учитывая, для эллипса коэффициенты
общего уравнения кривой второго порядка:
![]() =
=![]() ,
,
![]() =
=![]() ,
,
![]() =0,
=0,
![]() =–1,
=–1,
уравнение диаметра эллипса принимает
вид:
![]() ,
,
или
![]() =
=![]() =
=![]() .
.
Так как произведение:
![]() =–
=–![]()
симметрично относительно угловых
коэффициентов
![]()
и
![]() ,
,
то направления хорд и диаметров взаимно
обратимы: если направление хорд определено
угловым коэффициентом
![]() ,
,
то направление диаметров определяется
угловым коэффициентом
![]() ,
,
и наоборот!
Два
диаметра, угловые коэффициенты связаны
соотношением:
![]() =–
=–![]() ,
,
называются сопряжёнными.
Н етрудно
етрудно
заметить: если один из сопряжённых
диаметров эллипса располагаются в 1-й
и 3-й четвертях, то другой будет
располагаться во 2-й и в 4-й четвертях.
Если
значение углового коэффициента одного
из сопряжённых диаметров увеличивается,
то есть диаметр вращается против часовой
стрелки, то второй вращается в том же
направлении. Это совпадает с картиной
вращения сопряжённых диаметров
окружности.
Сопряжённые
диаметры эллипса не могут совпасть:
![]() =
=![]() ,
,
так как невозможно равенство:
![]() .
.
Если
![]() →0,
→0,
то
![]() →
→![]() .
.
В этом случае сопряжённые диаметры
совпадут с осями симметрии эллипса и
будут взаимно перпендикулярными.
Определим
диаметры для гиперболы.
П усть
усть
![]()
определяет направления хорд гиперболы.
Учитывая, для гиперболы коэффициенты
общего уравнения кривой второго порядка:
![]() =
=![]() ,
,
![]() =–
=–![]() ,
,
![]() =0,
=0,
![]() =–1,
=–1,
уравнение диаметра гиперболы принимает
вид:
![]() ,
,
или
![]() =
=![]() =
=![]() ,
,
откуда:
![]() =
=![]() .
.
Так как равенство симметрично относительно
угловых коэффициентов
![]()
и
![]() ,
,
то направления хорд и диаметров взаимно
обратимы: если направление хорд определено
угловым коэффициентом
![]() ,
,
то направление диаметров определяется
угловым коэффициентом
![]() ,
,
и наоборот! Видим также, что угловые
коэффициенты
![]()
и
![]()
одного знака.
Два
диаметра, угловые коэффициенты связаны
соотношением:
![]() =
=![]() ,
,
называются сопряжёнными.
Оба диаметра проходят в одной и той же
четверти, причём если
![]()
увеличивается, то
![]()
должен уменьшаться. Это значит, что при
изменении угловых коэффициентов
сопряжённых диаметров гиперболы эти
диаметры вращаются в противоположных
направлениях.
Так как
![]() =
=![]() ,
,
то при значениях
![]() =
=![]()
и
![]() =
=![]() .
.
Это значит, что при приближении диаметра
к асимптоте сопряжённый диаметр
приближается к той же асимптоте.
Если
![]() →0,
→0,
то
![]() →
→![]() .
.
В этом случае получаем взаимно
перпендикулярные сопряжённые диаметры,
совпадающие с осями гиперболы.
Определим
диаметры для параболы.
Пусть
![]()
определяет направления хорд параболы.
Учитывая, для параболы коэффициенты
общего уравнения кривой второго порядка:
![]() =0,
=0,
![]() =1,
=1,
![]() =–
=–
p,
![]() =0,
=0,
уравнение диаметра параболы принимает
вид:
![]() ,
,
или
![]() =
=![]()
– прямая, параллельная оси
![]() .
.
Это значит, что все диаметры параболы
параллельны оси
![]() .
.
Е сли
сли
диаметр и хорды перпендикулярны, то
диаметр
![]()
совпадает с осью
![]() .
.
Вывод:
общность кривых второго порядка при
решении задачи о диаметрах проявляется
в том, что все они имеют диаметры и для
их нахождения используют одно и то же
алгебраическое выражение.
☺☺
Пример 5–11:
Дана параллельная ортогональная проекция
окружности и её диаметра на некоторую
плоскость. Как построить проекцию
перпендикулярного диаметра этой
окружности?
Р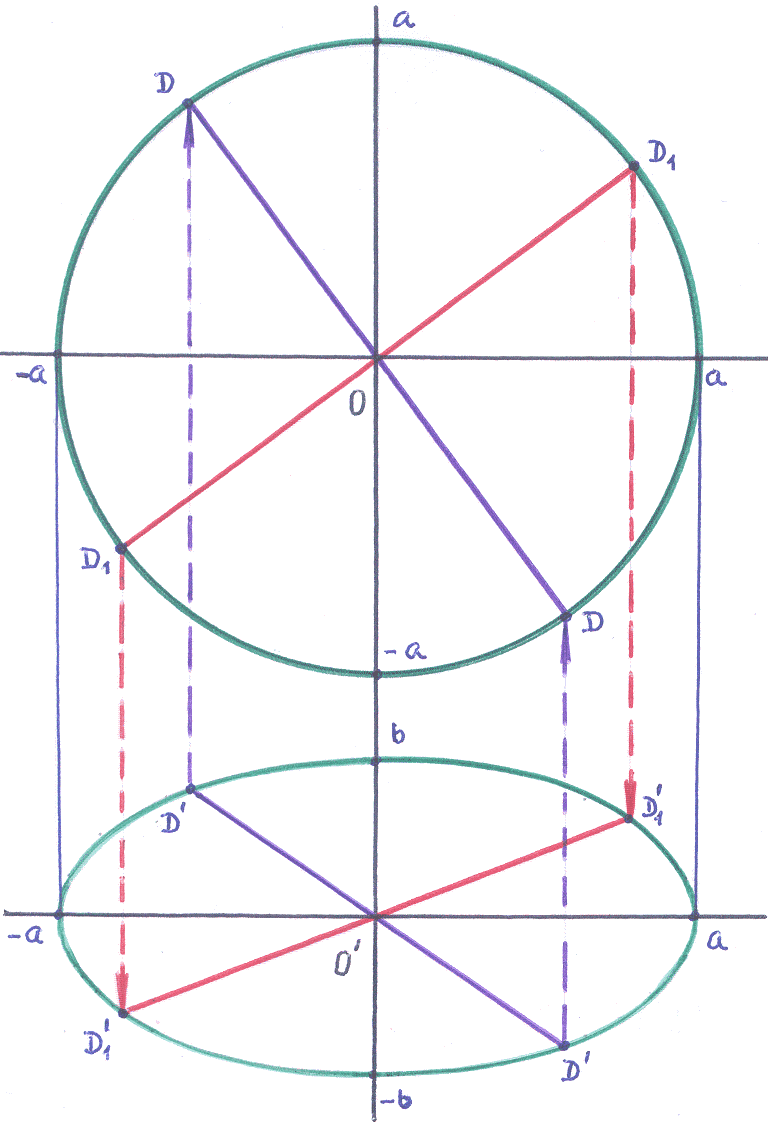 ешение:
ешение:
1). При
определении уравнений эллипса рассмотрен
геометрический способ построения
эллипса.
Для нас сейчас важно то, что ортогональное
параллельное проектирование превращает
окружность в эллипс. Отмечалось также,
что это равносильно сжатию окружности
с коэффициентом сжатия:
![]() =
=![]() .
.
2). По
условию мы имеем эллипс. Это значит, что
мы имеем диаметр окружности:
![]() =2
=2![]() .
.
Так как проекция окружности ортогональная,
то можем отметить центр окружности: на
перпендикуляре, идущем из центра эллипса,
и начертить окружность.
3). Отметим
на эллипсе один из его диаметров
![]() :
:
он проходит через центр эллипса. Нетрудно
отметить на окружности диаметр
![]() ,
,
который является проекцией отмеченного
диаметра
![]()
эллипса.
4). У
окружности отметим сопряжённый диаметр
![]() :
:
он перпендикулярен диаметру
![]() .
.
Отобразим диаметр
![]()
на эллипс. Получен диаметр
![]() ,
,
сопряжённый диаметру:
![]() .
.
Это и есть проекция перпендикулярного
диаметра окружности.
Ответ: указано в
тексте и на рисунке.
Замечание:
рассмотренный пример интересен тем,
что для нахождения сопряжённых диаметров
используются только геометрические
средства.
Пример 5–12:
Дан эллипс:
![]() .
.
Найти уравнения двух сопряжённых
диаметров этого эллипса, один из которых
проходит через точку
![]() (4,2).
(4,2).
Решение:
1). Учтём,
что все диаметры эллипса проходят через
начало координат:
![]() .
.
Для диаметра, проходящего через точку
![]() ,
,
вычисляем:
![]() =
=![]() .
.
2).
Воспользуемся выражением:
![]() =
=![]() =
=
![]() =
=
–![]()
для угловых коэффициентов сопряжённых
диаметров эллипса. Так как
![]() =
=![]() ,
,
то необходимо
![]() =–1.
=–1.
3). В
таком случае: если один диаметр имеет
уравнение
![]() =
=![]()
![]() ,
,
то другой:
![]() =–
=–![]() .
.
Ответ: один диаметр
имеет уравнение
![]() =
=![]()
![]() ,
,
другой:
![]() =–
=–![]() .
.
Пример 5–13:
Составить уравнение хорды эллипса
![]() ,
,
проходящей через точку
![]() (1,-2)
(1,-2)
и делящейся ею пополам.
Решение:
1). Учтём,
что все диаметры эллипса проходят через
начало координат:
![]() .
.
Для диаметра, проходящего через точку
![]() ,
,
вычисляем:
![]() =–2.
=–2.
Этот диаметр сопряжён искомой хорде.
2).
Воспользуемся условием:
![]() =
=![]() =
=
–![]() .
.
Это значит, что угловой коэффициент
искомой хорды
![]() =
=![]() .
.
3).
Уравнение хорды, проходящей через точку
![]()
и имеющей угловой коэффициент
![]() ,
,
можно записать в виде:
![]() ,
,
или
![]() .
.
Ответ: уравнение
хорды:
![]() .
.
Пример 5–14:
Составить уравнение диаметра гиперболы
![]()
для хорды, определяемой прямой
![]() .
.
Решение:
1). Так
как хорда имеет направление
![]() =2,
=2,
то сопряжённый ей диаметр имеет угловой
коэффициент
![]() =
=![]()
![]() =
=![]() .
.
2). Так
как диаметр
гиперболы проходит через начало
координат, то его уравнение:
![]() =
=![]()
![]() ,
,
или
![]() .
.
Ответ: уравнение
диаметра:
![]() .
.
Пример 5–15:
Составить уравнения сопряжённых
диаметров гиперболы
![]() ,
,
угол между которыми равен
![]() .
.
Решение:
1).
Воспользуемся выражением:
![]() =
=![]() =
=![]() .
.
2). Так
как
![]() =1
=1
=![]() ,
,
то из системы уравнений:

получим два решения:
![]() =–
=–![]() ,
,
![]() =–3,
=–3,
или
![]() =3,
=3,
![]() =
=![]() .
.
Так как диаметры проходят через начало
координат, пары сопряжённых диаметров:
а)
![]() =
=![]() ,
,
![]() =–3
=–3![]() ;
;
б)
![]() =3
=3![]() ,
,
![]() =
=![]()
![]() .
.
Ответ: уравнения
сопряжённых диаметров: а)
![]() =
=![]() ,
,
![]() =–3
=–3![]() ;
;
б)
![]() =3
=3![]() ,
,
![]() =
=![]()
![]() .
.
Пример 5–16:
Дана парабола:
![]() .
.
Через точку
![]() (–1,1)
(–1,1)
провести такую хорду, которая в этой
точке делилась бы пополам.
Решение:
1). Так
как хорда проходит через точку
![]() ,
,
то её уравнение запишем как:
![]() .
.
2). Из
уравнения параболы:
![]() =–4.
=–4.
Так как точка
![]()
есть середина хорды, то диаметр должен
через неё проходить! Из уравнения
диаметра:
![]() =
=![]()
получаем:
![]() ,
,
откуда
![]() =–4.
=–4.
3).
Уравнение
искомой хорды принимает вид:
![]() .
.
Ответ: уравнение
хорды:
![]() .
.
☻
Касательные
к кривым второго порядка.
Продолжим исследование кривых второго
порядка, используя общее для этих кривых
уравнение:
![]() .
.
(21)
Из
уравнения (21), используя канонические
уравнения кривых второго порядка,
получаем:
Окружность:
при
![]() =
=![]() =1,
=1,
![]() =0,
=0,
![]() =–
=–![]() ;
;
эллипс:
при
![]() =
=![]() ,
,
![]() =
=![]() ,
,
![]() =0,
=0,
![]() =–1.
=–1.
Гипербола:
при
![]() =
=![]() ,
,
![]() =–
=–![]() ,
,
![]() =0,
=0,
![]() =–1;
=–1;
парабола:
при
![]() =0,
=0,
![]() =1,
=1,
![]() =–
=–
p,
![]() =0.
=0.
Уравнение
(21) неявно
может определять либо функцию
![]() ,
,
либо
![]() .
.
Для определения касательной к кривой
![]()
или кривой
![]()
можно было бы воспользоваться понятием
производной. Мы поступим иначе:
воспользуемся определением касательной
рассмотрением предельного перехода по
отношению к секущей.
Обозначим
концы секущей: точки
![]()
![]()
и
![]()
![]() .
.
Так как точки
![]()
и
![]()
принадлежат кривой, то, используя
уравнение (20), можем записать:
![]() ,
, ![]() .
.
Вычитая
из первого равенства второе, получим
выражение:
![]() . (21)
. (21)
Рассмотрим два
случая:
1). Пусть
точка
![]()
не является вершиной линии второго
порядка, расположенной на оси
![]() ,
,
то есть
![]() .
.
Учитывая, что угловой коэффициент
секущей:
![]() =
=![]() ,
,
из равенства (21) получим:
![]() =
=![]() .
.
Предельное положение секущей при
неограниченном приближении точки
![]()
к точке
![]()
определяется выражением:
![]() =
=![]() =
=![]() . (22)
. (22)
2). Пусть
теперь точка
![]()
является вершиной линии второго порядка
и располагается на оси
![]() .
.
В этом случае
![]() =0
=0
и
![]() .
.
Разделим равенство (21) на разность:
![]() .
.
В этом случае получим: ![]() . (23)
. (23)
Так как
для всех кривых второго порядка:
![]() ,
,
то
![]() =0.
=0.
Это значит, что касательная к линии
второго порядка в вершине, лежащей на
оси
![]() ,
,
параллельна оси
![]() .
.
Общие
результаты применим для каждой из кривых
второго порядка.
Эллипс.
Так как для эллипса в общем уравнении:
A=![]() ,
,
B=![]() ,
,
C=0,
то выражение для углового коэффициента
касательной (22) принимает вид:
![]() =–
=–![]() .
.

Уравнение
касательной в точке
![]()
запишем, используя уравнение
![]() :
:
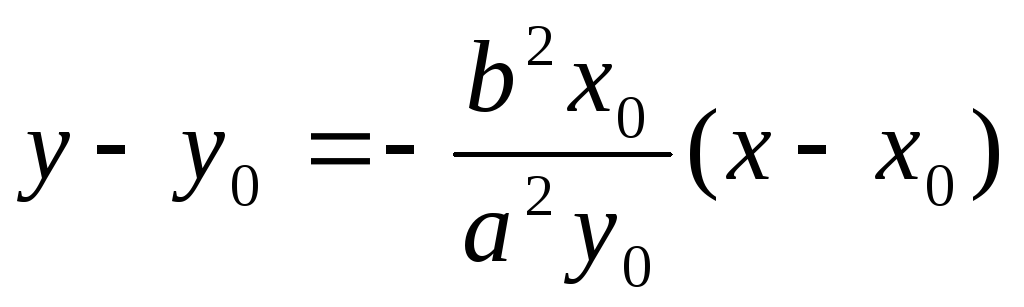
или
![]() =
=![]() .
.
Так как
точка
![]()
принадлежит эллипсу, последнее равенство
можно упростить, воспользовавшись
тождеством:
![]() =1.
=1.
Окончательно имеем уравнение касательной
к эллипсу:
![]() :
:
![]() =1. (24)
=1. (24)
Так как
окружность есть частный случай эллипса
при значениях
![]() ,
,
то уравнение касательной для окружности
имеет вид:
![]() =1. (25)
=1. (25)
Свойство
касательных эллипса:
касательные к эллипсу составляют равные
углы
с фокальными радиусами, проведёнными
в точку касания. Докажем это геометрически
изумительное свойство: лучи света,
испущенные из одного фокуса эллипса,
сбираются (все!) в другом фокусе (пусть
линия эллипса идеально отражающая)!
Для
доказательства свойства нам потребуется
рассмотреть треугольники
![]()
и
![]() ,
,
а именно доказать, что они подобны.
Для
нахождения отрезков
![]()
и
![]()
нормализуем уравнение касательной:
![]() ,
,
то есть уравнение:
![]()
или
![]() .
.
Для этого (вспомним!) необходимо умножить
уравнение на множитель
![]()
со знаком
![]() ,
,
если
![]() ,
,
и со знаком
![]() ,
,
если
![]() .
.
В нашем случае принимаем знак
![]() ,
,
а величина множителя:
 .
.
Тогда нормированное уравнение касательной:
![]() .
.
Учитывая:
![]()
![]()
и
![]()
![]() ,
,
найдём отклонения этих точек от
касательной
![]() :
:
![]() =
=
и
![]() =
=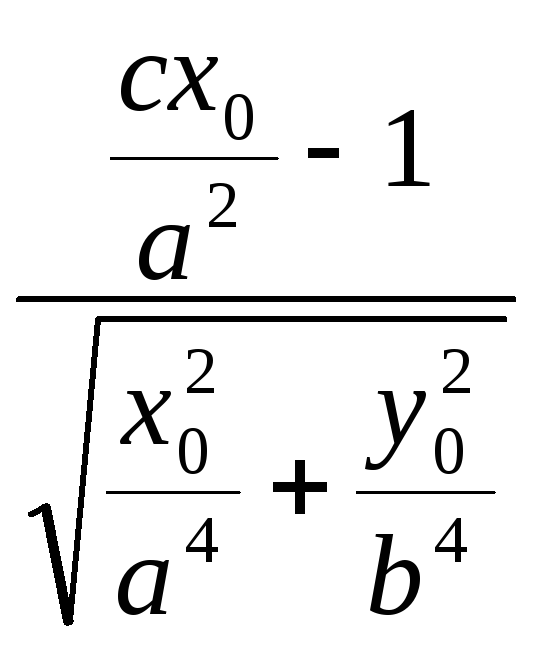 ,
,
причём:
![]() ,
,
![]() <0.
<0.
Для
доказательства подобия треугольников
![]()
и
![]()
составим отношение:
![]() =
=![]() =
= =
= =
=![]() =
=![]()
→ треугольники подобны.
Из
подобия треугольников
![]()
и
![]()
следует равенство углов:
![]()
и
![]() .
.
Свойство доказано.
Если
вращать эллипс вокруг его большой оси,
то получится эллиптическая поверхность
(это подробно рассматривается в Главе
6!). Если сделать эту поверхность изнутри
зеркальной, то (вспомним раздел физики
– оптику!) лучи, испускаемые источником,
помещённым в одном из фокусов, будут
собираться в другом фокусе.
☺☺
П ример
ример
5–17:
Даны две одинаковые зубчатые шестерни
эллиптической формы. Одна из них насажена
на ведущий вал (передаёт вращающий
момент), а вторая на ведомый (такая
конструкция называется редуктором).
Вычертить механизм зубчатой передачи
и проанализировать кинематику её
движения.
Решение:
1). В
соответствии с рисунком будем считать,
что ведущий вал зубчатого зацепления
помещён в фокус
![]()
нижней шестерёнки, а ведомый вал закреплён
в фокусе
![]()
верхней. Для работы зубчатой передачи
необходимо, чтобы расстояние
![]()
было неизменным. Это значит, что
выполняется равенство:
![]() =
=![]() .
.
2). Из
условия:
![]() =
=![]()
следует, что отрезки
![]()
и
![]()
принадлежат одной прямой. Тогда
![]() =
=![]()
и
![]() =
=![]() .
.
Из этого следует, что одновременно:
![]() =
=![]()
и отрезки
![]()
и
![]()
также принадлежат одной прямой.
3). Из
полученных в пункте 2) результатов имеем:
прямая
![]()
есть общая касательная находящихся в
зацеплении шестерёнок.
4). Теперь
не представляет большого труда вычертить
механизм зубчатого зацепления.
Вычерчивание верхнего эллипса (шестерёнки)
выполняем сжатием окружности радиуса
![]() .
.
На нижней дуге эллипса выбираем точку
![]() :
:
произвольно, но не посередине дуги (для
красоты!). На прямой:
![]() ,
,
отмечаем точку
![]() .
.
Аналогично строим точку
![]() .
.
Середина
отрезка
![]()
определяет центр нижнего эллипса (и
вспомогательной окружности!). Вычерчиваем
нижний эллипс. Рисунок готов!
5). Учтём,
что вектор скорости точки
![]()
направлен по общей касательной эллипсов,
а плечи этого вектора
![]()
относительно оси вращения
![]()
и
![]()
относительно
оси вращения
![]()
постоянно изменяются. Это значит, что
при постоянной угловой скорости ведущей
шестерёнки ведомая шестерёнка будет
вращаться с переменной угловой скоростью.
Это свойство редуктора с эллиптическими
шестерёнками используют в конструкциях
разных станков, например строгальных!
Ответ: в тексте
обосновано построение чертежа и
проанализированы кинематические
особенности эллиптического зубчатого
зацепления (редуктора).
☻
Найдём
условия того, что прямая
![]() :
:
![]()
касается эллипса
![]() ,
,
то есть совпадает с касательной эллипса
![]() :
:
![]() =
=![]()
в точке
![]()
![]() .
.
Известно,
что две прямые
![]()
и
![]()
совпадают, если
![]() =
=![]() =
=![]() .
.
В нашем случае это условие принимает
вид:
![]() ,
,
откуда
![]() =
=![]()
и
![]() =
=![]() .
.
Так как точка
![]()
принадлежит
![]() ,
,
то выполняется равенство:
![]() ,
,
или:
![]() . (26)
. (26)
Итак,
мы имеем необходимое условие (26) касания
заданной прямой
![]()
заданного эллипса. Будет ли это условие
достаточным? Пусть условие (26) выполняется.
Перепишем его в виде:
 .
.
Последнее
означает, что точка:
![]() =
=![]() ,
,
![]() =
=![]()
принадлежит эллипсу. Подставим координаты
точки
![]()
в уравнение касательной эллипса, то
есть в уравнение:
![]() =0.
=0.
Получаем:
![]() .
.
Это значит, если условие (26) выполняется,
то прямая
![]()
есть касательная эллипса. Таким образом,
условие (26) есть необходимое и достаточное
условие того, что
![]()
касается эллипса.
☺☺
Пример 5–18:
Найти уравнения касательных к эллипсу
![]() ,
,
параллельных прямой
![]() :
:![]() .
.
Найти расстояние между касательными.
Решение:
1).
Уравнение касательной должно иметь вид
![]() :
:
![]() =
=![]() ,
,
причём за счёт выбора соответствующего
значения параметра
![]()
можно добиться совпадения:
![]() =
=![]() .
.
Если
воспользоваться условием (26):
![]() ,
,
то для данного примера получим равенство:
![]() ,
,
откуда значение параметра
![]() =
=![]() 24.
24.
2 ).
).
Как и следовало ожидать (из геометрических
соображений!), у эллипса нашлось две
касательные, параллельные заданному
направлению. Одна
![]() :
:
![]()
и вторая
![]() :
:
![]() .
.
3). Найдём
расстояние
![]()
от точки (0,0) до касательной
![]() .
.
Для этого воспользуемся отклонением:
![]() =
=![]() .
.
Из этого следует:
![]() =
=![]() .
.
Расстояние между касательными равно
2![]() =
=![]() .
.
Ответ: касательные
![]() :
:
![]()
и
![]() :
:
![]() ,
,
расстояние 2![]() =
=![]() .
.
Замечание:
рассмотренный пример можно было решить
традиционным способом: найти производную
неявно заданной функции
![]()
и, приравняв её заданному прямой
![]()
угловому коэффициенту, из полученного
равенства вычислить координаты точки
касания
![]() ;
;
затем из условия принадлежности
![]()
касательной
![]()
вычислить параметр
![]() !
!
Здорово?
☻
Гипербола.
Так как для гиперболы в общем уравнении:
A=![]() ,
,
B=–![]() ,
,
C=0,
то выражение для углового коэффициента
касательной (22) принимает вид:
![]() =
=![]() .
.

Уравнение
касательной в точке
![]()
запишем, используя уравнение
![]() :
:

или
![]() =
=![]() .
.
Уравнение
касательной в точке
![]()
запишем, используя уравнение
![]() :
:
Так как
точка
![]()
принадлежит гиперболе, последнее
равенство можно упростить, воспользовавшись
тождеством:
![]() =1.
=1.
Окончательно имеем уравнение касательной
к гиперболе: ![]() :
:
![]() =1. (27)
=1. (27)
Свойство
касательных гиперболы:
касательные к гиперболе составляют
равные
углы
с фокальными радиусами, проведёнными
в точку касания.
Для
доказательства свойства нам потребуется
рассмотреть треугольники
![]()
и
![]() ,
,
а именно доказать, что они подобны.
Для
нахождения отрезков
![]()
и
![]()
нормализуем уравнение касательной:
![]() ,
,
то есть уравнение:
![]()
или
![]() .
.
Для этого (вспомним!) необходимо умножить
уравнение на множитель
![]()
со знаком
![]() ,
,
если
![]() ,
,
и со знаком
![]() ,
,
если
![]() .
.
В нашем случае принимаем знак
![]() ,
,
а величина множителя:
 .
.
Тогда нормированное уравнение касательной:
![]() .
.
Учитывая:
![]()
![]()
и
![]()
![]() ,
,
найдём отклонения этих точек от
касательной
![]() :
:
![]() =
=
и
![]() =
= ,
,
причём:
![]() .
.
Условие:
![]()
отражает тот факт, что фокусы гиперболы
располагаются по разные стороны
касательной, то есть находятся в разных
полуплоскостях.
Докажем
подобие треугольников
![]()
и
![]() для
для
случая, когда точка принадлежит правой
ветви гиперболы (используем симметрию
кривой!). Тогда можем записать:
![]() =
=![]() =
= =
= =
=![]() =
=![]()
→ треугольники подобны.
Из
подобия треугольников
![]()
и
![]()
следует равенство углов:
![]()
и
![]() .
.
Свойство доказано.
Если
вращать гиперболу вокруг её действительной
оси, то получится гиперболическая
поверхность – гиперболоид (это подробно
рассматривается в Главе 6!). Если сделать
эту поверхность изнутри зеркальной, то
(вспомним раздел физики – оптику!) лучи,
испускаемые источником, помещённым в
одном из фокусов, будем наблюдать так
(по направлению
![]() ),
),
будто их излучает другой фокус (мнимое
изображение первого фокуса!). Имеет
место расходящийся пучок лучей!
Замечание:
полученный для гиперболоида результат
превращает грозное оружие инженера
Гарина – гиперболоид инженера Гарина
в безобидную игрушку!
Найдём
условия того, что прямая
![]() :
:
![]()
касается гиперболы
![]() ,
,
то есть совпадает с касательной гиперболы
![]() :
:
![]() =
=![]()
в точке
![]() .
.
Известно,
что две прямые
![]()
и
![]()
совпадают, если
![]() =
=![]() =
=![]() .
.
В нашем случае это условие принимает
вид:
![]() ,
,
откуда
![]() =
=![]()
и
![]() =
=![]() .
.
Так как точка
![]()
принадлежит
![]() ,
,
то выполняется равенство:
![]() ,
,
или:
![]() . (27)
. (27)
Итак,
мы имеем необходимое условие (27) касания
заданной прямой
![]()
заданной гиперболы. Будет ли это условие
достаточным? Пусть условие (27) выполняется.
Перепишем его в виде:
 .
.
Последнее
означает, что точка:
![]() =
=![]() ,
,
![]() =
=![]()
принадлежит гиперболе. Подставим
координаты точки
![]()
в уравнение касательной гиперболы, то
есть в уравнение:
![]() =0.
=0.
Получаем:
![]() .
.
Это значит, если условие (27) выполняется,
то прямая
![]()
есть касательная гиперболы. Таким
образом, условие (27) есть необходимое и
достаточное условие того, что
![]()
касается гиперболы.
Замечание:
легко заметить, что условие (27) невозможно,
если
![]() ;
;
этому условию геометрически соответствуют
все случаи, когда угловой коэффициент
прямой
![]()
попадает в диапазон, определяемый
асимптотами гиперболы:
![]() .
.
☺☺
Пример 5–19:
Найти уравнения касательных к гиперболе
![]() ,
,
параллельных прямой
![]() :
:
![]() .
.
Р ешение:
ешение:
1).
Уравнение касательной должно иметь вид
![]() :
:
![]() =
=![]() ,
,
причём за счёт выбора соответствующего
значения параметра
![]()
можно добиться совпадения прямой
![]()
с касательной
![]() .
.
Проверим
выполнимость условия (27):
![]() .
.
Угловой коэффициент прямой
![]()
равен
![]() >
>![]()
→ касательная существует, и условие
(27) выполняется.
2).
Воспользуемся условием:
![]() .
.
В данном примере:
![]() =
=![]() .
.
Значение параметра
![]() =
=![]() 32.
32.
3). Как
и следовало ожидать (из геометрических
соображений!), у гиперболы нашлось две
касательные, параллельные заданному
направлению. Одна
![]() :
:
![]()
и вторая
![]() :
:
![]() .
.
Ответ: касательные
одна
![]() :
:
![]()
и вторая
![]() :
:
![]() .
.
Замечание:
важно не пропустить проверку углового
коэффициента прямой
![]() :
:
возможно не потребуется находить
касательную!
☻
Парабола.
Так как для гиперболы в общем уравнении:
A=0,
B=1,
C=–p,
то выражение для углового коэффициента
касательной (22) принимает вид:
![]() =
=![]() .
.

Уравнение
касательной в точке
![]()
запишем, используя уравнение
![]() :
:
![]()
или
![]() .
.
Так как
точка
![]()
принадлежит параболе, последнее равенство
можно упростить, воспользовавшись
тождеством:
![]() .
.
Окончательно имеем уравнение касательной
к параболе ![]() :
:
![]() ,
,
или
![]() . (28)
. (28)
Свойство
касательных параболы:
касательные к параболе составляют
равные
углы
с фокальным радиусом параболы и прямой,
параллельной оси параболы, и проходящей
через точку касания параболы. В
соответствии с рисунком это значит, что
угол
![]()
равен углу между касательной
![]()
и прямой
![]() ,
,
параллельной оси
![]() .
.
Для
доказательства свойства нам потребуется
рассмотреть треугольник
![]()
и доказать, что он равнобедренный.
Обозначим:
![]()
![]() .
.
Учитывая уравнение касательной (28)
получаем:
![]() =–
=–![]() .
.
В то же время у параболы:
![]() =
=![]() +
+![]() .
.
Вычислим также:
![]() =
=![]() +
+![]() =
=![]() +
+![]() .
.
Доказано, что треугольник
![]()
равнобедренный. Из этого следует, что
угол
![]() =
=![]() =
=![]() .
.
Но углы
![]()
и
![]()
равны как углы с параллельными сторонами.
Из этого следует равенство углов
![]() =
=![]() =
=![]() .
.
Свойство доказано!
Найдём
условия того, что прямая
![]() :
:
![]()
касается параболы
![]() ,
,
то есть совпадает с касательной параболы
![]() :
:
![]() =
=![]()
в точке
![]() .
.
Известно,
что две прямые
![]()
и
![]()
совпадают, если
![]() =
=![]() =
=![]() .
.
В нашем случае это условие принимает
вид:
![]() ,
,
откуда
![]() =
=![]()
и
![]() =
=![]() .
.
Так как точка
![]()
принадлежит
![]() ,
,
то выполняется равенство:
![]() ,
,
или:
![]() . (29)
. (29)
Итак,
мы имеем необходимое условие (29) касания
заданной прямой
![]()
заданной параболы. Будет ли это условие
достаточным? Пусть условие (29) выполняется.
Перепишем его в виде:  .
.
Последнее
означает, что точка:
![]() =
=![]() ,
,
![]() =
=![]()
принадлежит параболе. Подставим
координаты точки
![]()
в уравнение касательной параболы, то
есть в уравнение:
![]() .
.
Получаем:
![]() ,
,
или![]() .
.
Это значит, если условие (29) выполняется,
то прямая
![]()
есть касательная гиперболы. Таким
образом, условие (29) есть необходимое и
достаточное условие того, что
![]()
касается гиперболы.
Замечание:
легко заметить, что условие (29) невозможно
при значении
![]() ,
,
если
![]()
и
![]()
имеют разные знаки; это геометрически
невозможно, когда парабола расположена
справа от оси
![]() ,
,
а точка касания оказалась слева от неё.
Отметим
оптические свойства параболы: лучи
света, исходящие из фокуса параболы,
после зеркального отражения от параболы
образуют пучок, параллельный
оси параболы
(это учитывают при создании прожекторов
и теле- и радиоантенн)!
Замечание:
Это значит, что у инженера Гарина был
не гиперболоид (как пошутил Алексей
Толстой), а параболоид!
☺☺
Пример 5–20:
Найти уравнение касательной к параболе
![]() ,
,
параллельной прямой
![]() :
:
![]() .
.
Решение:
1 ).
).
Уравнение касательной должно иметь вид
![]() :
:
![]() ,
,
или
![]() ,
,
причём за счёт выбора соответствующего
значения параметра
![]()
можно добиться совпадения прямой
![]()
с касательной
![]() .
.
2).
Воспользуемся условием:
![]() .
.
В данном примере:
![]() .
.
Значение параметра
![]() =4.
=4.
Знаки
![]()
и
![]()
совпадают!
3). Как
и следовало ожидать (из геометрических
соображений!), у параболы одна касательная,
параллельная заданному направлению.
Одна
![]() :
:
![]() .
.
Ответ: касательная
одна
![]() :
:
![]() ,
,
или
![]() .
.
Рассмотрим несколько
примеров, в которых обобщается
использование свойств кривых второго
порядка.
☻
Пример 5–21:
Составить уравнение касательной к
эллипсу:
![]() ,
,
перпендикулярной прямой
![]() :
:![]() .
.
Решение:
1). Имея
![]() ,
,
легко записать уравнение касательной
эллипса, перпендикулярной
![]() ,
,
в виде
![]() :
:
![]() =
=![]() ,
,
причём за счёт выбора соответствующего
значения параметра
![]()
можно добиться совпадения:
![]() =
=![]() .
.
Если
воспользоваться условием (26):
![]() ,
,
то для данного примера получим равенство:
![]() ,
,
откуда значение параметра
![]() =
=![]() 10.
10.
2). Запишем
уравнения касательных, перпендикулярных
заданному направлению. Одна
![]() :
:
![]()
и вторая
![]() :
:
![]() .
.
Ответ: касательные
![]() :
:
![]()
и
![]() :
:
![]() .
.
Пример 5–22:
На эллипсе:
![]()
найти точку
![]() ,
,
ближайшую к прямой
![]() :
:![]()
и вычислить расстояние от точки M0
до этой прямой.
Решение:
1 ).
).
Учтём свойство эллипса по отношению к
его касательным: его верхняя половина
располагается под касательной, а нижняя
над касательной. Заметим также, что
рисунок не отражает окончательные
результаты решения задачи: взаимное
расположение всех геометрических фигур
на самом деле может оказаться другим.
Рисунок мы рассматриваем как эскиз
образа исходных данных задачи.
2). Так
как касательные:
![]()
и
![]()
должны быть параллельны прямой
![]() ,
,
то общим уравнением
для
них может быть запись:
![]() =
=![]() ,
,
причём за счёт выбора соответствующего
значения параметра
![]()
можно добиться совпадения:
![]()
с
![]()
и
![]() .
.
Если
воспользоваться условием (26):
![]() ,
,
то для данного примера получим равенство:
![]() ,
,
откуда значение параметра
![]() =
=![]() 24.
24.
Для верхней касательной имеем
![]() :
:![]() ,
,
или
![]() ,
,
для нижней касательной, соответственно
![]() :
:
![]() .
.
3).
Полученные результаты позволяют уточнить
взаимное расположение
![]() ,
,
![]() ,
,
![]()
и эллипса. Так как прямая
![]()
пересекает ось
![]()
в точке (0; 11.5), то ближе к прямой
![]()
располагается множество точек касательной
![]() .
.
Так как прямая
![]()
пересекает ось
![]()
в точке (0; 12), то она располагается выше
прямой
![]() .
.
Точка
![]()
определяется из полученных ранее
выражений с учётом окончательной записи
![]() :
:
![]() =
=![]() =
=![]() =–5,
=–5,
![]() =
=![]() =
=![]() =2.
=2.
4).
Нормализуя заданное уравнение, получаем
![]() :
:![]() .
.
Для нахождения расстояния между
параллельными прямыми:
![]()
и
![]()
воспользуемся точкой (0,12), принадлежащей
![]() ,
,
а не точкой
![]() .
.
Для выделенной точки отклонение от
![]() :
:
![]() =
=![]() =–
=–![]() .
.
5). Тогда
можем записать:
![]() =
=![]() =
=![]() .
.
Ответ: точка:
![]() (–5,2);
(–5,2);
расстояние:
![]() =
=![]() .
.
Пример 5–23: На
гиперболе:
![]()
найти точку
![]()
![]() ,
,
ближайшую к прямой
![]() :
:
![]()
и вычислить расстояние от точки
![]()
до этой прямой.
Решение:
1 ).
).
Учтём свойство гиперболы по отношению
к её касательным: её верхняя половина
располагается под касательной, а нижняя
над касательной. Заметим также, что
рисунок не отражает окончательные
результаты решения задачи: взаимное
расположение всех геометрических фигур
на самом деле может оказаться другим.
Рисунок мы рассматриваем как эскиз
образа исходных данных задачи.
2). Из
условия следует, что угловые коэффициенты
асимптот гиперболы: k=![]() .
.
Угловой коэффициент прямой
![]()
равен
![]() =
=![]() .
.
Проверим
выполнимость условия (27):
![]() .
.
Угловой коэффициент прямой
![]()
равен
![]() >
>![]()
→ касательная существует, и условие
(27) выполняется.
3). Так
как касательные:
![]()
и
![]()
должны быть параллельны прямой
![]() ,
,
то общим уравнением
для
них может быть запись:
![]() =
=![]() ,
,
причём за счёт выбора соответствующего
значения параметра
![]()
можно добиться совпадения:
![]()
с
![]()
и
![]() .
.
Воспользуемся
условием:
![]() .
.
В данном примере:
![]() =
=![]() .
.
Значение параметра
![]() =
=![]() 12.
12.
Это значит
![]() :
:![]() ,
,
![]() :
:
![]() .
.
4). Так
как прямая
![]()
пересекает ось
![]()
в точке
![]() ,
,
ближе к ней располагается прямая
![]() .
.
Это значит, по условию задачи нам нужна
точка
![]() .
.
Вычислим её координаты:
![]() =
=![]() =
=![]() =–6,
=–6,
![]() =
=![]() =
=![]() =3.
=3.
5).
Нормализуя заданное уравнение, получаем
![]() :
:![]() =0.
=0.
Для нахождения расстояния между
параллельными прямыми:
![]()
и
![]()
воспользуемся точкой (–4,0), принадлежащей
![]() ,
,
а не точкой
![]() .
.
Для выделенной точки отклонение от
![]() :
:
![]() =
=![]() ,
,
или
![]() =–
=–![]() .
.
6). Тогда
можем записать:
![]() =
=![]() =
=![]() .
.
Ответ: точка:
![]() (–6,3);
(–6,3);
расстояние:
![]() =
=![]() .
.
Пример 5–24:
На параболе:
![]()
найти точку
![]() ,
,
ближайшую к прямой
![]()
и вычислить расстояние от точки
![]()
до этой прямой.
Решение:
1). Учтём
свойство параболы по отношению к её
касательным: её верхняя половина
располагается под касательной, а нижняя
над касательной. Заметим также, что
рисунок не отражает окончательные
результаты решения задачи: взаимное
расположение всех геометрических фигур
на самом деле может оказаться другим.
Рисунок мы рассматриваем как эскиз
образа исходных данных задачи. Понятно,
что точка должна лежать на касательной
гиперболы, параллельной заданной прямой.
2 ).
).
Из условия следует, что угловой коэффициент
касательной должен быть:
![]() =–
=–![]() .
.
Это значит, что точка касания располагается
на нижней ветви параболы.
3).
Уравнение касательной должно иметь вид
![]() :
:
![]() ,
,
или
![]() ,
,
причём за счёт выбора соответствующего
значения параметра
![]()
можно добиться совпадения прямой
![]()
с касательной
![]() .
.
4).
Воспользуемся условием:
![]() .
.
В данном примере:
![]() .
.
Значение параметра
![]() =36.
=36.
Тогда уравнение касательной
![]() :
:![]()
4).
Вычислим координаты точки касания:
![]() =
=![]() =
=![]() =9
=9
и
![]() =
=![]() =
=![]() =–24.
=–24.
5).
Нормализуя заданное уравнение, получаем
![]() :
:![]()
![]() =0.
=0.
Для нахождения расстояния между
параллельными прямыми:
![]()
и
![]()
воспользуемся точкой (–9,0), принадлежащей
![]() ,
,
а не точкой
![]() .
.
Для выделенной точки отклонение от
![]() :
:
![]() =
=![]() =–10.
=–10.
6). Тогда
можем записать:
![]() =
=![]() =10.
=10.
Ответ: точка:
![]() (9,–24);
(9,–24);
расстояние:
![]() =10.
=10.
☻
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
tdayne |
Касательные к эллипсу
|
|
03/12/11 |
|
|
|
|
|
Someone |
Re: Касательные к эллипсу
|
||
23/07/05 |
А сколько общих точек у эллипса и его касательной?
|
||
|
|
|||
|
tdayne |
Re: Касательные к эллипсу
|
|
03/12/11 |
Хм, немного пытаюсь сообразить) Получается, что эта точка должна принадлежать и прямой, то есть можно подставить координаты в ее уравнение — 11.01.2012, 00:10 — Ан нет, 2 уравнения и 3 неизвестных — 11.01.2012, 00:11 — А сколько общих точек у эллипса и его касательной? одна) Но откуда взять 3е уравнение?
|
|
|
|
|
Someone |
Re: Касательные к эллипсу
|
||
23/07/05 |
Не понял, какие “три” уравнения. Я вижу только уравнение эллипса и уравнение семейства параллельных прямых.
|
||
|
|
|||
|
tdayne |
Re: Касательные к эллипсу
|
|
03/12/11 |
Разобрался Все получилось, ответ:
|
|
|
|
|
Someone |
Re: Касательные к эллипсу
|
||
23/07/05 |
Господи, какие премудрости. Я бы написал систему уравнений
|
||
|
|
|||
|
tdayne |
Re: Касательные к эллипсу
|
|
03/12/11 |
Единственное? Так касательных всегда же будет 2. Ну разве что исключая случай, когда исходная прямая и есть касательная
|
|
|
|
|
Someone |
Re: Касательные к эллипсу
|
||
23/07/05 |
А причём тут количество касательных? Вы помните, что я у Вас спросил в первом своём сообщении?
|
||
|
|
|||
|
tdayne |
Re: Касательные к эллипсу
|
|
03/12/11 |
Всё) Решил Вашу систему, ответ сошелся
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
фокусы которого лежат на оси абсцисс симметрично
относительно начала координат, зная, кроме того,
что:
и 2;
равна 10, а расстояние между фокусами 2c=8;
24, а расстояние между фокусами 2c=10;
его фокусами 2c=6 и эксцентриситет e=3/5.
равна 20, а эксцентриситет e=3/5.
10, а эксцентриситет e=12/13;
его директрисами равно 5 и расстояние между
фокусами 2c=4;
равна 8, а расстояние между директрисами равно 16;
6, а расстояние между директрисами равно 13;
его директрисами равно 32 и e=1/2.
уравнение эллипса, фокусы которого лежат на оси
ординат симметрично начала координат, зная,
кроме того, что:
соответственно 7 и 2;
равна 10, а расстояние между фокусами 2c=8;
его фокусами 2c=24 и эксцентриситет e=12/13.
16, а эксцентриситет e=3/5.
его фокусами 2c=6 и расстояние между директрисами
равно 50/3;
его директрисами равно 32/3 и эксцентриситет e=3/4.
каждого из следующих эллипсов:
эксцентриситет, уравнения директрис.
четырехугольника, две вершины которого лежат в
фокусах эллипса
совпадают с концами его малой оси.
эксцентриситет, уравнения директрис.
четырехугольника, две вершины которого лежат в
фокусах эллипса
концами его малой оси.
расстояние от фокуса F(c; 0) эллипса
односторонней с этим фокусом директрисы.
циркулем, построить фокусы эллипса
что изображены оси координат и задана масштабная
единица).
–3.
из точек A1(-2; 3), A2(2; -2), A3(2;
-4), A4(-1; 3), A5(-4; -3), A6(3; -1), A7(3;
-2), A8(2; 1), A9(0; 15), A10(0; -16) лежат на эллипсе
внутри и какие вне его.
линии опеределяются следующими уравнениями.
Изобразить эти линии на чертеже.
эллипса e=2/3, фокальный радиус точки М эллипса
равен 10. Вычислить расстояние от точки М до
односторонней с этим фокусом директрисы.
эллипса e=2/5, расстояние от точки эллипса до
директрисы равно 20. Вычислить расстояние от
точки М до фокуса, односторонней с этой
директрисой.
уравнения прямых, на которых лежат фокальные
радиусы точки М1.
459
точка M1(-4; 2,4) лежит
на эллипсе
М1.
эллипса e=1/3, центр его совпадает с началом
координат, один из фокусов (-2; 0). Вычислить
расстояние от точки М1 эллипса с абсциссой, равной 2, до
директрисы, односторонней с данным фокусом.
эллипса e=1/2, центр его совпадает с началом
координат, одна из директрис дана уравнением x=16.
Вычислить расстояние от точки M1
эллипса с абсциссой, равной –4, до
фокуса, одностороннего с данной директрисой.
эллипса
правого фокуса равно 14.
эллипса
левого фокуса равно 2,5.
большой оси. Определить расстояния от точек
пересечения этого перпендикуляра с эллипсом до
фокусов.
уравнения эллипса, фокусы которого расположены
на оси абсцисс симметрично относительно начала
координат, если даны:
и его малая полуось b=3;
-2) эллипса и его большая полуось
a=4;
М2(
и его эксцентриситет e=2/3;
-5/3) эллипса и его эксцентриситет
e=2/3;
12) эллипса и расстояние r1=20
от нее до левого фокуса.
и расстояние между его директрисами, равное 10.
эксцентриситет e эллипса, если:
из фокусов под углом 600;
фокусами виден и вершин малой оси под прямым
углом;
директрисами в три раза больше расстояния между
фокусами;
перпендикуляра, опущенного из центра эллипса на
его директрису, делится вершиной эллипса
пополам.
эллипса проведен перпендикуляр к его большой оси
(см. рис.). Определить, при каком значении
эксцентриситета эллипса отрезки
параллельны.
уравнение эллипса с полуосями a, b и центром C(x0, y0), если
известно, что оси симметрии эллипса параллельны
осям координат.
абсцисс в точке А(3; 0) и оси ординат в точке В(0; -4).
Составить уравнение этого эллипса, зная, что его
оси симметрии параллельны координатным осям.
является центром эллипса, касающегося обеих
координатных осей. Составить уравнение этого
эллипса, зная, что его оси симметрии параллельны
координатным осям.
каждое из следующих уравнений определяет эллипс,
и найти координаты его центра С, полуоси,
эксцентриситет и уравнения директрис:
линии определяются следующими уравнениями.
Изобразить эти линии на чертеже.
уравнение эллипса, зная, что:
равна 26 и фокусы суть F1(-10; 0), F2(14;0);
473.2
2 и фокусы суть F1(-1; -1), F2(1;
1);
473.3
эксцентриситет e=
473.4
расстояние между директрисами равно
474
эксцентриситет
фокус F (-4; 1) и уравнение соответствующей
директрисы
уравнение эллипса, если известны его
эксцентриситет e=1/2, фокус F(-4; 1) и уравнение
соответствующей директрисы
на эллипсе, фокус которого F(-1; -4), а
соответствующая директриса дана уравнением
уравнение эллипса, если известны его
эксцентриситет e=1/2, фокус F(3; 0) и уравнение
соответствующей директрисы
-1) лежит на эллипсе, фокус
которого F(1; 0), а соответствующая директриса дана
уравнением
-1) является концом малой оси
эллипса, фокусы которого лежат на прямой
уравнение этого эллипса, зная его эксцентриситет
e=
пересечения прямой
пересечения прямой
пересечения прямой
расположена прямая относительно эллипса:
пересекает ли, касается или проходит вне его,
если прямая и эллипс заданы следующими
уравнениями:
каких начениях m прямая
эллипса.
при котором прямая
уравнение касательной к эллипсу
точке M1(x1; y1).
касательные к эллипсу
в концах одного и того же диаметра, параллельны.
(Диаметром эллипса называется его хорда,
проходящая через его центр).
уравнения касательных к эллипсу
прямой
уравнения касательных к эллипсу
к прямой
прямой
ближайшую к прямой
этой прямой.
проведены касательные к эллипсу
их уравнения.
проведены касательные к эллипсу
уравнение хорды, соединяющей точки касания.
проведены касательные к эллипсу
расстояние d от точки Р до хорды эллипса,
соединяющей точки касания.
через точку А(4; -1) и касается прямой
уравнение этого эллипса при условии, что его оси
совпадают с осями координат.
уравнение эллипса, касающегося двух прямых
условии, что его ося совпадают с осями координат.
произведение расстояний от центра эллипса до
точки пересечения любой его касательной с
фокальной осью и до основания перпендикуляра,
опущенного из точки касания на фокульную ось,
если величина постоянная, равная квадрату
большой полуоси эллипса.
произвдение расстояний от фокусов до любой
касательной к эллипсу равно квадрату малой
полуоси.
эллипса, фокусы которого находятся в точках F1(-3;
0), F2(3; 0). Составить
уравнение этого эллипса.
уравнение эллипса, фокусы которого расположены
на оси абсцисс симметрично относительно начала
координат, если известны уравнение касательной к
эллипсу
прямая, касающаяся эллипса в некоторой точке М,
составляет равные углы с фокальными радиусами F1M, F2M и проходит
вне угла F1MF2.
эллипса
Ox направлен луч света. Известно, что
до эллипса, луч на него отразился. Составить
уравнение прямой, на которой лежит отраженный
луч.
пересечения эллипсов
эллипсы
в четырех точках, лежающих на окружности с
центром в начале координат, определить радиус R
этой окружности.
полуоси эллипса, полученного проектированием на
плоскость
плоскости
полуось которого равна 6, является проекцией
окружности радиуса R=12. Опредилть угол
эллипс и окружность.
круглого цилиндра является окружность радиуса
R=8. Определить полуоси эллипса, полученного в
сечении этого цилиндра плоскостью, наклоненной к
его оси под уголом
круглого цилиндра является окружность радиуса R=
цилиндра нужно его пересечь плоскостью, чтобы в
сечении получить эллипс с большой полуосью a=2.
сжатием (или равномерным растяжением) плоскости
к оси абсцисс называется такое преобразование
точек плоскости, при котором произвольная точка
M(x; y) перемещается в точку M’(x’; y’) (рис.1 ) так, что
x’=x, y’=qy, где q>0 – постоянная, называемая
коэффициентом равномерного сжатия. Аналогично
рпи помощи уравнения x’=qx, y’=y определяется
равномерное сжатия плоскости к оси Oy (рис. 2).
Определить, в какую линию преобразуется
окружность
равномерного сжатия плоскости к оси абсцисс q=4/5.

равномерного сжатия плоскости к оси Oy равен 3/4.
Определить уравнение линии, в которую при таком
сжатии преобразуется эллипс
линии, в которую преобразуется эллипс
равномерных сжатиях плоскости к координатным
осям, если коэффициенты равномерного сжатия
плоскости к осям Ox и Oy равны соответственно 4/3 и
6/7.
коэффициент q равномерного сжатия плоскости к
оси Ox, при котором эллипс
в эллипс
коэффициент q равномерного сжатия плоскости к
оси Oy, при котором эллипс
в эллипс
коэффициенты q1, q2 двух последовательных равномерных
сжатий плоскости к осям Ox и Oy, при которых
эллипс
 И эта же точка принадлежит эллипсу, то есть можно подставить
И эта же точка принадлежит эллипсу, то есть можно подставить 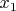 и
и  в его уравнение. Как раз получим 3 уравнения с тремя неизвестными.
в его уравнение. Как раз получим 3 уравнения с тремя неизвестными.  и
и  , находим
, находим 

 и посмотрел, когда она имеет единственное решение.
и посмотрел, когда она имеет единственное решение. спасибо.
спасибо.