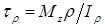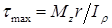Кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент T.
Брусья, испытывающие кручение, принято называть валами.
Внутренний крутящий момент
Внутренние скручивающие моменты появляются под действием внешних крутящих моментов mi, расположенных в плоскостях, перпендикулярных к продольной оси бруса.
Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.
Величина крутящего момента в любом сечении вала определяется методом сечений:
т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов mi, расположенных по одну сторону от рассматриваемого сечения.
Правило знаков внутренних скручивающих моментов:
Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.
В технике наиболее широко используются валы круглого поперечного сечения.
Теория кручения круглых валов основана на следующих гипотезах:
- поперечное сечение, плоское до деформации вала, остается плоским и после деформации;
- радиусы, проведенные мысленно в любом поперечном сечении, в процессе деформации вала не искривляются.
Напряжения при кручении
В поперечных сечениях вала при кручении имеют место только касательные напряжения.
Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле:
где Iρ — полярный момент инерции.
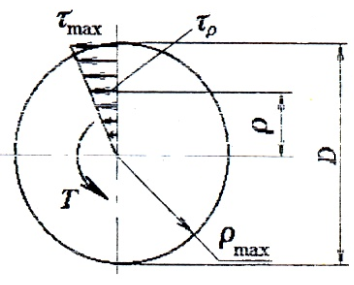
Эпюра касательных напряжений при кручении имеет следующий вид:
Касательные напряжения меняются по линейному закону и достигают максимального значения на контуре сечения при ρ= ρmax:
Здесь:
— полярный момент сопротивления.
Геометрические характеристики сечений:
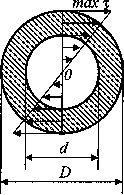
а) для полого вала:
б) для вала сплошного сечения (c=0)
в) для тонкостенной трубы (t<0,9)
где
— радиус срединной поверхности трубы.
Деформации
Деформации валов при кручении заключаются в повороте одного сечения относительно другого.
Угол закручивания вала на длине Z определяется по формуле:
Если крутящий момент и величина GIρ, называемая жесткостью поперечного сечения при кручении, постоянны, для участка вала длиной l имеем:
Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания:
Расчет валов сводится к одновременному выполнению двух условий:
- условию прочности:
- условию жесткости:
Для стальных валов принимается:
Используя условия прочности и жесткости, как и при растяжении – сжатии можно решать три типа задач:
- проверочный расчет, заключающийся в проверке выполнения условий прочности и жесткости при известных значениях крутящего момента, размеров и материала вала.
- Проектировочный расчет, при котором вычисляются диаметры:
при этом берется большее из найденных значений, а затем принимается стандартное значение по ГОСТ. - Определение грузоподъемности вала:
Из двух найденных значений крутящего момента необходимо принять меньшее.
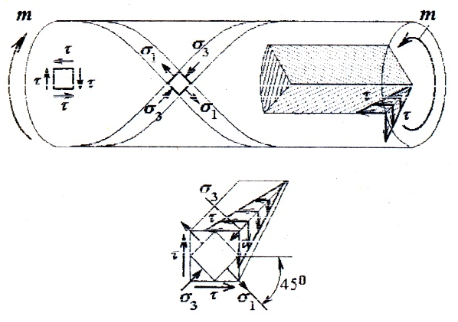
При кручении, наряду с касательными напряжениями в поперечных сечениях, в соответствии с законом парности, касательные напряжения возникают и в продольных сечениях. Таким образом, во всех точках вала имеет место чистый сдвиг.
Главные напряжения σ1 = τ, σ3 = -τ наклонены под углом α=±45о к образующей.
Потенциальная энергия упругой деформации определяется по формуле
или для участка вала при постоянном T и GIρ
Лекции по сопромату >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
В этой статье начнем говорить о кручении. Это одна из базисных тем в сопромате, как и растяжение-сжатие. Знания этой темы помогут тебе при изучении более сложных тем курса «сопротивление материалов».
Кручение – это такой вид деформации, при котором в сечениях стержня возникают крутящие моменты (T).
На кручение, как правило, работают детали, которые называются валами. Детали, которые широко используются в машиностроении.
Что такое крутящий момент?
Крутящий момент – это внутренний силовой фактор, возникающий в сечениях стержней испытывающих деформацию кручения.
На практике же стержни не работают исключительно на кручение, они могут и растягиваться, и изгибаться. Но это уже более продвинутые темы – сложное сопротивление. В этом же разделе будем рассматривать чистое кручение.
В чем измеряется крутящий момент и как обозначается?
Крутящие моменты обозначаются буквой – T (сокращённое с английского: Torque – крутящий момент), однако, часто в другой литературе ты можешь встретить обозначение — Мкр. Ты можешь использовать любое обозначение, какое больше нравиться, либо которое использует твой преподаватель.
В задачах тебе будут даны крутящие моменты, скорее всего, в Н·м либо кН·м.
Построение эпюры крутящих моментов
В этой статье расскажу, как строить эпюры при кручении: крутящих моментов, максимальных касательных напряжений и углов закручивания (углов поворотов).
На самом деле, многие рассматриваемые здесь принципы сильно похожи на те, что мы изучали ранее в уроке про построение эпюр при растяжении (сжатии). Здесь фактически будем делать всё то же самое, только оперировать другими обозначениями и названиями. После изучения того урока, с кручением у тебя точно не возникнет никаких трудностей.
В качестве примера, возьмём следующую расчётную схему:

Будем считать, что стержень изготовлен из стали (G = 8 · 1010 Па), а диаметры ступеней равны: d1=150 мм, d2=200 мм, d3=300 мм.
Под действием внешних моментов (M), их еще часто называют вращающими или скручивающими моментами, в поперечных сечениях стержня возникают внутренние моменты – крутящие (T).

Правило знаков для крутящих моментов
Чтобы построить эпюру крутящих моментов, необходимо задаться каким-то правилом знаков для крутящих моментов. В этой статье я буду использовать следующее правило:
- Если внешний момент (M), в плоскости сечения, поворачивает ПРОТИВ часовой стрелки, то крутящий момент (T) – положительный.

- Если внешний момент (M), в плоскости сечения, поворачивает ПО часовой стрелке, то крутящий момент (T) – отрицательный.

Можно учитывать знак крутящего момента ровно наоборот. Главное, придерживаться этого правила при расчёте всех участков и ориентироваться по полученным эпюрам: в какую сторону у тебя будут направлены внешние моменты, внутренние – крутящие моменты, куда будут поворачиваться сечения. Как видишь, знаки здесь нам нужны, чтобы задать определённые правила игры, а правило знаков – условное и не имеет физического смысла.
Расчёт крутящих моментов
Что же, давай, наконец, приступим к расчёту крутящих моментов. Пронумеруем расчётные участки:

Используя правило знаков, описанное выше, рассчитаем крутящие моменты на каждом участке:

По полученным значениям построим эпюру касательных напряжений:

Построение эпюры касательных напряжений при кручении
Касательные напряжения по высоте круглого сечения, будут распределены следующим образом:

Как видишь, касательные напряжения будут максимальны на поверхности стержня, они нас и будут интересовать больше всего, т. к. по ним выполняются прочностные расчёты, для них и будем строить эпюру – максимальных касательных напряжений.
Расчёт максимальных касательных напряжений
Максимальные касательные напряжения в поперечном сечении, можно определить по формуле:

где Wp — полярный момент сопротивлния, T — крутящий момент.
Полярный момент сопротивления для круглого сечения определяется по формуле:

Поэтому формулу для нахождения максимальных касательных напряжений для круглого поперечного сечения, можно записать в следующем виде:

По условию задачи диаметры участков известны. Осталось вычислить максимальные касательные напряжения на каждом участке:

По полученным значениям построим эпюру касательных напряжений:

Построение эпюры углов закручивания (поворотов)
Под действием внешних – скручивающих моментов, поперечные сечения стержня будут поворачиваться на определенный угол (φ). В этом разделе будем учиться определять эти углы закручивания (поворотов) поперечных сечений и строить эпюру.
Обозначим точки в характерных сечениях стержня:

Расчёт начинаем от жёсткой заделки и сразу можем записать, что в точке A, угол поворота равен нулю, т. к. здесь заделка ограничивает любые повороты сечения:
Чтобы рассчитать поворот сечения B, нужно учесть поворот предыдущего сечения:
А также, угол закручивания участка между расчётными сечениями:
Угол закручивания участка можно посчитать по формуле:

где l – длина участка; Ip – полярный момент инерции; G – модуль сдвига.
G – модуль сдвига (модуль упругости 2 рода) – определяется при испытании образцов на кручение, тем самым зависит от материала образца.
Модуль сдвига (G) известен, по условию задачи.
Формула для определения полярного момента инерции для круглого сечения следующая:

Зная диаметры, сразу вычислим полярные моменты инерции для каждого участка:

Определим угол закручивания сечения B, с учётом вышеуказанных формул:

Также можно перевести это значение в привычные градусы:

Для двух других сечений расчёт производится аналогичным образом.
Угол поворота сечения С

Угол поворота сечения D

По рассчитанным значениям, построим эпюру углов закручивания поперечных сечений:

Таким образом, свободный торец стержня, повернётся на 0.58 градуса, относительно неподвижного сечения A.
Расчеты на прочность при кручении
При кручении расчёты на прочность в целом похожи на расчёты при растяжении. Только здесь вместо нормальных напряжений расчёт ведётся по касательным напряжениям.
На кручение, как правило, работают детали, которые называются валами. Их назначение – передача крутящего момента от одного элемента к другому. При этом вал по всей длине имеет либо круглое сечение, либо кольцевое.
Условие прочности
За допустимое касательное напряжение [τ], часто в задачах по сопромату, принимают напряжение в два раза меньше, чем допустимое нормальное напряжение [σ]:

Максимальные касательные напряжения (τmax) в сечениях можно найти по формуле:

где T – крутящий момент в сечении;
Wp – полярный момент сопротивления сечения.
Полярные моменты сопротивления можно посчитать этим формулам.
Кручением
называется такой вид напряжённого
состояния, при котором в поперечном
сечении стержня возникает лишь один
силовой фактор — крутящий момент Мz.
Крутящий момент по определению равен
сумме моментов внутренних сил относительно
продольной оси стержня Oz. Нормальные
силы, параллельные оси Oz, вклада в
крутящий момент не вносят. С силами,
лежащими в плоскости поперечного сечения
стержня (интенсивности этих сил —
касательные напряжения
и
)
Мz
связывает вытекающее из его определения
уравнение равновесия статики (рис. 10.1)
Условимся
считать Mz
положительным, если со стороны отброшенной
части стержня видим его направленным
против часовой стрелки (рис. 10.2). Это
правило проиллюстрировано на рис. 1 и в
указанном соотношении, где крутящий
момент Мz
принят
положительным. Численно крутящий момент
равен сумме моментов внешних сил,
приложенных к отсеченной части стержня,
относительно оси Ог.
Рис.
10.1.
Связь крутящего момента с касательными
напряжениями
Рис.
10.2.
Иллюстрация положительного и отрицательного
крутящего момента
Рассмотрим
кручение стержней кругового поперечного
сечения. Исследование деформаций
упругого стержня с нанесенной на его
поверхности ортогональной сеткой рисок
(рис. 10.3) позволяет сформулировать
следующие предпосылки теории кручения
этого стержня:
-
поперечные
сечения остаются плоскими (выполняется
гипотеза Бернулли); -
расстояния
между поперечными сечениями не
изменяются, следовательно
;
-
контуры
поперечных сечений и их радиусы не
деформируются. Это означает, что
поперечные сечения ведут себя как
жесткие круговые пластинки, поворачивающиеся
при деформировании относительно оси
стержня Ог.
Отсюда следует, что любые деформации
в плоскости пластинки равны нулю, в том
числе и
;
-
материал
стержня подчиняется закону Гука.
Учитывая, что
,
из обобщенного закона Гука получаем.
Это означает, что в поперечных сечениях,
стержня возникают лишь касательные
напряжения
,
а вследствие закона парности касательных
напряжений, равные им напряжения
действуют и в сопряженных продольных
сечениях. Следовательно напряженное
состояние стержня — чистый
сдвиг.
Рис.
10.3.
Иллюстрация кручения: а)
исходное и б)
деформированное состояния
Выведем
формулу для касательных напряжений при
кручении призматического стержня
кругового поперечного сечения. Как
видно, поворот правого торцевого сечения
относительно неподвижного левого на
угол
(назовем
его углом закручивания стержня) вызывает
поворот продольных волокон на угол(угол
сдвига), поскольку на величинуискажаются
углы ортогональной сетки продольных и
поперечных рисок модели.
Двумя
смежными сечениями вырежем элемент
стержня длиной dz
и, поскольку нас интересуют деформации
элемента, левое сечение его будем считать
неподвижным (рис. 10.5). При повороте
правого сечения на угол
в
соответствии с гипотезой о недеформируемости
радиусов, правый конец волокнаАВ
(отстоящий от оси элемента на величину
полярного радиуса
)
будет перемещаться по дугеBB1,
вызывая поворот волокна на угол сдвига
Обратим
внимание на то, что сдвиг
и
связанное с ним касательное напряжениеперпендикулярны
радиусу.
Определим,
воспользовавшись законом Гука для
чистого сдвига
|
|
(10.1) |
Рис.
10.4.
Распределение касательных напряжений
при кручении.
Здесь
—
погонный угол закручивания стержня,
который остается пока неизвестным. Для
его нахождения обратимся к условию
статики, записав его в более удобной
для данного случая форме (рис. 10. 4,a)
|
|
(10.2) |
Подставляя
(10.1) в (10.2) и учитывая, что
где
Jp—;
полярный момент инерции поперечного
сечения (для круга с диаметром d
),
получаем
|
|
(10.3) |
Рис.
10.5.
Распределение напряжений для кольцевого
сечения
а)
разрушение дерева, б) разрушение
чугуна
Рис.
10.6.
Распределение исходных касательных и
главных напряжений:
Подставляя
выражение (10.3) в (10.1), получаем формулу
для касательных напряжений при кручении
призматического стержня кругового
поперечного сечения
|
|
(10.4) |
Как
видно из (10.4), сдвиги и касательные
напряжения пропорциональны расстоянию
от оси стержня. Обратим внимание на
структурные аналогии формул для
нормальных напряжений чистого изгиба
и касательных напряжений кручения.
Мерой
деформации стержня при кручении является
погонный угол закручивания стержня,
определяемый по (10.3). Поскольку величина
GJp
стоит в знаменателе формулы и при
заданной нагрузке (Mz
через нее выражается)
тем
меньше, чем большеGJp,
последнюю называют жесткостью
поперечного сечения при кручении.
Пользуясь
(3) для определения угла закручивания
элемента длиной dz
найдем
полный угол закручивания стержня длиной
l
|
|
(10.5) |
В
случае, если по длине стержня Мz
и DJp
постоянны, получаем
когда
эти величины кусочно-постоянны, то:
|
|
(10.6) |
Отметим,
что полученные формулы по структуре
аналогичны формулам для деформаций при
растяжении стержня.
Наибольшие
касательные напряжения возникают у
внешней поверхности стержня, т. е. при
где
Wр
— момент сопротивления при кручении
или полярный момент сопротивления
.
Полярный
момент сопротивления, стоящий в
знаменателе для максимальных касательных
напряжений, очевидно, является
геометрической характеристикой сечения,
а условие прочности стержня при кручении
принимает вид
|
|
(10.7) |
где
—
допускаемое напряжение на кручение.
Как
показали эксперименты и точное решение
этой задачи в теории упругости, все
гипотезы, сформулированные ранее для
стержня со сплошным круговым сечением,
остаются справедливыми и для стержня
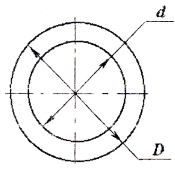
кольцевого поперечного сечения (рис.
10.7). Поэтому все выведенные ранее формулы
пригодны для расчета стержня кольцевого
сечения с той лишь разницей, что полярный
момент инерции определяется как разность
моментов инерции кругов с диаметрами
D и d
где
,
а момент сопротивления определяется
по формуле
Учитывая
линейный характер изменения касательных
напряжений по радиусу (рис. 10.7) и связанное
с этим лучшее использование материала,
кольцевое сечение следует признать
наиболее рациональным при кручении
стержня. Коэффициент использования
материала тем выше, чем меньше относительная
толщина трубы.
Как
отмечено ранее, напряженное состояние
при кручении стержня — чистый сдвиг,
являющийся частным случаем плоского
напряженного состояния. На площадках,
совпадающих с плоскостью поперечного
сечения и на парных им площадках
продольных сечений возникают экстремальные
касательные напряжения max-min
,
а главные напряжениядействуют
на площадках, наклоненных к оси стержня
под углами;
главное напряжение.
Особенности
напряженного состояния при кручении
нашли отражение в характере разрушения
стержней. Так, разрушение стержня из
дерева, плохо работающего на скалывание
вдоль волокон, происходит от продольных
трещин (рис. 8, a). Разрушение стержня из
хрупкого металла (например, чугуна)
происходит по винтовой линии, наклоненной
к образующим под углом 45o,
т. е. по траектории главного напряжения
(рис.
8,б).
ЭПЮРЫ
ВНУТРЕННИХ УСИЛИЙ ПРИ КРУЧЕНИИ
Рассмотрим
расчетную схему вала, нагруженного
двумя сосредоточенными моментами М
и 2М
и распределенными по длине: m,
рис. 10.7.
Методика
построения эпюры аналогична только что
рассмотренной методике при растяжении-сжатии.
а)
расчетная схема, б) первый участок, левая
часть в) второй участок, левая часть г)
третий участок, правая часть, д) эпюра
внутренних крутящих моментов
Рис.
10.7.
Построение эпюры внутренних крутящих
моментов:
В
исходных сечениях No 1,2 и 3 задаются
положительными значениями внутренних
крутящих моментов М1,
М2,
М3.
Пусть М=ml.
Для
первого участка (рис. 10.7 б):
Для
второго участка (рис.10.7 в):
Для
третьего участка (рис.10.7 г):
Границы
измерения параметра х3
в следующей системе координат:
Тогда:
Отмеченные
значения ординат откладываются на эпюре
внутренних крутящих моментов (рис.10.7
д).
Пример.
Стержень переменного круглого сечения
жестко заделан в концевых сечениях и
нагружен моментом М.
Требуется:
-
Определить
величины моментов в заделках. -
Построить
эпюры крутящих моментов Мz(z),
наибольших касательных напряжений
τ(z),
относительных углов закручивания Ѳ(z)
абсолютных углов закручивания ϕ(z).
Для этого составить на каждом участке
соответствующие аналитические выражения
и определить в буквенном виде значения
характерных ординат. -
Определить
из условия прочности и жесткости
допускаемую величину момента М. -
Построить
эпюру касательных напряжений в опасном
сечении(по напряжениям) при найденном
значении [М].
Данные к задаче:
D=8·10–² м;l=50·10–²м;
[τ]=80МПа; [Ѳ]=1 гр/м;G=8·10⁴МПа.
Кроме того, индивидуальность задания
определяется геометрией стержня и
величиной отношения диаметров.
=
= 0,85
Решение.
Прежде всего необходимо пояснить, как
определяется направление момента
условно считается, что если в кружочке
обозначения момента стоит точка, то как
бы стрела направлена на нас, если крестик,
то мы видим оперение стрелы. Так, на рис.
4.9 искомый момент М направлен по часовой
стрелке относительно оси стержня, если
смотреть с конца оси z.
Перед началом решения полезно определить
соотношения геометрических параметров
по участкам. Как принято, характерные
сечения обозначаем начальными буквами
латинского алфавита. Пронумеруем
участки: ①-ый участок АВ,②-ой участок
ВС и ③-ий участок СD, см.
рис.4.9. В качестве эталонного выберем
2-й участок, диаметр которого задан
непосредственно в данных к задаче. Все
геометрические параметры участков
выразим через эталонные. Итак, эталонные
параметры:
;
.
а) первый участок АВ:
б) второй участок ВС:
;
;
;
;
в) третий участок CD:
-
Определение
величины моментов в заделках.
Направляем
реактивные моменты МА
и МD
против направления действия момента
М. Уравнение равновесия:
(4.24)
Одно
уравнение с двумя неизвестными. В
качестве недостающих уравнений составим
уравнения совместимости перемещений
с помощью закона Гука см.(4.16) и принципа
независимости действия сил. Мысленно
попеременно отбрасывается связи,
накладываемые заделками в сечениях А
и D,
определим реактивные моменты, а уравнение
(4.24) используем в качестве проверочного
уравнения. Алгоритм решения данной
задачи такой же, как в примере при расчете
на растяжение-сжатие.
Отбрасываем
связь в сечении А. Определяем угол
поворота сечения А относительно сечения
D,
помня что в действительности этот угол
равен нулю.
Слагаемые,
содержащие МА,
взяты со знаком плюс, так как направление
момента МА
относительно оси z
против часовой стрелки. Соответственно
слагаемое с моментом М взято со знаком
минус.
Итак:
+
После
сокращений на l
и на
и сложений получим:
МА=0,407М.
Аналогично
для заделки в сечении D:
Или:
После
сокращений на l
и на
и сложений получим:
MD=0,593M
Подставим
полученные значения MA
и
MD
в
(4.24):
0,407М
– М + 0,593М=0; 0≡0.
Наносим
значения реактивных моментов на расчетную
схему, см.рис.4.9.
-
Построение
эпюр.
а)
эпюра крутящих моментов.
На
первом и втором участках рассмотрим
внешние моменты слева от сечения:
Мz(z1)
= Mz(z2)
= – MA
=0,407M
Так
как внешний момент МА
направлен против часовой стрелки
относительно оси z
и внутренний момент Мкр
также
направлен против часовой стрелки
относительно оси z,
вследствие совпадения направлений
внешней нормали и оси z,
то крутящий момент будет отрицательным.
На
третьем участке рассмотрим внешние
моменты справа от сечения:
Мz(z3)=MD=0,593M
В
этом случае внешняя нормаль не совпадает
с направлением оси z.
Строим
эпюру Mz(z),
см.рис.4.9.
б)эпюра
наибольших касательных напряжений на
контурах поперечных сечений.
;
;
;
Строим
эпюру τ(z),
см.рис.4.9.
в)
эпюра относительных углов закручивания.
Строим
эпюру Ѳ(z),
см.рис.4.9.
г)
эпюра абсолютных углов закручивания.
Согласно
выражению(4.17) при Ѳ = const
в пределах рассматриваемого участка ,
то эпюра Ү(А)=0, т.к. заделка
Абсолютный
угол закручивания в сечении В будет
определяться относительным углом
закручивания на первом участке:
Ү(В)=Ѳ(z1)·l1=-0,212
При
определении угла в сечении с необходимо
учитывать и угол в сечении B:
Ү(C)=Ү(B)+Ѳ(z2)·l2=
-0,424+(-0,407
)·2l=-1,238
Соответственно:
Ү(D)=Ү(C)+Ѳ(z3)·l3=
– 1,238+1,241
·l≈0
Определим
ошибку в вычислениях:
∆Ү=
т.е. вполне приемлемая точность в
расчетах.
Строим
эпюру Ү(z),
cм.рис.4.9.
-
Определение
допускаемого момента.
а)
из условия прочности.
Опасным,
то есть расчетным является любое сечение
третьего участка.
τmax
= 1,241
≤ [τ].
[M]τ
=
Коэффициент
106для
перевода единицы МН в Н.
б)
из условия жесткости.
В
данной задаче опасное сечение по условию
жесткости совпало с сечением по условию
прочности.
Ѳmax=1,241.
Необходимо
заданный допускаемый угол в градусной
мере перевести в радианную меру.
[Ѳ]=1
Окончательно
принимаем:
[M]=4518,6
Н·м
4.
Построение эпюры касательных напряжений
в любом сечении участка три, оказавшийся
опасным по величине напряжений.
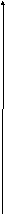
τm
х
D

При определении направлений касательных
напряжений учитываем направление
действия крутящего момента. На третьем
участке он положительный, то есть
относительно внешней нормали он направлен
против часовой стрелки. Соответственно
направляем напряжения. Стрелочки
напряжений ни в коем случае не могут
исходить из пространства высверленного
отверстия, см. рис. 4.10.
Из эпюры τ(z):
Коэффициент 10-6для перевода
единицы Па в МПа.
Наносим на эпюру значение τmax,
см. рис. 4.10.
РАСЧЕТ
ВАЛОВ
Рассмотрим
расчет вала на прочность и жесткость.
Пусть известна мощность W (кВт), передаваемая
вращающимся с заданным числом оборотов
в минуту (n) валом от источника мощности
(например, двигателя) к ее потребителю
(например, станку), а момент т, передаваемый
валом, требуется найти, так как численно
равный этому моменту крутящий момент
необходим для расчета вала.
Если
число оборотов вала в минуту п и
соответствующая угловая скорость
(с-1)
постоянны, а Ф — угол поворота вала в
данный момент времени t, то работа
вращательного движения А=тФ. Тогда
передаваемая валом мощность будет равна
Отсюда
кНм,
где
учтено, что
.
Если
мощность подается на вал через ведущий
шкив, а раздается потребителям через
несколько ведомых шкивов, то соответственно
определяются моменты на шкивах, а затем
строится эпюра крутящих моментов. Расчет
вала на прочность и жесткость ведется,
очевидно, по max Mz.
Определение
диаметра вала из условия прочности.
Условие прочности при кручении вала
имеет вид (10.7), где допускаемые напряжения
принимаются
пониженными по сравнению с допускаемыми
напряжениями обычного статического
расчета в связи с необходимостью учета
наличия концентраторов напряжений
(например, шпоночных канавок), переменного
характера нагрузки и наличия наряду с
кручением и изгиба вала.
Требуемое
значение Wp=dз/16
получаем из условия (10.7), принимая в нем
знак равенства
,
откуда
получаем формулу для диаметра вала
кругового сечения
|
|
(10.8) |
Определение
диаметра вала из условия жесткости.
Условие жесткости состоит в наложении
ограничения на погонный угол закручивания
вала
,
так как недостаточно жесткие валы не
обеспечивают устойчивой передачи
мощности и подвержены сильным колебаниям:
|
|
(10.9) |
Тогда,
учитывая, что
,
для диаметра вала из условия жесткости
имеем
|
|
(10.10) |
Аналогично
проводятся расчеты и для вала кольцевого
поперечного сечения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
У этого термина существуют и другие значения, см. Кручение.
Пример деформации кручения цилиндрического стержня
Деформация стержня прямоугольного сечения при кручении
Круче́ние — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары противоположных по направлению сил в его поперечной плоскости, точки приложения которых находятся на определённом удалении друг от друга. При этом данные силы образуют в поперечных сечениях тела единственный внутренний силовой фактор — крутящий момент. Примеры кручения: пружины растяжения-сжатия, валы.
При деформации кручения смещение каждой точки тела перпендикулярно к её расстоянию от оси приложенных сил и пропорционально этому расстоянию.
Угол закручивания цилиндрического стержня в границах упругих деформаций под действием момента T может быть определён из уравнения закона Гука для случая кручения
где:
-
— геометрический полярный момент инерции;
— длина стержня;
- G — модуль сдвига.
Отношение угла закручивания φ к длине 
Деформация кручения является частным случаем деформации сдвига.
Напряжения при кручении[править | править код]
Распределение касательных напряжений при кручении
Вращающийся стержень, не работающий на кручение, называют валом. Стержень, используемый как упругий элемент, который работает на скручивание, называется торсионом. Касательные напряжения 
,
где r — расстояние от оси кручения.
Очевидно, что касательные напряжения достигают наибольшего значения на поверхности вала при 

,
где Wp — полярный момент сопротивления.
Это даёт возможность записать условие прочности при кручении в таком виде:
.
Используя это условие, можно или по известным силовым факторам, которые создают крутящий момент Т, найти полярный момент сопротивления и далее, в зависимости от той или иной формы, найти размеры сечения, или наоборот — зная размеры сечения, можно вычислить наибольшую величину крутящего момента, которую можно допустить в сечении, которое в свою очередь, позволит найти допустимые величины внешних нагрузок.
Касательные напряжения в произвольной точке поперечного сечения вала. Максимальные касательные напряжения при кручении
Подставив выражение 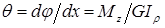
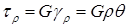
Наибольшие касательные напряжения (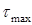
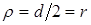
Формула наибольших касательных напряжений:
Введя обозначение 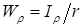
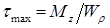

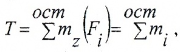
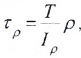
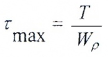
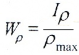
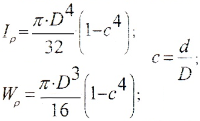
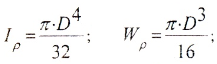
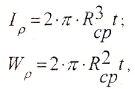
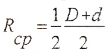
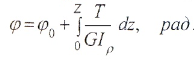
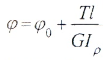
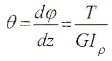
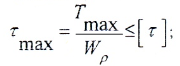
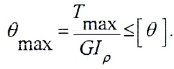
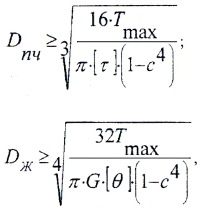
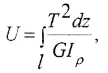
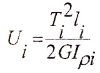





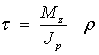
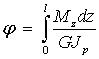

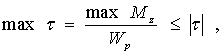

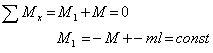

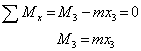























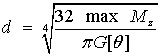







![tau_{max} = frac {T_{max}}{W_p} le [tau]](https://wikimedia.org/api/rest_v1/media/math/render/svg/609e79e5027bd3e3291f90a37ad417f2d5996a85)