ЮП
Юлия Попова
Гипотенуза прямоугольного треугольника равна 26 см, а площадь 120 см2. Найдите меньший катет.
Очень просто. Обозначим катеты как a и b. По теореме Пифагора a^2 + b^2 = 26^2 = 676. Как известно, площадь прямоугольного треугольника равна половине произведения катетов: a*b*0.5 = 120. Составляем систему из этих двух уравнений. Решаем подстановкой, допустим, возьмем катет a: a = 120/(0.5*b) = 120*2/b = 240/b. Далее подставляем в первое уравнение. Только не пугайся, числа большие: (240/b)^2 + b^2 = 676; 57600/b^2 + b^2 = 676. Умножаем обе части на b^2 (в этом отношении мы можем делать что угодно, ведь длина катета – величина положительная) : 57600 + b^4 = 676*b^2. Переносим все в левую часть:
b^4 – 676*b^2 +57600 = 0. Заменим b^2 на x, тогда b^4 = x^2: x^2 – 676x +57600 = 0. Решаем квадратное уравнение: дискриминант равен
D= (-676)^2 – 4*1*57600 =4*((338^2-57600)=4*( 114244 – 57600) =4* 56644= 4*4*49*289 = (2*2*7*17)^2=476^2. Далее находим корни: x1 = (676 – 476)/(2*1) = 200/2 = 162/2 =100. Т. е. x1 = 100, а значит b1 = корень квадратный из 100 = 10 (помним: длина катета – величина положительная) . Т. е. один катет мы уже нашли – он равен 10 см. Второй корень уравнения лучше не искать, второй катет можно найти из подстановки a = 240/b = 240/10 = 24. Все. Мы нашли катеты, они равны 10 см и 24 см соответственно. Задача решена. Можно сделать проверку: площадь равна 0.5*a*b = 0.5*10*24 = 120 см^2.
Как найти стороны прямоугольного треугольника, зная площадь
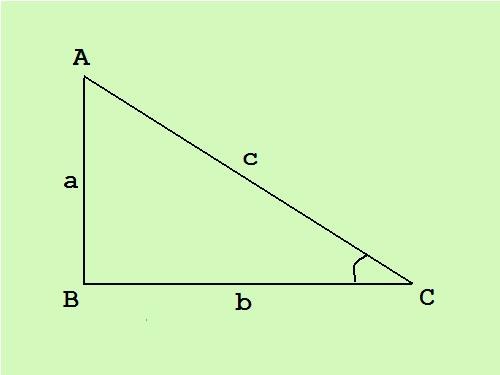
В прямоугольном треугольнике один угол прямой, другие два – острые. Сторона, противостоящая прямому углу, называется гипотенузой, другие две стороны – катеты. Зная площадь прямоугольного треугольника, можно вычислить стороны по известной формуле.
Инструкция
В прямоугольном треугольнике катеты перпендикулярны друг другу, следовательно, общая формула площади треугольника S = (c*h)/2 (где с – основание, а h – высота, проведенная к этому основанию) превращается в половину произведения длин катетов S = (a*b)/2.
Задача 1.
Найдите длины всех сторон прямоугольного треугольника, если известно, что длина одного катета превышает длину другого на 1 см, а площадь треугольника равна 28 см.
Решение.
Запишите основную формулу площади S = (a*b)/2 = 28. Известно, что b = a + 1, подставьте это значение в формулу: 28 = (a*(a+1))/2.
Раскройте скобки, получите квадратное уравнение с одной неизвестной a^2 + a – 56 = 0.
Найдите корни этого уравнения, для чего посчитайте дискриминант D = 1 + 224 = 225. Уравнение имеет два решения: a_1 = (-1 + √225)/2 = (-1 + 15)/2 = 7 и a_2 = (-1 – √225)/2 = (-1 – 15)/2 = -8.
Второй корень не имеет смысла, поскольку длина отрезка не может быть отрицательной величиной, так что a = 7 (см).
Найдите длину второго катета b = a + 1 = 8 (см).
Осталось найти длину третьей стороны. По теореме Пифагора для прямоугольного треугольника c^2 = a^2 + b^2 = 49 + 64, отсюда c = √(49 + 64) = √113 ≈ 10.6 (см).
Задача 2.
Найдите длины всех сторон прямоугольного треугольника, если известно, что его площадь равна 14 см, а угол ACB равен 30°.
Решение.
Запишите основную формулу S = (a*b)/2 = 14.
Теперь выразите длины катетов через произведение гипотенузы и тригонометрических функций по свойству прямоугольного треугольника:
a = c*cos(ACB) = c*cos(30°) = c*(√3/2) ≈ 0.87*c.
b = c*sin(ACB) = c*sin(30°) = c*(1/2) = 0.5*c.
Подставьте полученные значения в формулу площади:
14 = (0.87*0.5*c^2)/2, откуда:
28 ≈ 0.435*c^2 → c = √64.4 ≈ 8 (см).
Вы нашли длину гипотенузы, теперь найдите длины двух других сторон:
a = 0.87*c = 0.87*8 ≈ 7 (см), b = 0.5*c = 0.5*8 = 4 (см).
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
В некоторых задачах по геометрии требуется найти площадь прямоугольного треугольника, если известны длины его сторон. Так как длины сторон прямоугольного треугольника связаны теоремой Пифагора, а его площадь равна половине произведения длин катетов, то для решения этой задачи достаточно знать длины двух его любых сторон. Если же нужно решить обратную задачу – найти стороны прямоугольного треугольника по его площади, то потребуется дополнительная информация. Вам понадобится
Вам понадобится
Чтобы найти стороны равнобедренного прямоугольного треугольника по его площади, воспользуйтесь следующими формулами:К = √(2*Пл) или К = √2*√Пл и
Д = 2*√Пл, где
Пл – площадь треугольника,
К – длина катета треугольника,
Д – длина его гипотенузы.Длины сторон при этом будут выражаться в соответствующих площади линейных единицах измерения. Так, например, если площадь задана в квадратных сантиметрах (см²), то длины сторон будут измеряться в сантиметрах (см).Обоснование формул.
Площадь равнобедренного прямоугольного треугольника:
Пл = ½ * К², значит К² = 2 * Пл.
Теорема Пифагора для равнобедренного прямоугольного треугольника:
Д²=2 * К², значит Д = √2 * К.Пусть, например, площадь равнобедренного прямоугольного треугольника равняется 25 см². В этом случае, длина его катетов будет равняться:
К = √2 * √25 = 5√2, а длина гипотенузы:
Д = 2 * √25 = 10.
Чтобы найти длину сторон прямоугольного треугольника по его площади в общем случае, уточните значение какого-либо из дополнительных параметров. Это может быть соотношение катетов или соотношение катета и гипотенузы, один из острых углов треугольника, длина одной из сторон или его периметр.
Для расчета длин сторон треугольника в каждом конкретном случае воспользуйтесь теоремой Пифагора (Д² = К1² + К2²) и следующим равенством:Пл = ½ * К1 * К2, где
К1 и К2 – длины катетов.
Отсюда вытекает, что: К1 = 2Пл / К2 и, наоборот, К2 = 2Пл / К1.
Так, например, если соотношение катетов прямоугольного треугольника (К1/К2) равно Скк,
то К1 = Скк * К2 = Скк * 2Пл / К1, значит,К1 = √(2 * Скк * Пл)
К2 = √(2 * Скк * Пл) / Скк
Д = √((2 * Скк * Пл) + ((2 * Скк * Пл) / Скк))Пусть площадь прямоугольного треугольника – 25 см², а соотношение его катетов (К1/К2) равно 2, тогда по вышеприведенной формуле получается:К1 = √(2*2*25) = 10,
К2 = 10/2 = 5,
Д = √(10²+5²) = √125
Аналогично вычисляются длины сторон и в остальных случаях. Пусть, например, известны площадь (Пл) и периметр (Пе) прямоугольного треугольника.
Так как Пе = К1 + К2 + Д, а Д² = К1² + К2², то получается система из трех уравнений:К1 + К2 + Д = Пе
К1² + К2² = Д²
К1 * К2 = 2Пл,при решении которой в каждом конкретном случае определяются длины сторон треугольника.
Пусть, например, площадь прямоугольного треугольника 6, а периметр – 12 (соответствующих единиц).
В этом случае получается следующая система:К1+К2+Д = 12
К1² + К² = Д²
К1 * К2 = 12,
решив которую, можно узнать, что длины сторон треугольника равны 3, 4, 5.
Как найти катеты зная гипотенузу и площадь?
Всем спасибо!
На этой странице находится вопрос Как найти катеты зная гипотенузу и площадь?. Здесь же – ответы на него,
и похожие вопросы в категории Геометрия, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 5 – 9 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.
Как найти катет прямоугольного треугольника, если известна площадь и катет
s=69
bc (катет) = 23
Найди верный ответ на вопрос ✅ «Как найти катет прямоугольного треугольника, если известна площадь и катет s=69 bc (катет) = 23 …» по предмету 📙 Геометрия, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Геометрия » Как найти катет прямоугольного треугольника, если известна площадь и катет s=69 bc (катет) = 23
