Как найти стороны прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти стороны прямоугольного треугольника
Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Катет a =
Катет b =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Гипотенуза c =
Катет (известный) =
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
a = √c² – b²
b = √c² – a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² – 4² = √25 – 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Гипотенуза c =
Угол (прилежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Гипотенуза c =
Угол (противолежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см
См. также
Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.
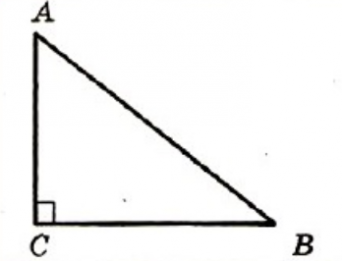
На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.
Свойства прямоугольного треугольника
- В прямоугольном треугольнике гипотенуза является наибольшей стороной.
- В прямоугольном треугольнике катет, лежащий напротив угла 300, равен половине гипотенузы. И обратно, если катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 300.
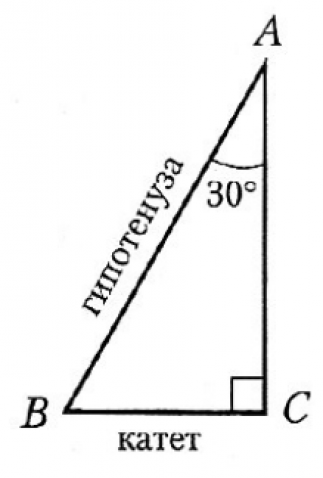
Например, пусть угол А=300, а гипотенуза АВ=28 см, то катет ВС будет равен 14 см, так как лежит напротив угла А=300. Или, например, если катет ВС=6 см, а гипотенуза АВ равна 12 см, то угол А (лежащий напротив катета ВС), равен 300.
- Сумма острых углов прямоугольного треугольника равна всегда 90 градусов.
- Медиана, проведенная к гипотенузе, равна её половине.
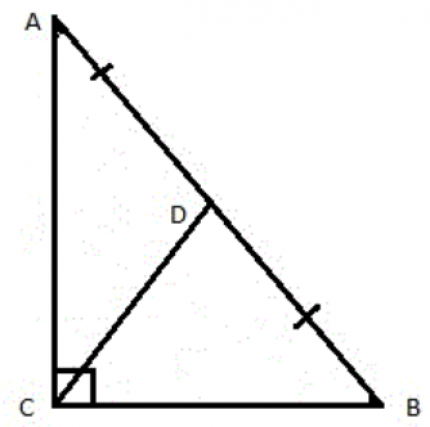
На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.
Признаки равенства прямоугольных треугольников
Существует 4 признака равенства прямоугольных треугольников:
- Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
- Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:
- по катетам;
- по катету и прилежащему острому углу;
- по гипотенузе и острому углу;
- по гипотенузе и катету.
Теорема Пифагора
Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».
Трактовка
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
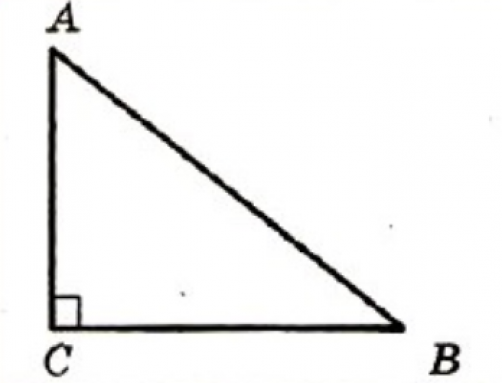
На рисунке в прямоугольном треугольнике АВ2=АС2+ВС2
Например, если в данном треугольнике катеты равны 9 и 12 см, то можно найти длину гипотенузы, используя теорему: АВ2=92+122=81+144=225=152, значит АВ=15 см.
Египетский треугольник
Определение
Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.
Пифагоровы тройки
Определение
Тройки чисел, которые удовлетворяют теореме Пифагора, называют Пифагоровы тройки, а сами числа – Пифагоровы числа. Например, такими являются числа 16, 12 и 20 – это числа, которые при подстановке в формулу теоремы, дают нам верное равенство: 162+122=202, 256+144=400, 400=400.
Даниил Романович | Просмотров: 7.8k
Прямоугольный треугольник – это треугольник, у которого один угол прямой (равен $90$ градусов).
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В$: $АС$ – противолежащий катет; $ВС$ – прилежащий катет.
Для острого угла $А$: $ВС$ – противолежащий катет; $АС$ – прилежащий катет.
1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
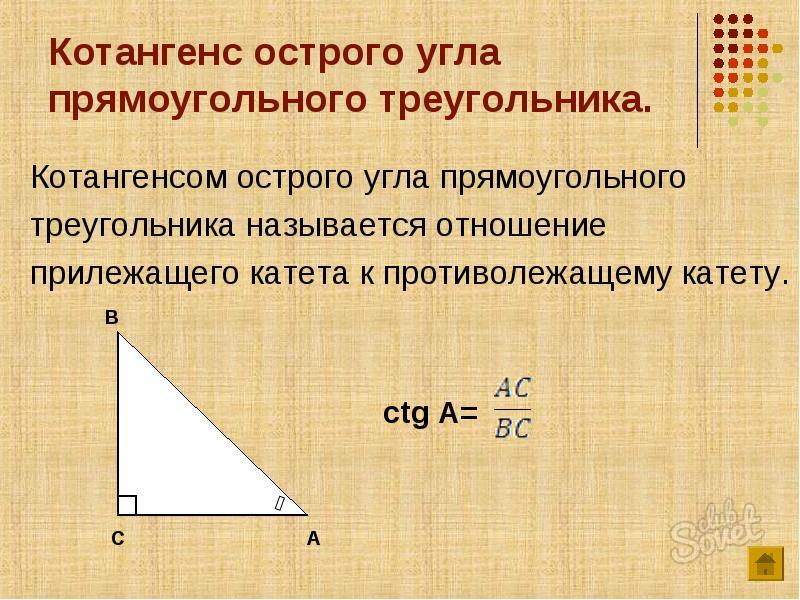
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
$sinB={AC}/{AB};$
$cosB={BC}/{AB};$
$tgB={AC}/{BC};$
$ctgB={BC}/{AC}.$
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
$sin BOA=sin BOC;$
$cos BOA=-cos BOC;$
$tg BOA=-tg BOC;$
$ctg BOA=-ctg BOC.$
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Площадь прямоугольного треугольника равна половине произведения его катетов
$S={AC∙BC}/{2}$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√{91}$. Найдите косинус внешнего угла при вершине $В$.
Решение:
Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то
$cosABD=-cosABC$
Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:
$cosABC={ВС}/{АВ}$
Катет $ВС$ мы можем найти по теореме Пифагора:
$ВС=√{10^2-√{91}^2}=√{100-91}=√9=3$
Подставим найденное значение в формулу косинуса
$cos ABC = {3}/{10}=0,3$
$cos ABD = – 0,3$
Ответ: $-0,3$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sinA={4}/{5}, AC=9$. Найдите $АВ$.
Решение:
Распишем синус угла $А$ по определению:
$sinA={ВС}/{АВ}={4}/{5}$
Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.
Применим теорему Пифагора, чтобы отыскать $«х»$
$АС^2+ВС^2=АВ^2$
$9^2+(4х)^2=(5х)^2$
$81+16х^2=25х^2$
$81=25х^2-16х^2$
$81=9х^2$
$9=х^2$
$х=3$
Так как длина $АВ$ составляет пять частей, то $3∙5=15$
Ответ: $15$
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
$CD^2=DB∙AD$
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
$CB^2=AB∙DB$
$AC^2=AB∙AD$
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
$AC∙CB=AB∙CD$
Прямоугольный треугольник
Определение и формулы прямоугольного треугольника
ОПРЕДЕЛЕНИЕ
Треугольник называется прямоугольным, если один из его углов прямой.
Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой.
Для прямоугольного треугольника справедливы следующие утверждения:
Прямоугольный треугольник
Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
(
A C^{2}+A B^{2}=B C^{2}
)
Сумма острых углов прямоугольного треугольника равна (
90^{circ}
) :
(
angle B+angle C=90^{circ}
)
Гипотенуза прямоугольного треугольника больше каждого их катетов:
(
A C>B C, A B>B C
)
Катет, лежащий против угла (
30^{circ}
) , равен половине гипотенузы.
Две высоты прямоугольного треугольника совпадают с его катетами.
Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.
Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности:
(
mathrm{AM}=mathrm{R}
)
Признаки равенства прямоугольных треугольников
По двум катетам: если два катета одного прямоугольного треугольника равны катетам другого прямоугольного треугольника, то такие треугольники равны.
По гипотенузе и катету: если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
По стороне и острому углу: Если сторона и прилежащий к ней острый угол одного прямоугольного треугольника соответственно равны стороне и прилежащему к ней острому углу другого прямоугольного треугольника, то такие треугольники равны
Подробнее про признаки равенства треугольников читайте по ссылке.
Тригонометрические соотношения в прямоугольном треугольнике
Тригонометрические соотношения в прямоугольном треугольнике
Площадь прямоугольного треугольника равна половине произведения катетов и вычисляется по формуле
(
S=frac{1}{2} a b
)
Примеры решения задач
ПРИМЕР 1
mathrm{ABC}
) катет (
mathrm{AC}
) равен 5 см, а (
angle C=60^{circ}
) . Найти гипотенузу (
mathrm{BC}
).
В прямоугольном треугольнике сумма острых углов равна (
90^{circ}
) значит
(
angle B=90^{circ}-angle C=30^{circ}
)
Также известно, что катет (
mathrm{AC}
) (рис. 1), лежащий против угла (
angle B=30^{circ}
) равен половине гипотенузы, т.е.
(
B C=2 A C=2 cdot 5=10
)
(
mathrm{BC}=10 mathrm{см.}
)
ПРИМЕР 2
В равнобедренном треугольнике (
mathrm{ABC}
) угол (
mathrm{A}
) – прямой, (
mathrm{BC=4 см}
). Найти площадь (
Delta A B C
)
Запишем для прямоугольного треугольника (
mathrm{ABC}
) теорему Пифагора:
(
B C^{2}=A C^{2}+A B^{2}
)
Так как этот треугольник равнобедренный, то (
A B=A C
). Тогда
(
B C^{2}=4^{2}=2 A C^{2} Rightarrow 2 A C^{2}=16
)
откуда (
A C=sqrt{8}
)
Площадь прямоугольного треугольника равна половине произведения катетов, т.е.
(
S=frac{1}{2} A B cdot A C=frac{1}{2} A C^{2}=4 mathrm{см}^{2}
)
(
mathrm{S}=4 mathrm{см} 2
)

Как найти катет прямоугольного треугольника
В жизни нам часто придется сталкиваться с математическими задачами: в школе, в университете, а затем помогая своему ребенку с выполнением домашнего задания. Люди определенных профессий будут сталкиваться с математикой ежедневно. Поэтому полезно запоминать или вспоминать математические правила. В этой статье мы разберем одно из них: нахождение катета прямоугольного треугольника.
1
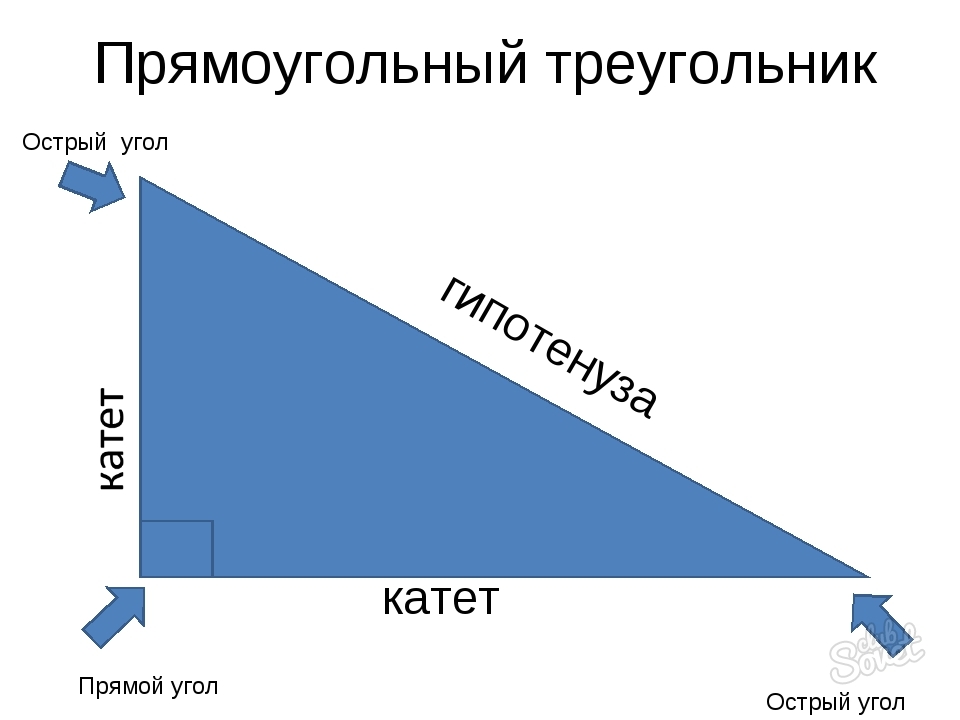
Что такое прямоугольный треугольник
Для начала вспомним, что такое прямоугольный треугольник. Прямоугольный треугольник – это геометрическая фигура из трех отрезков, которые соединяют точки, не лежащие на одной прямой, и один из углов этой фигуры равен 90 градусам. Стороны, образующие прямой угол, называются катетами, а сторона, которая лежит напротив прямого угла – гипотенузой.
2
Находим катет прямоугольного треугольника
Существует несколько способов, позволяющих узнать длину катета. Хотелось бы рассмотреть бы их подробнее.
Теорема Пифагора, чтобы найти катет прямоугольного треугольника
Если нам известны гипотенуза и катет, то мы можем найти длину неизвестного катета по теореме Пифагора. Звучит она так: “Квадрат гипотенузы равен сумме квадратов катетов”. Формула: c²=a²+b², где c – гипотенуза, a и b – катеты. Преобразовываем формулу и получаем: a²=c²-b².
Пример. Гипотенуза равна 5 см, а катет – 3 см. Преобразовываем формулу: c²=a²+b² → a²=c²-b². Далее решаем: a²=5²-3²; a²=25-9; a²=16; a=√16; a=4 (см).

Тригонометрические соотношения, чтобы найти катет прямоугольного треугольника
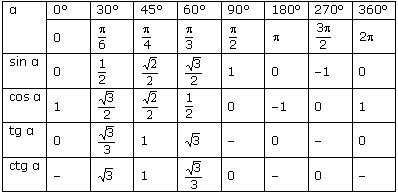
Также можно найти неизвестный катет, если известны любая другая сторона и любой острый угол прямоугольного треугольника. Есть четыре варианта нахождения катета при помощи тригонометрических функций: по синусу, косинусу, тангенсу, котангенсу. Для решения задач нам поможет таблица, которая находится чуть ниже. Рассмотрим эти варианты.
Найти катет прямоугольного треугольника при помощи синуса
Синус угла (sin) – это отношение противолежащего катета к гипотенузе. Формула: sin=a/c, где а – катет, лежащий против данного угла, а с – гипотенуза. Далее преобразуем формулу и получаем: a=sin*c.
Пример. Гипотенуза равна 10 см, угол А равен 30 градусов. По таблице вычисляем синус угла А, он равен 1/2. Затем по преобразованной формуле решаем: a=sin∠А*c; a=1/2*10; a=5 (см).

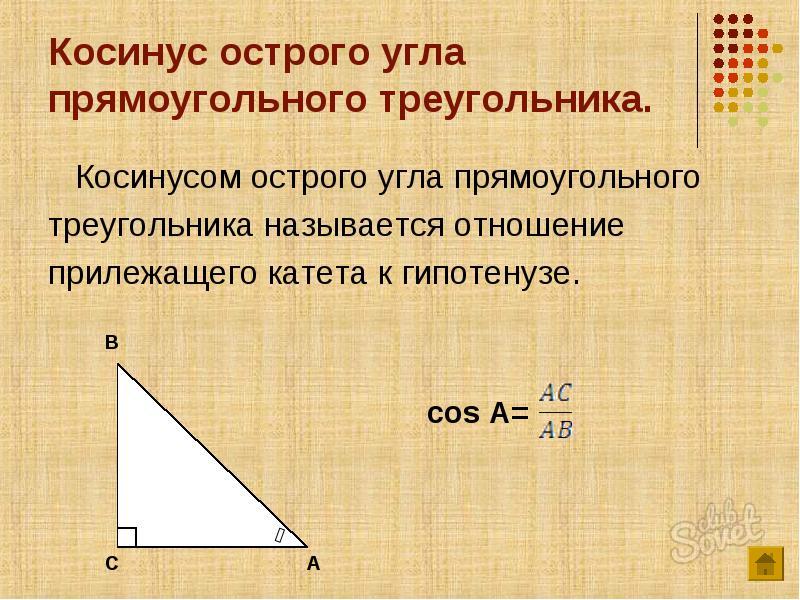
Найти катет прямоугольного треугольника при помощи косинуса
Косинус угла (cos) – это отношение прилежащего катета к гипотенузе. Формула: cos=b/c, где b – катет, прилежащий к данному углу, а с – гипотенуза. Преобразуем формулу и получим: b=cos*c.
Пример. Угол А равен 60 градусов, гипотенуза равна 10 см. По таблице вычисляем косинус угла А, он равен 1/2. Далее решаем: b=cos∠A*c; b=1/2*10, b=5 (см).
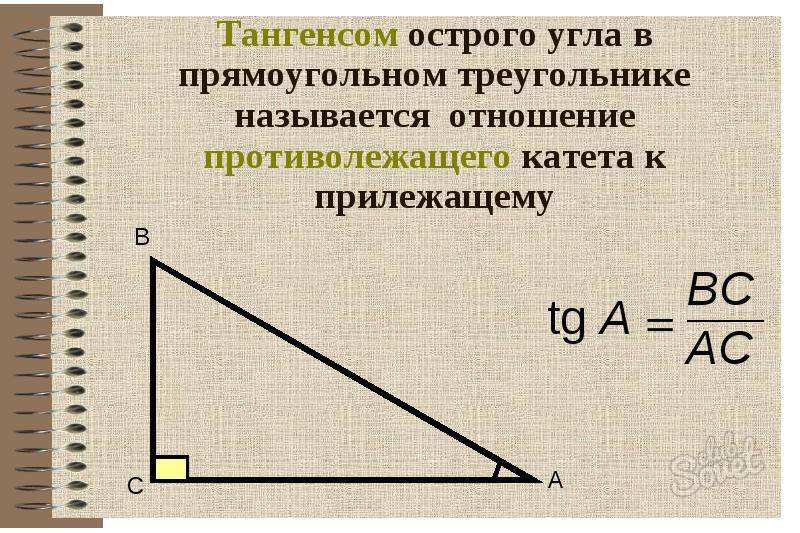
Найти катет прямоугольного треугольника при помощи тангенса
Тангенс угла (tg) – это отношение противолежащего катета к прилежащему. Формула: tg=a/b, где а – противолежащий к углу катет, а b – прилежащий. Преобразуем формулу и получаем: a=tg*b.
Пример. Угол А равен 45 градусов, гипотенуза равна 10 см. По таблице вычисляем тангенс угла А, он равен Решаем: a=tg∠A*b; a=1*10; a=10 (см).
Найти катет прямоугольного треугольника при помощи котангенса
Котангенс угла (ctg) – это отношение прилежащего катета к противолежащему. Формула: ctg=b/a, где b – прилежащий к углу катет, а – противолежащий. Иначе говоря, котангенс – это “перевернутый тангенс”. Получаем: b=ctg*a.
Пример. Угол А равен 30 градусов, противолежащий катет равен 5 см. По таблице тангенс угла А равен √3. Вычисляем: b=ctg∠A*a; b=√3*5; b=5√3 (см).
Итак, теперь вы знаете, как находить катет в прямоугольном треугольнике. Как видите, это не так уж и сложно, главное – запомнить формулы.
