Теорема пифагора
Определение теоремы пифагора
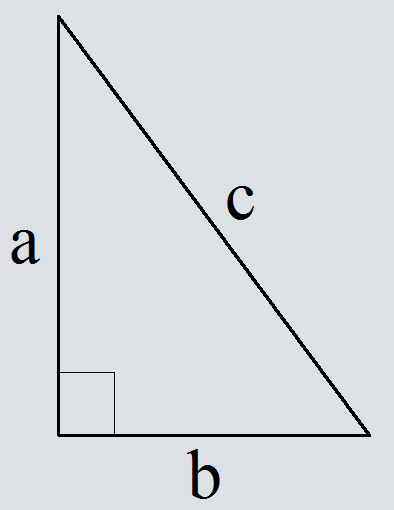
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Обозначив гипотенузу буквой – c, катеты буквами a и b получим следующее равенство
c2=a2+b2
Расчёт катета по теореме пифагора
Введите гипотенузу
c =
Введите катет
b =
Формула пифагора для катета
Где a, b – катеты прямоугольного треугольника,
с – гипотенуза прямоугольного треугольника
Расчёт гипотенузы по теореме пифагора
Введите первый катет
a =
Введите второй катет
b =
Формула пифагора для гипотенузы
Где a, b – катеты прямоугольного треугольника,
с – гипотенуза прямоугольного треугольника
Доказательство теоремы пифагора
Дано
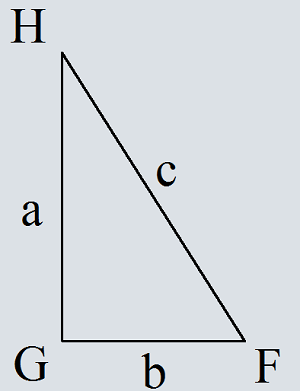
Прямоугольный треугольник с катетами a, b и гипотенузой c.
Доказать
c2=a2+b2
Доказательство
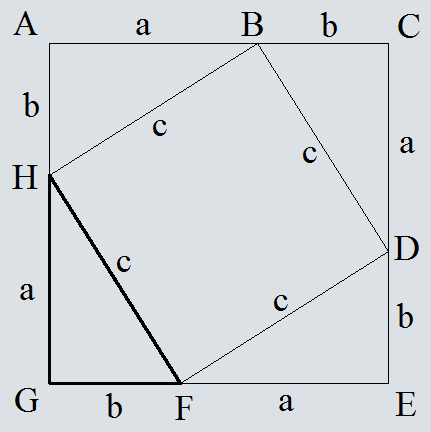
Достроим треугольник HFG до квадрата со стороной a+b.
Запишем площадь получевшегося квадрата двумя способами
S=(a+b)2
S=4*0.5*a*b +c2
Приравняем площади
(a+b)2=4*0.5*a*b +c2
a2+2*a*b +b2=2*a*b +c2
a2+b2=c2
Теорема доказана
В публикации представлены онлайн-калькуляторы и формулы для нахождения катета и гипотенузы в прямоугольном треугольнике по теореме Пифагора.
Инструкция по использованию: введите длины двух известных сторон треугольника (одного из катетов и гипотенузы или двух катетов), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина третьей стороны.
Содержание
скрыть
- Нахождение катета
- Нахождение гипотенузы
Нахождение катета
Формулы расчета
Нахождение гипотенузы
Формула расчета
Как найти стороны прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти стороны прямоугольного треугольника
Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Катет a =
Катет b =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Гипотенуза c =
Катет (известный) =
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
a = √c² – b²
b = √c² – a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² – 4² = √25 – 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Гипотенуза c =
Угол (прилежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Гипотенуза c =
Угол (противолежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см
См. также
Калькуляторы
- Найти сумму натуральных чисел от 1 до n
- Найти сумму натуральных чисел от M до N
- Возведение в степень
- Теореме Пифагора
- Калькулятор Фибоначчи
- Найти углы треугольника
- Найти углы прямоугольного треугольника
- Углы равнобедренного треугольника
- Углы ромба
- Углы параллелограмма
- Кубический корень
- Извлечение корня из числа
- Квадратный корень
- Факториал числа
- Радиус круга
- Радиус цилиндра
- Радиус шара
- Радиус вписанной окружности в правильный многоугольник
- Радиус окружности вписанной в треугольник
- Радиус окружности описанной вокруг треугольника
- Радиус вписанной и описанной окружности правильного треугольника
- Радиус вписанной окружности в прямоугольный треугольник
- Радиус вписанной и описанной окружности равнобедренного треугольника
- Теорема косинусов
- Теорема синусов
- Найти количество делителей числа
- Количество сторон многоугольника
- Число перестановок
Главная страница / Математические калькуляторы / Найти сторону треугольника по Теореме Пифагора
Добавить в закладки
Найти сторону треугольника по Теореме Пифагора
a =
b =
Знаков после запятой
Результат
Оставить комментарий (0)

Loading…
Поделиться в социальных сетях:
или https://correctcalc.ru/matematicheskie-kalkulyatory/teorema-pifagora/ скопировать ссылку на страницу
Теорема Пифагора – в прямоугольном треугольнике сумма квадратов катетов () равна квадрату гипотенузы.
Формула: a² + b² = c²
0 Комментариев |
; ; ; ; ;
Войти
Наш сайт использует файлы cookie, чтобы улучшить работу сайта, повысить его эффективность и удобство. Продолжая использовать сайт correctcalc.ru, вы соглашаетесь на использование файлов cookie.
Проценты
Процент от числа Процент одного числа от другого Прибавить процент к числу Вычесть процент из числа На сколько процентов одно число меньше другого На сколько процентов одно число больше другого Найти 100 процентов Процентное изменение Процентное соотношение Умножение на процент Деление на процент Разница в процентах Исходное значение Обратный прцент Число по проценту Снижение процентов
Математические
Сумма чисел от 1 до N Сумма чисел от M до N Возведение в степень Найти количество делителей числа Теорема Пифагора Фибоначи Найти углы треугольника Найти углы прямоугольного треугольника Углы равнобедренного треугольника Углы ромба Углы параллелограмма Кубический корень Извлечение корня из числа Квадратный корень Факториал числа Радиус круга Радиус цилиндра Радиус шара Радиус вписанной окружности в правильный многоугольник Радиус окружности вписанной в треугольник Радиус окружности описанной вокруг треугольника Радиус вписанной и описанной окружности правильного треугольника Радиус вписанной окружности в прямоугольный треугольник Радиус вписанной и описанной окружности равнобедренного треугольника Теорема косинусов Теорема синусов Количество сторон многоугольника Число перестановок
Дроби
Сложение дробей Вычитание дробей Деление дробей Умножение дробей Калькулятор сокращения дробей Возведения дробей в степень Перевод дроби в десятичную дробь Десятичная дробь в обыкновенную Смешанная дробь в обыкновенную Обыкновенная дробь в смешанную Обыкновенные дроби в проценты Калькулятор для сравнения дробей
Формула площади
Площадь прямоугольника Площадь треугольника Площадь кольца через радиусы Площадь круга Площадь квадрата Площадь квадрата по диагонали Площадь трапеции Площадь прямоугольного треугольника Площадь равнобедренного треугольника Площадь равностороннего треугольника Площадь параллелограмма Площадь эллипса Площадь четырехугольника Площадь сектора круга Площадь сегмента круга Площадь шара Площадь куба Площадь цилиндра Площадь пирамиды Площадь параллелепипеда Площадь конуса Площадь усеченного конуса Площадь тетраэдра Площадь призмы Площадь правильного многоугольника Площадь сектора кольца
Формула объема
Oбъема куба Oбъема параллелепипеда Объем конуса Объем призмы Объем цилиндра Объем шара Объем пирамиды Объем октаэдра Объем тетраэдра Объем усеченной пирамиды Объем усеченного конуса Объем шарового слоя Объем шарового сектора Объем шарового сегмента
Формула диагонали
Диагональ прямоугольника Диагональ квадрата Диагональ куба Диагональ прямоугольного параллелепипеда Диагонали ромба Диагонали параллелограмма Диагонали трапеции
Формула периметра
Периметр квадрата Периметр параллелограмма Периметр прямоугольника Периметр ромба Периметр трапеции Периметр треугольника Периметр четырехугольника Длина дуги Длина окружности круга Длина хорды окружности Периметр полукруга через диаметр Периметр полукруга через радиус
Формула высоты
Высота трапеции Высота ромба Высота параллелограмма Высота пирамиды Высота цилиндра Высота равнобедренного треугольника Высота равностороннего треугольникаа Высота треугольника
Формула стороны
Сторона треугольника Стороны прямоугольного треугольника Стороны равнобедренного треугольника Стороны равностороннего треугольника Стороны квадрата Стороны прямоугольника Стороны ромба Стороны параллелограмма Ребро пирамиды Ребро куба Боковое ребро параллелепипеда
Рассчет веса
Калькулятор индекса массы тела (ИМТ) Калькулятор идеального веса Процент жира-сухой мышечной массы Сколько воды нужно выпивать в день? Расчет количества мяса для шашлыка Расчет дней, за которые Вы сможете похудеть
Рассчет размера вещей
Калькулятор размеров обуви Калькулятор размеров мужской одежды Калькулятор размеров женской одежды Калькулятор размеров детской одежды
Животные
Сколько лет кошке по человеческим меркам
IT-специалисту
Перевод между системами счисления
Автомобилистам
Калькулятор расхода топлива
Бизнес калькуляторы
Сумма прописью онлайн Калькулятор НДС онлайн Калькулятор НДФЛ Сложный процент
Калькулятор дат
Количество дней между датами Количество недель между датами Сколько осталось до 23 февраля Сколько осталось до Нового года
Use the Pythagorean theorem to solve the length of any side of a right triangle or its area by entering known leg or hypotenuse values.
Solve For:
Solution and Steps:
Solution and Steps:
Steps to Solve
a= c² – b²
a= 5² – 3²
a= 25 – 9
a=16
a=4
Learn how we calculated this below
scroll down
On this page:
-
Calculator
-
What is the Pythagorean Theorem?
-
Pythagorean Theorem Formula
-
How to use the Pythagorean Theorem for Right Triangles
-
Find the Length of Leg a
-
Find the Length of Leg b
-
Find the Length of Hypotenuse c
-
Inverse Pythagorean Theorem
-
Pythagorean Triangles
What is the Pythagorean Theorem?
The Pythagorean theorem, sometimes called Pythagoras’ theorem, is an equation that relates the three sides of a right triangle, the two shorter sides (often called legs), and the longest side, called the hypotenuse.
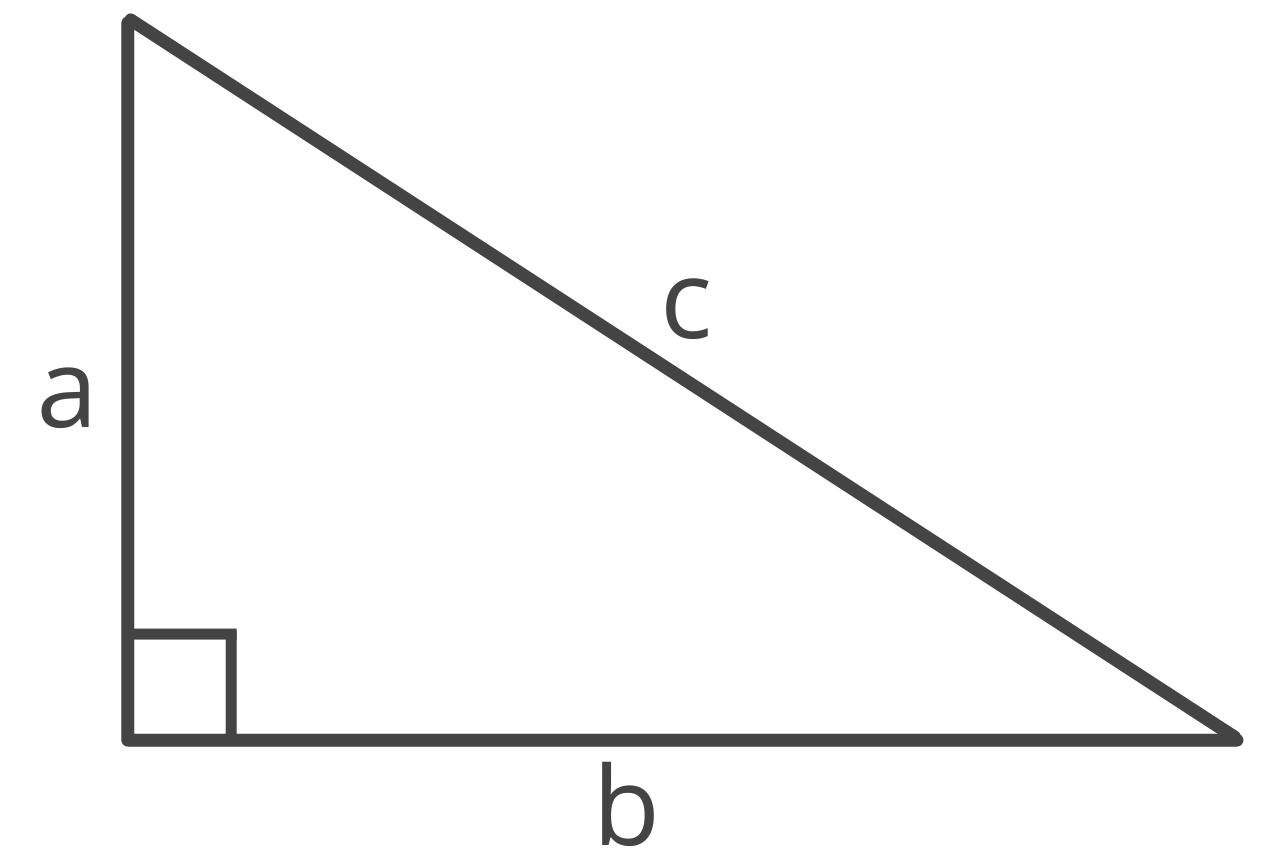
The Pythagorean theorem can be used to solve any side if the length of the other two sides is known.
The Pythagorean theorem states that the length of the hypotenuse squared is equal to the sum of the squares of each leg.
Pythagorean Theorem Formula
The Pythagorean theorem is expressed using the following equation, where a and b are the side lengths of the two legs, and c is the length of the hypotenuse:
a² + b² = c²
Thus, side a squared plus side b squared is equal to the square of the hypotenuse c.

How to use the Pythagorean Theorem for Right Triangles
Given the length of any two sides of a right triangle, the Pythagorean theorem is used to solve the length of the third side. To solve, replace the values of a, b, or c in the formula with the two known values and solve the equation.
The following formulas are derived from the Pythagorean theorem to solve for any side of a right triangle.
Find the Length of Leg a
The length of leg a can be found using the following formula:
a = c² – b²
The length of leg a is equal to the square root of c squared minus b squared.
Find the Length of Leg b
The length of leg b can be found using the following formula:
b = c² – a²
The length of leg b is equal to the square root of c squared minus a squared.
Find the Length of Hypotenuse c
The length of hypotenuse c can be found using the following formula:
c = a² + b²
The hypotenuse c is equal to the square root of a squared plus b squared.
Inverse Pythagorean Theorem
While the Pythagorean theorem relates the lengths of each side, the Inverse Pythagorean Theorem (sometimes called the Reciprocal Pythagorean Theorem) relates the side lengths to the height, or altitude, to the hypotenuse of a right triangle.
Since sides a and b are equal to the heights of the other side, the inverse Pythagorean theorem defines the relationship between the short sides and the height perpendicular to the hypotenuse.
The Inverse Pythagorean theorem states that if a right triangle with vertices A, B, and C is divided into two triangles by its height h at point D along side c, then the area of △ABC is equal to the area of △ACD plus the area of △BCD.
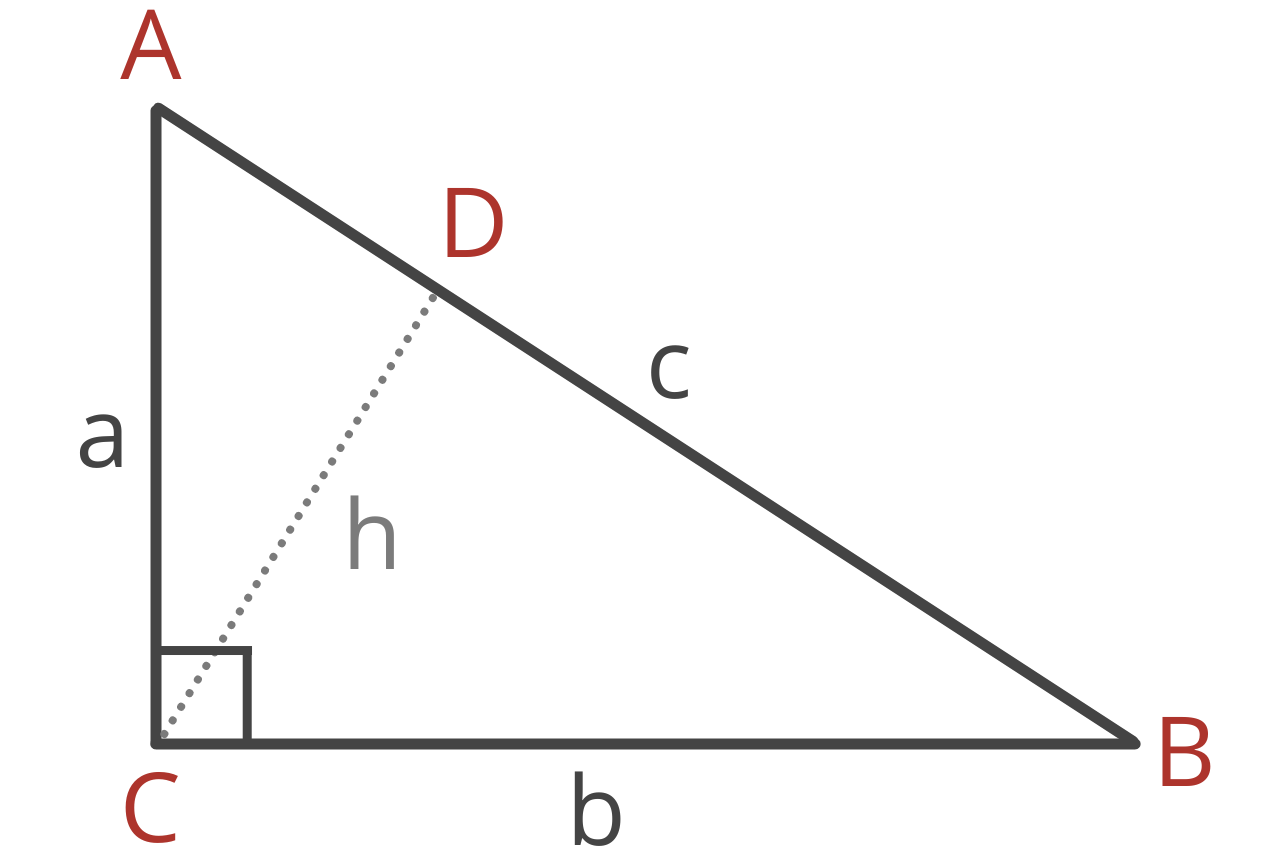
The length of the sides of these new triangles can be defined using the Pythagorean Theorem as follows:
1 / AC² + 1 / BC² = 1 / CD²
Note, AC, BC, and CD represent the length of the line segments connecting the respective vertices. This can be rewritten to more simply express the height of a right triangle:
1 / a² + 1 / b² = 1 / h²
Thus, the Inverse Pythagorean theorem says that the reciprocal of side a squared plus the reciprocal of side b squared is equal to the reciprocal of height h squared.
This can be further reduced to solve for the height given sides a, b, and c.
hc = ab
c = ab / h
You can also use our right triangle calculator to calculate the angles, area, or perimeter.
Pythagorean Triangles
A Pythagorean triangle is a special right triangle where each side length is a whole number. This is also called a Pythagorean triple.
The smallest Pythagorean triple is one with sides of lengths 3, 4, & 5. A primitive Pythagorean triple is a Pythagorean triple where the largest common divisor between them is 1.
For instance, the Pythagorean triple (3, 4, 5) is considered primitive since the largest common divisor is 1. On the other hand, the triple (9, 12, 15) is not primitive since the largest common divisor is 3.
Interestingly, both the area and inradius of a Pythagorean triple will also be whole numbers.
Some other examples of special right triangles are the 30 60 90 right triangle and the 45 45 90 right triangle.