в условии
в решении
в тексте к заданию
в атрибутах
Категория
Атрибут
Всего: 107 1–20 | 21–40 | 41–60 | 61–80 | 81–100 | 101–107
Добавить в вариант
Площадь прямоугольного треугольника равна
Один из острых углов равен 60°. Найдите длину катета, лежащего напротив этого угла.
Площадь прямоугольного треугольника равна
Один из острых углов равен 60°. Найдите длину катета, прилежащего к этому углу.
Площадь прямоугольного треугольника равна
Один из острых углов равен 60°. Найдите длину катета, лежащего напротив этого угла.
Площадь прямоугольного треугольника равна
Один из острых углов равен 60°. Найдите длину катета, лежащего напротив этого угла.
Площадь прямоугольного треугольника равна
Один из острых углов равен 60°. Найдите длину катета, лежащего напротив этого угла.
Площадь прямоугольного треугольника равна
Один из острых углов равен 60°. Найдите длину катета, прилежащего к этому углу.
Площадь прямоугольного треугольника равна
Один из острых углов равен 30°. Найдите длину гипотенузы.
Площадь прямоугольного треугольника равна
Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла.
Площадь прямоугольного треугольника равна
Один из острых углов равен 60°. Найдите длину катета, лежащего напротив этого угла.
Площадь прямоугольного треугольника равна
Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла.
Площадь прямоугольного треугольника равна
Один из острых углов равен 60°. Найдите длину катета, прилежащего к этому углу.
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Площадь прямоугольного треугольника равна
Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла.
Площадь прямоугольного треугольника равна
Один из острых углов равен 30°. Найдите длину гипотенузы.
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Площадь прямоугольного треугольника равна
Один из острых углов равен 30°. Найдите длину катета, прилежащего к этому углу.
Площадь прямоугольного треугольника равна
Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла.
Площадь прямоугольного треугольника равна
Один из острых углов равен 30°. Найдите длину катета, прилежащего к этому углу.
Площадь прямоугольного треугольника равна
Один из острых углов равен 60°. Найдите длину катета, прилежащего к этому углу.
Площадь прямоугольного треугольника равна
Один из острых углов равен 60°. Найдите длину катета, прилежащего к этому углу.
Всего: 107 1–20 | 21–40 | 41–60 | 61–80 | 81–100 | 101–107
Рассмотрим разновидность задания № (23) — геометрическая задача на нахождение длины катета.
Для выполнения необходимо вспомнить теорию.
Пример:
известно, что в прямоугольном треугольнике
ABC
с прямым углом
B
медиана
BM=5
, катет
AB=6
. Найди катет
BC
этого треугольника.
Как решить задание из примера?
Для получения максимального балла задание нужно оформлять разборчивым почерком с подробным решением. Обязательно должны присутствовать чертёж, дано и решение.

Рис. (1). Чертёж
Дано:
ΔABC
;
∠B=90°
;
BM
— медиана;
BM=5
;
AB=6
.
Решение:
Так как медиана в прямоугольном треугольнике, проведённая к гипотенузе, равна половине этой гипотенузы, то определим величину гипотенузы:
По теореме Пифагора, имеем:
BC=AC2
−AB2=102
−62=100
−36=64=8.
Ответ: 8.
Приветствую читателей и подписчиков канала Тесты_математика!
Предлагаю к рассмотрению геометрическую задачу из программы экзамена ОГЭ.
1. Задача 1.
Площадь прямоугольного треугольника равна 65. Найти меньший катет, если больший катет на 3 больше.
2. Задача 2.
У треугольника со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
3. Задача 3.
В треугольнике АВС известно, что АС = 54; ВМ- медиана, ВМ = 43. Найдите АМ.
Большинство читателей наверно сразу смогут решить эти задачи. формула известна. Остаётся не ошибиться, и выбрать верный ответ.
Для выбора одного ответа из нескольких предлагаем пройти тест, в котором и определится правильности выбора ответа.
Пройдите тест из трёх вопросов по геометрии. Выберите один ответ, нажмите на кнопку. Тест можно проходить сколько уголдно раз.
Тест.
Спасибо за просмотр задачи и решение теста.
Делитесь ответами и решением и результатом – в социальных сетях.
Подпишитесь на канал, Тесты_математика!
чтобы не пропустить новые публикации!
#задачи на логику, #головоломки, #математика, #тесты
Прямоугольный треугольник
Разбор сложных заданий в тг-канале:
В прямоугольном треугольнике
1. Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего или на косинус прилежащего к этому катету острого угла.
2. Катет прямоугольного треугольника равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к этому катету острого угла.
3. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
4. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, противолежащий этому катету, равен 30°.
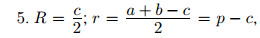
где a, b — катеты, а c — гипотенуза прямоугольного треугольника; r и R — радиусы вписанной и описанной окружностей соответственно
Теорема Пифагора и теорема, обратная теореме Пифагора
1. Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
2. Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то треугольник — прямоугольный
Средние пропорциональные в прямоугольном треугольнике
Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы (c) равен сумме квадратов катетов (a и b):
c2 = a2 + b2
Составим твой персональный план подготовки к ОГЭ
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Определение треугольника
Треугольник – многоугольник с тремя сторонами и тремя углами.

Угол ∠ A – угол, образованный сторонами A B и A C и противолежащий стороне B C .
Угол ∠ B – угол, образованный сторонами B A и B C и противолежащий стороне A C .
Угол ∠ C – угол, образованный сторонами C B и C A и противолежащий стороне A B .
Виды треугольников
Треугольник остроугольный, если все три угла в треугольнике острые.
Треугольник прямоугольный, если у него один из углов прямой ( = 90 ° ) .
Треугольник тупоугольный, если у него один из углов тупой.
Примеры:



Основные свойства треугольника:
- Против большей стороны лежит больший угол.
- Против равных сторон лежат равные углы.
- Сумма углов в треугольнике равна 180 ° .
- Если продолжить одну из сторон треугольника, например, A C , и взять на продолжении стороны точку D , образуется внешний угол ∠ B C D к исходному углу ∠ A C B .

Внешний угол равен сумме двух внутренних углов, не смежных с ним. ∠ B C D = 180 ° − ∠ A C B ∠ B C D = ∠ A + ∠ B
- Неравенство треугольника: любая из сторон треугольника меньше суммы двух других сторон и больше их разности.
Отрезки в треугольнике
Биссектриса угла – луч, выходящий из вершины угла и делящий его пополам.
Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне.
Свойства биссектрис треугольника:
- Биссектриса угла – геометрическое место точек, равноудаленных от сторон угла.
- Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам:

a b = m n
- Биссектрисы пересекаются в одной точке. Точка пересечения биссектрис – центр вписанной в треугольник окружности.
Замечание: биссектриса угла – это луч, а биссектриса треугольника – отрезок.
Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Свойства медиан треугольника:
- Медиана разбивает треугольник на два равновеликих треугольника (два треугольника, имеющих одинаковую площадь).
- Медианы треугольника пересекаются в одной точке. Точка пересечения медиан делит их в отношении 2:1, считая от вершины.

- Три медианы, проведенные в одном треугольнике, разбивают его на шесть равновеликих треугольников.

S 1 = S 2 = S 3 = S 4 = S 5 = S 6
Высота треугольника – это перпендикуляр, проведенный из вершины угла треугольника к прямой, содержащей противолежащую сторону этого треугольника.
Если треугольник остроугольный, то все три высоты будут лежать внутри треугольника. Если треугольник тупоугольный, то высоты, проведенные из вершин острых углов будут лежать вне треугольника, а высота, проведенная из вершины тупого угла будет лежать внутри треугольника.
Пример:


Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Свойство средней линии треугольника: средняя линия параллельна одной из его сторон и равна половине этой стороны.

m = a 2
Всего в треугольнике можно провести три средние линии. Три средние линии разбивают исходный треугольник на четыре равных треугольника. Площадь каждого маленького треугольника будет равна четверти площади большого треугольника.

Площадь треугольника
Площадь произвольного треугольника можно найти следующими способами:
- Полупроизведение стороны на высоту, проведенную к этой стороне.

S = 1 2 a ⋅ h a
- Полупроизведение двух сторон на синус угла между ними.

S = 1 2 a ⋅ b ⋅ sin α
- По формуле Герона.

S = p ( p − a ) ( p − b ) ( p − c ) p = a + b + c 2
Равнобедренный треугольник
Равнобедренным называется треугольник, у которого две стороны равны.
Равнобедренный треугольник может быть остроугольным, прямоугольным и тупоугольным.



Свойства равноберенного треугольника:
- В равнобедренном треугольнике углы при основании равны.
- В равнобедренном треугольнике медиана, высота и биссектриса, проведенные к основанию, совпадают.

Равносторонний треугольник
Равносторонним называется треугольник, у которого все стороны и все углы равны.

Площадь равностороннего треугольника находится по формуле S = a 2 3 4
Высота равностороннего треугольника находится по формуле h = a 3 2
Прямоугольный треугольник
Треугольник называется прямоугольным, если у него один из углов равен 90 ° .
Свойства прямоугольного треугольника:
- Сумма двух острых углов треугольника равна 90 ° .
- Катет, лежащий напротив угла в 30 ° , равен половине гипотенузы.
- Если катет равен половине гипотенузы, он лежит напротив угла в 30 ° .

a = c 2 c = 2 ⋅ a
- Медиана, проведенная из вершины прямого угла, равна половине гипотенузы.

m = c 2
- Пропорциональные отрезки в прямоугольном треугольнике

a = m ⋅ c b = n ⋅ c h = m ⋅ n
Теорема Пифагора
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

c 2 = a 2 + b 2
У прямоугольного треугольника катеты перпендикулярны друг другу, следовательно, площадь можно найти по формуле:
S = 1 2 a ⋅ b
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с треугольниками
Скачать домашнее задание к уроку 3.
