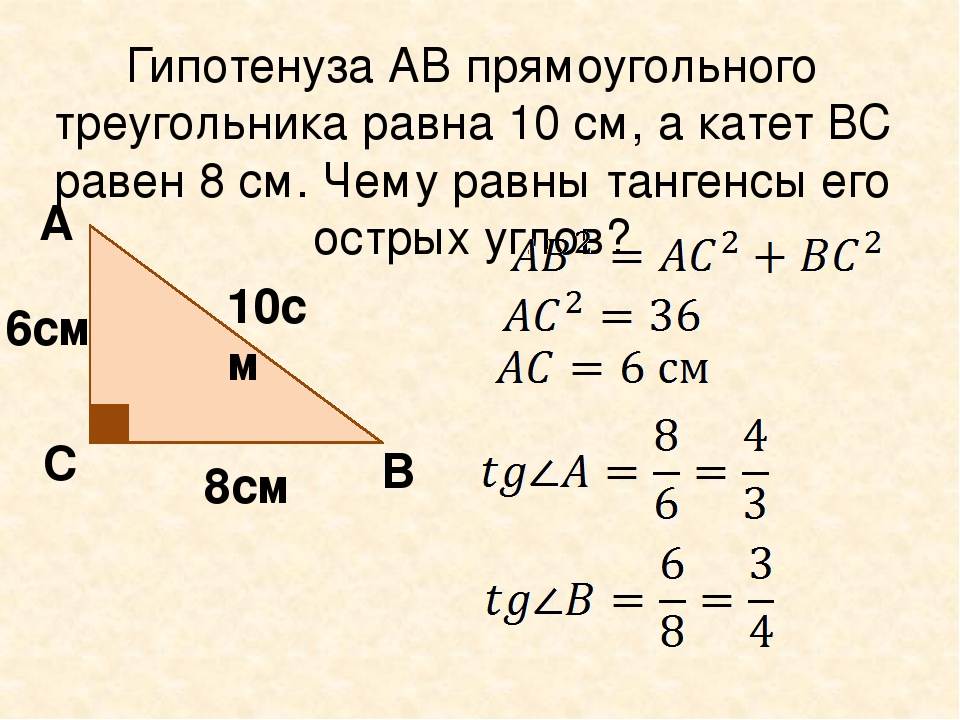
Уравнение прямоугольного треугольника – одно из наиболее узнаваемых в геометрии. Оно исходит из свойств прямоугольного треугольника и имеет следующий вид: а² + b² = c², где «a» и «b» – катеты, а «c» – гипотенуза.
Одна из задач, связанных с этим уравнением, заключается в том, чтобы найти сторону треугольника – катет – зная длину гипотенузы и одного из катетов. В этом блоке текста мы рассмотрим самый простой способ решить данную задачу.
Суть метода заключается в следующем: используя выражение для вычисления гипотенузы прямоугольного треугольника, решаем созданное квадратное уравнение. Вычисляем катет по известной гипотенузе и известному катету. Этот подход позволит найти требуемый катет.
Далее мы подробнее рассмотрим, каким образом это делать, и тщательно разберем все четыре возможные ситуации, чтобы вы могли сами решить любую задачу на поиск катета зная гипотенузу и один из катетов.
Основные понятия треугольника
Существует множество типов треугольников, которые отличаются между собой несколькими параметрами, такими как длина сторон, а также их взаимное расположение и отношения между углами.
Типы треугольников по длине сторон:
Равносторонний треугольник – треугольник, у которого все стороны равны по длине.
Равнобедренный треугольник – треугольник, у которого две стороны равны длине, а третья сторона отличается.
Разносторонний треугольник – треугольник, у которого все стороны имеют разное расстояние между собой.
Типы треугольников по углам:
Тупоугольный треугольник – треугольник, в котором один угол (угол А) превышает 90 градусов, самого большого угла, или прямого угла.
Прямоугольный треугольник – треугольник, который имеет один прямой угол (А).
Острый треугольник – треугольник, у которого все углы меньше 90 градусов.
Существенным свойством прямоугольного треугольника является следующее:
Теорема Пифагора – если в прямоугольном треугольнике правый угол А, цепной катет (ноликулярный) – б, гипотенуза – с, а противоположный катет – a, тогда квадрат гипотенузы с = a² + b².
Определение катетов и гипотенузы
Катеты – это две стороны, являющиеся противоположными углом, прямо противоположным углу. Катет тесно связан с другими сторонами треугольника путем теоремы Пифагора и других формул определенных для таких треугольников. Они могут быть найдены, если известна гипотенуза и один катет.
Гипотенуза – это самая длинная сторона прямоугольного треугольника. Гипотенуза соединяет два других угла треугольника. Как правило, в формуле пифагора гипотенуза является наименьшим пропорциональным знаком отношения между катетами, которые являются сторонами треугольника, расположенными под прямым углом друг к другу.
Теперь, давайте перейдем к определению катетов, зная гипотенузу и катет.
Это возможно с использованием формул, которые описывают свойства треугольника прямоугольного. Например, Формула Пифагора может быть использована для нахождения гипотенузы и является парой алгебраических уравнений, которые могут быть решены для того, чтобы найти сторону треугольника прямоугольного, например, в случае, когда одна сторона и гипотенуза известны.
Поскольку прямоугольный треугольник является треугольником с одним прямым углом и два касающихся угла, катеты и гипотенуза связаны функционально друг с другом путем теоремы Пифагора и других используемых формул.
Это заканчивает раздел статьи об определении катетов и гипотенузы.
Правильный треугольник
Определение правильного треугольника
Правильный треугольник – один из пяти основных типов треугольников в геометрии, наряду со сторонними треугольниками, равносторонними треугольниками, прямоугольными треугольниками и остроугольными и тупоугольными треугольниками.
Варианты оснований равнобедренного треугольника показывают, что все рёбра в него входят под одним углом. Это означает, что треугольник, образованный двумя основаниями и вершиной, является равнобедренным треугольником.
Площадь правильного треугольника
Площадь треугольника равна половине произведения его основания и высоты, однако если вы хотите быстро вычислить площадь правильного треугольника, вы можете воспользоваться следующим универсальным способом. Площадь правильного треугольника равна половине произведения его стороны и синуса угла между сторонами.
Вычисления треугольников могут быть полезными тем, кто изучает математику. Это может быть полезно для решения различных задач, как в повседневной жизни, так и в школах, колледжах и университетах.
Искривлённый треугольник
Определение искривлённого треугольника:
В неевклидовой геометрии, такой как гиперболическая геометрия, любая группа из трёх точек, никакие две из которых не лежат на одной прямой, определяет единственный треугольник. Это означает, что геометрия искривлённого треугольника основана на концепциях, отличных от стандартных треугольников в евклидовой геометрии.
Искривлённый треугольник в математике:
В математике, искривлённый треугольник может быть обнаружен в таких областях, как:
-
Гомология: Она связана с идеей искривлённых треугольников, когда мы рассматриваем искривлённые поверхности и трёхмерные пространства.
-
Тензорное исчисление: В ней можно изучать градиентные поля и искривлённые треугольники на искривлённых поверхностях.
-
Теория групп: В ней можно изучать искривлённые треугольники как представителей групп и их действия на пространствах.
Искривлённые треугольники могут быть изучены в математике, но их описание уходит далеко за рамки евклидовой геометрии. Они являются результатом исследований человечеством математических проявлений искривлённости и неевклидовых геометрий, которые приближают нас к пониманию сложного мира пространства и времени вокруг нас.
Правильный трапециевидно-обрезанный треугольник
Краткое описание
Правильный трапециевидно-обрезанный треугольник – это треугольник, который обладает следующими двумя свойствами: исходящие перпендикуляры из вершины основания являются показатель наушников величины основания, а основание трапеции является одной из сторон треугольника, которая не является красной стороной – гипотенузой.
Так, к примеру, если две стороны треугольника имеют размеры 3 см и 4 см, тогда гипотенуза могла бы быть равной 5 см, и тогда существует отношение пари произведений сторон треугольника (a, b, c): а/б = c/а, где a и b – катеты, а c – гипотенуза. В данном варианте a = 3 см, b = 4 см и c = 5 см, причем а/б = с/а = 2,5.
Свойства
Правильный трапециевидно-обрезанный треугольник обладает уникальными свойствами, которые можно объяснить исходя из понятия наушников: две стороны, которые являются боковыми, всегда расположены напрямую под основанием, и если бáзис – наклонная сторона, то две другие стороны будут перпендикулярны основанию трапеции.
Также следует заметить, что одна сторона гипотенузы треугольника может быть равна сумме сторон треугольников, в которых является основанием, так как при равном размере всех сторон треугольников их общая сторона гипотенузы является всегда равной сумме сторон оснований и гипотенузы соответствующих треугольников.
| Название стороны | Описание |
|---|---|
| Катеты | имеют равную длину и находятся между гипотенузой и основанием трапеции |
| Гипотенуза | самая длинная сторона, всегда находится между двумя катетами |
| Основание | имеет меньшую длину, чем катеты, и является наклонной стороной трапеции |
Таким образом, правильный трапециевидно-обрезанный треугольник обладает не только удивительным видом, но и прекрасными свойствами, которые позволяют ему обладать уникальными качествами среди других видов треугольников.
Треугольник Паскаля
Структура треугольника
Треугольник Паскаля состоит из двух древников, формирующих равнобедренный треугольник, и напоминает пирамидку чисел, которая расположена в виде ступеней. Каждый элемент строится на основе двух элементов из предыдущих строк: сверху и слева от него. Первая строка состоит из единицы, вторая – из чисел 1 и 1, а затем соответствующие номера строк складываются для получения новых чисел в последующих строках.
Квадратные треугольники
Квадратное треугольное число – это число, которое можно сформировать путём расположения равнобедренного треугольника с единичными цветами в таком порядке, чтобы каждая последующая строка была продолжением предыдущей. Первые четыре квадратных треугольных числа: 1, 3, 6, 10. Любая прямоугольная область, ограниченная треугольниками называется «треугольником Паскаля», потому что исключительные комбинации из данного набора каких-то элементов располагаются в этой области чисел, что позволяет анализировать сложную математическую статистику с помощью треугольника.
Зная катет и гипотенузу, можно решить эту задачу с помощью специальных формул. В треугольнике Паскаля сумма элементов каждой строки является квадратом числа ниже строки, которое находится справа от столбцов. Это происходит за счет представлений суммы и разности чисел каждого столбца в качестве квадратных треугольных чисел и их обратных, причем сумма квадратных треугольных чисел двух соседних столбцов составляет квадрат глубины треугольника, в которую уходит фигура.
Стиль CSS:
h2, h3 {
text-align: center;
font-weight: bold;
text-decoration: underline;
padding-bottom: 5px;
color: navy;
}
p {
text-align: justify;
font-family: Arial, sans-serif;
line-height: 1.6;
}
strong {
color: #F00;
}
em {
font-style: italic;
color: #00F;
}
Вычисление катетов по формуле Пифагора
| Входные данные | Формула Пифагора |
|---|---|
| Длина гипотенузы (a) | (a)^2 |
| Длина первого катета (b) | (b)^2 |
| Длина второго катета (c) | (c)^2 |
Чтобы найти неизвестные катеты, нужно решить это уравнение. Возьмем для примера треугольник и известно, что длина гипотенузы равна “a” и одна катет, назовем его “b”. Тогда мы можем представить формулу Пифагора следующим образом:
| Входные данные | Формула Пифагора |
|---|---|
| Длина гипотенузы (a) | a |
| Длина первого катета (b) | b |
| Длина второго катета (c) | √(a^2 – b^2) |
Здесь
означает квадратный корень. Получаемый ответ – это длина неизвестного катета, согласно теореме Пифагора.
Модификация Пифагоровой теоремы для трёх катетных треугольников
Однако, если мы имеем в виду систему из трёх подряд идущих катетных прямоугольных треугольников с общими катетами, то можно модифицировать Пифагорову теорему для таких случаев.
Проблема трёх катетных треугольников
Представим себе три подряд идущих катетных треугольника ABC, BCD и CDE. Это значит, что B и C – простые катеты, соответственно для треугольников ABC, BCD и CDE.
Модификация Пифагоровой теоремы

Если мы знаем гипотенузы a, b, и c обеих трёх треугольников и две стороны из трёх катетов, то можно определить третий катет. Для этого можно использовать модифицированную пифагорову теорему, выражая как:
d² = (b² – a²) и e² = (c² – b²).
Суммируя оба квадрата, мы можем определить третий катет p:
p² = (a² + c² – b²).
Таким образом, модифицированная Пифагорова теорема распространяется также на систему трех подряд идущих катетных прямоугольных треугольников с общими катетами, давая возможность определения недостающих сторон.
Вопрос-ответ:
Какие математические знания необходимо иметь, чтобы найти катет зная гипотенузу и угол между ними?
Чтобы найти катет, при условии выполнение гипотенузы и угла между ними, вам потребуется знания основ тригонометрии, а также понимание понятий катета и гипотенузы в прямоугольном треугольнике. В частности, вам понадобится умение работать с функциями синуса и косинуса, так как с их помощью вы сможете объяснить пропорции сторон прямоугольного треугольника.
Какую формулу следует использовать для нахождения катета в прямоугольном треугольнике, если известны гипотенуза и один из углов?
Для нахождения катета, если известны гипотенуза и один из углов (например, угол `A`), можно использовать следующую формулу: `a = b * sin(A)` или `b = a * sin(A)` (где `a` и `b` – катеты, `c` – гипотенуза и `A` – угол на стыке катетов и гипотенузы). Чтобы найти катеты, необходимо воспользоваться функции синуса для заданного угла, подставив гипотенузу и угол в соответствующую формулу.