поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,655 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,939 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
По теореме о сумме углов выпуклого многоугольника, сумма углов правильного пятиугольника равна 180º(5-2)=540º.
 Так как все углы правильного n-угольника равны между собой, каждый внутренний угол правильного пятиугольника равен 540º:5=108º (в частности, ∠A2A1A5=108º).
Так как все углы правильного n-угольника равны между собой, каждый внутренний угол правильного пятиугольника равен 540º:5=108º (в частности, ∠A2A1A5=108º).
Сумма внешних углов многоугольника, взятых по одному при каждой вершине, равна 360º. Поскольку все внешние углы правильного пятиугольника равны между собой, градусная мера каждого, например, угла 1, равна
∠1=360º:5=72º (можно было внешний угол искать как смежный с внутренним).
Каждый центральный угол правильного пятиугольника, например, угол A1O A2, равен
∠A1O A2=360º:5=72º.
Как и любой другой правильный многоугольник, правильный пятиугольник вписан в окружность и описан около окружности.
Соединив центр правильного многоугольника с его вершинами, получим пять равных равнобедренных треугольников.
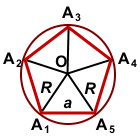
Основанием каждого такого треугольника равно стороне 5-угольника, боковые стороны равны радиусу описанной окружности, угол при вершине — центральному углу 5-угольника.
В треугольнике A1OA5
![]()
![]()
![]()
 Проведём из вершины высоту OF.
Проведём из вершины высоту OF.
По свойству равнобедренного треугольника, OF является также медианой и биссектрисой треугольника A1OA5, то есть
![]()
![]()
OF — радиус вписанной в A1A2A3A4A5 окружности: OF=r.
Рассмотрим прямоугольный треугольник A1OF.
По определению синуса,
![]()
откуда
![]()
![]()
Так как
![Rendered by QuickLaTeX.com [sin {36^o} = sqrt {frac{{5 - sqrt 5 }}{8}} ,]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-978b0fcccb82af5f73951d1811832f6d_l3.png)
то
![Rendered by QuickLaTeX.com [R = frac{a}{{2sqrt {frac{{5 - sqrt 5 }}{8}} }} = frac{{asqrt 8 }}{{2sqrt {5 - sqrt 5 } }} = frac{{a cdot 2sqrt 2 }}{{2sqrt {5 - sqrt 5 } }} = ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-37925508765b0e92c944807a15ed029f_l3.png)
![Rendered by QuickLaTeX.com [ = frac{{asqrt 2 }}{{sqrt {5 - sqrt 5 } }} = frac{{asqrt 2 cdot sqrt {5 + sqrt 5 } }}{{sqrt {5 - sqrt 5 } cdot sqrt {5 + sqrt 5 } }} = frac{{asqrt 2 cdot sqrt {5 + sqrt 5 } }}{{sqrt {{5^2} - {{(sqrt 5 )}^2}} }} = ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-3635f26a3c4a245681b619a78633459d_l3.png)
![]()
![]()
Таким образом, формула радиуса описанной около правильного пятиугольника окружности —
![]()
По определению котангенса,
![]()
![]()
Подставив значение котангенса 36°, получаем:
![]()
Итак, формула радиуса вписанной в правильный пятиугольник окружности
![]()
Применив формулу
![]()
можно найти площадь правильного пятиугольника. Здесь
![]()
следовательно, формула для нахождения площади A1A2A3A4A5
![]()
Все диагонали правильного пятиугольника равны.
Длина диагонали равна
![]()
Правильный пятиугольник
По теореме о сумме углов выпуклого многоугольника, сумма углов правильного пятиугольника равна 180º(5-2)=540º.
Так как все углы правильного n-угольника равны между собой, каждый внутренний угол правильного пятиугольника равен 540º:5=108º (в частности, ∠A2A1A5=108º).
Сумма внешних углов многоугольника, взятых по одному при каждой вершине, равна 360º. Поскольку все внешние углы правильного пятиугольника равны между собой, градусная мера каждого, например, угла 1, равна
∠1=360º:5=72º (можно было внешний угол искать как смежный с внутренним).
Каждый центральный угол правильного пятиугольника, например, угол A1O A2, равен
Как и любой другой правильный многоугольник, правильный пятиугольник вписан в окружность и описан около окружности.
Соединив центр правильного многоугольника с его вершинами, получим пять равных равнобедренных треугольников.
Основанием каждого такого треугольника равно стороне 5-угольника, боковые стороны равны радиусу описанной окружности, угол при вершине — центральному углу 5-угольника.
Проведём из вершины высоту OF.
По свойству равнобедренного треугольника, OF является также медианой и биссектрисой треугольника A1OA5, то есть
Рассмотрим прямоугольный треугольник A1OF.
Таким образом, формула радиуса описанной около правильного пятиугольника окружности —
Подставив значение котангенса 36°, получаем:
Итак, формула радиуса вписанной в правильный пятиугольник окружности
можно найти площадь правильного пятиугольника. Здесь
Все диагонали правильного пятиугольника равны.
Правильные многоугольники
Многоугольник – замкнутая ломаная линия. В школьной планиметрии изучают плоские линии, без самопересечений. Часть плоскости, ограниченная этой линией, также называется многоугольником. В этом смысле многоугольник имеет площадь. Многоугольник с n вершинами, а значит и с n сторонами, называется n-угольником.
Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.

На этом рисунке
1 – простая (без самопересечений) ломаная линия, имеет 6 звеньев и 7 вершин;
2 – шестизвенная ломаная, имеющая одно самопересечение;
3 – выпуклый многоугольник, пятиугольник;
4 – невыпуклый многоугольник, десятиугольник.
Итак, слово “правильный” в условии задачи сразу говорит нам о том, что все стороны и все углы многоугольника одинаковые. Количество углов (вершин) и количество сторон определяем по названию многоугольника. Далее в формулах и задачах будем обозначать это количество символом n.

и так далее.
правильный пятиугольник.
Чтобы построить другие правильные многоугольники, задайте количество сторон n (от 3-ёх до 12-ти).
Многоугольники можно вписывать в окружность или описывать вокруг неё. Однако, это получается не для всех и не всегда. Говоря математическим языком, не всегда существует окружность, которая удовлетворяет определению.
Если многоугольник вписан в окружность, то можно сказать, что окружность описана около многоугольника, или, наобррот, если многоугольник описан около окружности, то окружность вписана в него. Такие формулировки тоже встречаются в условиях геометрических задач. Чтобы не путаться запомним – вписанная фигура находится внутри описанной около неё.
 Четырехугольник вписан в окружность.
Четырехугольник вписан в окружность.
 Четырехугольник описан около окружности.
Четырехугольник описан около окружности.
Рассмотрим другие примеры.
Произвольный прямоугольник всегда можно вписать в окружность, но описать нельзя. Описать получится только тогда, когда прямоугольник – это квадрат.

Параллелограмм нельзя вписать в окружность. Описать можно только ромб.

В окружность можно вписать только равнобочную трапецию, описать около окружности тоже можно не всякую трапецию.

Существование вписанной и описанной окружности для произвольных многоугольников связано с величинами их углов и сторон. Есть специальные теоремы, позволяющие определить будет ли многоугольник являться вписанным и/или описанным. Сейчас мы на них останавливаться не будем. Сейчас важно отметить следующее:
 Треугольник вписан в зеленую окружность, описан вокруг синей.
Треугольник вписан в зеленую окружность, описан вокруг синей.
 Пятиугольник вписан в зеленую окружность, описан вокруг синей.
Пятиугольник вписан в зеленую окружность, описан вокруг синей.
Правильные многоугольники имеют центр, точнее совпадающие в одной точке центр симметрии, центр тяжести, центры вписанной и описанной окружностей. Если соединить с центром правильного n-угольника его вершины, то многоугольник разобьется на n равных равнобедренных треугольников.

Боковые стороны этих треугольников (на рисунке – зелёные отрезки) будут равны радиусу описанной окружности (R), а их основания (на рисунке – красные отрезки) равны стороне многоугольника (a).
Пользуясь таким чертежом, можно вычислять различные отрезки и углы в многоугольнике на основе знаний о равнобедренных треугольниках.
Например, угол AOB в пятиугольнике равен 360/5 = 72° (360° – полный круг). Угол OAB равен углу OBA и равен (180 − 72)/2 = 54°. Угол CAB = 2×54 = 108°. Сумма всех углов при вершинах пятиугольника 5×108 = 540°.
При решении задач на правильный многоугольник, часто бывает удобно дорисовать внешнюю (описанную) или внутреннюю (вписанную) окружность даже, если они не упоминаются в условии, и соединить вершины и точки касания с центром. Получатся равнобедренные или прямоугольные треугольники, о которых много известно, поэтому задачу будет решать легко.
 Синие треугольники равнобедренные потому, что их боковые стороны это радиусы одной и той же окруюности.
Синие треугольники равнобедренные потому, что их боковые стороны это радиусы одной и той же окруюности.
 Оранжевые треугольники прямоугольные потому, что касательная к окружности перпендикулярна её радиусу.
Оранжевые треугольники прямоугольные потому, что касательная к окружности перпендикулярна её радиусу.
На ОГЭ по математике в 9-ом классе и на ЕГЭ в 11-ом встречаются задачи с правильными многоугольниками, часто они включают в себя и вписанную или описанную окружность.
Задачи на правильные многоугольники
Внимание: задачи с решениями, но они временно скрыты. Сначала сделайте попытку решить задачу самостоятельно, и только после этого нажимайте кнопки “Посмотреть ответ” и “Посмотреть решение”. Cовпадать обязан только ответ. Способ решения может отличаться.
Доказать, что площадь правильного n-угольника можно вычислить по формуле S = pr, где p – полупериметр многоугольника, r – радиус вписанной окружности.
Ответ: S = pr
Середины сторон правильного восьмиугольника ABCDEFGH последовательно соединили. Какую часть площади исходного многоугольника занимает получившийся многоугольник KLMNPQRS ?
Ответ дайте в процентах, округлив до целых.
Примечание: Отношение сторон многоугольников можно найти иначе, например, достроить другие внутренние отрезки и рассмотреть прямоугольные треугольники.
Ответ: 85
В круг вписан правильный шестиугольник ABCDEF. Найти площадь круга, если радиус окружности, вписанной в треугольник ADE, равен r.
Определим площадь треугольника ADE двумя способами:
через произведение катетов [S = frac<cdot> <2>= frac><2>cdotfrac<2>cdotfrac<1> <2>= frac><8>; ] и через полупериметр и заданный радиус вписанной окружности [S = frac<2>cdot r = frac<2>cdot big(frac><2>+frac<2>+ xbig) = frac + 3) > <4>]
Теперь можно составить уравнение и решить его относительно х.
[ frac> <8>= frac + 3)> <4>] [ frac> <2>= frac + 3)> <1>] [x = frac <2r(sqrt<3>+ 3)><sqrt<3>> = 2r(1 + sqrt<3>)] Так как AD = x – диаметр окружности, то её площадь можно найти по формуле [S = frac <pi d^2> <4>= frac <pi (2r)^2 (1 + sqrt<3>)^2> <4>= pi r^2(1 +2 sqrt <3>+ 3) = pi r^2(4 + 2sqrt<3>) = 2pi r^2(2 + sqrt<3>)]
Ответ: 2πr 2 (2 + √3 _ )
Найти отношение площади правильного двадцатичетырёхугольника, вписанного в некоторую окружность, к площади правильного двенадцатиугольника, вписанного в ту же окружность.
Ответ: 4sin15° ≈ 1,04
 Точка O – центр правильного шестиугольника ABCDEF, в котором AC = 10,5. Найдите радиус окружности, касающейся окружностей, описанных около треугольников AOB, COD и EOF.
Точка O – центр правильного шестиугольника ABCDEF, в котором AC = 10,5. Найдите радиус окружности, касающейся окружностей, описанных около треугольников AOB, COD и EOF.
Примечание: Если Вы не догадались использовать свойство медиан треугольника, то можно рассматривать треугольники AOC, AOH и т.п., теорему косинусов или теорему Пифагора. Ответ будет получен с чуть большим объёмом вычислений.
Ответ: 7
 Точка O – центр правильного шестиугольника ABCDEF со стороной 7. Найдите радиус окружности, касающейся окружностей, описанных около треугольников BOD, DOF и BOF.
Точка O – центр правильного шестиугольника ABCDEF со стороной 7. Найдите радиус окружности, касающейся окружностей, описанных около треугольников BOD, DOF и BOF.
Правильный пятиугольник — построение, свойства и формулы
Бывают задачи на построение и нахождение некоторых геометрических параметров правильного пятиугольника. Построить фигуру непросто. Для этого математики рекомендуют несколько методик, позволяющих выполнить операцию более точно или за короткий промежуток времени. У фигуры есть свойства, а также формулы, позволяющие найти ее геометрические характеристики.

Точное построение фигуры
Специалисты рекомендуют некоторую последовательность действий, по которым построить правильный пятиугольник очень просто. Для операции необходимы обыкновенная тетрадь в клеточку, циркуль, карандаш, резинка и линейка. Следует выполнить некоторые шаги:
Если все пункты алгоритма выполнены правильно, то должен получиться пентагон, изображенный на рисунке 1:

Этот способ следует применять для точных построений и чертежей деталей. Однако для решения задач, в которых необходимо схематически изобразить пятиугольник, этот вариант не подойдет.
Алгоритм Биона
Прием Биона является менее точным методом, чем первый. Он позволяет построить любой правильный многоугольник, вписанный в произвольный круг. Для операции необходимо воспользоваться алгоритмом (шаблоном) Биона, имеющим такой вид:

Погрешность построения многоугольника с 5, 7, 9 и 10 сторонами при использовании алгоритма довольно маленькая. Ее значения равно 3,2%. Однако при n>10 погрешность составляет не более 11%.
Приближенные методы
Существует несколько методов, позволяющих приближенно изобразить фигуру. Однако оптимальным является построение пентагона (рис. 2), используя две окружности (описанную и вписанную).
Метод известного математика А. Дюрера является оптимальным среди остальных, поскольку на построение затрачивается минимальное количество времени. Для его реализации следует выполнить определенные шаги алгоритма Дюрера:

Существует еще один метод — построение пятиугольника из десятиугольника, который вписан в окружность. Для этого следует соединить его вершины через одну. Однако способ рекомендуется применять только в том случае, когда исходная фигура уже имеется. Кстати, его следует строить также методом А. Дюрера.
Математики рекомендуют еще один простой способ. Для его реализации необходимо начертить окружность с диаметром АD. После этого его нужно поделить на 3 равные части, то есть AB = BC = CD. Затем из точки С следует опустить перпендикуляры на окружность. Обозначить места пересечения точками E и F. Проделать такую же процедуру с точкой B, обозначив пересечения точками G и H. Остается лишь соединить все точки отрезками.
Признаки и свойства
Не всегда получается верно идентифицировать пятиугольник. Для этого математики предлагают признаки, которые применимы только к правильной фигуре. К ним можно отнести следующие:
Следует отметить, что признаки справедливы для любого правильного многогранника. Пять осей симметрии имеет правильный пятиугольник (сколько сторон, столько и осей). Пентагон обладает некоторыми свойствами, которые будут очень полезны при решении задач. К ним можно отнести следующие:

Однако свойств недостаточно при решении задач, поскольку существуют некоторые формулы и соотношения для нахождения основных параметров пентагона.
Расчет параметров
С помощью соотношений можно легко найти необходимые характеристики любой фигуры. Однако в некоторых источниках не указаны условные обозначения известного параметра пентагона. Это существенно затрудняет понимание формулы, а также ее дальнейшее использование. Перед изучением следует нарисовать фигуру и обозначить некоторые величины, которыми могут быть диагонали, стороны, апофемы и радиусы.

Рекомендуется использовать различные литеры или буквенные обозначения. Недопустимо пронумеровывать вершины, поскольку при вычислениях можно ошибиться. Нельзя использовать вместо букв цифры при обозначениях. Например, пентагон ABCDE является правильной записью. Допускается применение чисел в индексах, а именно, в пятиугольнике правильного типа ABCDE при пересечении его диагоналей образовался пентагон A1B1C1D1E1.
Математики рекомендуют обозначать только промежуточные фигуры или их проекции литерами с индексами. Для каждой новой фигуры следует вводить другие обозначения. Не следует использовать зарезервированные переменные. Например, центр окружности в точке P является недопустимой записью, поскольку такой буквой обозначается периметр.
Условные обозначения
Для нахождения основных величин пентагона следует обозначить некоторые его параметры. Фигура имеет следующие обозначения:
Значения сторон равны между собой. Площадь правильного пятиугольника — характеристика двумерной фигуры, которая показывает ее размерность. Периметром называется сумма всех 5 сторон. Полупериметр вычисляется по следующему соотношению: p = P / 2. Диагонали — отрезки, проведенные из одной вершины к противоположной (несмежной).
Соотношения и формулы
После обозначений следует переходить к рассмотрению основных формул, при помощи которых можно вычислять параметры фигуры. Сторону можно найти, воспользовавшись такими соотношениями:
Радиус вписанной окружности в пентагон можно найти, используя тригонометрические функции. Однако существует также формула, позволяющая вычислить приближенное значение. Это необходимо в том случае, когда под рукой нет специального онлайн-калькулятора, компьютера или таблиц Брадиса. Формулы для нахождения радиуса вписанной окружности:

Математики также рекомендуют описать вокруг пентагона окружность. Это расширит возможности по поиску его основных характеристик. Однако ее радиус следует вычислить. Формулы для его нахождения выглядят таким образом:
Периметр определяется просто: Р = 5а. Значение полупериметра эквивалентно половине периметра, то есть p = P / 2 = 5a / 2 = 2,5a. Площадь можно найти, используя такие формулы:

Высота правильного пятиугольника (h) — отрезок, проведенный из центра на любую из сторон. Она делит ее на две равные части, поскольку является биссектрисой и медианой равнобедренного треугольника. У последнего две стороны — радиусы описанной окружности, а третья — сторона пентагона. Высота называется также апофемой и проекцией на «а». Вычисляется ее значение по формуле h = a * tg(72) / 2.
Величина Ф является отношением площади пентагона (S) к площади (S1) правильного пятиугольника, полученного при пересечении диагоналей первого: S / S1 = Ф^4 = 3Ф + 2 = (3 * 5^(1/2) + 7) / 2. Длина диагонали находится по такому соотношению: d = [Ф * 5^(1/2) * R]^(1/2).
Таким образом, при решении задач необходимо знать основные признаки, свойства, соотношения и формулы для нахождения основных характеристик пентагона. Практика обязательна, поскольку теоретические знания без практического применения бесполезны.
[spoiler title=”источники:”]
http://mathematichka.ru/school/geom_figures/Regular_polygon_1.html
http://sprint-olympic.ru/uroki/geometrija/85022-pravilnyi-piatiygolnik-postroenie-svoistva-i-formyly.html
[/spoiler]
Какова градусная мера каждого угла правильного пятиугольника?
MichaelMS
Профи
(664),
закрыт
12 лет назад
Лучший ответ
Советы Депутатам
Искусственный Интеллект
(223891)
12 лет назад
У меня получилось 108 градусов.
Соединим все углы с центром и получим 5 треугольников. Угол при центре 360: 5 = 72
на 2 оставшихсяугла остается 180 – 72 = 108
2 угла соседних треугольников и будут в сумме составлять искомый угол правильного пятиугольника
Остальные ответы
God of war
Просветленный
(42452)
12 лет назад
Сумма всех углов равна 360 градусов. Получается, в правильном пятиугольнике каждый угол равен 72 градусам.
Rellik 123
Мудрец
(15240)
12 лет назад
ну ты мозг
Похожие вопросы
Загрузить PDF
Загрузить PDF
В геометрии угол — это фигура, которая образована двумя лучами, которые выходят из одной точки (она называется вершиной угла). В большинстве случаев единицей измерения угла является градус (°) — помните, что полный угол или один оборот равен 360°. Найти значение угла многоугольника можно по его типу и значениям других углов, а если дан прямоугольный треугольник, угол можно вычислить по двум сторонам. Более того, угол можно измерить с помощью транспортира или вычислить с помощью графического калькулятора.
-

1
Сосчитайте число сторон многоугольника. Чтобы вычислить внутренние углы многоугольника, сначала нужно определить, сколько у многоугольника сторон. Обратите внимание, что число сторон многоугольника равно числу его углов.[1]
- Например, у треугольника 3 стороны и 3 внутренних углов, а у квадрата 4 стороны и 4 внутренних углов.
-

2
Вычислите сумму всех внутренних углов многоугольника. Для этого воспользуйтесь следующей формулой: (n – 2) x 180. В этой формуле n — это количество сторон многоугольника. Далее приведены суммы углов часто встречающихся многоугольников:[2]
- Сумма углов треугольника (многоугольника с 3-мя сторонами) равна 180°.
- Сумма углов четырехугольника (многоугольника с 4-мя сторонами) равна 360°.
- Сумма углов пятиугольника (многоугольника с 5-ю сторонами) равна 540°.
- Сумма углов шестиугольника (многоугольника с 6-ю сторонами) равна 720°.
- Сумма углов восьмиугольника (многоугольника с 8-ю сторонами) равна 1080°.
-

3
Разделите сумму всех углов правильного многоугольника на число углов. Правильный многоугольник это многоугольник с равными сторонами и равными углами. Например, каждый угол равностороннего треугольника вычисляется так: 180 ÷ 3 = 60°, а каждый угол квадрата находится так: 360 ÷ 4 = 90°.[3]
- Равносторонний треугольник и квадрат — это правильные многоугольники. А у здания Пентагона (Вашингтон, США) и дорожного знака «Стоп» форма правильного восьмиугольника.
-

4
Вычтите сумму всех известных углов из общей суммы углов неправильного многоугольника. Если стороны многоугольника не равны друг другу, и его углы также не равны друг другу, сначала сложите известные углы многоугольника. Теперь полученное значение вычтите из суммы всех углов многоугольника — так вы найдете неизвестный угол.[4]
- Например, если дано, что 4 угла пятиугольника равны 80°, 100°, 120° и 140°, сложите эти числа: 80 + 100 + 120 + 140 = 440. Теперь вычтите это значение из суммы всех углов пятиугольника; эта сумма равна 540°: 540 – 440 = 100°. Таким образом, неизвестный угол равен 100°.
Совет: неизвестный угол некоторых многоугольников можно вычислить, если знать свойства фигуры. К примеру, в равнобедренном треугольнике две стороны равны и два угла равны; в параллелограмме (это четырехугольник) противоположные стороны равны и противоположные углы равны.
Реклама
-

1
Помните, что в любом прямоугольном треугольнике один угол всегда равен 90°. Это так, даже если прямой угол никак не отмечен или его значение не указано. Таким образом, один угол прямоугольного треугольника всегда известен, а другие углы можно вычислить с помощью тригонометрии.[5]
-

2
Измерьте длину двух сторон треугольника. Самая длинная сторона прямоугольного треугольника называется гипотенузой. Прилежащая сторона это сторона, которая находится возле неизвестного угла. Противолежащая сторона — это сторона, которая находится напротив неизвестного угла. Измерьте две стороны, чтобы вычислить неизвестные углы треугольника.[6]
Совет: воспользуйтесь графическим калькулятором, чтобы решить уравнения, или найдите онлайн-таблицу со значениями синусов, косинусов и тангенсов.
-

3
Вычислите синус угла, если вам известны противолежащая сторона и гипотенуза. Для этого подставьте значения в уравнение: sin(x) = противолежащая сторона ÷ гипотенуза. Например, противолежащая сторона равна 5 см, а гипотенуза равна 10 см. Разделите 5/10 = 0,5. Таким образом, sin(x) = 0,5, то есть x = sin-1 (0,5).[7]
- Если у вас есть графический калькулятор, введите 0,5 и нажмите клавишу sin-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 30°.
-

4
Вычислите косинус угла, если вам известны прилежащая сторона и гипотенуза. Для этого подставьте значения в уравнение: cos(x) = прилежащая сторона ÷ гипотенуза. Например, прилежащая сторона равна 1,67 см, а гипотенуза равна 2 см. Разделите 1,67/2 = 0,83. Таким образом, cos(x) = 0,83, то есть x = cos-1 (0,83).[8]
- Если у вас есть графический калькулятор, введите 0,83 и нажмите клавишу cos-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 33,6°.
-

5
Вычислите тангенс угла, если вам известны противолежащая и прилежащая стороны. Для этого подставьте значения в уравнение: tg(x) = противолежащая сторона ÷ прилежащая сторона. Например, противолежащая сторона равна 75 см, а прилежащая сторона равна 75 см. Разделите 75/100 = 0,75. Таким образом, tg(x) = 0,75, то есть x = tg-1 (0,75).[9]
- Если у вас есть графический калькулятор, введите 0,75 и нажмите клавишу tg-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 36,9°.
Реклама
Советы
- Названия углов соответствуют их значениям. Угол в 90° — это прямой угол. Угол в 180° — это развернутый угол. Угол, который лежит между 0° и 90° — это острый угол. Угол, который лежит между 90° и 180° — это тупой угол. Угол, который лежит между 180° и 360° — это невыпуклый угол.
- Если сумма двух углов равна 90°, они называются дополнительными. Запомните: два острых угла прямоугольного треугольника всегда являются дополнительными. Если же сумма двух углов равна 180°, они называются смежными.
Реклама
Об этой статье
Эту страницу просматривали 236 588 раз.
