Определение кажущейся молекулярной массы и параметров состояния смеси
В
теорию газовых смесей введено понятие
о средней
(кажущейся) молекулярной массе смеси
см,
т.е. о молекулярной массе такого
воображаемого однородного газа, который
по своим свойствам аналогичен
рассматриваемой смеси.
Находится
кажущаяся молекулярная масса следующим
образом. Из определения киломоля вытекает
равенство, справедливое для любого
однородного газа:
![]() , (24)
, (24)
где n
– количество вещества компонента, моль.
Для смеси по
аналогии можно записать:
![]() . (25)
. (25)
Отсюда, из равенства:
![]() (26)
(26)
следует,
что:
 , (27)
, (27)
где ![]() ;
;![]() ;
;
…;![]() – мольные доли компонентов смеси,моль.
– мольные доли компонентов смеси,моль.
Поскольку
![]() то среднюю молекулярную массу можно
то среднюю молекулярную массу можно
выразить:
![]() . (28)
. (28)
Если
известен массовый состав смеси, то
кажущуюся молекулярную массу смеси
вычисляют по уравнению:
 . (29)
. (29)
Если
известен объемный состав смеси (объемная
доля компонентов), то плотность смеси
газов можно вычислить из соотношений:
![]() . (30)
. (30)
Если
газовая смесь задана массовыми долями,
то плотность смеси можно определить из
соотношения:
 . (31)
. (31)
Удельный
объем смеси представляет величину,
обратную плотности смеси:
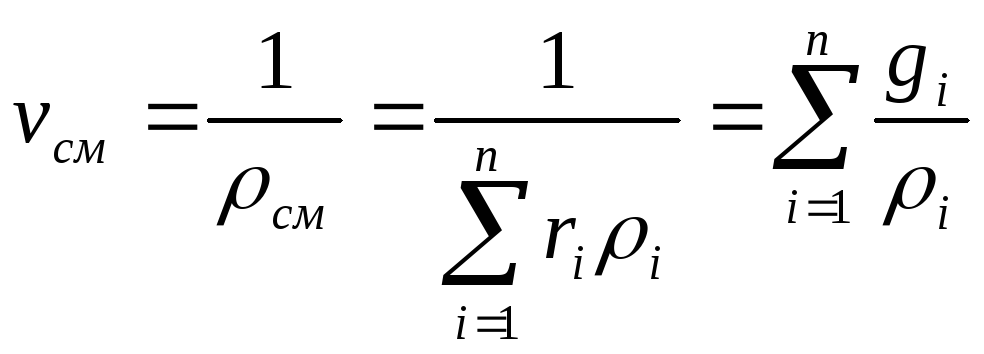 . (32)
. (32)
Объемные
доли компонентов смеси удобно использовать
для вычисления парциальных давлений
ее составных частей. Из уравнения:
![]() , (33)
, (33)
следует,
что:
![]() , (34)
, (34)
т.е.
для любого компонента смеси можно
записать:
![]() . (35)
. (35)
24 Теплоемкость
Теплоемкостью
называется количество теплоты, которое
необходимо подвести к какой-либо
количественной единице рабочего тела,
чтобы нагреть ее на
1 градус (1
°С или 1
К).
Истинная
теплоемкость
– производная количества теплоты по
температуре, она определяется в виде
отношения:
![]() , (36)
, (36)
откуда:
 . (37).
. (37).
Теплоемкость
зависит от характера процесса, при
котором подводится или отводится
теплота, поэтому при экспериментальном
определении ее значения обычно используют
два термодинамических процесса,
протекающих при постоянном объеме
![]() и давлении
и давлении![]() .
.
Значения теплоемкостей![]() и
и![]() для различных веществ сведены в таблицы.
для различных веществ сведены в таблицы.
Подведенная
при постоянном объеме теплота, когда
dl=0,
расходуется только на изменение
внутренней энергии. При постоянном
давлении некоторое количество теплоты
идет также на совершение работы, поэтому
для изменения температуры рабочего
тела на 1 градус при P
= const
требуется большее количество теплоты,
чем при v
= const
и, следовательно
![]() .
.
В
зависимости от способа определения
количества рабочего тела (т.е. от
количественной единицы измерения
рабочего тела, которую необходимо
нагреть) теплоемкости делят на:
Все
они связаны м/у собой соотношениями:
![]() ; (38)
; (38)
![]() ; (39)
; (39)
![]() . (40)
. (40)
Теплоемкости
![]() и
и![]() газа не зависят ни от объема, ни от
газа не зависят ни от объема, ни от
давления, и являются однозначными
функциями температуры. Иногда, в
приближенных расчетах, зависимостью
от температуры пренебрегают и значения
теплоемкости принимают постоянными.
Тогда в соответствии с выражением (37):
![]() . (41)
. (41)
В
большинстве случаев функцию С=f(Т)
(см. рисунок 3) приходится учитывать и
использовать для определения количества
подведенной или отведенной теплоты,
которая численно равна площади под
характеристикой 1-2 процесса. Количество
теплоты можно найти, если использовать
средние значения теплоемкости Сср,
при V = const
или Р = const
определяются отношением:
![]() . (42)
. (42)

Рисунок 3 –
Зависимость теплоемкости от температуры
В
этом случае площадь а34в, равна площади
а12в. С помощью Сср,
можно рассчитать количество теплоты
по формуле аналогичной выражению (42).
Если
необходимо получить количество
подведенной теплоты в интервале
температур T1
– T2
, то
поступают следующим образом: сначала
определяют количество теплоты
![]() ,
,
![]() ,
,
а затем:
![]() . (43)
. (43)
Для
многих теплотехнических расчетов
зависимость С=f(Т)
принимают линейной, тогда:
![]() . (44)
. (44)
В этом случае
![]() , (45)
, (45)
тогда:
![]() . (46)
. (46)
Если
рабочим телом является смесь газов, то
ее теплоемкость зависит от состава
смеси:
 (47)
(47)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

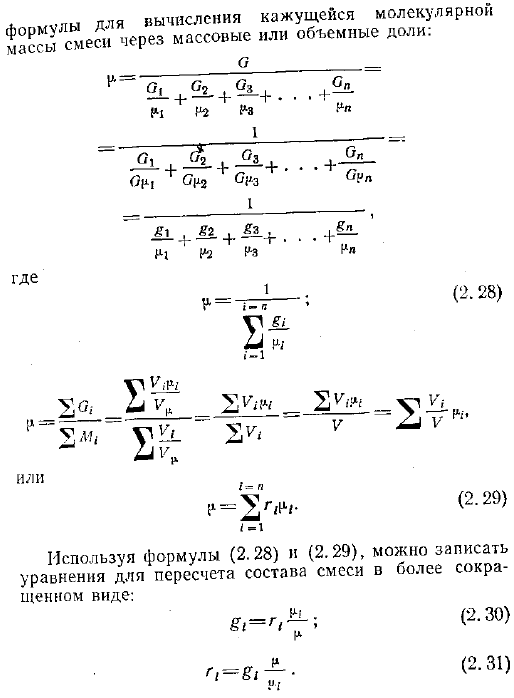


Кажущаяся молекулярная масса смеси
- Для смешанных газов, понятие молекулярной массы является произвольным. Напомним, что молекулярная атомная масса-это относительное число, которое указывает, во сколько раз больше массы молекулы атома.
При установившемся режиме следует рассматривать три погрешности, обусловленные теплопроводностью, неполным восстановлением температуры и излучением, и, кроме того, благодаря неустановившимся температурам дополнительно может появиться погрешность, обусловленная тепло- емкостью.
Людмила Фирмаль
Это вещество составляет 1 12 массы атома углерода или более. Конечно, единственно верное значение для смеси показать нельзя, так как в смеси газов присутствуют молекулы разной массы Молекулярная масса. Таким образом, для характеристики смеси вводится понятие кажущейся молекулярной массы.
- Формула 2. 19, молекулярная масса компонента выражается как отношение массы газа к числу молей конкретного газа. 2.26 Аналогично, кажущаяся молекулярная масса газогазовой смеси представляет собой отношение общей массы смеси к общему числу молей всех компонентов Да. 2М м 2.27.
В таком случае надо попытаться увеличить теплообмен конвекцией, уменьшив диаметр термометра (очень тонкие проволочные термопары) или искусственно увеличив скорость газа, обтекающего термометр.
Людмила Фирмаль
Выражение 2.19 или — Экспресс 6 А4 долларов По формулам 2.20 и 2.23 из LG,-Vy, можно найти. Мул для вычисления кажущихся молекул YsGy смесь по массовой доле или объемной доле О л 21 ч — -.. — Х 3 Один 01 г. −23- 4 -Мне очень жаль.- — H 7 2 Один Один Куда Один Из VII — 1 2. Двадцать восемь Ул У. Р. Х0 -,,, 2 — 2 2 2 г В Или 2.29 северный 2Г П I-1 Используя формулы 2.28 и 2.29, можно описать уравнения для пересчета состава смеси в более сокращенном виде. Г 2.30 2.31
Смотрите также:
- Методические указания по теплотехнике

Выразим формально газовую постоянную смеси R по формуле (1.6), введя кажущуюся молекулярную массу смеси ц,. [c.41]
Газовую постоянную смеси газов (/ (. ) можно выразить или через газовые постоянные отдельных компонентов, входящих в смесь, или через кажущуюся молекулярную массу смеси [c.30]
Кажущуюся молекулярную массу смеси определяем из уравнения (30) [c.32]
Заметим, что величину р = СШ, т. е. отношение массы всей смеси в килограммах к общему числу киломолей, называют иногда кажущейся молекулярной массой смеси. [c.181]
Полезное во многих расчетах понятие кажущейся молекулярной массы смеси р,см можно определить следующим образом [c.148]
Кажущаяся молекулярная масса смеси 148 Карно теорема 52 [c.458]
Здесь [,1см – так называемая кажущаяся молекулярная масса смеси, равная [c.10]
Кажущаяся молекулярная масса смеси. При расчетах с идеально-газовыми смесями удобно пользоваться так называемой кажущейся молекулярной массой смеси, являющейся -отношением массы смеси к суммарному количеству молей компонентов [c.21]
Кажущаяся молекулярная масса смеси 21 Калорические свойства вещества 39, 95, 114, 141, 154, 164, 171, 183 Калория 27 [c.505]
При расчетах удобно использовать понятие кажущейся молекулярной массы смеси [c.142]
В механических смесях молекулы отдельных газов не вступают в химическое соединение, поэтому нельзя говорить о действительной молекулярной массе смеси. Вследствие этого вводится условное представление о средней (кажущейся) молекулярной массе смеси, под которой понимается молекулярная масса воображаемого газа, заменяющего действительную смесь и состоящего из одинаковых, средних по массе молекул. Масса такой средней молекулы равна массе смеси, деленной на число ее молекул. [c.30]
Найдем кажущуюся молекулярную массу смеси вычисляем ее для каждого компонента g . [c.28]
По уравнению (46) можно определить кажущуюся молекулярную массу смеси, если она задана объемными долями. [c.28]
Определим кажущуюся молекулярную массу смеси по уравнению [c.29]
Определить мольные доли Zi каждого газа в смеси, кажущуюся молекулярную массу смеси, удельную газовую постоянную, о ий объем смеси, парциальные давления и объемы. [c.24]
Определить массовые я объемные доли двуокиси углерода и кислорода, кажущуюся молекулярную массу смеси и ее газовую постоянную после того, как перегородка будет убрана и процесс смешения закончится. [c.26]
При расчетах, производимых с газовыми смесями, удобно пользоваться некоторой условной величиной — средней (кажущейся) молекулярной массой смеси. [c.112]
По аналогии с этим кажущейся молекулярной массой смеси газов называется отнощение общей массы смеси к общему числу молей всех компонентов [c.30]
Кроме того, газовая постоянная смеси может быть вычислена по уравнению (2. 12), если известна кажущаяся молекулярная масса смеси ,1. [c.32]
Кажущуюся молекулярную массу смеси определяем по формуле [c.36]
Кажущаяся молекулярная масса смеси р,. Согласно закону Авогадро плотности газов пропорциональны их молекулярным массам, поэтому после замены р а ц уравнение (1-30) приводится к виду [c.20]
Кажущаяся молекулярная масса смеси л. В соответствии с уравнением (1-11) молекулярные массы газа пропорциональны их плотностям, поэтому, заменяя в уравнении (1-34) р на г, получаем [c.21]
Пример 1-7. Атмосферный воздух состоит по объему нз 21% кислорода и 79% азота. При нормальных условиях определить плотность, газовую постоянную и кажущуюся молекулярную массу смеси. Найти также парциальное давление компонентов. [c.23]
Молекулярную массу смеси [Хт в расчетах часто называют кажущейся молекулярной массой смеси, которая равна отношению массы сМеси G к суммарному количеству вещества компонентов G в молях. [c.25]
Из уравнения (26) легко получить значение так называемой кажущейся молекулярной массы газовой смеси [c.29]
Чтобы решать практические задачи, касающиеся газовых смесей, необходимо уметь определять по давлениям отдельных компонентов давление смеси, находить парциальные давления компонентов смеси по давлению смеси, выполнять пересчет объемного состава на массовый и, наоборот, определять плотность, удельный объем, газовую постоянную смеси и ее кажущуюся молекулярную массу. [c.29]
Для решения ряда практических задач удобно пользоваться понятием о кажущейся молекулярной массе газовой смеси. Под последней понимают величину численно равную киломолю смеси. [c.30]
Молекулярную массу смеси называют кажущейся, так как в действительности для газовой смеси понятия киломоля и молекулярной [c.31]
Пользуясь понятиями массовых и объемных долей и кажущейся молекулярной массы, а также приведенными выше выражениями, для них можно вывести ряд формул, удобных для решения задач на газовые смеси. В табл. 3-1 дается сводка этих формул. [c.33]
В соответствии с уравнением (1-55) кажущаяся молекулярная масса рассматриваемой смеси одноатомного и двухатомного газов равна [c.489]
Средняя (кажущаяся) молекулярная масса и газовая постоянная смеси [c.30]
Средняя (кажущаяся) молекулярная масса влаж-. него воздуха р может быть определена, как для смеси идеальных газов, по уравнению (1.64), т. е. [c.80]
Величину Но называют кажущимся -молекулярным весом смеси. Часто Цо называют средним молекулярным весом или средним кажущимся молекулярным весом. Такое название она получила потому, что является условной величиной, реально не существующей. Как отмечалось в параграфе 2.7, молекулярный вес характеризует массу реальных молекул, из которых состоит газ. Всякая же рассматриваемая нами газовая смесь состоит из разнородных молекул отдельных газов, причем эти молекулы все время остаются в смеси неизменными и никакие осредненные молекулы из данных молекул не образовываются. Следовательно, понятие о кажущемся молекулярном весе смеси приобретает определенный смысл в том случае, если мы представим себе такой реально существующий однородный газ, молекулярный вес которого численно равен кажущемуся молекулярному весу смеси при их одинаковых весах и одинаковых числах молей. В этом случае упомянутый однородный газ и смесь по определенным своим физическим свойствам будут тождественны (одинаковы), что позволяет распространять на смесь некоторые законы, установленные для однородных газов. [c.46]
Рассмотрим газовую смесь, составленную из трех компонентов и заданную по массе. Определим газовую постоянную смеси, кажущуюся молекулярную массу, удельный объем и плотность. [c.22]
c.148
]
Техническая термодинамика Изд.3 (1979) — [
c.21
]
Подборка по базе: Расчет газовой смеси.docx, СТ 60 специальные газовые средства.ppt, Давление твердых тел.doc, Масса смеси.docx, Расчет основных рабочих параметров корчевателя-собирателя.docx, Практическая работа на тему _Анализ содержания УМК _Английский в, Статья_ Требования к созданию рабочих программ, в соответствии с, курс тел.docx, Улучшение условий труда рабочих или компенсационные выплаты (про, Улучшение условий труда рабочих или компенсационные выплаты (про
Задание: В тетрадях написать конспект, разобрать примеры решения задач.
Газовые смеси. Смеси рабочих тел.
1. Газовые смеси.
1) Газовые смеси – обычно имеются в виду соединения горючих составных частей топлива и воздуха при горении.

Как известно, горение представляет собой химический процесс соединения горючих составных частей топлива с кислородом воздуха. В результате этого процесса получается газовая смесь, состоящая из кислорода, азота, углекислого, газа, водяного пара и некоторых других газов.
Состав этих смесей, или, как их называют, продуктов сгорания топлива, может быть самым разнообразным и зависит как от состава топлива, так и от условий, при которых происходит сгорание (в частности, от количества подводимого воздуха).
2) Иногда топливо заставляют сгорать при недостаточном количестве воздуха (в газогенераторе). В этом случаев состав продуктов сгорания топлива входят в значительном количестве водород, окись углерода и другие продукты неполно го сгорания. Такие газовые смеси способны к дальнейшему соединению с кислородом (сгоранию) и при этом выделяют тепло, а поэтому они применяются как горючие газы, часто их употребляют в качестве топлива в двигателях внутреннего сгорания.
Газовая смесь может также быть получена в газогенераторе, где происходит сгорание при недостатке кислорода. газогенератор

3) Кроме того к газовым смесям относятся продукты сгорания топлива, а также горючие газы:

Горючий газ, добываемый из недр земли (естественный газ), также представляет собой газовую смесь; она состоит главным образом из метана (СН4), различных углеводоро¬дов, углекислого газа, азота и др.
В свою очередь, к смесям не относятся однородные газы, например, пар (рабочее тело в паросиловых установках). Кроме пара все остальные рабочие тела являются смесями и рассматриваются как смеси идеальных газов.
2. Уравнение состояния идеального газа для компонентов смесей.
С однородным газом приходится иметь дело главным образом в паросиловых установках, где рабочим телом служит по преимуществу водяной пар. В остальных случаях в качестве рабочего тела используется газовая смесь. Поэтому необходимо уметь вычислять для такой смеси все те величины, о которых шла речь в предыдущих параграфах. Газовые смеси, встречающиеся в теплотехнических расчетах, рассматриваются как идеальные газы; они подчиняются законам Бойля — Мариотта и Гей-Люссака.
Уравнение аналогично уравнению идеального газа для однородного газа
![]()
Когда мы имеем дело со смесями газов, важно знать, что они имеют такие характеристики, как парциальный объем и парциальное давление. Для начала определим, что такое смесь идеальных газов.
Смесь идеальных газов – это смесь нескольких газообразных веществ, которые при заданных условиях не будут вступать в определенные химические реакции.
При смене условий (например, повышении температуры, понижении давления) газовая смесь все же может вступать во взаимодействие.
3. Понятие парциального давления для смеси
Парциальное давление – это особая характеристика, описывающая состояние компонентов смеси идеальных газов. Сформулируем основное определение:
Парциальным называется давление pi, которое могло бы создаваться i-ым газом в смеси при условии отсутствия остальных газов и сохранения исходного объема и температуры.
Формула парциального давления будет выглядеть так:

Объем смеси здесь обозначен буквой V, ее температура – T.
Для нахождения давления смеси идеальных газов нужно воспользоваться законом Дальтона: р = р1 + р2 +..+рn, тогда
 , где
, где  – знак суммирования компонентов
– знак суммирования компонентов
4. Понятие парциального объема для смеси
У газовой смеси также есть такая характеристика, как парциальный объем.
Парциальный объем Vi газа в газовой смеси – это такой объем, который мог бы иметь газ при условии отсутствия всех остальных газов и сохранении исходной температуры и объема.
Если речь идет о смеси идеальных газов, то к ней применим закон Амага:

Нам известно, что параметры, определяющие состояние смеси идеальных газов, будут подчиняться уравнению Менделеева-Клайперона.
Формула будет выглядеть так: 
Все параметры данного уравнения будут относиться ко всей смеси. Это же уравнение удобнее записать так:
pV = mRsmTpV
Здесь параметры  означают
означают
удельную газовую постоянную смеси.
5. Параметры смеси1) Массовая доли смеси 
Масса газовой смеси равна сумме масс всех входящих в нее: 
2) Объёмная доля каждого компонета газа.
где ri – объёмная доля i-го газа; Vi – парциальный объём i-го газа; V – объём смеси газов.
3) Существует
взаимосвязь массовых и объемных долей смеси.
Ее несложно получить, выразив массы газов через произведение их объемов на плотности, а отношение плотностей при одинаковых параметрах, в соответствии с законом Авогадро, заменив отношением молярных масс:

4) К
ажущаяся молярная масса смеси μсм – это величина, которая определяется путём деления массы смеси mсм, кг, на число молей смеси νсм, моль
Кажущаяся молярная масса смеси: 
Эта величина имеет условный характер (ее иногда называют кажущейся молекулярной массой) из следующих соображений. По отношению к отдельному газу молекулярная масса — отвлеченное число, характеризующее массу действительно существующей молекулы. Так как газовая смесь — совокупность разнородных молекул, по отношению к такой смеси понятие о молекулярной массе может быть применено в том смысле, что эта смесь как бы заменяется газом, состоящим из однородных фиктивных («средних») молекул, совокупность которых образует газ, соответствующий действительной смеси. Эта величина вводится для удобства при расчетах.
В теплотехнических расчетах в громадном большинстве случаев пользуются объемными долями, так как прибор, которым пользуются для определения состава продуктов сгорания — газоанализатор, дает результаты анализа в объемных долях.
5) К
ажущуюся молярную массу смеси по её химическому составу
μсм= r1 μ1+ r2 μ2+…+ rn, где r – объемные доли компонентов
6) Г
азовая постоянная смеси
Rсм = g1·R1+ g2·R2+……+ gn·Rn,
где  газовая постоянная компонентов смеси
газовая постоянная компонентов смеси
7) Вычисление
относительного объемного состава газовой смеси по относительному массовому составу
На практике часто необходим взаимный пересчёт из массовых и объёмных долей. Рекомендуется использовать следующие выражения:


Решение задач
Задача 1. Какой объем V занимает смесь газов — азота массой m1=1 кг и гелия массой m2=1 кг — при нормальных условиях?
Дано: Решение:
m1=1 кг V = V1 + V2
m2=1 кг Уравнение Менделеева-Клайперона: 
V-? Откуда: 


Задача 2. Дана смесь газов, состоящая из 1 кг углекислого газа и 0,5 кг O2. Если считать их идеальными, какой объем они будут занимать при давлении в 1 атм? Температура смеси равна 300К.
Дано:
M = 1 кг (CO2)
m = 0,5 кг (O2)
р =1 атм = 10·105Па
Т = 300К
Vс-?
Решение
1) Вычислим общую массу газовой смеси.
m = mO2 + mCO2
Значит, m = 1 + 0,5=1,5
2) Вычислим массовые компоненты смеси:

gO2=0,5/1,5=0,33; gСO2=1/1,5=0,67
3) Найдем газовую постоянную смеси:
Rсм = g1·R1+ g2·R2, где

Rсм=8,31(0,33/32⋅10−3+0,67/46⋅10−3)= 200 ДжкгК.
4) Объем смеси вычисляем с помощью уравнения Менделеева-Клайперона:

Vsm=1,5⋅200⋅300/105=0,9 м3V
Ответ: 0,9 м3.
Задача 3. В баллоне объемом 25 литров находится 20 г азота и 2 г гелия при 301К. Найдите давление в баллоне.
Дано:
V= 25л = 0,025м3
m1 = 20·10-3кг
m2 = 2·10-3кг
р-?
Решение:
1) Уравнение Менделеева-Клайперона: 
Для двух газов: 

2) Запишем закон Дальтина

Ответ: p = 105 Па.
Задача 4 Газовая смесь, состоящая из кислорода и азота, находится в баллоне под давлением p=1 МПа. Определить парциальные давления p1 кислорода и p2 азота, если массовая доля g1кислорода в смеси равна 0,2
Дано:
P =1 МПа
g 1 = 0,2
р1,р2-?
Решение:
Закон Дальтона: р = р1 + р2
 , следовательно
, следовательно 


Выразим  , подставляем в давление р2
, подставляем в давление р2


р1 = р – р2 =0,18МПа
Задача 5. Сухой воздух состоит в основном из кислорода и азота. Если пренебречь остальными составными частями воздуха, то можно считать, что массовые доли кислорода и азота соответственно g1=0,232, g2=0,768. Определить относительную молекулярную массу Mr воздуха.
Дано:
g1=0,232,
g2=0,768
μ-?
Решение:
Если известен массовый состав смеси, то по нему можно найти её мольный состав. Массы отдельных газов mi и полную массу смеси т можно выразить через число моль следующим образом: m1=μ1 ν1; m2=μ2 ν2;
νсм = ν1 + ν2
 Упростим:
Упростим: 
Тогда 
Задача 6.. Найти молярную массу смеси кислорода массой m1 =25г и и азота массой m2=75 г
Дано:
m1 = 25·10-3кг
m2 = 75·10-3кг
μсм-?
Решение:
Молярная масса смеси: 
Масса смеси m = m1 + m2

Задача для самостоятельного решения:
Имеется сосуд объемом 1 м3, в котором находится 0,10⋅10−3 кгг гелия и 0,5⋅10−3 кг водорода. Постоянная температура равна 290 К. Вычислите давление смеси и парциальное давление гелия в нем.
Контрольные вопросы:
1. Что называется смесью газов
2. Назовите параметры смеси газов: массовые доли, объемные доли
3. Как найти парциальное давление смеси газов
4. Как найти кажущуюся молярную массу смеси газов
5. Как вычислить относительный объемный состав газовой смеси по относительному массовому составу
6. Как определить газовую постоянную смеси?
An Introduction to Enhanced Oil Recovery
Amirhossein Mohammadi Alamooti, Farzan Karimi Malekabadi, in Fundamentals of Enhanced Oil and Gas Recovery from Conventional and Unconventional Reservoirs, 2018
1.9.3 Natural Gas Properties
Gas is defined as a light fluid with low viscosity and density having significant compressibility. Natural gas is composed of hydrocarbon and nonhydrocarbon compounds. Hydrocarbons composing gas fluid are chiefly the lightest, including methane, ethane, propane, butane, pentane, and a small amount of heavier components. Nitrogen, carbon dioxide, and hydrogen sulfide are the most nonhydrocarbon compounds found in natural gas. In order to simulate reservoirs and investigate different scenarios, modeling reservoir fluid behavior is essential. In other words, pressure–volume–temperature study and physical properties for reservoir fluids should be carried out. The required physical properties in gas reservoirs for solving problems are: apparent molecular weight, density, specific gravity, compressibility factor, gas formation volume factor, and gas viscosity.
1.9.3.1 Apparent Molecular Weight
Apparent molecular weight for gases is mathematically defined as follows:
MWa=∑yiMWi
where MWa is apparent molecular weight of mixture, yi is mole fraction of component I, and MWi is molecular weight of component i.
1.9.3.2 Density
In order to analyze fluid phase behavior, studying the relationship between pressure, volume, and temperature is necessary. For ideal gases the mathematical relationship is expressed as:
PV=nRT
where P is pressure, V is volume, R is universal gas constant, and T is temperature. The term n is numbers of moles of gas. On the other hand, molecular weight is defined as the weight of the gas divided by numbers of moles:
MW=mn
So the pressure–volume–temperature relationship for ideal gases can be rewritten as:
PV=mMWRT
Density is defined as the ratio of mass to the corresponding volume:
ρ=mV
So,
ρ=P⋅MWRT
where ρ is density, m is mass, V is volume, R is universal gas constant, and T is temperature.
1.9.3.3 Specific Gravity
The term specific gravity is expressed as the gas density to the air density under the same condition (pressure and temperature).
γ=ρgasρair
where γ is specific gravity, ρgas is gas density, and ρair is air density.
In the case of standard conditions, the behavior of gases is close to ideal gases; therefore the specific gravity can be rewritten as:
γ=(Psc⋅MWgas)/(RTsc)(Psc⋅MWair)/(RTsc)
γ=MWgasMWair=MWgas28.96
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128130278000011
Field guidelines
M. Rafiqul Islam, in Reservoir Development, 2022
7.3.4.1.1 Natural gas properties
- ▪
-
Apparent molecular weight, Ma
(7.11)Ma=∑i=1yiMi
where yi is the mole fraction and Mi is the molecular weight of ith component.
- ▪
-
Specific gravity, γg
(7.12)γg=ρgρair,γg=Ma28.96
- ▪
-
Compressibility factor (gas deviation factor), z
(7.13)z=VactualVIdeal,z=fyiPT
where VIdeal is the gas volume if it is treated as an ideal gas.
- ▪
-
Isothermal gas compressibility coefficient, cg
(7.14)cg=−1v∂v∂PT,cg=1P−1z∂z∂PT
where v is the specific volume of the gas.
- ▪
-
Gas formation volume factor, Bg
(7.15)Bg=VP,TVStd
where Vstd is the volume of the gas at standard condition.
- ▪
-
Gas expansion factor, Eg
(7.16)Eg=1Bg
- ▪
-
Viscosity, μg μg = f(yi, P, T)
In Chapter 2, fluid characterization rules, derived from the origin and age of petroleum fluids, are presented. In Chapter 4, various applications are suggested for different types of crude oil. This characterization would optimize sustainability and maximize profit without compromising sustainability.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128200537000044
Basic Principles
Maurice Stewart, Ken Arnold, in Gas-Liquid And Liquid-Liquid Separators, 2008
1.3.2 Molecular Weight and Apparent Molecular Weight
The number of moles is defined as follows:
(1.2)Mole=MassMolecular weight
expressed as
(1.3)n=mM
or in units as
(1.4)lb−mole=lblblb−mole
Molecular weight is defined as the sum of the atomic weights of the various elements present.
Example 1.1: Molecular Weight Calculation
Given:
Determine the molecular weight of ethane, C2H6
Solution:
| Element | No. of Atoms | Atomic Weight | Product | ||
|---|---|---|---|---|---|
| C | 2 | × | 12 | = | 24 |
| H | 6 | × | 1 | = | 6 |
| Molecular weight | = | 30 lb/(lb−mol) |
Up to now, we have addressed only pure substances. We now have to consider hydrocarbon mixtures. However, first we must discuss apparent molecular weight and specific gravity. It is not correct to say that a hydrocarbon mixture has a molecular weight; rather, it is an apparent molecular weight. Apparent molecular weight is defined as the sum of the products of the mole fractions of each component times the molecular weight of that component. This is shown in Equation (1.5):
(1.5)MW=∑yi(MW)i
where
yi = molecular fraction of ith component
MWi = molecular weight of ith component
∑yi = 1
Now, let us look at an example of the application of apparent molecular weight that will also result with a number that we will use often throughout this book.
Example 1.2: Determine the apparent molecular weight of dry air, which is a gas mixture consisting of nitrogen, oxygen, and small amounts of Argon
Given:
Determine he apparent molecular weight of air given its approximate composition
| Gas Composition | |
|---|---|
| Component | Mole fraction |
| Nitrogen | 0.78 |
| Oxygen | 0.21 |
| Argon | 0.01 |
| Total | 1.00 |
Solution:
- 1
-
Look up the molecular weight of each component from the physical constant table
(MW)N=28;(MW)O=32;(MW)A=40
- 2
-
Multiply the mole fraction of each component by its molecular weight
(MW)AIR=∑yi(MW)i=yN(MW)N+yO(MW)O+yA(MW)A=(0.78×28)+(0.21×32)+(0.01×40)=29 lb/(lb−mole)
We will now define the specific gravity of a gas.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780750689793000015
Reservoir-Fluid Properties
Tarek Ahmed, in Reservoir Engineering Handbook (Fifth Edition), 2019
Solution
- Step 1.
-
Calculate the apparent molecular weight of the liquid and gas phase:
Mo=100.253Mg=24.99
- Step 2.
-
Calculate the coefficients A and B:
A=46.2362.4100.253=0.00739B=18.2162.424.99=0.01168
- Step 3.
-
Calculate the parachor of C7 + from Equation 2-125:
Pchc7+=69.9+2.3215=564.4
- Step 4.
-
Construct the following working table:
Component Pch Axi Byi Pch(Axi – Byi) C1 77 0.00333 0.0090 –0.4361 C2 108 0.00037 0.00093 –0.0605 C3 150.3 0.00037 0.00070 –0.0497 n-C4 189.9 0.00022 0.00047 –0.0475 n-C5 231.5 0.00007 0.00023 –0.0370 C6 271.0 0.000074 0.00023 –0.0423 C7 + 564.4 0.00296 0.000117 1.6046 0.9315 - Step 5.
-
σ = (0.9315)4 = 0.753 dynes/cm
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128136492000025
Reservoir-Fluid Properties
Tarek Ahmed, in Reservoir Engineering Handbook (Fourth Edition), 2010
Solution
- Step 1.
-
Calculate the apparent molecular weight of the liquid and gas phase:
Mo=100.253 Mg=24.99
- Step 2.
-
Calculate the coefficients A and B:
A=46.23(62.4) (100.253)=0.00739B=18.21(62.4) (24.99)=0.01168
- Step 3.
-
Calculate the parachor of C7+ from Equation 2-125:
(Pch)C7+=69.9+(2.3) (215)=564.4
- Step 4.
-
Construct the following working table:
Component Pch Axi Byi Pch(Axi − Byi) C1 77 0.00333 0.0090 −0.4361 C2 108 0.00037 0.00093 −0.0605 C3 150.3 0.00037 0.00070 −0.0497 n-C4 189.9 0.00022 0.00047 −0.0475 n-C5 231.5 0.00007 0.00023 −0.0370 C6 271.0 0.000074 0.00023 −0.0423 C7+ 564.4 0.00296 0.000117 1.6046 0.9315 - Step 5.
-
σ = (0.9315)4 = 0.753 dynes/cm
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9781856178037500109
Vapor-Liquid Phase Equilibria
Tarek Ahmed, in Reservoir Engineering Handbook (Fifth Edition), 2019
Solution
- Step 1.
-
Calculate the apparent molecular weight of the crude oil to give Ma = 113.5102.
- Step 2.
-
Calculate the density of the bubble-point crude oil by using the Standing and Katz correlation to yield po = 44.794 lb/ft3.
- Step 3.
-
Flash the original composition through the first separator by generating the equilibrium ratios by using the Standing correlation (Equation 15-20) to give:
Component zi Ki xi yi CO2 0.0008 3.509 0.0005 0.0018 N2 0.0164 39.90 0.0014 0.0552 C1 0.2840 8.850 0.089 0.7877 C2 0.0716 1.349 0.0652 0.0880 C3 0.1048 0.373 0.1270 0.0474 i – C4 0.0420 0.161 0.0548 0.0088 n – C4 0.0420 0.120 0.0557 0.0067 i – C5 0.0191 0.054 0.0259 0.0014 n – C5 0.0191 0.043 0.0261 0.0011 C6 0.0405 0.018 0.0558 0.0010 C7 + 0.3597 0.0021 0.4986 0.0009 With nL = 0.7209 and nv = 0.29791.
- Step 4.
-
Use the calculated liquid composition as the feed for the second separator and flash the composition at the operating condition of the separator.
Component zi Ki xi yi CO2 0.0005 3.944 0.0005 0.0018 N2 0.0014 46.18 0.0008 0.0382 C1 0.089 10.06 0.0786 0.7877 C2 0.0652 1.499 0.0648 0.0971 C3 0.1270 0.4082 0.1282 0.0523 i – C4 0.0548 0.1744 0.0555 0.0097 n – C4 0.0557 0.1291 0.0564 0.0072 i – C5 0.0259 0.0581 0.0263 0.0015 n – C5 0.0261 0.0456 0.0264 0.0012 C6 0.0558 0.0194 0.0566 0.0011 C7 + 0.4986 0.00228 0.5061 0.0012 With nL = 0.9851 and nv = 0.0149.
- Step 5.
-
Repeat the above calculation for the stock-tank stage to give:
Component zi Ki xi yi CO2 0.0005 81.14 0000 0.0014 N2 0.0008 1,159 0000 0.026 C1 0.0784 229 0.0011 0.2455 C2 0.0648 27.47 0.0069 0.1898 C3 0.1282 6.411 0.0473 0.3030 i – C4 0.0555 2.518 0.0375 0.0945 n – C4 0.0564 1.805 0.0450 0.0812 i – C5 0.0263 0.7504 0.0286 0.0214 n – C5 0.0264 0.573 0.02306 0.0175 C6 0.0566 0.2238 0.0750 0.0168 C7 + 0.5061 0.03613 0.7281 0.0263 With nL = 0.6837 and nv = 0.3163.
- Step 6.
-
Calculate the actual number of moles of the liquid phase at the stock-tank conditions from Equation 15-39:
nLst=10.72090.98510.6837=0.48554
- Step 7.
-
Calculate the total number of moles of the liberated gas from the entire surface separation system:
nv=1–nLst=1–0.48554=0.51446
- Step 8.
-
Calculate apparent molecular weight of the stock-tank oil from its composition to give (Ma)st = 200.6.
- Step 9.
-
Calculate the density of the stock-tank oil by using the Standing correlation to give:
ρost=50.920
γ=50.920/62.4=0.81660°/60°
- Step 10.
-
Calculate the API gravity of the stock-tank oil:
API=141.5/0.816–131.5=41.9
- Step 11.
-
Calculate the gas solubility from Equation 15-42 to give:
Rs=2130.3310.5144650.920.48554200.6=573.0scf/STB
- Step 12.
-
Calculate Bo from Equation 15-43 to give:
Bo=113.510250.9244.7940.48554200.6=1.325bbl/STB
To optimize the operating pressure of the separator, the above steps should be repeated several times under different assumed pressures and the results, in terms of API, Bo, and Rs, should be expressed graphically and used to determine the optimum pressure.
Note that at low pressures, e.g., p < 1000, equilibrium ratios are nearly independent of the overall composition zi or the convergence pressure and can be considered only a function pressure and temperature. Under this condition, i.e, p < 1000, the equilibrium ratio for any component i can be expressed as:
Ki=Aip
The temperature-dependent coefficient Ai is a characterization parameter of component i that accounts for the physical properties of the component. The above expression suggests that the Ki varies linearly at a constant temperature with 1/p. For example, suppose that a hydrocarbon mixture exists at 300 psi and 100°F. Assume that the mixture contains methane and we want to estimate the equilibrium ratio of methane (or any other components) when the mixture is flashed at 100 psi and at the same temperature of 100°F. The recommended procedure is summarized in the following steps:
- Step 1.
-
Because at low pressure the equilibrium ratio is considered independent of the overall composition of the mixture, use the equilibrium ratio charts of Appendix A to determine the Ki value of methane at 300 psi and 100°F:
KC1=10.5
- Step 2.
-
Calculate the characterization parameter Ai of methane from the above proposed relationship:
10.5=Ai500Ai=10.5300=3,150
- Step 3.
-
Calculate the K; of methane at 100 psi and 100°F from:
KC1=3,150100=31.5
In many low-pressure applications of flash calculations at constant temperature, it might be possible to characterize the entire hydrocarbon mixture as a binary system, i.e., two-component system. Because methane exhibits a linear relationship with pressure of a wide range of pressure values, one of the components that forms the binary system should be methane. The main advantage of such a binary system is the simplicity of performing flash calculations because it does not require an iterative technique.
Reconsider Example 15-6 where flash calculations were performed on the entire system at 400 psia and 72°F. To perform flash calculations on the feed for the second separator at 350 psi and 72oF, follow these steps:
- Step 1.
-
Select methane as one of the binary systems with the other component defined as ethane-plus, i.e., C2 +, which lumps the remaining components. Results of Example 15-6 show:
- ○
-
KC1=8.85
- ○
-
yC1=0.7877
- ○
-
xC2=0.089
- ○
-
yC2+=1.0−0.7877=0.2123
- ○
-
xC2+=1.0−0.089=0.911
- Step 2.
-
From the definition of the equilibrium ratio, calculate the K value of C2 +:
KC2+=yC2+xC2+=0.21230.9110=0.2330
- Step 3.
-
Calculate the characterization parameter A; for methane and C2 +:
AC1=KC1p=8.85400=3,540AC2+=KC2+p=0.233400=93.2
The equilibrium ratio for each of the two components (at a constant temperature) can then be described by:
KC1=3,540pKC2+=93.2p
- Step 4.
-
Calculate the Ki value for each component at the second separator pressure of 350 psi:
KC1=3,540350=10.11KC2+=93.2350=0.266
- Step 5.
-
Using the flash calculations procedure as outlined previously for a binary system, calculate the composition and number of moles of the gas and liquid phase at 350 psi:
- ○
-
Solve for xC1 and xC2 +:
xC1=1−K2K1−K2=1.0−0.26610.11−0.2660=0.0746xC2+=1−xC1=1.0−0.0746=0.9254
- ○
-
Solve for yC1 and yC2 +:
yC1=xC1K1=0.074610.11=0.754yC2+=1−yC1=1.0−0.754=0.246
- ○
-
Solve for number of moles of the vapor and liquid phase:
nv=z1−x1x1K1−1=0.089−0.07460.074610.11−1=0.212nL=1−nv=1.0−0.212=0.788
The above calculations are considered meaningless without converting moles of liquid n1 into volume, which requires the calculation of the liquid density at separator pressure and temperature. Notice:
V=nLMaρo
where Ma is the apparent molecular weight of the separated liquid and is given by (for a binary system):
Ma=xC1MC1+xC2+MC2+
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128136492000153
Petroleum reservoir properties
Boyun Guo, in Well Productivity Handbook (Second Edition), 2019
2.2.2.2 Gas pseudocritical pressure and temperature
In a similar way to determining gas apparent molecular weight by using the gas composition data, the mixing rule can also be used to estimate the critical properties of a gas on the basis of the critical properties of the compounds it contains. The gas critical properties determined in such a way are called pseudocritical properties. Gas pseudocritical pressure (ppc) and pseudocritical temperature (Tpc) are, respectively, expressed as
(2.20)ppc=∑i=1Ncyipci
and
(2.21)Tpc=∑i=1NcyiTci
where pci and Tci are the critical pressure and the critical temperature of compound i, respectively.
2.2 Sample problem
For the gas composition given in Table 2.1, estimate the gas apparent molecular weight, specific gravity, pseudocritical pressure, and pseudocritical temperature of the gas.
Solution
This problem may be solved using the spreadsheet program MixingRule.xls, as shown in Table 2.3.
Table 2.3. Results given by the spreadsheet program MixingRule.xls.
| MixingRule.xls | |||||||
|---|---|---|---|---|---|---|---|
| Description: This spreadsheet calculates gas apparent molecular weight, specific gravity, pseudocritical pressure, and pseudocritical temperature based on gas composition. | |||||||
| Instruction: (1) Update gas composition data (yi); (2) view result. | |||||||
| Compound | yi | MWi | yiMWi | pci (psia) | yipci (psia) | Tci, (°R) | yiTci (°R) |
| C1 | 0.775 | 16.04 | 12.43 | 673 | 521.58 | 344 | 266.60 |
| C2 | 0.083 | 30.07 | 2.50 | 709 | 58.85 | 550 | 45.65 |
| C3 | 0.021 | 44.10 | 0.93 | 618 | 12.98 | 666 | 13.99 |
| i-C4 | 0.006 | 58.12 | 0.35 | 530 | 3.18 | 733 | 4.40 |
| n-C4 | 0.002 | 58.12 | 0.12 | 551 | 1.10 | 766 | 1.53 |
| i-C5 | 0.003 | 72.15 | 0.22 | 482 | 1.45 | 830 | 2.49 |
| n-C5 | 0.008 | 72.15 | 0.58 | 485 | 3.88 | 847 | 6.78 |
| C6 | 0.001 | 86.18 | 0.09 | 434 | 0.43 | 915 | 0.92 |
| C7+ | 0.001 | 114.23 | 0.11 | 361 | 0.36 | 1024 | 1.02 |
| N2 | 0.050 | 28.02 | 1.40 | 227 | 11.35 | 492 | 24.60 |
| CO2 | 0.030 | 44.01 | 1.32 | 1073 | 32.19 | 548 | 16.44 |
| H2S | 0.020 | 34.08 | 0.68 | 672 | 13.45 | 1306 | 26.12 |
| 1.000 | MWa = | 20.71 | ppc = | 661 | Tpc = | 411 | |
| γg = | 0.71 |
If the gas composition is not known, but gas-specific gravity is given, the pseudocritical pressure and temperature can be estimated using various charts or correlations that have been developed empirically. Two simple correlations are
(2.22)ppc=709.604−58.718γg
(2.23)Tpc=170.491+307.344γg
which are valid for sweet gases—that is, those in which H2S < 3%, N2 < 5%, and the total content of inorganic compounds is less than 7%.
Corrections for impurities in sour gases are always necessary and can be determined using either charts or correlations. One is the Wichert-Aziz (1972) correction, expressed as
(2.24)A=yH2S+yCO2
(2.25)B=yH2S
(2.26)ε3=120(A0.9−A1.6)+15(B0.5−B4.0)
(2.27)Tpc′=Tpc−ε3(correctedTpc)
(2.28)Ppc′=PpcTpc′Tpc+B(1−B)ε3(correctedppc)
Other correlations with impurity corrections to compensate for inorganic components are also available (Ahmed, 1989):
(2.29)ppc=678−50(γg−0.5)−206.7yN2+440yCO2+606.7yH2S
(2.30)Tpc=326+315.7(γg−0.5)−240yN2−83.3yCO2+133.3yH2S
Applications of the pseudocritical pressure and temperature are normally found in petroleum engineering using pseudo-reduced pressure and temperature, defined as
(2.31)ppr=pppc
(2.32)Tpr=TTpc
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128182642000026
Properties of Petroleum Fluids
In Well Productivity Handbook, 2008
2.4.1 Gas Specific Gravity
Gas specific gravity is defined as the ratio of the apparent molecular weight of the gas to that of air. The molecular weight of air is usually taken as 28.97 (approximately 79% nitrogen and 21% oxygen). Therefore, the gas specific gravity can be expressed as
(2.18)γg=MWα28.97
where MWa is the apparent molecular weight of the gas, which can be calculated on the basis of its composition. Gas composition is usually determined in laboratories and is reported in mole fractions of the gas components. For example, if yi is the mole fraction of component i, the apparent molecular weight of the gas can be calculated using the mixing rule:
(2.19)MWa=∑i−1NcyiMWi
where MWi is the molecular weight of component i, and Nc is the number of components in the gas. The necessary molecular weights of compounds can be found in textbooks on organic chemistry or petroleum fluids, such as that by Ahmed (1989). Gas specific gravity varies between 0.55 and 0.9.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9781933762326500090
Properties of Petroleum Fluids
Boyun Guo PhD, … Xuehao Tan PhD, in Petroleum Production Engineering (Second Edition), 2017
2.3.1 Specific Gravity of Gas
“Specific gravity gas” is defined as the ratio of the apparent molecular weight of the gas to that of air. The molecular weight of air is usually taken as equal to 28.97 (~79% nitrogen and 21% oxygen). Therefore, the gas-specific gravity is
(2.18)γg=MWa28.97,
where MWa is the apparent molecular weight of gas, which can be calculated on the basis of gas composition. Gas composition is usually determined in a laboratory and reported in mole fractions of components in the gas. Let yi be the mole fraction of component i, and the apparent molecular weight of the gas can be formulated using a mixing rule such as
(2.19)MWa=∑i=1NcyiMWi,
where MWi is the molecular weight of component i, and Nc is number of components. The molecular weights of compounds (MWi) can be found in textbooks on organic chemistry or petroleum fluids such as that by Ahmed (1989). Gas-specific gravity varies between 0.55 and 0.9.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128093740000027
