Не все так просто, как утверждает уважаемая Ангела. Вопрос непростой и дискуссионный. Согласно классической механике масса тела есть просто производное от количества молекул в веществе, которое, уж точно, не изменится при его нагревании. Может увеличиться объем утюга, можно учесть изменение удельной плотности чугуна (жалкие проценты), но классическая механика (по Ньютону) говорит, что вес – это произведение массы на ускорение свободного падения. Масса, возможно увеличилась, хотя есть сведения что у чугуна удельная плотность уменьшается с увеличением температуры.
А вот господин Альберт Эйнштейн почему-то утверждает, что масса и энергия связаны в один пучок.
В соответствии с его знаменитой теорией относительности E=M*C^2, M-масса тела, С- скорость света. Что же мы имеем по этой формуле? Изменилась энергия, утюг нагрели ( но еще не бросили со скоростью, близкой к скорости света). Раз нагрели, значит увеличили энергию. А если принять скорость света за постоянную, то значит, увеличилась масса тела.
Опять парадокс между классической и релятивистской механикой. Я не берусь отвечать на вопрос, я просто хочу поблагодарить автора за такие нетривиальные вопросы, только не знаю как.
Формула для расчета количества теплоты
Допустим, на нужно узнать, какое количество теплоты получила при нагревании железная деталь. Масса детали $3 space кг$. Деталь нагрелась от $20 degree C$ до $300 degree C$.
Возьмем значение теплоемкости железа из таблицы — $460 frac{Дж}{кг cdot degree C}$. Объясним смысл этой величины: на нагревание куска железа массой $1 space кг$ на $1 degree C$ необходимо затратить количество теплоты, равное $460 space Дж$.
- Масса детали у нас в 3 раза больше, значит, на ее нагрев потребуется в 3 раза большее количество теплоты — $1380 space Дж$
- Температура изменилась не на $1 degree C$, а на $280 degree C$
- Значит, необходимо в 280 раз большее количество теплоты: $1380 space Дж cdot 280 = 386 400 space Дж$
Тогда, формула для расчета количества теплоты, необходимой для нагревания тела или выделяемого им при охлаждении примет вид:
$Q = cm(t_2 — t_1)$,
где $Q$ — количество теплоты, $c$ — удельная теплоемкость вещества, из которого состоит тело, $m$ — масса тела, $t_1$ — начальная температура тела, $t_2$ — конечная температура тела.
Чтобы рассчитать количество теплоты, которое необходимо затратить для нагревания тела или выделяемое им при охлаждении, нужно удельную теплоемкость умножить на массу тела и на разность конечной и начальной температур.
Рассмотрим подробнее особенности расчета количества теплоты на примерах решения задач.
Видео
Формула расчета теплоты при изменении температуры
Элементарное количество теплоты обозначим как $delta Q$. Обратим внимание, что элемент тепла, которое получает (отдает) система при малом изменении ее состояния не является полным дифференциалом. Причина этого состоит в том, что теплота является функцией процесса изменения состояния системы.
Элементарное количество тепла, которое сообщается системе, и температура при этом меняется от Tдо T+dT, равно:
где C – теплоемкость тела. Если рассматриваемое тело однородно, то формулу (1) для количества теплоты можно представить как:
где $c=frac{C}{m}$ – удельная теплоемкость тела, m – масса тела, $c_{mu}=c cdot mu$ — молярная теплоемкость, $mu$ – молярная масса вещества, $nu=frac{m}{mu}$ – число молей вещества.
Если тело однородно, а теплоемкость считают независимой от температуры, то количество теплоты ($Delta Q$), которое получает тело при увеличении его температуры на величину $Delta t = t_2 — t_1$ можно вычислить как:
где t2, t1 температуры тела до нагрева и после. Обратите внимание, что температуры при нахождении разности ($Delta t$) в расчетах можно подставлять как в градусах Цельсия, так и в кельвинах.
Единицы измерения количества теплоты
Основной единицей измерения количества теплоты в системе СИ является: [Q]=Дж
Внесистемная единица теплоты, которая часто встречается в технических расчетах. [Q]=кал (калория). 1 кал=4,1868 Дж.
Примеры решения задач
Определить вещество, лежащее в основе тела, если при нагревании его с 200 до 600К ему передалось 4,*106Дж. Масса тела 40 кг.
Решение
Чтобы решить задачу, необходимо узнать удельную теплоемкость этого вещества, затем — по таблице узнать его название.
C=Q÷mΔT
C=4,*106÷40*400=,25*103Дж/кгК
По таблице находим, что такую удельную теплоемкость имеет олово.
Масса воды в сосуде 800г, температура 60оС. В эту воду помещают лед с температурой -10оС. Какой массы лед был помещен, если термодинамическое равновесие установилось, когда температура воды стала равной 40оС.
Решение
Из таблиц определяем, что удельная теплоемкость воды равна 4,2*103Дж/кгК, льда -2,1*103Дж/кгК. λ льда (удельная теплота плавления) =3,33*105Дж/кг.
Для состояния теплового баланса характерно:
с2m2(to-t2)+λm2+c1m2(t3-to)+c1m1(t3-t1)=
Находим m2:
m2=c1m1(t1-t3)⁄(c2(to-t2)+λ+c1(t3-t))
Подставляя значения, находим величину массы, равную 0,13 кг.
Определить Q, выделившееся при охлаждении 20 л масла, если его температура снизилась с 60оС до 20оС.
Первым делом, для перехода в систему СИ заменяем объем, выраженный в литрах, на единицу м3:20л=,02м3.
Q=cmΔT.
В то же время m=ρV/
Найдя в таблице ρ, высчитываем массу масла: m=90*,02=18кг
Разница температур составила 40оС.
Q=1800*18*40=1296(кДж).
Теги
Количество теплоты. Удельная теплоёмкость

1. Изменение внутренней энергии путём совершения работы характеризуется величиной работы, т.е. работа является мерой изменения внутренней энергии в данном процессе. Изменение внутренней энергии тела при теплопередаче характеризуется величиной, называемой количеством теплоты.
Количеством теплоты называется изменение внутренней энергии тела в процессе теплопередачи без совершения работы.
Количество теплоты обозначают буквой ( Q ). Так как количество теплоты является мерой изменения внутренней энергии, то его единицей является джоуль (1 Дж).
При передаче телу некоторого количества теплоты без совершения работы его внутренняя энергия увеличивается, если тело отдаёт какое-то количество теплоты, то его внутренняя энергия уменьшается.
2. Если в два одинаковых сосуда налить в один 100 г воды, а в другой 400 г при одной и той же температуре и поставить их на одинаковые горелки, то раньше закипит вода в первом сосуде. Таким образом, чем больше масса тела, тем большее количество теплоты требуется ему для нагревания. То же самое и с охлаждением: тело большей массы при охлаждении отдаёт большее количество теплоты. Эти тела сделаны из одного и того же вещества и нагреваются они или охлаждаются на одно и то же число градусов.
[ Qsim m ]
3. Если теперь нагревать 100 г воды от 30 до 60 °С, т.е. на 30 °С, а затем до 100 °С, т.е. на 70 °С, то в первом случае на нагревание уйдёт меньше времени, чем во втором, и, соответственно, на нагревание воды на 30 °С, будет затрачено меньшее количество теплоты, чем на нагревание воды на 70 °С. Таким образом, количество теплоты прямо пропорционально разности конечной ( (t_2,^circ C) ) и начальной ( (t_1,^circ C) ) температур: ( Qsim(t_2-t_1) ).
4. Если теперь в один сосуд налить 100 г воды, а в другой такой же сосуд налить немного воды и положить в неё такое металлическое тело, чтобы его масса и масса воды составляли 100 г, и нагревать сосуды на одинаковых плитках, то можно заметить, что в сосуде, в котором находится только вода, температура будет ниже, чем в том, в котором находятся вода и металлическое тело. Следовательно, чтобы температура содержимого в обоих сосудах была одинаковой нужно воде передать большее количество теплоты, чем воде и металлическому телу. Таким образом, количество теплоты, необходимое для нагревания тела зависит от рода вещества, из которого это тело сделано.
5. Зависимость количества теплоты, необходимого для нагревания тела, от рода вещества характеризуется физической величиной, называемой удельной теплоёмкостью вещества.
Физическая величина, равная количеству теплоты, которое необходимо сообщить 1 кг вещества для нагревания его на 1 °С (или на 1 К), называется удельной теплоёмкостью вещества.
Такое же количество теплоты 1 кг вещества отдаёт при охлаждении на 1 °С.
Удельная теплоёмкость обозначается буквой ( c ). Единицей удельной теплоёмкости является 1 Дж/кг °С или 1 Дж/кг К.
Значения удельной теплоёмкости веществ определяют экспериментально. Жидкости имеют большую удельную теплоёмкость, чем металлы; самую большую удельную теплоёмкость имеет вода, очень маленькую удельную теплоёмкость имеет золото.
Удельная теплоёмкость свинца 140 Дж/кг °С. Это значит, что для нагревания 1 кг свинца на 1 °С необходимо затратить количество теплоты 140 Дж. Такое же количество теплоты выделится при остывании 1 кг воды на 1 °С.
Поскольку количество теплоты равно изменению внутренней энергии тела, то можно сказать, что удельная теплоёмкость показывает, на сколько изменяется внутренняя энергия 1 кг вещества при изменении его температуры на 1 °С. В частности, внутренняя энергия 1 кг свинца при его нагревании на 1 °С увеличивается на 140 Дж, а при охлаждении уменьшается на 140 Дж.
Количество теплоты ( Q ), необходимое для нагревания тела массой ( m ) от температуры ( (t_1,^circ C) ) до температуры ( (t_2,^circ C) ), равно произведению удельной теплоёмкости вещества, массы тела и разности конечной и начальной температур, т.е.
[ Q=cm(t_2{}^circ-t_1{}^circ) ]
По этой же формуле вычисляется и количество теплоты, которое тело отдаёт при охлаждении. Только в этом случае от начальной температуры следует отнять конечную, т.е. от большего значения температуры отнять меньшее.
6. Пример решения задачи. В стакан, содержащий 200 г воды при температуре 80 °С, налили 100 г воды при температуре 20 °С. После чего в сосуде установилась температура 60 °С. Какое количество теплоты получила холодная вода и отдала горячая вода?
При решении задачи необходимо выполнять следующую последовательность действий:
- записать кратко условие задачи;
- перевести значения величин в СИ;
- проанализировать задачу, установить, какие тела участвуют в теплообмене, какие тела отдают энергию, а какие получают;
- решить задачу в общем виде;
- выполнить вычисления;
- проанализировать полученный ответ.
1. Условие задачи.
Дано:
( m_1 ) = 200 г
( m_2 ) = 100 г
( t_1 ) = 80 °С
( t_2 ) = 20 °С
( t ) = 60 °С
______________
( Q_1 ) — ? ( Q_2 ) — ?
( c_1 ) = 4200 Дж/кг · °С
2. СИ: ( m_1 ) = 0,2 кг; ( m_2 ) = 0,1 кг.
3. Анализ задачи. В задаче описан процесс теплообмена между горячей и холодной водой. Горячая вода отдаёт количество теплоты ( Q_1 ) и охлаждается от температуры ( t_1 ) до температуры ( t ). Холодная вода получает количество теплоты ( Q_2 ) и нагревается от температуры ( t_2 ) до температуры ( t ).
4. Решение задачи в общем виде. Количество теплоты, отданное горячей водой, вычисляется по формуле: ( Q_1=c_1m_1(t_1-t) ).
Количество теплоты, полученное холодной водой, вычисляется по формуле: ( Q_2=c_2m_2(t-t_2) ).
5. Вычисления.
( Q_1 ) = 4200 Дж/кг · °С · 0,2 кг · 20 °С = 16800 Дж
( Q_2 ) = 4200 Дж/кг · °С · 0,1 кг · 40 °С = 16800 Дж
6. В ответе получено, что количество теплоты, отданное горячей водой, равно количеству теплоты, полученному холодной водой. При этом рассматривалась идеализированная ситуация и не учитывалось, что некоторое количество теплоты пошло на нагревание стакана, в котором находилась вода, и окружающего воздуха. В действительности же количество теплоты, отданное горячей водой, больше, чем количество теплоты, полученное холодной водой.
Содержание
- ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
- Ответы
ПРИМЕРЫ ЗАДАНИЙ
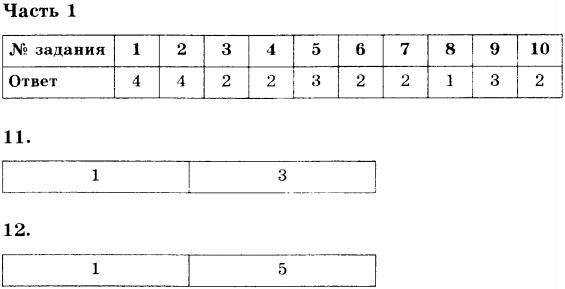
Часть 1
1. Удельная теплоёмкость серебра 250 Дж/(кг · °С). Что это означает?
1) при остывании 1 кг серебра на 250 °С выделяется количество теплоты 1 Дж
2) при остывании 250 кг серебра на 1 °С выделяется количество теплоты 1 Дж
3) при остывании 250 кг серебра на 1 °С поглощается количество теплоты 1 Дж
4) при остывании 1 кг серебра на 1 °С выделяется количество теплоты 250 Дж
2. Удельная теплоёмкость цинка 400 Дж/(кг · °С). Это означает, что
1) при нагревании 1 кг цинка на 400 °С его внутренняя энергия увеличивается на 1 Дж
2) при нагревании 400 кг цинка на 1 °С его внутренняя энергия увеличивается на 1 Дж
3) для нагревания 400 кг цинка на 1 °С его необходимо затратить 1 Дж энергии
4) при нагревании 1 кг цинка на 1 °С его внутренняя энергия увеличивается на 400 Дж
3. При передаче твёрдому телу массой ( m ) количества теплоты ( Q ) температура тела повысилась на ( Delta t^circ ). Какое из приведённых ниже выражений определяет удельную теплоёмкость вещества этого тела?
1) ( frac{mDelta t^circ}{Q} )
2) ( frac{Q}{mDelta t^circ} )
3) ( frac{Q}{Delta t^circ} )
4) ( QmDelta t^circ )
4. На рисунке приведён график зависимости количества теплоты, необходимого для нагревания двух тел (1 и 2) одинаковой массы, от температуры. Сравните значения удельной теплоёмкости (( c_1 ) и ( c_2 )) веществ, из которых сделаны эти тела.
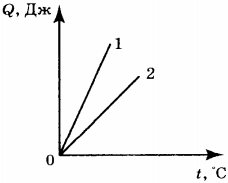
1) ( c_1=c_2 )
2) ( c_1>c_2 )
3) ( c_1<c_2 )
4) ответ зависит от значения массы тел
5. На диаграмме представлены значения количества теплоты, переданного двум телам равной массы при изменении их температуры на одно и то же число градусов. Какое соотношение для удельных теплоёмкостей веществ, из которых изготовлены тела, является верным?
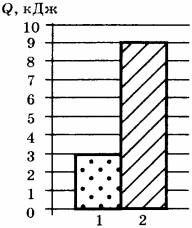
1) ( c_1=c_2 )
2) ( c_1=3c_2 )
3) ( c_2=3c_1 )
4) ( c_2=2c_1 )
6. На рисунке представлен график зависимости температуры твёрдого тела от отданного им количества теплоты. Масса тела 4 кг. Чему равна удельная теплоёмкость вещества этого тела?
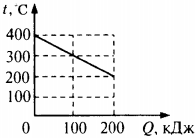
1) 500 Дж/(кг · °С)
2) 250 Дж/(кг · °С)
3) 125 Дж/(кг · °С)
4) 100 Дж/(кг · °С)
7. При нагревании кристаллического вещества массой 100 г измеряли температуру вещества и количество теплоты, сообщённое веществу. Данные измерений представили в виде таблицы. Считая, что потерями энергии можно пренебречь, определите удельную теплоёмкость вещества в твёрдом состоянии.

1) 192 Дж/(кг · °С)
2) 240 Дж/(кг · °С)
3) 576 Дж/(кг · °С)
4) 480 Дж/(кг · °С)
8. Чтобы нагреть 192 г молибдена на 1 К, нужно передать ему количество теплоты 48 Дж. Чему равна удельная теплоёмкость этого вещества?
1) 250 Дж/(кг · К)
2) 24 Дж/(кг · К)
3) 4·10-3 Дж/(кг · К)
4) 0,92 Дж/(кг · К)
9. Какое количество теплоты необходимо для нагревания 100 г свинца от 27 до 47 °С?
1) 390 Дж
2) 26 кДж
3) 260 Дж
4) 390 кДж
10. На нагревание кирпича от 20 до 85 °С затрачено такое же количество теплоты, как для нагревания воды такой же массы на 13 °С. Удельная теплоёмкость кирпича равна
1) 840 Дж/(кг · К)
2) 21000 Дж/(кг · К)
3) 2100 Дж/(кг · К)
4) 1680 Дж/(кг · К)
11. Из перечня приведённых ниже высказываний выберите два правильных и запишите их номера в таблицу.
1) Количество теплоты, которое тело получает при повышении его температуры на некоторое число градусов, равно количеству теплоты, которое это тело отдаёт при понижении его температуры на такое же число градусов.
2) При охлаждении вещества его внутренняя энергия увеличивается.
3) Количество теплоты, которое вещество получает при нагревании, идёт главным образом на увеличение кинетической энергии его молекул.
4) Количество теплоты, которое вещество получает при нагревании, идёт главным образом на увеличение потенциальной энергии взаимодействия его молекул
5) Внутреннюю энергию тела можно изменить, только сообщив ему некоторое количество теплоты
12. В таблице представлены результаты измерений массы ( m ), изменения температуры ( Delta t ) и количества теплоты ( Q ), выделяющегося при охлаждении цилиндров, изготовленных из меди или алюминия.

Какие утверждения соответствуют результатам проведённого эксперимента? Из предложенного перечня выберите два правильных. Укажите их номера. На основании проведенных измерений можно утверждать, что количество теплоты, выделяющееся при охлаждении,
1) зависит от вещества, из которого изготовлен цилиндр.
2) не зависит от вещества, из которого изготовлен цилиндр.
3) увеличивается при увеличении массы цилиндра.
4) увеличивается при увеличении разности температур.
5) удельная теплоёмкость алюминия в 4 раза больше, чем удельная теплоёмкость олова.
Часть 2
C1.Твёрдое тело массой 2 кг помещают в печь мощностью 2 кВт и начинают нагревать. На рисунке изображена зависимость температуры ( t ) этого тела от времени нагревания ( tau ). Чему равна удельная теплоёмкость вещества?
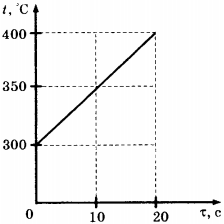
1) 400 Дж/(кг · °С)
2) 200 Дж/(кг · °С)
3) 40 Дж/(кг · °С)
4) 20 Дж/(кг · °С)
Ответы
Количество теплоты. Удельная теплоёмкость
3.1 (62.81%) 64 votes
Так как речь идет о насыщенном паре, то считаем, что сосуд закрыт. Найдем объем пара Vn1 в сосуде при температуре T = 373 К:
Vn1 = V – Vb,
где V = 3 л, Vb = m/ρ1 — объем воды, m = 0,75 кг, ρ1 = 958 кг/м3 — плотность воды при 100°С. Масса m1 насыщенного пара при T = 373 К будет равна:
m1 = ρn1∙Vn1,
где ρn1 = 588,5 г/м3 — плотность насыщенного пара при Т = 373 К. Тогда
[m_{1} =rho _{n1} cdot left(V-frac{m}{rho _{1} } right),]
m1 = 1,305 г.
Так как вода взята при температуре кипения, то нагревание ее на 1 К приведет к ее парообразованию. Определим, вся ли вода превратиться в пар.
Плотность насыщенного пара при Т = 374 К равна ρn2 = 608 г/м3 (значение взято приблизительно). Для того, чтобы плотность пара достигла этого значения в объеме V = 3 л понадобиться всего mn = 1,824 г (mn = ρn2∙V). Следовательно, воды испариться меньше 1 г. Поэтому изменением объема пара Vn1 (и объемным расширением воды из-за малого изменения температуры) можно пренебречь.
В итоге получаем, что масса m2 насыщенного пара при T = 374 К будет равна:
[m_{2} =rho _{n2} cdot V_{n1} =rho _{n2} cdot left(V-frac{m}{rho _{1} } right),]
m2 = 1,348 г.
Изменение массы насыщенного пара
Δm = 0,043 г.
Примечание. Для более точных расчетов надо знать правильную плотность насыщенного пара при Т = 374 К.
По формуле Эйнштейна Е = мс2
Изменение Е считаем – “Массу воды” умн. “на удельную теплоемкость воды ” и умн. “на разность температур”.
Полученное изменение Е делим на скорость света в квадрате
Получаем изменение (прирост) первоначальной массы) .
(результат очень мал, за пределами точности современных измерений) .
См. Соколовский Ю. И. Элементарный задачник по теории относительности. М. 1971 г. с. 21 № 69 ( задача отнесена к категории ЛЕГКИХ)
У Соколовского – не “масса литра воды”, а “масса воды”
В задачнике по физике для школ
Задачу любопытную нашел,
Простую, но довольно интересную:
«Насколько возрастет масса воды
При нагревании ее от десяти
До сотни градусов по Цельсию? »
Задачу дал в «ответах» , но мне стали говорить,
Что «массу» на «объем» здесь надо заменить!
Проверив все, условий я не изменил,
И заслужил эпитеты «придурок» и «дебил» !
Возможно, что такое написали сгоряча.
Но надо ж, наконец, ее решить, друзья!
