Как найти кинематическую вязкость воздуха

Рассмотрены основные физические свойства воздуха: плотность воздуха, его динамическая и кинематическая вязкость, удельная теплоемкость, теплопроводность, температуропроводность, число Прандтля и энтропия. Свойства воздуха даны в таблицах в зависимости от температуры при нормальном атмосферном давлении.

Плотность воздуха в зависимости от температуры

Представлена подробная таблица значений плотности воздуха в сухом состоянии при различных температурах и нормальном атмосферном давлении. Чему равна плотность воздуха? Аналитически определить плотность воздуха можно, если разделить его массу на объем, который он занимает при заданных условиях (давление, температура и влажность). Также можно вычислить его плотность по формуле уравнения состояния идеального газа. Для этого необходимо знать абсолютное давление и температуру воздуха, а также его газовую постоянную и молярный объем. Это уравнение позволяет вычислить плотность воздуха в сухом состоянии.

На практике, чтобы узнать какова плотность воздуха при различных температурах, удобно воспользоваться готовыми таблицами. Например, приведенной таблицей значений плотности атмосферного воздуха в зависимости от его температуры. Плотность воздуха в таблице выражена в килограммах на кубический метр и дана в интервале температуры от минус 50 до 1200 градусов Цельсия при нормальном атмосферном давлении (101325 Па).

Плотность воздуха в зависимости от температуры — таблица

t, °С	ρ, кг/м3	t, °С	ρ, кг/м3	t, °С	ρ, кг/м3	t, °С	ρ, кг/м3
-50	1,584	20	1,205	150	0,835	600	0,404
-45	1,549	30	1,165	160	0,815	650	0,383
-40	1,515	40	1,128	170	0,797	700	0,362
-35	1,484	50	1,093	180	0,779	750	0,346
-30	1,453	60	1,06	190	0,763	800	0,329
-25	1,424	70	1,029	200	0,746	850	0,315
-20	1,395	80	1	250	0,674	900	0,301
-15	1,369	90	0,972	300	0,615	950	0,289
-10	1,342	100	0,946	350	0,566	1000	0,277
-5	1,318	110	0,922	400	0,524	1050	0,267
0	1,293	120	0,898	450	0,49	1100	0,257
10	1,247	130	0,876	500	0,456	1150	0,248
15	1,226	140	0,854	550	0,43	1200	0,239

При 25°С воздух имеет плотность 1,185 кг/м³. При нагревании плотность воздуха снижается — воздух расширяется (его удельный объем увеличивается). С ростом температуры, например до 1200°С, достигается очень низкая плотность воздуха, равная 0,239 кг/м³, что в 5 раз меньше ее значения при комнатной температуре. В общем случае, снижение плотности газов при нагреве позволяет проходить такому процессу, как естественная конвекция и применяется, например, в воздухоплавании.

Если сравнить плотность воздуха относительно плотности воды, то воздух легче на три порядка — при температуре 4°С плотность воды равна 1000 кг/м³, а плотность воздуха составляет 1,27 кг/м³. Необходимо также отметить значение плотности воздуха при нормальных условиях. Нормальными условиями для газов являются такие, при которых их температура равна 0°С, а давление равно нормальному атмосферному. Таким образом, согласно таблице, плотность воздуха при нормальных условиях (при НУ) равна 1,293 кг/м³.

Динамическая и кинематическая вязкость воздуха при различных температурах

При выполнении тепловых расчетов необходимо знать значение вязкости воздуха (коэффициента вязкости) при различной температуре. Эта величина требуется для вычисления числа Рейнольдса, Грасгофа, Релея, значения которых определяют режим течения этого газа. В таблице даны значения коэффициентов динамической μ и кинематической ν вязкости воздуха в диапазоне температуры от -50 до 1200°С при атмосферном давлении.

Коэффициент вязкости воздуха с ростом его температуры значительно увеличивается. Например, кинематическая вязкость воздуха равна 15,06·10^-6 м²/с при температуре 20°С, а с ростом температуры до 1200°С вязкость воздуха становиться равной 233,7·10^-6 м²/с, то есть увеличивается в 15,5 раз! Динамическая вязкость воздуха при температуре 20°С равна 18,1·10^-6 Па·с.

При нагревании воздуха увеличиваются значения как кинематической, так и динамической вязкости. Эти две величины связаны между собой через величину плотности воздуха, значение которой уменьшается при нагревании этого газа. Увеличение кинематической и динамической вязкости воздуха (как и других газов) при нагреве связано с более интенсивным колебанием молекул воздуха вокруг их равновесного состояния (согласно МКТ).

Динамическая и кинематическая вязкость воздуха (в таблице даны значения вязкости, увеличенные в 10⁶ раз)

t, °С	μ·106, Па·с	ν·106, м2/с	t, °С	μ·106, Па·с	ν·106, м2/с	t, °С	μ·106, Па·с	ν·106, м2/с
-50	14,6	9,23	70	20,6	20,02	350	31,4	55,46
-45	14,9	9,64	80	21,1	21,09	400	33	63,09
-40	15,2	10,04	90	21,5	22,1	450	34,6	69,28
-35	15,5	10,42	100	21,9	23,13	500	36,2	79,38
-30	15,7	10,8	110	22,4	24,3	550	37,7	88,14
-25	16	11,21	120	22,8	25,45	600	39,1	96,89
-20	16,2	11,61	130	23,3	26,63	650	40,5	106,15
-15	16,5	12,02	140	23,7	27,8	700	41,8	115,4
-10	16,7	12,43	150	24,1	28,95	750	43,1	125,1
-5	17	12,86	160	24,5	30,09	800	44,3	134,8
0	17,2	13,28	170	24,9	31,29	850	45,5	145
10	17,6	14,16	180	25,3	32,49	900	46,7	155,1
15	17,9	14,61	190	25,7	33,67	950	47,9	166,1
20	18,1	15,06	200	26	34,85	1000	49	177,1
30	18,6	16	225	26,7	37,73	1050	50,1	188,2
40	19,1	16,96	250	27,4	40,61	1100	51,2	199,3
50	19,6	17,95	300	29,7	48,33	1150	52,4	216,5
60	20,1	18,97	325	30,6	51,9	1200	53,5	233,7

Удельная теплоемкость воздуха при температуре от -50 до 1200°С

Представлена таблица удельной теплоемкости воздуха при различных температурах. Теплоемкость в таблице дана при постоянном давлении (изобарная теплоемкость воздуха) в интервале температуры от минус 50 до 1200°С для воздуха в сухом состоянии. Чему равна удельная теплоемкость воздуха? Величина удельной теплоемкости определяет количество тепла, которое необходимо подвести к одному килограмму воздуха при постоянном давлении для увеличения его температуры на 1 градус. Например, при 20°С для нагревания 1 кг этого газа на 1°С в изобарном процессе, требуется подвести 1005 Дж тепла.

Удельная теплоемкость воздуха увеличивается с ростом его температуры. Однако, зависимость массовой теплоемкости воздуха от температуры не линейная. В интервале от -50 до 120°С ее величина практически не меняется — в этих условиях средняя теплоемкость воздуха равна 1010 Дж/(кг·град). По данным таблицы видно, что значительное влияние температура начинает оказывать со значения 130°С. Однако, температура воздуха влияет на его удельную теплоемкость намного слабее, чем на вязкость. Так, при нагреве с 0 до 1200°С теплоемкость воздуха увеличивается лишь в 1,2 раза – с 1005 до 1210 Дж/(кг·град).

Следует отметить, что теплоемкость влажного воздуха выше, чем сухого. Если сравнить теплоемкость воды и воздуха, то очевидно, что вода обладает более высоким ее значением и содержание воды в воздухе приводит к увеличению удельной теплоемкости.

Удельная теплоемкость воздуха при различных температурах — таблица

t, °С	Cp, Дж/(кг·град)	t, °С	Cp, Дж/(кг·град)	t, °С	Cp, Дж/(кг·град)	t, °С	Cp, Дж/(кг·град)
-50	1013	20	1005	150	1015	600	1114
-45	1013	30	1005	160	1017	650	1125
-40	1013	40	1005	170	1020	700	1135
-35	1013	50	1005	180	1022	750	1146
-30	1013	60	1005	190	1024	800	1156
-25	1011	70	1009	200	1026	850	1164
-20	1009	80	1009	250	1037	900	1172
-15	1009	90	1009	300	1047	950	1179
-10	1009	100	1009	350	1058	1000	1185
-5	1007	110	1009	400	1068	1050	1191
0	1005	120	1009	450	1081	1100	1197
10	1005	130	1011	500	1093	1150	1204
15	1005	140	1013	550	1104	1200	1210

Теплопроводность, температуропроводность, число Прандтля воздуха

В таблице представлены такие физические свойства атмосферного воздуха, как теплопроводность, температуропроводность и его число Прандтля в зависимости от температуры. Теплофизические свойства воздуха даны в интервале от -50 до 1200°С для сухого воздуха. По данным таблицы видно, что указанные свойства воздуха существенно зависят от температуры и температурная зависимость рассмотренных свойств этого газа различна.

Теплопроводность воздуха λ при повышении температуры увеличивается во всем диапазоне, достигая при 1200°С величины 0,0915 Вт/(м·град). Другие теплофизические свойства воздуха такие, как его температуропроводность a и число Прандтля Pr, по-разному реагируют на изменение температуры. Температуропроводность, как и вязкость воздуха сильно зависит от температуры и при нагревании, например с 0 до 1200°С, ее значение увеличивается почти в 17 раз.

Число Прандтля воздуха слабо зависит от температуры и при нагревании этого газа его величина сначала снижается до величины 0,674, а затем начинает расти, и при температуре 1200°С достигает значения 0,724.

Физические свойства атмосферного воздуха — таблица

t, °С	λ·102, Вт/(м·град)	а·106, м2/с	Pr	t, °С	λ·102, Вт/(м·град)	а·106, м2/с	Pr
-50	2,04	12,7	0,728	170	3,71	45,7	0,682
-40	2,12	13,8	0,728	180	3,78	47,5	0,681
-30	2,2	14,9	0,723	190	3,86	49,5	0,681
-20	2,28	16,2	0,716	200	3,93	51,4	0,68
-10	2,36	17,4	0,712	250	4,27	61	0,677
0	2,44	18,8	0,707	300	4,6	71,6	0,674
10	2,51	20	0,705	350	4,91	81,9	0,676
20	2,59	21,4	0,703	400	5,21	93,1	0,678
30	2,67	22,9	0,701	450	5,48	104,2	0,683
40	2,76	24,3	0,699	500	5,74	115,3	0,687
50	2,83	25,7	0,698	550	5,98	126,8	0,693
60	2,9	27,2	0,696	600	6,22	138,3	0,699
70	2,96	28,6	0,694	650	6,47	150,9	0,703
80	3,05	30,2	0,692	700	6,71	163,4	0,706
90	3,13	31,9	0,69	750	6,95	176,1	0,71
100	3,21	33,6	0,688	800	7,18	188,8	0,713
110	3,28	35,2	0,687	850	7,41	202,5	0,715
120	3,34	36,8	0,686	900	7,63	216,2	0,717
130	3,42	38,6	0,685	950	7,85	231,1	0,718
140	3,49	40,3	0,684	1000	8,07	245,9	0,719
150	3,57	42,1	0,683	1100	8,5	276,2	0,722
160	3,64	43,9	0,682	1200	9,15	316,5	0,724

Будьте внимательны! Теплопроводность воздуха в таблице указана в степени 10². Не забудьте разделить на 100! Температуропроводность воздуха указана в степени 10⁶. Допускается интерполяция значений физических свойств воздуха в приведенных таблицах.

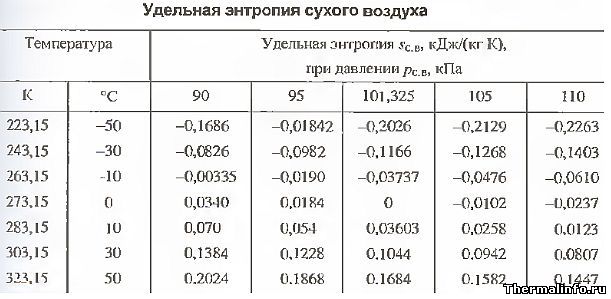
Энтропия сухого воздуха

В таблице представлены значения такого теплофизического свойства воздуха, как удельная энтропия. Значения энтропии даны для сухого воздуха в  размерности кДж/(кг·град) в зависимости от температуры и давления. Удельная энтропия указана в таблице в интервале температуры от -50 до 50°С при давлении воздуха от 90 до 110 кПа. Следует отметить, что при нормальном атмосферном давлении (101,325 кПа) и температуре, например 30°С, удельная энтропия воздуха равна 0,1044 кДж/(кг·град).

Источники:

1. Михеев М.А., Михеева И.М. Основы теплопередачи.
2. Богданов С.Н., Бурцев С.И., Иванов О.П., Куприянова А.В. Холодильная теника. Кондиционирование воздуха. Свойства веществ: Справ./ Под ред. С.Н. Богданова. 4-е изд., перераб. и доп. — СПб.: СПбГАХПТ, 1999.- 320 с.

Механика сплошных сред
Сплошная среда
Классическая механика Закон сохранения массы · Закон сохранения импульса
Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость
Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение
Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнение Громеки — Лэмба · Уравнение Бернулли · Уравнения Навье — Стокса · Уравнение вихря · Уравнение диффузии · Закон Гука
См. также: Портал:Физика

Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате макроскопическая работа, затрачиваемая на это перемещение, рассеивается в виде тепла. Твёрдые тела (стекло, металлы, полупроводники, диэлектрики, ферромагнетики)^[1] также могут обладать вязкостью, но внутреннее трение в твёрдых телах в силу специфики явления обычно рассматривается отдельно в теории упругости и пластичности.

Механизм внутреннего трения в жидкостях и газах заключается в том, что движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.

Вязкость газов и жидкостей характеризуют динамическим коэффициентом вязкости (единица измерения в Международной системе единиц (СИ) — паскаль-секунда, Па·с, в системе СГС — пуаз, П; 1 Па·с = 10 П, 1 сП = 10⁻³ Па·с = 1 мПа·с) или кинематическим коэффициентом вязкости (единица измерения в СИ — м²/c, в СГС — стокс, Ст; 1 Ст = см²/с = 10⁻⁴ м²/с, 1 сСт = 1 мм²/с = 10⁻⁶ м²/с; внесистемная единица — градус Энглера). Кинематический коэффициент вязкости — отношение динамического коэффициента к плотности вещества. Классические методы измерения вязкости включают, например, измерение времени вытекания заданного объёма через калиброванное отверстие под действием силы тяжести. Прибор для измерения вязкости называется вискозиметром.

Переход вещества из жидкого состояния в стеклообразное обычно связывают с достижением вязкости порядка 10¹¹—10¹² Па·с.

Сила вязкого трения[править | править код]

Если параллельные плоские тела площадью S каждое, находящиеся на малом расстоянии h, движутся в той же плоскости со скоростью друг относительно друга, а пространство между телами заполнено жидкостью или газом, то на каждое из них действует сила, в простейшем случае пропорциональная относительной скорости и площади S и обратно пропорциональная расстоянию между телами h:

Коэффициент пропорциональности, зависящий от природы жидкости или газа, называют коэффициентом динамической вязкости. Этот закон был предложен Исааком Ньютоном в 1687 году и носит его имя (закон вязкости Ньютона). Экспериментальное подтверждение закона было получено в начале XIX века в опытах Кулона с крутильными весами и в экспериментах Хагена и Пуазёйля с течением воды в капиллярах^[2].

Эта сила называется силой вязкого трения. Её качественное отличие от сухого трения, кроме прочего, в том, что она пропорциональна скорости. Следовательно, при наличии только вязкого трения и сколь угодно малой внешней силы тело обязательно придёт в движение, то есть для вязкого трения не существует трения покоя.

Вторая вязкость[править | править код]

Вторая вязкость, или объёмная вязкость, — внутреннее трение при переносе импульса в направлении движения. Влияет только при учёте сжимаемости и (или) при учёте неоднородности коэффициента второй вязкости по пространству.

Если динамическая (и кинематическая) вязкость характеризует деформацию чистого сдвига, то вторая вязкость характеризует деформацию объёмного сжатия.

Объёмная вязкость играет большую роль в затухании звука и ударных волн и экспериментально определяется путём измерения этого затухания.

Вязкость газов[править | править код]

В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле

где  — средняя скорость теплового движения молекул, − средняя длина свободного пробега. Из этого выражения в частности следует, что вязкость не очень разреженных газов практически не зависит от давления, поскольку плотность прямо пропорциональна давлению, а длина пробега  — обратно пропорциональна. Такой же вывод следует и для других кинетических коэффициентов для газов, например, для коэффициента теплопроводности. Однако этот вывод справедлив только до тех пор, пока разрежение газа не становится столь малым, что отношение длины свободного пробега к линейным размерам сосуда (число Кнудсена) не становится по порядку величины равным единице; в частности, это имеет место в сосудах Дьюара (термосах).

С повышением температуры вязкость большинства газов увеличивается, это объясняется увеличением средней скорости молекул газа , растущей с температурой как .

Влияние температуры на вязкость газов[править | править код]

В отличие от жидкостей, вязкость газов увеличивается с увеличением температуры (у жидкостей она уменьшается при увеличении температуры).

Формула Сазерленда может быть использована для определения вязкости идеального газа в зависимости от температуры:^[3]

где

 — динамическая вязкость (в Па·с) при заданной температуре ;

 — контрольная вязкость (в Па·с) при некоторой контрольной температуре ;

 — заданная температура в кельвинах;

 — контрольная температура в кельвинах;

 — постоянная Сазерленда для того газа, вязкость которого требуется определить.

Эту формулу можно применять для температур в диапазоне 0 < < 555 K и при давлениях менее 3,45 МПа с ошибкой менее 10 %, обусловленной зависимостью вязкости от давления.

Постоянная Сазерленда и контрольные вязкости газов при различных температурах приведены в таблице ниже:

Газ	, K	, K	, мкПа·с
Воздух	120	291,15	18,27
Азот	111	300,55	17,81
Кислород	127	292,25	20,18
Углекислый газ	240	293,15	14,8
Угарный газ	118	288,15	17,2
Водород	72	293,85	8,76
Аммиак	370	293,15	9,82
Оксид серы(IV)	416	293,65	12,54
Гелий	79,4[4]	273	19[5]

Вязкость жидкостей[править | править код]

Динамическая вязкость[править | править код]

Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Для так называемых ньютоновских жидкостей (которых вокруг нас большинство) справедлив общий закон внутреннего трения — закон Ньютона:

Коэффициент вязкости (коэффициент динамической вязкости, динамическая вязкость) может быть получен на основе соображений о движениях молекул. Очевидно, что будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля — Андраде:

Иная формула, представляющая коэффициент вязкости, была предложена Бачинским^[6]. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества . Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение

где:

 — константа, характерная для определённой жидкости;

 — собственный объём, занимаемый частицами жидкости.

Динамическая вязкость жидкостей уменьшается с увеличением температуры и растёт с увеличением давления.

Кинематическая вязкость[править | править код]

В технике, в частности, при расчёте гидроприводов и в триботехнике, часто приходится иметь дело с величиной

и эта величина получила название кинематической вязкости^[7].

Здесь  — плотность жидкости;  — коэффициент динамической вязкости.

Кинематическая вязкость в старых источниках часто указана в сантистоксах (сСт). В СИ эта величина переводится следующим образом: 1 сСт = 1 мм²/c = 10⁻⁶ м²/c.

Условная вязкость[править | править код]

Условная вязкость — величина, косвенно характеризующая гидравлическое сопротивление течению, измеряемая временем истечения заданного объёма раствора через вертикальную трубку (определённого диаметра). Измеряют в градусах Энглера (по имени немецкого химика К. О. Энглера), обозначают — °ВУ. Определяется отношением времени истечения 200 мл испытываемой жидкости при данной температуре из специального вискозиметра ко времени истечения 200 мл дистиллированной воды из того же прибора при 20 °С. Условную вязкость до 16 °ВУ переводят в кинематическую по таблице ГОСТ, а условную вязкость, превышающую 16 °ВУ, по формуле

где  — кинематическая вязкость (в м²/с), а  — условная вязкость (в °ВУ) при температуре t.

Ньютоновские и неньютоновские жидкости[править | править код]

Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. В уравнении Навье — Стокса для ньютоновской жидкости имеет место аналогичный вышеприведённому закон вязкости (по сути, обобщение закона Ньютона, или закон Навье — Стокса^[8]):

где  — тензор вязких напряжений.

Среди неньютоновских жидкостей по зависимости вязкости от скорости деформации различают псевдопластики и дилатантные жидкости. Моделью с ненулевым напряжением сдвига (действие вязкости подобно сухому трению) является модель Бингама. Если вязкость меняется с течением времени, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.

С повышением температуры вязкость многих жидкостей падает. Это объясняется тем, что кинетическая энергия каждой молекулы возрастает быстрее, чем потенциальная энергия взаимодействия между ними. Поэтому все смазки всегда стараются охладить, иначе это грозит простой утечкой через узлы.^{[источник не указан 1007 дней]}

Вязкость аморфных материалов[править | править код]

Вязкость аморфных материалов (например, стекла или расплавов) — это термически активизируемый процесс^[9]:

где

 — энергия активации вязкости (Дж/моль);

 — температура (К);

 — универсальная газовая постоянная (8,31 Дж/моль·К);

 — некоторая постоянная.

Вязкое течение в аморфных материалах характеризуется отклонением от закона Аррениуса: энергия активации вязкости изменяется от большой величины при низких температурах (в стеклообразном состоянии) на малую величину при высоких температурах (в жидкообразном состоянии). В зависимости от этого изменения аморфные материалы классифицируются либо как сильные, когда , или ломкие, когда . Ломкость аморфных материалов численно характеризуется параметром ломкости Доримуса : сильные материалы имеют , в то время как ломкие материалы имеют .

Вязкость аморфных материалов весьма точно аппроксимируется двуэкспоненциальным уравнением^[10]

с постоянными , , , и , связанными с термодинамическими параметрами соединительных связей аморфных материалов.

В узких температурных интервалах недалеко от температуры стеклования это уравнение аппроксимируется формулами типа VTF или сжатыми экспонентами Кольрауша.

Если температура существенно ниже температуры стеклования, , двуэкспоненциальное уравнение вязкости сводится к уравнению типа Аррениуса

с высокой энергией активации , где  — энтальпия разрыва соединительных связей, то есть создания конфигуронов, а  — энтальпия их движения. Это связано с тем, что при аморфные материалы находятся в стеклообразном состоянии и имеют подавляющее большинство соединительных связей неразрушенными.

При двуэкспоненциальное уравнение вязкости также сводится к уравнению типа Аррениуса

но с низкой энергией активации . Это связано с тем, что при аморфные материалы находятся в расправленном состоянии и имеют подавляющее большинство соединительных связей разрушенными, что облегчает текучесть материала.

Относительная вязкость[править | править код]

В технических науках часто пользуются понятием относительной вязкости, под которой понимают отношение коэффициента динамической вязкости (см. выше) раствора к коэффициенту динамической вязкости чистого растворителя:

где

μ — динамическая вязкость раствора;

μ₀ — динамическая вязкость растворителя.

Вязкость некоторых веществ[править | править код]

Для авиастроения и судостроения наиболее важно знать вязкости воздуха и воды.

Вязкость воздуха[править | править код]

Вязкость воздуха зависит в основном от температуры.
При 15,0 °C вязкость воздуха составляет 1,78⋅10⁻⁵ кг/(м·с) = 17,8 мкПа·с = 1,78⋅10⁻⁵ Па·с. Можно найти вязкость воздуха как функцию температуры с помощью программ расчёта вязкостей газов^[11].

Вязкость воды[править | править код]

Динамическая вязкость воды составляет 8,90·10⁻⁴ Па·с при температуре около 25 °C. Как функция температуры: T = A × 10^B/(T−C), где A = 2,414·10⁻⁵ Па·с, B = 247,8 K, C = 140 K.

Значения динамической вязкости жидкой воды при разных температурах вплоть до точки кипения приведены в таблице:

Температура, °C	Вязкость, мПа·с
10	1,308
20	1,002
30	0,7978
40	0,6531
50	0,5471
60	0,4668
70	0,4044
80	0,3550
90	0,3150
100	0,2822

Динамическая вязкость разных веществ[править | править код]

Ниже приведены значения коэффициента динамической вязкости некоторых ньютоновских жидкостей:

Вязкость отдельных видов газов

Газ	при 0 °C (273 K), мкПа·с	при 27 °C (300 K), мкПа·с
воздух	17,4	18,6
водород	8,4	9,0
гелий		20,0
аргон		22,9
ксенон	21,2	23,2
углекислый газ		15,0
метан		11,2
этан		9,5

Вязкость жидкостей при 25 °C

Жидкость	Вязкость, Па·с	Вязкость, мПа·с
ацетон	3,06·10−4	0,306
бензол	6,04·10−4	0,604
кровь (при 37 °C)	(3—4)·10−3	3—4
касторовое масло	0,985	985
кукурузный сироп	1,3806	1380,6
этиловый спирт	1.074·10−3	1.074
этиленгликоль	1,61·10−2	16,1
глицерин (при 20 °C)	1,49	1490
мазут	2,022	2022
ртуть	1,526·10−3	1,526
метиловый спирт	5,44·10−4	0,544
моторное масло SAE 10 (при 20 °C)	0,065	65
моторное масло SAE 40 (при 20 °C)	0,319	319
нитробензол	1,863·10−3	1,863
жидкий азот (при 77K)	1,58·10−4	0,158
пропанол	1,945·10−3	1,945
оливковое масло	0,081	81
пек	2,3·108	2,3·1011
серная кислота	2,42·10−2	24,2
вода	8,94·10−4	0,894

Примечания[править | править код]

Литература[править | править код]

• R. H. Doremus. J. Appl. Phys., 92, 7619—7629 (2002).
• M. I. Ojovan, W. E. Lee. J. Appl. Phys., 95, 3803—3810 (2004).
• M. I. Ojovan, K. P. Travis, R. J. Hand. J. Phys.: Condensed Matter, 19, 415107 (2007).
• Л. И. Седов. Механика сплошной среды. Т. 1. — М.: Наука, 1970. — 492 с.
• П. Н. Гедык, М. И. Калашникова. Смазка металлургического оборудования. — М.: Металлургия, 1976. — 380 с.
• И. Ф. Голубев. Вязкость газов и газовых смесей. — М.: Физматлит, 1959.
• Ред. Ф. Н. Тавадзе Внутреннее трение в металлах, полупроводниках, диэлектриках и ферромагнетиках. — М., Наука, 1978. — 235 c.

Ссылки[править | править код]

• Аринштейн А. Сравнительный вискозиметр Жуковского // Квант, № 9, 1983.
• Измерение вязкости нефтепродуктов
• Булкин П. С. Попова И. И., Общий физический практикум. Молекулярная физика
• Градус условной вязкости // Большой энциклопедический политехнический словарь. — 2004.
• Вязкость воды

Вязкость воздуха

Коэффициент динамической вязкости воздуха можно определить по формуле Милликена:

$$mu=9.80665cdot(1.745cdot10^{-6}+5.03cdot10^{-9}cdot t)$$

Перевод динамической вязкости $mu$ в кинематическую $nu$ при помощи плотности $rho$:

$$nu=frac{mu}{rho}$$