Как найти кинетический момент двух тел - Сайт, где вы сможете решить свои вопросы

Вычисление кинетического момента при различных движениях твердого тела

Будем
приближенно моделировать твердое тело
неизменяемой системой n
материальных
точек, распределенных по объёму тела.

1. Поступательное
движение твёрдого тела

Учитывая,
что при поступательном движении твёрдого
тела скорости всех его точек одинаковы
и вынося скорость
за знак суммирования, получим

Таким
образом,
,
гдеМ
— масса тела.

В полученной
формуле отсутствует знак суммирования,
и, следовательно, она справедлива и для
твердого тела с непрерывно распределенной
массой.

2. Вращательное
движение твёрдого тела вокруг неподвижной
оси

Кинетический
момент тела относительно оси вращения
z
равен

где

– расстояние от k-ой
точки до оси вращения,
(–
угловая скорость тела).

Следовательно,

(13.11)

Вынося за знак
суммирования угловую скорость в равенстве
(13.11), получим

Следовательно,
,
где
– момент инерции тела относительно оси
z.

Для твердого тела
с непрерывно распределенной массой
момент инерции будет представлять
соответствующий интеграл.

3. Плоскопараллельное
движение твёрдого тела

Из
кинематики известно, что введением
вспомогательных осей, за которые
примем оси Кёнига Cx₂y₂z₂
(рис. 13.6), плоское движение тела в
плоскости Oxy
раскладывается на переносное
поступательное движение вместе с
осями Кёнига и относительное вращательное
движение тела вокруг оси
.
Тогда на основании формулы
(13.10) кинетический момент тела
относительно осиz
перпендикулярной
плоскости движения тела равен
сумме момента количества движения

центра
масс так, как если бы в нём была
сосредоточена масса всего тела
относительно оси z
и кинетического момента тела в его
относительном вращательном движении
вокруг оси, проходящей через центр масс
тела
:

(13.12)

Теорема об изменении кинетического момента

Рис.13.7

Пусть
точки механической системы М_k массой
m_k движутся
относительно инерциальной системы
отсчёта Oxyz
со скоростью
(k=1,2,…,n).
Выберем произвольную подвижную точку
А
за центр. Определим положение точек
механической системы М_k
относительно точки А
радиус-вектором
(рис. 13.7).

Тогда
кинетический момент механической
системы относительно точки А
равен

(13.13)

Продифференцируем
обе части равенства (13.13) по времени,
получим

(13.14)

где
–
ускорения точек относительно инерциальной
системы отсчёта, вызванные действием
равнодействующих внешних сили равнодействующих внутренних сили, следовательно

Тогда

(13.15)

В
равенстве (13.15)

Обозначая
главный момент внешних сил относительно
точки А
–
и учитывая, что главный момент внутренних
сил механической системы относительно
точки равен нулю, получим

Таким образом

(13.16)

где
М
– масса всей системы,
–
скорость центра масс.

Равенство
(13.16) выражает теорему об изменении
кинетического момента относительно
подвижной точки: производная
по времени от кинетического момента
для произвольной подвижной точки равна
сумме главного момента внешних сил
системы относительно той же точки и
векторного
произведения
количества движения системы на скорость
этой точки.

Теорема
чаще применяется для неподвижной точки
(V_O
= 0):

(13.17)

Производная по
времени от кинетического момента
механической системы относительно
неподвижной точки равна главному моменту
внешних сил относительно той же точки.

В
проекциях на оси х,
у,
z
получим три скалярных равенства:

(13.18)

Если
в равенстве (13.16) за точку А
принять подвижный центр масс, теорема
будет иметь вид:

Следовательно,
теорема об изменении кинетического
момента механической системы для
неподвижного центра O
и для центра масс С
имеют
одинаковый вид.

Следствия
из теоремы об изменении кинетического
момента механической системы для
неподвижной точки

1.
Внутренние силы непосредственно не
влияют на изменение кинетического
момента.

2.
Если главный момент внешних сил
относительно некоторой неподвижной
точки равен нулю, то кинетический момент
системы относительно того же центра не
изменяется по модулю и направлению.

Если

,
то

и, следовательно, .

3.
Если главный момент внешних сил
относительно некоторой неподвижной
оси равен нулю, то кинетический момент
механической системы относительно этой
оси не изменяется по величине.

Если

,
то

и, следовательно, .

Пример
1. Скамейка Жуковского.
Круглая горизонтальная платформа может
вращаться с пренебрежимо малым трением
вокруг вертикальной оси. В первоначальный
момент на платформе стоит человек с
гантелями в опущенных руках. Платформу
раскрутили. Как изменится её угловая
скорость, если стоящий на ней человек
расставит руки с гантелями на уровне
плеч?

Решение.
Внешними силами механической системы,
состоящей из платформы с человеком,
будут силы тяжести платформы, человека
с гантелями и реакции опор о поверхность
параллельные оси вращения платформы.
Следовательно,
.
Тогда из третьего следствия теоремы об
изменении кинетического момента
механической системы
и, следовательно,

(13.19)

где
– момент инерции механической системы
в первый момент при опущенных руках с
гантелями,₁
– угловая скорость в этот момент времени,
– момент инерции механической системы
при расставленных руках,₂– соответствующая
угловая скорость системы. При этом
,
так как во втором случае будут больше
расстояния от гантелей до оси вращения
платформы с человеком.

Тогда
из равенства (13.19) угловая скорость при
расставленных руках уменьшится ₂< ₁.

Пример
2. Управление вращением платформы с
помощью маховика.
Механическая система состоит из
горизонтальной платформы, которая может
вращаться с пренебрежимо малым трением
вокруг вертикальной оси z
и маховика, ось которого совпадает с
осью вращения платформы. Маховик
раскрутили (за счёт внутренних сил) до
угловой скорости 
из состояния покоя. Определить угловую
скорость 
платформы.

Решение.
Как и в первом примере, внешние силы
(силы тяжести платформы и маховика,
реакции опор платформы о поверхность)
параллельны оси вращения z
и, следовательно,
.
Из третьего следствия теоремы об
изменении кинетического момента
механической системы

Пусть
–
момент инерции маховика,–
момент инерции платформы относительно
оси вращения. Кинетический момент
маховика относительно оси вращения
равенесли предположить, что платформа будет
вращаться в ту же сторону, что и маховик.
Кинетический момент платформы относительно
оси вращения равен

Тогда,
учитывая, что механическая система
вращается из состояния покоя, получаем

Откуда

Знак (-) означает,
что платформа будет вращаться в сторону,
противоположную вращению маховика.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание:

Кинетический момент точки и системы:

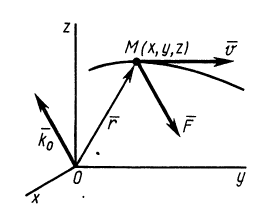
Рис. 47

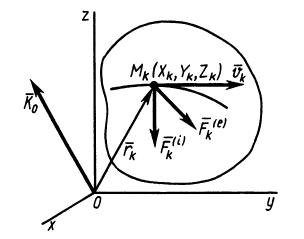
Рис. 48

Наряду с количеством движения в качестве векторной меры движения можно использовать кинетический момент, или момент количества движения. Для материальной точки массой 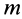, движущейся со скоростью 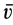, кинетическим моментом 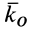относительно какого-либо центра 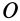(рис. 47), т. е.

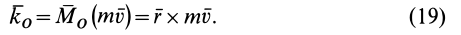
Кинетический момент 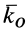приложен к точке , относительно которой он вычисляется.

Проецируя обе части (19) на прямоугольные декартовы оси, получаем кинетические моменты точки относительно этих осей координат, если точка является началом осей координат:

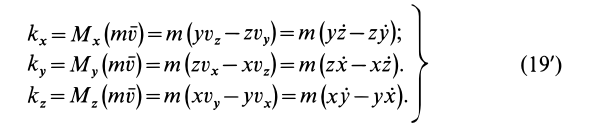
В физике кинетический момент точки иногда называют моментом импульса точки.

Единица кинетического момента в С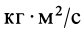И — , или .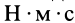

Для механической системы кинетическим моментом 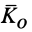(или главным моментом количества движения системы относительно какой-либо точки 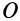) называют векторную сумму кинетических моментов точек этой системы, взятых относительно точки 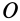(рис. 48), т. е.

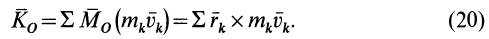
Кинетический момент системы 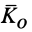приложен к точке 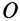, относительно которой он вычисляется.

Если спроецировать (20) на прямоугольные декартовы оси координат, то получим проекции кинетического момента на эти оси, или кинетические моменты относительно осей координат:

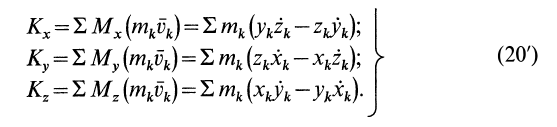
Кинетический момент относительно оси вращения при вращательном движении твердого тела

Вычислим кинетический момент твердого тела относительно оси вращения, когда тело вращается вокруг этой неподвижной оси с угловой скоростью 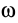(рис. 49). По определению кинетического момента относительно оси [(см. формулы (20′)] имеем

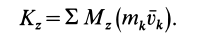
Но при вращении тела вокруг оси 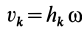, причем количество движения точки 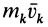перпендикулярно отрезку 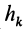и лежит в плоскости, перпендикулярной оси вращения 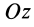. Следовательно, момент количества движения относительно оси 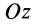для одной точки

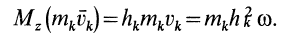
Для всего тела

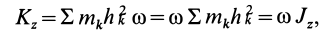
т. е.

Таким образом, кинетический момент тела относительно оси вращения при вращательном движении равен произведению угловой скорости тела на его момент инерции относительно оси вращения. Знак кинетического момента относительно оси совпадает со знаком угловой скорости вращения вокруг этой оси: при вращении против часовой стрелки кинетический момент положительный; при вращении по часовой стрелке — отрицательный.

Дополнительно без вывода приведем формулы для кинетических моментов относительно двух других осей координат 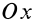и 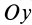, перпендикулярных оси вращения 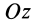. Имеем

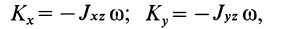
где 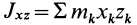и 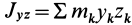— центробежные моменты инерции.

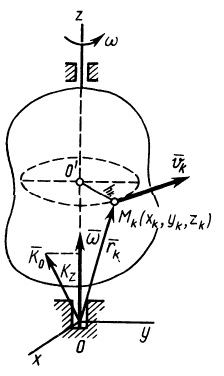
Рис. 49

Эти формулы можно получить как частный случай более общих формул для случая вращения твердого тела вокруг неподвижной точки. Они могут быть получены и непосредственно.

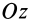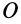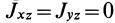Если ось вращения является главной осью инерции для точки , то и, следовательно 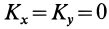для этой точки. В этом случае кинетический момент 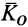относительно точки 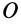направлен по оси вращения. В общем случае 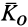не направлен по оси вращения, так как имеет не равные нулю проекци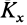и и 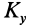на оси координат, перпендикулярные оси вращения .

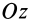Теорема об изменении кинетического момента точки

Для материальной точки основной закон динамики можно представить в виде

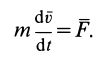
Умножая обе части этого соотношения слева векторно на радиус-вектор 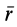(см. рис. 48), получаем

В правой части этой формулы имеем момент силы относительно неподвижной точки 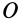. Преобразуем левую часть, применив формулу производной от векторного произведения:

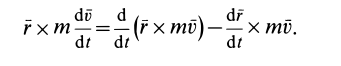
Но

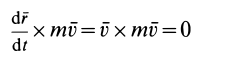
как векторное произведение параллельных векторов.

После этого из (22) получаем

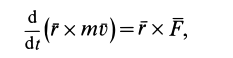
или

Таким образом, первая производная по времени от кинетического момента точки относительно какого-либо центра равна моменту силы относительно того же центра.

Это и есть теорема об изменении кинетического момента для точки.

Проецируя (23) на прямоугольные декартовы оси координат, получаем теоремы об изменении кинетического момента точки относительно этих осей координат:

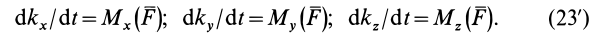
Теорема об изменении кинетического момента системы

Если к точкам системы приложить все внешние и внутренние силы (рис. 48), то для каждой точки системы можно выразить теорему об изменении кинетического момента в форме (23), т. е.

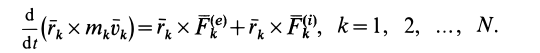
Суммируя правые и левые части этих соотношений по всем точкам системы и заменяя суммы производных производной от суммы, получаем

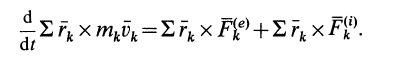
Так как, по свойству внутренних сил,

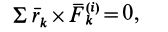
а по определению кинетического момента системы,

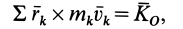
то

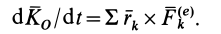
Если обозначить главный момент всех внешних сил 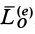, т. е.

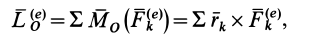
то теорему об изменении кинетического момента системы можно представить в виде

Следовательно, первая производная по времени от кинетического момента системы относительно какой-либо точки равна векторной сумме моментов внешних сил, действующих на систему, относительно той же точки.

В эту теорему входит кинетический момент системы 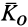в ее движении относительно инерциальной системы отсчета, причем кинетический момент и моменты внешних сил вычисляются относительно неподвижной в этой системе отсчета точки 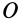. Получим теорему об изменении кинетического момента системы такого же движения, но выберем в качестве точки при вычислении кинетического момента и моментов внешних сил точку 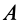, движущуюся относительно инерциальной системы отсчета со скоростью .

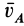По определению кинетического момента системы относительно точки 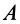имеем (рис. 50)

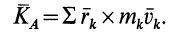
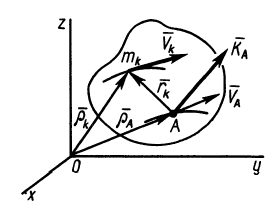
Рис. 50

Вычислим производную по времени от кинетического момента 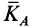по правилу дифференцирования векторных произведений. Получим

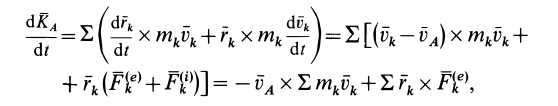
так как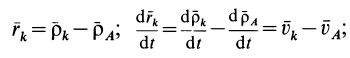

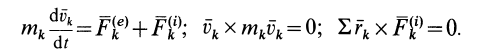
Учитывая, что 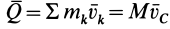, получим

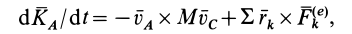
или

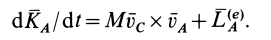
Рассмотрим частные случаи этой теоремы.

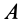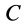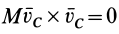1. Если точка совпадает с центром масс , то и теорема принимает форму

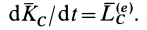
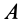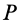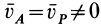2. Если в случае плоского движения твердого тела выбрать в качестве точки мгновенный центр скоростей , то , так как в рассматриваемом случае 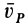есть скорость движения мгновенного центра скоростей по неподвижной центроиде, а она не равна нулю в отличие от скорости точки тела, совпадающей с точкой 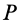, которая равна нулю. Очевидно, 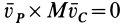, если 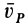параллельна 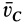, т.е. если касательные к центроидам и траектории центра масс параллельны или, что то же самое, центр масс находится на нормали к центроидам в точке 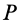. Тогда

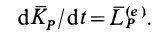
Эти частные случаи показывают, что для подвижных точек центра масс для любой системы и мгновенного центра скоростей при плоском движении твердого тела в рассмотренном случае теорема об изменении кинетического момента для абсолютного движения имеет ту же форму, что и для неподвижной точки .

Внутренние силы непосредственно не влияют на изменение кинетического момента системы. Они могут влиять на него только через внешние силы, т. е. неявно.

Проецируя (24) на прямоугольные декартовы оси координат, получаем теоремы об изменении кинетического момента системы относительно этих осей координат, т. е.

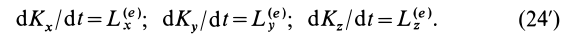
Теорема об изменении кинетического момента позволяет изучать вращательное движение твердого тела вокруг оси и точки или вращательную часть движения тела в общем случае движения свободного твердого тела.

Законы сохранения кинетических моментов

Выведем законы сохранения кинетических моментов для системы, рассматривая материальную точку как механическую систему, у которой число точек равно единице. Естественно, что для одной материальной точки все действующие на нее силы являются внешними. Возможны следующие частные случаи теоремы об изменении кинетического момента системы.

1. Если главный момент внешних сил системы относительно точки равен нулю, т. е. 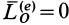, то, согласно (24), кинетический момент системы 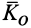относительно той же точки постоянен по модулю и направлению, т. е.

Этот частный случай теоремы об изменении кинетического момента системы называют законом сохранения кинетического момента. В проекциях на прямоугольные декартовы оси координат по этому закону

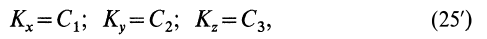
где 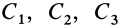— постоянные величины.

Соотношения (25′) являются первыми интегралами дифференциальных уравнений движения системы (3). Закон сохранения кинетического момента системы показывает, что одни внутренние силы не могут изменить кинетический момент системы, так же как они не изменяют ее количество движения.

2. Если сумма моментов всех внешних сил системы относительно оси 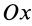равна нулю, т. е. 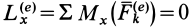, то из (24′) следует, что

Следовательно, кинетический момент системы относительно какой-либо координатной оси постоянен, если сумма моментов внешних сил относительно этой оси равна нулю, что, в частности, наблюдается, когда внешние силы параллельны оси или пересекают ее. В частном случае для тела или системы тел, которые все вместе могут вращаться вокруг неподвижной оси, и если при этом

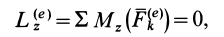
то

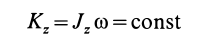
или

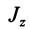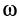где и — момент инерции системы тел и их угловая скорость относительно оси вращения в произвольный момент времен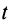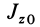и ; и 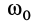— момент инерции тел и их угловая скорость в момент времени, выбранный за начальный, например при .

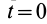Закон сохранения кинетического момента в форме (27) используют в своей деятельности акробаты, прыгуны, танцоры и т. д. Наглядно его можно продемонстрировать в опыте на скамье Жуковского (рис. 51). Если человек с гирями в руках встанет на горизонтальную платформу скамьи Жуковского, которая может вращаться вокруг вертикальной оси почти без трения, и затем ему сообщить угловую скорость вокруг этой оси, то

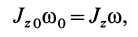
так как внешние силы или параллельны оси вращения (силы веса человека, гирь и платформы), или пересекают ось (реакции подшипника, если пренебречь силами трения).

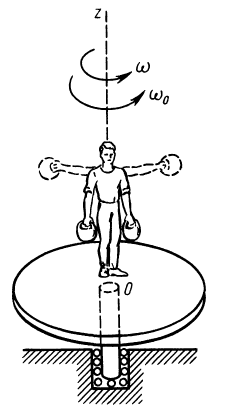
Рис. 51

Следовательно, если человек увеличит момент инерции, например разведением рук с гирями в сторону, то угловая скорость вращения уменьшится, и наоборот. В действительности угловая скорость хотя и медленно, но все время уменьшается вследствие наличия сопротивления воздуха и трения в подшипнике скамьи.

Пример:

Однородный горизонтальный диск радиусом 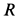и силой тяжести 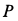может вращаться без трения вокруг вертикальной оси. Как изменится угловая скорость диска, если первоначально стоящий на диске на расстоянии 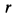от его оси человек с силой тяжести 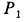пойдет по окружности радиусом 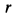по диску с относительной скоростью 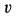(рис. 52)?

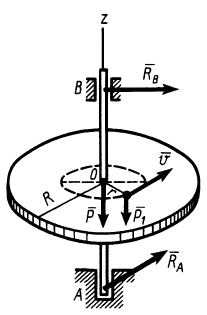
Рис. 52

Решение:

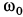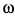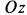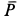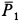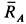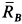Пусть угловая скорость диска вначале была , а потом вследствие движения человека по диску стала . Так как внешние силы для системы, состоящей из человека и диска, параллельны оси (силы тяжести и ) или ее пересекают (реакции и ), то

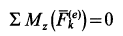
и, следовательно,

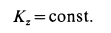
Составим 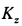для двух моментов времени и приравняем друг другу. В начальный момент, когда человек стоит, кинетический момент системы определяется как

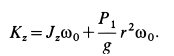
После того как человек пойдет по диску, его кинетический момент станет равным кинетическому моменту от вращения вместе с диском плюс кинетический момент от относительного движения по диску, если человек идет в сторону вращения диска, т. е.

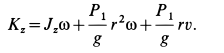
Приравнивая полученные выражения кинетических моментов, получаем

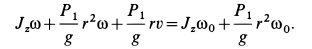
Отсюда

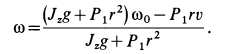
Для однородного диска

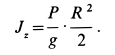
Поэтому угловая скорость

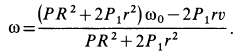
Угловая скорость диска от движения по нему человека уменьшилась на 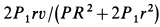. Если вместо диска рассматривать земной шар, то движение по нему материальных объектов (воздуха, течения воды и т. д.), которые имеют не равную нулю проекцию скорости на касательную к параллелям, вызовет изменение угловой скорости вращения Земли. Она уменьшится, если проекции скорости положительны для направления по вращению земного шара, и увеличится, если против вращения.

Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси

Из теоремы об изменении кинетического момента (24′) получим дифференциальное уравнение вращения твердого тела вокруг неподвижной оси 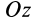(рис. 53). Имеем

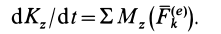
Для случая вращения твердого тела вокруг неподвижной оси, согласно (21), имеем

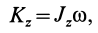
где 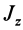— постоянный для твердого тела момент инерции относительно неподвижной оси вращения; 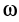— угловая скорость. Учитывая это, получаем

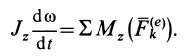
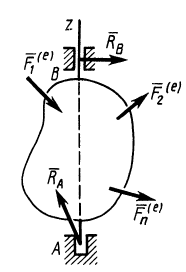
Рис. 53

Если ввести угол поворота тела 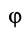, учитывая, что 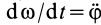, имеем

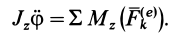
Это и есть дифференциальное уравнение вращения твердого тела вокруг неподвижной оси. Оно полностью аналогично дифференциальному уравнению поступательного движения твердого тела в проекции на какую-либо ось, например на ось .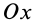

В дифференциальное уравнение вращения тела вокруг неподвижной оси вместо координаты 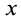входит угол поворота 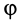, вместо массы тела 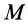—момент инерции относительно оси вращения 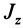, вместо суммы проекций внешних сил на ось 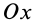— сумма моментов внешних сил относительно оси вращения 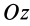или так называемый вращательный момент внешних сил.

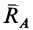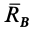Реакции подшипников и оси вращения являются внешними силами, но их моменты относительно оси вращения равны нулю, так как они пересекают ось, если пренебречь силами трения.

В частном случае, когда

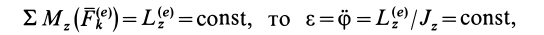
т. е. вращение тела происходит с постоянным угловым ускорением.

Если

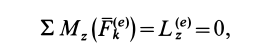
то

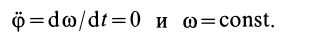
Это случай равномерного вращения тела по инерции без действия вращательного момента внешних сил.

Дифференциальное уравнение вращательного движения твердого тела в общем случае позволяет решать две основные задачи: по заданному вращению тела определять вращающий момент внешних сил и по заданному вращательному моменту и начальным условиям находить вращение тела. При решении второй задачи для нахождения угла поворота как функции времени приходится интегрировать дифференциальное уравнение вращательного движения. Методы его интегрирования полностью аналогичны рассмотренным выше методам интегрирования дифференциального уравнения прямолинейного движения точки.

Движение точки под действием центральной силы

Теорема площадей:

Наряду с введенными в кинематике точки скоростью 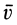и ускорением 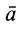можно ввести другие характеристики движения точки, например секторные скорость и ускорение. Секторной скоростью точк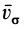и или 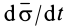относительно точки 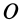(рис. 54) называют векторную величину, определяемую по формуле

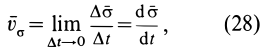
где 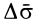— вектор, численно равный заштрихованной на рисунке площади, ометаемой радиусом-вектором 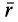движущейся точки за время 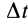; направление вектора 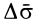берется по перпендикуляру к заштрихованной площади так, чтобы с конца этого вектора при ометании заштрихованной площади видеть поворот радиуса-вектора 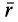против часовой стрелки.

Для случая движения точки по плоскости секторная скорость перпендикулярна этой плоскости, если точка 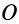выбрана в той же плоскости, в которой движется точка. Секторная скорость всегда приложена в той точке, относительно которой она вычисляется.

Секторное ускорение 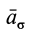можно ввести как производную по времени от вектора секторной скорости, т. е.

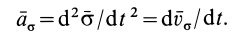
Секторную скорость можно выразить через момент линейной скорости 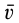относительно точки :

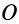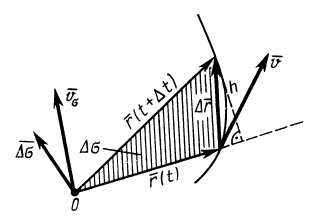
Рис. 54

Векторное произведение 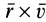, согласно определению, имеет такое же направление, как и 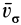. Следовательно, для доказательства формулы (29) достаточно показать, что величины левой и правой частей одинаковы. Вычислим левую часть формулы (29):

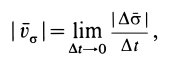
но

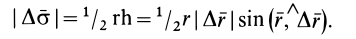
Следовательно,

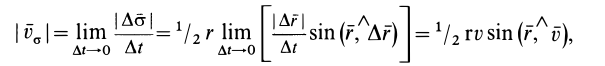
что совпадает с модулем векторного произведения, стоящим справа в формуле (29).

Если движение точки происходит в плоскости, то секторную скорость можно считать алгебраической величиной. В этом случае секторную скорость точки часто выражают в полярных координатах. Из формулы (29) секторная скорость

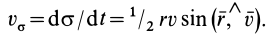
Но из кинематики точки в полярной системе координат на плоскости известно (рис. 55), что .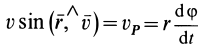

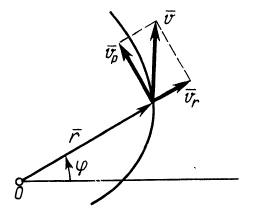
Рис. 55

Следовательно,

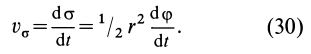
Формула (30) выражает секторную скорость в полярных координатах в случае плоского движения точки.

Используя формулу (29), кинетический момент через секторную скорость можно выразить в виде

Соответственно теорему об изменении кинетического момента (23) для точки можно выразить через секторную скорость формулой

В форме (32) теорему об изменении кинетического момента для точки называют теоремой площадей.

Движение точки под действием центральной силы

Центральной силой 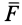называют такую силу, линия действия которой при движении точки ее приложения проходит через одну и ту же точку 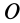, называемую центром центральной силы.

Центральная сила может быть притягивающей (направленной к центру) и отталкивающей (направленной от центра). Так как для центральной силы _момент силы относительно своего центра равен нулю, т. е. 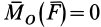, то, следовательно, по теореме об изменении кинетического момента для точки (23),

В проекциях на прямоугольные оси декартовой системы с началом в точке 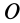по (33) имеем:

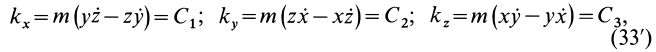
где 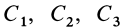— постоянные величины.

Умножая первое соотношение (33′) на 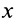, второе — на 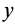, третье — на 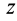и складывая, получаем 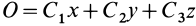, т.е. координаты движущейся точки 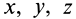удовлетворяют уравнению плоскости, проходящей через начало координат.

Следовательно, траектория точки, движущейся под действием центральной силы, является плоской кривой, лежащей в плоскости, проходящей через центр силы.

Так как при движении точки под действием центральной силы

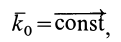
то, учитывая формулу (31), имеем

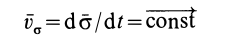
и, следовательно,

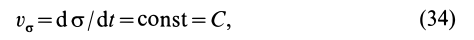
или

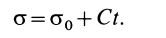
Формула (34) выражает так называемый интеграл площадей: при движении точки под действием центральной силы секторная скорость является постоянной величиной и, следовательно, ометаемая радиусом-вектором площадь пропорциональна времени.

Учитывая формулу (30), интеграл площадей (34) в полярных координатах можно представить в виде

В этой форме интеграл площадей широко используется при рассмотрении движения планет вокруг Солнца и вообще различных спутников, в частности искусственных спутников Земли.

Теорема об изменении кинетического момента системы в относительном движении по отношению к центру масс

Рассмотрим относительное движение системы только относительно системы координат, движущейся поступательно вместе с центром масс системы.

Прежде чем рассмотреть теорему, выведем формулу для вычисления кинетического момента системы.

Формула для кинетического момента системы

Пусть механическая система совершает движение относительно основной системы координат 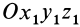. Возьмем подвижную систему координат 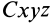с началом в центре масс системы 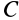, движущуюся поступательно относительно основной системы координат. Из рис. 56 следует, что для любого момента времени .

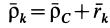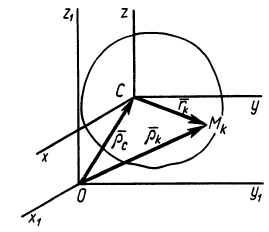
Рис. 56

Дифференцируя это тождество по времени, получаем

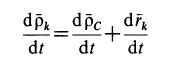
или

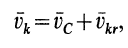
где 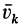— абсолютная скорость точки 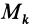, 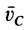— абсолютная скорость центра масс; 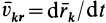— относительная скорость точки 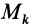относительно подвижной системы координат 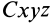. При поступательном движении подвижной системы координат ее угловая скорость 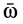равна нулю и по формуле Бура полная производная по времени от радиуса-вектора 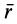совпадает с локальной производной, равной относительной скорости.

Согласно определению кинетического момента 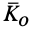относительно неподвижной точки 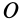, для абсолютного движения системы относительно системы координат 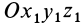по формуле (20) имеем

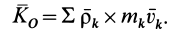
Подставляя в эту формулу значения 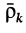и 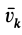, после небольших преобразований получаем

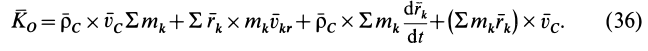
В этой формуле 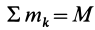— масса системы. Кроме того, последние два слагаемых равны нулю. Действительно, по определению радиуса-вектора центра масс относительно этого центра масс имеем

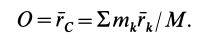
Следовательно, 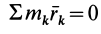и последнее слагаемое в (36) тоже равно нулю.

Другое слагаемое можно предварительно преобразовать:

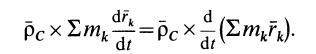
Это слагаемое также равно нулю, так как все время 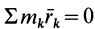. Формула (36) принимает следующий окончательный вид:

где .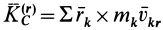

Величина 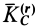является кинетическим моментом системы относительно центра масс для относительного движения относительно системы координат, движущейся поступательно вместе с центром масс, т. е. системы координат .

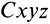Формула (37) показывает, что кинетический момент абсолютного движения системы относительно неподвижной точки равен векторной сумме кинетического момента центра масс относительно той же точки, если бы в центре масс была сосредоточена вся масса системы, и кинетического момента системы относительно центра масс для относительного движения системы по отношению к подвижной системе координат, движущейся поступательно вместе с центром масс.

Теорема об изменении кинетического момента системы в относительном движении по отношению к центру масс. Для абсолютного движения системы и неподвижной точки теорема об изменении кинетического момента имеет вид

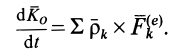
Подставляя сюда значения 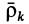и 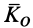по формуле (37) и производя дифференцирование и группировку членов, получаем

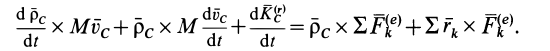
Перенося из правой части в левую первое слагаемое и учитывая, что

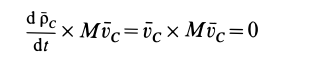
как векторное произведение параллельных векторов, после объединения слагаемых имеем

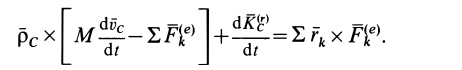
В этой формуле выражение в квадратных скобках равно нулю на основании теоремы о движении центра масс системы (18) и, следовательно, формула примет вид

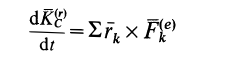
или

где 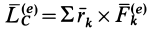является главным моментом всех внешних сил относительно центра масс.

Формула (38) и выражает рассматриваемую теорему об изменении кинетического момента системы относительно центра масс для относительного движения системы по отношению к системе координат, движущейся поступательно с центром масс; она формулируется так же, как если бы центр масс был неподвижной точкой.

Эту теорему применяют для изучения вращательной части плоского движения и движения свободного твердого тела вокруг центра масс.

Дифференциальные уравнения плоского движения твердого тела

Используя теоремы о движении центра масс и изменении кинетического момента системы относительно центра масс для относительного движения системы по отношению к системе координат, движущейся поступательно с центром масс, получим дифференциальные уравнения плоского движения твердого тела.

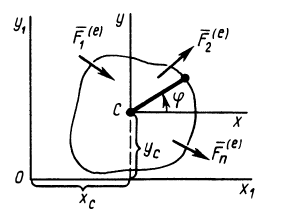
Рис. 57

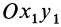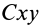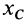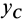В плоскости движения центра масс тела, совершающего плоское движение, выберем неподвижную систему координат , относительно которой рассматривается движение, и движущуюся поступательно вместе с центром масс систему (рис. 57). Пусть и — координаты центра масс тела относительно неподвижной системы координат. Тогда по теореме о движении центра масс получим два следующих дифференциальных уравнения плоского движения твердого тела:

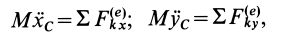
где 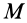— масса тела.

Третье дифференциальное уравнение плоского движения твердого тела получим из теоремы об изменении кинетического момента в относительном движении по отношению к центру масс (38) в проекции на подвижную ось :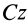

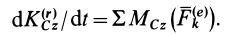
Плоское движение твердого тела можно считать состоящим из поступательного движения вместе с центром масс 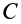и вращения вокруг подвижной оси 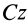. Для случая вращения вокруг оси кинетический момент относительно этой оси вычисляется по формуле

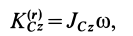
где 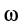— угловая скорость; 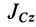— момент инерции тела относительно оси .

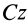Так как 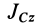является величиной постоянной, то после подстановки 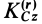в теорему об изменении’ кинетического момента в относительном движении получим

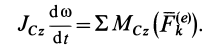
Если ввести угол поворота 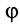вокруг подвижной оси 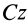, то получим следующее дифференциальное уравнение:

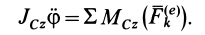
Таким образом, для твердого тела, совершающего плоское движение и, следовательно, имеющего три степени свободы, соответственно получим следующие три дифференциальных уравнения:

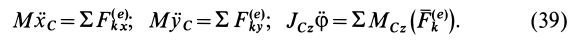
С помощью этих уравнений можно решать две основные задачи: по заданному плоскому движению твердого тела находить действующие на тело внешние силы и по заданным внешним силам и начальным условиям определять его движение. При решении этих задач должны быть заданы масса тела 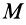и его момент инерции.

Заказать решение задач по теоретической механике

Теорема Резаля

Теореме об изменении кинетического момента системы можно дать следующее кинематическое истолкование. Из кинематики точки известно, что скорость точки можно рассматривать как скорость конца радиуса-вектора, следящего за движущейся точкой, или как скорость изменения самого радиуса-вектора, если он проведен в движущуюся точку из какой-либо неподвижной точки (рис. 58). Траектория движущейся точки при этом является годографом радиуса-вектора г, а скорость точки направлена по касательной к этому годографу и равна первой производной по времени от радиуса-вектора. Аналогично этому, и производную по времени от кинетического момента можно рассматривать как своеобразную скорость конца этого вектора при движении по годографу кинетического момента (рис. 59). Эта скорость не является обычной скоростью точки, так как кинетический момент имеет иную размерность, чем радиус-вектор. Это есть скорость изменения вектора кинетического момента.

Таким образом, если обозначить через 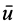скорость конца кинетического момента, т. е. 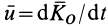, то теорему об изменении кинетического момента системы (24) можно представить в новой форме — в виде так называемой теоремы Резаля:

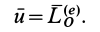
Теорему Резаля можно сформулировать так: при движении механический системы скорость точки, совпадающей с концом вектора кинетического момента при движении по годографу этого вектора, равна по величине и параллельна по направлению главному моменту всех внешних сил системы. Точка, относительно которой вычисляются кинетический момент системы и главный момент внешних сил, одна и та же.

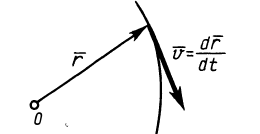
Рис. 58

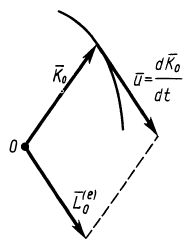
Рис. 59

В форме теоремы Резаля может быть сформулирована и теорема об изменении кинетического момента в относительном движении по отношению к центру масс.

Теорема Резаля особенно удобна для приближенного исследования движения быстровращающихся гироскопов.

Аналогично и теорему об изменении количества движения для системы можно сформулировать в форме теоремы Резаля для количества движения: при движении механической системы скорость точки, совпадающей с концом вектора количества движения при движении по его годографу, равна по величине и параллельна по направлению главному вектору всех внешних сил, действующих на систему.

Теорема об изменении кинетической энергии
Потенциальное силовое поле
Закон сохранения механической энергии
Принцип Даламбера
Геометрия масс
Свойства внутренних сил системы
Дифференциальное уравнение движения системы
Теоремы об изменении количества движения и о движении центра масс

Источник

Макеты страниц

Кинетический момент твердого тела (общий случай)

Во многих случаях в качестве механической системы выступают твердое тело и система твердых тел.

В динамике твердого тела часто возникает необходимость во введении вспомогательной системы координатных осей, начало которой находится в центре масс тела и которые движутся, оставаясь все время параллельными самим себе (поступательно движутся вместе с центром масс). Такие оси называются осями Кёнига.

Рис. 32.

При вычислении кинетического момента твердое тело мысленно разбиваем на N малых частиц (материальных точек) и вводим две вспомогательные системы координат с началом в центре масс С — систему осей Кёнига и систему Cxyz, оси которой неизменно связаны с движущимся телом (как бы «вморожены» в тело) (рис. 32). Тогда Рис. 32 движение материальных точек тела относительно основной (неподвижной) системы координат Oxyz можем рассматривать как сложное движение, состоящее из переносного (движение осей Кёнига) и относительного (движение точек тела относительно осей Кёнига). Соответственно, скорости точек тела в выражении для кинетического момента будут являться абсолютными скоростями и вычисляться при помощи теоремы сложения скоростей по формулам

Здесь учтено, что переносное движение является поступательным, поэтому переносные скорости точек тела все одинаковы и равны скорости центра масс.

Подставим это выражение в формулу для определения кинетического момента системы (в данном случае — тела):

Первая сумма приводится к виду

и представляет собой момент относительно центра О количества движения тела , приложенного в центре масс тела. Вторая сумма определяет главный момент относительных количеств движения точек тела относительно того же центра О.

Введем в рассмотрение главный момент относительных количеств движения тела относительно центра масс

где — радиусы-векторы материальных точек тела, проведенные из центра масс, и покажем, что имеет место равенство . Для этого выразим абсолютные радиусы-векторы через радиус-вектор центра масс и относительные радиусы-векторы

и подставим в выражение для

Но первый член в полученной сумме равен нулю, так как равна нулю величина . Действительно, для этой величины последовательно можем написать:

так как сохраняет постоянное значение (равное нулю). Следовательно, имеет место равенство .

В результате для вычисления кинетического момента твердого тела относительно неподвижного центра О получаем следующую общую формулу:

Напомним, что в этой формуле М — масса тела, — радиус-вектор центра масс, проведенный из неподвижного центра О, — скорость центра масс, — кинетический момент тела в его относительном движении по отношению к осям Кёнига, вычисленный относительно центра масс.

Отметим частные случаи.

Тело движется поступательно. В этом случае относительное движение отсутствует — положение тела не изменяется относительно осей Кёнига. Относительные скорости частиц () равны нулю, вместе с ними равен нулю и относительный кинетический момент тела .

Следовательно, для определения кинетического момента остается только первый член в полученной общей формуле, т. е.

Так как формулу можно записать и в другом виде:

Из нее следует, что кинетический момент поступательно движущегося тела относительно некоторого неподвижного центра равен моменту относительно этого центра количества движения тела, приложенного в его центре масс. Правило сохраняется и при вычислении кинетических моментов тела относительно координатных осей .

Тело вращается вокруг неподвижной оси. В этом случае удобно действовать непосредственно, не прибегая к разложению движения на переносное и относительное.

Выберем моментный центр О на оси вращения тела, ось вращения совместим с осью неподвижной системы координат Oxyz (рис. 33). Выделим в теле частицу (материальную точку) с массой и радиусом-вектором . Тогда для скорости частицы можем записать

Рис. 33.

Здесь — орты осей Oxyz; — проекции вектора угловой скорости тела на эти оси; — координаты выделенной частицы.

В полученном выражении коэффициенты при ортах равны проекциям скорости частицы на соответствующие координатные оси. Следовательно, для проекций количества движения выделенной частицы будем иметь выражения

Для момента количества движения частицы относительно точки О с учетом полученных равенств получаем

Отсюда следуют формулы для моментов количества движения частицы относительно координатных осей

Суммируя соответствующие моменты для всех материальных точек тела, определяем проекции на оси Oxyz кинетического момента всего тела:

Из этих формул основное значение для дальнейшего имеет формула

определяющая проекцию кинетического момента вращающегося тела на направление оси вращения.

Сравнивая проекции кинетического момента тела с проекциями угловой скорости , видим, что векторы угловой скорости и кинетического момента вращающегося тела не направлены вдоль одной прямой (см. также рис. 33). Векторы и будут коллинеарными лишь в том случае, если выполняются равенства .

Вращающееся твердое тело (ротор), для которого выполняются условия (центр масс лежит на оси вращения) и (ось вращения является главной осью инерции), называется статически и динамически уравновешенным. Таковы, например, однородный круглый диск, однородный круглый цилиндр, однородный шар при их вращении вокруг одной из своих осей симметрии.

Иногда требуется знать проекции кинетического момента на оси , неизменно связанные с самим движущимся телом — . Вид формул для их вычисления сохраняется, только моменты инерции и угловую скорость следует задавать теперь в осях :

Пример. На круглой горизонтальной платформе массы и радиуса R стоит человек массы (рис. 34). Платформа и человек вначале неподвижны. Что будет происходить с платформой, если человек будет двигаться по ней с относительной скоростью по окружности радиуса . Трением в опорах пренебречь, платформу считать однородным круглым диском.

Рис. 34.

Решение. Выберем в качестве системы платформу вместе с находящимся на ней человеком, принимаемым за материальную точку М. Внешними силами будут вес платформы , вес человека , реакции подпятника А и подшипника В. Момент каждой из этих сил относительно оси вращения платформы (оси z) равен нулю, поэтому равен нулю и главный момент внешних сил относительно этой оси. Следовательно, кинетический момент системы относительно оси z остается при движении постоянным, равным своему начальному значению

В начале движения платформа и человек неподвижны, поэтому , и это равенство принимает вид

Если человек будет перемещаться по платформе с некоторой абсолютной скоростью v, то его количество движения имеет относительно оси момент

Но кинетический момент всей системы равен нулю, поэтому платформа начнет вращаться, а ее кинетический момент относительно оси вращения будет равным и противоположным по знаку моменту количества движения человека .

Для определения угловой скорости платформы составим выражение для кинетического момента системы относительно оси :

Так как платформа вращается, движение человека (точки М) будет сложным движением. По теореме сложения скоростей для абсолютной скорости v получаем:

Условие сохранения кинетического момента теперь запишется так:

Отсюда находим

В заключение заметим, что теорема об изменении кинетического момента выполняется только по отношению к неподвижному центру и неподвижным координатным осям. Однако существует единственная подвижная точка, относительно которой теорема продолжает оставаться справедливой. Такой точкой является центр масс (системы или тела). Теорема сохраняется и по отношению к осям Кенига. Доказательство этих положений мы опускаем.

Оглавление

Предисловие
Введение в динамику
Динамика точки
Две основные задачи динамики точки
Дифференциальные уравнения движения материальной точки
Способы решения основных задач динамики точки
Лекция 12. Способы интегрирования дифференциального уравнения прямолинейного движения материальной точки
Дифференциальное уравнение и начальные условия прямолинейного движения
Определение закона движения точки под действием силы, зависящей только от времени
Определение закона движения точки под действием силы, зависящей только от положения
О нахождении закона движения при постоянной силе и силе, зависящей только от скорости
Лекция 13. Колебательные движения материальной точки
Свободные колебания
Вынужденные колебания
Явление резонанса
Влияние сопротивления на свободные и вынужденные колебания
Динамика системы
Механическая система
Масса и центр масс системы
Момент инерции относительно оси
Моменты инерции относительно координатных осей
Моменты инерции твердого тела
Осевые моменты инердии некоторых твердых тел
Радиус инерции
Главные оси инерции
Классификация сил, действующих на точки системы
Свойства внутренних сил
Дифференциальные уравнения движения механической системы
Теорема о движении центра масс
Законы сохранения движения дентра масс
Общие теоремы динамики
Основные динамические величины механической системы
Теорема об изменении количества движения
Законы сохранения количества движения
О вычислении количества движения
Интегральная форма теоремы об изменении количества движения
Лекция 16. Теорема об изменении кинетического момента
Кинетический момент
Теорема об изменении кинетического момента
Законы сохранения кинетического момента
Кинетический момент твердого тела (общий случай)
Дифференциальные уравнения движения твердого тела
Физический маятник и его малые колебания
Лекция 17. Теорема об изменении кинетической энергии
Работа силы
Работа силы тяжести
Работа упругой силы пружины
Работа силы трения скольжения
Работа пары сил трения качения
Потенциальные силы
Вычисление потенциальной энергии
Теорема об изменении кинетической энергии
Вычисление кинетической энергии твердого тела
О решении задач при помощи теоремы об изменении кинетической энергии
Общие принципы механики
Принцип Даламбера для материальной точки
Принцип Даламбера для механической системы
Определение главного вектора и главного момента сил инерции твердого тела
Тело движется поступательно с ускорением
Тело совершает вращательное движение
Тело совершает плоскопараллельное движение
Лекция 19. Принцип возможных перемещений
Возможные перемещения
Уравнения связей. Классификация связей по виду их уравнений
Связи идеальные и неидеальные
Принцип возможных перемещений
Применение принципа возможных перемещений
Лекция 20. Принцип Даламбера-Лагранжа и общее уравнение динамики. Уравнения движения механической системы в обобщенных координатах
Принцип Даламбера-Лагранжа
Общее уравнение динамики
Обобщенные координаты и обобщенные силы
Уравнения движения механической системы в обобщенных координатах
Рекомендуемая литература

Источник

Момент импульса

Размерность	L²MT⁻¹
Единицы измерения
СИ	м²·кг/с
СГС	см²·г/с
Примечания
псевдовектор

Моме́нт и́мпульса (момент импульса относительно точки, также: кинетический момент, угловой момент, орбитальный момент, момент количества движения) — физическая величина, характеризующая количество вращательного движения и зависящая от того, сколько массы вращается, как она распределена в пространстве и с какой угловой скоростью происходит вращение^[1].

Для одной материальной точки момент импульса равен векторному произведению радиус-вектора точки на её импульс, для системы точек — сумме таких произведений. Стандартное обозначение: , единица измерения в СИ: м²кг/с. Величина зависит от выбора положения начала отсчёта радиус-векторов O.

Момент импульса замкнутой системы сохраняется. Он является одним из трёх аддитивных (энергия, импульс, момент импульса) интегралов движения. При наличии внешних сил производная момента импульса по времени равна моменту сил (относительно того же начала O).

Основное использование понятия момента импульса относится к задачам, связанным с реальным вращением (особенно при наличии центральной или осевой симметрии; тогда О обычно выбирается в центре или на оси). Но величина может быть вычислена и в других ситуациях, например для прямолинейного движения частицы мимо произвольной точки O, не лежащей на линии движения и условно принимаемой за центр.

В случае вращения твёрдого тела вокруг фиксированной оси часто используется не сам момент импульса, а его проекция ${displaystyle L_{parallel }}$ на эту ось — такая величина называется моментом импульса относительно оси.

Понятие момента импульса было изначально введено в классической механике, но имеет обобщения в квантовой механике и электродинамике.

Момент импульса в классической механике[править | править код]

Связь между силой F, моментом силы τ, импульсом и моментом импульса

Определение[править | править код]

Момент импульса материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:

{mathbf {L}}={mathbf {r}}times {mathbf {p}}

где — радиус-вектор частицы относительно выбранного неподвижного начала отсчёта, — импульс частицы.

Из определения момента импульса следует его аддитивность: для системы, состоящей из нескольких материальных точек, выполняется

${displaystyle mathbf {L} =sum limits _{i}mathbf {L} _{i}=sum _{i}mathbf {r} _{i}times mathbf {p} _{i}}$

Количество частиц может быть бесконечным, например в случае твёрдого тела с распределённой массой.

Так как момент импульса задаётся векторным произведением, он является псевдовектором, перпендикулярным обоим векторам и .

Момент импульса можно вычислить относительно любого начала отсчета O (получающиеся при этом разные значения связаны очевидным образом); однако чаще всего (для удобства и определённости) его вычисляют относительно центра масс, закреплённой точки вращения твердого тела или другой чем-то выделенной точки.

Выбор точки O иногда связан с характером задачи. Так, при рассмотрении орбитального движения планеты вокруг Солнца за начало отсчёта естественно взять Солнце, а при анализе её же собственного вращения — центр этой планеты. Естественно, получатся два разных момента импульса: ${displaystyle mathbf {L} _{mathrm {orbit} }}$ и ${displaystyle mathbf {L} _{mathrm {spin} }}$ .

Вычисление в общем случае[править | править код]

Если имеется материальная точка массой , двигающаяся со скоростью и находящаяся в точке, описываемой радиус-вектором , то и момент импульса вычисляется по формуле

{displaystyle mathbf {L} =mathbf {r} times mmathbf {v} }

Чтобы рассчитать момент импульса тела, его надо разбить на бесконечно малые кусочки ( rho — плотность) и просуммировать их моменты как моменты импульса материальных точек, то есть взять интеграл:

${displaystyle mathbf {L} =int limits _{V}{mathbf {dL} }=int limits _{V}{mathbf {r} times mathbf {v} ,dm}=int limits _{V}{mathbf {r} times mathbf {v} ,rho dV}}$

На практике rho задаётся как функция трёх координат и необходимо выполнение тройного интегрирования:

{displaystyle mathbf {L} =iiint {(xmathbf {i} +ymathbf {j} +zmathbf {k} )times mathbf {v} ,rho (x,y,z),dx,dy,dz}}

Если считать, что — обобщённая функция, включающая, возможно, и дельтообразные члены, то эта формула применима и к распределённым, и к дискретным системам.

Случай фиксированной оси[править | править код]

Важным случаем использования понятия «момент импульса» является движение вокруг неизменной оси. В такой ситуации часто рассматривают не сам момент импульса (псевдовектор), а его проекцию на ось как псевдоскаляр, знак которого зависит от направления вращения:

${displaystyle L_{parallel }=pm |mathbf {r_{perp }} times mathbf {p_{perp }} |}$

Параллельность-перпендикулярность (, perp ) имеются в виду по отношению к оси; ${displaystyle mathbf {r} =mathbf {r_{perp }} +mathbf {r_{parallel }} }$ , ${displaystyle mathbf {p} =mathbf {p_{perp }} +mathbf {p_{parallel }} }$ . При этом ${displaystyle r_{perp }}$ — расстояние от оси до материальной точки, называемое «плечом». Величина указанной проекции, в отличие от самого момента, не меняется при сдвиге начала отсчёта O на оси. Для распределённой системы

${displaystyle L_{parallel }=pm left|int {mathbf {r_{perp }} times mathbf {v_{perp }} ,rho dV}right|}$

Если при этом все точки тела движутся по окружностям (вращаются) с одинаковой угловой скоростью omega , то есть численно ${displaystyle v=omega r_{perp }}$ , то для материальной точки массой или для системы будет, соответственно,

${displaystyle L_{parallel }=pm omega mr_{perp }^{2}quad }$

или ${displaystyle quad L_{parallel }=pm omega int {r_{perp }^{2},rho dV}}$

Величину ${displaystyle L_{parallel }}$ иногда называют моментом импульса относительно оси. Символ параллельности у и знак перед выражением могут опускаться, если очевидно, о чём идёт речь.

Для абсолютно твёрдого тела, величина последнего интеграла называется моментом инерции относительно оси вращения и обозначается . Тогда запись обретает вид ${displaystyle ,L_{parallel }=pm Iomega ,}$ или, в векторной форме, . Если известен момент инерции относительно оси, проходящей через центр масс тела, а вращение происходит вокруг другой, но параллельной ей оси, то необходимый момент инерции находится по теореме Штайнера.

Сохранение момента импульса[править | править код]

Закон сохранения момента импульса: суммарный момент импульса относительно любой неподвижной точки для замкнутой системы остается постоянным со временем.

Производная момента импульса по времени есть момент силы:

${displaystyle {frac {dmathbf {L} }{dt}}=sum _{i}{frac {dmathbf {r} _{i}}{dt}}times mathbf {p} _{i}+sum _{i}mathbf {r} _{i}times {frac {dmathbf {p} _{i}}{dt}}=sum _{i}mathbf {r} _{i}times mathbf {F} _{i}=mathbf {tau _{ext}} }$

Таким образом, требование замкнутости системы может быть ослаблено до требования равенства нулю главного (суммарного по всем частицам ) момента внешних сил:

${displaystyle mathbf {L} =mathrm {constant} leftrightarrow mathbf {tau _{ext}} =0}$

где ${displaystyle mathbf {tau _{ext}} }$ — момент сил, приложенных к системе частиц. (Но конечно, если внешние силы вообще отсутствуют, это требование также выполняется.) Аналогичный закон сохранения справедлив для момента импульса относительно фиксированной оси.

По теореме Нётер закон сохранения момента импульса следует из изотропии пространства, то есть из инвариантности пространства по отношению к повороту на произвольный угол. При повороте на произвольный бесконечно малый угол , радиус-вектор частицы с номером изменятся на ${displaystyle delta mathbf {r} _{i}=delta varphi times mathbf {r} _{i}}$ , а скорости — ${displaystyle delta mathbf {v} _{i}=delta varphi times mathbf {v} _{i}}$ . Функция Лагранжа системы при таком повороте не изменится, вследствие изотропии пространства. Поэтому

$delta mathcal L = mathcal L(mathbf{r}_i + deltamathbf{r}_i,; mathbf{v}_i + deltamathbf{v}_i) - mathcal L(mathbf{r}_i,; mathbf{v}_i) = sum limits_i left( frac{partial mathcal L}{partial mathbf r_i} delta varphi timesmathbf r_i + frac{partial mathcal L}{partial mathbf v_i} delta varphi times mathbf v_i right)= 0.$

С учётом $frac{partial {mathcal {L}}}{partial {mathbf v_{i}}} = mathbf {p_{i}},; frac{partial mathcal {L}}{partial mathbf {r_{i}}} = mathbf {dot p_{i}}$ , где ${mathbf p}_{i}$ — обобщенный импульс -той частицы, каждое слагаемое в сумме из последнего выражения можно переписать в виде

$dot {mathbf p_i} ,delta varphi times mathbf r_i + mathbf p_i,delta varphi times mathbf {dot r_i}.$

Теперь, пользуясь свойством смешанного произведения, совершим циклическую перестановку векторов, в результате чего получим, вынося общий множитель:

$delta mathcal L = delta varphi sum limits_i left( mathbf r_i times dot {mathbf p_i} + dot {mathbf r_i} times mathbf p_i right) = delta varphi frac{d}{dt} sum limits_i (mathbf r_i times mathbf p_i) = delta varphi frac{d mathbf L}{dt} = 0,$

где — момент импульса системы. Ввиду произвольности , из равенства следует ${displaystyle {frac {dmathbf {L} }{dt}}=0.}$

Смежные понятия[править | править код]

При рассмотрении задач, связанных с вращением, фигурируют понятия, частично упоминавшиеся выше:

момент импульса относительно оси (термин состоит из четырёх слов) — проекция момента импульса на ось;
момент инерции твёрдого тела (см. также моменты инерции некоторых тел);
момент силы (он же: крутящий момент, вращательный момент, вертящий момент);
импульс момента силы ${displaystyle int limits _{t_{1}}^{t_{2}}mathbf {r} times mathbf {F} (t);dt}$ (единица измерения — Н·м·с) — мера воздействия момента силы относительно данной оси за данный промежуток времени (во вращательном движении).

Несмотря на созвучность с «моментом импульса», эти понятия не синонимичны термину «момент импульса» и несут самостоятельный смысл.

Момент импульса в электродинамике[править | править код]

При описании движения заряженной частицы в электромагнитном поле канонический импульс не является инвариантным. Как следствие, канонический момент импульса тоже не инвариантен. Тогда берётся реальный импульс, который также называется «кинетическим импульсом»:

${displaystyle mathbf {p} -{frac {emathbf {A} }{c}},}$

где — электрический заряд, — скорость света, — векторный потенциал. Таким образом, гамильтониан (инвариантный) заряженной частицы массы в электромагнитном поле:

$H =frac{1}{2m} left( mathbf{p} -frac {e mathbf{A} }{c}right)^2 + evarphi,$

где varphi — скалярный потенциал. Из этого потенциала следует закон Лоренца. Инвариантный момент импульса, или «кинетический момент импульса», определяется следующим образом:

$K= mathbf{r} times left( mathbf{p} -frac {e mathbf{A} }{c}right).$

Момент импульса в квантовой механике[править | править код]

Оператор момента[править | править код]

В квантовой механике момент импульса квантуется, то есть он может изменяться только по «квантовым уровням» между точно определёнными значениями. Проекция на любую ось момента импульса частиц, обусловленного их пространственным движением, должна быть целым числом, умноженным на hbar ( с чертой — постоянная Планка, поделенная на 2 pi ).

Эксперименты показывают, что большинство частиц имеют постоянный внутренний момент импульса, который не зависит от их движения через пространство. Этот спиновый момент импульса всегда кратен hbar/2 для фермионов и hbar для бозонов. Например, электрон в состоянии покоя имеет момент импульса hbar/2 .^[2]

В классическом определении момент импульса зависит от 6 переменных ${displaystyle r_{x}}$ , ${displaystyle r_{y}}$ , ${displaystyle r_{z}}$ , $p_{x}$ , $p_{y}$ , и $p_{z}$ . Переводя это на квантовомеханические определения, используя принцип неопределенности Гейзенберга, получаем, что невозможно вычислить все шесть переменных одновременно с любой точностью. Поэтому есть ограничение на то, что мы можем узнать или подсчитать о практическом моменте импульса. Это значит, что лучшее, что мы можем сделать — это подсчитать одновременно величину вектора момента импульса и какой-либо одной его компоненты (проекции).

Математически полный момент импульса в квантовой механике определяется как оператор физической величины из суммы двух частей, связанных с пространственным движением — в атомной физике такой момент называют орбитальным, и внутренним спином частицы — соответственно, спиновым. Первый оператор действует на пространственные зависимости волновой функции:

{displaystyle {hat {mathbf {L} }}={hat {mathbf {r} }}times {hat {mathbf {p} }}}

где и — координатный и импульсный оператор, соответственно, а второй — на внутренние, спиновые. В частности, для одной частицы без электрического заряда и без спина, оператор углового момента может быть записан как:

{displaystyle {hat {mathbf {L} }}=-ihbar (mathbf {r} times nabla )}

где nabla — оператор набла. Это часто встречающаяся форма оператора момента импульса, но не самая главная, она имеет следующие свойства:

$[L_i,; L_j ] = i hbar varepsilon_{ijk} L_k, quadleft[L_i,; mathbf{L}^2 right] = 0$

где $varepsilon_{ijk}$ — Символ Леви-Чивиты;

и даже более важные подстановки с гамильтонианом частицы без заряда и спина:

Симметрия вращения[править | править код]

Операторы момента импульса обычно встречаются при решении задач сферической симметрии в сферических координатах. Тогда момент импульса в пространственном отображении:

${displaystyle -{frac {1}{hbar ^{2}}}mathbf {L} ^{2}={frac {1}{sin theta }}{frac {partial }{partial theta }}left(sin theta {frac {partial }{partial theta }}right)+{frac {1}{sin ^{2}theta }}{frac {partial ^{2}}{partial varphi ^{2}}}.}$

Когда находят собственные значения этого оператора, получают следующее:

${displaystyle L^{2}mid l,;mrangle ={hbar }^{2}l(l+1)mid l,;mrangle ,}$

L_z mid l,; m rang = hbar m mid l,; m rang,

где , — целые числа, такие что а
$lang theta ,; varphi mid l,; m rang = Y_{l,;m}(theta,;varphi)$
— сферические функции.

Примечания[править | править код]

↑ Pivarski, Jim Spin. Symmetry Magazine (март 2013). Дата обращения: 28 апреля 2014. Архивировано 15 апреля 2014 года.
↑ [Информация с сайта Нобелевского комитета (англ.). Дата обращения: 3 ноября 2017. Архивировано 18 мая 2008 года. Информация с сайта Нобелевского комитета (англ.)]

Литература[править | править код]

Биденхарн Л., Лаук Дж. Угловой момент в квантовой физике. Теория и приложения. — М.: Мир, 1984. — Т. 1. — 302 с.
Блохинцев Д. И. Основы квантовой механики. — М.: Наука, 1976. — 664 с.
Боум А. Квантовая механика: основы и приложения. — М.: Мир, 1990. — 720 с.
Варшалович Д. А., Москалев А. Н., Херсонский В. К. Квантовая теория углового момента. — Л.: Наука, 1975. — 441 с.
Зар Р. Теория углового момента. О пространственных эффектах в физике и химии. — М.: Мир, 1993. — 352 с.

Источник

Вычисление кинетического момента при различных движениях твердого тела

Теорема об изменении кинетического момента

Кинетический момент относительно оси вращения при вращательном движении твердого тела

Теорема об изменении кинетического момента точки

Теорема об изменении кинетического момента системы

Законы сохранения кинетических моментов

Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси

Движение точки под действием центральной силы

Движение точки под действием центральной силы

Теорема об изменении кинетического момента системы в относительном движении по отношению к центру масс

Формула для кинетического момента системы

Дифференциальные уравнения плоского движения твердого тела

Теорема Резаля

Кинетический момент твердого тела (общий случай)

Момент импульса в классической механике[править | править код]

Определение[править | править код]

Вычисление в общем случае[править | править код]

Случай фиксированной оси[править | править код]

Сохранение момента импульса[править | править код]

Смежные понятия[править | править код]

Момент импульса в электродинамике[править | править код]

Момент импульса в квантовой механике[править | править код]

Оператор момента[править | править код]

Симметрия вращения[править | править код]

Примечания[править | править код]

Литература[править | править код]

Вам также может понравиться

Как найти оттиск печати

Как найти кадастровую стоимость формула

Как от суммы найти 3000

Добавить комментарий Отменить ответ