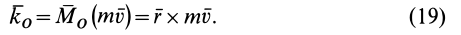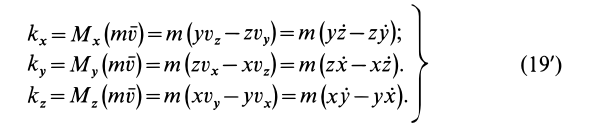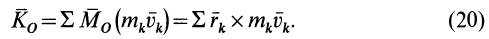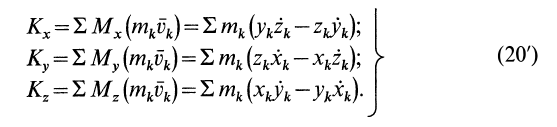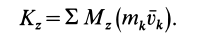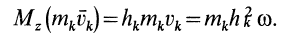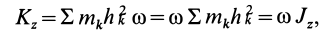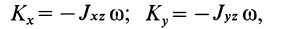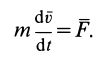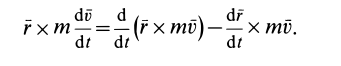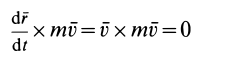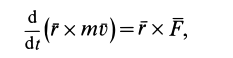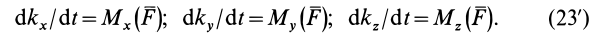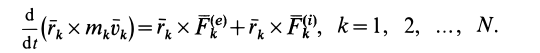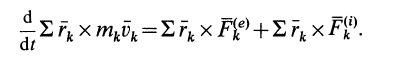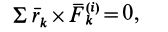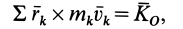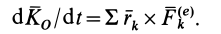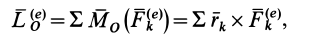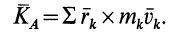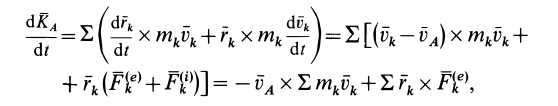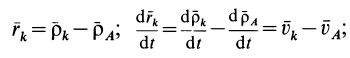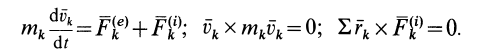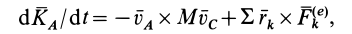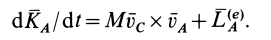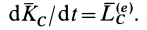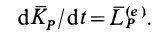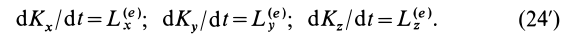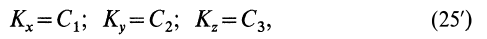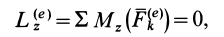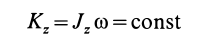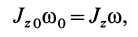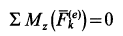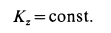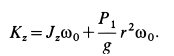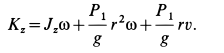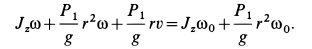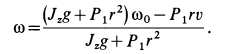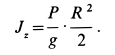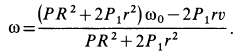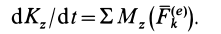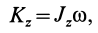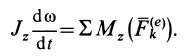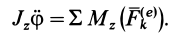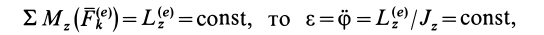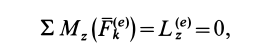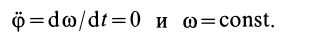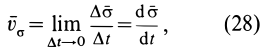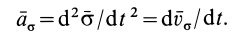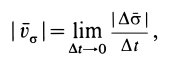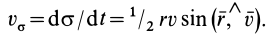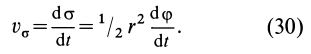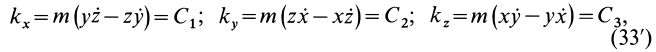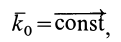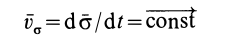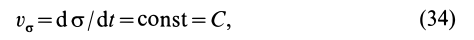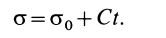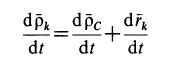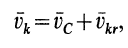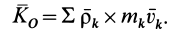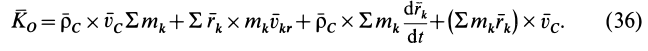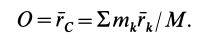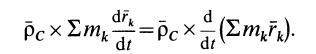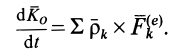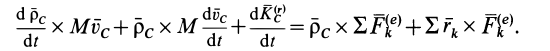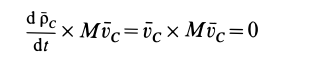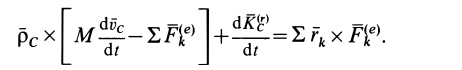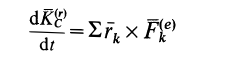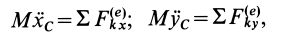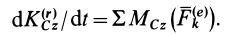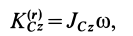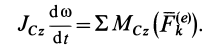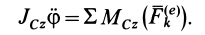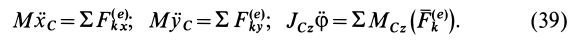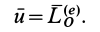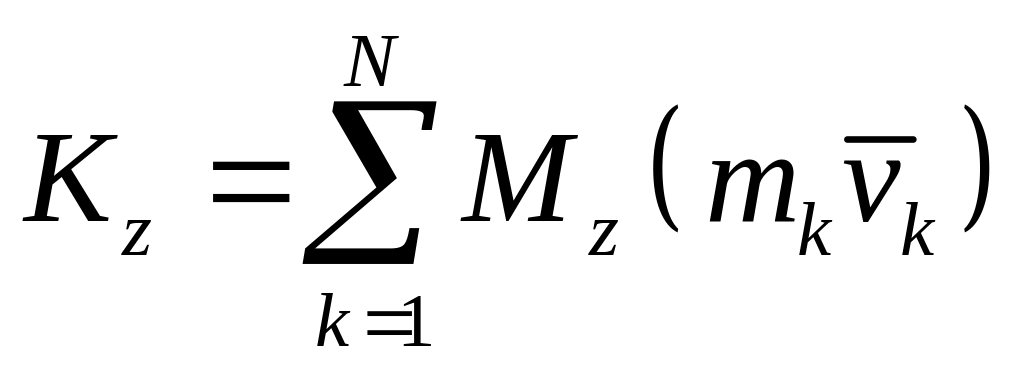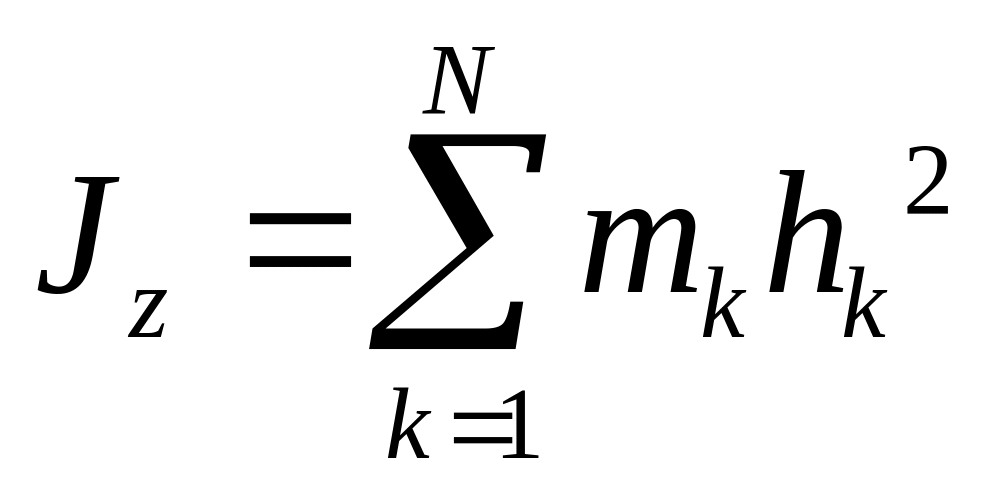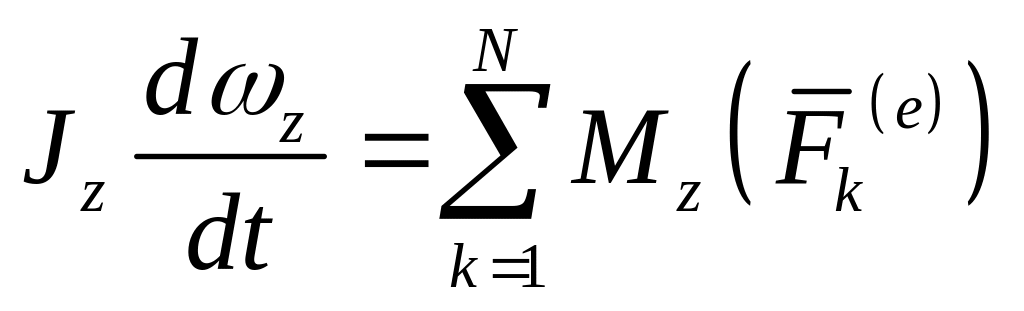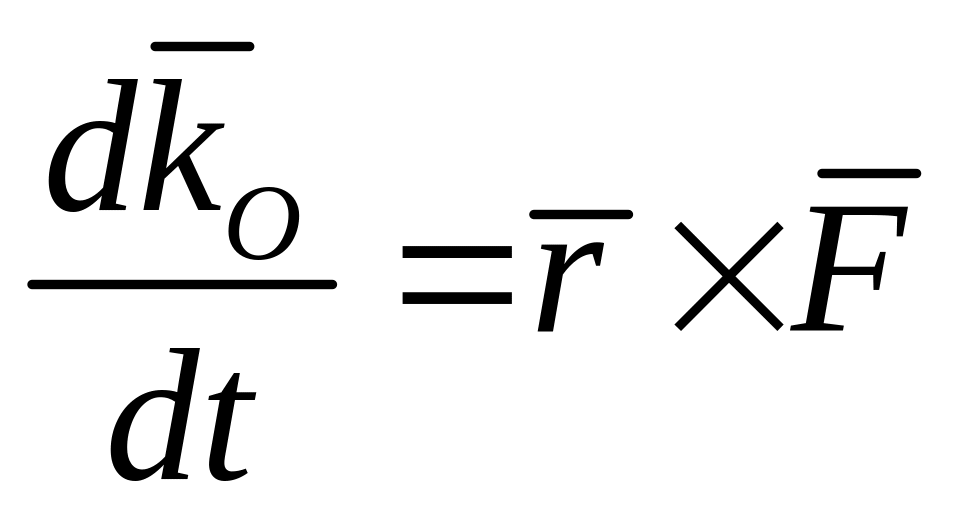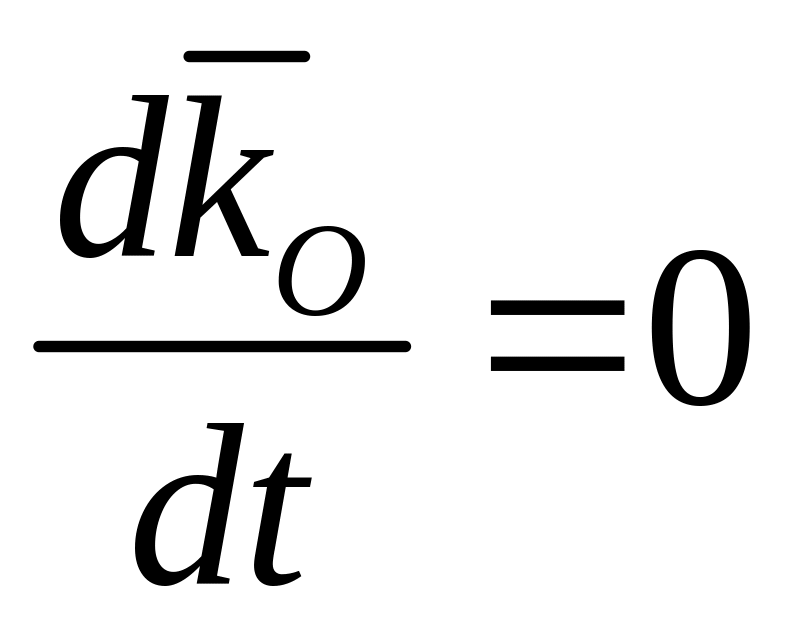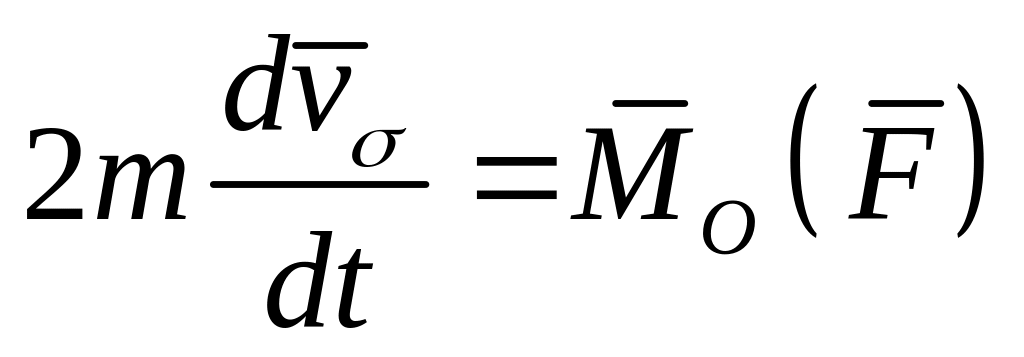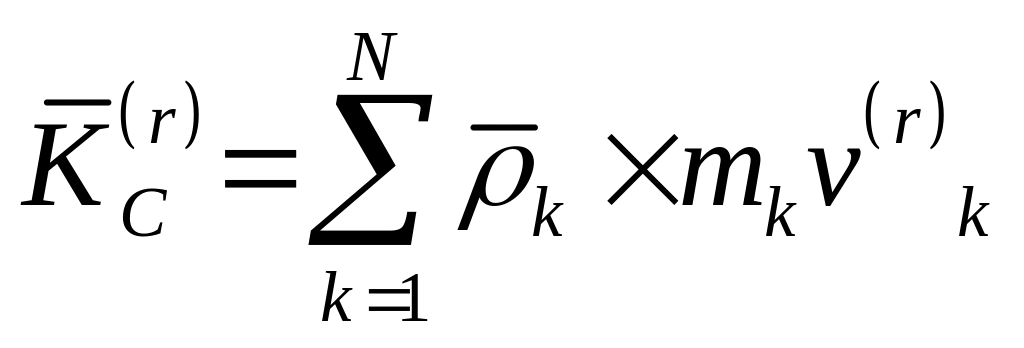Содержание:
Кинетический момент точки и системы:
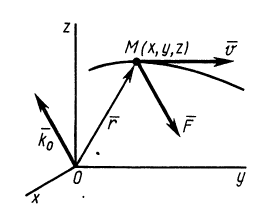
Рис. 47
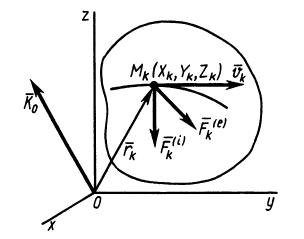
Рис. 48
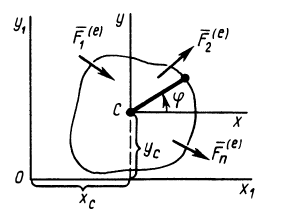
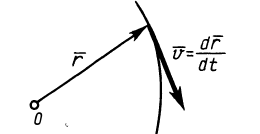
Наряду с количеством движения в качестве векторной меры движения можно использовать кинетический момент, или момент количества движения. Для материальной точки массой 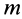
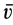
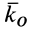
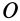
Кинетический момент 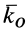
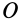
Проецируя обе части (19) на прямоугольные декартовы оси, получаем кинетические моменты точки относительно этих осей координат, если точка 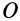
В физике кинетический момент точки иногда называют моментом импульса точки.
Единица кинетического момента в СИ — 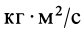
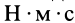
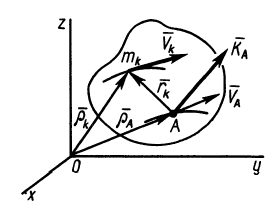
Для механической системы кинетическим моментом 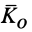
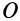
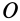
Кинетический момент системы 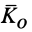
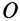
Если спроецировать (20) на прямоугольные декартовы оси координат, то получим проекции кинетического момента на эти оси, или кинетические моменты относительно осей координат:
Кинетический момент относительно оси вращения при вращательном движении твердого тела
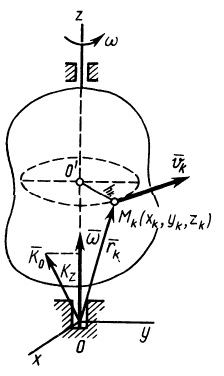
Вычислим кинетический момент твердого тела относительно оси вращения, когда тело вращается вокруг этой неподвижной оси с угловой скоростью 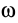
Но при вращении тела вокруг оси 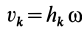
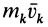
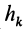
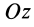
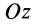
Для всего тела
т. е.
Таким образом, кинетический момент тела относительно оси вращения при вращательном движении равен произведению угловой скорости тела на его момент инерции относительно оси вращения. Знак кинетического момента относительно оси совпадает со знаком угловой скорости вращения вокруг этой оси: при вращении против часовой стрелки кинетический момент положительный; при вращении по часовой стрелке — отрицательный.
Дополнительно без вывода приведем формулы для кинетических моментов относительно двух других осей координат 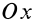
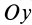
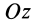
где 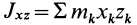
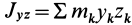
Рис. 49
Эти формулы можно получить как частный случай более общих формул для случая вращения твердого тела вокруг неподвижной точки. Они могут быть получены и непосредственно.
Если ось вращения 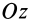
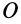
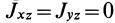
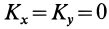
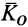
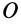
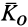
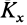
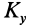
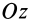
Теорема об изменении кинетического момента точки
Для материальной точки основной закон динамики можно представить в виде
Умножая обе части этого соотношения слева векторно на радиус-вектор 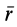
В правой части этой формулы имеем момент силы относительно неподвижной точки 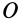
Но
как векторное произведение параллельных векторов.
После этого из (22) получаем
или
Таким образом, первая производная по времени от кинетического момента точки относительно какого-либо центра равна моменту силы относительно того же центра.
Это и есть теорема об изменении кинетического момента для точки.
Проецируя (23) на прямоугольные декартовы оси координат, получаем теоремы об изменении кинетического момента точки относительно этих осей координат:
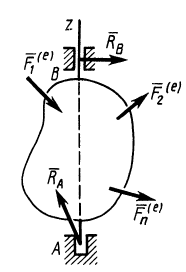
Теорема об изменении кинетического момента системы
Если к точкам системы приложить все внешние и внутренние силы (рис. 48), то для каждой точки системы можно выразить теорему об изменении кинетического момента в форме (23), т. е.
Суммируя правые и левые части этих соотношений по всем точкам системы и заменяя суммы производных производной от суммы, получаем
Так как, по свойству внутренних сил,
а по определению кинетического момента системы,
то
Если обозначить главный момент всех внешних сил 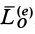
то теорему об изменении кинетического момента системы можно представить в виде
Следовательно, первая производная по времени от кинетического момента системы относительно какой-либо точки равна векторной сумме моментов внешних сил, действующих на систему, относительно той же точки.
В эту теорему входит кинетический момент системы 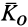
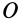
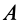
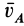
По определению кинетического момента системы относительно точки 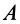
Рис. 50
Вычислим производную по времени от кинетического момента 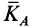
так как
Учитывая, что 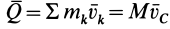
или
Рассмотрим частные случаи этой теоремы.
1. Если точка 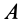
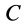
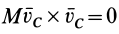
2. Если в случае плоского движения твердого тела выбрать в качестве точки 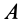
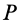
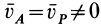
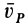
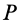
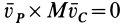
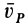
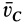
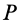
Эти частные случаи показывают, что для подвижных точек центра масс для любой системы и мгновенного центра скоростей при плоском движении твердого тела в рассмотренном случае теорема об изменении кинетического момента для абсолютного движения имеет ту же форму, что и для неподвижной точки 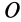
Внутренние силы непосредственно не влияют на изменение кинетического момента системы. Они могут влиять на него только через внешние силы, т. е. неявно.
Проецируя (24) на прямоугольные декартовы оси координат, получаем теоремы об изменении кинетического момента системы относительно этих осей координат, т. е.
Теорема об изменении кинетического момента позволяет изучать вращательное движение твердого тела вокруг оси и точки или вращательную часть движения тела в общем случае движения свободного твердого тела.
Законы сохранения кинетических моментов
Выведем законы сохранения кинетических моментов для системы, рассматривая материальную точку как механическую систему, у которой число точек равно единице. Естественно, что для одной материальной точки все действующие на нее силы являются внешними. Возможны следующие частные случаи теоремы об изменении кинетического момента системы.
1. Если главный момент внешних сил системы относительно точки 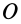
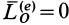
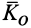
Этот частный случай теоремы об изменении кинетического момента системы называют законом сохранения кинетического момента. В проекциях на прямоугольные декартовы оси координат по этому закону
где 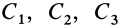
Соотношения (25′) являются первыми интегралами дифференциальных уравнений движения системы (3). Закон сохранения кинетического момента системы показывает, что одни внутренние силы не могут изменить кинетический момент системы, так же как они не изменяют ее количество движения.
2. Если сумма моментов всех внешних сил системы относительно оси 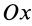
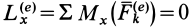
Следовательно, кинетический момент системы относительно какой-либо координатной оси постоянен, если сумма моментов внешних сил относительно этой оси равна нулю, что, в частности, наблюдается, когда внешние силы параллельны оси или пересекают ее. В частном случае для тела или системы тел, которые все вместе могут вращаться вокруг неподвижной оси, и если при этом
то
или
где 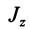
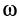
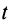
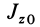
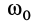
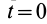
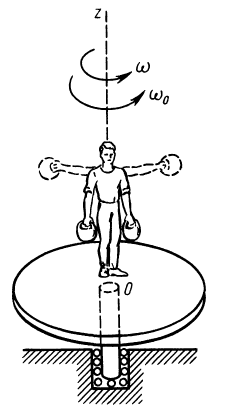
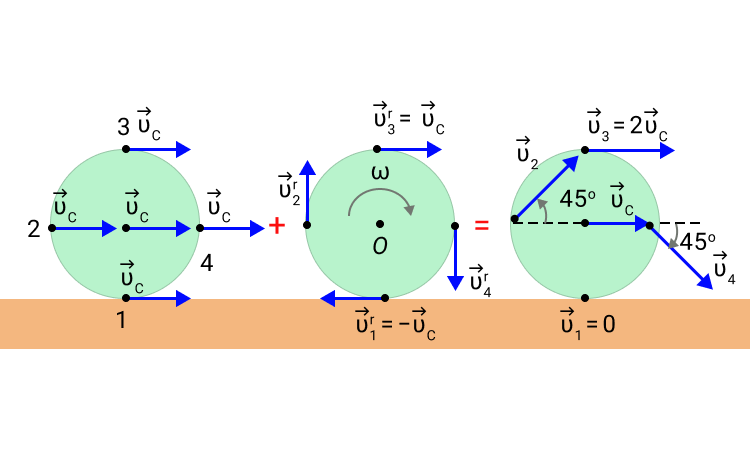
Закон сохранения кинетического момента в форме (27) используют в своей деятельности акробаты, прыгуны, танцоры и т. д. Наглядно его можно продемонстрировать в опыте на скамье Жуковского (рис. 51). Если человек с гирями в руках встанет на горизонтальную платформу скамьи Жуковского, которая может вращаться вокруг вертикальной оси почти без трения, и затем ему сообщить угловую скорость вокруг этой оси, то
так как внешние силы или параллельны оси вращения (силы веса человека, гирь и платформы), или пересекают ось (реакции подшипника, если пренебречь силами трения).
Рис. 51
Следовательно, если человек увеличит момент инерции, например разведением рук с гирями в сторону, то угловая скорость вращения уменьшится, и наоборот. В действительности угловая скорость хотя и медленно, но все время уменьшается вследствие наличия сопротивления воздуха и трения в подшипнике скамьи.
Пример:
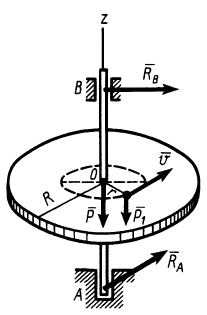
Однородный горизонтальный диск радиусом 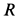
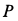
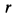
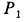
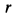
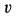
Рис. 52
Решение:
Пусть угловая скорость диска вначале была 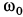
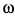
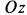
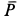
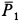
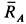
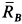
и, следовательно,
Составим 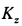
После того как человек пойдет по диску, его кинетический момент станет равным кинетическому моменту от вращения вместе с диском плюс кинетический момент от относительного движения по диску, если человек идет в сторону вращения диска, т. е.
Приравнивая полученные выражения кинетических моментов, получаем
Отсюда
Для однородного диска
Поэтому угловая скорость
Угловая скорость диска от движения по нему человека уменьшилась на 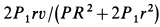
Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси
Из теоремы об изменении кинетического момента (24′) получим дифференциальное уравнение вращения твердого тела вокруг неподвижной оси 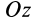
Для случая вращения твердого тела вокруг неподвижной оси, согласно (21), имеем
где 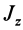
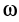
Рис. 53
Если ввести угол поворота тела 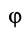
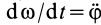
Это и есть дифференциальное уравнение вращения твердого тела вокруг неподвижной оси. Оно полностью аналогично дифференциальному уравнению поступательного движения твердого тела в проекции на какую-либо ось, например на ось 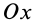
В дифференциальное уравнение вращения тела вокруг неподвижной оси вместо координаты 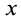
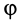
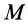
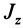
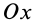
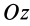
Реакции подшипников 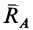
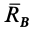
В частном случае, когда
т. е. вращение тела происходит с постоянным угловым ускорением.
Если
то
Это случай равномерного вращения тела по инерции без действия вращательного момента внешних сил.
Дифференциальное уравнение вращательного движения твердого тела в общем случае позволяет решать две основные задачи: по заданному вращению тела определять вращающий момент внешних сил и по заданному вращательному моменту и начальным условиям находить вращение тела. При решении второй задачи для нахождения угла поворота как функции времени приходится интегрировать дифференциальное уравнение вращательного движения. Методы его интегрирования полностью аналогичны рассмотренным выше методам интегрирования дифференциального уравнения прямолинейного движения точки.
Движение точки под действием центральной силы
Теорема площадей:
Наряду с введенными в кинематике точки скоростью 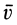
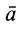
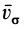
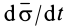
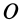
где 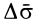
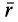
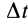
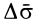
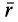
Для случая движения точки по плоскости секторная скорость перпендикулярна этой плоскости, если точка 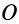
Секторное ускорение 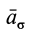
Секторную скорость можно выразить через момент линейной скорости 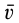
Рис. 54
Векторное произведение 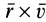
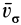
но
Следовательно,
что совпадает с модулем векторного произведения, стоящим справа в формуле (29).
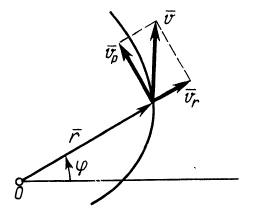
Если движение точки происходит в плоскости, то секторную скорость можно считать алгебраической величиной. В этом случае секторную скорость точки часто выражают в полярных координатах. Из формулы (29) секторная скорость
Но из кинематики точки в полярной системе координат на плоскости известно (рис. 55), что 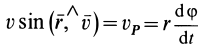
Рис. 55
Следовательно,
Формула (30) выражает секторную скорость в полярных координатах в случае плоского движения точки.
Используя формулу (29), кинетический момент через секторную скорость можно выразить в виде
Соответственно теорему об изменении кинетического момента (23) для точки можно выразить через секторную скорость формулой
В форме (32) теорему об изменении кинетического момента для точки называют теоремой площадей.
Движение точки под действием центральной силы
Центральной силой 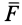
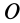
Центральная сила может быть притягивающей (направленной к центру) и отталкивающей (направленной от центра). Так как для центральной силы _момент силы относительно своего центра равен нулю, т. е. 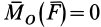
В проекциях на прямоугольные оси декартовой системы с началом в точке 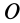
где 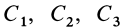
Умножая первое соотношение (33′) на 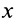
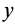
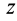
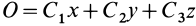
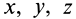
Следовательно, траектория точки, движущейся под действием центральной силы, является плоской кривой, лежащей в плоскости, проходящей через центр силы.
Так как при движении точки под действием центральной силы
то, учитывая формулу (31), имеем
и, следовательно,
или
Формула (34) выражает так называемый интеграл площадей: при движении точки под действием центральной силы секторная скорость является постоянной величиной и, следовательно, ометаемая радиусом-вектором площадь пропорциональна времени.
Учитывая формулу (30), интеграл площадей (34) в полярных координатах можно представить в виде
В этой форме интеграл площадей широко используется при рассмотрении движения планет вокруг Солнца и вообще различных спутников, в частности искусственных спутников Земли.
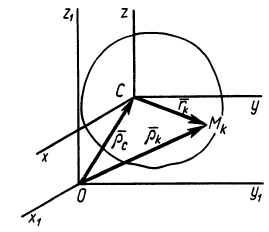
Теорема об изменении кинетического момента системы в относительном движении по отношению к центру масс
Рассмотрим относительное движение системы только относительно системы координат, движущейся поступательно вместе с центром масс системы.
Прежде чем рассмотреть теорему, выведем формулу для вычисления кинетического момента системы.
Формула для кинетического момента системы
Пусть механическая система совершает движение относительно основной системы координат 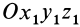
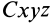
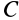
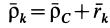
Рис. 56
Дифференцируя это тождество по времени, получаем
или
где 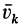
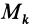
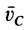
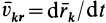
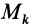
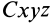
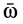
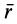
Согласно определению кинетического момента 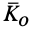
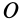
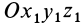
Подставляя в эту формулу значения 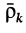
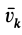
В этой формуле 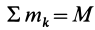
Следовательно, 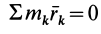
Другое слагаемое можно предварительно преобразовать:
Это слагаемое также равно нулю, так как все время 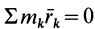
где 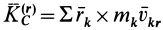
Величина 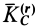
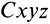
Формула (37) показывает, что кинетический момент абсолютного движения системы относительно неподвижной точки 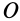
Теорема об изменении кинетического момента системы в относительном движении по отношению к центру масс. Для абсолютного движения системы и неподвижной точки 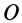
Подставляя сюда значения 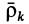
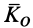
Перенося из правой части в левую первое слагаемое и учитывая, что
как векторное произведение параллельных векторов, после объединения слагаемых имеем
В этой формуле выражение в квадратных скобках равно нулю на основании теоремы о движении центра масс системы (18) и, следовательно, формула примет вид
или
где 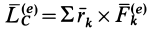
Формула (38) и выражает рассматриваемую теорему об изменении кинетического момента системы относительно центра масс для относительного движения системы по отношению к системе координат, движущейся поступательно с центром масс; она формулируется так же, как если бы центр масс был неподвижной точкой.
Эту теорему применяют для изучения вращательной части плоского движения и движения свободного твердого тела вокруг центра масс.
Дифференциальные уравнения плоского движения твердого тела
Используя теоремы о движении центра масс и изменении кинетического момента системы относительно центра масс для относительного движения системы по отношению к системе координат, движущейся поступательно с центром масс, получим дифференциальные уравнения плоского движения твердого тела.
Рис. 57
В плоскости движения центра масс тела, совершающего плоское движение, выберем неподвижную систему координат 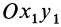
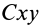
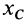
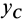
где 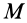
Третье дифференциальное уравнение плоского движения твердого тела получим из теоремы об изменении кинетического момента в относительном движении по отношению к центру масс (38) в проекции на подвижную ось 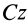
Плоское движение твердого тела можно считать состоящим из поступательного движения вместе с центром масс 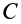
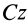
где 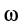
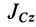
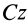
Так как 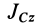
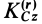
Если ввести угол поворота 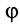
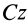
Таким образом, для твердого тела, совершающего плоское движение и, следовательно, имеющего три степени свободы, соответственно получим следующие три дифференциальных уравнения:
С помощью этих уравнений можно решать две основные задачи: по заданному плоскому движению твердого тела находить действующие на тело внешние силы и по заданным внешним силам и начальным условиям определять его движение. При решении этих задач должны быть заданы масса тела 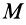
- Заказать решение задач по теоретической механике
Теорема Резаля
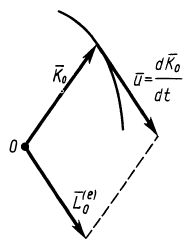
Теореме об изменении кинетического момента системы можно дать следующее кинематическое истолкование. Из кинематики точки известно, что скорость точки можно рассматривать как скорость конца радиуса-вектора, следящего за движущейся точкой, или как скорость изменения самого радиуса-вектора, если он проведен в движущуюся точку из какой-либо неподвижной точки (рис. 58). Траектория движущейся точки при этом является годографом радиуса-вектора г, а скорость точки направлена по касательной к этому годографу и равна первой производной по времени от радиуса-вектора. Аналогично этому, и производную по времени от кинетического момента можно рассматривать как своеобразную скорость конца этого вектора при движении по годографу кинетического момента (рис. 59). Эта скорость не является обычной скоростью точки, так как кинетический момент имеет иную размерность, чем радиус-вектор. Это есть скорость изменения вектора кинетического момента.
Таким образом, если обозначить через 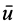
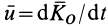
Теорему Резаля можно сформулировать так: при движении механический системы скорость точки, совпадающей с концом вектора кинетического момента при движении по годографу этого вектора, равна по величине и параллельна по направлению главному моменту всех внешних сил системы. Точка, относительно которой вычисляются кинетический момент системы и главный момент внешних сил, одна и та же.
Рис. 58
Рис. 59
В форме теоремы Резаля может быть сформулирована и теорема об изменении кинетического момента в относительном движении по отношению к центру масс.
Теорема Резаля особенно удобна для приближенного исследования движения быстровращающихся гироскопов.
Аналогично и теорему об изменении количества движения для системы можно сформулировать в форме теоремы Резаля для количества движения: при движении механической системы скорость точки, совпадающей с концом вектора количества движения при движении по его годографу, равна по величине и параллельна по направлению главному вектору всех внешних сил, действующих на систему.
- Теорема об изменении кинетической энергии
- Потенциальное силовое поле
- Закон сохранения механической энергии
- Принцип Даламбера
- Геометрия масс
- Свойства внутренних сил системы
- Дифференциальное уравнение движения системы
- Теоремы об изменении количества движения и о движении центра масс
-
Кинетический момент твёрдого тела относительно оси вращения.
Главный момент
количеств движения вращающегося тела
относительно неподвижной оси вращения
равен произведению момента инерции
тела относительно оси вращения на
проекцию угловой скорости вращения
тела на ось вращения.
|
|
Пусть твёрдое тело
вращается вокруг неподвижной оси Oz
с угловой скоростью
.
Определи главный момент количеств
движения этого тела относительно оси
Oz.
Согласно определению
(10)
Проекция скорости
точки
тела на касательную к траектории её
движения
а момент количества
движения относительно оси Oz
где
.
Подставив
в (10), получим
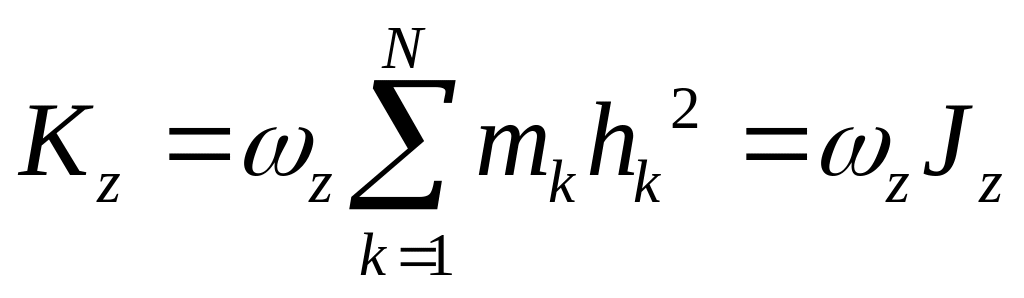
Где
– момент инерции тела относительно оси
вращения
.
Окончательно имеем:
Знак
– главного момента количеств движения
твёрдого тела относительно оси вращения
– определяется знаком проекции угловой
скорости
-
Дифференциальные уравнения вращения тела вокруг неподвижной оси.
В случае вращения
вокруг неподвижной оси тело имеет одну
степень свободы. По теореме об изменении
главного момента количеств движения
мех. системы относительно оси вращения
Oz

Где для твёрдого
тела
.
Тогда
|
|
Это выражение
называется дифференциальным уравнением
вращения твёрдого тела вокруг неподвижной
оси. Его можно записать в виде
или

Начальные условия
для случая вращения твёрдого тела вокруг
неподвижной оси следующие:
-
Движение точки под действием центральной силы, теорема площадей.
Рассмотрим движение
точки М
массой m
под действием силы
,
линия действия которой проходит через
центр О во всё время движения точки М.
Такую силу называют центральной.
Траектория
материальной точки, движущейся под
действием центральной силы, является
плоской привой, лежащей в плоскости,
проходящей через центр силы.
Согласно определению
центральной силы, момент силы
относительно
точки О
и из
следует,
что
или
В проекциях:
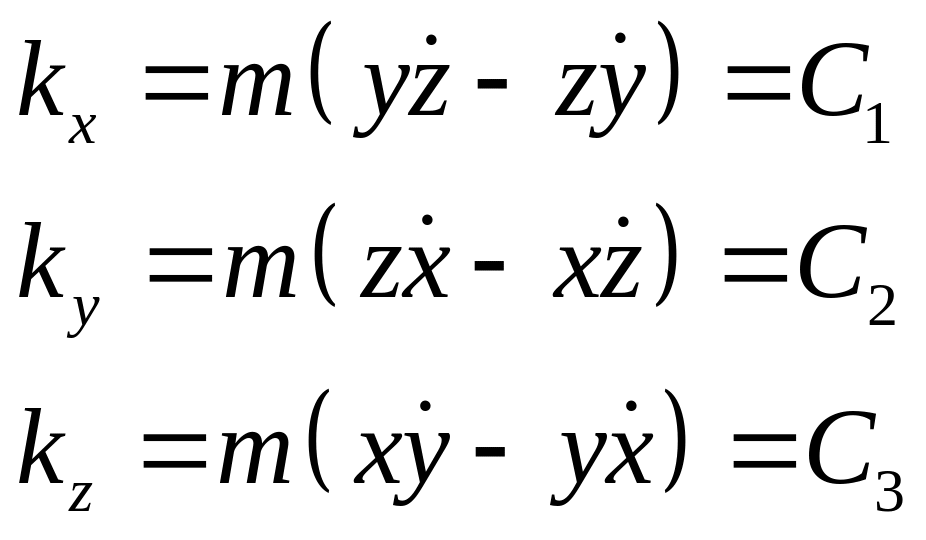
Умножая первое на
x,
второе на у,
третье на z
и складывая полученные выражения,
получаем
Т.е. координаты
точки М(x,y,z)
удовлетворяют уравнению плоскости,
проходящей через начала координат.
Теорема площадей.
Запишем выражение
для момента количества движения
материальной точки
,
используя формулу
для
секторной скорости
Преобразуем

или
|
|
Записанную в таком
виде теорему об изменении момента
количества движения материальной точки
называют теоремой
площадей.
-
Кинетический момент системы материальных точек при сложном движении.
Главный момент
количеств движения механической системы
относительно неподвижного центра О для
абсолютного движения системы равен
векторной сумме момента вектора
количество абсолютного движения системы
(приложенного в центре масс) относительно
того же центра, и главного момента
количеств движения системы относительно
центра масс для относительного движения
системы по отношению к центру масс
.
|
(11)
В проекции на
|
Введем подвижную
систему координат CXYZ,
которая двигается поступательно по
отношению к инерциальной системе отсчета
Оxyz
и начало которой связано с центром масс
С системы. Подвижную СК CXYZ
называют кенинговой
системой координат. продифференцируем
по времени выражение

Тогда
Согласно формуле
Бура

Но при поступательном
движении системы CXYZ
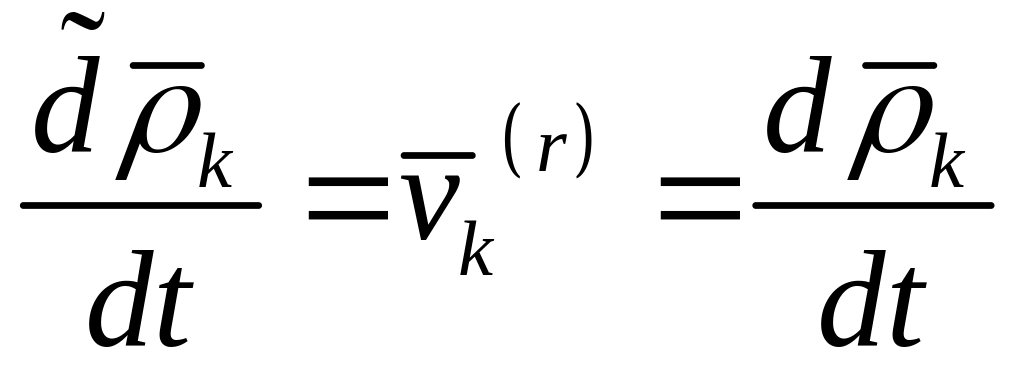
Главный момент
кол-ва движения мех. системы относительно
неподвижного центра О для абсолютного
движения системы относительно неподвижной
(инерциальной) системы координат Oxyz
равен
Подставляя сюда
выражения для
и
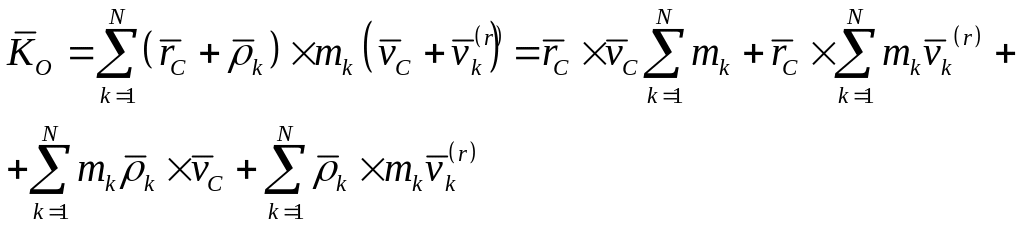
Здесь
так как радиус-вектор центра масс
относительно центра масс
,
а следовательно

Т.е. количество
движения системы в её движении относительно
центра масс равно нулю.
Таким образом:
(11)
Где
– главный момент количеств движения
мех. системы относительно центра масс
для относительного движения системы
по отношению к центру масс (по отношению
к СК CXYZ,
движущейся поступательно вместе с
центром масс)
В проекции на ось
Oz
(CZ)
формула (11) принимает вид
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Кинетический момент системы относительно центра и относительно оси. Кинетический момент вращающегося твердого тела относительно оси вращения
Кинетическим моментом системы относительно какого-либо центра 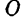
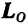
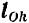
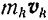
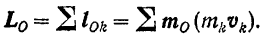
Кинетическим моментом системы относительно какой-либо оси называется главный момент 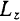
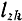
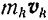
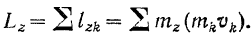
Так же как и главные моменты сил относительно центра и оси, проходящей через этот центр (стр. 115), кинетический момент 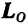
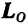
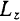
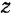
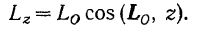
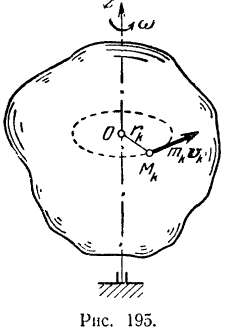
Проекция кинетического момента системы относительно какого-либо центра на любую ось, проходящую через этот центр, равна кинетическому моменту данной системы относительно этой оси.
Установим теперь формулу для вычисления кинетического момента в особо важном для практики случае. Пусть какое-либо твердое тело (рис. 195) вращается вокруг неподвижной оси 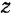
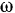
Найдем кинетический момент 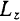
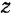
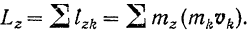
Отметим на рис. 195 вектор 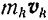
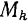
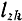
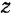
Так как все точки вращающегося тела движутся в плоскостях, перпендикулярных к оси вращения, и плечо вектора 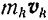
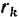
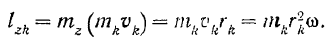
Различные точки тела имеют разную массу 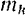
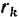
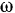
Следовательно,
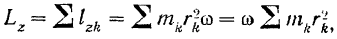
где
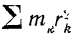
есть согласно формуле (139) момент инерции 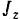
Таким образом, мы получаем:
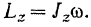
Кинетический момент вращающегося твердого тела относительно его оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость тела.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
|
|
Макеты страниц
Кинетический момент твердого тела (общий случай)
Во многих случаях в качестве механической системы выступают твердое тело и система твердых тел.
В динамике твердого тела часто возникает необходимость во введении вспомогательной системы координатных осей, начало которой находится в центре масс тела и которые движутся, оставаясь все время параллельными самим себе (поступательно движутся вместе с центром масс). Такие оси называются осями Кёнига.

Рис. 32.
При вычислении кинетического момента твердое тело мысленно разбиваем на N малых частиц (материальных точек) и вводим две вспомогательные системы координат с началом в центре масс С — систему 



Здесь учтено, что переносное движение является поступательным, поэтому переносные скорости 

Подставим это выражение в формулу для определения кинетического момента системы (в данном случае — тела):

Первая сумма приводится к виду

и представляет собой момент относительно центра О количества движения тела 


Введем в рассмотрение главный момент относительных количеств движения тела относительно центра масс

где 





и подставим в выражение для 

Но первый член в полученной сумме равен нулю, так как равна нулю величина 

так как 

В результате для вычисления кинетического момента твердого тела относительно неподвижного центра О получаем следующую общую формулу:

Напомним, что в этой формуле М — масса тела, 


Отметим частные случаи.
Тело движется поступательно. В этом случае относительное движение отсутствует — положение тела не изменяется относительно осей Кёнига. Относительные скорости частиц 


Следовательно, для определения кинетического момента остается только первый член в полученной общей формуле, т. е.

Так как 

Из нее следует, что кинетический момент поступательно движущегося тела относительно некоторого неподвижного центра равен моменту относительно этого центра количества движения тела, приложенного в его центре масс. Правило сохраняется и при вычислении кинетических моментов тела относительно координатных осей 
Тело вращается вокруг неподвижной оси. В этом случае удобно действовать непосредственно, не прибегая к разложению движения на переносное и относительное.
Выберем моментный центр О на оси вращения тела, ось вращения совместим с осью 






Рис. 33.
Здесь 



В полученном выражении коэффициенты при ортах равны проекциям скорости частицы на соответствующие координатные оси. Следовательно, для проекций количества движения 

Для момента количества движения частицы относительно точки О с учетом полученных равенств получаем

Отсюда следуют формулы для моментов количества движения частицы 

Суммируя соответствующие моменты для всех материальных точек тела, определяем проекции на оси Oxyz кинетического момента 

Из этих формул основное значение для дальнейшего имеет формула

определяющая проекцию кинетического момента вращающегося тела на направление оси вращения.
Сравнивая проекции кинетического момента тела с проекциями угловой скорости 



Вращающееся твердое тело (ротор), для которого выполняются условия 

Иногда требуется знать проекции кинетического момента на оси 



Пример. На круглой горизонтальной платформе массы 




Рис. 34.
Решение. Выберем в качестве системы платформу вместе с находящимся на ней человеком, принимаемым за материальную точку М. Внешними силами будут вес платформы 



В начале движения платформа и человек неподвижны, поэтому 

Если человек будет перемещаться по платформе с некоторой абсолютной скоростью v, то его количество движения 


Но кинетический момент всей системы равен нулю, поэтому платформа начнет вращаться, а ее кинетический момент относительно оси вращения 

Для определения угловой скорости платформы составим выражение для кинетического момента системы относительно оси 

Так как платформа вращается, движение человека (точки М) будет сложным движением. По теореме сложения скоростей для абсолютной скорости v получаем:

Условие сохранения кинетического момента 

Отсюда находим

В заключение заметим, что теорема об изменении кинетического момента выполняется только по отношению к неподвижному центру и неподвижным координатным осям. Однако существует единственная подвижная точка, относительно которой теорема продолжает оставаться справедливой. Такой точкой является центр масс (системы или тела). Теорема сохраняется и по отношению к осям Кенига. Доказательство этих положений мы опускаем.
Оглавление
- Предисловие
- Введение в динамику
- Динамика точки
- Две основные задачи динамики точки
- Дифференциальные уравнения движения материальной точки
- Способы решения основных задач динамики точки
- Лекция 12. Способы интегрирования дифференциального уравнения прямолинейного движения материальной точки
- Дифференциальное уравнение и начальные условия прямолинейного движения
- Определение закона движения точки под действием силы, зависящей только от времени
- Определение закона движения точки под действием силы, зависящей только от положения
- О нахождении закона движения при постоянной силе и силе, зависящей только от скорости
- Лекция 13. Колебательные движения материальной точки
- Свободные колебания
- Вынужденные колебания
- Явление резонанса
- Влияние сопротивления на свободные и вынужденные колебания
- Динамика системы
- Механическая система
- Масса и центр масс системы
- Момент инерции относительно оси
- Моменты инерции относительно координатных осей
- Моменты инерции твердого тела
- Осевые моменты инердии некоторых твердых тел
- Радиус инерции
- Главные оси инерции
- Классификация сил, действующих на точки системы
- Свойства внутренних сил
- Дифференциальные уравнения движения механической системы
- Теорема о движении центра масс
- Законы сохранения движения дентра масс
- Общие теоремы динамики
- Основные динамические величины механической системы
- Теорема об изменении количества движения
- Законы сохранения количества движения
- О вычислении количества движения
- Интегральная форма теоремы об изменении количества движения
- Лекция 16. Теорема об изменении кинетического момента
- Кинетический момент
- Теорема об изменении кинетического момента
- Законы сохранения кинетического момента
- Кинетический момент твердого тела (общий случай)
- Дифференциальные уравнения движения твердого тела
- Физический маятник и его малые колебания
- Лекция 17. Теорема об изменении кинетической энергии
- Работа силы
- Работа силы тяжести
- Работа упругой силы пружины
- Работа силы трения скольжения
- Работа пары сил трения качения
- Потенциальные силы
- Вычисление потенциальной энергии
- Теорема об изменении кинетической энергии
- Вычисление кинетической энергии твердого тела
- О решении задач при помощи теоремы об изменении кинетической энергии
- Общие принципы механики
- Принцип Даламбера для материальной точки
- Принцип Даламбера для механической системы
- Определение главного вектора и главного момента сил инерции твердого тела
- Тело движется поступательно с ускорением
- Тело совершает вращательное движение
- Тело совершает плоскопараллельное движение
- Лекция 19. Принцип возможных перемещений
- Возможные перемещения
- Уравнения связей. Классификация связей по виду их уравнений
- Связи идеальные и неидеальные
- Принцип возможных перемещений
- Применение принципа возможных перемещений
- Лекция 20. Принцип Даламбера-Лагранжа и общее уравнение динамики. Уравнения движения механической системы в обобщенных координатах
- Принцип Даламбера-Лагранжа
- Общее уравнение динамики
- Обобщенные координаты и обобщенные силы
- Уравнения движения механической системы в обобщенных координатах
- Рекомендуемая литература
Для кинематического описания процесса вращения твердого тела нужно ввести такие понятия как угловое перемещение Δφ, угловое ускорение ε и угловая скорость ω:
ω=∆φ∆t, (∆t→0),ε=∆φ∆t, (∆t→0).
Углы выражаются в радианах. За положительное направление вращения принимается направление против часовой стрелки.
Когда твердое тело вращается относительно неподвижной оси, все точки этого тела перемещаются с одинаковыми угловыми скоростями и ускорениями.
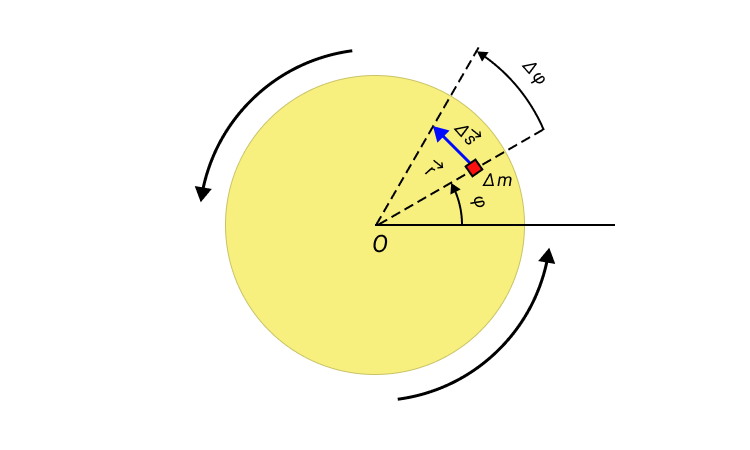
Рисунок 1. Вращение диска относительно оси, проходящей через его центр O.
Если угловое перемещение Δφ мало, то модуль вектора линейного перемещения ∆s→ некоторого элемента массы Δm вращающегося твердого тела можно выразить соотношением:
∆s=r∆ϕ,
в котором r – модуль радиус-вектора r→.
Между модулями угловой и линейной скоростей можно установить связь посредством равенства
v=rω.
Модули линейного и углового ускорения также взаимосвязаны:
a=aτ=rε.
Векторы v→ и a→=aτ→ направлены по касательной к окружности радиуса r.
Также нам необходимо учесть возникновение нормального или центростремительного ускорения, которое всегда возникает при движении тел по окружности.
Модуль ускорения выражается формулой:
an=v2r=ω2r.
Если разделить вращающееся тело на небольшие фрагменты Δmi, обозначить расстояние до оси вращения через ri, а модули линейных скоростей через vi, то запись формулы кинестетической энергии вращающегося тела будет иметь вид:
Ek=∑iνmvi22=∑i∆m(riω)22=ω22∑i∆miri2.
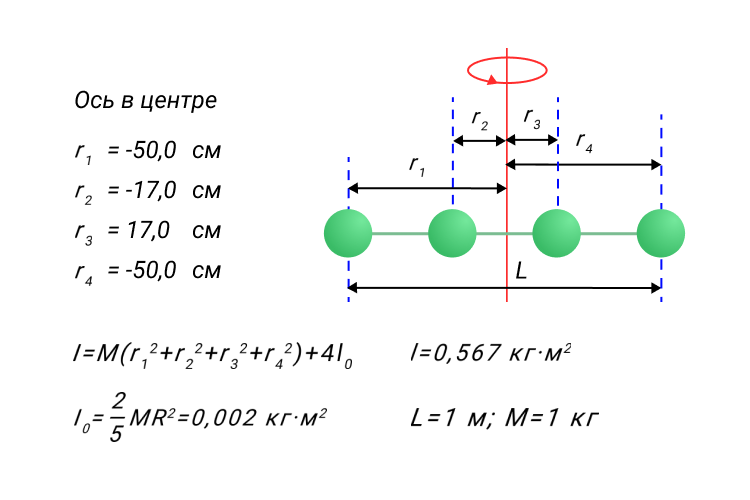
Физическая величина ∑i∆miri2 носит название момента инерции I тела относительно оси вращения. Она зависит от распределения масс вращающегося тела относительно оси вращения:
I=∑i∆miri2.
В пределе при Δm→0 эта сумма переходит в интеграл. Единица измерения момента инерции в СИ – килограмм–метр в квадрате (кг·м2). Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде:
Ek=Iω22.
В отличие от выражения, которое мы использовали для описания кинестетической энергии поступательно движущегося тела mv22, вместо массы m в формулу входит момент инерции I. Также мы принимаем во внимание вместо линейной скорости v угловую скорость ω.
Если для динамики поступательного движения основную роль играет масса тела, то в динамике вращательного движения имеет значение момент инерции. Но если масса – это свойство рассматриваемого твердого тела, которое не зависит от скорости движения и других факторов, то момент инерции зависит от того, вокруг какой оси вращается тело. Для одного и того же тела момент инерции будет определяться различными осями вращения.
В большинстве задач считается, что ось вращения твердого тела проходит через центр его массы.
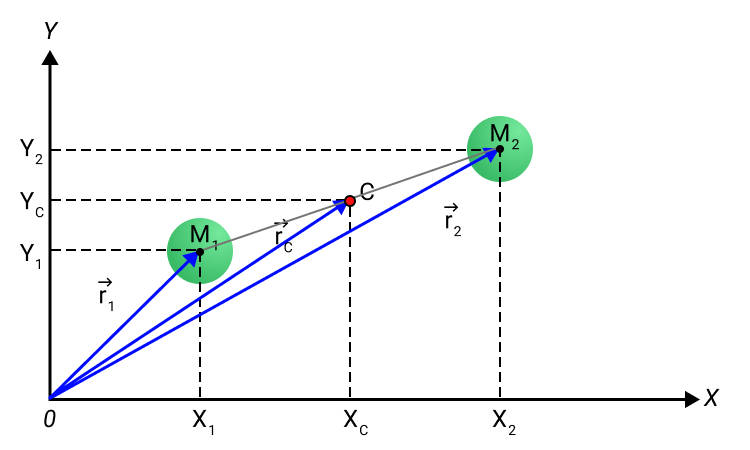
Положение xC, yC центра масс для простого случая системы из двух частиц с массами m1 и m2, расположенными в плоскости XY в точках с координатами x1, y1 и x2, y2 определяется выражениями:
xC=m1x1+m2x2m1+m2, yC=m1y1+m2y2m1+m2.
Рисунок 2. Центр масс C системы из двух частиц.
В векторной форме это соотношение принимает вид:
rC→=m1r1→+m2r2→m1+m2.
Аналогично, для системы из многих частиц радиус-вектор rC→ центра масс определяется выражением
rC→=∑miri→∑mi.
Если мы имеем дело с твердым телом, состоящим из одной части, то в приведенном выражении суммы для rC→ необходимо заменить интегралами.
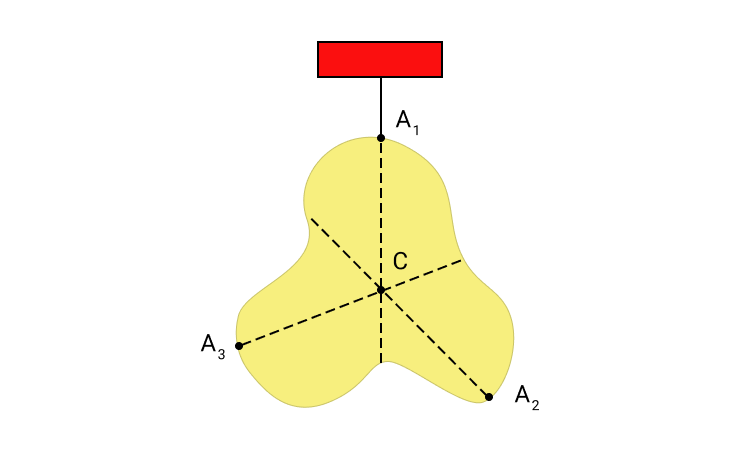
Центр масс в однородном поле тяготения совпадает с центром тяжести. Это значит, что если мы возьмем тело сложной формы и подвесим его за центр масс, то в однородном поле тяготения это тело будет находиться в равновесии. Отсюда следует способ определения центра масс сложного тела на практике: его необходимо последовательно подвесить за несколько точек, одновременно отмечая по отвесу вертикальные линии.
Рисунок 3. Определение положения центра масс C тела сложной формы. A1, A2, A3 точки подвеса.
На рисунке мы видим тело, которое подвешено за центр масс. Оно находится в состоянии безразличного равновесия. В однородном поле тяготения равнодействующая сил тяжести приложена к центру масс.
Мы можем представить любое движение твердого тела как сумму двух движений. Первое поступательное, которое производится со скоростью центра масс тела. Второе – это вращение относительно оси, которая проходит через центр масс.
Предположим. Что у нас есть колесо, которое катится по горизонтальной поверхности без проскальзывания. Все точки колеса во время движения перемещаются параллельно одной плоскости. Такое движение мы можем обозначить как плоское.
Теорема о движении центра масс
Кинестетическая энергия вращающегося твердого тела при плоском движении будет равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, которая проведена через центр масс и располагается перпендикулярно плоскостям, в которых движутся все точки тела:
Ek=mvC22+ICω22,
где m – полная масса тела, IC – момент инерции тела относительно оси, проходящей через центр масс.
Рисунок 4. Качение колеса как сумма поступательного движения со скоростью vC→ и вращения с угловой скоростью ω=vCR относительно оси O, проходящей через центр масс.
В механике используется теорема о движении центра масс.
Любое тело или несколько взаимодействующих тел, которые представляют собой единую систему, обладают центром масс. Этот центр масс под воздействием внешних сил перемещается в пространстве как материальная точка, в которой сосредоточена вся масса системы.
На рисунке мы изобразили движение твердого тела, на которое действуют силы тяжести. Центр масс тела движется по траектории, которая близка к параболе, тогда как траектория остальных точек тела является более сложной.
Рисунок 5. Движение твердого тела под действием силы тяжести.
Теорема Штейнера о параллельном переносе оси вращения
Рассмотрим случай, когда твердое тело движется вокруг некоторой неподвижной оси. Момент инерции этого тела инерции I можно выразить через момент инерции IC этого тела относительно оси, проходящей через центр масс тела и параллельной первой.
Рисунок 6. К доказательству теоремы о параллельном переносе оси вращения.
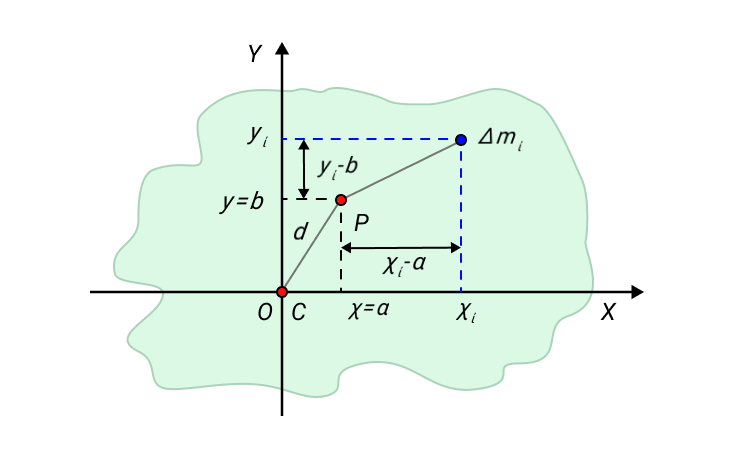
Для примера возьмем твердое тело, форма которого произвольна. Обозначим центр масс С. Выберем систему координат ХУ с началом координат 0. Совместим центр масс и начало координат.
Одна из осей проходит через центр масс С. Вторая ось пересекает произвольно выбранную точку Р, которая расположена на расстоянии d от начала координат. Выделим некоторый малый элемент массы данного твердого тела Δmi.
По определению момента инерции:
IC=∑∆mi(xi2+yi2),IP=∑mi(xi-a)2+yi-b2
Выражение для IP можно переписать в виде:
IP=∑∆mi(xi2+yi2)+∑∆mi(a2+b2)-2a∑∆mixi-2b∑∆miyi.
Два последних члена уравнения обращаются в нуль, так как начало координат в нашем случае совпадает с центром масс тела.
Так мы пришли к формуле теоремы Штейнера о параллельном переносе оси вращения.
Для тела, которое вращается относительно произвольной неподвижной оси, момент инерции, согласно теореме Штейнера, равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.
IP=IC+md2,
где m – полная масса тела.
Рисунок 7. Модель момента инерции.
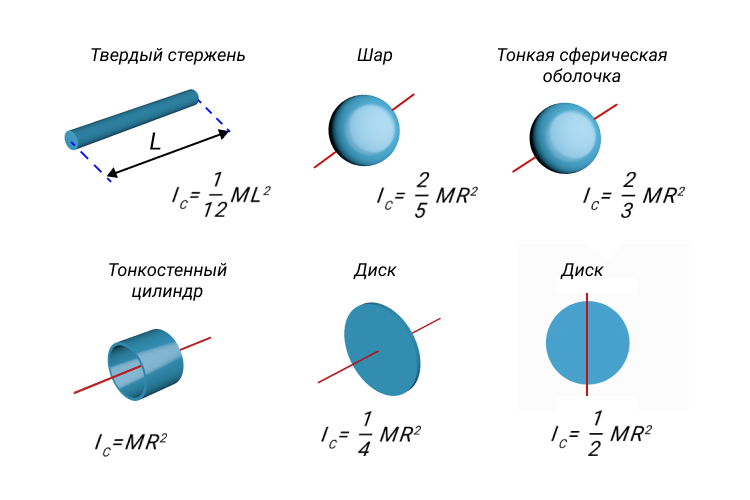
На рисунке ниже изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.
Рисунок 8. Моменты инерции IC некоторых однородных твердых тел.
Основное уравнение динамики вращательного движения твердого тела
В тех случаях, когда мы имеем дело с твердым телом, которое вращается относительно неподвижной оси, мы можем обобщить второй закон Ньютона. На рисунке ниже мы изобразили твердое тело произвольной формы, вращающееся относительно некоторой оси, проходящей через точку О. Ось вращения расположена перпендикулярно плоскости рисунка.
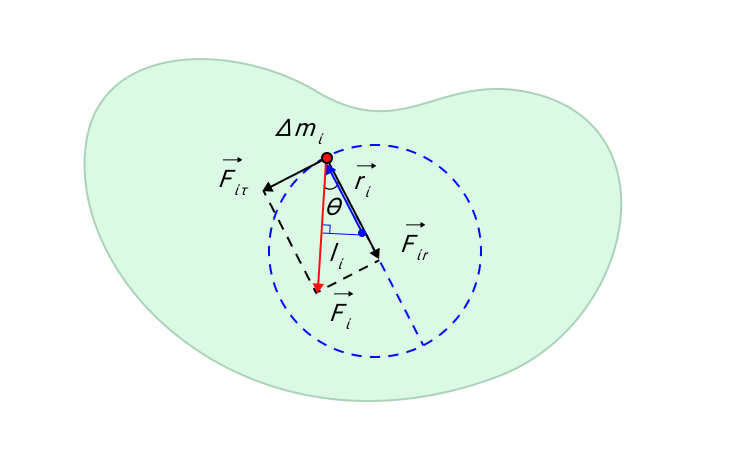
Δmi – это произвольный малый элемент массы, на который оказывают воздействие внешние и внутренние силы. Равнодействующая всех сил есть Fi→. Ее можно разложить на две составляющие: касательную составляющую Fiτ→ и радиальную Fir→. Радиальная составляющая Fir→ создает центростремительное ускорение an.
Рисунок 9. Касательная Fiτ→ и радиальная Fir→ составляющие силы Fi→ действующей на элемент Δmi твердого тела.
Касательная составляющая Fiτ→ вызывает тангенциальное ускорение aiτ→ массы Δmi. Второй закон Ньютона, записанный в скалярной форме, дает
∆miaiτ=Fiτsin θ или ∆miriε=Fisin θ,
где ε=aiτri – угловое ускорение всех точек твердого тела.
Если обе части написанного выше уравнения умножить на ri, то мы получим:
∆miri2ε=Firisin θ=Fili=Mi.
Здесь li – плечо силы, Fi,→Mi – момент силы.
Теперь нужно аналогичные соотношения записать для всех элементов массы Δmi вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:
∑∆miri2ε=∑Mi.
Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.
∑M=∑Miвнешн+∑Miвнутр.
Но сумма моментов всех внутренних сил согласно третьему закону Ньютона равна нулю, поэтому в правой части остается только сумма моментов всех внешних сил, которые мы будем обозначать через M. Так мы получили основное уравнение динамики вращательного движения твердого тела.
Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими.
Iε=M
Обычно за положительное направление вращения принимают направление против часовой стрелки.
Возможна и векторная форма записи основного уравнения динамики вращательного движения, при которой величины ω→, ε→, M→ определяются как векторы, направленные по оси вращения.
Закон сохранения момента импульса
В разделе, посвященном поступательному движению тела, мы ввели понятие импульса тела p→. По аналогии с поступательным движением для вращательного движения мы вводим понятие момента импульса.
Момент импульса вращающегося тела – это физическая величина, которая равняется произведению момента инерции тела I на угловую скорость ω его вращения.
Для обозначения момента импульса используется латинская буква L.
L=lω
Поскольку ε=∆ω∆t; ∆t→0, уравнение вращательного движения можно представить в виде:
M=Iε=I∆ω∆t или M∆t=I∆ω=∆L.
Получаем:
M=∆L∆t; (∆t→0).
Мы получили это уравнение для случая, когда I = const. Но оно будет справедливо и тогда, когда момент инерции тела будет изменяться в процессе движения.
Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L=Iω относительно данной оси сохраняется: ∆L=0, если M=0.
Следовательно,
L=lω=const.
Так мы пришли к закону сохранения момента импульса.
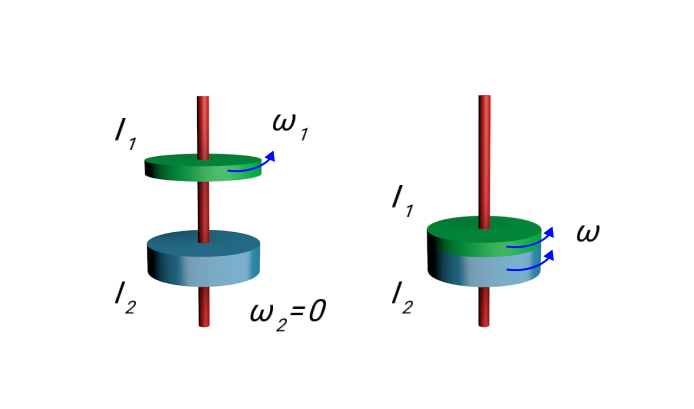
В качестве примера приведем рисунок, на котором изображено неупругое вращательное столкновение дисков, которые насажены на общую для них ось.
Рисунок 10. Неупругое вращательное столкновение двух дисков. Закон сохранения момента импульса: I1ω1=(I1+I2)ω.
Мы имеем дело с замкнутой системой. Для любой замкнутой системы закон сохранения момента импульса будет справедливым. Он выполняется и в условиях экспериментов по механике, и в условиях космоса, когда планеты движутся по своим орбитам вокруг звезды.
Мы можем записать уравнение динамики вращательного движения как для неподвижной оси, так и для оси, которая перемещается равномерно или с ускорением. Вид уравнения не изменится и в том случае, если ось движется ускоренно. Для этого должно выполняться два условия: ось должна проходить через центр массы тела, а ее направление в пространстве остается неизменным.
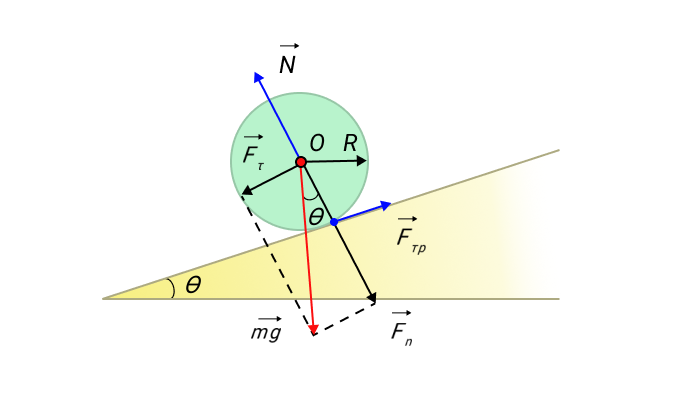
Предположим, что у нас есть тело (шар или цилиндр), которое катится по наклонной плоскости с некоторым трением.
Рисунок 11. Качение симметричного тела по наклонной плоскости.
Ось вращения O проходит через центр масс тела. Моменты силы тяжести mg→ и силы реакции N→ относительно оси O равны нулю. Момент M создает только сила трения: M = FтрR.
Уравнение вращательного движения:
ICε=ICaR=M=FтрR,
где ε – угловое ускорение катящегося тела, a – линейное ускорение его центра масс, IC – момент инерции относительно оси O, проходящей через центр масс.
Второй закон Ньютона для поступательного движения центра масс записывается в виде:
ma=mg sin α-Fтр.
Исключая из этих уравнений Fтр, получим окончательно:
α=mg sin θICR2+m.
Из этого выражения видно, что быстрее будет скатываться с наклонной плоскости тело, обладающее меньшим моментом инерции. Например, у шара IC=25mR2, а у сплошного однородного цилиндра IC=12mR2. Следовательно, шар будет скатываться быстрее цилиндра.