Как найти кинетическую энергию альфа частицы

Спрятать решение

Источник: Рым­ке­вич А. П. Сбор­ник задач по фи­зи­ке для 9−11 клас­сов, М.: «Про­све­ще­ние», 1990 (№ 1164)

Символическая
запись атомного ядра

,

где
– символ химического элемента,– зарядовое число, совпадающее с атомным
номером (число протонов в ядре),– массовое число (сумма числа протонов
и нейтронов в ядре).

Разность суммы
масс покоя входящих в ядро нуклонов и
массы покоя ядра называется дефектом
массы

,

где
– масса протона,– масса нейтрона,– масса ядра.

Энергия связи ядра
вычисляется по формуле

,

где при практических
расчетах удобно использовать массу,
выраженную в атомных единицах массы, а
квадрат скорости света
.

Для расчетов
энергии связи (дефекта масс) удобнее
пользоваться выражением, куда входят
не массы ядер, а массы нейтральных
атомов:

,

где
– масса атома водорода,– масса атома данного химического
элемента.

Удельная энергия
связи (энергия связи на нуклон)

.

Энергия, выделяющаяся
(поглощающаяся) в ходе ядерной реакции,
вычисляется по формуле

,

где в первой скобке
стоит сумма масс покоя частиц, вступающих
в реакцию, а во второй – сумма масс покоя
продуктов ядерной реакции.

Символическая
запись ядерной реакции может быть дана
в развернутом виде, например,

,

или в сокращенном
виде

.

В ходе любой ядерной
реакции должны выполняться законы
сохранения зарядового и массового
чисел.

Символические
обозначения некоторых частиц, участвующих
в ядерных реакциях:
– протон,– нейтрон,– дейтрон (ядро изотопа водорода),– тритон (ядро изотопа водорода),– альфа-частица (ядро изотопа гелия),– электрон,– позитрон,– нейтрино,– антинейтрино,– гамма-квант.

Закон радиоактивного
распада

,

где
– число радиоактивных атомов в начальный
момент времени,– число нераспавшихся атомов к моменту
времени,– постоянная радиоактивного распада.

Период полураспада
(промежуток времени, в течение которого
распадается половина первоначального
количества радиоактивных атомов) связан
с постоянной распада соотношением

.

Величина, обратная
постоянной распада

,

называется средним
временем жизни радиоактивного атома.

Активность
радиоактивного образца определяется
как отношение числа
ядер, распавшихся в изотопе, к промежутку
времени,
за которое произошел распад

.

Примеры решения задач

Задача 1. Определить
энергию, которая может выделиться при
образовании из протонов и нейтронов
одного моля гелия
.

Решение

Вычислим дефект
массы процесса, в ходе которого из двух
протонов и двух нейтронов образуется
ядро атома гелия. Поскольку в таблицах
приведены массы покоя атомов, а не ядер,
добавим к каждому протону по электрону
(в результате получится атом водорода),
а к ядру атома гелия добавим два электрона
(в результате получится атом гелия). В
результате получим

.
(2.3.1)

Используя табличные
данные (,,),
находим

(2.3.2)

При помощи (2.3.2)
определяем энергетический эффект от
слияния протонов и нейтронов в атом
гелия

.

Как известно, число
частиц в одном моле любого вещества
равно постоянной Авогадро, поэтому при
образовании из протонов и нейтронов
одного моля гелия должна выделиться
энергия

.

Задача 2. Под
действием протонов могут происходить
реакции термоядерного деления:

а)
;
б).

Какие изотопы
используются в качестве мишеней в этих
реакциях? Определить энергию
,
выделяющуюся в ходе реакций.

Решение

Для ответа на
первый вопрос воспользуемся законами
сохранения зарядового и массового
чисел. Для первой реакции это позволяет
записать уравнения

,
,

решая которые
получаем

,
,

что позволяет при
помощи таблицы Менделеева определить
первую мишень:

.

Аналогичные
вычисления для второй реакции дают
ответ:

.

Теперь аналогично
задаче 1 определяем энергетический
выход реакция, предполагая, что
кинетической энергией бомбардирующих
мишени протонов можно пренебречь:

а)
;

б)
.

Сравнение полученных
значений с энергией покоя протона
,
показывает, что использованное при
решении пренебрежение кинетической
энергией протона справедливо только
для нерелятивистских протонов.

Задача 3. Протоны
с кинетической энергией
бомбардируют литиевую мишень, в результате
чего наблюдается ядерная реакция.
Найти кинетическую энергию каждой
альфа-частицы и угол между направлениями
их разлета, если разлет происходит
симметрично по отношению к направлению
налетающих протонов.

Решение

Воспользуемся для
решения задачи законами сохранения
импульса и энергии. Суммарная кинетическая
энергия альфа-частиц очевидно равняется
сумме кинетической энергии протона и
энергетическому выходу ядерной реакции:

.
(2.3.3)

Обозначая угол,
который образует импульс альфа-частицы
с импульсом протона через
,
и проектируя закон сохранения импульса
на направление движения протона, получаем

.
(2.3.4)

Используя
классическую формулу связи кинетической
энергии и импульса (это оправдано, так
как рассматриваемые в задаче энергии
намного меньше энергий покоя участвующих
в реакции частиц)

(2.3.5)

и формулу
энергетического выхода ядерной реакции

,
(2.3.6)

из (2.3.3), (2.3.4) находим

,
(2.3.7)

.
(2.3.8)

Подстановка в
(2.3.7), (2.3.8) числовых значений с учетом
найденного при решении предыдущей
задачи энергетического выхода реакции
дает:

,

.

Задача 4. За время
начальное количество некоторого
радиоактивного изотопа уменьшилось враза. Во сколько разоно уменьшится за время?

Решение

Воспользуемся
законом радиоактивного распада

.
(2.3.9)

Согласно условию
задачи

,
.
(2.3.10)

Логарифмируя
первое из уравнений (2.3.10), получаем

,

что после подстановки
во второе уравнение (2.3.10) дает

.

Задача 5. Известно,
что из радиоактивного полония
массойза времядня в результате его распада образуется
гелий объемомпри нормальных условиях. Определить по
этим данным период полураспада данного
изотопа полония.

Решение

Начальное число
атомов полония найдем из формулы
молекулярно-кинетической теории

.
(2.3.11)

Число распавшихся
атомов полония в предположении, что не
происходит других реакций альфа-распада,
будет равно образовавшемуся числу
атомов гелия, которое можно определить
при помощи уравнения состояния идеального
газа

.
(2.3.12)

Из закона
радиоактивного распада находим

,
(2.3.13)

что после подстановки
(2.3.11), (2.3.12) дает уравнение

.
(2.3.14)

Учитывая формулу
связи постоянной распада и периода
полураспада
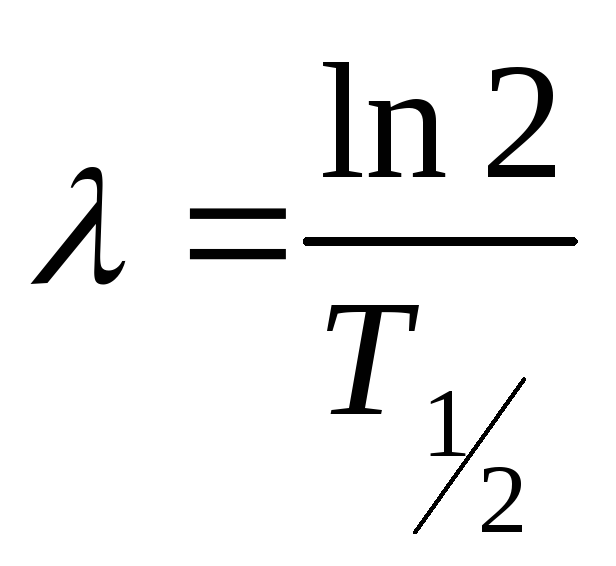и решая уравнение (2.3.14) с учетом,
находим значение периода полураспада

.

2021-03-26   

Определите минимальное значение кинетической энергии $alpha$-частицы, необходимое для осуществления реакции

$^{4} He + ^{7} Li rightarrow ^{10} B + n$,

если реакция идет с поглощением энергии $Q = 2,85 МэВ$. Ядро лития неподвижно.

Решение:

До реакции мы имеем $alpha$-частицу, или ядро атома гелия, и ядро лития, а после реакции образуются ядро бора и нейтрон. Если мы подсчитаем суммарные энергии покоя частиц до реакции и после реакции, то увидим, что энергия покоя ядра бора и нейтрона больше, чем энергия покоя а -частицы и ядра лития. Эта разность как раз и равна поглощаемой энергии $Q$ при данной реакции. Такие ядерные реакции, проходящие с поглощением энергии, называют эндотермическими реакциями. Реакции, идущие, наоборот, с выделением энергии, называют экзотермическими. Отсюда понятно, что если исходные частицы неподвижны, то эндотермическая реакция не пойдет. Значит, налетающая на мишень частица должна обладать некоторой минимальной энергией, при которой начнется реакция. Величину этой энергии называют пороговой.

Наиболее удобно рассмотреть процесс неупругого взаимодействия частиц в системе отсчета, связанной с центром масс системы. Обозначим скорость $alpha$-частицы в лабораторной системе отсчета через $v_{ alpha}$. Тогда скорость движения центра масс равна

$u = frac{m_{ alpha }v_{ alpha } }{m_{ alpha } + m_{Li} }$,

где $m_{ alpha }$ и $m_{Li}$ – массы $alpha$-частицы и ядра лития. Скорость $alpha$-частицы в системе центра масс составляет

$v_{ alpha ц} = v_{ alpha } – u = frac{m_{Li}v_{ alpha } }{m_{ alpha }+ m_{Li} }$

– здесь за положительное направление выбрано направление скорости $alpha$-частицы в лабораторной системе отсчета. Скорость ядра лития в системе центра масс равна

$v_{Liц} = – u = – frac{m_{ alpha } v_{ alpha } }{m_{ alpha } + m_{Li} }$.

В этой системе отсчета при пороговой скорости $alpha$-частицы образовавшееся ядро бора и нейтрон должны покоиться. Запишем закон сохранения полной энергии до реакции и после реакции:

$m_{ alpha }c^{2} + frac{m_{ alpha }v_{ alpha ц}^{2} }{2} + m_{Li}c^{2} + frac{m_{Li} v{Liц}^{2} }{2} = m_{B}c^{2} + m_{n}c^{2}$

– энергии частиц здесь записаны для нерелятивистского случая. Подставляя в это уравнение выражения для $v_{ alpha ц}$ и $v_{Li ц}$ и учитывая, что

$m_{B}c^{2} + m_{n}c^{2} – ( m_{ alpha} c^{2} + m_{Li}c^{2}) = Q$,

получим

$frac{m_{ alpha }m_{Li} v_{ alpha }^{2} }{2(m_{ alpha} + m_{Li} ) } = Q$.

Отсюда находим минимальную кинетическую энергию $alpha$-частицы в лабораторной системе отсчета:

$E_{k} = frac{m_{ alpha}v_{ alpha }^{2} }{2} = left ( 1 + frac{m_{ alpha } }{m_{Li} } right )Q = 4,48 МэВ$.

Альфа-частица представляет собой ядро гелия. Если у атома гелия убрать электронную оболочку, то останется эта частица. Она состоит из двух протонов и двух нейтронов, имеет сферическую форму с радиусом 10^-5 метра. Масса альфа-частицы составляет 6,68 * 10^-27 килограмм.

История открытия

На рубеже XIX-XX веков два физика с мировым именем открыли существование альфа-частиц. Это были новозеландский физик Эрнест Резерфорд, который работал в Канаде в городе Монреале, и французский химик и физик Поль Вийяр, который ставил свои эксперименты в Париже. Эти два ученых изучали различные виды радиации по их свойствам проникать через различные среды, а также по их взаимодействию с искусственным магнитным полем.

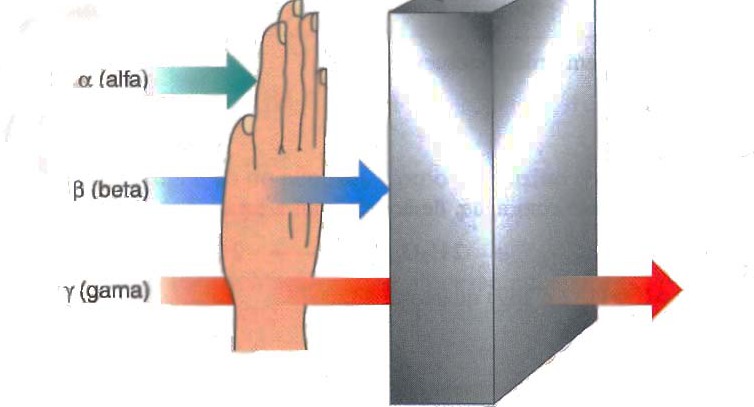
В результате этих экспериментов Резерфорд выделил три типа радиоактивного излучения: альфа, бета и гамма. Альфа-лучи были определены как лучи, имеющие наименьшую проникающую способность через различные предметы среди изучаемых видов радиации.

Элементарные частицы: протоны и нейтроны

В физике любой частице принято приписывать две основные характеристики – электрический заряд и массу, так как эти критерии определяют во многом ее свойства и поведение в конкретных физических условиях.

Как было сказано выше, альфа-частица состоит из двух протонов и двух нейтронов. Протон представляет собой элементарную частицу, имеющую массу 1,6726 * 10^-27 кг и заряд +1,602 * 10^–19 Кл. Что касается нейтрона, то его масса в 1,00137 раз больше, чем у протона, то есть составляет 1,67489*10^-27 кг. Заряд нейтрона равен нулю, то есть эта частица является электрически нейтральной (отсюда и название – “нейтрон”).

Альфа-частицы и их заряд

Заряд и массу альфа-частицы можно определить, если принимать во внимание названные выше цифры, а также учитывать, что сама частица состоит из двух протонов и двух нейтронов. Заряд альфа-частицы является положительным и равен +3,204 * 10^–19 Кл. Отметим, что значение +1,602 * 10^–19 Кл принято в физике называть элементарным зарядом, поскольку он равен по модулю этим же величинам у протона и электрона. Таким образом, заряд альфа-частицы равен +2 элементарных заряда.

Масса альфа-частицы

Если учитывать аддитивное свойство физической величины “масса”, то можно рассчитать самостоятельно, сколько весит альфа-частица. Приведенные выше цифры для протонов и нейтронов говорят, что масса альфа-частицы равна 6,69498 * 10^-27 кг. Получается эта цифра, если сложить массы в покое двух протонов и двух нейтронов. В итоге отношение масс протона и альфа-частицы приблизительно составляет 1/4. То есть альфа-частица в четыре раза тяжелее протона.

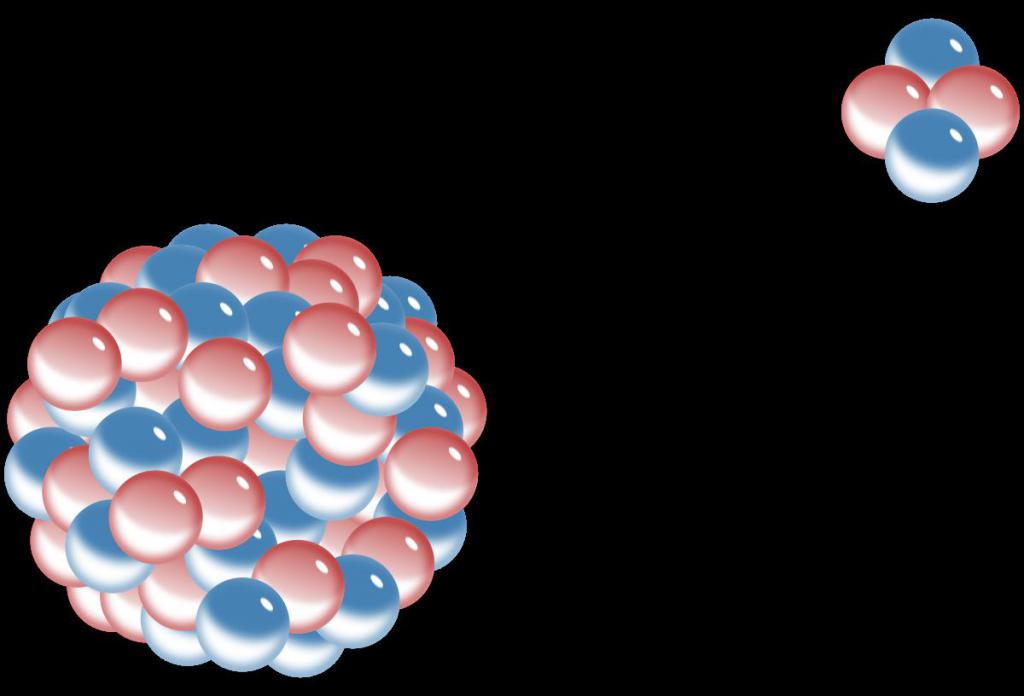
Однако множество проведенных экспериментов по установлению точной массы этой частицы говорят, что масса покоя альфа-частицы составляет 6,68 * 10 * 10^-27 кг, то есть она меньше на 0,015 * 10^-27 кг полученного выше значения. Куда же девается разница? Ответ на этот вопрос достаточно прост – она переходит в энергию. Дело в том, что при образовании альфа-частицы из протонов и нейтронов в результате ядерных взаимодействия между ними выделяется энергия в виде электромагнитного излучения, два протона и два нейтрона переходят в более выгодное энергетическое состояние – нашу альфа-частицу.

Энергия образования

Чтобы рассчитать энергию образования альфа-частицы, следует воспользоваться знаменитым уравнением Эйнштейна, которое связывает массу и энергию через одну из фундаментальных постоянных нашей Вселенной – скорость света. Это уравнение имеет вид: E = mc², где E – энергия, m – масса, c – скорость света в вакууме.

Зная, что при образовании альфа-частицы масса ее компонентов уменьшается на 0,015 * 10^-27 кг, а также зная, что скорость света составляет 3 * 10⁸ м/с, получаем энергию, которая выделяется во время этого процесса. Она равна E = 0,015 * 10^-27 * 9 * 10¹⁶ = 1,35 * 10^-12 Дж. В физике элементарных частиц принято энергии записывать в электрон-вольтах (эВ). Один электрон-вольт равен 1,602177 * 10⁻¹⁹ Дж. Тогда энергия образования альфа-частицы равна 8,426 * 10⁶ эВ, или 8,426 МэВ (мегаэлектрон-вольт).

Чтобы понять, насколько велика эта энергия, можно провести простой расчет. Представим, что вся энергия образования альфа-частицы переводится на ее ускорение. Пользуясь уравнением Лоренца для нерелятивистских скоростей, то есть полагая, что кинетическая энергия-альфа частицы равна mv²/2, где v – скорость ее движения, получаем, что этой энергии образования будет достаточно, чтобы разогнать альфа-частицу до скорости 2 * 10⁷ м/c, что составляет 6,7 % от скорости света в вакууме. Отметим, что задавать вопрос о том, на сколько увеличится масса альфа-частицы при таких скоростях, не имеет смысла, поскольку увеличением ее массы можно пренебречь, так как она составит всего 0,015/6,68 * 100 = 0,2 %.

Основные физические свойства

Альфа-частица тяжелее в 4 раза протона и в 8000 раз – электрона, то есть для мира элементарных частиц она обладает большой массой. Напомним, что масса одного протона или одного нейтрона в атомных единицах (а.е.м.) равна 1, а заряд протона равен +1 в единицах элементарного заряда, то есть альфа-частица имеет заряд +2, а массу – 4. Тогда отношение заряда к массе альфа-частицы равно +1/2 = +0,5.

Поскольку она обладает электрическим зарядом, пролетая через электрическое или магнитное поле, она взаимодействует с ним. Чтобы определить направление силы, которая действует на альфа-частицу в магнитном поле, необходимо воспользоваться так называемым правилом левой руки: четыре пальца следует расположить вдоль вектора движения альфа частицы, а ладонь повернуть таким образом, чтобы линии магнитной индукции входили в нее. Тогда оттопыренный под прямым углом большой палец укажет направление действующей силы на движущуюся заряженную частицу.

Альфа-частицы могут разгоняться до больших скоростей, достигающих величин 15 млн км/с, то есть 5 % от скорости света. Ввиду большой массы и огромных скоростей они приобретают значительную кинетическую энергию, которая может составлять до 10 МэВ.

Проникающая способность

Поскольку альфа-частица обладает значительной массой (по сравнению с массой электрона), а также электрическим зарядом, который по модулю превышает заряд электрона в 2 раза, то ее проникающая способность, то есть способность проходить через слой вещества, является незначительной.

Во время своего движения альфа-частица испытывает столкновения с атомами, передавая им значительное количество энергии, которая приводит к ионизации атомов, то есть к отрыву электронов от них. Например, проходя всего 5 см в воздухе, альфа-частица испытывает огромное число столкновений и практически полностью теряет свою кинетическую энергию.

Любое твердое вещество легко задерживает альфа-частицу. Так, она не может пройти через слой из нескольких листов бумаги, а алюминиевая пластина толщиной всего 0,1 мм задерживает поток любой интенсивности из альфа-частиц. Еще раз отметим, хотя проникающая способность этой частицы мала, она очень сильно ионизирует всякое вещество, через которое движется.

Альфа-частица – продукт радиоактивного распада

Несмотря на то что альфа-частица состоит из протонов и нейтронов, из этих элементарных частиц она в природе не образуется, а получается в результате радиоактивного альфа-распада некоторых химических элементов.

Альфа-распад является одним из видов радиоактивного распада, в результате которого атомное ядро некоторого химического элемента, испуская альфа-частицу, превращается в ядро другого элемента, масса которого на 4 а.е.м. меньше, чем эта величина у родительского ядра, а порядковый номер в таблице Менделеева на 2 единицы меньше, чем у исходного элемента.

Альфа-распад бывает спонтанным (происходит произвольным образом в природе) и вынужденным (вызван в результате какого-либо специального воздействия на атомное ядро). Спонтанный распад характерен только для очень тяжелых атомных ядер. Так, самым легким элементом, который испытывает спонтанный альфа-распад, является теллурий 106. Уран 238 также претерпевает альфа-распад с образованием технеция 234.

Поскольку альфа-частица обладает двойным положительным элементарным зарядом, она при распаде радиоактивного ядра быстро захватывает электроны, образуя при этом атом гелия. Именно по этой причине во многих породах с большим содержанием альфа-радиоактивных элементов имеются полости, заполненные газом гелием, например в минералах, богатых ураном или торием. Основным источником альфа-частиц на Земле является благородный газ радон, который находится в почве, воде, воздухе и различных типах горных пород.