Как найти кинетическую энергию через ускорение - Сайт, где вы сможете решить свои вопросы

Придавая телу ускорения и заставляя его двигаться с определенной скоростью, мы совершаем некоторую работу. Данная работа запасается в виде кинетической энергии тела.

[contents]

Кинетическая энергия тела, энергия движения, рассчитывается по формуле:

W_к= mas=(1/2)*mu²

Где:
W_к — Кинетическая энергия тела, энергия движения (Джоуль),
m — масса тела (кг),
s — перемещение тела (метр)
u — скорость тела (м/c)
a — ускорение тела (м/c²)

Рассчитать (найти) кинетическую энергию тела онлайн

Найти кинетическую энергию тела онлайн через ускорение, перемещение и скорость тела

Рассчитаем кинетическую энергию по формуле:

W_к= mas

Кинетическая энергия, найти массу тела онлайн

Масса тела через кинетическую энергию рассчитывается по формуле:

m= W_к/ as = (W_к*2) / u²

Кинетическая энергия, найти скорость тела онлайн

Из формул, указанных выше, мы также легко можем рассчитать скорость тела, зная массу и кинетическую энергию.

Найти изменение кинетической энергии по скорости

Изменение величины скорости от u₁ до u₂ приводит к изменению кинетической энергии, которое рассчитывается по формуле:

ΔW_к= (m / 2)*(u₂²−u₁²)

W_к — Кинетическая энергия тела, энергия движения (Джоуль),
m — масса тела (кг),
s — перемещение тела (метр)
u1 — начальная скорость тела (м/c)

u2 — конечная скорость тела (м/c)
a — ускорение тела (м/c²)

Источник

Download Article

When there are no opposing forces, a moving body tends to keep moving with a steady velocity as we know from Newton’s first law of motion. If, however, a resultant force does act on a moving body in the direction of its motion, then it will accelerate per Newton’s second law The work done by the force will become converted into increased kinetic energy in the body. We derive the expression for kinetic energy from these basic principles.

1
Begin with the Work-Energy Theorem. The work that is done on an object is related to the change in its kinetic energy.
2
Rewrite work as an integral. The end goal is to rewrite the integral in terms of a velocity differential.
Advertisement
3
Rewrite force in terms of velocity. Note that mass is a scalar and can therefore be factored out.
- ${begin{aligned}Delta K&=int m{mathbf {a}}cdot {mathrm {d}}{mathbf {r}}\&=mint {frac {{mathrm {d}}{mathbf {v}}}{{mathrm {d}}t}}cdot {mathrm {d}}{mathbf {r}}end{aligned}}$
4
Rewrite the integral in terms of a velocity differential. Here, it is trivial, because dot products commute. Recall the definition of velocity as well.
- ${begin{aligned}Delta K&=mint {frac {{mathrm {d}}{mathbf {r}}}{{mathrm {d}}t}}cdot {mathrm {d}}{mathbf {v}}\&=mint {mathbf {v}}cdot {mathrm {d}}{mathbf {v}}end{aligned}}$
5
Integrate over change in velocity. Typically, initial velocity $v_{{0}}$ is set to 0.
- ${begin{aligned}Delta K&={frac {1}{2}}mv^{{2}}-{frac {1}{2}}mv_{{0}}^{{2}}\&={frac {1}{2}}mv^{{2}}end{aligned}}$

1
Begin with the Work-Energy Theorem. The work that is done on an object is related to the change in its kinetic energy.
2
Rewrite work in terms of acceleration. Note that using algebra alone in this derivation restricts us to constant acceleration.
- ${begin{aligned}Delta K&=FDelta x\&=maDelta xend{aligned}}$
- Here, is the displacement.
3
Relate velocity, acceleration, and displacement. There are several constant acceleration kinematic equations that relate time, displacement, velocity, and acceleration. The “timeless” equation which does not contain time is below.
- $v^{{2}}=v_{{0}}^{{2}}+2aDelta x$
- When an object starts from rest, $v_{{0}}=0.$
4
Solve for acceleration. Remember, initial velocity is 0.
- $a={frac {v^{{2}}}{2Delta x}}$
5
Substitute acceleration into the original equation and simplify.
- ${begin{aligned}Delta K&=mleft({frac {v^{{2}}}{2Delta x}}right)Delta x\&={frac {1}{2}}mv^{{2}}end{aligned}}$

Add New Question

Question

How do I calculate kinetic energy using the equations of motion?

K=1/2mv^2. You can take any equation of motion, solve for v and then substitute in the equation above. I could provide more help if you gave the specific equation.
Question

How do I calculate potential and kinetic energy involving projectile of a ball without given mass?

You can not, since energy is a function of both mass and velocity. If you know the velocity but not the mass, you can turn it into a function of mass, since velocity becomes a constant; you could have K = 7m, where m is the mass. Just be sure to mind your units.
Question

Why are we using the timeless equation?

We’re using the timeless equation because we know that the kinetic energy of something shouldn’t depend on time. So by using this equation, we can arrive at the answer in the simplest possible way. Otherwise, we would have to find a way to cancel the time variable that would be introduced.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

Thanks for submitting a tip for review!

About This Article

Thanks to all authors for creating a page that has been read 141,822 times.

Did this article help you?

Get all the best how-tos!

You’re all set!

Источник

Виды энергии:
	Механическая	Потенциальная Кинетическая
‹♦›	Внутренняя
	Электромагнитная	Электрическая Магнитная
	Химическая
	Ядерная
	Гравитационная
	Вакуума
Гипотетические:
	Тёмная
См. также: Закон сохранения энергии

Кинети́ческая эне́ргия — скалярная функция, являющаяся мерой движения материальных точек, образующих рассматриваемую механическую систему, и зависящая только от масс и модулей скоростей этих точек^[1]. Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии^[2]. Для движения со скоростями значительно меньше скорости света кинетическая энергия записывается как

${displaystyle T=sum {{m_{i}v_{i}^{2}} over 2},}$

где индекс нумерует материальные точки. Часто выделяют кинетическую энергию поступательного и вращательного движения^[3]. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением^[4]. Когда тело не движется, его кинетическая энергия равна нулю. Возможные обозначения кинетической энергии: , ${displaystyle E_{mathrm {kin} }}$ , и другие. В системе СИ она измеряется в джоулях (Дж), в СГС — в эргах.

Упрощённо, кинетическая энергия — это работа, которую необходимо совершить, чтобы тело массой разогнать из состояния покоя до скорости . Либо, наоборот, это работа, которую может совершить, останавливаясь, тело массой , обладающее начальной скоростью .

История и этимология понятия[править | править код]

Прилагательное «кинетический» происходит от греческого слова κίνησις (kinesis, «движение»). Дихотомия между кинетической энергией и потенциальной энергией восходит к аристотелевским концепциям потенциальности и актуальности^[en]^[5] .

Принцип классической механики, согласно которому E ∝ mv²/2, был впервые разработан Готфридом Лейбницем и Иоганном Бернулли, описавшими кинетическую энергию как живую силу (лат. vis viva)^[6]. Вильгельм Гравезанд из Нидерландов предоставил экспериментальные доказательства этой связи. Сбрасывая грузы с разной высоты на глиняный блок, он определил, что глубина их проникновения пропорциональна квадрату скорости удара. Эмили дю Шатле осознала значение данного эксперимента и опубликовала объяснение^[7].

Понятия «кинетическая энергия» и «работа» в их нынешнем научном значении восходят к середине XIX века. В 1829 году Гаспар-Гюстав Кориолис опубликовал статью Du Calcul de l’Effet des Machines, в которой излагалась математика того, что по сути является кинетической энергией. Создание и введение в оборот самого термина «кинетическая энергия» приписывают Уильяму Томсону (лорду Кельвину) c 1849—1851 гг.^[8]^[9]. Ренкин, который ввел термин «потенциальная энергия» в 1853 году^[10], позже цитировал У. Томсона и П. Тэйта с заменой слова «кинетическая» на «фактическая»^[11].

Кинетическая энергия в классической механике[править | править код]

Случай одной материальной точки[править | править код]

По определению, кинетической энергией материальной точки массой называется величина

${displaystyle T={{mv^{2}} over 2}}$

при этом предполагается, что скорость точки всегда значительно меньше скорости света. С использованием понятия импульса () данное выражение примет вид ${displaystyle T=p^{2}/2m}$ .

Если vec{F} — равнодействующая всех сил, приложенных к точке, выражение второго закона Ньютона запишется как . Скалярно умножив его на перемещение материальной точки и учитывая, что , причём ${displaystyle {rm {d}}(v^{2})/{rm {d}}t={rm {d}}({vec {v}}cdot {vec {v}})/{rm {d}}t=2{vec {v}}cdot {rm {d}}{vec {v}}/{rm {d}}t}$ , получим ${displaystyle {vec {F}}{rm {d}}{vec {s}}={rm {d}}(mv^{2}/2)={rm {d}}T}$ .

Если система замкнута (внешние силы отсутствуют) или равнодействующая всех сил равна нулю, то стоящая под дифференциалом величина остаётся постоянной, то есть кинетическая энергия является интегралом движения.

Случай абсолютно твёрдого тела[править | править код]

При рассмотрении движения абсолютно твёрдого тела его можно представить как совокупность материальных точек. Однако, обычно кинетическую энергию в таком случае записывают, используя формулу Кёнига, в виде суммы кинетических энергий поступательного движения объекта как целого и вращательного движения:

${displaystyle T={frac {Mv^{2}}{2}}+{frac {Iomega ^{2}}{2}}.}$

Здесь — масса тела, — скорость центра масс, и — угловая скорость тела и его момент инерции относительно мгновенной оси, проходящей через центр масс^[12].

Кинетическая энергия в гидродинамике[править | править код]

В гидродинамике вместо массы материальной точки рассматривают массу единицы объёма, то есть плотность жидкости или газа . Тогда кинетическая энергия, приходящаяся на единицу объёма, двигающегося со скоростью vec{v} , то есть плотность кинетической энергии ${displaystyle w_{T}={rm {d}}T/{rm {d}}V}$ (Дж/м³), запишется:

${displaystyle w_{T}=rho {frac {v_{alpha }v_{alpha }}{2}},}$

где по повторяющемуся индексу , означающему соответствующую проекцию скорости, предполагается суммирование.

Поскольку в турбулентном потоке жидкости или газа характеристики состояния вещества (в том числе, плотность и скорость) подвержены хаотическим пульсациям, физический интерес представляют осреднённые величины. Влияние гидродинамических флуктуаций на динамику потока учитывается методами статистической гидромеханики, в которой уравнения движения, описывающие поведение средних характеристик потока, в соответствии с методом О. Рейнольдса, получаются путём осреднения уравнений Навье-Стокса^[13]. Если, в согласии с методом Рейнольдса, представить , ${displaystyle v_{alpha }={overline {v_{alpha }}}+v'_{alpha }}$ , где черта сверху — знак осреднения, а штрих — отклонения от среднего, то плотность кинетической энергии приобретёт вид:

${displaystyle {overline {w_{T}}}={frac {1}{2}}{overline {rho v_{alpha }v_{alpha }}}=E_{s}+E_{st}+E_{t},}$

где ${displaystyle E_{s}={overline {rho }},{overline {v_{alpha }}},{overline {v_{alpha }}}/2}$ — плотность кинетической энергии, связанной с упорядоченным движением жидкости или газа, ${displaystyle E_{t}={overline {rho }},{overline {v'_{alpha },v'_{alpha }}}/2+{overline {rho 'v'_{alpha }v'_{alpha }}}/2}$ — плотность кинетической энергии, связанной с неупорядоченным движением («плотность кинетической энергии турбулентности»^[13], часто называемой просто «энергией турбулентности»), а ${displaystyle E_{st}=S_{alpha }{overline {v_{alpha }}}}$ — плотность кинетической энергии, связанная с турбулентным потоком вещества ( ${displaystyle S_{alpha }={overline {rho 'v'_{alpha }}}}$ — плотность флуктуационного потока массы, или «плотность турбулентного импульса»). Эти формы кинетической энергии жидкости обладают разными трансформационными свойствами при преобразовании Галилея: кинетическая энергия упорядоченного движения ${displaystyle E_{s}}$ зависит от выбора системы координат, в то время как кинетическая энергия турбулентности ${displaystyle E_{t}}$ от него не зависит. В этом смысле кинетическая энергия турбулентности дополняет понятие внутренней энергии.

Подразделение кинетической энергии на упорядоченную и неупорядоченную (флуктуационную) части зависит от выбора масштаба осреднения по объёму или по времени. Так, например, крупные атмосферные вихри циклоны и антициклоны, порождающие определённую погоду в месте наблюдения, рассматриваются в метеорологии как упорядоченное движение атмосферы, в то время как с точки зрения общей циркуляции атмосферы и теории климата это — просто большие вихри, относимые к неупорядоченному движению атмосферы.

Кинетическая энергия в квантовой механике[править | править код]

В квантовой механике кинетическая энергия представляет собой оператор, записывающийся, по аналогии с классической записью, через импульс, который в этом случае также является оператором (, — мнимая единица):

${displaystyle {hat {T}}={frac {{hat {p}}^{2}}{2m}}=-{frac {hbar ^{2}}{2m}}Delta }$

где hbar — редуцированная постоянная Планка, nabla — оператор набла, Delta — оператор Лапласа. Кинетическая энергия в таком виде входит в важнейшее уравнение квантовой механики — уравнение Шрёдингера^[14].

Кинетическая энергия в релятивистской механике[править | править код]

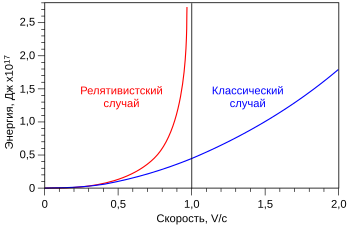
Зависимости кинетической энергии от скорости в классическом и релятивистском случаях для массы в 1 кг

Если в задаче допускается движение со скоростями, близкими к скорости света, кинетическая энергия материальной точки определяется как:

${displaystyle T={frac {mc^{2}}{sqrt {1-v^{2}/c^{2}}}}-mc^{2},}$

где

— масса материальной точки,

— скорость движения в выбранной инерциальной системе отсчёта,

— скорость света в вакууме ( ${displaystyle mc^{2}}$

— энергия покоя).

Кинетическая энергия в этой формуле может быть разложена в ряд Маклорена по степеням :

${displaystyle T=mc^{2}left({frac {1}{2}}(v/c)^{2}+{frac {3}{8}}(v/c)^{4}+cdots right).}$

При скоростях много меньших скорости света ( v ll c ) пренебрегаем членами разложения с высшими степенями и выражение для переходит в классическую формулу ${displaystyle Tapprox 1/2cdot mv^{2}}$ .

Как и в классическом случае, имеет место соотношение , получаемое посредством умножения на выражения второго закона Ньютона (в виде ${displaystyle {vec {F}}=mcdot {rm {d}}({vec {v}}/{sqrt {1-v^{2}/c^{2}}})/{rm {d}}t}$ ).

Релятивистское соотношение между кинетической энергией и импульсом p записывается в виде

${displaystyle T={sqrt {p^{2}c^{2}+m^{2}c^{4}}}-mc^{2}=mc^{2}left({sqrt {{frac {p^{2}}{m^{2}c^{2}}}+1}}-1right).}$

Разложив это выражение по степеням ${displaystyle p^{2}/(m^{2}c^{2}),}$ получаем

${displaystyle T=mc^{2}left({frac {p^{2}}{2m^{2}c^{2}}}-{frac {p^{4}}{8m^{4}c^{4}}}+{frac {3p^{6}}{48m^{6}c^{6}}}-cdots right)={frac {p^{2}}{2m}}-{frac {p^{4}}{8m^{3}c^{2}}}+{frac {3p^{6}}{48m^{5}c^{4}}}-cdots ,}$

первый член которого равен нерелятивистскому выражению кинетической энергии через импульс, а последующие члены — релятивистские поправки к этому выражению, которые малы при

Свойства кинетической энергии[править | править код]

Аддитивность. Это свойство означает, что кинетическая энергия механической системы, состоящей из материальных точек, равна сумме кинетических энергий всех материальных точек, входящих в систему^[1].
Инвариантность по отношению к повороту системы отсчёта. Кинетическая энергия не зависит от положения точки и направления её скорости, а зависит лишь от модуля скорости или от квадрата её скорости^[1].
Неинвариантность по отношению к смене системы отсчёта в общем случае. Это ясно из определения, так как скорость претерпевает изменение при переходе от одной системы отсчёта к другой.
Сохранение. Кинетическая энергия не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Это свойство инвариантно по отношению к преобразованиям Галилея^[1]. Свойства сохранения кинетической энергии и второго закона Ньютона достаточно, чтобы вывести математическую формулу кинетической энергии^[15]^[16].

Физический смысл кинетической энергии[править | править код]

Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии^[2]:

${displaystyle A_{12}=T_{2}-T_{1}.}$

Это равенство актуально как для классической, так и для релятивистской механики (получается интегрированием выражения между состояниями 1 и 2).

Соотношение кинетической и внутренней энергии[править | править код]

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров) как единое целое, можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — постоянная Больцмана.

См. также[править | править код]

Теорема о кинетической энергии системы
Потенциальная энергия
Закон сохранения энергии
Хаос
Энтальпия
Негэнтропия
Термодинамика
Парадокс кинетической энергии

Примечания[править | править код]

↑ ¹ ² ³ ⁴ Айзерман, 1980, с. 49.
↑ ¹ ² Сивухин Д. В. § 22. Работа и кинетическая энергия. // Общий курс физики. — М.: Наука, 1979. — Т. I. Механика. — С. 131. — 520 с.
↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
↑ Батыгин В. В., Топтыгин И. Н. 3.2. Кинематика релятивистских частиц // Современная электродинамика, часть 1. Микроскопическая теория. — Москва, Ижевск: Институт компьютерных исследований, 2002. — С. 238. — 736 с. — 1000 экз. — ISBN 5-93972-164-8.
↑ Brenner, Joseph. Logic in Reality. — illustrated. — Springer Science & Business Media, 2008. — P. 93. — ISBN 978-1-4020-8375-4. Архивная копия от 25 января 2020 на Wayback Machine Extract of page 93 Архивировано 4 августа 2020 года.
↑ Мах Э. Механика. Историко-критический очерк её развития. — Ижевск: «РХД», 2000. — С. 252. — 456 с. — ISBN 5-89806-023-5.
↑ Judith P. Zinsser. Emilie Du Châtelet : daring genius of the Enlightenment. — New York: Penguin Books, 2007. — viii, 376 pages, 16 unnumbered pages of plates с. — ISBN 0-14-311268-6, 978-0-14-311268-6.
↑ Crosbie Smith. Energy and empire : a biographical study of Lord Kelvin. — Cambridge [Cambridgeshire]: Cambridge University Press, 1989. — xxvi, 866 pages с. — ISBN 0-521-26173-2, 978-0-521-26173-9. Архивировано 25 января 2022 года.
↑ John Theodore Merz. A history of European thought in the nineteenth century. — Gloucester, Mass.: Peter Smith, 1976. — 4 volumes с. — ISBN 0-8446-2579-5, 978-0-8446-2579-9.
↑ William John Macquorn Rankine. XVIII. On the general law of the transformation of energy // The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. — 1853-02. — Т. 5, вып. 30. — С. 106–117. — ISSN 1941-5990 1941-5982, 1941-5990. — doi:10.1080/14786445308647205.
↑ W.J. Macquorn Rankine. XIII. On the phrase “Potential energy,” and on the definitions of physical quantities // The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. — 1867-02. — Т. 33, вып. 221. — С. 88–92. — ISSN 1941-5990 1941-5982, 1941-5990. — doi:10.1080/14786446708639753.
↑ Голубева О. В. Теоретическая механика. — М.: «Высшая школа», 1968. — С. 243—245. Архивировано 23 августа 2017 года.
↑ ¹ ² Монин А. С., Яглом А. М. Статистическая гидромеханика. Часть 1. — М.: Наука, 1965. — 639 с.
↑ Блохинцев Д. И. Основы квантовой механики Архивная копия от 15 февраля 2022 на Wayback Machine, 5-е изд. Наука, 1976. — 664 с., см. § 26.
↑ Айзерман, 1980, с. 54.
↑ Сорокин В. С. «Закон сохранения движения и мера движения в физике» Архивная копия от 1 января 2015 на Wayback Machine // УФН, 59, с. 325—362, (1956)

Литература[править | править код]

Айзерман М. А. Классическая механика. — М.: Наука, 1980. — 368 с.
Фриш С. Э. Курс общей физики. В 3-х тт. Т.1. Физические основы механики. Молекулярная физика. Колебания и волны. 13-е изд. — СПб.: Лань, 2010. — 480 с. — ISBN 978-5-8114-0663-0.
Сивухин Д. В. Общий курс физики. Т. 1. Механика. 5-е изд. — М.: Физматлит, 2006. — 560 с. — ISBN 5-9221-0715-1.

Источник

Загрузить PDF

Существует два вида энергии: потенциальная и кинетическая. Потенциальная энергия — это энергия одного объекта по отношению к другому, которая зависит от их взаимного расположения.^[1] Например, если вы стоите на вершине холма, то ваша потенциальная энергия будет отличаться от той, которой вы обладали бы у подножия этого холма. Кинетическая энергия — это энергия движущегося объекта.^[2] Кинетическая энергия возникает при колебаниях, вращении и поступательном движении (перемещении тела из одного места в другое).^[3] Кинетическую энергию любого объекта легко вычислить, если известны его масса и скорость.^[4]

1
Запомните формулу для вычисления кинетической энергии. Формула для нахождения кинетической энергии (КЕ) имеет следующий вид: KE = 0,5 x mv². Здесь m — масса, которая показывает, как много в данном объекте материи, а v — скорость, то есть мера того, насколько быстро объект меняет свое положение в пространстве.^[5]
- Ответ должен быть выражен в стандартных единицах измерения кинетической энергии, джоулях (Дж). Один джоуль эквивалентен 1 кг * м²/с².
2
Определите массу объекта. Если в исходном условии не дана масса, ее придется определить самостоятельно. Для этого можно взвесить предмет и найти массу в килограммах (кг).
- Настройте весы. Прежде чем взвешивать предмет, необходимо выставить на весах ноль. Это называется тарировкой весов.^[6]
- Положите объект на весы. Осторожно положите предмет на весы и запишите его массу в килограммах.
- При необходимости переведите граммы в килограммы. В конечную формулу необходимо подставить значение массы в килограммах.
3
Найдите скорость объекта. Часто в условии задачи дается скорость объекта. Если скорость не дана, ее можно найти по пройденному расстоянию и затраченному для этого времени.^[7] Скорость измеряется в метрах в секунду (м/с).
- Чтобы определить скорость, необходимо расстояние поделить на время: V = d/t. Скорость является векторной величиной, то есть имеет абсолютное значение и направление. Абсолютное значение соответствует величине скорости, а направление указывает на то, куда движется объект.
- Например, скорость объекта может составлять 80 м/с или –80 м/с, в зависимости от направления движения.
- Чтобы вычислить скорость, просто поделите пройденное расстояние на затраченное время.
Реклама

1
Запишите формулу. Кинетическая энергия (KE) вычисляется по следующей формуле: KE = 0,5 x mv². Здесь m — масса, которая показывает, как много в данном объекте материи, а v — скорость, то есть мера того, насколько быстро объект меняет свое положение в пространстве.^[8]
- Ответ записывается в джоулях (Дж). Это стандартная единица измерения кинетической энергии. Один джоуль эквивалентен 1 кг * м²/с².
2
Подставьте в формулу массу и скорость. Если в условии задачи не дана масса или скорость, необходимо найти их. Предположим, что заданы обе эти величины, и необходимо решить следующую задачу: Найдите кинетическую энергию женщины массой 55 кг, которая бежит со скоростью 3,87 м/с. В условии даны масса и скорость, поэтому их можно сразу подставить в формулу:^[9]
- KE = 0,5 x mv²
- KE = 0,5 x 55 x (3,87)²
3
Проведите вычисления. После подстановки массы и скорости можно рассчитать кинетическую энергию (KE). Возведите скорость в квадрат и умножьте полученное значение на массу и на 0,5. Помните, что ответ должен получиться в джоулях (Дж).^[10]
- KE = 0,5 x 55 x (3,87)²
- KE = 0,5 x 55 x 14,97
- KE = 411,675 Дж
Реклама

1
Запишите формулу. Кинетическая энергия (KE) вычисляется по следующей формуле: KE = 0,5 x mv². Здесь m — масса, которая показывает, как много в данном объекте материи, а v — скорость, то есть мера того, насколько быстро объект меняет свое положение в пространстве.^[11]
- Ответ записывается в джоулях (Дж). Это стандартная единица измерения кинетической энергии. Один джоуль эквивалентен 1 кг * м²/с².
2
Подставьте в формулу известные значения. В некоторых задачах дается кинетическая энергия и масса, или кинетическая энергия и скорость. Сначала необходимо подставить в формулу все известные величины.
- Пример 1: чему равна скорость предмета, если его масса составляет 30 кг и он имеет кинетическую энергию 500 Дж?
  - KE = 0,5 x mv²
  - 500 Дж = 0,5 x 30 x v²
- Пример 2: чему равна масса предмета, если его кинетическая энергия составляет 100 Дж, и он движется со скоростью 5 м/с?
  - KE = 0,5 x mv²
  - 100 Дж = 0,5 x m x 5²
3
Преобразуйте уравнение, чтобы найти неизвестную величину. Путем алгебраических преобразований перенесите искомую величину по одну, а все известные величины — по другую сторону знака равенства.
- Пример 1: чему равна скорость предмета, если его масса составляет 30 кг и он имеет кинетическую энергию 500 Дж?
  - KE = 0,5 x mv²
  - 500 Дж = 0,5 x 30 x v²
  - Умножим массу на 0,5: 0,5 x 30 = 15
  - Поделим кинетическую энергию на получившееся значение: 500/15 = 33,33
  - Извлечем квадратный корень, чтобы найти скорость: 5,77 м/с
- Пример 2: чему равна масса предмета, если его кинетическая энергия составляет 100 Дж, и он движется со скоростью 5 м/с?
  - KE = 0,5 x mv²
  - 100 Дж = 0,5 x m x 5²
  - Возведем скорость в квадрат: 5² = 25
  - Умножим полученное значение на 0,5: 0,5 x 25 = 12,5
  - Поделим кинетическую энергию на эту величину: 100/12,5 = 8 кг
Реклама

Об этой статье

Эту страницу просматривали 29 513 раз.

Была ли эта статья полезной?

Источник

Вначале выводится формула потенциальной энергии, а из нее уже выводится формула кинетической энергии. Формулу потенциальной энергии получил Исаак Ньютон в своей знаменитой книге “Математические начала натуральной философии”. Он рассуждал примерно следующим образом.

Пусть на моей ладони лежит некий предмет. Буду поднимать ладонь с предметом очень медленно и равномерно таким образом, чтобы сила реакции ладони N уравновешивалась силой тяжести предмета P, а кинетическая энергия была бы практически равна нулю из-за очень малой скорости. Куда девается работа A = INT (P dh) = mgh, производимая мною над предметом? Она преобразуется в скрытую потенциальную энергию предмета, которая может перейти в явную кинетическую, если позволить предмету свободно падать.

Теперь смотрите, какая была допущена ошибка Ньютоном. Если на предмет действуют сразу несколько сил F1, F2, F3 и так далее, то для вычисления суммарной энергии, производимой всеми силами вместе, нужно подставлять под знак интеграла результирующую силу, а не одну из частных сил. А Ньютон подставил частную силу, силу веса. Так как в рассмотренном им случае результирующая сила равна нулю (сила веса уравновешивается силой реакции ладони), правильный расчет покажет нулевую работу. А если работа равна нулю, значит энергия предмета не меняется. И если она была равна нулю в начальной точке подъема, то останется равной нулю независимо от высоты подъема. Иными словами, потенциальной энергии в природе не существует. Но на практике мы прекрасно знаем, что подъем любого тяжелого предмета сопровождается затратами энергии. Значит, полученный вывод о нулевой работе ошибочен? Нет, он правилен. Просто работа будет выполняться не над поднимаемым предметом, а над чем-то иным. И формула mgh описывает не потенциальную энергию предмета, а энергию чего-то иного.

Теперь переходим к кинетической энергии. В кинематике (наука о равномерном и неравномерном движении) есть такая формула V1 V1 – V0 V0 = 2aS для ускоренного движения, где V0 – начальная скорость, V1 – конечная скорость, a – ускорение, S – длина проходимого пути. Если в начальный момент времени скорость предмета V0 была равна нулю, то выражая произведение ускорения на длину и подставляя его в формулу потенциальной энергии, получим mVV/2, то есть формулу кинетической энергии. А теперь будем рассуждать. Если комплекс mgh описывает не потенциальную энергию предмета, а что-то иное, тогда получаемая из него формула mVV/2 также будет описывать не кинетическую энергию предмета, а энергию чего-то иного. А чего именно – это я сейчас попробую разъяснить.

Когда мы поднимаем любой предмет, мы преодолеваем сопротивление не предмета, а гравитационного поля. Следовательно, будем совершать работу над гравитационным полем и увеличивать его энергию на величину Е = mgh. А когда мы бросаем предмет, мы через его ускоренное движение деформируем структуру окружающего нас физического вакуума, совершаем над ним работу и увеличиваем его энергию на величину Е = mVV/2. Таким образом, вместо потенциальной энергии существует энергия гравитационного поля, а вместо кинетической энергии существует энергия физического вакуума.

Источник

Рассчитать (найти) кинетическую энергию тела онлайн

Найти кинетическую энергию тела онлайн через ускорение, перемещение и скорость тела

Кинетическая энергия, найти массу тела онлайн

Кинетическая энергия, найти скорость тела онлайн

Найти изменение кинетической энергии по скорости

About This Article

Did this article help you?

История и этимология понятия[править | править код]

Кинетическая энергия в классической механике[править | править код]

Случай одной материальной точки[править | править код]

Случай абсолютно твёрдого тела[править | править код]

Кинетическая энергия в гидродинамике[править | править код]

Кинетическая энергия в квантовой механике[править | править код]

Кинетическая энергия в релятивистской механике[править | править код]

Свойства кинетической энергии[править | править код]

Физический смысл кинетической энергии[править | править код]

Соотношение кинетической и внутренней энергии[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Об этой статье

Была ли эта статья полезной?

Вам также может понравиться

Как найти отрезок соединяющий середины сторон параллелограмма

Как найти площадь груга

Как найти реплей боя в вот

Добавить комментарий Отменить ответ