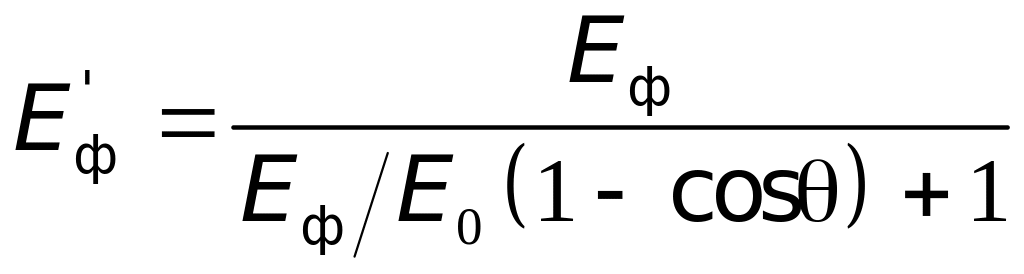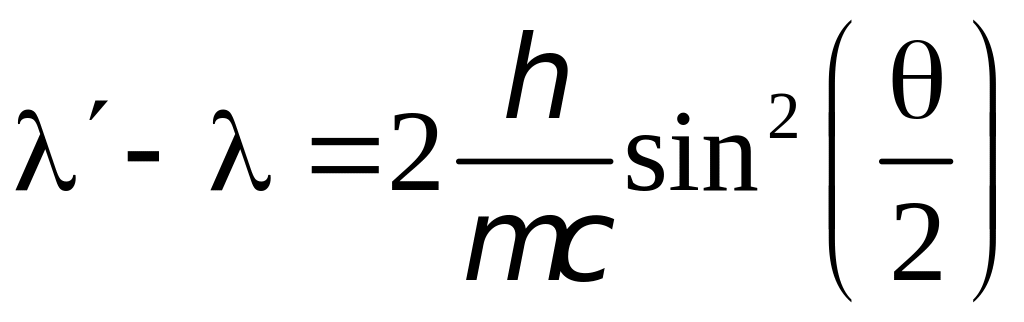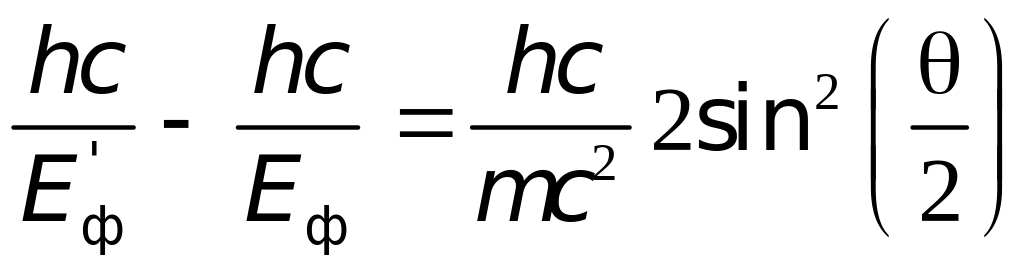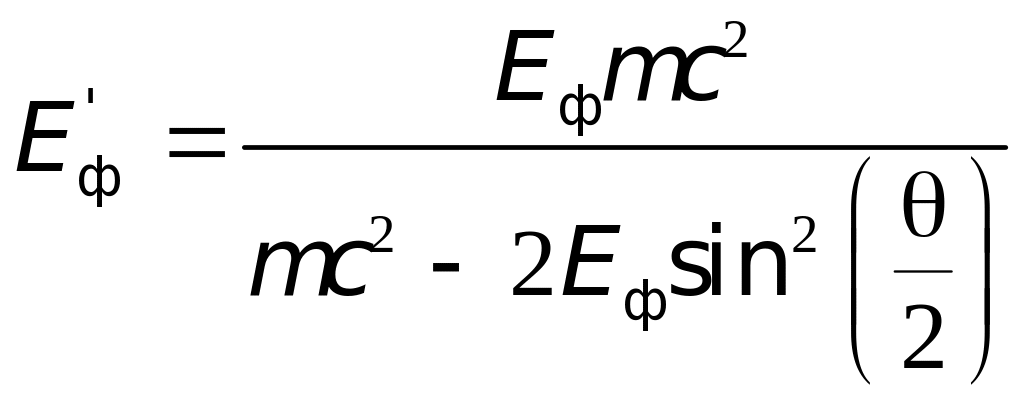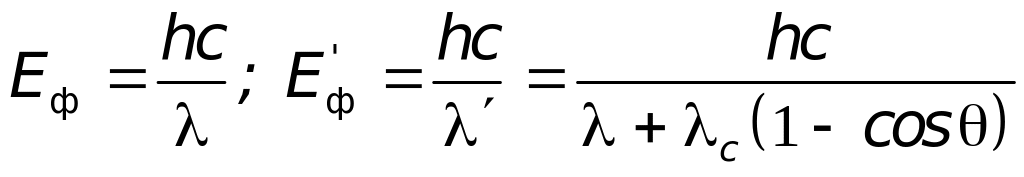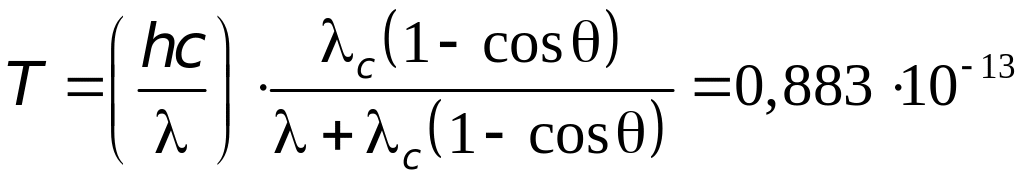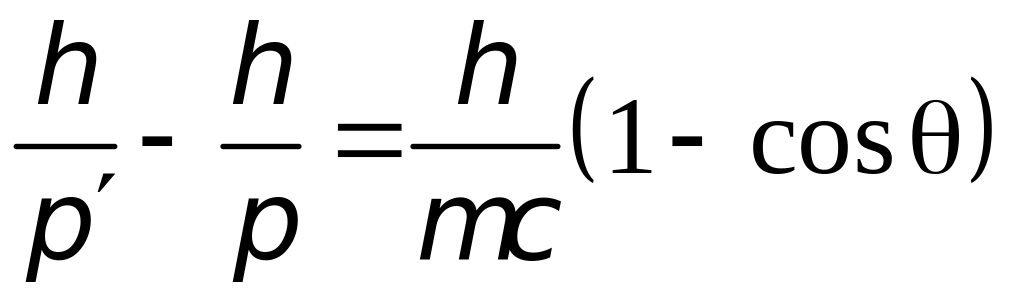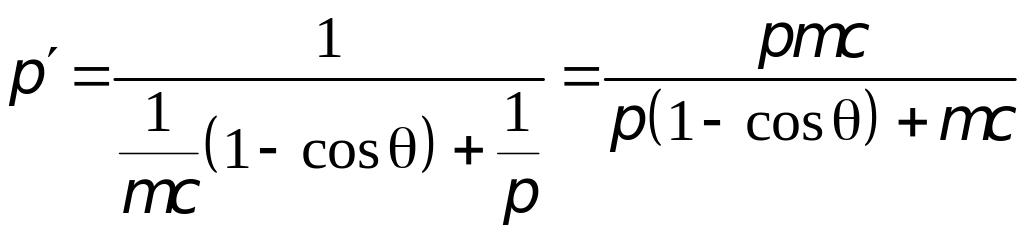Как найти кинетическую энергию электрона отдачи

В
1922 году А. Комптон, исследуя рассеяние
рентгеновского излучения различными
веществами обнаружил, что в нем наряду
с исходной длиной волны

появляется смещенная линия с длиной
волны


>

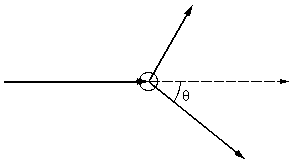
(Рис.8).

Рис.8 Схема установки
по изучению эффекта Комптона

Это
изменение длины волны получило название
комптоновского смещения, а само явление
эффекта Комптона. Комптоновское смещение

не зависит от длины волны

и от природы рассеивающего вещества и
определяется формулой:

,

где

– масса электрона или другой заряженной
частицы,

–
комптоновская длина волны этой частицы,

и 
– длины волн
падающего и рассеянного излучения;
–угол
рассеяния. Для электрона

2,42пм.

Все
закономерности эффекта Комптона можно
объяснить, если рассмотреть упругое
столкновение рентгеновского кванта с
покоящимся электроном, слабо связанным
с атомом. Происходит процесс, напоминающий
удар двух биллиардных шаров, когда один
шар (рентгеновский квант) налетает на
покоящийся шар (электрон) и в результате
абсолютно упругого удара шары (рассеянный
квант и электрон) разлетаются под
некоторым углом. Налетающий квант с
энергией

передает часть своей энергии электрону,
поэтому рассеянный квант имеет меньшую
энергию и, следовательно, большую длину
волны. Энергия рентгеновского кванта
(десятки кэВ) на несколько порядков
превосходит энергию связи электрона в
атоме (десятки эВ), поэтому наиболее
слабо связанные с атомом электроны
внешних оболочек можно считать свободными
и покоящимися.

Законы
сохранения энергии при комптоновском
упругом рассеянии.

Закон сохранения
импульса имеет вид:

,

где

и

– волновые векторы падающего и рассеянного
фотонов (модуль волнового вектора равен

).
Графическая иллюстрация закона сохранения
импульса приведена на Рис. 9. Закон
сохранения энергии записывается в виде:

(

используется
релятивистская формула, т.к. энергия
падающего кванта сравнима в энергией
покоя электрона). Здесь

–постоянная
Планка, с –
скорость света,

– масса электрона,

– импульс электрона,

и


– длины падающей и рассеянной волн.

Рис.9
Графическая иллюстрация закона сохранения
импульса в эффекте Комптона

В
эффекте Комптона участвуют только
свободные электроны, которые слабо
связаны с атомами. Если же энергия связи
электрона больше энергии фотона, то
такой электрон не будет свободным и
эффект Комптона не возникает. В этом
случае фотон взаимодействует с жестко
связанной системой электрон – ядро и
«отскакивает» от нее, практически не
изменяя своей энергии и длины волны. В
реальном веществе фотоны сталкиваются
как со свободными, так и с сильно
связанными электронами, поэтому и
возникают оба компонента рассеяния с
длинами волн

и

.

Эффект
Комптона не может происходить под
действием квантов видимого света (с
длинами волн 400 – 700 нм), поскольку их
энергия составляет 3 – 1,8 эВ соответственно,
что на 5 порядков меньше энергии покоя
электрона – 511000 эВ.

Кинетическая
энергия электрона отдачи:

,
где

– энергия падающего фотона и

– энергия рассеянного фотона.

Соотношение
между энергией падающего

и рассеянного

фотонов при комптоновском рассеянии:

,
откуда

,
где

 = 0,511 МэВ
– энергия покоя электрона.

Примеры решения задач

Задача
1. В результате
эффекта Комптона фотон при соударении
с электро-ном был рассеян на угол 90.
Энергия

рассеянного фотона равна 0,4 МэВ.
Опре-делите энергию фотона

до рассеяния.

Решение.
Выразим в
формуле Комптона

длины волн

и

через энергии

и

соответствующих фотонов, воспользовавшись
соотношением

,

,
откуда

=
1,85 Мэв,

где

= 0,51 МэВ, 1 МэВ = 1,6·10^-13
Дж.

Задача
2. Гамма-фотон
с длиной волны 1,2 пм в результате
комптоновского рассеяния на свободном
электроне отклонился от первоначального
направления на угол 60.
Определите кинетическую энергию и
импульс электрона отдачи. До столкновения
электрон покоился.

Решение.
Из закона
сохранения энергии кинетическая энергия
электрона отдачи равна

,
где

и

– энергия падающего и рассеянного
фотонов.

Выражая
энергию падающего и рассеянного фотона
через его длину волны и используя формулу
изменения длины волны фотона при
комптоновском рассеянии, получим:

.

Для
кинетической энергии электрона находим

Дж.
= 0,521 МэВ.

пм
– комптоновская длина волны электрона.
Кинетическая энергия электрона сравнима
с его энергией покоя

,
поэтому его импульс найдем по
релятивистской формуле

=
4,8·10^-22кг·м/c.

Задача
3. Фотон с
импульсом 5,4410^–22
кгм/с
в результате эффекта Компто-

на
был рассеян на свободном электроне на
угол 30.
Найти импульс рассеянного фотона.

Решение.
Выражая
импульс фотона через его длину волны и
используя формулу изменения длины волны

при эффекте Комптона получим:

,
или

,

откуда

= 4,310^–22
кгм/с.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Решение.
Кинетическая энергия электрона отдачи равна разности энергии падающего фотона и энергии рассеянного фотона:

W_еО = W_Ф – W_рф     (1).

Определим длину волны фотона.
Формула комптоновской длины волны получается из формулы де-бройлевской длины волны путём замены скорости частицы υ на скорость света c:

[ {{lambda }_{K}}=frac{h}{{{m}_{0}}cdot c} (2). ]

Где: h = 6,62∙10^-34 Дж∙с – постоянная Планка, m₀ = 9,1∙10^-31 кг – масса электрона, с = 3∙10⁸ м/с – скорость света.
Энергию фотона определим по формуле:

[ {{W}_{Phi }}=frac{hcdot c}{{{lambda }_{K}}}=frac{hcdot ccdot {{m}_{0}}cdot c}{h}={{m}_{0}}cdot {{c}^{2}} (3). ]

Энергию рассеянного фотона определим по формуле:

[ {{W}_{pPhi }}={{frac{hcdot c}{lambda ‘}}^{2}} (4). ]

λ` – длина волны рассеянного фотона.
Запишем формулу для вычисления изменения длины волны при рассеянии:

[ begin{align}
  & Delta lambda =lambda ‘-lambda ={{lambda }_{K}}cdot (1-cos alpha ), alpha ={{90}^{0}}, Delta lambda ={{lambda }_{K}}, lambda ‘=2cdot {{lambda }_{K}} (5). \
 & {{W}_{pPhi }}=frac{hcdot c}{2cdot {{lambda }_{K}}}=frac{hcdot ccdot {{m}_{0}}cdot c}{2cdot h}=frac{{{m}_{0}}cdot {{c}^{2}}}{2} (6). \
end{align} ]

Подставим (6) и (4) в (1) определим кинетическую энергия электрона отдачи:

[ {{W}_{eO}}=frac{{{m}_{0}}cdot {{c}^{2}}}{2}. ]

W_еО =40,95∙10^-15 Дж.

Данная тема будет посвящена решению задач, связанных с
расчетом энергии и импульса фотонов.

Задача 1. Определите энергию, массу и импульс фотона,
если соответствующая ему длина волны равна 1,6 ∙ 10⁻¹²
м.

ДАНО:	РЕШЕНИЕ Энергия фотона определяется по формуле Массу фотона можно определить из формулы Импульс фотона

Ответ: W
= 1,2 ∙ 10⁻¹³ Дж; m = 1,4 ∙ 10⁻³⁰ кг; р =  4,1
∙ 10⁻²² кг ∙ м/с.

Задача 2. Электрон, пройдя разность потенциалов 4,9 В,
сталкивается с атомом ртути и переводит его в первое возбужденное состояние.
Какую длину волны имеет фотон, соответствующий переходу атома ртути в
нормальное состояние?

ДАНО:	РЕШЕНИЕ Определим энергию, которую приобретает электрон, пройдя в электростатическом поле ускоряющую разность потенциалов Энергия вылетевшего фотона Приравняем эти два уравнения Тогда длина волны фотона

Ответ: длина волны фотона равна 250
нм.

Задача 3. Работа выхода электрона из металла 4,5 эВ.
Энергия падающего фотона 4,9 эВ. Если свет падает на пластинку нормально, а
электрон вылетает перпендикулярно пластинке, то чему равно изменение модуля
импульса металлической пластинки при вылете из нее одного электрона?

ДАНО:

РЕШЕНИЕ Рассматриваемая система (металлическая пластинка — фотон — электрон) не является замкнутой. Однако фотоэффект практически безинерционен, так как с момента облучения металла светом до вылета электронов проходит около одной миллиардной доли секунды. Так как время взаимодействия очень мало, то для рассматриваемой системы должен выполняться закон сохранения импульса Импульс системы в начальном состоянии будет определяться только импульсом падающего фотона, так как в начальный момент времени пластинка не движется Импульс системы в конечном состоянии будет складываться из импульса вылетевшего электрона и импульса, который приобрела пластинка Тогда закон сохранение импульса Изменение импульса пластинки Запишем закон сохранения импульса в проекциях на нормаль Импульс, переданный фотоном Импульс, преданный электроном Из уравнения Эйнштейна для фотоэффекта Тогда импульс переданный электроном Тогда изменение модуля импульса металлической пластины

Ответ: изменение модуля импульса
пластинки равно 3,44 ∙ 10⁻²⁵ кг ∙ м/с

Задача 4. Энергия фотона рентгеновского излучения 0,3
МэВ. Фотон был рассеян при соударении со свободным покоящимся электроном, в
результате чего его длина волны увеличилась на 0,0025 нм. Определить: энергию
рассеянного фотона; угол, под которым вылетел электрон отдачи; кинетическую
энергию электрона отдачи.

ДАНО:

РЕШЕНИЕ Согласно условию задачи, при рассеянии рентгеновского излучения на электронах, происходит увеличение его длины волны. Этот эффект, который называют эффектом Комптона, объясняется тем, что фотон, как и любая частица, обладает определенным импульсом и что акт рассеяния представляет собой упругое столкновение фотона с электроном, аналогичное соударению упругих шариков. При этом выполняется как закон сохранения импульса, так и закон сохранения энергии. Упруго соударяясь с электроном, фотон передает ему часть импульса и энергии. Энергия фотона, как известно, определяется по формулам Уменьшение энергии фотона означает уменьшение частоты рентгеновского излучения и увеличение его длины волны. Энергия рассеянного фотона Длина волны рассеянного излучения Длина волны падающего излучения Длина волны рассеянного излучения Тогда энергия рассеянного фотона Проверим размерности Определим угол, под которым вылетает электрон отдачи. Для этого нарисуем вспомогательный рисунок, на котором укажем ситуацию до столкновения фотона с электроном и после. Так как время взаимодействия фотона с электроном мало, то систему «фотон-электрон» можно считать замкнутой, и для нее должен выполняться закон сохранения импульса Закон сохранения импульса в проекциях на ось Ох Закон сохранения импульса в проекциях на ось Оу Тогда Импульс падающего фотона Энергия падающего фотона Аналогично для рассеянного фотона Тогда И Формула Комптона Тогда Комптоновская длина волны электрона Тогда Закон сохранения энергии Тогда кинетическая энергия электрона отдачи

Ответ: W’
= 0,2 МэВ; φ = 31^о; W_k = 0,1 МэВ.