Как найти кинетическую энергию формула 10 класс

Как найти кинетическую энергию формула 10 класс

Энергия – важнейшее понятие и термин в механике. Что такое энергия, и что она значит? Существует множество определений, и вот одно из них.

Что такое энергия?

Энергия в физике – это способность тела совершать работу. 

Кинетическая энергия

Что такое кинетическая энергия?

Рассмотрим тело, которое двигалось под действием каких-то сил, изменило свою скорость с v1→ до v2→. В этом случае силы, действующие на тело, совершили определенную работу A. 

Работа всех сил, действующих на тело, равна работе равнодействующей силы. 

Кинетическая энергия

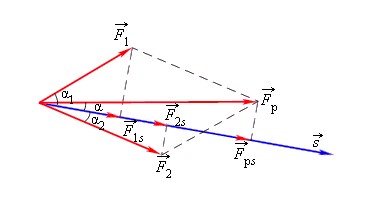
Fр→=F1→+F2→

A=F1·s·cosα1+F2·s·cosα2=Fрcosα.

Как находить связь между изменением скорости тела и работой, совершенной действующими на тело силами. Для простоты будем считать, что на тело действует одна сила F→, направленная вдоль прямой линии. Под действием этой силы тело движется равноускоренно и прямолинейно. В этом случае векторы F→, v→, a→, s→ совпадают по направлению и их можно рассматривать как алгебраические величины. 

Работа силы F→ равна A=Fs. Перемещение тела выражается формулой s=v22-v122a. Отсюда:

A=Fs=F·v22-v122a=ma·v22-v122a

A=mv22-mv122=mv222-mv122.

Если вычислять, то работа, совершенная силой, пропорционально изменению квадрата скорости тела. 

Определение. Кинетическая энергия

Кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости. Вот как выглядит формула кинетической энергии:

EK=mv22.

Кинетическая энергия – это энергия движения тела. При нулевой скорости она равна нулю.

Теорема о кинетической энергии

Вновь будем работать с рассмотренным примером и сформулируем теорему о кинетической энергии тела.

Теорема о кинетической энергии

Работа приложенной к телу силы равна изменению кинетической энергии тела. Данное утверждение справедливо и тогда, когда тело движется под действием изменяющейся по модулю и направлению силы. 

A=EK2-EK1.

Таким образом, кинетическая энергия тела массы m, движущегося со скоростью v→, будет измеряться (при измерении) и равна работе, которую сила должна совершить, чтобы разогнать тело до этой скорости.

A=mv22=EK.

Чтобы остановить тело, нужно совершить работу 

A=-mv22=-EK

Потенциальная энергия

Что будет означать или обозначать кинетическая энергия?

Кинетическая энергия – это энергия движения. Наряду с кинетической энергией есть еще такой вид энергии как потенциальная энергия, то есть энергия взаимодействия тел, которая будет вычисляться и зависеть от их положения. Кинетическая и потенциальная энергии рассматриваются параллельно.

Формула потенциальной энергии:

E пот = m * g * h

Например, тело поднято над поверхностью земли. Чем выше оно поднято, тем больше будет потенциал-я энергия. Когда тело движется и падает вниз под действием силы тяжести (притяжения), эта сила совершает работу. Причем работа силы тяжести определяется только вертикальным перемещением тела и не зависит от траектории.

Потенциальная энергия

Важно!

Вообще о потенциально энергии можно говорить только в контексте тех сил, работа которых не зависит от формы траектории тела. Такие силы называются консервативными.

Примеры консервативных сил: сила тяжести, сила упругости.

Когда тело движется вертикально вверх, сила тяжести совершает отрицательную работу. 

Рассмотрим вычисление на примере, когда шар переместился из точки с высотой h1 в точку с высотой h2. 

Потенциальная энергия

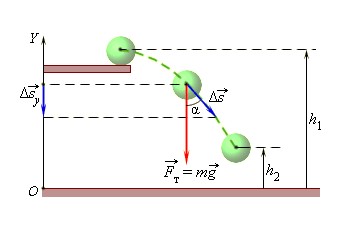
При этом сила тяжести совершила работу, равную 

A=-mg(h2-h1)=-(mgh2-mgh1).

Эта работа равна изменению величины mgh, взятому с противоположным знаком. 

Величина ЕП=mgh – потенциальна энергия в поле силы тяжести. На нулевом уровне (на земле) потенциальную энергию тела можно не рассчитывать: она равна нулю.

Определение. Потенциальная энергия

Потенциальная энергия – часть полной механической энергии системы, с нахождением в поле консервативных сил. Потенциальная энергия зависит от положения точек, составляющих систему. Механическая энергия – это сумма потенциальной и кинетической энергий, которые есть в компонентах механической системы.

Можно говорить о потенциальной энергии в поле силы тяжести, потенциальной энергии сжатой пружины (пружинной энергии) и т.д. 

Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.

A=-(EП2-EП1).

Ясно, что потенциальная энергия зависит от выбора нулевого уровня (начала координат оси OY). Подчеркнем, что физический смысл имеет изменение потенциальной энергии при перемещении тел друг относительно друга. При любом выборе нулевого уровня изменение потенциальной энергии будет одинаковым.

При расчете движения тел в поле гравитации Земли, но на значительных расстояниях от нее, во внимание нужно принимать закон всемирного тяготения (зависимость силы тяготения от расстояния до цента Земли). Приведем формулу, выражающую зависимость потенциальной энергии тела.

EП=-GmMr.

Здесь G – гравитационная постоянная, M – масса Земли.

Потенциальная энергия пружины

Представим, что в первом случае мы взяли пружину и удлинили ее на величину x. Во втором случае мы сначала удлинили пружину на 2x, а затем уменьшили на x. В обоих случаях пружина оказалась растянута на x, но это было сделано разными способами. 

При этом работа силы упругости при изменении длины пружины на x в обоих случаях была одинакова и равна

Aупр=-A=-kx22.

Величина Eупр=kx22 называется потенциальной энергией сжатой пружины. Она равна работе силы упругости при переходе из данного состояния тела в состояние с нулевой деформацией.

Если перед вами часто поднимается вопрос определения и характеристики энергии, как явления, вам стоит подумать о сохранении описанной выше информации.

Источник
Виды энергии:
Atwood machine.svg Механическая  Потенциальная
 Кинетическая
‹♦› Внутренняя
Sun corner.svg Электромагнитная  Электрическая
 Магнитная
Oil&gas portal logo.PNG Химическая
Radiation symbol alternate.svg Ядерная
G Гравитационная
emptyset Вакуума
Гипотетические:
{displaystyle } Тёмная
См. также: Закон сохранения энергии

Кинети́ческая эне́ргия — скалярная функция, являющаяся мерой движения материальных точек, образующих рассматриваемую механическую систему, и зависящая только от масс и модулей скоростей этих точек[1]. Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии[2]. Для движения со скоростями значительно меньше скорости света кинетическая энергия записывается как

{displaystyle T=sum {{m_{i}v_{i}^{2}} over 2},}

где индекс i нумерует материальные точки. Часто выделяют кинетическую энергию поступательного и вращательного движения[3]. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением[4]. Когда тело не движется, его кинетическая энергия равна нулю. Возможные обозначения кинетической энергии: T, {displaystyle E_{mathrm {kin} }}, K и другие. В системе СИ она измеряется в джоулях (Дж), в СГС — в эргах.

Упрощённо, кинетическая энергия — это работа, которую необходимо совершить, чтобы тело массой m разогнать из состояния покоя до скорости v. Либо, наоборот, это работа, которую может совершить, останавливаясь, тело массой m, обладающее начальной скоростью v.

История и этимология понятия[править | править код]

Прилагательное «кинетический» происходит от греческого слова κίνησις (kinesis, «движение»). Дихотомия между кинетической энергией и потенциальной энергией восходит к аристотелевским концепциям потенциальности и актуальности[en][5] .

Принцип классической механики, согласно которому E ∝ mv2/2, был впервые разработан Готфридом Лейбницем и Иоганном Бернулли, описавшими кинетическую энергию как живую силу (лат. vis viva)[6]. Вильгельм Гравезанд из Нидерландов предоставил экспериментальные доказательства этой связи. Сбрасывая грузы с разной высоты на глиняный блок, он определил, что глубина их проникновения пропорциональна квадрату скорости удара. Эмили дю Шатле осознала значение данного эксперимента и опубликовала объяснение[7].

Понятия «кинетическая энергия» и «работа» в их нынешнем научном значении восходят к середине XIX века. В 1829 году Гаспар-Гюстав Кориолис опубликовал статью Du Calcul de l’Effet des Machines, в которой излагалась математика того, что по сути является кинетической энергией. Создание и введение в оборот самого термина «кинетическая энергия» приписывают Уильяму Томсону (лорду Кельвину) c 1849—1851 гг.[8][9]. Ренкин, который ввел термин «потенциальная энергия» в 1853 году[10], позже цитировал У. Томсона и П. Тэйта с заменой слова «кинетическая» на «фактическая»[11].

Кинетическая энергия в классической механике[править | править код]

Случай одной материальной точки[править | править код]

По определению, кинетической энергией материальной точки массой m называется величина

{displaystyle T={{mv^{2}} over 2}},

при этом предполагается, что скорость точки v всегда значительно меньше скорости света. С использованием понятия импульса ({displaystyle {vec {p}}=m{vec {v}}}) данное выражение примет вид {displaystyle T=p^{2}/2m}.

Если vec{F} — равнодействующая всех сил, приложенных к точке, выражение второго закона Ньютона запишется как {displaystyle {vec {F}}=m{vec {a}}}. Скалярно умножив его на перемещение материальной точки {{rm {d}}}{vec s}={vec v}{{rm {d}}}t и учитывая, что {displaystyle {vec {a}}={rm {d}}{vec {v}}/{rm {d}}t}, причём {displaystyle {rm {d}}(v^{2})/{rm {d}}t={rm {d}}({vec {v}}cdot {vec {v}})/{rm {d}}t=2{vec {v}}cdot {rm {d}}{vec {v}}/{rm {d}}t}, получим {displaystyle {vec {F}}{rm {d}}{vec {s}}={rm {d}}(mv^{2}/2)={rm {d}}T}.

Если система замкнута (внешние силы отсутствуют) или равнодействующая всех сил равна нулю, то стоящая под дифференциалом величина T остаётся постоянной, то есть кинетическая энергия является интегралом движения.

Случай абсолютно твёрдого тела[править | править код]

При рассмотрении движения абсолютно твёрдого тела его можно представить как совокупность материальных точек. Однако, обычно кинетическую энергию в таком случае записывают, используя формулу Кёнига, в виде суммы кинетических энергий поступательного движения объекта как целого и вращательного движения:

{displaystyle T={frac {Mv^{2}}{2}}+{frac {Iomega ^{2}}{2}}.}

Здесь {displaystyle M} — масса тела, v — скорость центра масс, {vec omega } и {displaystyle I} — угловая скорость тела и его момент инерции относительно мгновенной оси, проходящей через центр масс[12].

Кинетическая энергия в гидродинамике[править | править код]

В гидродинамике вместо массы материальной точки рассматривают массу единицы объёма, то есть плотность жидкости или газа {displaystyle rho ={rm {d}}M/{rm {d}}V}. Тогда кинетическая энергия, приходящаяся на единицу объёма, двигающегося со скоростью vec{v}, то есть плотность кинетической энергии {displaystyle w_{T}={rm {d}}T/{rm {d}}V} (Дж/м3), запишется:

{displaystyle w_{T}=rho {frac {v_{alpha }v_{alpha }}{2}},}

где по повторяющемуся индексу {displaystyle {alpha }=x,y,z}, означающему соответствующую проекцию скорости, предполагается суммирование.

Поскольку в турбулентном потоке жидкости или газа характеристики состояния вещества (в том числе, плотность и скорость) подвержены хаотическим пульсациям, физический интерес представляют осреднённые величины. Влияние гидродинамических флуктуаций на динамику потока учитывается методами статистической гидромеханики, в которой уравнения движения, описывающие поведение средних характеристик потока, в соответствии с методом О. Рейнольдса, получаются путём осреднения уравнений Навье-Стокса[13]. Если, в согласии с методом Рейнольдса, представить rho =overline {rho }+rho ', {displaystyle v_{alpha }={overline {v_{alpha }}}+v'_{alpha }}, где черта сверху — знак осреднения, а штрих — отклонения от среднего, то плотность кинетической энергии приобретёт вид:

{displaystyle {overline {w_{T}}}={frac {1}{2}}{overline {rho v_{alpha }v_{alpha }}}=E_{s}+E_{st}+E_{t},}

где {displaystyle E_{s}={overline {rho }},{overline {v_{alpha }}},{overline {v_{alpha }}}/2} — плотность кинетической энергии, связанной с упорядоченным движением жидкости или газа, {displaystyle E_{t}={overline {rho }},{overline {v'_{alpha },v'_{alpha }}}/2+{overline {rho 'v'_{alpha }v'_{alpha }}}/2} — плотность кинетической энергии, связанной с неупорядоченным движением («плотность кинетической энергии турбулентности»[13], часто называемой просто «энергией турбулентности»), а {displaystyle E_{st}=S_{alpha }{overline {v_{alpha }}}} — плотность кинетической энергии, связанная с турбулентным потоком вещества ({displaystyle S_{alpha }={overline {rho 'v'_{alpha }}}} — плотность флуктуационного потока массы, или «плотность турбулентного импульса»). Эти формы кинетической энергии жидкости обладают разными трансформационными свойствами при преобразовании Галилея: кинетическая энергия упорядоченного движения {displaystyle E_{s}} зависит от выбора системы координат, в то время как кинетическая энергия турбулентности {displaystyle E_{t}} от него не зависит. В этом смысле кинетическая энергия турбулентности дополняет понятие внутренней энергии.

Подразделение кинетической энергии на упорядоченную и неупорядоченную (флуктуационную) части зависит от выбора масштаба осреднения по объёму или по времени. Так, например, крупные атмосферные вихри циклоны и антициклоны, порождающие определённую погоду в месте наблюдения, рассматриваются в метеорологии как упорядоченное движение атмосферы, в то время как с точки зрения общей циркуляции атмосферы и теории климата это — просто большие вихри, относимые к неупорядоченному движению атмосферы.

Кинетическая энергия в квантовой механике[править | править код]

В квантовой механике кинетическая энергия представляет собой оператор, записывающийся, по аналогии с классической записью, через импульс, который в этом случае также является оператором ({displaystyle {hat {p}}=-jhbar nabla }, {displaystyle j} — мнимая единица):

{displaystyle {hat {T}}={frac {{hat {p}}^{2}}{2m}}=-{frac {hbar ^{2}}{2m}}Delta }

где hbar  — редуцированная постоянная Планка, nabla  — оператор набла, Delta  — оператор Лапласа. Кинетическая энергия в таком виде входит в важнейшее уравнение квантовой механики — уравнение Шрёдингера[14].

Кинетическая энергия в релятивистской механике[править | править код]

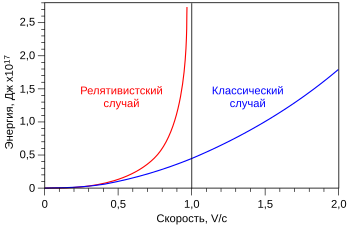
Зависимости кинетической энергии от скорости в классическом и релятивистском случаях для массы в 1 кг

Если в задаче допускается движение со скоростями, близкими к скорости света, кинетическая энергия материальной точки определяется как:

{displaystyle T={frac {mc^{2}}{sqrt {1-v^{2}/c^{2}}}}-mc^{2},}
где m — масса материальной точки,
v — скорость движения в выбранной инерциальной системе отсчёта,
c — скорость света в вакууме ({displaystyle mc^{2}} — энергия покоя).

Кинетическая энергия в этой формуле может быть разложена в ряд Маклорена по степеням {displaystyle v/c}:

{displaystyle T=mc^{2}left({frac {1}{2}}(v/c)^{2}+{frac {3}{8}}(v/c)^{4}+cdots right).}

При скоростях много меньших скорости света (v ll c) пренебрегаем членами разложения с высшими степенями и выражение для T переходит в классическую формулу {displaystyle Tapprox 1/2cdot mv^{2}}.

Как и в классическом случае, имеет место соотношение {displaystyle {vec {F}}{rm {d}}{vec {s}}={rm {d}}T}, получаемое посредством умножения на {{rm {d}}}{vec s}={vec v}{{rm {d}}}t выражения второго закона Ньютона (в виде {displaystyle {vec {F}}=mcdot {rm {d}}({vec {v}}/{sqrt {1-v^{2}/c^{2}}})/{rm {d}}t}).

Релятивистское соотношение между кинетической энергией и импульсом p записывается в виде

{displaystyle T={sqrt {p^{2}c^{2}+m^{2}c^{4}}}-mc^{2}=mc^{2}left({sqrt {{frac {p^{2}}{m^{2}c^{2}}}+1}}-1right).}

Разложив это выражение по степеням {displaystyle p^{2}/(m^{2}c^{2}),} получаем

{displaystyle T=mc^{2}left({frac {p^{2}}{2m^{2}c^{2}}}-{frac {p^{4}}{8m^{4}c^{4}}}+{frac {3p^{6}}{48m^{6}c^{6}}}-cdots right)={frac {p^{2}}{2m}}-{frac {p^{4}}{8m^{3}c^{2}}}+{frac {3p^{6}}{48m^{5}c^{4}}}-cdots ,}

первый член которого равен нерелятивистскому выражению кинетической энергии через импульс, а последующие члены — релятивистские поправки к этому выражению, которые малы при {displaystyle pll mc.}

Свойства кинетической энергии[править | править код]

  • Аддитивность. Это свойство означает, что кинетическая энергия механической системы, состоящей из материальных точек, равна сумме кинетических энергий всех материальных точек, входящих в систему[1].
  • Инвариантность по отношению к повороту системы отсчёта. Кинетическая энергия не зависит от положения точки и направления её скорости, а зависит лишь от модуля скорости или от квадрата её скорости[1].
  • Неинвариантность по отношению к смене системы отсчёта в общем случае. Это ясно из определения, так как скорость претерпевает изменение при переходе от одной системы отсчёта к другой.
  • Сохранение. Кинетическая энергия не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Это свойство инвариантно по отношению к преобразованиям Галилея[1]. Свойства сохранения кинетической энергии и второго закона Ньютона достаточно, чтобы вывести математическую формулу кинетической энергии[15][16].

Физический смысл кинетической энергии[править | править код]

Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии[2]:

{displaystyle A_{12}=T_{2}-T_{1}.}

Это равенство актуально как для классической, так и для релятивистской механики (получается интегрированием выражения {displaystyle {vec {F}}{rm {d}}{vec {s}}={rm {d}}T} между состояниями 1 и 2).

Соотношение кинетической и внутренней энергии[править | править код]

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров) как единое целое, можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — постоянная Больцмана.

См. также[править | править код]

  • Теорема о кинетической энергии системы
  • Потенциальная энергия
  • Закон сохранения энергии
  • Хаос
  • Энтальпия
  • Негэнтропия
  • Термодинамика
  • Парадокс кинетической энергии

Примечания[править | править код]

  1. ↑ 1 2 3 4 Айзерман, 1980, с. 49.
  2. ↑ 1 2 Сивухин Д. В. § 22. Работа и кинетическая энергия. // Общий курс физики. — М.: Наука, 1979. — Т. I. Механика. — С. 131. — 520 с.
  3. ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
  4. ↑ Батыгин В. В., Топтыгин И. Н. 3.2. Кинематика релятивистских частиц // Современная электродинамика, часть 1. Микроскопическая теория. — Москва, Ижевск: Институт компьютерных исследований, 2002. — С. 238. — 736 с. — 1000 экз. — ISBN 5-93972-164-8.
  5. ↑ Brenner, Joseph. Logic in Reality. — illustrated. — Springer Science & Business Media, 2008. — P. 93. — ISBN 978-1-4020-8375-4. Архивная копия от 25 января 2020 на Wayback Machine Extract of page 93 Архивировано 4 августа 2020 года.
  6. ↑ Мах Э.  Механика. Историко-критический очерк её развития. — Ижевск: «РХД», 2000. — С. 252. — 456 с. — ISBN 5-89806-023-5.
  7. ↑ Judith P. Zinsser. Emilie Du Châtelet : daring genius of the Enlightenment. — New York: Penguin Books, 2007. — viii, 376 pages, 16 unnumbered pages of plates с. — ISBN 0-14-311268-6, 978-0-14-311268-6.
  8. ↑ Crosbie Smith. Energy and empire : a biographical study of Lord Kelvin. — Cambridge [Cambridgeshire]: Cambridge University Press, 1989. — xxvi, 866 pages с. — ISBN 0-521-26173-2, 978-0-521-26173-9. Архивировано 25 января 2022 года.
  9. ↑ John Theodore Merz. A history of European thought in the nineteenth century. — Gloucester, Mass.: Peter Smith, 1976. — 4 volumes с. — ISBN 0-8446-2579-5, 978-0-8446-2579-9.
  10. ↑ William John Macquorn Rankine. XVIII. On the general law of the transformation of energy // The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. — 1853-02. — Т. 5, вып. 30. — С. 106–117. — ISSN 1941-5990 1941-5982, 1941-5990. — doi:10.1080/14786445308647205.
  11. ↑ W.J. Macquorn Rankine. XIII. On the phrase “Potential energy,” and on the definitions of physical quantities // The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. — 1867-02. — Т. 33, вып. 221. — С. 88–92. — ISSN 1941-5990 1941-5982, 1941-5990. — doi:10.1080/14786446708639753.
  12. ↑ Голубева О. В. Теоретическая механика. — М.: «Высшая школа», 1968. — С. 243—245. Архивировано 23 августа 2017 года.
  13. ↑ 1 2 Монин А. С., Яглом А. М. Статистическая гидромеханика. Часть 1. — М.: Наука, 1965. — 639 с.
  14. ↑ Блохинцев Д. И. Основы квантовой механики Архивная копия от 15 февраля 2022 на Wayback Machine, 5-е изд. Наука, 1976. — 664 с., см. § 26.
  15. ↑ Айзерман, 1980, с. 54.
  16. ↑ Сорокин В. С. «Закон сохранения движения и мера движения в физике» Архивная копия от 1 января 2015 на Wayback Machine // УФН, 59, с. 325—362, (1956)

Литература[править | править код]

  • Айзерман М. А. Классическая механика. — М.: Наука, 1980. — 368 с.
  • Фриш С. Э. Курс общей физики. В 3-х тт. Т.1. Физические основы механики. Молекулярная физика. Колебания и волны. 13-е изд. — СПб.: Лань, 2010. — 480 с. — ISBN 978-5-8114-0663-0.
  • Сивухин Д. В. Общий курс физики. Т. 1. Механика. 5-е изд. — М.: Физматлит, 2006. — 560 с. — ISBN 5-9221-0715-1.
Источник

На
прошлом уроке мы с вами узнали, что скалярная физическая величина, которая
характеризует процесс перемещения тела под действием силы и равная произведению
модуля силы на модуль перемещения и на косинус угла между ними, называется механической
работой.

Также
мы упоминали о том, что величиной, характеризующей способность системы
совершить работу и являющейся функцией состояния системы, является механическая
энергия.

Давайте
с вами вспомним, как энергия тела зависит от его скорости. Пусть у нас есть
материальная точка массой т, совершающая некоторое перемещение под
действием постоянной силы, направленной вдоль перемещения.

Выберем
координатную ось ОХ так, чтобы её положительное направление совпадало с
направлением векторов силы и перемещения.

Теперь
вспомним, что согласно второму закону Ньютона единственным результатом действия
этой силы будет сообщение материальной точке ускорения:

Проще
говоря, действующая сила изменяет скорость точки. Кроме того, как мы уже знаем,
она будет совершать работу. Тогда логично предположить, что есть некая связь
между работой силы и изменением скорости тела. Учитывая, что в выбранной
системе координат модуль перемещения точки равен изменению её координаты,
запишем формулу для определения работы силы:

Так
как точка движется с ускорением, то изменение её координаты при переходе из
начального положения в конечное можно найти по известной формуле из
кинематики: 

Теперь
подставим выражения для силы и изменения координаты точки в формулу для работы:

Сократив
ускорение и выполнив почленное умножение, получим формулу, связывающую работу
равнодействующей силы с изменением величины «Эм Вэ квадрат, пополам».

Из
курса физики седьмого класса вам должно быть известно, что физическая
величина, равная половине произведения массы материальной точки на квадрат её
скорости, называется кинетической энергией. Ей обладают любые движущиеся
тела.

Как
видно из формулы, кинетическая энергия тела — величина скалярная, которая
зависит от модуля скорости тела, но не зависит от её направления.

Давайте
перепишем уравнение для работы силы с учётом введённых обозначений:

Полученная
нами формула выражает математическую запись теоремы об изменении
кинетической энергии: изменение кинетической энергии материальной точки при её
перемещении равно работе равнодействующей всех сил, действующих на неё.

Эта
теорема справедлива для любых сил, действующих на материальную точку: будь то
сила упругости, сила трения или сила тяжести.

Из
теоремы следует, что изменение кинетической энергии зависит только от скорости
точки в начальном и конечном положениях. При этом неважно, каким образом изменялась
скорость и под действием каких сил это изменение происходило.

Отметим,
что если начальная скорость точки в какой-либо инерциальной системе отсчёта
равна нулю, то её кинетическая энергия будет равна работе, которую необходимо
совершить, чтобы покоящейся точке сообщить скорость. А поскольку скорость
тела зависит от выбора инерциальной системы отсчёта, то и кинетическая энергия
также зависит от выбора системы отсчёта. Так, например, для водителя, сидящего
неподвижно относительно машины, она равна нулю в системе отсчёта, связанной с
машиной, и отлична от нуля в системе отсчёта, связанной с Землёй.

Теперь
давайте проделаем такой опыт. Возьмём гирю известной массы и с помощью
невесомой и нерастяжимой нити равномерно поднимем её на некоторую высоту h
над поверхностью стола. Очевидно, что в этом случае сила натяжения нити, равная
по модулю силе тяжести, действующей на гирю, совершила работу:

Теперь,
с помощью неподвижного блока и нити соединим гирю с цилиндром, примерно такой
же массы, что и гиря. Что произойдёт, если отпустить гирю? Правильно, она
вернётся на прежний уровень, а цилиндр при этом поднимется. А за счёт чего
совершилась работа по подъёму цилиндра? Скорее всего, за счёт работы силы, с
которой Земля притягивает к себе гирю. Значит, способность совершать работу по
подъёму цилиндра приобрела не гиря сама по себе, а силы взаимодействия системы
«гиря — Земля». Мерой этой способности является физическая величина, называемая
потенциальной энергией.

Таким
образом, потенциальная энергия — это количественная мера способности сил
взаимодействия механической системы совершать работу.

Термин
«потенциальная энергия» впервые был введён в XIX
веке шотландским физиком Уильямом Джоном Ранкином.

В
механике принято выделять два вида потенциальной энергии: это потенциальная
энергия тела в гравитационном поле Земли и потенциальная энергия упруго
деформированного тела.

Потенциальная
энергия тела в поле тяготения — это энергия, обусловленная взаимодействием тела
с Землёй и равная произведению массы тела на ускорение свободного падения и на
высоту тела над поверхностью Земли:

Из
определения следует, что потенциальная энергия тела в поле тяготения Земли
зависит от их взаимного расположения. Однако стоит отметить, что записанная
нами формула справедлива только для материальных точек. Во всех остальных
случаях под высотой следует понимать высоту, на которой находится центр тяжести
тела. При этом его высота должна быть намного меньше радиуса Земли.

Потенциальная
энергия упруго деформированного тела — это энергия, обусловленная
взаимодействием частей одного и того же тела. Она равна половине произведения
коэффициента упругости тела на квадрат его удлинения или сжатия:

Последние
наши две формулы хоть и описывают одну и ту же физическую величину, но
отличаются друг от друга. Это связано с тем, что сила тяжести в данном месте
Земли является величиной постоянной. А вот сила упругости при деформировании
тела линейно меняется.

Обобщив
две формулировки потенциальной энергии для тела, находящегося в поле тяготения,
и упруго деформированного тела, можно сказать, что потенциальная энергия —
это энергия системы, определяемая взаимным расположением тел или частей тела
друг относительно друга и характером сил взаимодействия между ними.

Источник

Кинетическая энергия


Кинетическая энергия

4.4

Средняя оценка: 4.4

Всего получено оценок: 68.

4.4

Средняя оценка: 4.4

Всего получено оценок: 68.

Если система может совершить работу, то говорят, что она обладает энергией. Энергия — важная характеристика системы. Она не может исчезать и появляться, но имеет несколько видов и может переходить из одного вида в другой. Одним из таких видов является кинетическая энергия. В статье дадим определение этого понятия, выведем формулу кинетической энергии.

Формула кинетической энергии

Совершение работы в механике означает, что некоторая сила действует на материальную точку и перемещает ее. Согласно второму закону Ньютона материальная точка при этом получает некоторое ускорение, и ее скорость меняется.

Рис. 1. Второй закон Ньютона.

Из кинематики известно, что если точка на пути $S$ двигалась с ускорением $a$, то ее начальная скорость $v_0$ и конечная $v$ связаны следующим соотношением:

$$v^2=v_0^2+2aS$$

Поскольку на всём пути ускорение материальной точки постоянно, то и сила, действующая на точку, также постоянна. Для нахождения работы, которую совершила эта сила, необходимо величину силы $F$ умножить на путь $S$, найденный из этой формулы. Получаем:

$$A={Fover a}{v^2-v_0^2over 2}$$

По второму закону Ньютона ${Fover a}=m$. Подставляя это соотношение в формулу работы, получаем:

$$A={mv^2over 2}-{mv_0^2over 2}$$

Из этой формулы видно, что работа, произведенная силой, равна разности двух величин, формулы которых различаются только скоростью. То есть эти величины характеризуют способность материальной точки совершать работу при изменении скорости, а значит, являются выражением энергии.

Величину, равную половине произведения массы на квадрат скорости материальной точки, называют кинетической энергией материальной точки. Формула кинетической энергии (обозначение — латинская буква $Е$):

$$E={mv^2over 2}$$

Кинетическая энергия тела имеет те же единицы измерения, что и работа, — Джоуль (Дж).

Кинетическая энергия

Рис. 2. Кинетическая энергия.

Свойства кинетической энергии

Если выписать в таблицу значения кинетической энергии движущейся материальной точки в разные моменты и работу, совершенную силой при этом, можно доказать теорему об изменении кинетической энергии.

Изменение кинетической энергии материальной точки за некоторое время равно работе, совершенной за это время силой, действующей на точку.

Таким образом, если работа силы положительна, то кинетическая энергия тела увеличивается, а если отрицательна — то уменьшается. Энергия, которой обладает движущаяся материальная точка, равна работе, которую надо совершить, чтобы разогнать ее от нуля до имеющейся скорости.

Важным свойством кинетической энергии является ее относительность. Действительно, скорость — величина, зависящая от системы отсчета. Следовательно, можно сделать вывод, что и кинетическая энергия в разных системах отсчета будет различной. К примеру, для внешнего наблюдателя движущийся автомобиль имеет большую кинетическую энергию, а для пассажира этого автомобиля его энергия равна нулю.

Если в системе имеется несколько независимых движущихся тел, то полная кинетическая энергия системы равна сумме кинетических энергий составляющих.

Рис. 3. Кинетическая энергия системы тел.

Еще одним свойством кинетической энергии является независимость от ее причины и источника. Движущееся тело будет обладать равной кинетической энергией независимо от того, что послужило причиной движения — то ли гравитационные силы, то ли силы упругости пружины, то ли внутренняя энергия топлива. Кинетическая энергия тела всегда будет зависеть только от его массы и скорости.

Заключение

Что мы узнали?

Кинетическая энергия материальной точки — это величина, равная половине произведения массы точки на квадрат ее скорости. Изменение кинетической энергии материальной точки за некоторое время равно работе, совершенной за это время силой, действующей на точку.

Тест по теме

Доска почёта

Доска почёта

Чтобы попасть сюда – пройдите тест.

  • Карим Шаяхметов

    10/10

Оценка доклада

4.4

Средняя оценка: 4.4

Всего получено оценок: 68.

А какая ваша оценка?

Источник

Содержание:

Кинетическая энергия:

Иногда значение работы можно найти, не используя понятия силы и перемещения, на основании характеристики изменения энергии тела.

Рассмотрим тело массой m, на которое действует сила F. Направление действия силы совпадает с направлением перемещения. Работа, которую выполняет эта сила,

A = Fs.
Согласно второму закону механики Ньютона значение силы 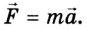Кинетическая энергия в физике - формулы и определения с примерами

Как известно, модуль перемещения равен:

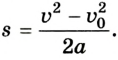
Кинетическая энергия в физике - формулы и определения с примерами

Поэтому 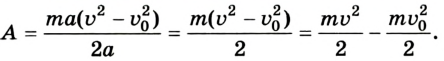Кинетическая энергия в физике - формулы и определения с примерами

Как известно, выражение 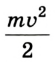Кинетическая энергия в физике - формулы и определения с примерами называется кинетической энергией. Следовательно, для расчета работы достаточно определить только массу тела и его начальную и конечную скорости, т. е. знать изменение кинетической энергии тела. Такой метод удобен, поскольку им можно пользоваться даже в случае переменной силы и произвольной траектории.

Физическая величина, описывающая состояние движущегося тела и изменение которой определяет работу, называется кинетической энергией.

Для измерения энергии, как и работы, используется единица джоуль (Дж), названная в честь английского ученого Д. Джоуля.

Кинетической энергией обладает тело, движущееся в данной системе отсчета с определенной скоростью: 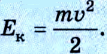Кинетическая энергия в физике - формулы и определения с примерами
Скорость тела, измеренная в разных системах отсчета, будет иметь разное значение, т. е. она является относительной величиной. Поэтому кинетическая энергия тела постоянной массы тоже величина относительная и в разных системах отсчета имеет разное значение.

Рассмотрим, например, два железнодорожных вагона, массы которых составляют по 2 • 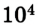Кинетическая энергия в физике - формулы и определения с примерами кг, движущиеся в одном направлении со скоростями 15 м/с и 10 м/с относительно железнодорожного полотна, причем первый догоняет второго. Их кинетическая энергия соответственно будет:

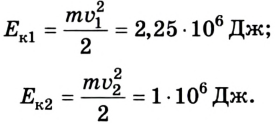
Кинетическая энергия в физике - формулы и определения с примерами

Если же систему отсчета связать со вторым вагоном, то первый будет двигаться со скоростью 5 м/с , а второй – со скоростью v = 0. В этом случае

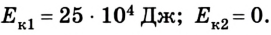
Кинетическая энергия в физике - формулы и определения с примерами

Следовательно, при расчетах в разных инерциальных системах отсчета следует учитывать, что кинетическая энергия в случае перехода из одной системы в другую будет изменяться.

Что такое кинетическая энергия

Кинетическая энергия (от греческого слова кинетикос – тот, что приводит в движение) – это энергия, которой тело обладает вследствие собственного движения.

Кинетической энергией обладает ветер, её используют для сообщения движения ветряным двигателям. Движущиеся массы воздуха оказывают давление на наклонные плоскости крыльев ветряных двигателей и заставляют их вращаться. На рисунке 175, а изображена ветряная мельница, в которой за счёт энергии ветра мелют зерно. Современные довольно мощные ветряные двигатели (рис. 175, б) используют для того, чтобы вырабатывать электроэнергию, качать из скважин воду и подавать её в водонапорные башни.

Движущаяся вода или нагретый пар, вращая турбины электростанции, теряет часть своей кинетической энергии и выполняет работу. Самолёт, летящий высоко в небе, кроме потенциальной обладает и кинетическуй энергией. Если тело находится в состоянии покоя, т. е. его скорость относительно Земли равна нулю, то и его кинетическая энергия относительно Земли будет равна нулю.

Опытами установлено, что чем больше масса тела и скорость, с которой оно движется, тем больше его кинетическая энергия. Выявленная зависимость математически выражается такой формулой: 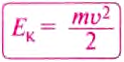Кинетическая энергия в физике - формулы и определения с примерами

где 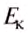Кинетическая энергия в физике - формулы и определения с примерами — кинетическая энергия тела; 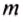Кинетическая энергия в физике - формулы и определения с примерами — масса тела; 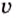Кинетическая энергия в физике - формулы и определения с примерами— скорость движения тела.

Определение кинетической энергии

Наблюдения явлений природы показывают, что работа может выполняться при движении тел. Так, движущийся тепловоз, стыкуясь с вагоном, перемещает его на некоторое расстояние. Выполняется работа и в том случае, когда брошенный камень разбивает лед. Выстреленная из ружья пуля пробивает доску и т. п. Если потенциальной энергией обладают тела, на которые действует сила, то в упомянутых выше случаях работа выполняется потому, что они осуществляли перемещение, двигались.

Какой энергией обладают движущиеся тела

Энергию движущегося тела называют кинетической энергией. 

Кинетическая энергия является физической величиной ее значение можно рассчитывать. Для этого необходимо знать, от каких физических величин она зависит.

Как рассчитывают кинетическую энергию

Поставим желоб под некоторым углом к поверхности стола. На некотором расстоянии от его нижнего конца поставим брусок. На средней части желоба разместим маленький стальной шарик и отпустим его. Скатившись по желобу, шарик ударится о брусок и переместит его на некоторое расстояние. Отметим расстояние, на которое сместился брусок.

Поместим шарик в верхней части желоба и отпустим его. В этом случае, скатившись желобом к основе, шарик приобрел большую скорость, чем раньше. Ударившись в брусок, он переместит его на большее расстояние, чем в предыдущем опыте, соответственно выполнив большую работу.

Таким образом, кинетическая энергия тела зависит от его скорости. Эта зависимость нелинейная, что заметно на графике зависимости кинетической энергии тела от его скорости. График имеет вид кривой линии (рис. 126).

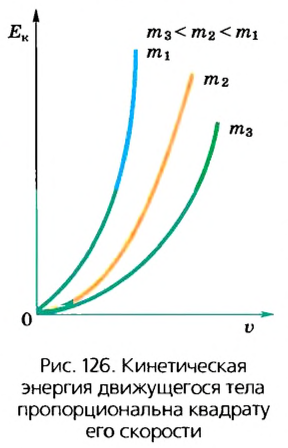
Кинетическая энергия в физике - формулы и определения с примерами

Кинетическая энергия тела относительна

Как известно, скорость тела является относительной величиной и зависит от выбора тела отсчета. Поэтому и кинетическая энергия является величиной относительной. Если артиллерийский снаряд, попав в стену, причиняет значительные разрушения, то снаряд, посланный вдогонку сверхзвуковому самолету, не причинит ему существенных повреждений, поскольку скорость снаряда относительно самолета будет небольшой.

Последствия столкновения автомобилей в случае их движения навстречу друг другу будут всегда более ощутимы, чем тогда, когда один автомобиль догоняет другой.

Кинетическая энергия зависит и от массы тела. Если повторим предыдущие опыты с шариком большей массы, то увидим, что перемещения бруска в этом случае будет большим. Эта зависимость линейная, поэтому можно сказать, что кинетическая энергия тела пропорциональна его массе (рис. 127).

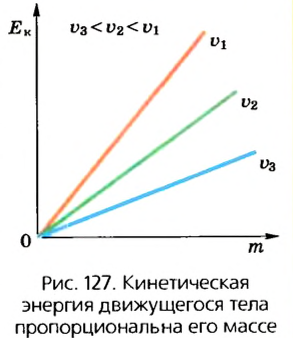
Кинетическая энергия в физике - формулы и определения с примерами

Как рассчитать кинетическую энергию

Чтобы рассчитать кинетическую энергию, используют формулу:

Кинетическая энергия в физике - формулы и определения с примерами

где Кинетическая энергия в физике - формулы и определения с примерами — масса тела; Кинетическая энергия в физике - формулы и определения с примерами — скорость тела.

Кинетическая энергия разных физических тел используется для выполнения механической работы. Так, опытные водители автомобилей время от времени отсоединяют двигатель от колес, выключая сцепление, и этим экономят топливо. Работа по преодолению сил трения выполняется за счет кинетической энергии автомобиля. Конструкторы работают над моделью городского автобуса, который начинает движение за счет энергии раскрученного во время стоянки большого маховика. Это дает возможность существенно уменьшить выбросы вредных газов в атмосферу и экономить топливо.

В южных областях Украины, в частности на Крымском полуострове, используют ветряные электростанции, которые работают за счет кинетической энергии потоков воздуха — ветра (рис. 128).

Кинетическая энергия в физике - формулы и определения с примерами

  • Заказать решение задач по физике

Кинетическая энергия тела

Рассмотрим движение тела массой т под действием нескольких сил, например движение санок (см. рис. 124). Предположим также, что сила натяжения веревок постоянна, а следовательно, постоянной будет и результирующая сила 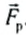Кинетическая энергия в физике - формулы и определения с примерами. Она совпадает по направлению с перемещением тела или противоположна ему. Эта сила, естественно, вызывает ускорение санок, т. е. изменяет их скорость. Кроме того, она совершает работу. Следовательно, между работой результирующей силы и изменением скорости санок должна существовать связь.

Рассмотрим случай, когда проекция результирующей силы на направление движения положительна, т. е. санки движутся равноускоренно с ускорением а, которое находится из второго закона Ньютона:
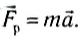Кинетическая энергия в физике - формулы и определения с примерами    (1)

Работа результирующей силы:
A = Fp△r,    (2)
где △r— модуль перемещения тела за некоторый промежуток времени. Подставим выражение (1) в (2). В результате получим:
A = ma△r.    (3)

При равноускоренном одномерном движении модуль перемещения △r и изменение скорости связаны соотношением:
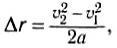Кинетическая энергия в физике - формулы и определения с примерами    (4)
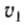где Кинетическая энергия в физике - формулы и определения с примерами и Кинетическая энергия в физике - формулы и определения с примерами 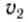— начальная и конечная скорости тела, которое совершило перемещение △r с ускорением а.

Соотношение (3) с учетом (4) примет вид:
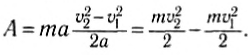Кинетическая энергия в физике - формулы и определения с примерами    (5) 

Полученная формула связывает работу результирующей силы, действующей на тело, с изменением величины 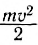Кинетическая энергия в физике - формулы и определения с примерами. Эта величина называется кинетической энергией тела и обычно обозначается К.
Кинетическая энергия тела — это энергия движения. Она равна половине произведения массы тела на квадрат его скорости:
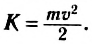Кинетическая энергия в физике - формулы и определения с примерами      (6)

Тогда формула (5) примет вид:
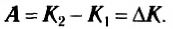Кинетическая энергия в физике - формулы и определения с примерами      (7)

Итак, работа результирующей силы, действующей на тело, равна изменению кинетической энергии тела. Как вы уже знаете, изменение какой-то величины равно разности конечного значения и начального. Из формулы (7) очевидно следует, что кинетическая энергия выражается в тех же единицах, что и работа, т. е. в СИ в джоулях.

Когда результирующая сила действует по направлению движения тела и, следовательно, совершает положительную работу, то K2>K1. Это означает, что кинетическая энергия тела увеличивается. Понятно, что, если результирующая сила направлена в сторону, противоположную движению, она совершает отрицательную работу, и кинетическая энергия тела уменьшается. Следует отметить, что, хотя мы получили формулу (7) для частного случая равноускоренного и прямолинейного движения, она справедлива и в случае изменяющейся во времени результирующей силы. Поэтому формулу (7) часто называют теоремой о кинетической энергии.

Итак, любое движущееся тело (рис. 127, 128) обладает кинетической энергией. Поскольку скорость тела зависит от выбора инерциальной системы отсчета, то и кинетическая энергия также зависит от выбора системы отсчета. Очевидно, что, как и работа, кинетическая энергия является скалярной физической величиной. Она не зависит от направления движения тела, а определяется его массой и квадратом скорости.

Главные выводы:

  1. Кинетическая энергия тела — это энергия движения. Она равна половине произведения массы тела на квадрат его скорости и зависит от выбора системы отсчета.
  2. Изменение кинетической энергии равно работе всех сил, действующих на тело.
  3. Кинетическая энергия измеряется в тех же единицах, что и работа.
  • Закон сохранения и превращения механической энергии
  • Работа, мощность и энергия
  • Движение и силы
  • Давление в физике
  • Взаимодействие тел
  • Механическая энергия и работа
  • Золотое правило механики
  • Потенциальная энергия
Источник

Добавить комментарий