Средняя кинетическая энергия хаотического движения молекул


4.5
Средняя оценка: 4.5
Всего получено оценок: 83.
4.5
Средняя оценка: 4.5
Всего получено оценок: 83.
Согласно молекулярно-кинетической теории в неподвижном теле, находящемся в состоянии механического покоя, молекулы и атомы находятся в постоянном хаотическом (несогласованном) движении. Кинетическая энергия молекул, движущихся внутри вещества, определяет то, что все называют температурой вещества. Можно ли, зная температуру, найти кинетическую энергию хаотического теплового движения молекул?
Кинетическая энергия движущейся частицы
Формула для кинетической энергии Ек движущегося со скоростью v тела массой m была получена в разделе механики. Это соотношение справедливо не только для поведения тел видимых размеров, но и для микрочастиц (молекул, атомов, электронов и т.п.):
$Ек = {m * v^2over 2}$ (1),
Полная кинетическая энергию вещества Епк получается сложением энергий всех отдельных частиц:
$Е^п_к = Е_1+ Е_2 + Е_3 +…. Е_N$ (2),
где N — полное число частиц в веществе.

Найти суммарную кинетическую энергию всего вещества с помощью формул (1) и (2), конечно, невозможно: ведь для этого необходимо знать массы и скорости всех частиц, а также их общее количество. Если учесть, что только в одном моле вещества находится огромное число молекул (6,023*1023!), то становится понятно, что для решения этой задачи требуется другой подход.
Наблюдениями и исследованиями процессов передачи тепла ученые занимались задолго до нахождения формул молекулярно-кинетической теории. Для того чтобы придать понятиям “теплый”, “холодный” и т.п. более четкий, числовой вид, были изобретены термометры. Один из первых термометров придумал знаменитый Галилео Галилей, живший в Италии с 1564 г. по 1642 г.
Эксперименты показывали, что чем горячее вещество, тем быстрее (“энергичнее”) двигаются частицы. После изобретения микроскопа появилась возможность визуально наблюдать броуновское движение частиц, которые начинали перемещаться быстрее при нагревании.
Оказывается в 1 см3 при 00С и 760 мм.рт.ст. находится 2,7*1019 молекул. Чтобы ощутить насколько велико это число приведем такой пример. Предположим, что газ удаляется из крохотного сосуда объемом 1 см3 с такой скоростью, что в каждую секунду “убегает” миллион молекул. Нетрудно подсчитать, что сосуд опустеет через миллион лет!
Молекулярно-кинетический подход
Уже к середине ХIX века стало понятно, что пытаться описывать движение каждого атома — дело безнадежное, т.к. ни один прибор не сможет отследить все молекулы и атомы. Вместо такого, “лобового”, подхода системы, состоящие из большого числа частиц стали рассматривать, не пытаясь учесть свойства отдельных атомов, а усредняя эти свойства по большой их совокупности.
В 1859 г. английский физик Максвелл с помощью такого подхода получил для давления p одноатомного газа формулу:
$p = {1over 3} * n * m * v^2_c$ (3),
где: n — концентрация молекул, m — масса молекул, v2c = <v2>ср — среднее арифметическое квадратов скоростей молекул.
Температура вещества — мера кинетической энергии
Ранее для идеального газа был открыт закон Клапейрона-Менделеева, связавший в единое уравнение такие физические параметры, как давление p, объем V и температуру T (по шкале Кельвина):
$p * V = {mover μ} * R * T$ (4),
где:
μ — молярная масса газа, R = 8,3157 джоуль/моль/градус — универсальная газовая постоянная.
В то же время газовая постоянная R равна:
$R = k * N_a$ (5),
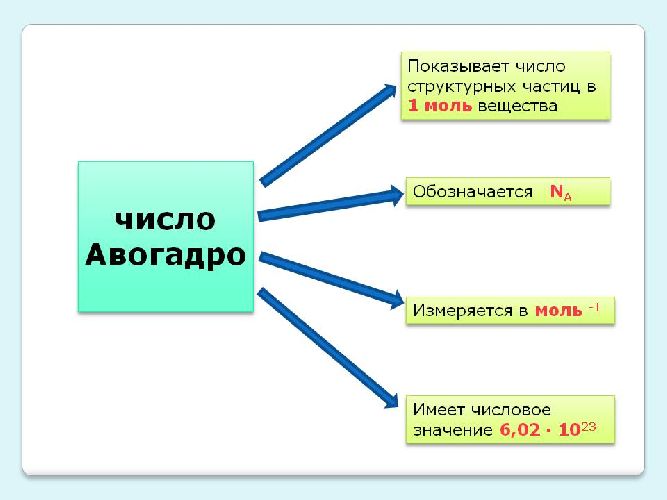
где: k =1,38*10-23 Дж/К — постоянная Больцмана, Na — число Авогадро.
Тогда, подставив в уравнение (4) R из уравнения (5), разделив обе части уравнения (4) на объем V и воспользовавшись тем, что:
${mover μ} * {Naover V } = n$ — концентрация молекул, получим из формулы (4) выражение для давления в виде:
$p = n * k * T$ (6).
Из формул для величины давления p (3) и (6) получаем:
$p = {1over 3} * n * m * v^2_c = n * k * T$ (7).
Далее, сократив обе части уравнения на n, и умножив обе части на 3/2, получим:
${m * v^2over 2} = { 3 over 2} * k * T$ (8).
В левой части уравнения, пользуясь формулой (1), получаем выражение для средней кинетической энергии хаотического движения молекул:
$Е_к = { 3 over 2} * k * T$ (9).
Последняя формула (9) демонстрирует, что температура является мерой кинетической энергии молекул. Если газ одноатомный, то вся его энергия — это энергия поступательного движения.
Из формулы (9) следует еще один важный вывод: средняя кинетическая энергия поступательного движения для разных газов будет одинаковой не зависимо от массы молекул, и будет зависеть только от величины температуры.

Что мы узнали?
Итак, мы узнали что суммарная кинетическая энергия вещества складывается из кинетических энергий отдельных частиц. Кинетическая энергия движения частиц, усредненная по их числу, определяет температуру вещества. С помощью уравнения Менделеева-Клапейрона (4) и формулы для давления (3) получили соотношение, связывающее среднюю кинетическую энергию хаотического движения молекул с температурой вещества T.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Кристина Тараканова
11/11
Оценка доклада
4.5
Средняя оценка: 4.5
Всего получено оценок: 83.
А какая ваша оценка?
Согласно молекулярно-кинетической теории в неподвижном теле, находящемся в состоянии механического покоя, молекулы и атомы находятся в постоянном хаотическом (несогласованном) движении. Кинетическая энергия молекул, движущихся внутри вещества, определяет то, что все называют температурой вещества. Можно ли, зная температуру, найти кинетическую энергию хаотического теплового движения молекул?

Содержание
- Кинетическая энергия движущейся частицы
- Молекулярно-кинетический подход
- Температура вещества — мера кинетической энергии
- Что мы узнали?
Кинетическая энергия движущейся частицы
Формула для кинетической энергии Ек движущегося со скоростью v тела массой m была получена в разделе механики. Это соотношение справедливо не только для поведения тел видимых размеров, но и для микрочастиц (молекул, атомов, электронов и т.п.):
$Ек = {m * v^2over 2}$ (1),
Полная кинетическая энергию вещества Епк получается сложением энергий всех отдельных частиц:
$Е^п_к = Е_1+ Е_2 + Е_3 +…. Е_N$ (2),
где N — полное число частиц в веществе.

Рис. 1. Хаотически движущиеся с разными скоростями молекулы в веществе.
Найти суммарную кинетическую энергию всего вещества с помощью формул (1) и (2), конечно, невозможно: ведь для этого необходимо знать массы и скорости всех частиц, а также их общее количество. Если учесть, что только в одном моле вещества находится огромное число молекул (6,023*1023!), то становится понятно, что для решения этой задачи требуется другой подход.
Наблюдениями и исследованиями процессов передачи тепла ученые занимались задолго до нахождения формул молекулярно-кинетической теории. Для того чтобы придать понятиям “теплый”, “холодный” и т.п. более четкий, числовой вид, были изобретены термометры. Один из первых термометров придумал знаменитый Галилео Галилей, живший в Италии с 1564 г. по 1642 г.
Эксперименты показывали, что чем горячее вещество, тем быстрее (“энергичнее”) двигаются частицы. После изобретения микроскопа появилась возможность визуально наблюдать броуновское движение частиц, которые начинали перемещаться быстрее при нагревании.
Оказывается в 1 см3 при 00С и 760 мм.рт.ст. находится 2,7*1019 молекул. Чтобы ощутить насколько велико это число приведем такой пример. Предположим, что газ удаляется из крохотного сосуда объемом 1 см3 с такой скоростью, что в каждую секунду “убегает” миллион молекул. Нетрудно подсчитать, что сосуд опустеет через миллион лет!
Молекулярно-кинетический подход
Уже к середине ХIX века стало понятно, что пытаться описывать движение каждого атома — дело безнадежное, т.к. ни один прибор не сможет отследить все молекулы и атомы. Вместо такого, “лобового”, подхода системы, состоящие из большого числа частиц стали рассматривать, не пытаясь учесть свойства отдельных атомов, а усредняя эти свойства по большой их совокупности.
В 1859 г. английский физик Максвелл с помощью такого подхода получил для давления p одноатомного газа формулу:
$p = {1over 3} * n * m * v^2_c$ (3),
где: n — концентрация молекул, m — масса молекул, v2c = <v2>ср — среднее арифметическое квадратов скоростей молекул.
Температура вещества — мера кинетической энергии
Ранее для идеального газа был открыт закон Клапейрона-Менделеева, связавший в единое уравнение такие физические параметры, как давление p, объем V и температуру T (по шкале Кельвина):
$p * V = {mover μ} * R * T$ (4),
где:
μ — молярная масса газа, R = 8,3157 джоуль/моль/градус — универсальная газовая постоянная.

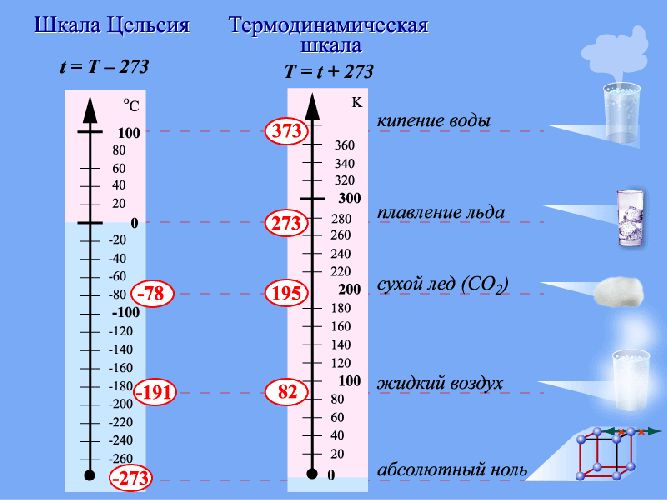
Рис. 2. Температуры по шкалам Кельвина и Цельсия.
В то же время газовая постоянная R равна:
$R = k * N_a$ (5),
где: k =1,38*10-23 Дж/К — постоянная Больцмана, Na — число Авогадро.

Рис. 3. Число Авогадро.
Тогда, подставив в уравнение (4) R из уравнения (5), разделив обе части уравнения (4) на объем V и воспользовавшись тем, что:
${mover μ} * {Naover V } = n$ — концентрация молекул, получим из формулы (4) выражение для давления в виде:
$p = n * k * T$ (6).
Из формул для величины давления p (3) и (6) получаем:
$p = {1over 3} * n * m * v^2_c = n * k * T$ (7).
Далее, сократив обе части уравнения на n, и умножив обе части на 3/2, получим:
${m * v^2over 2} = { 3 over 2} * k * T$ (8).
В левой части уравнения, пользуясь формулой (1), получаем выражение для средней кинетической энергии хаотического движения молекул:
$Е_к = { 3 over 2} * k * T$ (9).
Последняя формула (9) демонстрирует, что температура является мерой кинетической энергии молекул. Если газ одноатомный, то вся его энергия — это энергия поступательного движения.
Из формулы (9) следует еще один важный вывод: средняя кинетическая энергия поступательного движения для разных газов будет одинаковой не зависимо от массы молекул, и будет зависеть только от величины температуры.
Что мы узнали?
Итак, мы узнали что суммарная кинетическая энергия вещества складывается из кинетических энергий отдельных частиц. Кинетическая энергия движения частиц, усредненная по их числу, определяет температуру вещества. С помощью уравнения Менделеева-Клапейрона (4) и формулы для давления (3) получили соотношение, связывающее среднюю кинетическую энергию хаотического движения молекул с температурой вещества T.
Предыдущая
ФизикаТретий закон Ньютона – формула и определение, как направлены силы
Следующая
ФизикаРабота силы упругости – формула, измерение, определение
Физика, 10 класс
Урок №19. Температура. Энергия теплового движения молекул
На уроке рассматриваются понятия: температура и тепловое равновесие; шкалы Цельсия и Кельвина; абсолютная температура как мера средней кинетической энергии теплового движения частиц вещества, зависимость давления от концентрации молекул и температуры.
Глоссарий по теме:
Макроскопические параметры – величины объём V, давление p и температура t, характеризующие состояние макроскопических тел без учёта их молекулярного строения.
Температура характеризует степень нагретости тела (холодное, тёплое, горячее).
Температура (от лат. temperatura — надлежащее смешение, соразмерность, нормальное состояние) – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.
Тепловым равновесием называют – такое состояние тел, при котором температура во всех точках системы одинакова.
Тепловым или термодинамическим равновесием, изолированной системы тел, называют состояние, при котором все макроскопические параметры в системе остаются неизменными.
Термометр — это прибор для измерения температуры путём контакта с исследуемым телом. Различают жидкостные, газовые термометры, термопары, термометры сопротивления.
Абсолютная температура Т прямо пропорциональна температуре Θ (тета), выражаемой в энергетических единицах (Дж).
Абсолютный нуль – предельная температура, при которой давление идеального газа обращается в нуль при фиксированном объёме или объём идеального газа стремится к нулю при неизменном давлении.
Абсолютный нуль – температура, при которой прекращается тепловое движение молекул.
Абсолютная шкала температур (Шкала Кельвина) – здесь нулевая температура соответствует абсолютному нулю, а каждая единица температуры равна градусу по шкале Цельсия.
Кельвин – единица абсолютной температуры в Международной системе измерений (СИ).
Постоянная Больцмана – коэффициент , связывает температуру Θ энергетических единицах (Дж) с абсолютной температурой Т (К).
, связывает температуру Θ энергетических единицах (Дж) с абсолютной температурой Т (К).
Абсолютная температура есть мера средней кинетической энергии молекул.
Давление газа прямо пропорционально концентрации его молекул и абсолютной температуре Т.
Закон Авогадро – в равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул
Обязательная литература:
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 195 – 203.
Дополнительная литература:
- Смородинский Я.А. Температура. – 3-е издание. – М.: Бюро Квантум, 2007. (Библиотечка «Квант». Вып. 103. Приложение к журналу «Квант» № 5/2007.) С. 5— 25.
- Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. – С. 111-115.
- Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. – С. 65 – 67.
- Орлов В.А., Сауров Ю.А. Практика решения физических задач. 10-11классы. – М.: Вентана-Граф, 2014. – С. 98-99.
- http://kvant.mccme.ru/1991/09/idealnyj_gaz_-_universalnaya_f.htm
Теоретический материал для самостоятельного изучения
Измеряя расположение звёзд на небе, расстояния на земле, время, люди знали, для чего они это делают и изобретали, телескопы, часы, прототипы современных линеек. О температуре такого же сказать было нельзя. О том, что такое тепловое равновесие и что означает степень нагрева тела (температура), существовали разные мнения. Но человек с незапамятных времен точно знал, что, когда два тела плотно соприкасаются, между ними устанавливается, выражаясь современным языком, тепловое равновесие.
Любое макроскопическое тело или группа макроскопических тел при неизменных внешних условиях самопроизвольно переходят в состояние теплового равновесия.
Тепловым равновесием называют такое состояние тел, при котором температура во всех точках системы одинакова.
Температура (от лат. temperatura — надлежащее смешение, соразмерность, нормальное состояние) – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.
К числу характеристик состояния макроскопических тел (твёрдых тел, жидкостей, газов) и процессов изменения их состояний, относят объём, давление и температуру. Эти величины описывают в целом тела, состоящие из большого числа молекул, а не отдельные молекулы. При этом микроскопические процессы внутри тела не прекращаются при тепловом равновесии: расположения молекул всё время меняются и меняются их скорости при столкновениях.
Величины объём, давление и температуру, характеризующие состояние макроскопических тел без учёта их молекулярного строения, называют макроскопическими параметрами.
Тепловым или термодинамическим равновесием, изолированной системы тел, называют состояние, при котором все макроскопические параметры в системе остаются неизменными.
Для точной характеристики нагретости тела, необходим прибор, способный измерить температуры тел и дать возможности их сравнения.
Термометр — это прибор для измерения температуры путём контакта с исследуемым телом. Различают жидкостные, газовые термометры, термопары, термометры сопротивления.
В 1597 году Галилей создал термоскоп, в собственных сочинениях учёного нет описания этого прибора, но его ученики засвидетельствовали этот факт. Аппарат представлял собой устройство для поднятия воды при помощи нагревания.
Изобретение термометра, данные которого не зависели бы от перепадов атмосферного давления, произошли благодаря экспериментам физика Э. Торричелли, ученика Галилея.
Во всех приборах, изобретённых в XVIII веке, измерение температуры было относительно расширению столбика воды, спирта или ртути и произвольности выбора начала отсчёта, т.е. нулевой температуры. Наполняющие их вещества замерзали или кипели и этими термометрами нельзя было измерять очень низкие или очень высокие температуры. Необходимо было изобрести такую шкалу, чтобы избавиться от зависимости выбранного вещества, на основе которого формировалось градуирование.
Шкала, предложенная шведским учёным Андерсом Цельсием в 1742 г., точно устанавливала положение двух точек: 0 и 100 градусов. По шкале Цельсия температура обозначается буквой t, измеряется в градусах Цельсия (ºС).
На территории Англии и США используется шкала Фаренгейта. Такая шкала была предложена немецким учёным Даниелем Габриелем Фаренгейтом в 1724 г.: 0 °F — температура смеси снега с нашатырём или поваренною солью, 96 °F —температура здорового человеческого тела, во рту или под мышкой.
Рене Антуан де Реомюр не одобрял применения ртути в термометрах вследствие малого коэффициента расширения ртути. В 1730 году изобрёл водно-спиртовой термометр и предложил шкалу от 0 до 80°.
Шкала Реомюра очень долго использовалась на родине учёного во Франции вплоть до настоящего времени.
Различные жидкости при нагревании расширяются не одинаково. Поэтому расстояния на шкале между нулевой отметкой 0 °C и 100 °C будут разными.
Однако существует способ создать тело, которое приближенно обладает нужными качествами. Это идеальный газ. Было замечено, что в отличие от жидкостей все разряжённые газы – водород, гелий, кислород – расширяются при нагревании одинаково и одинаково меняют своё давление при изменении температуры. Это свойство газов позволяет избавиться в термометрах от одного существенного недостатка шкалы Цельсия – произвольности выбора начала отсчёта, то есть нулевой температуры.
При тепловом равновесии, если давление и объём газа массой m постоянны, то средняя кинетическая энергия молекул газа должна иметь строго определённое значение, как и температура.
Практически такую проверку произвести непосредственно невозможно, но с помощью основного уравнения молекулярно-кинетической теории её можно выразить через макроскопические параметры:

 ;
;  ;
;  ;
;  ;
; 

Если кинетическая энергия действительно одинакова для всех газов в состоянии теплового равновесия, то и значение давления р должно быть тоже одинаково для всех газов при постоянном значении отношения объёма к числу молекул. Подтвердить или опровергнуть данное предположение может только опыт.

Возьмём несколько сосудов, заполненных различными газами, например, водородом, гелием и кислородом. Сосуды имеют определённые объёмы и снабжены манометрами, для измерения давления газов в сосудах. Массы газов известны, тем самым известно число молекул в каждом сосуде. Приведём газы в состояние теплового равновесия. Для этого поместим их в тающий лёд и подождём, пока не установится тепловое равновесие и давление газов перестанет меняться.
Здесь устанавливается тепловое равновесие и все газы имеют одинаковую температуру 0 °С. При этом показания манометра показывают разное давление р, объёмы сосудов V изначально были разными и число молекул N различно, так как газы, закаченные в баллоны разные. Найдём отношение для водорода всех параметров для одного моля вещества:

Такое значение отношения произведения давления газа на его объём к числу молекул получается для всех газов при температуре тающего льда. Обозначим это отношение через Θ0 (тета нулевое):

Таким образом, предположение, что средняя кинетическая энергия, а также давление р в состоянии теплового равновесия одинаковы для всех газов, если их объёмы и количества вещества одинаковы или если отношение

Если же сосуды с газами поместить в кипящую воду при нормальном атмосферном давлении, то согласно эксперименту, отношение макроскопических параметров будет также одинаковым для всех газов, но значение будет больше предыдущего

Отсюда следует, что величина Θ растёт с повышением температуры и не зависит от других параметром, кроме температуры. Этот опытный факт позволяет рассматривать величину Θ тета как естественную меру температуры и измерять в энергетических единицах — джоулях.
А теперь вместо энергетической температуры введём температуру, которая будет измеряться в градусах. Будем считать величину тета Θ прямо пропорциональной температуре Т, где k- коэффициент пропорциональности

Так как  , то тогда
, то тогда 
По этой формуле вводится температура, которая даже теоретически не может быть отрицательной, так как все величины левой части этого равенства больше или равны нулю. Следовательно, наименьшим значением этой температуры является нуль, при любом другом параметре p, V, N равным нулю.
Предельную температуру, при которой давление идеального газа обращается в нуль при фиксированном объёме или при которой объём идеального газа стремится к нулю при неизменном давлении, называют абсолютным нулём температуры.
Тепловое движение молекул непрерывно и бесконечно, а при абсолютном нуле молекулы поступательно не двигаются. Следовательно, абсолютный нуль температур при наличии молекул вещества не может быть достигнут. Абсолютный нуль температур — это самая низкая температурная граница, верхней не существует, та «наибольшая или последняя степень холода», существование которой предсказывал М.В. Ломоносов.
В 1848 г. английскому физику Вильяму Томсону (лорд Кельвин) удалось построить абсолютную температурную шкалу (её в настоящее время называют шкалой Кельвина), которая имеет две основные точки 0 К (или абсолютный нуль) и 273К, точка в которой вода существует в трёх состояниях (в твёрдом, жидком и газообразном).
Абсолютная температурная шкала — шкала температур, в которой за начало отсчёта принят абсолютный нуль. Температура здесь обозначается буквой T и измеряется в кельвинах (К).
На шкале Цельсия, есть две основные точки: 0°С (точка, в которой тает лёд) и 100°С (кипение воды). Температура, которую определяют по шкале Цельсия, обозначается t. Шкала Цельсия имеет как положительные, так и отрицательные значения.
Из опыта мы определили значения величины Θ (тета) при 0 °С и 100 °С. Обозначим абсолютную температуру при 0 °С через Т1, а при 100 °С через Т2. Тогда согласно формуле:



Отсюда можно вычислить коэффициент k, который связывает температуру в Θ энергетических единицах (Дж) с абсолютной температурой Т (К)
k = 1,38 • 10-23 Дж/К – постоянная Больцмана.
Зная постоянную Больцмана, можно найти значение абсолютного нуля по шкале Цельсия. Для этого найдём сначала значение абсолютной температуры, соответствующее 0°С:

 значение абсолютной температуры.
значение абсолютной температуры.
Один кельвин и один градус шкалы Цельсия совпадают. Поэтому любое значение абсолютной температуры Т будет на 273 градуса выше соответствующей температуры t по Цельсию:


Теперь выведем ещё одну зависимость температуры от средней кинетической энергии молекул. Из основного уравнения молекулярно-кинетической теории и уравнения для определения абсолютной температуры


Здесь видно, что левые части этих уравнений равны, значит правые равны тоже.

Средняя кинетическая энергия хаотического поступательного движения молекул газа пропорциональна абсолютной температуре.
Абсолютная температура есть мера средней кинетической энергии движения молекул.
Из выведенных формул мы можем получить выражение, которое показывает зависимость давления газа от концентрации молекул и температуры



Из этой зависимости вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же. Отсюда следует закон Авогадро, известный нам из курса химии.
Закон Авогадро: в равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
Рассмотрим задачи тренировочного блока урока.
1. При температуре _______ (370C; 2830C; 270C) средняя кинетическая энергия поступательного движения молекул равна 6,21·10-21Дж.
Дано:

k = 1,38 • 10-23 Дж/К – постоянная Больцмана
t -?
Решение:
Запишем значение средней кинетической энергии хаотического поступательного движения молекул с зависимостью от абсолютной температуры:

Отсюда выразим Т:


Соотношение между абсолютной температурой и температурой в градусах Цельсия:

Подставим значение абсолютной температуры:

Правильный вариант ответа:
2. При температуре 290 К и давлении 0,8 МПа, средняя кинетическая энергия молекул равна __________ Дж, а концентрация составляет молекул ___________ м-3.
Дано:
Т = 290К
р = 0,8 МПа =0,8·106 Па
k = 1,38 • 10-23 Дж/К – постоянная Больцмана
Ек -? n – ?
Решение:
Значение средней кинетической энергии хаотического поступательного движения молекул:

Подставив значение абсолютной температуры, найдём ответ:

Определим концентрацию газа из соотношения:



Правильный вариант ответа: 6·10-21; 2·1026 м-3.
KeFiRo4eK
Знаток
(302),
закрыт
7 лет назад
Определите кинетическую энергию хаотического поступательного движения всех молекул любого газа в баллоне емкостью 10л и давлении 0.4*10^5 Па
Заранее спасибо!
Лучший ответ
Тугеус Владимир
Искусственный Интеллект
(174877)
10 лет назад
По уравнению внутренней энергии газа Е = 3/2vRT, где v – количество вещества в молях.
По уравнению Менделеева-Клапейрона рV = vRT, отсюда Е = 3/2рV. Подставь сюда и сосчитай!
Остальные ответы
решу
Мастер
(1216)
3 года назад
Физика Определите суммарную кинетическую энергию хаотического поступательного движения молекул газа в баллоне вместимостью 10 л при давлении 0,4 МПа. На какую высоту можно поднять мальчика массой 50 кг, использовав такую энергию?
Подробное решение тут —->>> https://www.youtube.com/watch?v=Nah4k0SWIZk
Похожие вопросы
Материал из PhysBook
Перейти к: навигация, поиск
Микро- и макропараметры системы
Содержание
-
1 Микро- и макропараметры системы
-
1.1 Макропараметры
- 1.1.1 Средние скорости молекул газов
- 1.2 См. также
-
1.1 Макропараметры
-
2 Идеальный газ
- 2.1 Вывод основного уравнения
-
3 Температура – мера средней кинетической энергии молекул
- 3.1 См. также
Атомы и молекулы, взаимодействую друг с другом, образуют разнообразные вещества (системы). Если число частиц невелико (десятки, сотни), то мы имеем микросистему. Если число частиц системы во много раз больше (миллионы и более), то такую систему называют макросистемой. Например, газ, состоящий из очень большого числа молекул — это макросистема. Большое число частиц системы приводит к появлению у нее новых свойств, которыми отдельные частицы не обладают. Например, давление газа есть результат непрерывного действия всех молекул на стенки сосуда, хотя не каждая молекула сталкивается со стенками. Для описания состояния макросистемы вводят параметры, которые называются параметрами состояния. Различают микропараметры и макропараметры состояния.
Микропараметры — это параметры, характеризующие отдельную частицу. Например, масса молекулы, ее скорость, энергия.
Макропараметры
Макропараметры — это параметры, характеризующие систему в целом. Например, объем V, давление p, средняя скорость молекул  , температура T, концентрация n и т.д. Значения этих параметров могут быть установлены с помощью измерительных приборов.
, температура T, концентрация n и т.д. Значения этих параметров могут быть установлены с помощью измерительных приборов.
Объем газа V — это объем сосуда, в котором газ находится. В Си измеряется в м3. Часто используется несистемная единица измерения 1 литр: 1 л = 10-3 м3.
Давление р — скалярная физическая величина, равная отношению силы F к значению площади S площадки, на которую эта сила действует:  . Газ оказывает давление вследствие столкновений молекул со стенками сосуда. В Си единица давления 1 Н/м2 = 1 Па (Паскаль). Внесистемные единицы измерения — 1 мм.рт.ст и 1 атмосфера. Нормальное давление равно одной физической атмосфере. 1 физическая атмосфера = 1 атм = 760 мм.рт.ст, 1 техническая атмосфера = 1 ат = 736 мм.рт.ст. 1 мм.рт.ст. = 133Па.
. Газ оказывает давление вследствие столкновений молекул со стенками сосуда. В Си единица давления 1 Н/м2 = 1 Па (Паскаль). Внесистемные единицы измерения — 1 мм.рт.ст и 1 атмосфера. Нормальное давление равно одной физической атмосфере. 1 физическая атмосфера = 1 атм = 760 мм.рт.ст, 1 техническая атмосфера = 1 ат = 736 мм.рт.ст. 1 мм.рт.ст. = 133Па.
- Более строгое определение давления: давление р — скалярная физическая величина, равная отношению проекции силы на направление нормали к площадке, на которую сила действует, к значению площади этой площади.
Концентрация молекул n — это число молекул N в единице объема, т.е.  . Измеряется в 1/м3 = м–3.
. Измеряется в 1/м3 = м–3.
Температура — скалярная физическая величина, характеризующий степень нагретости тела.
По шкале Цельсия температура обозначается буквой t, измеряется в градусах Цельсия (ºС). За 1 ºС принята одна сотая промежутка от температуры плавления льда (0 ºС) до температуры кипения воды (100 ºС).
Абсолютная температурная шкала — шкала температур, в которой за начало отсчета принят абсолютный нуль. Температура здесь обозначается буквой T, измеряется в кельвинах (К). За единицу измерения в этой шкале принят один градус Цельсия, т.е. изменение на один кельвин (1 К) равно изменению на один градус Цельсия.
T = (t + 273) К или t = (T – 273) ºС,
где T — абсолютная термодинамическая температура (К); t — температура по шкале Цельсия (ºС).
Средние скорости молекул газов
Движение молекул газа подчиняется законам статистической физики. В каждый момент времени скорости отдельных молекул могут значительно отличаться друг от друга, но их средние значения одинаковы и при расчетах используются не мгновенные скорости отдельных молекул, а не которые средние значения. Различают среднюю арифметическую  и среднюю квадратичную
и среднюю квадратичную  скорости хаотического движения молекул.
скорости хаотического движения молекул.
Пусть имеется N молекул, скорости которых соответственно υ1, υ2, …, υN. Средняя арифметическая скорость хаотического движения молекул (при грубом приближении) по модулю определяется как сумма модулей скоростей молекул газа, деленная на их общее число:

Средняя квадратичная скорость хаотического движения молекул

где  — средний квадрат скорости движения молекул. Его не следует смешивать с квадратом средней скорости:
— средний квадрат скорости движения молекул. Его не следует смешивать с квадратом средней скорости:  .
.
- Более строгое определение средней скорости дано тут.
См. также
- Аксенович Л.А. и др. Физика в средней школе // 6.12. Температура и тепловое равновесие системы. 6.13. Измерение температуры. 6.14. Абсолютная температурная шкала. Абсолютный нуль
- Кикоин А. Температура, теплота, термометр //Квант. — 1990. — № 8. — С. 10-19
- Мякишев Г.Я. Давление газа в сосуде //Квант. — 1987. — № 9. — С. 41-42
- Температура
Идеальный газ
Рассмотрим свойства газов на основе МКТ. Для этого введем физическую модель идеального газа, в которой приняты следующие допущения:
1) размеры молекул малы по сравнению со средним расстоянием между ними; молекулы можно принимать за материальные точки;
2) силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях;
3) молекулы сталкиваются друг с другом как абсолютно упругие шары, движение которых описывается законами механики.
Таким образом, идеальным называется газ, в котором можно пренебречь собственным объемом молекул и межмолекулярным взаимодействием (кроме столкновений).
При небольших давлениях и не очень низких температурах реальные газы близки к идеальному газу. Например, водород, кислород при нормальных условиях в атмосфере можно рассматривать как идеальные газы.
При высоких давлениях молекулы газа находятся так близко, что между ними возникают заметные силы взаимодействия. Пренебречь их собственным объемом нельзя, и газ уже не является идеальным.
Основное уравнение МКТ идеального газа — это уравнение, связывающее микро- и макропараметры идеального газа. Одно из этих уравнений имеет вид:

где p — давление газа (Па); n — концентрация молекул (м–3); m0 — масса одной молекулы газа (кг); 〈v2 〉 — среднее значение квадрата скорости молекул (м/с2). Это уравнение называют еще уравнением Клаузиуса.
Давление можно выразить через среднюю кинетическую энергию молекул:  , где 〈Ek 〉 – средняя кинетическая энергия одной молекулы газа (Дж). Подставляя 〈Ek 〉 в уравнение Клаузиуса, получаем
, где 〈Ek 〉 – средняя кинетическая энергия одной молекулы газа (Дж). Подставляя 〈Ek 〉 в уравнение Клаузиуса, получаем

Вывод основного уравнения
- Аксенович Л.А. и др. Физика в средней школе // 6.11. Основное уравнение МКТ идеального газа
- Кикоин А.К. Давление идеального газа //Квант. — 1983. — № 10. — С. 35-37
Температура – мера средней кинетической энергии молекул
Можно провести следующий эксперимент. Взять сосуды с разными газами. Определить предварительно их объемы, массы и рассчитать число молекул (по формуле  ), затем поместить сосуды в тающий лед. После наступления теплового равновесия определить давление p и рассчитать отношение
), затем поместить сосуды в тающий лед. После наступления теплового равновесия определить давление p и рассчитать отношение  . Опыт показывает, что оно одинаково для всех газов. Затем эти сосуды помещают в кипящую воду. Опять это отношение для всех газов одинаковое, но большее первого значения. Проделав опыт несколько раз при разных температурах, можно заметить, что отношение
. Опыт показывает, что оно одинаково для всех газов. Затем эти сосуды помещают в кипящую воду. Опять это отношение для всех газов одинаковое, но большее первого значения. Проделав опыт несколько раз при разных температурах, можно заметить, что отношение  . Обозначим коэффициент пропорциональности k, тогда:
. Обозначим коэффициент пропорциональности k, тогда:
 или
или 
где p — давление газа (Па); n — концентрация молекул (м–3); T — температура газа (К); k — постоянная Больцмана, равная 1,38·10–23 Дж/К.
Сравнивая выражения (3) и (2), получаем
 или
или 
Данная формула верна для расчёта средней энергии поступательного движения молекулы или для расчёта средней кинетической энергии одноатомной молекулы. Если учитывать, наряду с поступательным движением и вращение молекулы, то средняя кинетическая энергии молекулы с жесткой связью (без колебании атомов в молекуле) будет равна

где i — степень свободы. Для одноатомного газа (например, инертные газы) i = 3, для двухатомного — i =5.
Температура – это величина, характеризующая среднюю кинетическую энергию поступательного движения молекул идеального газа:

Эта формула позволяет установить физический смысл абсолютной температуры Т. Этот макроскопический параметр характеризует среднее значение кинетической энергии хаотического теплового движения одной молекулы в состоянии термодинамического равновесия. Интересно отметить, что средняя энергия теплового движения молекул зависит только от температуры газа. При данной температуре средняя кинетическая энергия поступательного хаотического движения молекул не зависит ни от химического состава газа, ни от массы молекул, ни от давления газа, ни от объема, занимаемого газом.
Так как абсолютная температура не может равняться нулю, то и средняя энергия теплового движения молекул то же не может равняться нулю, т.е. молекулы находятся в постоянном движении.
См. также
- Аксенович Л.А. и др. Физика в средней школе // 6.12. Температура и тепловое равновесие системы. 6.13. Измерение температуры. 6.14. Абсолютная температурная шкала. Абсолютный нуль
- Городецкий Е.Е. Идеальный газ — универсальная физическая модель //Квант. — 1991. — № 9. — С. 33-36
- Кикоин А. Температура, теплота, термометр //Квант. — 1990. — № 8. — С. 10-19
- *Стасенко А.Л. Кладовые энергии молекулы //Квант. — 1995. — № 5. — С. 36-38
Смотреть HD
видео онлайн
бесплатно 2022 года
