Дегтярев Роман
Ученик
(225),
на голосовании
8 лет назад
Маховик начинает вращаться с постоянным угловым ускорением 0,4 рад/с2. Через 10 с от начала движения момент импульса маховика равен 60 кг м2/с. Найдите кинетическую энергию маховика через 25 с после начала движения
Голосование за лучший ответ
Анатолий Ушаков
Мыслитель
(6194)
8 лет назад
Маховик начинает вращаться с постоянным угловым ускорением ε = 0,4 рад/с². Через 10 с от начала движения момент импульса маховика равен 60 кг м²/с. Найдите кинетическую энергию маховика через 25 с после начала движения
угловое ускорение
ε = ω/t
момент импульса
L=Jω1; где J момент инерции
ω = εt
ω1=ω(10) = 4 сˉ¹
J = L/ω1 = 60/4 = 15 кг м²
Кинетическая энергия вращающегося тела
W = J ω2² /2
ω2=ω(25) = 10 сˉ¹
W = 15*100 /2 = 750 дж
Тема: Какую кинетическую энергию приобретает маховик? (Прочитано 3861 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Какую кинетическую энергию приобретает маховик в результате действия на него в течение t = 10 с постоянного вращающего момента М = 20 Н∙м? Момент инерции маховика J = 200 кг∙м2. Сделать рисунок.
« Последнее редактирование: 25 Апреля 2015, 22:53 от Сергей »
Записан
Решение.
Кинетическая энергия которую приобретает маховик равна работе вращающего момента за это время.
А = Т = М∙φ (1).
φ – угол поворота маховика, который вращается равноускоренно из состояния покоя.
[ varphi =frac{varepsilon cdot {{t}^{2}}}{2} (2). ]
ε – угловое ускорение.
Запишем основной закон динамики, выразим угловое ускорение, подставим в (2) (2) подставим в (1) определим кинетическую энергию которую приобретет маховик.
[ M=Jcdot varepsilon (3), varepsilon =frac{M}{J}, varphi =frac{Mcdot {{t}^{2}}}{Jcdot 2}, T=frac{{{M}^{2}}cdot {{t}^{2}}}{Jcdot 2} (4). ]
Т = 100 Дж.
« Последнее редактирование: 07 Мая 2015, 06:05 от alsak »
Записан
Определим
кинетическую энергию твёрдого тела,
вращающегося вокруг неподвижной оси.
Разобьем это тело на n
материальных точек. Каждая точка движется
с линейной скоростью υi=ωri,
тогда кинетическая энергия точки
или
Полная
кинетическая энергия вращающегося
твердого тела равна сумме кинетических
энергий всех его материальных точек:
(3.22)
(J
– момент инерции тела относительно оси
вращения)
Если
траектории всех точек лежат в параллельных
плоскостях (как у цилиндра, скатывающегося
с наклонной плоскости, каждая точка
перемещается в своей плоскости рис ),
это плоское
движение.
В соответствии с принципом Эйлера
плоское движение всегда можно бесчисленным
количеством способов разложить на
поступательное и вращательное движение.
Если шарик падает или скользит вдоль
наклонной плоскости, он двигается только
поступательно; когда же шарик катится
– он ещё и вращается.
Если
тело совершает поступательное и
вращательное движения одновременно,
то его полная кинетическая энергия
равна
(3.23)
Из
сопоставления формул кинетической
энергии для поступательного и
вращательного движений видно, что мерой
инертности при вращательном движении
служит момент инерции тела.
§ 3.6 Работа внешних сил при вращении твёрдого тела
При
вращении твёрдого тела его потенциальная
энергия не изменяется, поэтому элементарная
работа внешних сил равна приращению
кинетической энергии тела:
dA
= dE
или
Учитывая,
что Jβ
= M,
ωdr
= dφ,
имеем α
тела на конечный угол φ
равна
(3.25)
При
вращении твёрдого тела вокруг неподвижной
оси работа внешних сил определяется
действием момента этих сил относительно
данной оси. Если момент сил относительно
оси равен нулю, то эти силы работы не
производят.
Примеры решения задач
Пример
2.1. Маховик
массой m
=5кг и радиусом r
= 0,2 м вращается вокруг горизонтальной
оси с частотой ν0=720
мин-1
и при торможении останавливается за t
=20 с. Найти тормозящий момент и число
оборотов до остановки.
Решение
Для
определения тормозящего момента применим
основное уравнение динамики вращательного
движения
IΔω
= MΔt
где
I=mr2–
момент инерции диска; Δω
=ω
– ω0,
причём ω
=0 конечная угловая скорость, ω0=2πν0
– начальная. М –тормозящий момент сил,
действующих на диск.
Зная
все величины, можно определить тормозящий
момент
-mr2
2πν0=МΔt
(1)
откуда
(2)
Из
кинематики вращательного движения угол
поворота за время вращения диска до
остановки может быть определён по
формуле
(3)
где β–угловое ускорение.
По условию задачи: ω =ω0
– βΔt, так как ω=0, ω0
= βΔt
Тогда выражение (2) может быть записано
в виде:
Пример 2.2. Два
маховика в виде дисков одинаковых
радиусов и масс были раскручены до
скорости вращения n=
480 об/мин и предоставили самим себе. Под
действием сил трения валов о подшипники
первый остановился через t
=80 с, а второй сделал N=
240 оборотов до остановки. У какого и
маховика момент сил трения валов о
подшипники был больше и во сколько раз.
Решение:
Момент сил терния М1
первого маховика найдём, воспользовавшись
основным уравнением динамики вращательного
движения
M1Δt
= Iω2–
Iω1
где Δt
– время действия момента сил трения,
I=mr2
– момент инерции
маховика , ω1=
2πν и ω2=
0– начальная и конечная угловые скорости
маховиков
Тогда
Момент сил трения М2
второго маховика выразим через связь
между работой А сил трения и изменением
его кинетической энергии ΔEк:
где Δφ = 2πN
– угол поворота, N
-число оборотов маховика.
Тогда , откуда
Отношение
будет равно
Момент сил трения второго маховика в
1.33 раза больше.
Пример
2.3. Масса
однородного сплошного диска m, массы
грузов m1
и m2
(рис.15). Скольжения и трения нити в оси
цилиндра нет. Найти ускорение грузов и
отношение натяжений нити
в процессе движения.
Решение
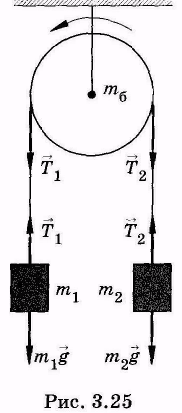
поэтому, когда m1
и m2
будут совершать поступательное движение,
цилиндр будет совершать вращение
относительно оси, проходящей через
точку О. Положим для определённости,
что m2
> m1
.
Тогда груз m2
опускается и цилиндр вращается по
часовой стрелке. Запишем уравнения
движения тел, входящих в систему
Первые два
уравнения записаны для тел с массами
m1
и m2
, совершающих поступательное движение,
а третье уравнение – для вращающегося
цилиндра. В третьем уравнении слева
стоит суммарный момент сил, действующих
на цилиндр (момент силы T1
взят
со знаком минус, так как сила T1
стремится
повернуть цилиндр против часовой
стрелки). Справа I – момент инерции
цилиндра относительно оси О, который
равен
где R – радиус цилиндра; β –
угловое ускорение цилиндра.
Так как
проскальзывания нити нет, то
. С учётом выражений для I и β получим:
Складывая уравнения системы, приходим
к уравнению
Отсюда находим
ускорение a
грузов
Далее легко
найти T1
и T2
и их отношение
Из полученного
уравнения видно, что натяжения нитей
будут одинаковы, т.е. =1,
если масса цилиндра будет гораздо меньше
массы грузов.
Пример
2.4. Полый
шар массой m = 0,5 кг имеет внешний радиус
R = 0,08м и внутренний r = 0,06м. Шар вращается
вокруг оси, проходящей через его центр.
В определённый момент на шар начинает
действовать сила, в результате чего
угол поворота шара изменяется по закону
.
Определить момент приложенной силы.
Решение
Решаем задачу,
используя основное уравнение динамики
вращательного движения .
Основная трудность – определить момент
инерции полого шара, а угловое ускорение
β находим как .
Момент инерции I полого шара равен
разности моментов инерции шара радиуса
R и шара радиуса r:
где ρ – плотность материала шара. Находим
плотность, зная массу полого шара
Отсюда определим плотность материала
шара
Так как
Для момента силы M получаем следующее
выражение:
Пример
2.5. Тонкий
стержень массой 300г и длиной 50см вращается
с угловой скоростью 10с-1
в
горизонтальной плоскости вокруг
вертикальной оси, проходящей через
середину стержня. Найдите угловую
скорость, если в процессе вращения в
той же плоскости стержень переместится
так, что ось вращения пройдёт через
конец стержня.
Решение
Используем
закон сохранения момента импульса
(1)
(Ji-момент
инерции стержня относительно оси
вращения).
Для
изолированной системы тел векторная
сумма моментов импульса остаётся
постоянной. Вследствие того, что
распределение массы стержня относительно
оси вращения изменяется момент инерции
стержня также изменяется в соответствии
с (1):
J0ω1
=
J2ω2.
(2)
Известно,
что момент инерции стержня относительно
оси, проходящей через центр масс и
перпендикулярной стержню, равен
J0
=
mℓ2/12.
(3)
По
теореме Штейнера
J
=J0
+mа2
(J-момент
инерции стержня относительно произвольной
оси вращения; J0
–
момент инерции относительно параллельной
оси, проходящей через центр масс; а–
расстояние от центра масс до выбранной
оси вращения).
Найдём
момент инерции относительно оси,
проходящей через его конец и перпендикулярной
стержню:
J2
=J0
+mа2,
J2
= mℓ2/12
+m(ℓ/2)2
=
mℓ2/3.
(4)
Подставим
формулы (3) и (4) в (2):
mℓ2
ω1/12
=
mℓ2
ω2/3
откуда
ω2
=
ω1/4
ω2
=10с-1/4=2,5с-1
Пример
2.6.
Человек массой m=60кг,
стоящий на краю платформы массой М=120кг,
вращающейся по инерции вокруг неподвижной
вертикальной оси с частотой ν1=12мин-1,
переходит к её центру. Считая платформу
круглым однородным диском, а человека
– точечной массой, определите, с какой
частотой ν2
будет
тогда вращаться платформа.
Дано:
m=60кг,
М=120кг, ν1=12мин-1
= 0,2с-1.
Найти:
ν1
Решение:
Согласно
условию задачи, платформа с человеком
вращается по инерции, т.е. результирующий
момент всех сил, приложенных к вращающейся
системе, равен нулю. Поэтому для системы
«платформа-человек» выполняется закон
сохранения момента импульса
I1ω1=
I2ω2
где
–
момент инерции системы, когда человек
стоит на краю платформы (учли, что момент
инерции платформы, равен(R
– радиус п
момент инерции человека на краю платформы
равенmR2).
–
момент инерции системы, когда человек
стоит в центре платформы (учли, что
момент человека, стоящего в центре
платформы, равен нулю). Угловая скорость
ω1=
2π ν1
и
ω1=
2π ν2.
Подставив
записанные выражения в формулу (1),
получаем
откуда
искомая частота вращения
Ответ:
ν2=24мин-1.
Соседние файлы в папке Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Unit Converter
Enter the flywheel moment of inertia (kg-m^2) and the angular velocity (rad/s) into the calculator to determine the Flywheel Energy.
- All Energy Calculators
- Inertia Acceleration Calculator
- Mass Moment of Inertia Calculator (Point Mass)
- Inertia Force Calculator
- Orbital Kinetic Energy Calculator
- Flywheel Power Calculator
- Flywheel Torque Calculator
Flywheel Energy Formula
The following equation is used to calculate the Flywheel Energy.
Variables:
- Where Ef is the Flywheel Energy (Joules)
- I is the flywheel moment of inertia (kg-m^2)
- w is the angular velocity (rad/s)
To calculate the kinetic energy of a flywheel, multiply the moment of inertia by the square of the angular velocity, then divide by 2.
How to Calculate Flywheel Energy?
The following two example problems outline the steps and information needed in order to calculate the Flywheel Energy.
Example Problem #1:
- First, determine the flywheel momentum of inertia (kg-m^2). In this example, the flywheel moment of inertia (kg-m^2) is measured to be 9.
- Next, determine the angular velocity (rad/s). For this problem, the angular velocity (rad/s) is calculated to be 5.
- Finally, calculate the Flywheel Energy using the formula above:
Ef = .5*I*w^2
Inserting the values from above and solving the equation with the imputed values gives:
Ef = .5*9*5^2 = 112.5 (Joules)
Example Problem #2:
Using the same process as example problem 1, we first define the needed variables outlined by the formula. In this case, the values are provide as:
flywheel moment of inertia (kg-m^2) = 9
angular velocity (rad/s) = 3
Entering these values into the formula or calculator above gives us:
Ef = .5*9*3^2 = 40.5 (Joules)
Кинетическая энергия твердого тела
При применении теоремы об изменении кинетической энергии системы часто приходится вычислять кинетическую энерпно движущегося твердого гела. Найдем ее выражение при важнейших видах движения тела.
Тело движется поступательно
Пели тело движется поступательно, то скорости всех его точек в каждый момент равны между собой. Следовательно. в данном случае кинетическая энергия тела
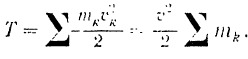
Обозначая 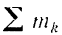
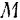
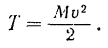
Кинетическая энергия 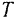
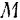
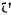
Таким образом, кинетическая энергии поступательно движущегося тела, как этого и можно было ожидать, вычисляется совершенно одинаково с кинетической энергией материальной точки.
Но формуле (208) вычисляется также и кинетическая энергия любой системы, движущейся так, что модули скоростей всех ее точек одинаковы.
Тело вращается вокруг неподвижной оси.
Модуль 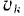
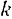
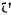
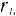
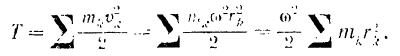
Но
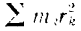
есть момент инерции 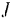
Следовательно, при вращательном движении тела
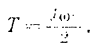
Кинетическая энергии 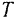
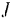
Сравнивая формулу (209) с формулой (208) можно заметить что строение их аналогично. В формуле (209) роль линейной скорости точки играет угловая скорость тела, а роль массы момент инерции тела (мера его инерции при вращательном движении.
Тело совершает плоское движение.
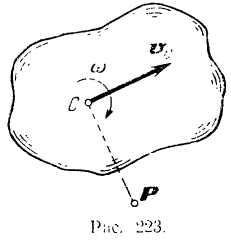
Пусть тело совершает плоское движение. Представим себе сечение тела (рис. 223) плоскостью проходящей через центр тяжести 
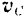
Зная это. нетрудно найти и положение мгновенного центра скоростей фигуры. Он лежит (см. § 63) па перпендикуляре. восстановленном из какой-либо точки фигуры к направлению скорости этой точки, на расстоянии, разном отношению скорости данной точки к угловой скорости фигуры. Следовательно, искомое расстояние
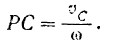
При плоском движении тола скорости его точек каждый момент распределяются так, как будто бы тело вращается в этот момент вокруг мгновенной оси (см. § 64), проходящей через соответствующий данному моменту мгновенный центр скоростей фигуры и перпендикулярной к ее плоскости.
Но кинетическая энергия тела
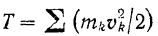
зависит только от массы каждой его точки и ее скорости, и поэтому соответствующую данному моменту кинетическую энергию тела, совершающего плоское движение, можно вычислить по формуле (209):
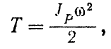
где 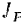
Пользование формулой (209) для нахождения кинетической энергии тела при его плоском движении затрудняется тем, что требует для каждого момента времени определения положения мгновенной оси вращения тела и вычисления соответствующего ей момента инерции тела. Преобразуем полученную формулу, воспользовавшись теоремой о моментах инерции относительно параллельных осей (§ 80). Согласно этой теореме
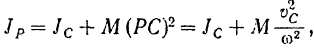
где 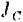
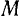
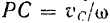
Подставив полученное выражение для момента инерции 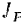
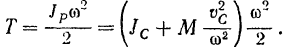
Раскрыв скобки и произведя сокращение, окончательно получим:
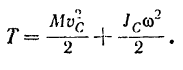
Кинетическая энергия тела при его плоском движении равна сумме тех кинетических анергий, которые имело бы данное тело при его поступательном движении со скоростью центра масс тела и при его вращательном движении вокруг оси, проходящей через центр масс тела и перпендикулярной к неподвижной плоскости, параллельно которой движется тело.
Данную формулировку нетрудно запомнить, если принять во внимание, что всякое плоское движение может быть разложено на поступательное движение со скоростью полюса и вращательное движение вокруг полюса (§61).
Только в отличие от кинематики выбор полюса здесь не произволен. При вычислении по формуле (210) кинетической энергии тела при его плоском движении за полюс надо обязательно выбирать центр масс тела. Если за полюс принять другую точку тела, то мы получим иную, чем (210), формулу для его кинетической энергии.
Пример задачи:
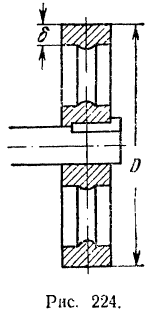
Маховое колесо (рис. 224), пес обода которого 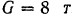
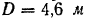
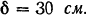
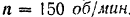
Решение:
По теореме о кинетической энергии системы
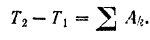
Кинетическую энергию маховика в конце рассматриваемого периода его работы определим по формуле (209) 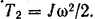
Изменение кинетической энергии маховика происходит только за счет приложенного к нему постоянного вращающего момента, работа которого согласно формуле (202) равна
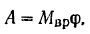
где 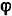
Таким образом, уравнение кинетической энергии системы принимает вид
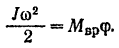
Отсюда искомый момент сил равен
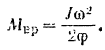
Момент инерции 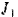
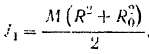
Наружный радиус обода
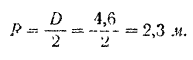
Внутренний радиус обода
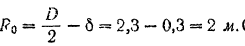
Следовательно, момент инерции обода
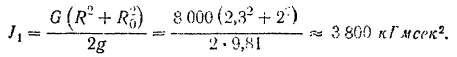
Момент инерции спиц и втулки
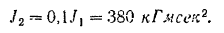
Момент инерции всего маховика
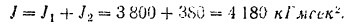
Угловая скорость маховика
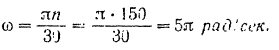
Угол, на который повернется маховик, сделав
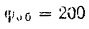
оборотов, равен
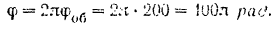
Подставляя числовые данные, определяем весомый момент сил
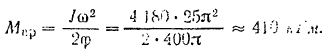
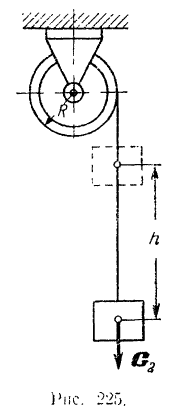
Пример задачи:
На шкив (рис. 225) радиуса 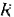
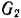
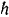
Решение:
Так как система сначала находилась в покое, то се начальная кинетическая энергия 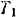
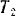
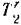
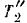
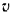
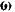
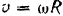
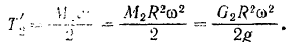
Кинетическая энергия шкива равна
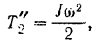
где 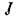
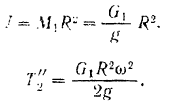
А кинетическая энергия всей системы
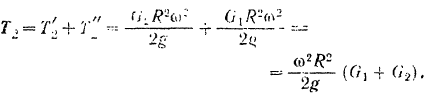
Так как кинетической энергии системы происходит только за счет работы силы тяжести опускающегося на высоту 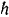
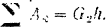
Таким образом, уравнение кинетической энергии системы приобретает вид
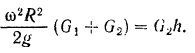
Отсюда искомая угловая скорость шкива
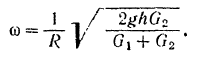
Пример задачи:
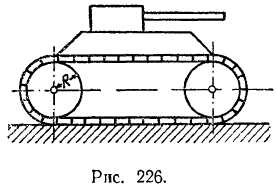
Танк (рис. 226) приводится в движение двигателем. который вращает четыре колеса (по два с каждой стороны). Колеса своими выступами захватывают гусеницы. Определить скорость танка через 10 сек после начала его движения, если средняя полезная мощность двигателя танка 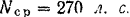
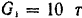
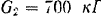
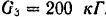
Решение:
Рассматриваемая система состоит; 1) из поступательно движущегося корпуса танка, 2) двух гусениц, каждая из которых движется поступательно вместе с танком и одновременно с той же скоростью совершает движение относительно корпуса танка, и 3) четырех колес, вращающихся вокруг своих осей и вместе с ними перемещающихся поступательно, т. е. совершающих плоское движение.
Кинетическая энергия корпуса танка равна
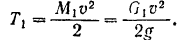
Кинетическая энергия гусениц
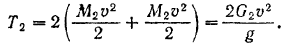
Скорость точек оси колеса равна поступательной скорости танка. Следовательно, угловая скорость колеса 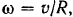
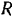
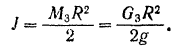
Таким образом, кинетическая энергия колес:
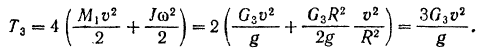
Кинетическая энергия всего танка
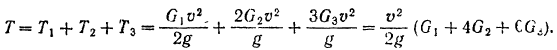
Так как в начале движения танка его кинетическая энергия равна нулю, то уравнение (207) кинетической энергии системы принимает вид
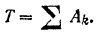
Следовательно, полезная работа двигателя, приводящего в движение танк,
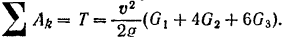
Средняя полезная мощность двигателя (в лошадиных силах)
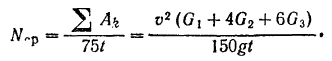
Отсюда скорость танка через 10 сек после начала его движения
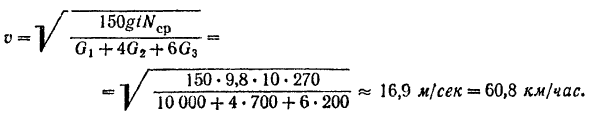
Пример задачи:
Шестерня I (рис. 227), ось которой проходит через точку 
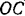

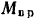
Радиус шестерни I (сателлита) — 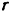
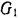
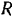
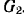
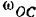
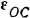
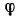
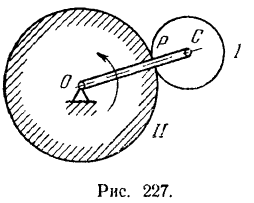
Решение:
Рассматривая кривошип и шестерню I как одну систему, применим к ней теорему об изменении кинетической энергии системы:
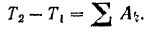
Так как вначале система была неподвижна, то 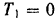
Находим кинетическую энергию 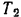
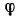
Кривошип совершает вращательное движение вокруг неподвижной оси 
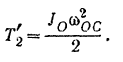
Момент инерции однородного стержня относительно оси, проходящей через его конец (задача 71).
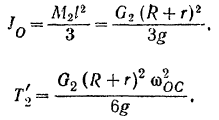
Шестерня I совершает плоское движение. По формуле (210) ее кинетическая энергия
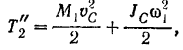
где 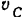
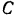
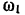
Точка 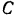
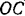
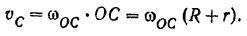
Мгновенный центр 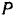
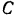
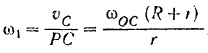
Момент инерции шестерни I (однородного сплошною цилиндр) относительно ее центральной оси:
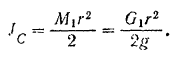
Подставляя найденные значения угловой скорости, скорости центра масс и момента инерции в выражение для кинетической энергии шестерни I, находим:
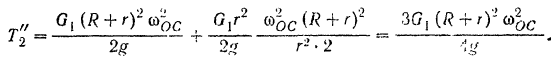
Кинетическая энергия осой системы
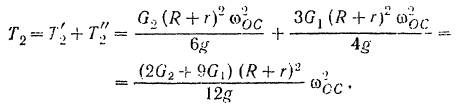
Вычисляем теперь сумму 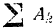
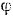
Механизм расположен в горизонтальной плоскости. Следовательно, работа сил тяжести, приложенных ко всем частям системы, равна нулю. Трением в осях мы пренебрегаем. Таким образом, изменение кинетической энергии нашей системы происходит только за счет работы постоянного вращающего момента 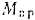
Таким образом, в соответствии с формулой (202)
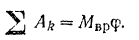
Подставляя найденные значения
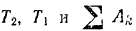
уравнение кинетической энергии системы, получаем:
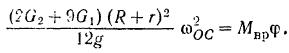
Отсюда искомая угловая скорость кривошипа
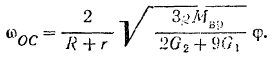
Для того чтобы определить угловое ускорение кривошипа, продифференцируем по времени обе часта уравнения кинетической энергии:
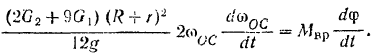
Принимая во внимание, что
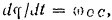
и сокрушая на 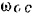
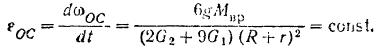
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы: